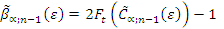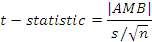2.1. The Mixedwood Growth Model
MGM models the growth of pure or mixed stands of four major boreal species: white spruce (
Picea glauca (Moench) Voss) (SW), lodgepole pine (
Pinus contorta var.
latifolia Engelm.) (PL), trembling aspen (
Populus tremuloides Michx
.) (AW), and black spruce (
Picea mariana (Mill.) B.S.P.) (SB). The model utilizes individual tree growth (height increment and diameter increment) and survival functions to project a list of trees into the future. MGM includes sub-models developed separately for: (1)
Juvenile trees having a diameter at breast height (DBH) less than 4.0 cm; (2)
Mid-rotation trees having a DBH greater than or equal to 4.0 cm and that is less than 80% of their maximum height, defined by the asymptote of the height
vs. DBH curve; and (3)
Old-Growth trees taller than 80% of their maximum height. Site index and competition from other trees are key drivers of the growth functions. A full description of the model functions and parameters by species and sub-models can be found online [
1].
The model can be initialized using a tree list or stand table, including juvenile trees <1.3 m height. Tree lists can also be created using stand summary data: species, average height and diameter at breast height (DBH), breast height age for each tree (or total age for trees <1.3 m), and an estimate of site index for each species. The growth and survival relationships were developed using Alberta data, although regional variants for British Columbia, Saskatchewan, and Manitoba allow use of local species codes, site curves, and tree-volume estimation equations.
Outputs summarize both tree and stand characteristics. Summaries are provided as yield tables and charts portraying averages and totals for the conifer and hardwood components including estimates of above ground tree biomass. Linkage to the Stand Visualization System [
16] is also built into the model, to provide visual snapshots of the stand structure (assuming random tree locations) at any stage of development.
2.2. Description of Validation Datasets
Four datasets were used for the validation: the Alberta Sustainable Resource Development (ASRD) Stand Dynamics System (SDS) juvenile permanent sample plots (PSPs), the Western Boreal Growth and Yield Association (WESBOGY) juvenile PSPs, ASRD mature stand PSPs (ASRD), and Saskatchewan Ministry of the Environment PSP data (SSK). These datasets contain a range of forest stand types (species mixtures and structure), and include a range of productivity (site index) and stand ages (juvenile, mid-rotation and mature) and varying projection lengths. The SDS and WESBOGY datasets contain some silvicultural manipulations (chiefly site preparation and juvenile thinning). These data provide a basis for the rigorous testing of model performance. Summary details on plots and re-measurements for the data sources are found in (
Table 1,
Table 2,
Table 3,
Table 4 and
Table 5).
Four datasets were used for the validation: the Alberta Sustainable Resource Development (ASRD) Stand Dynamics System (SDS) juvenile permanent sample plots (PSPs), the Western Boreal Growth and Yield Association (WESBOGY) juvenile PSPs, ASRD mature stand PSPs (ASRD), and Saskatchewan Ministry of the Environment PSP data (SSK). These datasets contain a range of forest stand types (species mixtures and structure), and include a range of productivity (site index) and stand ages (juvenile, mid-rotation and mature) and varying projection lengths. The SDS and WESBOGY datasets contain some silvicultural manipulations (chiefly site preparation and juvenile thinning). These data provide a basis for the rigorous testing of model performance. Summary details on plots and re-measurements for the data sources are found in (
Table 1,
Table 2,
Table 3,
Table 1 and
Table 5).
Table 1.
Summary statistics (mean, min. and max.) for age and projection length, as well as the average site index for aspen, pine and spruce types by validation dataset and species group.
Table 1.
Summary statistics (mean, min. and max.) for age and projection length, as well as the average site index for aspen, pine and spruce types by validation dataset and species group.
| Dataset | Species | n | Initial Age (years) | Projection Length (years) | Aspen Site Index (m) | Pine Site Index (m) | Spruce Site Index (m) |
|---|
| Mean | Min | Max | Mean | Min | Max | Mean | Mean | Mean |
|---|
| ASRD | AW | 124 | 74 | 28 | 130 | 28 | 5 | 41 | 18.7 | - | - |
| | CD | 184 | 147 | 40 | 435 | 32 | 13 | 43 | 17.8 | - | 15.2 |
| | DC | 90 | 108 | 42 | 198 | 30 | 7 | 42 | 17.6 | - | 19.3 |
| | SW | 104 | 154 | 66 | 435 | 29 | 6 | 39 | - | - | 15.3 |
| SDS | AW | 51 | 5 | 1 | 10 | 14 | 9 | 19 | 19.8 | - | - |
| | SW | 13 | 5 | 2 | 7 | 16 | 11 | 22 | - | - | 20.1 |
| | MX | 16 | 6 | 2 | 9 | 16 | 13 | 19 | 18.3 | - | 18.3 |
| WESBOGY | AW | 93 | 7 | 5 | 10 | 6 | 1 | 9 | 20.9 | - | - |
| | SW | 62 | 7 | 5 | 10 | 6 | 1 | 9 | 17.6 | - | - |
| | MX | 307 | 7 | 5 | 10 | 6 | 1 | 9 | 20.8 | - | 17.3 |
| SASK | AW | 20 | 71 | 46 | 103 | 15 | 10 | 29 | 18.9 | - | - |
| | CD | 20 | 105 | 67 | 160 | 21 | 12 | 32 | 15.6 | 16.9 | 17.8 |
| | DC | 20 | 97 | 54 | 160 | 21 | 13 | 33 | 17.5 | 17.1 | 16.3 |
| | SW | 20 | 91 | 63 | 140 | 16 | 8 | 29 | - | 17.0 | - |
Table 2.
The summary of observed stand parameters (volume (m3 ha−1), basal area (m2 ha−1), DBH (cm), height (m), density (stems ha−1) and top height (m)), as well as the validation statistics (average mean bias (AMB), standard deviation of the residuals (SD_resid), relative mean bias (RMB), efficiency (EF) and the equivalence cutoff (EQ) for the conifer and deciduous components by species group (AW, CD, DC, and SW) for the ASRD dataset.
Table 2.
The summary of observed stand parameters (volume (m3 ha−1), basal area (m2 ha−1), DBH (cm), height (m), density (stems ha−1) and top height (m)), as well as the validation statistics (average mean bias (AMB), standard deviation of the residuals (SD_resid), relative mean bias (RMB), efficiency (EF) and the equivalence cutoff (EQ) for the conifer and deciduous components by species group (AW, CD, DC, and SW) for the ASRD dataset.
| Species Group | n | Variable | Conifer | Deciduous |
|---|
| Observed | Statistics of Model Fit | Observed | Statistics of Model Fit |
|---|
| Mean | Min | Max | SD | AMB | SD_resid | RMB (%) | EF | EQ | Mean | Min | Max | SD | AMB | SD_resid | RMB (%) | EF | EQ |
|---|
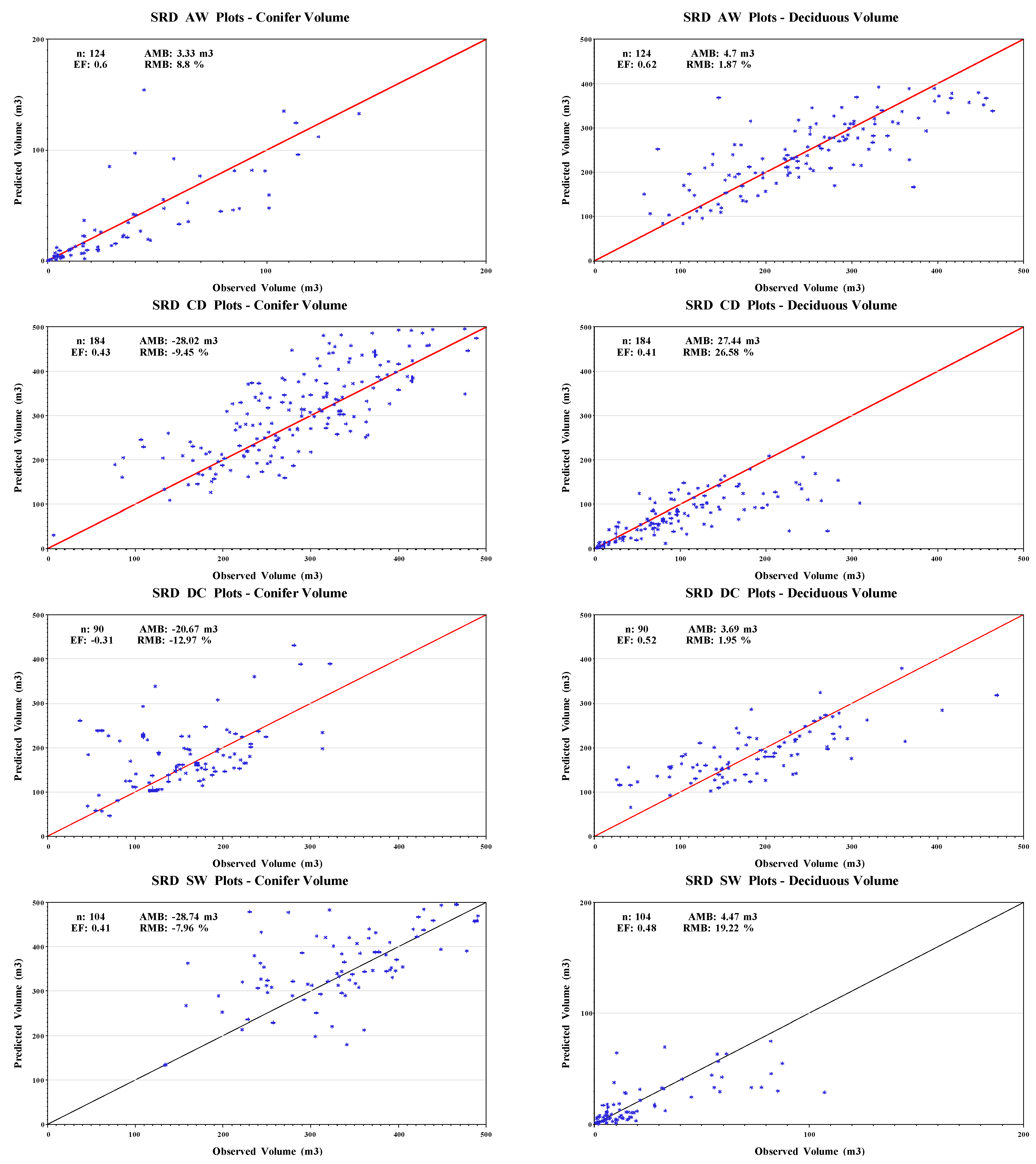
| AW | 124 | Volume (m3 ha−1) | 37.83 | 0.33 | 142.05 | 36.07 | 3.33 | 22.68 | 8.80 | 0.60 | 6.81 | 251.00 | 57.82 | 510.92 | 98.02 | 4.70 | 60.02 | 1.87 | 0.62 | 17.57 |
| | | Basal Area (m2 ha−1) | 4.10 | 0.12 | 13.23 | 3.56 | 0.71 | 1.98 | 17.34 | 0.65 | 0.61 | 27.75 | 6.78 | 53.72 | 8.94 | 1.68 | 5.88 | 6.05 | 0.53 | 1.67 |
| | | DBH (cm) | 34.77 | 11.70 | 67.20 | 13.82 | 4.88 | 5.63 | 14.05 | 0.71 | 5.91 | 27.52 | 12.87 | 47.20 | 8.61 | −0.82 | 1.90 | −2.96 | 0.94 | 1.38 |
| | | Height (m) | 21.26 | 6.70 | 31.48 | 6.17 | −1.75 | 2.83 | −8.25 | 0.71 | 2.34 | 21.57 | 10.68 | 30.34 | 4.06 | −1.16 | 1.77 | −5.42 | 0.73 | 1.51 |
| | | Density (stems ha−1) | 61 | 5 | 296 | 70 | −0.81 | 25.09 | −1.34 | 0.87 | 6.67 | 598 | 79 | 1920 | 440 | 75.08 | 124.36 | 12.55 | 0.89 | 95.73 |
| | | Top Height (m) | 22.15 | 8.00 | 30.64 | 6.14 | −1.79 | 3.72 | −8.07 | 0.55 | 2.44 | 23.82 | 12.30 | 32.51 | 4.04 | −1.54 | 1.80 | −6.44 | 0.66 | 1.91 |
| CD | 184 | Volume (m3 ha−1) | 296.52 | 7.00 | 547.10 | 95.59 | −28.02 | 66.39 | −9.45 | 0.43 | 38.55 | 103.25 | 2.87 | 309.34 | 73.39 | 27.44 | 50.56 | 26.58 | 0.41 | 34.07 |
| | | Basal Area (m2 ha−1) | 31.75 | 1.55 | 58.25 | 10.12 | −0.84 | 6.77 | −2.65 | 0.55 | 3.81 | 10.39 | 0.46 | 29.01 | 6.76 | 2.95 | 4.76 | 28.43 | 0.33 | 3.22 |
| | | DBH (cm) | 27.34 | 13.93 | 50.10 | 6.49 | 1.46 | 2.82 | 5.35 | 0.78 | 1.91 | 35.69 | 17.82 | 66.40 | 8.46 | 0.02 | 4.63 | 0.07 | 0.73 | 1.07 |
| | | Height (m) | 21.04 | 10.70 | 28.61 | 3.83 | −0.45 | 1.61 | −2.14 | 0.82 | 0.84 | 23.80 | 15.45 | 32.07 | 3.40 | −0.83 | 2.13 | −3.47 | 0.57 | 1.19 |
| | | Density (stems ha−1) | 626 | 44 | 2765 | 471 | −58.16 | 151.40 | −9.29 | 0.90 | 81.41 | 106 | 10 | 474 | 83 | 29.62 | 65.16 | 27.88 | 0.26 | 38.24 |
| | | Top Height (m) | 25.99 | 10.70 | 34.71 | 4.05 | −0.79 | 1.80 | −3.03 | 0.79 | 1.04 | 24.29 | 15.45 | 32.07 | 3.46 | −0.71 | 2.19 | −2.93 | 0.58 | 1.21 |
| DC | 90 | Volume (m3 ha−1) | 159.43 | 37.16 | 321.96 | 63.79 | −20.67 | 69.92 | −12.97 | −0.31 | 33.48 | 189.86 | 25.89 | 643.18 | 97.57 | 3.69 | 67.57 | 1.95 | 0.52 | 22.78 |
| | | Basal Area (m2 ha−1) | 15.77 | 4.56 | 31.60 | 5.61 | −1.07 | 6.24 | −6.78 | −0.27 | 3.00 | 19.29 | 2.87 | 50.33 | 8.52 | 0.99 | 5.81 | 5.15 | 0.52 | 1.93 |
| | | DBH (cm) | 29.84 | 15.13 | 49.04 | 6.92 | 1.53 | 3.09 | 5.13 | 0.75 | 2.39 | 32.16 | 13.16 | 46.50 | 6.35 | −0.26 | 2.87 | −0.80 | 0.79 | 0.96 |
| | | Height (m) | 22.60 | 13.34 | 30.89 | 3.07 | −1.42 | 2.43 | −6.32 | 0.16 | 2.03 | 23.52 | 15.27 | 31.20 | 3.03 | −1.08 | 1.99 | −4.63 | 0.44 | 1.65 |
| | | Density (stems ha−1) | 244 | 40 | 729 | 151 | −39.94 | 85.94 | −16.39 | 0.60 | 56.06 | 270 | 20 | 1470 | 220 | 25.70 | 86.39 | 9.52 | 0.83 | 43.19 |
| | | Top Height (m) | 25.62 | 15.60 | 34.88 | 3.12 | −1.81 | 2.51 | −7.05 | 0.01 | 2.31 | 24.86 | 15.77 | 32.49 | 2.82 | −1.58 | 2.03 | −6.34 | 0.16 | 1.99 |
| SW | 104 | Volume (m3 ha−1) | 361.14 | 133.94 | 594.37 | 101.41 | −28.74 | 73.01 | −7.96 | 0.41 | 43.34 | 23.27 | 0.69 | 107.32 | 25.74 | 4.47 | 17.97 | 19.22 | 0.48 | 7.45 |
| | | Basal Area (m2 ha−1) | 38.20 | 12.52 | 62.53 | 10.62 | −1.11 | 6.94 | −2.91 | 0.58 | 4.20 | 2.71 | 0.12 | 10.49 | 2.71 | 0.60 | 1.90 | 22.23 | 0.45 | 0.79 |
| | | DBH (cm) | 25.69 | 16.68 | 46.72 | 5.49 | −0.41 | 3.03 | −1.60 | 0.69 | 1.03 | 26.06 | 11.40 | 54.20 | 8.88 | 0.36 | 3.86 | 1.40 | 0.81 | 1.30 |
| | | Height (m) | 21.40 | 13.09 | 28.91 | 2.77 | −0.83 | 1.71 | −3.90 | 0.53 | 1.28 | 19.73 | 10.18 | 28.86 | 3.56 | −0.84 | 2.05 | −4.01 | 0.62 | 1.18 |
| | | Density (stems ha−1) | 782 | 64 | 2299 | 424 | 55.60 | 207.58 | 7.11 | 0.74 | 93.87 | 51 | 5 | 235 | 50 | 8.52 | 28.79 | 16.77 | 0.64 | 13.71 |
| | | Top Height (m) | 26.97 | 17.91 | 32.82 | 2.92 | −0.45 | 1.50 | −1.67 | 0.71 | 0.81 | 19.88 | 10.18 | 28.86 | 3.58 | −0.76 | 2.04 | −3.85 | 0.63 | 1.19 |
Table 3.
The summary of observed stand increment (volume increment (m3 ha−1 y−1), DBH increment (cm y−1), height increment (m y−1), and top height increment (m y−1)), and the validation statistics (average mean bias (AMB), standard deviation of the residuals (SD_resid), relative mean bias (RMB), as well as the t-test statistics (t-statistic and p-value) for AMB, for the conifer and deciduous components by species group (AW, CD, DC, and SW) ASRD dataset.
Table 3.
The summary of observed stand increment (volume increment (m3 ha−1 y−1), DBH increment (cm y−1), height increment (m y−1), and top height increment (m y−1)), and the validation statistics (average mean bias (AMB), standard deviation of the residuals (SD_resid), relative mean bias (RMB), as well as the t-test statistics (t-statistic and p-value) for AMB, for the conifer and deciduous components by species group (AW, CD, DC, and SW) ASRD dataset.
| Group | Species Variable | Observed | Statistics of Model Fit | t-test for AMB |
|---|
| n | Mean | AMB | SD_Resid | RMB (%) | t-value | p-value |
|---|
| AW | Volume Inc (m3 ha−1 y−1) | 124 | 4.309 | −1.856 | 1.873 | −43.08 | −11.039 | <0.001 |
| Deciduous | DBH Inc (cm y−1) | | 0.263 | −0.031 | 0.063 | −11.69 | −5.408 | <0.001 |
| | Height Inc (m y−1) | | 0.120 | −0.059 | 0.117 | −49.52 | −5.655 | <0.001 |
| | Top Height Inc (m y−1) | | 0.055 | −0.076 | 0.128 | −136.22 | −6.574 | <0.001 |
| CD | Volume Inc (m3 ha−1 y−1) | 184 | 3.807 | −0.811 | 2.247 | −21.31 | −4.898 | <0.001 |
| Conifer | DBH Inc (cm y−1) | | 0.169 | 0.048 | 0.090 | 28.52 | 7.298 | <0.001 |
| | Height Inc (m y−1) | | 0.109 | −0.016 | 0.049 | −14.31 | −4.293 | <0.001 |
| | Top Height Inc (m y−1) | | 0.061 | −0.024 | 0.056 | −39.59 | −5.900 | <0.001 |
| DC | Volume Inc (m3 ha−1 y−1) | 90 | 2.687 | −0.873 | 1.384 | −32.49 | −5.984 | <0.001 |
| Deciduous | DBH Inc (cm y−1) | | 0.242 | −0.011 | 0.096 | −4.46 | −1.071 | 0.287 |
| | Height Inc (m y−1) | | 0.099 | −0.038 | 0.067 | −38.54 | −5.402 | <0.001 |
| | Top Height Inc (m y−1) | | 0.040 | −0.054 | 0.077 | −136.30 | −6.646 | <0.001 |
| SW | Volume Inc (m3 ha−1 y−1) | 104 | 4.967 | −1.485 | 2.475 | −29.89 | −6.118 | <0.001 |
| Conifer | DBH Inc (cm y−1) | | 0.154 | −0.014 | 0.093 | −9.11 | −1.538 | 0.127 |
| | Height Inc (m y−1) | | 0.127 | −0.034 | 0.060 | −26.56 | −5.751 | <0.001 |
| | Top Height Inc (m y−1) | | 0.092 | −0.016 | 0.060 | −16.97 | −2.672 | 0.009 |
Table 4.
The summary of the mean deciduous or coniferous volume increment (m3 ha−1 y−1), as well as the standard deviation of the residual volume (SD) by projection length classes for the species group (AW, CD, DC, and SW) in the ASRD dataset.
Table 4.
The summary of the mean deciduous or coniferous volume increment (m3 ha−1 y−1), as well as the standard deviation of the residual volume (SD) by projection length classes for the species group (AW, CD, DC, and SW) in the ASRD dataset.
| Species Group | n | Average Projection Length | Actual Mean Deciduous Volume Increment | Residual Deciduous Volume Increment | SD Residual Volume Increment | Species Group | n | Average Projection Length | Actual Mean Conifer Volume Increment | Residual Coniferous Volume Increment | SD Residual Volume |
|---|
| AW | 56 | 8 | 3.72 | −2.93 | 1.48 | CD | 123 | 10 | 3.67 | −0.23 | 2.97 |
| | | 18 | 3.99 | −2.46 | 1.14 | | | 20 | 3.53 | −0.83 | 2.61 |
| | | 26 | 4.23 | −2.02 | 1.03 | | | 27 | 3.55 | −0.70 | 2.41 |
| | | 35 | 4.38 | −1.58 | 0.93 | | | 33 | 3.57 | −0.38 | 2.14 |
| DC | 42 | 11 | 2.45 | −1.69 | 1.16 | SW | 50 | 12 | 4.43 | −1.62 | 2.84 |
| | | 18 | 2.70 | −1.19 | 1.06 | | | 19 | 4.72 | −1.49 | 3.00 |
| | | 26 | 2.83 | −0.82 | 0.83 | | | 26 | 4.91 | −1.36 | 2.96 |
| | | 34 | 2.99 | −0.41 | 1.14 | | | 34 | 5.34 | −0.86 | 2.65 |
Table 5.
The summary of observed stand parameters (DBH (cm), height (m), density (stems ha−1) and top height (m)), as well as the validation statistics (average mean bias (AMB), standard deviation of the residuals (SD_resid), relative mean bias (RMB), efficiency (EF) and the equivalence cutoff (EQ) for the conifer and deciduous components by species group (AW, SW and MX) for the SDS dataset.
Table 5.
The summary of observed stand parameters (DBH (cm), height (m), density (stems ha−1) and top height (m)), as well as the validation statistics (average mean bias (AMB), standard deviation of the residuals (SD_resid), relative mean bias (RMB), efficiency (EF) and the equivalence cutoff (EQ) for the conifer and deciduous components by species group (AW, SW and MX) for the SDS dataset.
| Species Group | n | Variable | Conifer | Deciduous |
|---|
| Observed | Statistics of Model Fit | Observed | Statistics of Model Fit |
|---|
| Mean | Min | Max | SD | AMB | SD_resid | RMB (%) | EF | EQ | Mean | Min | Max | SD | AMB | SD_resid | RMB (%) | EF | EQ |
|---|
| AW | 51 | DBH (cm) | 2.23 | 0.50 | 5.46 | 1.13 | −0.26 | 1.04 | −11.51 | 0.11 | 0.51 | 4.30 | 1.25 | 8.77 | 1.58 | 0.02 | 1.11 | 0.47 | 0.51 | 0.47 |
| | | Height (m) | 2.60 | 1.44 | 5.23 | 0.76 | −0.15 | 0.74 | −5.70 | 0.01 | 0.34 | 6.19 | 2.60 | 9.16 | 1.60 | 0.00 | 0.93 | −0.06 | 0.66 | 0.43 |
| | | Density (stems ha−1) | 2368 | 250 | 14000 | 2856 | −526.72 | 1166.71 | −22.25 | 0.80 | 828.68 | 9343 | 1000 | 36000 | 6259 | −910.30 | 4776.33 | −9.74 | 0.40 | 2055.49 |
| | | Top Height (m) | 3.39 | 1.31 | 7.91 | 1.41 | −0.09 | 1.29 | −2.56 | 0.17 | 0.54 | 10.00 | 5.47 | 16.20 | 2.45 | 1.25 | 1.43 | 12.52 | 0.39 | 1.70 |
| SW | 13 | DBH (cm) | 4.38 | 0.80 | 9.21 | 2.98 | −0.04 | 1.78 | −0.89 | 0.64 | 1.53 | 2.06 | 0.33 | 7.80 | 2.48 | −1.85 | 1.18 | −89.47 | 0.14 | 2.64 |
| | | Height (m) | 3.58 | 1.68 | 6.85 | 1.60 | −0.22 | 0.92 | −6.24 | 0.65 | 0.79 | 3.12 | 1.44 | 7.75 | 2.16 | −1.42 | 1.28 | −45.52 | 0.16 | 2.15 |
| | | Density (stems ha−1) | 3000 | 750 | 9500 | 2636 | −347.39 | 564.13 | −11.58 | 0.94 | 630.00 | 4281 | 250 | 17000 | 5723 | −4019.41 | 6347.50 | −93.88 | −0.76 | 7149.69 |
| | | Top Height (m) | 5.01 | 1.68 | 7.90 | 2.27 | 0.20 | 1.34 | 3.98 | 0.65 | 1.15 | 4.13 | 1.55 | 11.80 | 3.53 | −1.60 | 2.79 | −38.74 | 0.14 | 2.97 |
| MX | 16 | DBH (cm) | 4.39 | 1.67 | 7.93 | 1.98 | 0.11 | 1.34 | 2.49 | 0.54 | 1.05 | 4.28 | 1.49 | 7.75 | 1.87 | −0.79 | 1.35 | −18.50 | 0.29 | 1.41 |
| | | Height (m) | 3.98 | 2.39 | 6.74 | 1.23 | −0.05 | 0.85 | −1.35 | 0.52 | 0.68 | 5.77 | 2.01 | 9.83 | 2.19 | −0.82 | 1.61 | −14.25 | 0.31 | 1.56 |
| | | Density (stems ha−1) | 3188 | 750 | 9000 | 2850 | −393.50 | 669.29 | −12.35 | 0.92 | 701.25 | 4953 | 1000 | 15250 | 4262 | −206.08 | 3101.90 | −4.16 | 0.47 | 2377.50 |
| | | Top Height (m) | 5.95 | 3.52 | 8.88 | 1.83 | 0.49 | 1.36 | 8.30 | 0.37 | 1.07 | 8.99 | 2.60 | 12.30 | 2.41 | 0.63 | 1.79 | 7.05 | 0.37 | 1.44 |
For each of the validation datasets, individual plots were categorized by dominant species: pure types which included white spruce (SW) and trembling aspen (AW); and mixed types: conifer (white spruce leading) (CD), deciduous leading (DC), or if there were too few PSPs to differentiate by leading species, a general mixedwood category (MX) was used. Pure species groups were defined as having 80% or greater basal area of the primary species, while mixed types had between 50% and 80% of their basal area represented by the primary species. Since basal area proportions varied over the re-measurements, plots were categorized at the time they were closest to maturity, i.e., the last measurement for the juvenile plots, and the first measurement for the mature plots.
2.2.1. ASRD—Mature Permanent Sample Plot Data
The Alberta Sustainable Resource Development (ASRD) PSPs were initiated by the province in the 1960s and were continually installed until the 1990s. They were originally intended to aid in the determination of the optimal rotation age of various stand types, and were therefore placed in near-mature to mature stands. We used 524 ASRD PSPs in this validation, of which 78 were single plots and 801 were from clusters of two to four plots several tree-lengths apart. Each of the clustered plots was considered independent. The plots had up to six re-measurements, of which the first and last were used for the validation. Detailed information on plot design and measurement protocol can be found in the PSP field procedures manual
Alberta Land and Forest Service, 1998 [
17]. For these ASRD mature PSPs, four stand type categories were created: two pure (AW and SW), and two mixed (CD and DC). Site index estimates were obtained from measurement of either trees destructively sampled adjacent to each plot, or estimated using measured heights of top height trees (thickest 100 ha
−1), based on sub-regional site index equations [
18,
19]. Stand volume was compiled from tree height and DBH data using sub-regional equations [
20].
For this validation, 22 plots (17 CD and 5 SW plots) from the mature ASRD dataset were removed because they exhibited dramatic reductions in stand density over one projection period due to windthrow.
2.2.2. Juvenile Stand Dynamics System Plot Data
The Stand Dynamics System (SDS) PSPs were part of a program initiated by the province in the 1980s to develop growth and yield information for young post-harvest stands. We used the 80 aspen-spruce PSPs from the SDS program in this validation. For deciduous (AW) and deciduous-leading (DC), we restricted our validation to data from the four 1.78 m (10 m
2) circular regeneration plots (40 m
2 total area). Additional information is contained in the larger plots (250 m
2, 1000 m
2) into which these are nested; however, the tagging thresholds used in these larger plots (height >1.3 m and DBH >9.1 cm, respectively) make it impossible to separate the effects of mortality and new establishment from density changes due to trees growing through the tagging limit. For white spruce and conifer (spruce) leading mixedwoods, we used data from all plots. Also in very high density stands (>50 trees in each 10 m
2 subplot; ~50,000 stems ha
−1), additional trees were simply tallied into 10 cm height classes. These partial tallies at high density create some ambiguity in distinguishing ingress from mortality over time, but there was no way to remove this ambiguity without ignoring the high density dynamics. Detailed information on plot design and measurement protocols can be found in the Stand Dynamics System field procedures manual [
21]. For the SDS PSPs, three stand type categories were created, two pure (AW and SW) and one mixed (MX). Site index for the primary species was estimated using measured heights of top height trees taken at the last re-measurement, and using sub-regional site index equations [
18,
19].
2.2.3. WESBOGY Juvenile Permanent Sample Plot Data
The Western Boreal Growth and Yield Association (WESBOGY) has a series of long-term study plots, established from 1990 to 2004. These plots are placed in post-harvest, mixed aspen–white spruce stands and consist of control (untreated) aspen, and five manipulated aspen densities (0, 200, 500, 1500 and 4000 stems ha
−1). White spruce was planted in these stands at controlled densities of 0, 500 and 1000 stems ha
−1. We used data from nine installations (462 plots) from the WESBOGY study in this validation. The data were from 400 m
2 plots, with the exception of the natural (control) aspen plots which, owing to the high density, were taken from four 4m
2 sub-plots, combined to form a single 16 m
2 plot. Detailed information on plot design and measurement protocols can be found in the WESBOGY procedures manual [
22] and in Bokalo
et al. [
23]. For the WESBOGY PSPs, three stand types were assessed, two pure (AW and SW) and one mixed (MX). Site index values were estimated as for the SDS plots.
2.2.4. Saskatchewan Mature Permanent Sample Plot Data
This validation dataset from Saskatchewan was a random sub-sample of 80 permanent sample plots from the 1122 PSPs maintained by the Saskatchewan Ministry of Environment and Weyerhaeuser Company. The database included measurements made by Weyerhaeuser Company as part of their forest management agreement from 1994 to 2000. Detailed information on plot design and measurement protocols can be found in the Weyerhaeuser permanent sample plot procedures manual [
24]. Compilation and sub-sampling protocols can be found in Tansanu and Bokalo [
25]. For the Saskatchewan PSPs, four species categories were created, consisting of two pure (AW and SW) and two mixed (CD and DC). Site index was estimated using measured heights of top height trees and unpublished regional site index equations [
26]. Volumes were estimated using regional taper equations [
27].
2.3. Validation Methods
Our model validation used the first plot measurement to initialize MGM, we then projected the treelist to the final re-measurement where the observed stand conditions were evaluated against the MGM predictions. Using only the final measurement for validation provided the longest possible growth interval and eliminated autocorrelation issues that can arise when multiple measurements from individual stands are used. MGM projections used sub-regional site index equations [
18] and sub-regional volume equations [
20]. Because we were projecting PSPs, no mortality adjustments were used. The model was validated using both scatter plots and statistical tests for stand level model outputs (depending on dataset) that include the state variables volume (m
3 ha
−1), basal area (m
2 ha
−1), average DBH (cm), average height (m), top height (m), density (stems ha
−1) and quadratic mean diameter (QMD, cm). Annual periodic growth rate (volume-, height-, DBH- and top height increment) was also used for validation because it removes the influence of initial size and directly evaluates the performance of the component relationships. Annual periodic volume increment was calculated as the annualized difference in yield over the projection period, adding back the volume which was lost to mortality during this interval [
28]. There were no removals over the projection periods and ingress was not included. Validation using increment was done on the ASRD, SDS and WESBOGY datasets.
Validation of volume increment with respect to projection length for the ASRD dataset used a subsample of plots with the longest projection lengths. This kept the number of observations constant in order to remove effects of sample size and data variability on the results. For all projection length classes, the first measurement represents the initial volume from which volume increment is calculated.
Since volume vs. stand age (“yield”) curves are the most important product of the model for users, we used residual plots for volume to assess potential biases with respect to site index, initial stand density and projection length. As projection lengths varied from 5 to 40 years, bias was also assessed in approximately 10-year projection intervals, as well as at the final re-measurement.
We did not examine volume and basal area predictions for the juvenile datasets (SDS and WESBOGY) since these variables have low values and are highly dependent on the density distribution above and below breast height (1.3 m; volume and basal area calculations do not include trees shorter than 1.3 m).
Top height was defined as the average height of the thickest 100 stems ha−1 of each species. Basal area, quadratic mean diameter, density, and top height are readily measurable in the field, and are useful for tracking stand performance against the model. Average height and DBH are additional simple metrics of tree size.
Except for Saskatchewan data, the results were examined for both the conifer and deciduous stand components based on the four stand types (AW, SW, CD, DC) and—in the cases where there was insufficient data to separate CD and DC—the MX group. For brevity, in the pure species groups, only the dominant species component will be discussed.
2.4. Validation Metrics
Plots of observed (
Y )
vs. predicted
![Forests 04 00001 i001]()
data with a line
![Forests 04 00001 i002]()
) representing the perfect fit were used to visually assess the goodness-of-fit and identify model biases [
29,
30]. Plots of residuals (predicted
![Forests 04 00001 i001]()
− observed (
Y )) against stand characteristics such as site index and initial stand density, as well as projection length, were used to detect undesirable patterns in the residuals and a change in bias over the range of the parameter.
Five statistical metrics—average model bias (AMB), relative model bias percent (RMB), efficiency (EF) [
7,
11,
29,
31], the paired
t-test for equivalence (EQ) [
13,
32] and the traditional
t-test—were used to evaluate model performance. Average model bias (Equation (1)) is the average of the residual errors, presented in the units of the parameter being predicted, and is described by:
where (
Yi),
![Forests 04 00001 i004]()
are as above and (
n) is the number of observations. A model with an AMB of 0 would indicate no bias. Interpretation of the AMB should include an understanding of the significance of the error in terms of the accuracy of measurements for the different parameters.
The relative model bias (RMB, Equation (2)) relates the average mean bias to the observed mean estimator expressed as a percentage, providing an indication of the magnitude of the AMB (average error).
where
![Forests 04 00001 i006]()
is the average of the observed values. These metrics have the statistical convention of being negative for overestimates and positive for underestimates. The combination of the two metrics, AMB and RMB, provide the end user with an overall assessment of bias.
Efficiency (Equation (3)) is a dimensionless statistic that relates the model predictions to the observed data in a manner similar to that of the coefficient of determination (
R2) and is described by:
where the variables are as defined above. The efficiency statistic has a theoretical upper bound of one indicating a perfect model fit, a value of 0 indicates the model is no better than the mean. Unlike the coefficient of determination (
R2, which has a lower bound of 0), an EF value of less than 0 indicates a poorer fit than simply using the overall mean. Poor efficiency indicates poor precision or large variability in the individual errors, thus providing some sense of how well the model will predict any single plot.
Equivalence (EQ) tests are frequently used for model evaluation [
13]. Typically the test is used to determine whether model predictions fit the test data within a user defined range of deviation. This range can be absolute (e.g., ±20 m
3 for volume) or relative (e.g., a percentage of the mean or standard error), and is chosen by the user (e.g., 10%, 20%). If the model is rejected at an initially chosen deviation, the user may well analyze for equivalence again with a wider deviation. Since the model may be the user’s only option, we feel a useful innovation was to reverse the equivalence test, and report which level of deviance the model would be deemed “just equivalent.” The user can then decide if this is an acceptable range.
In the paired t-test for equivalence (EQ), the null hypothesis (Equation (4)) is that the difference between the predicted and the observed values are significantly different. To obtain equivalence, there must be significant evidence to reject the null hypothesis and accept the alternative hypothesis (Equation (5)).
where
p refers to the predicted and
o the observed.
If
Yi represents the observed and
![Forests 04 00001 i010]()
represents the predicted, the mean difference is
![Forests 04 00001 i011]()
with a standard deviation (
![Forests 04 00001 i012]()
and standard error (
![Forests 04 00001 i013]()
).
The calculated
t-statistic (
td) defining the confidence interval is calculated as
The cutoff
![Forests 04 00001 i015]()
for a given probability level and criterion (
ε) defines the region of indifference and is calculated as:
where
![Forests 04 00001 i017]()
denotes the quantile function of the F-distribution with 1,
n− 1 degrees of freedom and the non-centrality parameter (
![Forests 04 00001 i018]()
) =
n × ε [
32]. Epsilon (
ε) is a subjectively chosen but meaningful criterion, expressed relative to the standard deviation (
![Forests 04 00001 i012]()
and represents the desired accuracy level (region of indifference) where any differences between observed and predicted are considered irrelevant.
When the
t-statistic falls within the region of indifference (|
t| <
![Forests 04 00001 i019]()
), the null hypothesis is rejected and it is concluded that the two datasets are considered significantly similar, or equivalent. The power
![Forests 04 00001 i020]()
for a given criterion (
ε) at a probability level (
α) can be computed using:
where is the cumulative distribution function for the non-central
t distribution [
13].
Normally, the desired level of accuracy or cutoff is selected a priori, however, this leads simply to a result where we accept or reject the null hypothesis. Since the only factor that is not fixed is the criterion (ε) (if α is fixed at the usual 0.05 level), we solved for the criterion that represents the threshold where the test shifted from accepting the null hypothesis to rejecting it, while maintaining a power greater than 0.7. From a model validation perspective, the user needs to only decide if the criterion and associated power are acceptable for their application. In the case where the user would like to test different combinations of cutoff and power, we present sufficient information to complete these calculations.
For validating periodic annual increment, a
t-test (
α = 0.05) tested the null hypothesis that the AMB is not significantly different from 0 (
H0 :
μp -
μo = 0). A
t-statistic (Equation (9)) smaller than the critical
t-value (Student’s
t-table) will lead to the acceptance of the null hypothesis (
p-value greater than 0.05) indicating no statistically significant bias.
where
s is the standard deviation of the residual differences.
p-values less than 0.05 indicate a statistically significant bias.
 data with a line
data with a line  ) representing the perfect fit were used to visually assess the goodness-of-fit and identify model biases [29,30]. Plots of residuals (predicted
) representing the perfect fit were used to visually assess the goodness-of-fit and identify model biases [29,30]. Plots of residuals (predicted  − observed (Y )) against stand characteristics such as site index and initial stand density, as well as projection length, were used to detect undesirable patterns in the residuals and a change in bias over the range of the parameter.
− observed (Y )) against stand characteristics such as site index and initial stand density, as well as projection length, were used to detect undesirable patterns in the residuals and a change in bias over the range of the parameter.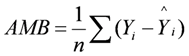
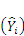 are as above and (n) is the number of observations. A model with an AMB of 0 would indicate no bias. Interpretation of the AMB should include an understanding of the significance of the error in terms of the accuracy of measurements for the different parameters.
are as above and (n) is the number of observations. A model with an AMB of 0 would indicate no bias. Interpretation of the AMB should include an understanding of the significance of the error in terms of the accuracy of measurements for the different parameters. 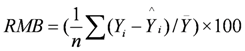
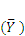 is the average of the observed values. These metrics have the statistical convention of being negative for overestimates and positive for underestimates. The combination of the two metrics, AMB and RMB, provide the end user with an overall assessment of bias.
is the average of the observed values. These metrics have the statistical convention of being negative for overestimates and positive for underestimates. The combination of the two metrics, AMB and RMB, provide the end user with an overall assessment of bias.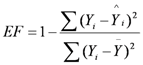
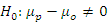
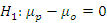
 represents the predicted, the mean difference is
represents the predicted, the mean difference is  with a standard deviation (
with a standard deviation ( 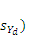 and standard error (
and standard error (  ).
).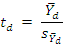
 for a given probability level and criterion (ε) defines the region of indifference and is calculated as:
for a given probability level and criterion (ε) defines the region of indifference and is calculated as:
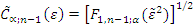
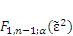 denotes the quantile function of the F-distribution with 1, n− 1 degrees of freedom and the non-centrality parameter (
denotes the quantile function of the F-distribution with 1, n− 1 degrees of freedom and the non-centrality parameter (  ) = n × ε [32]. Epsilon (ε) is a subjectively chosen but meaningful criterion, expressed relative to the standard deviation (
) = n × ε [32]. Epsilon (ε) is a subjectively chosen but meaningful criterion, expressed relative to the standard deviation ( 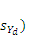 and represents the desired accuracy level (region of indifference) where any differences between observed and predicted are considered irrelevant.
and represents the desired accuracy level (region of indifference) where any differences between observed and predicted are considered irrelevant.  ), the null hypothesis is rejected and it is concluded that the two datasets are considered significantly similar, or equivalent. The power
), the null hypothesis is rejected and it is concluded that the two datasets are considered significantly similar, or equivalent. The power  for a given criterion (ε) at a probability level (α) can be computed using:
for a given criterion (ε) at a probability level (α) can be computed using: