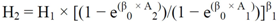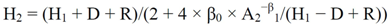Site Index Curves for Young Hybrid Larch Growing on Former Farmland in Sweden
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Site

| Variable | Unit | No. localities/plots | Mean | SD | Min. | Max. |
|---|---|---|---|---|---|---|
| Stand characteristics | ||||||
| Stand size | m2 | 26 | 1197 | 158 | 465 | 2374 |
| Height | m | 26 | 14.2 | 5.5 | 7.9 | 28.6 |
| Age | years | 26 | 23 | 10 | 17 | 49 |
| Diameter | cm | 26 | 16.4 | 7.3 | 6.7 | 33.9 |
| Stem number | stems ha−1 | 26 | 993 | 557 | 266 | 2165 |
| Basal area | m2 ha−1 | 26 | 18.1 | 9.5 | 4.3 | 35.7 |
| Plot characteristics | ||||||
| Plot size | m2 | 42 | 753 | 464 | 400 | 2200 |
| Height | m | 42 | 14.3 | 3.2 | 8.0 | 27.8 |
| Diameter | cm | 42 | 18.4 | 4.1 | 7.6 | 36.4 |
2.2. Soil Sampling
2.3. Construction of Site Index Curves
- where β0, β1 are parameters.
- • A Hossfield-based model proposed by Cieszewski and Bella [39]:where D = β0/Kβ1; R = [(H1 − D)2 + 4 × β0 × H1/A1β1]0.5 K; β0, β1 are parameters.
- • A model derived by Cieszewski [40] (Equation (21)):where P = Z0 × (Z02 + (2 × β1 × H1)/A1β0)0.5; Z0 = H1 − β2 β0; β1, β2 are parameters.
2.4. Statistical Analysis
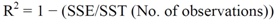
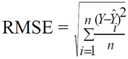
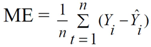
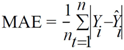
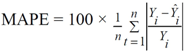
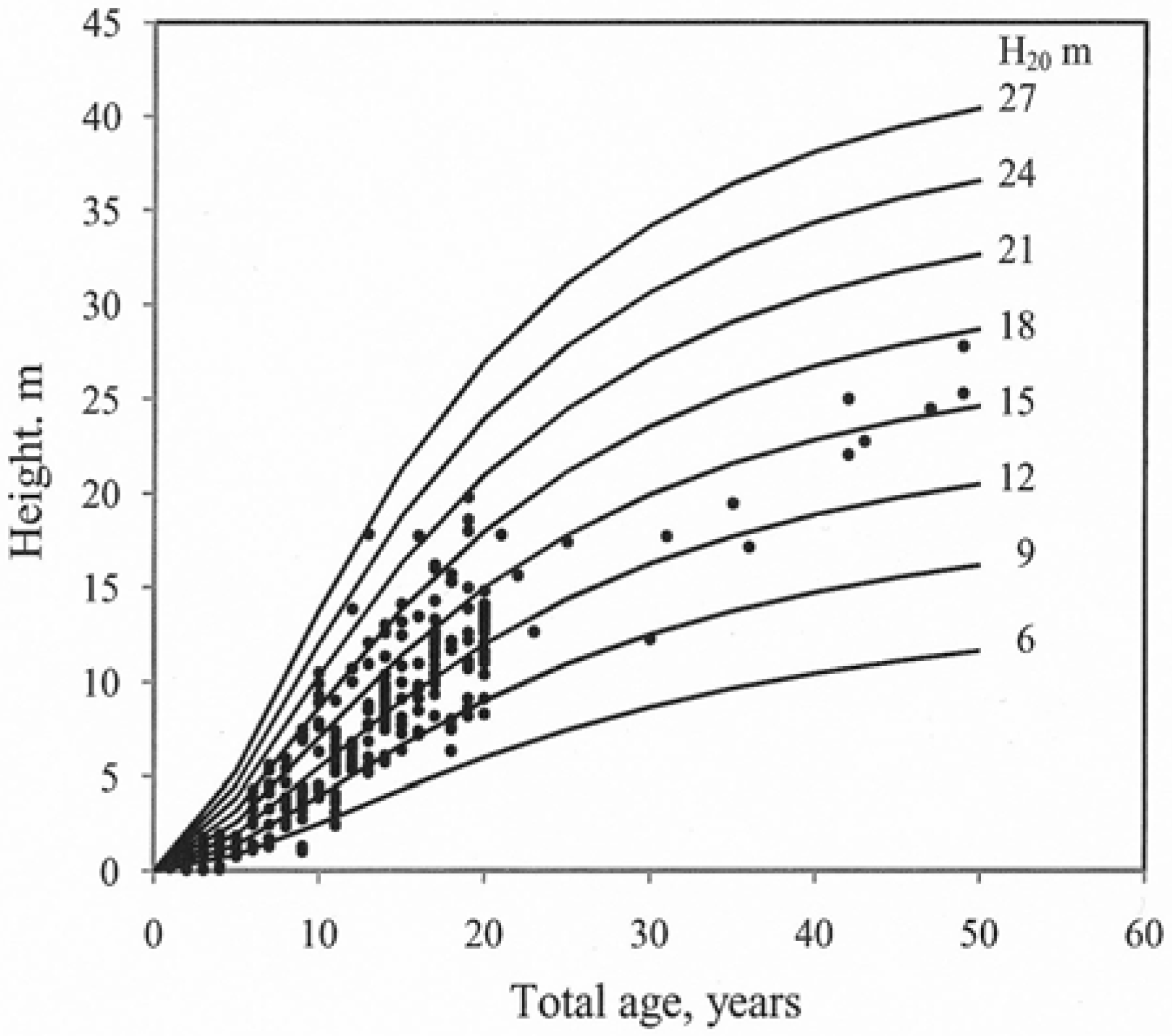
3. Results
| Model | Number of difference | Parameters | Parameter estimates | Se | Rmse M | R2 | Me M | Mae M | Mape % | Rmse 1 M | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Total age | |||||||||||
| 1 | 3024 | β0 | −0.0205 | 0.0010 | 1.18 | 0.98 | 0.07 | 0.79 | 12.73 | 1.18 | |
| β1 | 1.5520 | 0.0183 | |||||||||
| 2 | 3024 | β0 | 238.4000 | 6.1271 | 1.22 | 0.98 | −0.03 | 0.83 | 13.46 | 1.22 | |
| β1 | 1.4072 | 0.0129 | |||||||||
| K | 1.8257 | 0.0456 | |||||||||
| 3 | 3024 | β0 | 1.7187 | 0.0127 | 0.90 | 0.99 | 0.07 | 0.66 | 10.69 | 0.90 | |
| β1 | 4857.4000 | 9.7000 | |||||||||
| β2 | 24.9287 | 0.3240 | |||||||||
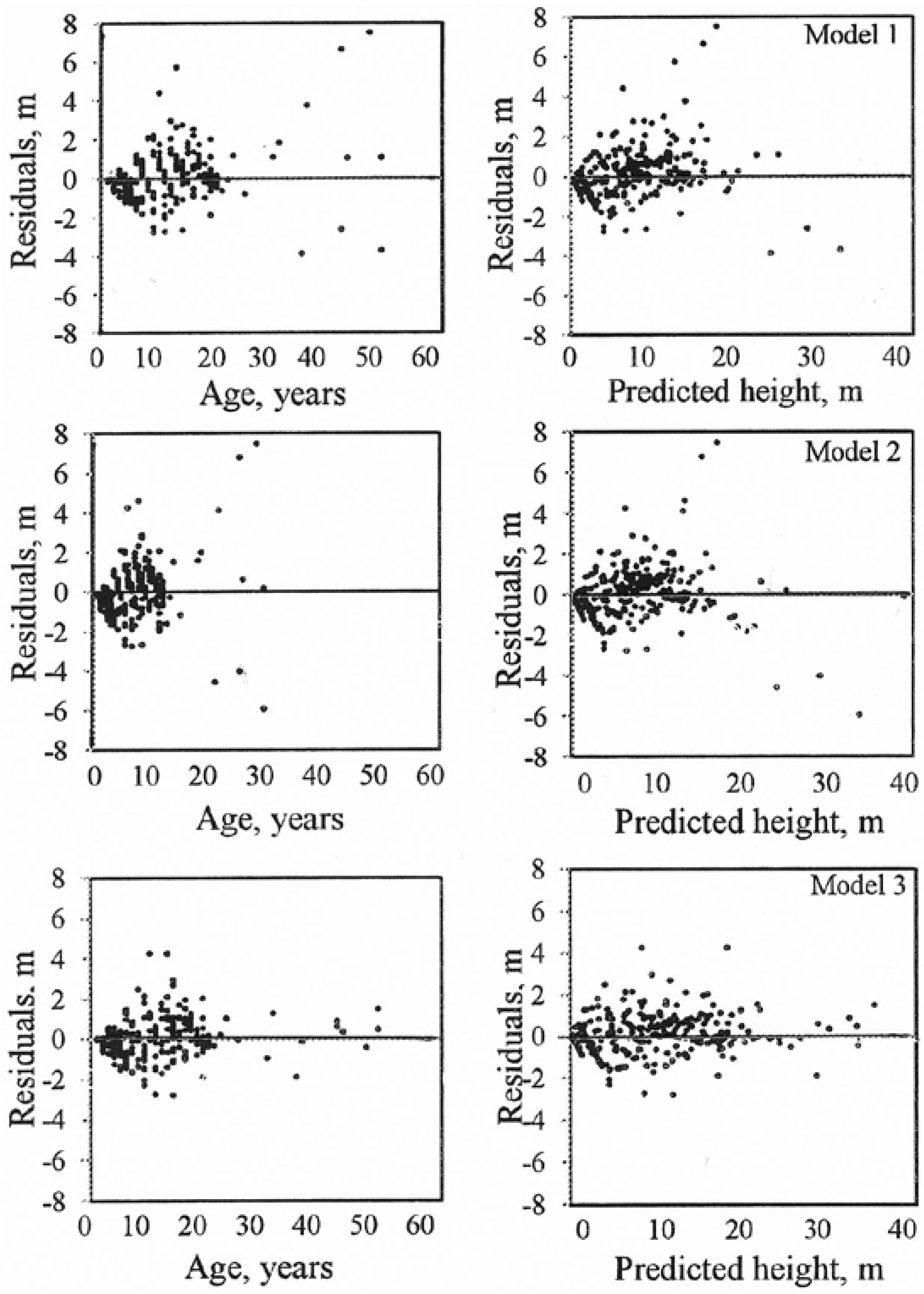
| MRES for Models | ||||
|---|---|---|---|---|
| Age class | Number of observation | 1 | 2 | 3 |
| 1–10 | 1575 | −0.24 | −0.35 | −0.12 |
| 11–20 | 1323 | 0.36 | 0.29 | 0.28 |
| 21–30 | 45 | 0.24 | 0.06 | 0.02 |
| 31–40 | 27 | 0.65 | 0.57 | −0.21 |
| >40 | 54 | 1.73 | 0.91 | 0.60 |
| Total | 3024 | 0.07 | −0.03 | 0.07 |
4. Discussion
 ”, site index for Japanese larch in Norway reported by Wielgolaski et al. (1993), H40 = 26 and 29 m “
”, site index for Japanese larch in Norway reported by Wielgolaski et al. (1993), H40 = 26 and 29 m “  ” and for Japanese larch in Denmark (Andersen, 1950), Bon B, “
” and for Japanese larch in Denmark (Andersen, 1950), Bon B, “  ”.
”.
 ”, site index for Japanese larch in Norway reported by Wielgolaski et al. (1993), H40 = 26 and 29 m “
”, site index for Japanese larch in Norway reported by Wielgolaski et al. (1993), H40 = 26 and 29 m “  ” and for Japanese larch in Denmark (Andersen, 1950), Bon B, “
” and for Japanese larch in Denmark (Andersen, 1950), Bon B, “  ”.
”.
5. Conclusions
Acknowledgements
Conflict of Interest
References
- Schmidt, W.C. Around the world with Larix: An introduction. In Ecology and Management of Larix Forests: A Look Ahead, Proceedings of an International Symposium, Whitefish, MT, USA, 5–9 October 1992; USDA Forest Service: Golden, CO, USA; pp. 6–10.
- Schotte, G. Lärken och dess betydelse för svensk skoghushållning (in Swedish). Medd. Stat. Skogsförsöksanst. 1917, 922, 13–14. [Google Scholar]
- Swedish Forest Agency, Swedish Statistical Yearbook of Forestry 2011; Swedish Forest Agency: Jönköping, Sweden, 2011.
- Cook, D.B. Characteristics of dunkfeld larch and its parent species. J. For. 1946, 80, 844–845. [Google Scholar]
- Dallimore, W.; Jackson, A.B.; Harrison, S.G. A Handbook of Conifer and Ginkgoaceae, 4th ed; St. Martins Press: New York, NY, USA, 1967; p. 729. [Google Scholar]
- Rawinski, J.J.; Bowler, J.A.; Noste, N.V. Soil Properties Related to Coniferous Seedling Height Growth in Southern Wiscounsin; Research Note NC-254; United States Department of Agriculture (USDA), North Central Forest Experiment Station: Saint Paul, MN, USA, 1992; p. 3. [Google Scholar]
- Larsson-Stern, M. Aspects of Hybrid Larch (Larix × eurolepis A. Henry) as a Potential Tree Species in Southern Swedish Forestry. Ph.D. Dissertation, Swedish University of Agricultural Sciences, Uppsala, Sweden, 2003. [Google Scholar]
- Vollbrecht, G.; Stenlid, J. Transfer of the P-type of Heterobasidion annosum form old-growth stumps of Picea abies and Larix × eurolepis. Eur. J. For. Path. 1999, 29, 153–159. [Google Scholar] [CrossRef]
- Hägglund, B. Evaluation of forest site productivity. Commonw. For. Bur. For. Abstr. 1981, 42, 515–527. [Google Scholar]
- Beamont, J.-F.; Ung, C.H.; Bernier-Cardou, M. Relating site index to ecological factors in black spruce stands: Tests of hypothesis. For. Sci. 1999, 45, 484–491. [Google Scholar]
- Bailey, R.L.; Clutter, J.L. Base-Age invariant polymorphic site curves. For. Sci. 1974, 20, 155–159. [Google Scholar]
- Clutter, J.L.; Fortson, J.C.; Pienaar, L.V.; Brister, G.H.; Bailey, R.L. Timber Management: A Quantitative Approach; John Wiley & Sons.: New York, NY, USA, 1983; pp. 30–62. [Google Scholar]
- Monserud, R.A. Height growth and site index curves for inland Douglas-fir based on stem analysis data and forest habitat types. For. Sci. 1984, 30, 945–965. [Google Scholar]
- Borders, B.E.; Bailey, R.L.; Ware, K.D. Slash pine site index from a polymorphic model by joining (splining) nonpolynomial segments with an algebraic difference method. For. Sci. 1984, 30, 411–423. [Google Scholar]
- Cieszewski, C.J.; Bailey, R.L. Generalize algebraic difference approach: Theory based deviation of dynamic site equations with polymorphism and variable asymptotes. For. Sci. 2000, 46, 116–126. [Google Scholar]
- Eriksson, H.; Johansson, U.; Kiviste, A. A site-index model for pure and mixed stands of Betula pendula and Betula pubescens in Sweden. Scand. J. For. Res. 1997, 12, 49–156. [Google Scholar]
- Elfving, B.; Kiviste, A. Construction of site index equations for Pinus sylvestris L. using permanent plot data in Sweden. For. Ecol. Manag. 1997, 98, 125–134. [Google Scholar] [CrossRef]
- Trincado, G.V.; Kiviste, A.; von Gadow, K. Preliminary site index models for native roble (Nothofagus oblique) and rauli (N. Alpine) in Chile. J. For. Sci. 2002, 32, 322–333. [Google Scholar]
- Adame, P.; Cañellas, I.; Roig, S.; del Río, M. Modeling dominant height growth and site index curves rebollo oak (Quercus pyrenaica Willd). Ann. For. Sci. 2006, 63, 629–940. [Google Scholar]
- De Santos-Posadas, H.M.; Montero-Mata, M.; Kanninen, M. Dynamic dominant height growth curves for Terminalia Amazonia (Gmel). Excell in Costa Rica. Artícul. Agrociencia. 2006, 40, pp. 521–532. Available online: http://www.citeulike.org/group/15200/article/9308792 (accessed on 17 August 2012).
- Diéguez-Aranda, U.; Burkhart, H.E.; Amateis, R.L. Dynamic site model for loblolly pine (Pinus taeda L.) plantations in the United States. For. Sci. 2006, 52, 262–272. [Google Scholar]
- Diéguez-Aranda, U.; Grandaz-Arias, J.A.; Álvarez-Gonzáles, J.G.; Gadow, K.V. Site quality curves for birch stands in North Western Spain. Silva Fenn. 2006, 40, 631–644. [Google Scholar]
- Kiveste, A.; Kiveste, K. Algebraic difference equations for stand height, diameter, and volume depending on stand age and site factors for Estonian state forests. Math. Comput. For. Nat. Res. Sci. 2009, 1, 67–77. [Google Scholar]
- Nord-Larsen, T.; Meilby, H.; Skovsgaard, J. Site specific height growth models for six common tree species in Denmark. Scand. J. For. Res. 2009, 24, 194–204. [Google Scholar] [CrossRef]
- Diaz-Marato, I.J.; Fernández-Parajes, J.; Vila-Lameiro, P.; Baracala-Pérez, E. Site index model for natural stands of rebollo oak (Quercus pyrenaica Willd.) in Galicia, NW Iberian Peninsula. Cienc. For. St. Maria 2010, 20, 57–68. [Google Scholar]
- Schober, R. Ertragstafel Fűr Europäische Lärche. Grűnberg in Hessen (in German); Im Selbstverlag des Verfassers: Grünber, Germany, 1946. [Google Scholar]
- Wiksten, Å. Några exempel på den sibiriska lärkens (Larix sibirica Lebed) produktionsförmåga i Sverige (in Swedish). Medd. från Stat. Skogsforskn. Inst. 1962, 51, 43. [Google Scholar]
- Vuokila, Y. Lehtikuusen kuutioimisyhtälöt ja-taulukot (in Swedish). Commun. Inst. For. Fenn. 1960, 51, 89. [Google Scholar]
- Ekö, P.M.; Larsson-Stern, M.; Albrektsson, A. Growth and yield of hybrid larch (Larix × eurolepis A. Henry) in Southern Sweden. Scand. J. For. Res. 2004, 19, 320–328. [Google Scholar] [CrossRef]
- Wielgolaski, F.M. Growth Studies in Plantations of Larix decidua Mill. and L. Kaempferi Carr. in Western Norway. I. Site-Index curves; Norsk Institutt for Skogforskning: Aas, Norway, 1993. [Google Scholar]
- Fries, J. Vårtbjörkens produktion i svealand och södra norrland (in Swedish). Stud. For. Suec. 1964, 14, 303. [Google Scholar]
- Johansson, T. Biomass equations for determining fractions of pendula and pubescent birches growing on abandoned farmland and some practical implications. Biomass Bioenergy 1999, 16, 223–238. [Google Scholar] [CrossRef]
- Ekström, G. Klassifikation av Svenska Åkerjordar (in Swedish); Geological Survey of Sweden: Stockholm, Sweden, 1929; pp. 1–161. [Google Scholar]
- Newberry, J.D. A note on Carmean’s estimate of height from analysis data. For. Sci. 1991, 37, 368–369. [Google Scholar]
- Carmean, W.H. Site index curves for upland oaks in the Central States. For. Sci. 1972, 18, 109–120. [Google Scholar]
- Borders, B.E.; Bailey, R.L.; Clutter, M.L. Forest growth models: Parameter estimations using real growth series. In Forest Growth Modeling and Prediction; General Technical Report NC-120; Ek, A.R., Shirley, S.R., Burk, T.E., Eds.; U.S. Department of Agriculture, Forest Service, North Central Forest Experiment Station: Newtown Square, PA, USA, 1988; pp. 660–667. [Google Scholar]
- Goelz, J.C.G.; Burk, T.E. Development of a well behaved site index equation: Jack pine in north central Ontario. Can. J. For. Res. 1992, 22, 776–784. [Google Scholar] [CrossRef]
- Richards, F.J. A flexible growth function for empirical use. J. Exp. Bot. 1959, 10, 290–300. [Google Scholar] [CrossRef]
- Cieszewski, C.J.; Bella, I.E. Polymorphic height and site index curves for Lodgepole pine in Alberta. Can. J. For. Res. 1989, 19, 1151–1160. [Google Scholar] [CrossRef]
- Cieszewski, C.J. Three models of deriving advanced dynamic site equations demonstrated on inland Douglas-fir site curves. Can. J. For. Res. 2001, 31, 165–173. [Google Scholar] [CrossRef]
- SAS, Version 9.1, SAS Institute Inc.: Cary, NC, USA, 2006.
- Zar, J.H. Biostatistical Analysis; Prentice-Hall: Englewood Cliffs, NJ, USA, 2009. [Google Scholar]
- Parresol, B.R.; Hotvedt, J.E.; Cao, Q.V. A volume and taper prediction system for bald cypress. Can. J. For. Res. 1987, 17, 250–259. [Google Scholar] [CrossRef]
- Kozak, A.; Kozak, R. Does cross validation provide additional information in the evaluation of regression models? Can. J. For. Res. 2003, 33, 976–987. [Google Scholar] [CrossRef]
- Rayner, M.E. Site index and dominant height growth curves for regrowth karri (Eucalyptus diversicolor F. Muell) in South-Western Australia. For. Ecol. Manag. 1991, 44, 261–283. [Google Scholar] [CrossRef]
- Wang, M.; Rennolls, K.; Borders, B.E. Base-Age invariant site index models from a generalized algebraic parameter prediction approach. For. Sci. 2008, 54, 625–632. [Google Scholar]
- Nord-Larsen, T. Developing dynamic site index curves for European beech (Fagus sylvatica L.) in Denmark. For. Sci. 2006, 52, 173–181. [Google Scholar]
- Kozak, A. Effect of multicollinearity and auto correlation on the variable-exponent taper equations. Can. J. Res. 1997, 27, 619–629. [Google Scholar] [CrossRef]
- Huang, S. Development of compatible height and site index models for young and mature stands within an ecosystem-based management framework. In Empirical and Process Based Models for Forest Trees and Stand Growth Simulation; Amaro, A., Tomé, M., Eds.; Empirical and Process Based Models for Forest Trees and Stand Growth Simulation: Oeiras, Portugal, 1997; pp. 61–98. [Google Scholar]
- Devan, J.S.; Burkhart, H.E. Polymorphic site index equations for loblolly pine based on a segmented polynomial differential model. For. Sci. 1982, 28, 544–555. [Google Scholar]
- Carmean, W.H.; Lenthall, D.J. Height growth and site-index curves for jack pine in north central Ontario. Can. J. For. Res. 1989, 19, 215–224. [Google Scholar] [CrossRef]
- Andersen, M. Form factor investigations and yield tables for Japanese larch in Denmark. Forstlige Forsøgsvœsen i Dan. 1950, 19, 331–410. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Johansson, T. Site Index Curves for Young Hybrid Larch Growing on Former Farmland in Sweden. Forests 2012, 3, 723-735. https://doi.org/10.3390/f3030723
Johansson T. Site Index Curves for Young Hybrid Larch Growing on Former Farmland in Sweden. Forests. 2012; 3(3):723-735. https://doi.org/10.3390/f3030723
Chicago/Turabian StyleJohansson, Tord. 2012. "Site Index Curves for Young Hybrid Larch Growing on Former Farmland in Sweden" Forests 3, no. 3: 723-735. https://doi.org/10.3390/f3030723
APA StyleJohansson, T. (2012). Site Index Curves for Young Hybrid Larch Growing on Former Farmland in Sweden. Forests, 3(3), 723-735. https://doi.org/10.3390/f3030723