Solving University Course Timetabling Problems Using Constriction Particle Swarm Optimization with Local Search

Abstract

Course timetabling is a combinatorial optimization problem and has been confirmed to be an NP-complete problem. Course timetabling problems are different for different universities. The studied university course timetabling problem involves hard constraints such as classroom, class curriculum, and other variables. Concurrently, some soft constraints need also to be considered, including teacher’s preferred time, favorite class time etc. These preferences correspond to satisfaction values obtained via questionnaires. Particle swarm optimization (PSO) is a promising scheme for solving NP-complete problems due to its fast convergence, fewer parameter settings and ability to fit dynamic environmental characteristics. Therefore, PSO was applied towards solving course timetabling problems in this work. To reduce the computational complexity, a timeslot was designated in a particle’s encoding as the scheduling unit. Two types of PSO, the inertia weight version and constriction version, were evaluated. Moreover, an interchange heuristic was utilized to explore the neighboring solution space to improve solution quality. Additionally, schedule conflicts are handled after a solution has been generated. Experimental results demonstrate that the proposed scheme of constriction PSO with interchange heuristic is able to generate satisfactory course timetables that meet the requirements of teachers and classes according to the various applied constraints.

1. Introduction

Course timetabling is a scheduling problem. However, it is far more complicated than general scheduling as it involves teachers, students, classrooms, and courses. From a broader perspective, course arrangement includes many interrelated issues, such as exams, meetings, administrative allocation, etc. [1]. The study by Even and Itai [2] proved that the course timetabling problem is an NP-complete problem. Conventionally, course timetabling has been conducted manually. Due to the large variety of constraints, resource limitations and complicated human factors involved, course timetabling often takes a lot of time and manpower. Using computers to perform course timetabling, however, can not only consolidate the preferences of the people concerned but can also enable achievement of high satisfaction in spite of the many constraints. Obviously, this results in saving a lot of time and thus manpower.

Ever since the 1960s, scholars have been studying course timetabling problems. Hertz [3] proposed using tabu search as the study method to deal with course timetabling problems in two stages (TATI/TAG) and emphasized that the approach is suitable for handling problems in large-scale course timetabling and test scheduling. Mooney et al. [1] came up with a nonlinear integer programming model, setting preference values according to the status of each teacher, to establish the maximum classroom utilization rate and teachers’ priority in course timetabling. Masood [4] employed a two-stage multi-objective scheduling model for allocation of teachers, courses, and time. Werra [5] suggested a restricted coloring theory and used mathematical concepts to apply the theory in course timetabling. Ross et al. discussed the state of the art in applying evolutionary algorithms to tackle timetabling problems of various kinds [6]. Cambazard et al. [7] used local search and constraint programming techniques for solving post enrolment-based course timetabling problems. An initial solution generated by Largrangian relaxation and improved by simulated annealing for solving master course timetable was proposed by Gunawan et al. [8]. Genetic algorithm (GA) was applied to deal with university timetabling derived from various limitations and constraints [9]. Ant colony optimization (ACO) algorithm was used to solve the post enrollment course timetabling problem by Nothegger et al. [10]. Meanwhile, Shiau [11] solved course scheduling problems by applying hybrid particle optimization. Tassopoulos and Beligiannis [12] applied hybrid particle swarm optimization to create feasible different Greek high school timetables. A memetic computing scheme named hybrid harmony search (HHS) algorithm for solving a university course timetabling problem was proposed by Al-Betar et al. [13]. The HHS integrates particle swarm optimization and hill climbing to balance exploitation and exploration search. Moreover, a hybrid genetic algorithm and tabu search approach was suggested for solving post enrolment course timetabling problems by Jat and Yang [14].

Considering the great impact of course timetabling results on teaching quality and learning interest, this study allows teachers and classes to express their expected course timeslots and preferences to help produce course timetabling results that can better meet the expectations of all involved as well as prevent negative influence on teaching and learning as a result of inappropriate course timetabling. As stated above, many approximation, heuristics and metaheuristics based algorithms such as nonlinear programming, coloring theory, evolutionary algorithm, local search, GA, PSO, and tabu search were developed for solving a variety of course timetabling problems. Those algorithms focused on how to efficiently seek the best solution in solution space. Among the many algorithms developed for solving scheduling problems, particle swarm optimization (PSO) has been proven to be capable of achieving remarkable performance. The advantages of less parameter settings required and fast convergence make it a popular algorithm applied to a variety of optimization problems. For this reason, PSO has been adopted in this study combined with interexchange local search because of its powerful search capacity, to find the solutions needed for optimal scheduling. Most studies have applied conventional PSO, but herein, a new methodology named standard PSO is applied and investigated. Hence, two types of particle swarm optimization are applied; one with inertia weights and the other with constriction factors. To reduce the computational complexity, particle encoding is based on timeslots rather than the traditional study hour. Moreover, a local search is involved for further exploring the neighboring solution space to enhance the solution quality.

2. Course Timetabling Problem

The course timetabling problem investigated in this work involves resource allocation constraints; under limited resources the conditions with regard to teachers, courses, students, and teaching facilities have to be met. The constraints vary with the environment, system and other factors of each college. Usually, constraints are divided into hard and soft constraints. Hard constraints are the ones that have to be met and must not be violated while the soft ones should be met and not be violated. In most Taiwanese universities, a class consists of a large group of students who share a major and go to most classes together. The hard constraints taken into consideration in this study include:

(1)

Each teacher can only teach one class in the same timeslot (teaching two courses at the same time is prohibited).

(2)

Each classroom can only be used for one course in the same timeslot (having two courses taught in the same classroom at the same time is not permitted).

(3)

Each class can only attend one course in any given timeslot.

(4)

A three-credit course must be arranged in consecutive hours, not on two separate days or with an interrupting lunch break.

(5)

No courses are to be conducted in the third and fourth hours each Thursday as that is the time for the weekly school (class) assembly and for the class tutor.

(6)

According to regulations, teachers holding first-level supervisory positions are to teach two classes each week.

(7)

Teachers concurrently holding first-level and second-level administrative positions or supervisory positions of academic units are not to teach any classes on Thursday afternoon.

Concurrently, the soft constraints taken into consideration are as follows:

(1)

Class time conflicts between the required courses of each year should be avoided to facilitate students’ course retake and credit makeup.

(2)

Course timetabling should be conducted according to the timeslot preferences of teachers and students as well as the levels of preference.

(3)

Each teacher may not teach more hours than the limit stipulated by the undergraduate department or graduate institute.

(4)

Each full-time teacher must teach classes for at least three days a week.

3. Particle Swarm Optimization Algorithm

Particle Swarm Optimization (PSO) was developed by Kennedy and Eberhart [15] in 1995. In PSO, a bird of a flock is represented as a particle, and the swarm is composed of a group of particles. The position of each particle can be regarded as the Candidate Solution to an optimization problem. Every particle is given a Fitness Function designed in correspondence with the corresponding problem. When each particle moves to a new position in the search space, it will remember its personal best (P_best). In addition to remembering its own information, each particle will also exchange information with the other particles and remember the global best (G_best). Then, each particle will revise its velocity and direction in accordance with its P_best and the G_best to move toward the optimal value and find the optimal solution. With the advantages of simple and easy application, less parameter setting required, and decent performance, PSO has been adopted in many fields, such as TSP [16], flowshop [17], VRP [18], task-resource assignment in grid [19], special scheduling [20,21], etc. Hence, it has also been applied in this study to establish the optimal timetabling for university courses.

To begin a PSO algorithm, the initial velocity and position of each particle in a group of particles are randomly determined. Then, the evolving process is as follows:

(1)

The initial position and velocity of each particle in the Nth dimension are determined randomly.

(2)

The fitness value of each particle is assessed according to the defined objective function.

(3)

If the fitness value of each particle’s current location is better than its P_best, the P_best is set to the current position.

(4)

The fitness value of the particle is compared with that of the G_best. If it is better, the G_best is updated.

(5)

Equation (1) as shown below is applied to update the velocity and position of each particle.

(6)

The process is repeated from Step 2 until the termination criterion is met or the optimal solution in the universe is obtained.

$$\begin{array}{l}{V}_{id}^{t+1}=V_{id}^t+c_1\times Rand1\times (P_{id}-X_{id})+c_2\times Rand2\times (P_{gd}-X_{id})\\ X_{id}^{t+1}=X_{id}^t+V_{id}^{t+1}\end{array}$$

(1)

In the equation,

• V_id is the velocity component of the ith particle in the dth dimension.
• X_id is the position component of the ith particle in the dth dimension.
• c₁ is the cognitive learning factor.
• c₂ is the social learning factor.
• P_id is the position component of the P_best of the ith particle in the dth dimension.
• P_gd is the position component of the G_best in the dth dimension.
• Rand() is a random number between [0, 1].

3.1. The Inertia Weights

Since PSO was founded, many derivative algorithms have been developed. In Equation (1), the particle advancement guided by cognitive and social learning factors belongs to the local search ability, whereas Term 1 on the right hand side of Equation (1) is the advancement along the velocity direction of the particle itself and belongs to the global search ability. Therefore, Shi and Eberhart (1998) proposed the inertial weight value concept [22] and added an inertial weight value (w) to the original PSO algorithm, Equation (1), to balance the global search ability and the local search ability, as shown in Equation (2) and thereby boost the capability to locate the optimal solution and convergence rate.

$$\begin{array}{l}{V}_{id}^{t+1}=\omega V_{id}^t+c_1\times Rand1\times (P_{id}-X_{id})+c_2\times Rand2\times (P_{gd}-X_{id})\\ X_{id}^{t+1}=X_{id}^t+V_{id}^{t+1}\end{array}$$

(2)

This version of PSO is the most commonly used and is referred to as the conventional PSO in this study.

3.2. Constriction Factors

Clerc [23] (1999) proposed the constriction factor method; a constriction factor is added into the PSO prototype to ensure stable convergence. Eberhart and Shi [24] conducted a comparative analysis on inertia weights and constriction factors and discovered that the best convergence effect can be achieved by defining V_max = X_max (the maximum velocity is confined to the maximum position range) when a constriction factor is applied. Bratton and Kennedy later defined this as the Standard PSO (SPSO) [25]. The particle velocity update equation modified according to the constriction factor based PSO is as shown below:

$$\begin{array}{l}{V}_{id}^{t+1}=K[V_{id}^t+c_1\times Rand1\times (P_{id}-X_{id})+c_2\times Rand2\times (P_{gd}-X_{id})]\\ K=\frac{2}{2-\phi -\sqrt{{\phi }^2-4\kappa }}, \phi =c_1+c_2, \phi >4\end{array}$$

(3)

In the equation, K is the constriction factor and constant φ is the sum of learning factors c₁ and c₂. Kennedy and Clerc [26] discovered in their study that when constant φ is smaller than four, convergence of the entire swarm cannot be guaranteed. On the other hand, when it is larger than four, not only do the particles move quickly and achieve convergence, but the convergence can also take place at an appropriate velocity. Normally, the settings are K = 0.72984, and c₁ = c₂ = 2.05. In this study, experiments were conducted with the conventional PSO and the SPSO and the results comparatively analyzed.

3.3. Particle Encoding

The four main factors in course timetabling are teachers, courses, students (classes), and classrooms together with other teaching facilities. The combination of these four factors is defined as the particle position and each particle represents a solution group. The objective is to obtain the optimal particle position, (the optimal course timetabling solution). Due to teachers’ preference, the 3 h of 3-credit courses must be consecutive, without a lunch break within. Hence, the first, second and third hours are considered a timeslot, the second, third, and fourth hours another timeslot, and so forth. Basically, there are 40 course hours in a week’s timetable for Taiwanese universities, i.e., 8 h a day, 5 days a week. To reduce the complexity of timetabling and particle encoding and decrease computational complexity, 20 timeslots are designated in the course timetabling instead of using a 40-period weekly class schedule. Restated, the 8 class hours in each day are separated into 4 timeslots and there are 20 timeslots each week (4 timeslots a day, 5 days a week as shown in Figure 1). As a result, the 40-hour weekly class schedule is reduced to a 20-timeslot class schedule and the encoding of the particles can thus be simplified while the complexity in calculation also decreases. Subsequently, the 20-timeslot class schedule of each teacher is designated as a particle with a one-dimensional vector (Figure 2). Similarly, each class schedule and each classroom schedule are also designated as particles with one-dimensional vectors. In the end, each particle has three dimensions and each dimension represents a one-dimensional vector corresponding to the schedule of the teacher, class, and classroom respectively.

Figure 1. Representation of timeslots for course timetabling.

Figure 1. Representation of timeslots for course timetabling.

Figure 2. Particle encoding scheme.

Figure 2. Particle encoding scheme.

If there are 10 teachers, the particle position vector then has the value of 20 × 10 = 200 elements. The elements in the particle are between 1 and 200. There are 5 days a week and 4 timeslots per day. Elements 1–20 stand for the class schedule of the first teacher, 21–40 for the second teacher, 41 to 60 for the third teacher, and so on as shown in Figure 2. First, each particle is initialized and the range of the initial position is set between 0 and 9 as shown in Figure 3. The range of the initial velocity is set between −0.5 and 0.5. The position vector X_h = [X_hi], i = 1–200 is established to represent the particle position; h is the particle and i is the element. Next, the element value of X_hi is rounded to the nearest integer [0, 9] and temporarily stored in S_hi. Then, sequencing is conducted according to the initial value of S_hi as shown in Figure 4 to extract numbers of maximum values of the S_hi, the quantity to be extracted depending on the number of hours each teacher teaches. Suppose the first and the second teachers teach three courses each and three maximum values are then extracted as shown in Figure 5. The timeslot arrangement for these two teachers is made according to the position numbers of these three maximum S_hi values to find out whether there is any conflict between the teacher, class, and classroom schedules. If there is no conflict, the course code is put in the teaching schedule of the first teacher, the class schedule, and the schedule of the classroom. If there is any conflict, the time slot arrangement is then exchanged with the timeslot in the fourth arrangement as shown in Figure 6. If any conflict appears again, the exchange is made with the timeslots in the fifth arrangement, and so on. The teacher’s preference values corresponding to the teacher schedule and the class’s preference values corresponding to the class schedule are then added up to calculate the fitness value. Next, the fitness value of each particle is assessed, the personal best (P_best) and global best (G_best) are updated, and finally the velocity and position of each particle are updated.

Figure 3. Particle initialization.

Figure 3. Particle initialization.

Figure 4. S_hi after sorting.

Figure 4. S_hi after sorting.

Figure 5. Three maximum values extracted.

Figure 5. Three maximum values extracted.

Figure 6. Example of a conflict process of a teacher’s schedule.

Figure 6. Example of a conflict process of a teacher’s schedule.

Since each week is divided into 20 timeslots, when, for example, a 3-hour course is arranged in the first timeslot (the first, second and third hours) on Monday, it will be impossible for that teacher to have another 3-hour course in the second timeslot (the second, third and fourth hours) and the fourth hour in the morning will be left idle. If Tuesday afternoon is open, it means two 2-hour courses, one 4-hour course, or one 3-hour course can be arranged. In other words, the system has to be able to assess whether a 2-hour, 3-hour, or 4-hour course is suitable. If a 2-hour course is arranged, another 2-hour course can be scheduled. If it is a 3-hour or 4-hour course, only one course can be scheduled.

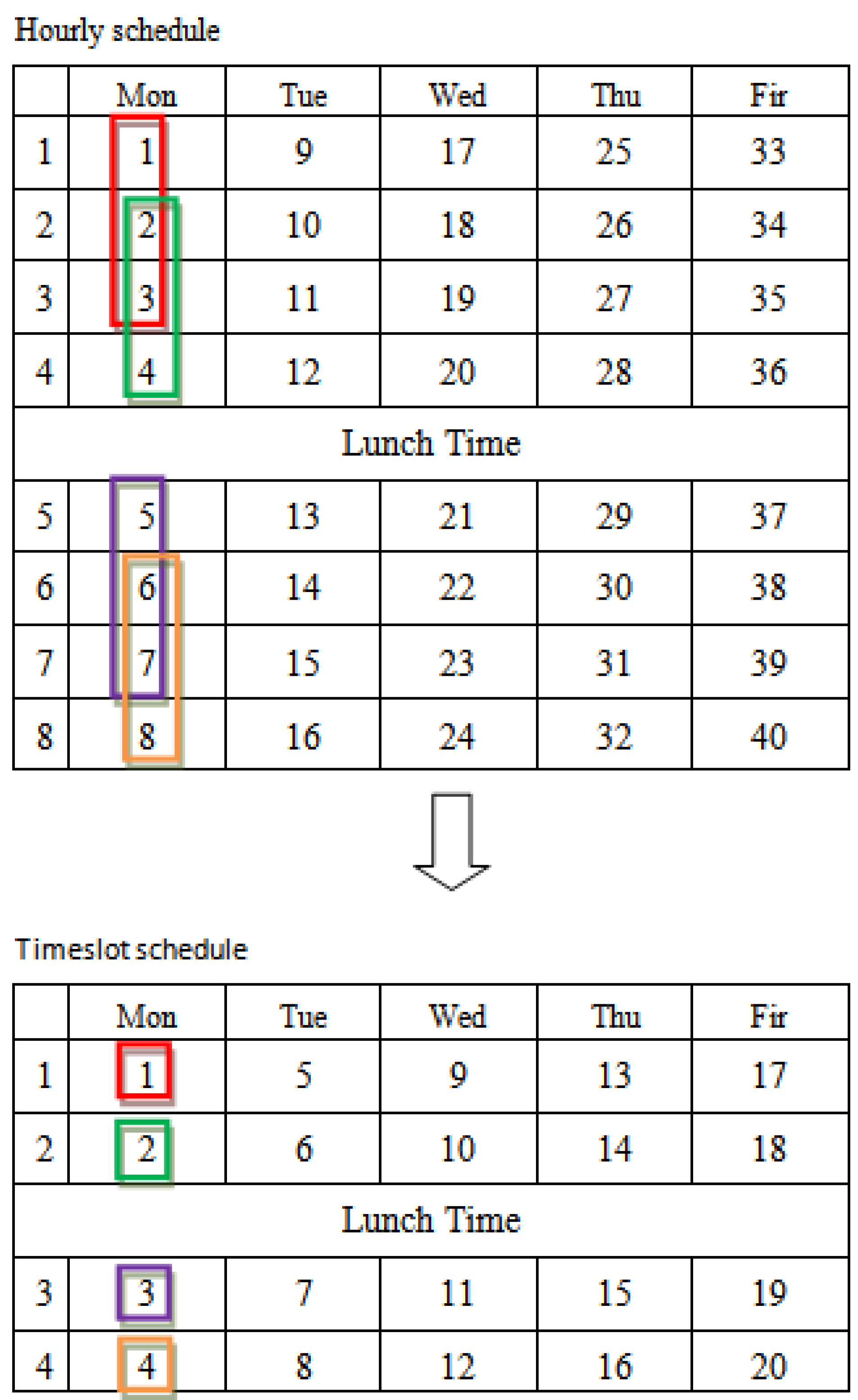
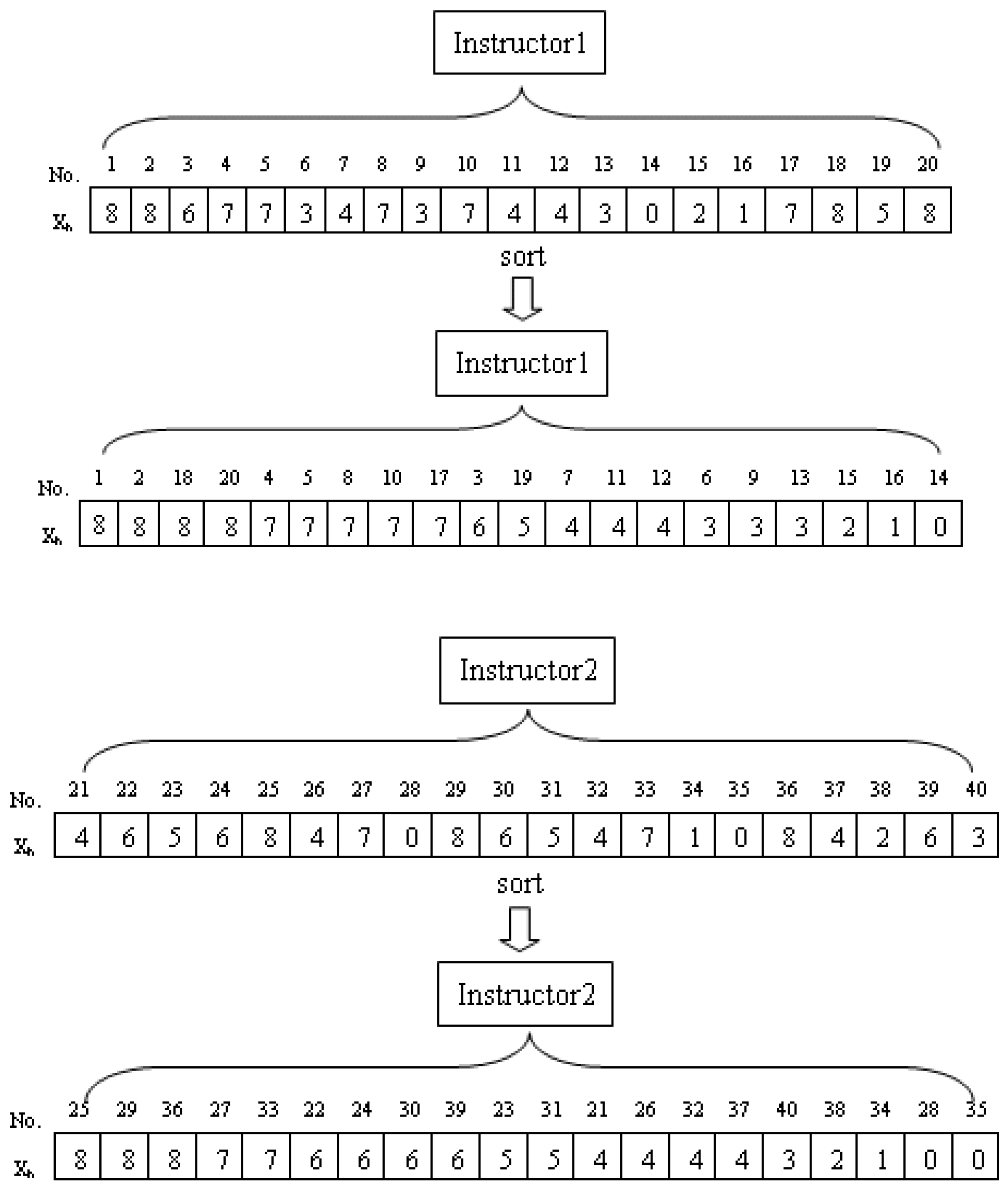
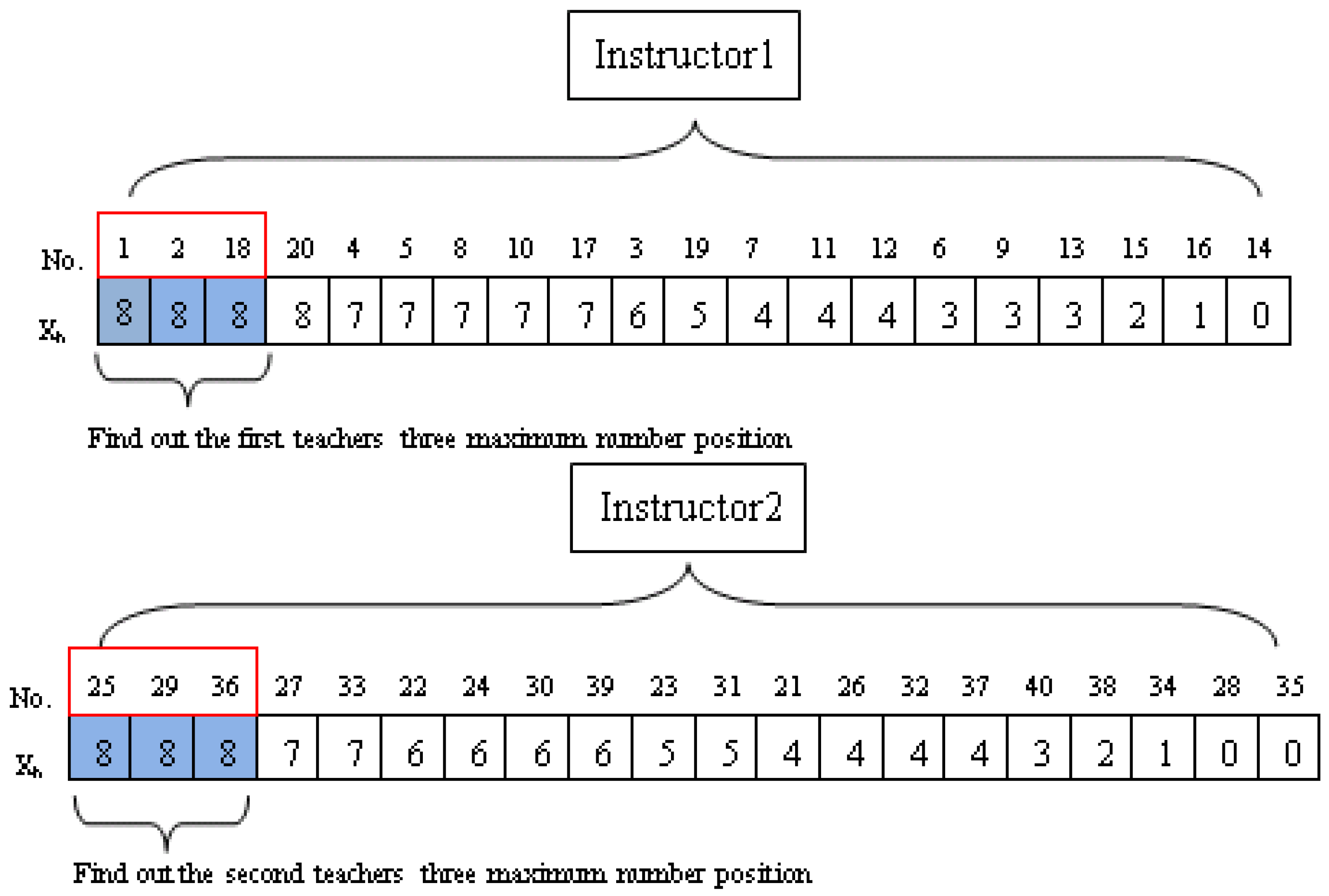
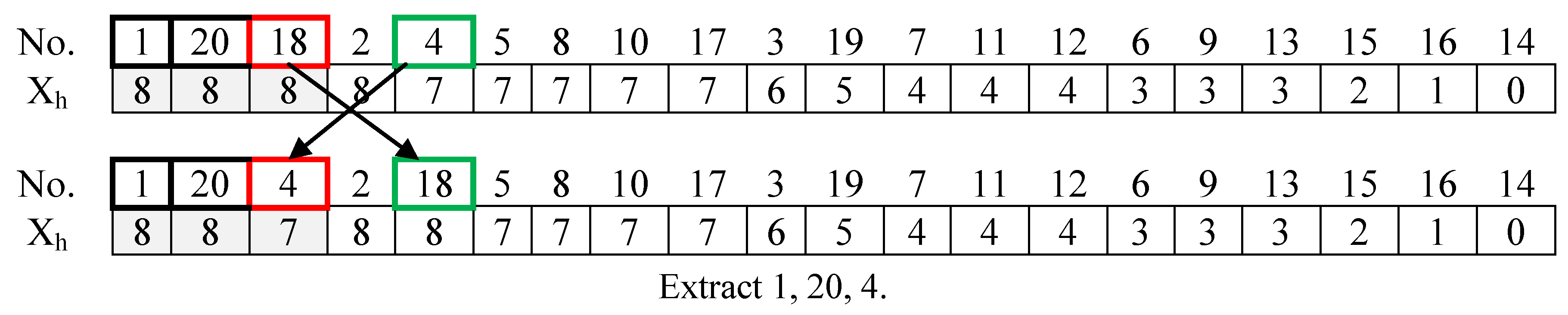
3.4. Fitness Function

In this study, the overall satisfaction is affected by the satisfactions of the class and teacher. The preferred timeslot and level of preference filled in by each class and teacher are assessed to understand the priorities in course timetabling. Five represents the most favorite timeslot, 4 the second favorite, 3 an acceptable timeslot, 2 a mediocre timeslot, and 1 the least favorite timeslot. A value of −10 represents a timeslot where no classes should be scheduled. In the evolving process of the PSO scheme, 10 timeslots are avoided to prevent situations where a teacher is not available. Table 1 shows an example of preferred timeslots, based on the results of a questionnaire administered.

Table 1. Preference timeslot example.

Timeslot	Mon	Tue	Wed	Thu	Fir
1	1	5	3	5	4
2	1	4	2	5	3
Lunch Break
3	2	4	2	−10	2
4	2	4	−10	−10	2

Table 1. Preference timeslot example.

Timeslot	Mon	Tue	Wed	Thu	Fir
1	1	5	3	5	4
2	1	4	2	5	3
Lunch Break
3	2	4	2	−10	2
4	2	4	−10	−10	2

The principal objective of this study was to find the optimal satisfaction of teachers and classes with the results of course timetabling. Since soft constraints can increase such satisfaction, the fitness function (satisfaction value) is defined as the result of subtracting the soft constraint penalty function from the total value of teacher and class satisfactions of the course timetable. Hence, the definition of the fitness function in this work is as shown in Equation (4).

$$fitness={\sum }_t{preference\_level}_t+{\sum }_c{preference\_level}_c-{\sum }_i{Penalty}_i$$

(4)

In the equation, preference_level_t represents t teacher’s preference level, and preference_level_c the c class’s preference level. Penalty_i is the penalty function for violation of the ith soft constraint. The fitness function is applied in the iteration to measure the fitness value. The larger it is, the better the solution the particle represents and the fewer are the soft constraints violated.

3.5. PSO with Local Search

As the search by PSO in the solution space evolves, movement is made according to the personal best of each particle and the global best. Therefore, after generation evolution, the search area decreases and there is a high probability that each particle will be trapped on the local optimal solution and become unable to escape from the local optima. Although the particles have good searching capability in local areas, they are unable to find better solutions outside these areas and thus lose the opportunity to locate the optimal solution in the universe. Hence, in this study, local search mechanisms are consolidated and a disturb mechanism [27] is added in the movement of the particles to increase the probability of particles escaping from the local optimal solution and to find the optimal solution in the universe quickly. Local search is performed after the movement and position change of particles in PSO. The areas around the position of each particle obtained using PSO are examined in the hope of finding a better solution to update the p_best and the g_best. The interchange heuristic, which swaps two randomly selected elements, is applied to the local search to explore the adjacent solution space, thereby improving the quality of the solution by helping to avoid convergence to the locally optimal solution. Such complementation boosts the performance of PSO through optimization of the solution search.

4. Experimental Results and Discussion

This study was conducted by analyzing a situation involving 16 teachers, 10 classes, and 10 classrooms. The goal was to produce the most satisfactory class schedule to meet the various constraints as well as the expectations of the teachers and the classes. The influence of the different parameters in the algorithm on the level of satisfaction with the course timetabling results was also examined and the experimental results proved the adopted framework was effective.

The course timetabling process was further analyzed as follows:

(1)

Prioritization of teachers

The prioritization of teachers in course timetabling will have a significant effect on the results of course timetabling, therefore, no specific teacher’s timetable should be assigned first and they are thus assigned randomly.

(2)

Course data

The data regarding the courses a teacher will teach needs to be established before the semester begins. Such data includes the teacher code, course code, class code of the class to take the course in question, teacher’s status, number of class hours, classroom, etc.

(3)

Classroom data

Classrooms involve certain particular factors. A teacher is assigned to maintain and manage each one of the classrooms of the Computer Science and Information Engineering Department where this study was performed and all the classes to be taught by a teacher are normally arranged to be conducted in the classroom that the teacher is assigned to maintain and manage. Restated, if classroom A is placed under the management of teacher A, the courses that teacher A teaches will be preferably conducted in classroom A. Since the number of teachers in the department is larger than the number of classrooms, some classrooms are placed under the management of two or more teachers.

(4)

Handling of teacher, class and classroom schedules conflicts

A class time conflict may happen when two teacher timeslots, classroom timeslots and course timeslots overlap and it becomes an infeasible solution. To avoid an endless search for solutions to class time conflicts in all timeslots, such conflicts are singled out from timeslots as being infeasible solutions and assessed whether they should be discarded according to the satisfaction level.

4.1. Particle Quantity Analysis

Figure 7 shows the results of analysis of the evolution of 5, 10, 15, 20, 25, 30 and 35 particles to observe the influence of different numbers of particles on the overall fitness value of course timetabling. The response of standard PSO (denoted by SPSO) and conventional PSO (denoted by PSO) to the quantity of particles is tested. Apparently, larger numbers of particles do not result in better fitness values. When the evolution of each quantity of particles is conducted for 6000 generations, the best fitness value comes from when the number of particles is 30.

Figure 7. Swarm sizes verse average fitness (SPSO: X = 0.72984, c₁ = 2, c₂ = 2, V_max = 3; PSO: w = 0.7, c₁ = 2, c₂ = 2, V_max = 3).

Figure 7. Swarm sizes verse average fitness (SPSO: X = 0.72984, c₁ = 2, c₂ = 2, V_max = 3; PSO: w = 0.7, c₁ = 2, c₂ = 2, V_max = 3).

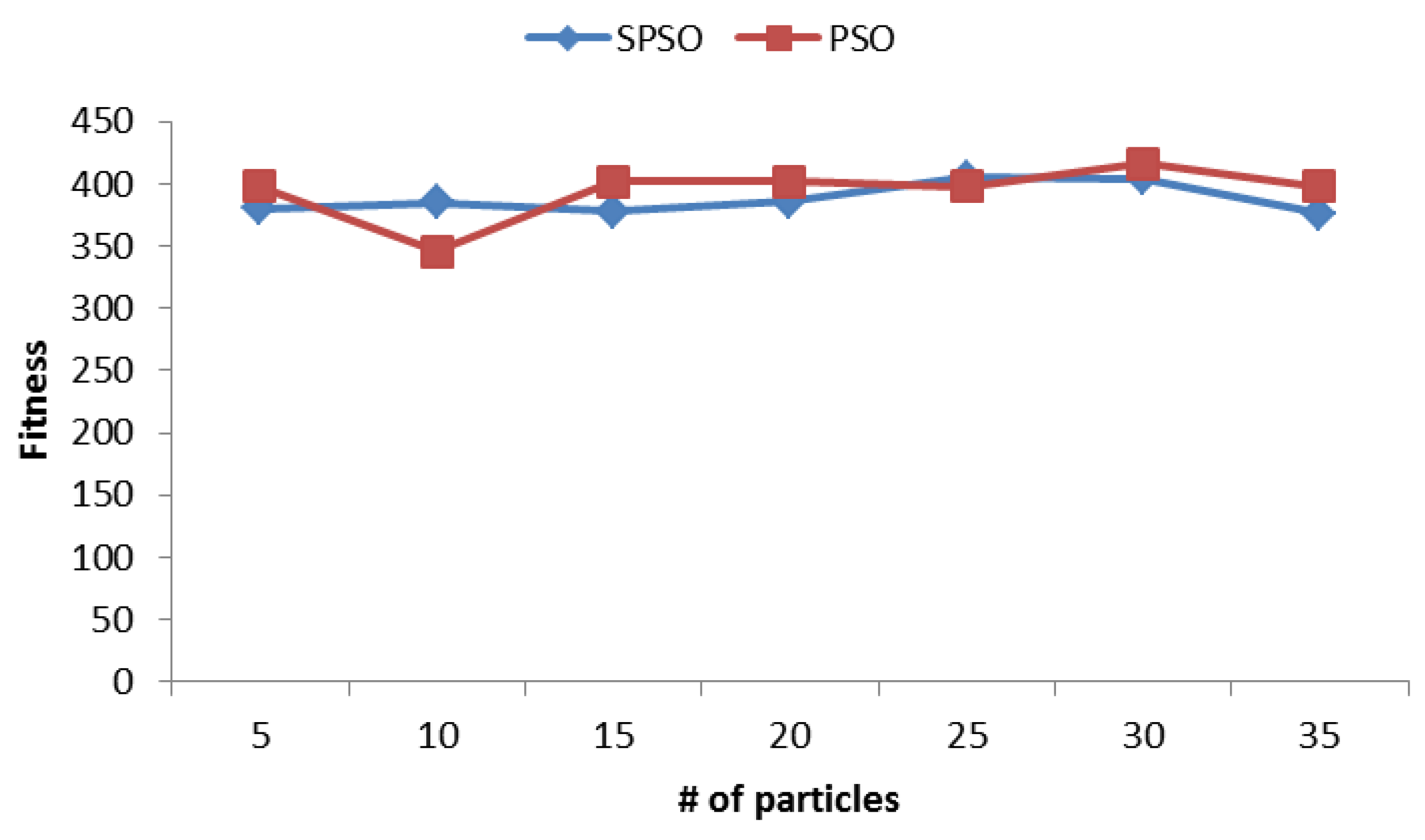
4.2. Inertia Weight Analysis

The w, inertia weight value setting will have an effect on the velocity of particle position update and also indirectly on the next position the particle will move to. If the w value setting is inappropriate, it is impossible to explore unknown areas and the search for the personal best and global best will also be affected. Figure 8 shows the satisfaction (fitness) value obtained from tests conducted (6000 iterations) with PSO using different w and V_max values. Apparently, there is higher satisfaction obtained when w = 0.8 and V_max = 3.

Figure 8. Particle swarm optimization (PSO), c₁ = 2, c₂ = 2.

Figure 8. Particle swarm optimization (PSO), c₁ = 2, c₂ = 2.

4.3. Learning Factor Analysis

Using the better average satisfaction value obtained when w = 0.8 to analyze learning factors c₁ and c₂, testing results with PSO are shown in Figure 9. The average fitness (380.5714) for c₁ = 2, c₂ = 2 is higher than the average fitness (373.1429) for c₁ = 2.05, c₂ = 2.05. Figure 10, testing with SPSO, indicates that the results are also better when c₁ = 2.0, c₂ = 2.0 (average fitness is 378.7143 for c₁ = 2.0, c₂ = 2.0 and 373.1429 for c₁ = 2.05, c₂ = 2.0.5), the same as the outcome of using PSO.

Figure 9. PSO comparison between c₁ = c₂ = 2 and c₁ = c₂ = 2.05 (w = 0.8).

Figure 9. PSO comparison between c₁ = c₂ = 2 and c₁ = c₂ = 2.05 (w = 0.8).

Figure 10. SPSO comparison between c₁ = c₂ = 2 and c₁ = c₂ = 2.05 (χ = 0.72984).

Figure 10. SPSO comparison between c₁ = c₂ = 2 and c₁ = c₂ = 2.05 (χ = 0.72984).

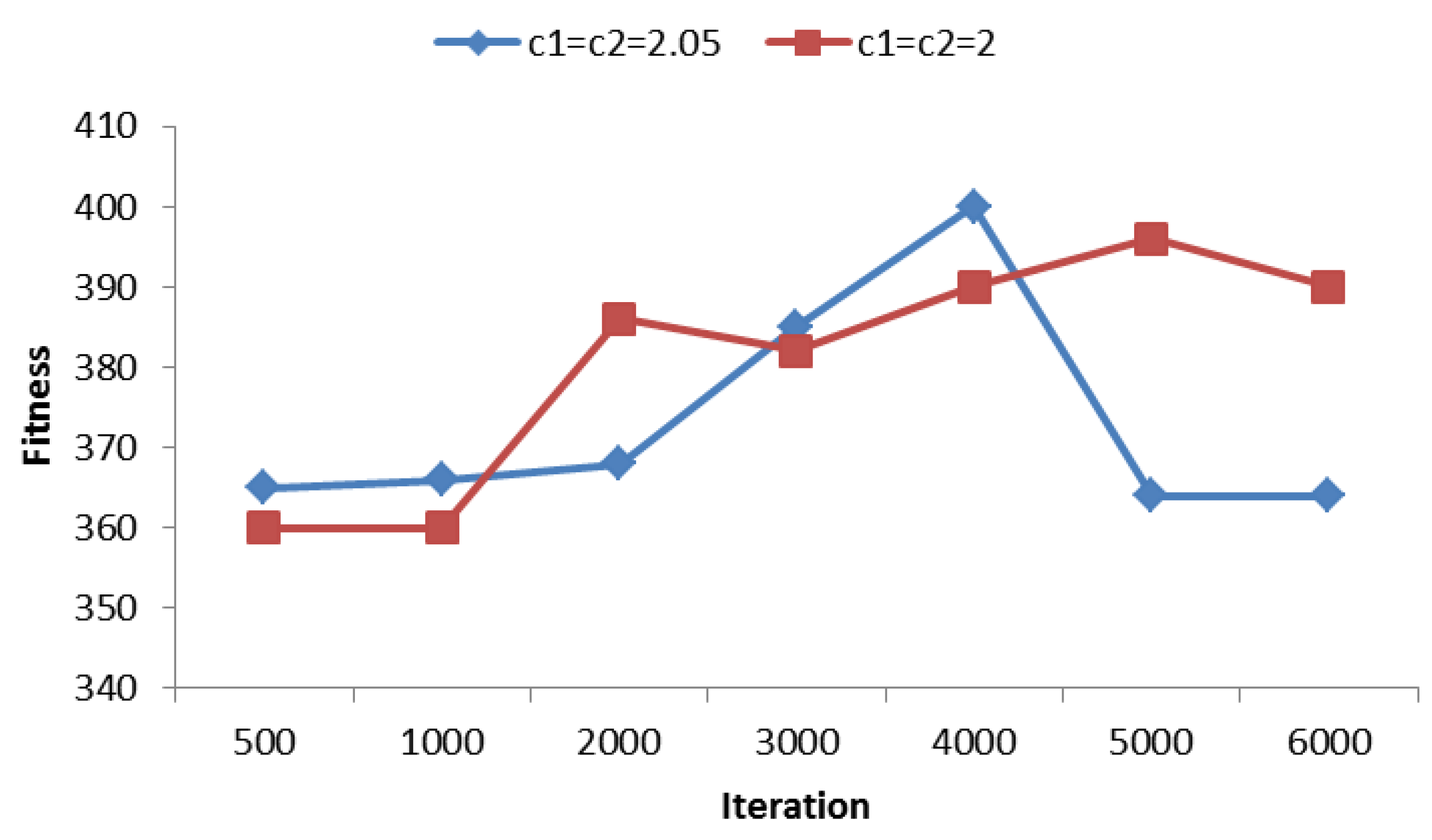
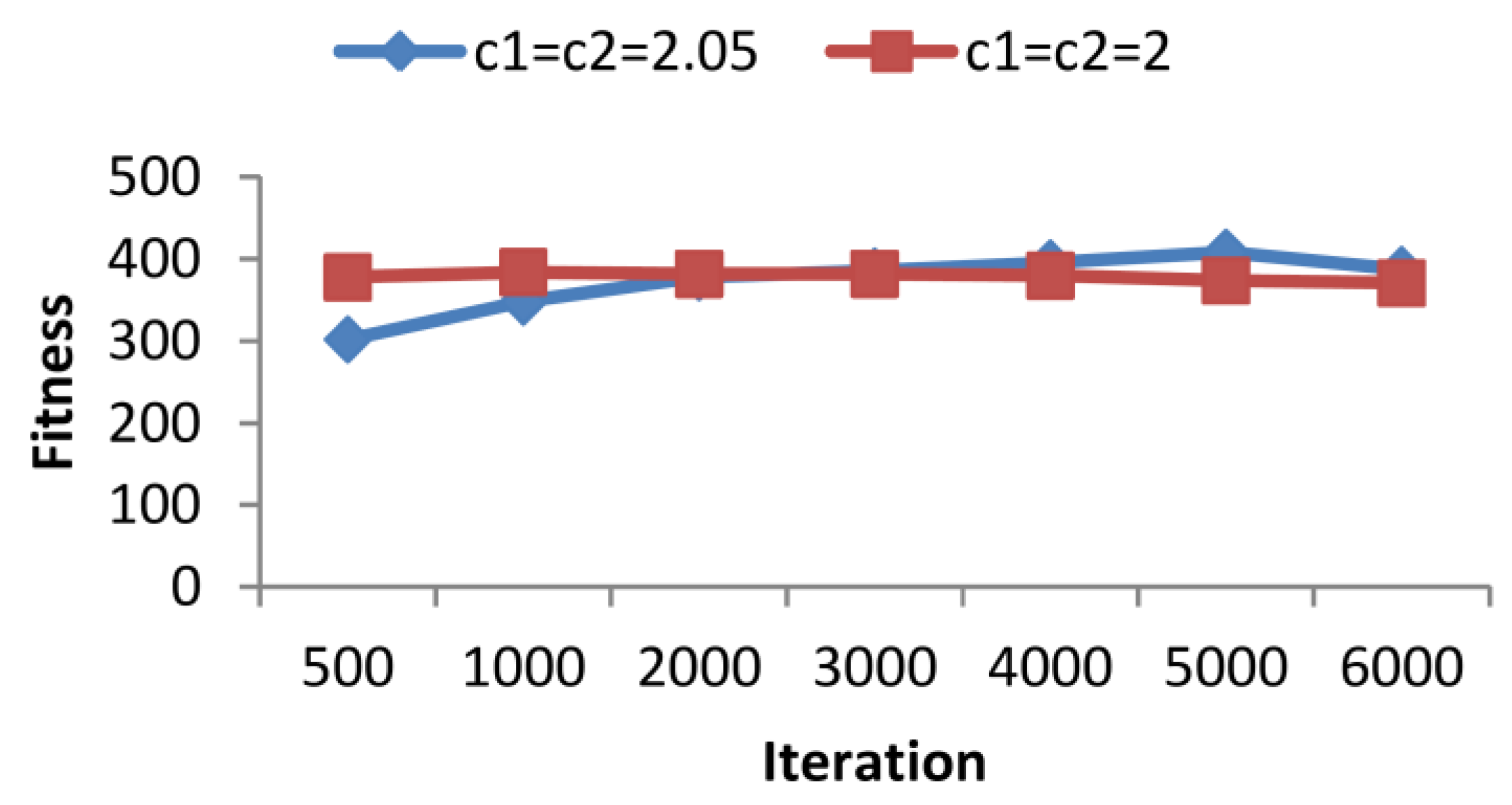
4.4. Performance Comparison between PSO and SPSO with/without Local Search

In this Section, PSO, SPSO, PSOLS (PSO with local search) and SPSOLS (SPSO with local search), associated with corresponding learning factors and V_max are applied to analyze the differences in search performance. The results are as shown in Table 2, Table 3, Table 4 and Table 5. They indicate that after local search is added, regardless of the differences of learning factors and other parameters, the outcomes are significantly better than those obtained by using PSO or SPSO alone. For PSOLS, when c₁ = 2, c₂ = 2, w = 0.8 and V_max = 4, the average satisfaction level (406.8) is higher than when c₁ = 2, c₂ = 2, w = 0.8 and V_max = 3. Additionally, for SPSOLS, c₁ = 2, c₂ = 2, χ = 0.72984 and V_max = 3 yields higher average satisfaction level (411.6) than applying c₁ = 2, c₂ = 2, χ = 0.72984 and V_max = 4. Moreover, the performance by utilizing SPSOLS is better than that of applying PSOLS. This confirms that SPSOLS can improve the quality of the solutions as proposed in this study.

Table 2. Performance comparison among PSO and PSOLS (PSO with local search) (c₁ = 2.05, c₂ = 2.05, w = 0.8).

Iteration	PSO V = −3~3	PSOLS V = −3~3	PSO V = −4~4	PSOLS V = −4~4
2000	384	398	368	402
3000	370	402	385	414
4000	380	402	400	396
5000	396	416	396	410
6000	375	404	380	402
Average	381	404.4	385.8	404.8

Table 2. Performance comparison among PSO and PSOLS (PSO with local search) (c₁ = 2.05, c₂ = 2.05, w = 0.8).

Iteration	PSO V = −3~3	PSOLS V = −3~3	PSO V = −4~4	PSOLS V = −4~4
2000	384	398	368	402
3000	370	402	385	414
4000	380	402	400	396
5000	396	416	396	410
6000	375	404	380	402
Average	381	404.4	385.8	404.8

Table 3. Performance comparison among PSO and PSOLS (c₁ = 2, c₂ = 2, w = 0.8).

Iteration	PSO V = −3~3	PSOLS V = −3~3	PSO V = −4~4	PSOLS V = −4~4
2000	362	386	386	400
3000	370	403	382	412
4000	396	404	390	412
5000	390	404	374	390
6000	368	402	361	420
Average	377.2	399.8	378.6	406.8

Table 3. Performance comparison among PSO and PSOLS (c₁ = 2, c₂ = 2, w = 0.8).

Iteration	PSO V = −3~3	PSOLS V = −3~3	PSO V = −4~4	PSOLS V = −4~4
2000	362	386	386	400
3000	370	403	382	412
4000	396	404	390	412
5000	390	404	374	390
6000	368	402	361	420
Average	377.2	399.8	378.6	406.8

Table 4. Performance comparison among SPSO and SPSOLS (SPSO with local search) (c₁ = 2.05, c₂ = 2.05, w = 0.72984).

Iteration	SPSO V = −3~3	SPSOLS V = −3~3	SPSO V = −4~4	SPSOLS V = −4~4
2000	381	398	376	378
3000	371	384	392	410
4000	396	418	394	410
5000	380	384	374	419
6000	392	415	392	418
Average	384	399.8	385.6	407

Table 4. Performance comparison among SPSO and SPSOLS (SPSO with local search) (c₁ = 2.05, c₂ = 2.05, w = 0.72984).

Iteration	SPSO V = −3~3	SPSOLS V = −3~3	SPSO V = −4~4	SPSOLS V = −4~4
2000	381	398	376	378
3000	371	384	392	410
4000	396	418	394	410
5000	380	384	374	419
6000	392	415	392	418
Average	384	399.8	385.6	407

Table 5. Performance comparison among SPSO and SPSOLS (c₁ = 2, c₂ = 2, χ = 0.72984).

Iteration	SPSO V = −3~3	SPSOLS V = −3~3	SPSO V = −4~4	SPSOLS V = −4~4
2000	400	412	375	401
3000	408	416	394	412
4000	402	416	410	424
5000	398	390	380	412
6000	406	424	398	408
Average	402.8	411.6	391.4	411.4

Table 5. Performance comparison among SPSO and SPSOLS (c₁ = 2, c₂ = 2, χ = 0.72984).

Iteration	SPSO V = −3~3	SPSOLS V = −3~3	SPSO V = −4~4	SPSOLS V = −4~4
2000	400	412	375	401
3000	408	416	394	412
4000	402	416	410	424
5000	398	390	380	412
6000	406	424	398	408
Average	402.8	411.6	391.4	411.4

Finally, course timetabling that achieves the optimal satisfaction for the 16 teachers, 10 classes and 10 classrooms is simulated using PSOLS and SPSOLS. The number of particles was set at 30, the number of evolutions 6000, c₁ = 2, c₂ = 2, and V = −4~4 (for PSOLS)/V = −3~3 (for SPSOLS) to run the experiment. The changes in the fitness are as shown in Figure 11 and Figure 12.

Figure 11. Fitness evolution of SPSOLS (c₁ = 2, c₂ = 2, χ = 0.72984, V = −3~3).

Figure 11. Fitness evolution of SPSOLS (c₁ = 2, c₂ = 2, χ = 0.72984, V = −3~3).

Figure 12. Fitness evolution PSOLS (c₁ = 2, c₂ = 2, w = 0.8, V = −4~4).

Figure 12. Fitness evolution PSOLS (c₁ = 2, c₂ = 2, w = 0.8, V = −4~4).

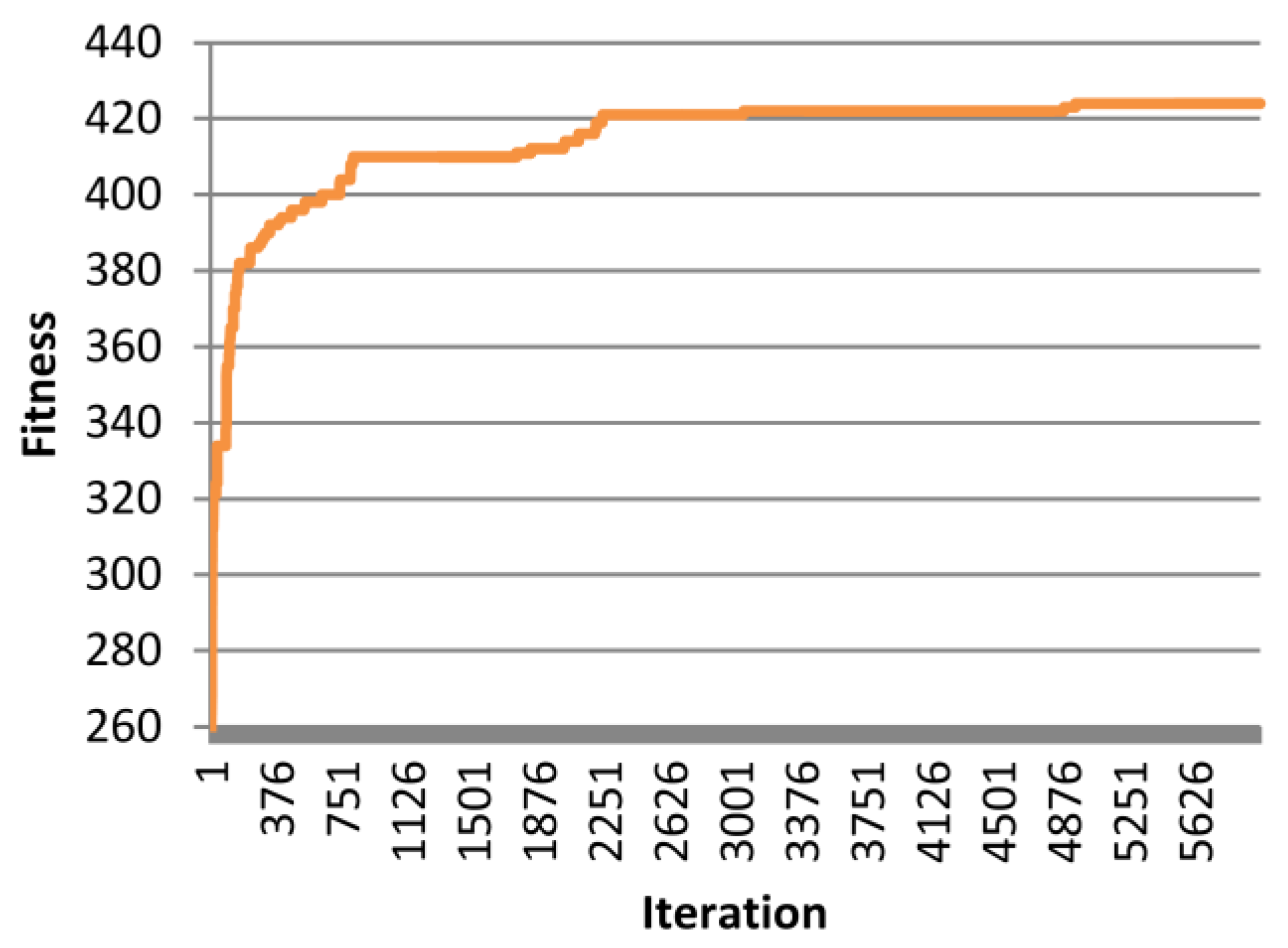
5. Conclusions

PSO is a promoting scheme for solving complex problems such as course timetabling. A new PSO named standard PSO (SPSO) has been applied and investigated. Thus, this work discusses the application of different types of PSO (PSO and SPSO) to find solutions to solve optimization problems in university course timetabling. Concurrently, to reduce the computational complexity, particle encoding is designated on the basis of timeslot rather than study hour. Moreover, an interchange heuristic is included to explore the neighboring solution space and enhance solution quality. The solutions found in accordance with the characteristics of the problem have been able to improve the satisfaction of the teachers and classes toward the schedule. Any conflicts between the teacher schedules, the class schedules, or the classroom schedules were also handled in this work. Additionally, premature convergence was prevented by adding an interchange local search mechanism. The following conclusions have been established:

(1)

With local search added in PSO and SPSO, the satisfaction (fitness value) of the teachers and classes is better than the fitness value obtained without adding local search. This confirms that the quality of solutions can be improved by applying the proposed scheme in this paper.

(2)

The results from application of different parameters show that use of SPSOLS obtains the best solution (the best fitness of 424 and maximum average fitness of 411.6). Restated, SPSOLS outperforms PSOLS.

The above conclusions indicate that application of the concept of combining SPSO with local search proposed in this study in finding solutions to optimization problems in course timetabling is sound and results in better solutions.