The Influence of Pore Size on the Indentation Behavior of Metallic Nanoporous Materials: A Molecular Dynamics Study
Abstract
:1. Introduction
2. Simulation Methods
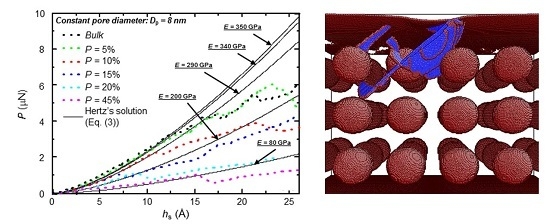
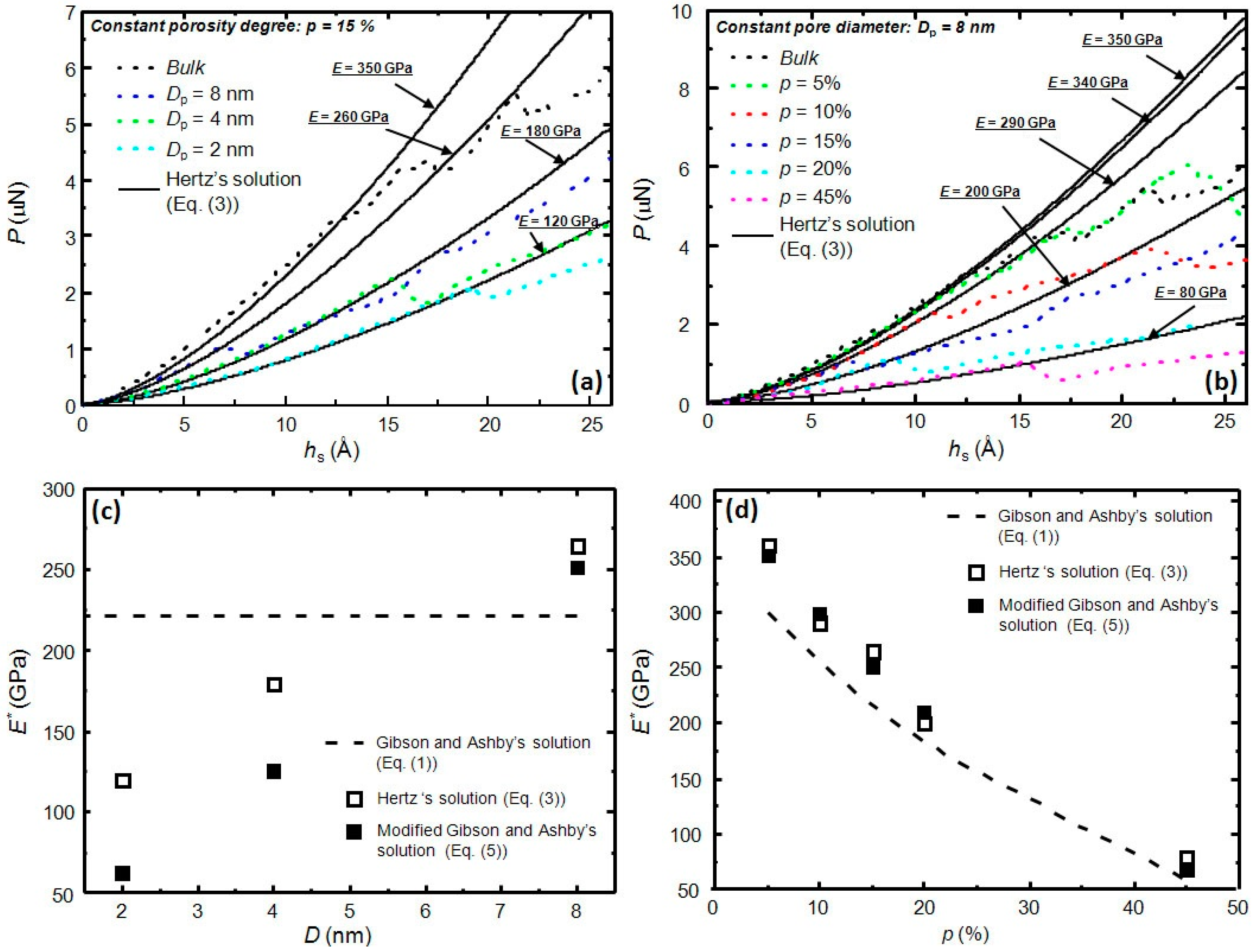
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sun, W.; Kherani, N.P.; Hirschman, K.D.; Gadeken, L.L.; Fauchet, P.M. A Three-Dimensional Porous Silicon p-n Diode for Betavoltaics and Photovoltaics. Adv. Mater. 2005, 17, 1230–1233. [Google Scholar] [CrossRef]
- Liu, J.; Cao, L.; Huang, W.; Li, Z. Fabrication and Temperature-Dependent Field-Emission Properties of Bundlelike VO2 Nanostructures. ACS Appl. Mater. Interfaces 2011, 3, 3552–3558. [Google Scholar] [CrossRef] [PubMed]
- Otsubo, K.; Haraguchi, T.; Sakata, O.; Fujiwara, A.; Kitagawa, H. Step-by-Step Fabrication of a Highly Oriented Crystalline Three-Dimensional Pillared-Layer-Type Metal-Organic Framework Thin Film Confirmed by Synchrotron X-ray Diffraction. J. Am. Chem. Soc. 2012, 134, 9605–9608. [Google Scholar] [CrossRef] [PubMed]
- Xiong, Q.; Tu, J.; Lu, Y.; Chen, J.; Yu, Y.; Wang, X.; Gu, C. Three-dimensional porous nano-Ni/Fe3O4 composite film: Enhanced electrochemical performance for lithium-ion batteries. J. Mater. Chem. 2012, 22, 18639–18645. [Google Scholar] [CrossRef]
- Huan, T.N.; Ganesh, T.; Kim, K.S.; Kim, S.; Han, S.-H.; Chung, H. A three-dimensional gold nanodendrite network porous structure and its application for an electrochemical sensing. Biosens. Bioelectron. 2011, 27, 183–186. [Google Scholar] [CrossRef] [PubMed]
- Pellicer, E.; Cabo, M.; Rossinyol, E.; Solsona, P.; Suriñach, S.; Baró, M.D.; Sort, J. Nanocasting of Mesoporous In-TM (TM = Co, Fe, Mn) Oxides: Towards 3D Diluted-Oxide Magnetic Semiconductor Architectures. Adv. Funct. Mater. 2013, 23, 900–911. [Google Scholar] [CrossRef]
- Blaker, J.J.; Maquet, V.; Jérôme, R.; Boccaccini, A.R.; Nazhat, S.N. Mechanical properties of highly porous PDLLA/Bioglass composite foams as scaffolds for bone tissue engineering. Acta Biomater. 2005, 1, 643–652. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Fu, Z.-Y.; Su, B.-L. Hierarchically Structured Porous Materials for Energy Conversion and Storage. Adv. Funct. Mater. 2012, 22, 4634–4667. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structures and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Williford, R.E.; Li, X.S.; Addleman, R.S.; Fryxell, G.E.; Baskaran, S.; Birnbaum, J.C.; Coyle, C.; Zemanian, T.S.; Wang, C.; Courtney, A.R. Mechanical stability of templated mesoporous silica thin films. Microporous Mesoporous Mater. 2005, 85, 260–266. [Google Scholar] [CrossRef]
- Murillo, J.S.; Bachlechner, M.E.; Campo, F.A.; Barbero, E.J. Structure and mechanical properties of silica aerogels and xerogels modeled by molecular dynamics simulation. J. Non Cryst. Solids 2010, 356, 1325–1331. [Google Scholar] [CrossRef]
- Cohen-Tanugi, D.; Grossman, J.C. Mechanical Strength of Nanoporous Graphene as a Desalination Membrane. Nano Lett. 2014, 14, 6171–6178. [Google Scholar] [CrossRef] [PubMed]
- Andrews, E.W.; Huang, J.S.; Gibson, L.J. Creep behavior of a closed-cell aluminum foam. Acta Mater. 1999, 47, 2927–2935. [Google Scholar] [CrossRef]
- Volkert, C.A.; Lilleodden, E.T.; Kramer, D.; Weissmüller, J. Approaching the theoretical strength in nanoporous Au. Appl. Phys. Lett. 2006, 89. [Google Scholar] [CrossRef]
- Hodge, A.M.; Biener, J.; Hayes, J.R.; Bythrow, P.M.; Volkert, C.A.; Hamza, A.V. Scaling equation for yield strength of nanoporous open-cell foams. Acta Mater. 2007, 55, 1343–1349. [Google Scholar] [CrossRef]
- Mameka, N.; Wang, K.; Markmann, J.; Lilleodden, E.T.; Weissmüller, J. Nanoporous Gold-Testing Macro-scale Samples to Probe Small-scale Mechanical Behavior. Mater. Res. Lett. 2016, 4, 27–36. [Google Scholar] [CrossRef]
- Dávila, L.P.; Erhart, P.; Bringa, E.M.; Meyers, M.A.; Lubarda, V.A.; Schneider, M.S.; Becker, R.; Kumar, M. Atomistic modeling of shock-induced void collapse in copper. Appl. Phys. Lett. 2005, 86. [Google Scholar] [CrossRef]
- Rudd, R.E. Void growth in bcc metals simulated with molecular dynamics using the Finnis-Sinclair potential. Philos. Mag. 2009, 89, 3133–3161. [Google Scholar] [CrossRef]
- Ruestes, C.J.; Bringa, E.M.; Stukowski, A.; Nieva, J.F.R.; Tang, Y.; Meyers, M.A. Plastic deformation of a porous bcc metal containing nanometer sized voids. Comput. Mater. Sci. 2014, 88, 92–102. [Google Scholar] [CrossRef]
- Yuan, F.; Wu, X. Scaling laws and deformation mechanisms of nanoporous copper under adiabatic uniaxial strain compression. AIP Adv. 2014, 4. [Google Scholar] [CrossRef]
- Plimpton, S.J. Fast parallel algorithms for short-range molecular-dynamics. J. Comp. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Mishin, Y.; Mehl, M.J.; Papaconstantopoulos, D.A.; Voter, A.F.; Kress, J.D. Structural stability and lattice defects in copper: Ab initio, tight-binding, and embedded-atom calculations. Phys. Rev. B 2001, 63. [Google Scholar] [CrossRef]
- Ziegenhain, G.; Urbassek, H.M.; Hartmaier, A. Influence of crystal anisotropy on elastic deformation and onset of plasticity in nanoindentation: A simulational study. J. Appl. Phys. 2010, 107. [Google Scholar] [CrossRef]
- Liu, X.; Yuan, F.; Wei, Y. Grain size effect on the hardness of nanocrystal measured by the nanosize indenter. Appl. Surf. Sci. 2013, 279, 159–166. [Google Scholar] [CrossRef]
- Salehinia, I.; Lawrence, S.K.; Bahr, D.F. The effect of crystal orientation on the stochastic behavior of dislocation nucleation and multiplication during nanoindentation. Acta Mater. 2013, 61, 1421–1431. [Google Scholar] [CrossRef]
- Hertz, H. Miscellaneous Papers; Macmillan and Co.: London, UK, 1896. [Google Scholar]
- Fang, T.-H.; Weng, C.-I.; Chang, J.-G. Molecular dynamics analysis of temperature effects on nanoindentation measurement. Mater. Sci. Eng. A 2003, 357, 7–12. [Google Scholar] [CrossRef]
- Poncharal, P.; Wang, Z.L.; Ugarte, D.; De Heer, W.A. Electrostatic deflections and electromechanical resonances of carbon nanotubes. Science 1999, 283, 1513–1516. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.-B.; Wang, L.-F.; Hoyce, H.J.; Gao, Q.; Liao, X.-Z.; Mai, Y.-W.; Tan, H.H.; Zou, J.; Ringer, S.P.; Gao, H.-J.; et al. Super deformability and Young’s modulus of GaAs nanowires. Adv. Mater. 2011, 23, 1356–1360. [Google Scholar] [CrossRef] [PubMed]
- Cuenot, S.; Frétigny, C.; Demoustier-Champagne, S.; Nysten, B. Surface tension effect on the mechanical properties of nanomaterials measured by atomic force microscopy. Phys. Rev. B 2004, 69. [Google Scholar] [CrossRef]
- Li, J. AtomEye: An efficient atomistic configuration viewer. Model. Simul. Mater. Sci. Eng. 2003, 11, 173–177. [Google Scholar] [CrossRef]

© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esqué-de los Ojos, D.; Pellicer, E.; Sort, J. The Influence of Pore Size on the Indentation Behavior of Metallic Nanoporous Materials: A Molecular Dynamics Study. Materials 2016, 9, 355. https://doi.org/10.3390/ma9050355
Esqué-de los Ojos D, Pellicer E, Sort J. The Influence of Pore Size on the Indentation Behavior of Metallic Nanoporous Materials: A Molecular Dynamics Study. Materials. 2016; 9(5):355. https://doi.org/10.3390/ma9050355
Chicago/Turabian StyleEsqué-de los Ojos, Daniel, Eva Pellicer, and Jordi Sort. 2016. "The Influence of Pore Size on the Indentation Behavior of Metallic Nanoporous Materials: A Molecular Dynamics Study" Materials 9, no. 5: 355. https://doi.org/10.3390/ma9050355
APA StyleEsqué-de los Ojos, D., Pellicer, E., & Sort, J. (2016). The Influence of Pore Size on the Indentation Behavior of Metallic Nanoporous Materials: A Molecular Dynamics Study. Materials, 9(5), 355. https://doi.org/10.3390/ma9050355