First Exploratory Study on the Ageing of Rammed Earth Material
Abstract
:1. Introduction
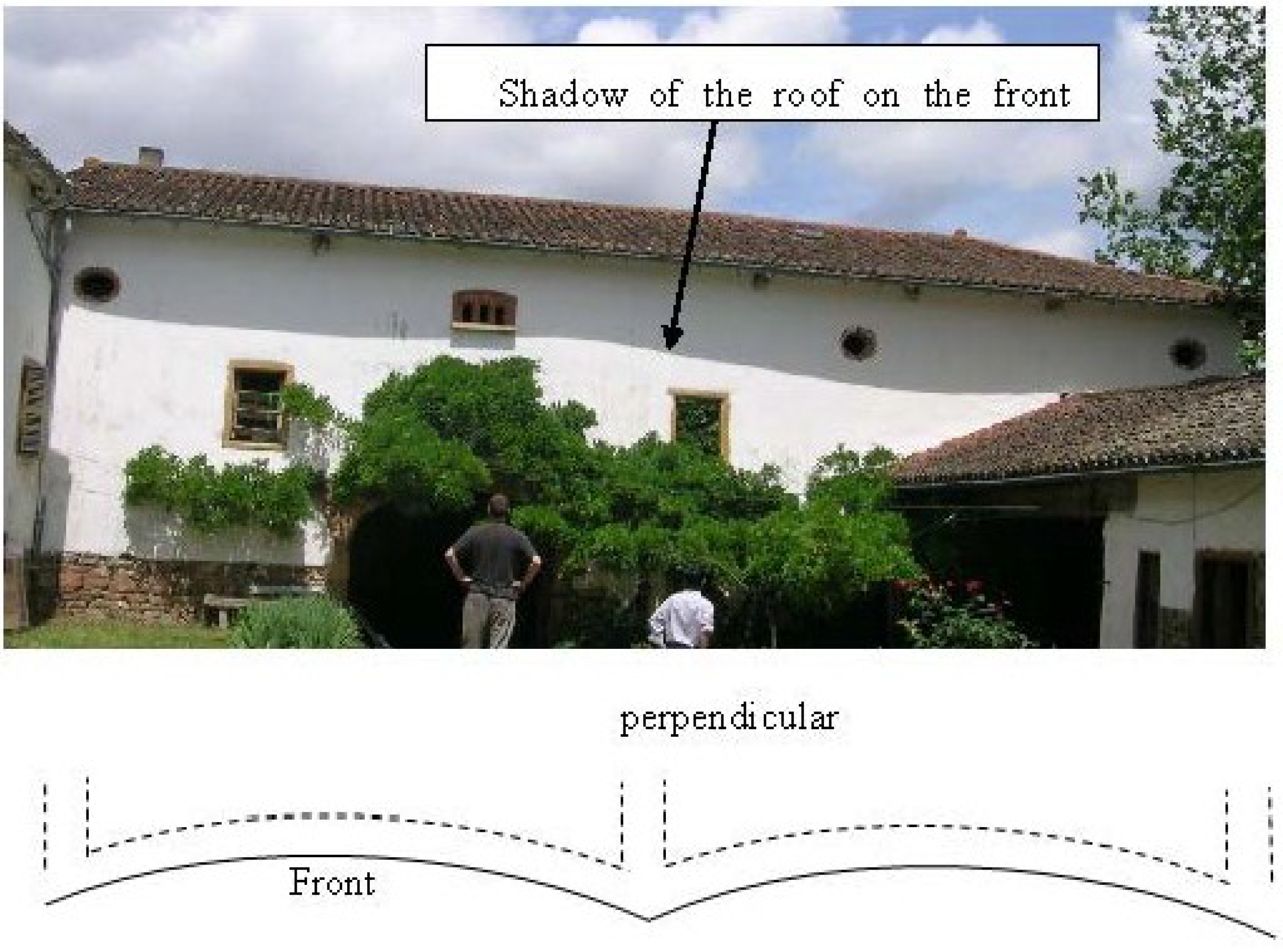
2. Characterizing 22 Years Old RE Walls
2.1. Presentation of Studied Walls

2.2. In-Situ Dynamic Measurement
2.2.1. Measurement Device
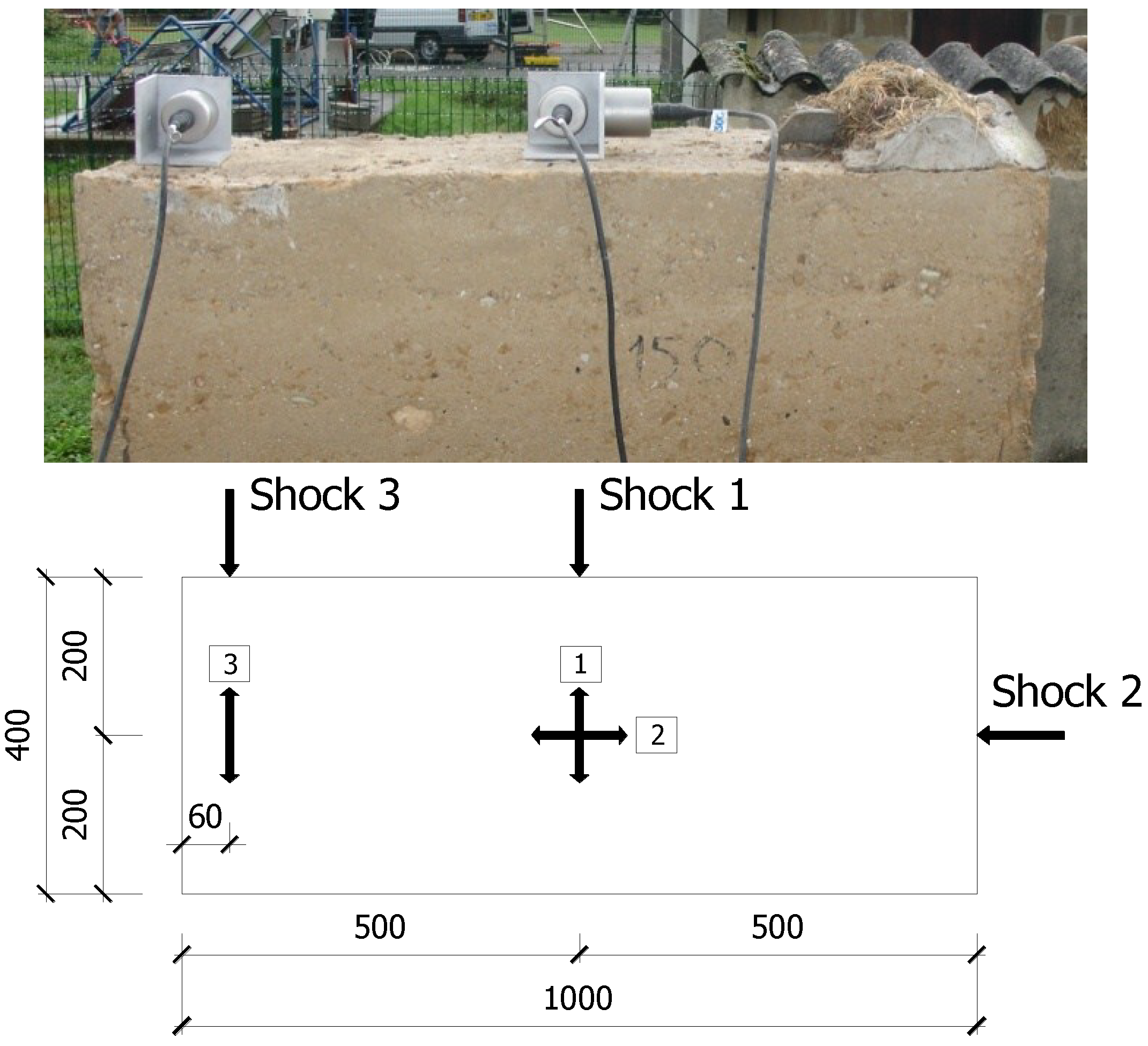
2.2.2. Frequencies Measured in-Situ

| Walls | Moduli identified (MPa) | Measurements | Model | ||
|---|---|---|---|---|---|
| Wall A | 104 | 12.25 ± 0.05 | 16.25 ± 0.12 | 12.25 | 16.48 |
| Wall B | 98 | 11.87 ± 0.08 | 16.20 ± 0.09 | 11.87 | 15.97 |
| Wall C | 90 | 11.38 ± 0.10 | 15.38 ± 0.22 | 11.38 | 15.31 |
2.2.3. Finite Element Modelling (FEM) of the Walls
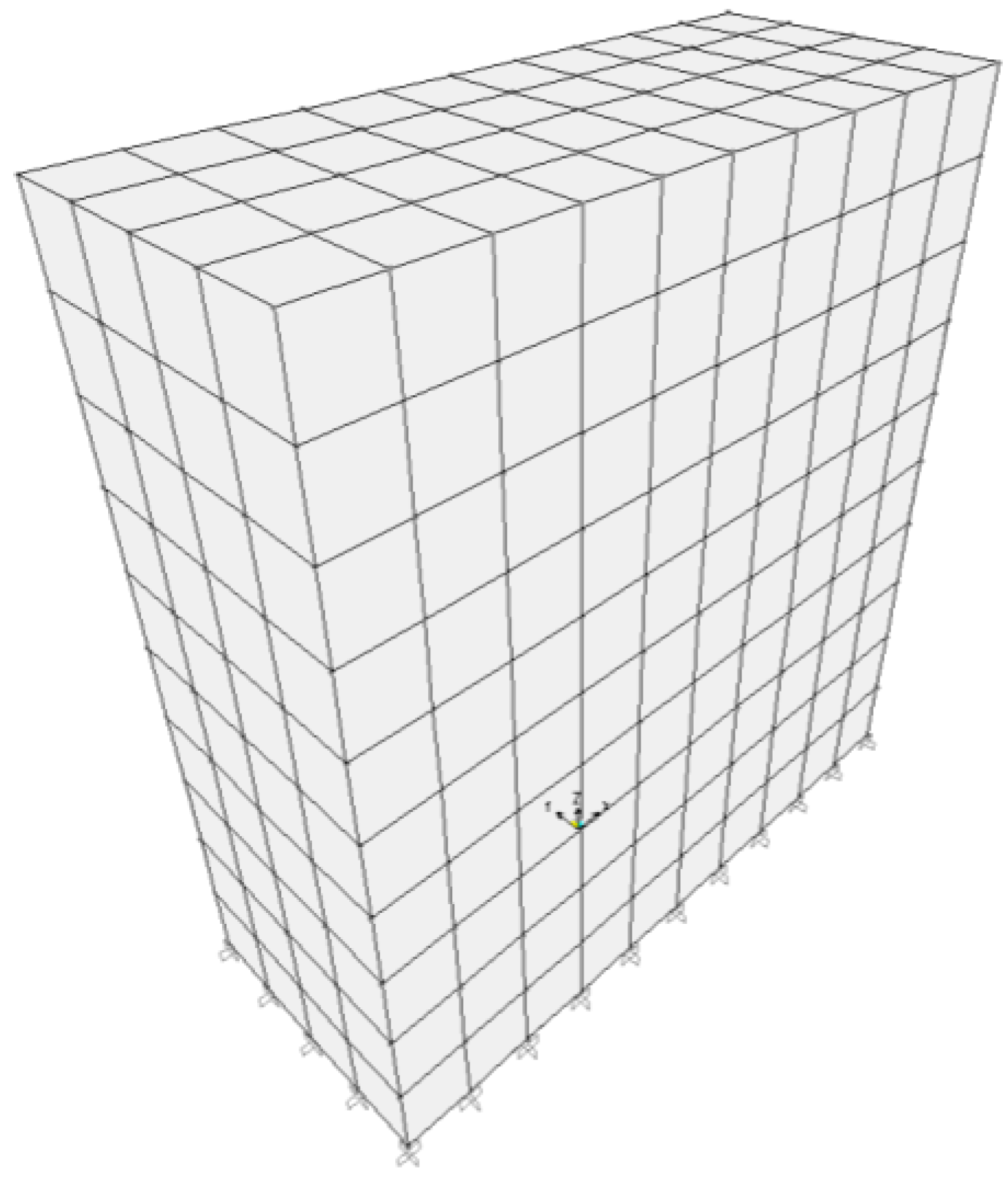
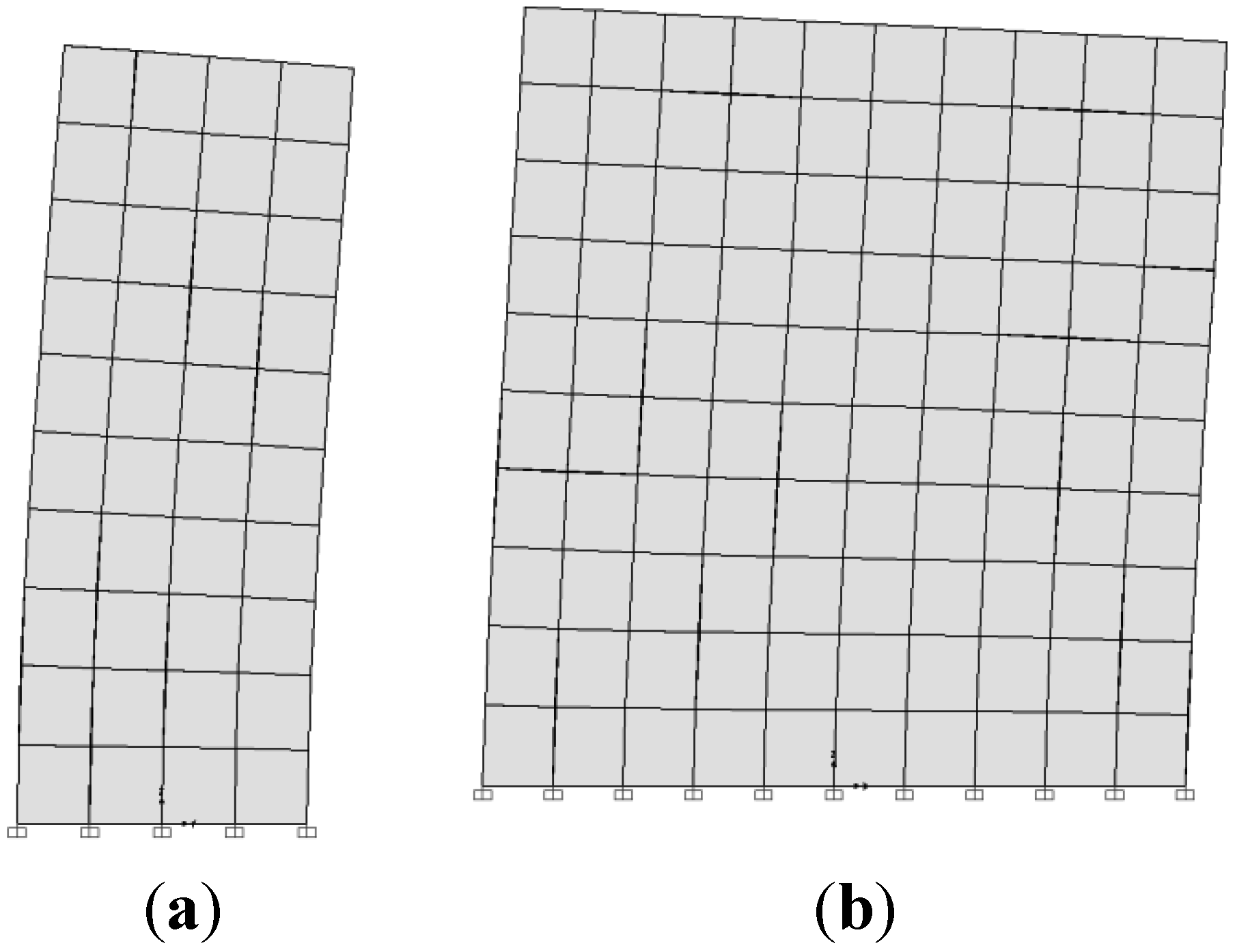
3. Laboratory Static Tests
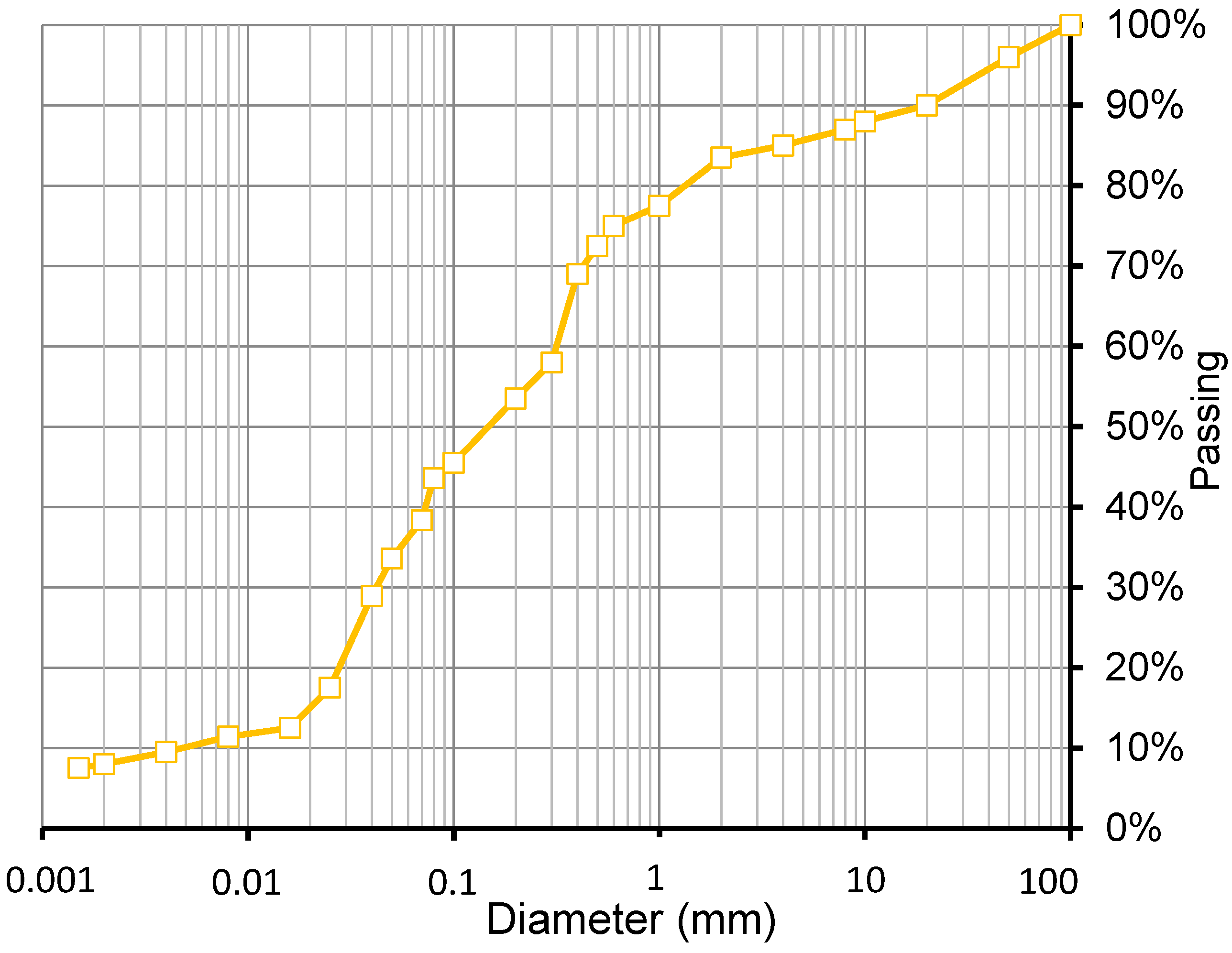
3.1. Cutting out the Specimens

3.2. Density Measurement
3.3. Unconfined Compression Test
- ⇨
- Eh = K∙E1/3, where K is the correction factor to correct modulus measured on specimen height.
- ⇨
- E1/3new/E1/3old = Ehnew/Ehold
| Test direction | Density | Moisture content | Ultimate stress (MPa) | Ultimate strain | E (MPa) |
|---|---|---|---|---|---|
| Perpendicular to layers | 1.82 | 1.4% | 0.89 ± 0.10 | 0.013 ± 0.001 | 98 ± 6 |
| Parallel to layers | 1.82 | 1.3% | 0.82 ± 0.08 | 0.012 ± 0.001 | 93 ± 5 |
4. Characterizing the “New” Rammed Earth
4.1. Manufacture of Specimens and Compression Tests
- -
- Two specimens (0.4 × 0.4 × 0.7) m3
- -
- Two specimens (0.4 × 0.4 × 0.2) m3


4.2. Results
| Test direction | Density | Moisture content | Ultimate stress (MPa) | Ultimate strain | E (MPa) |
|---|---|---|---|---|---|
| Perpendicular to layers | 1.91 | 1.8% | 1.35 ± 0.1 | 0.008 ± 0.001 | 263 ± 12 |
| Parallel to layers | 1.91 | 1.7% | 1.18 ± 0.1 | 0.007 ± 0.001 | 287 ± 8 |
5. Discussion and the Creep Coefficient
- -
- damage of the sample during the “old” specimens’ taking: however, the in-situ dynamic tests give the similar results of modulus. So, it is not this possibility.
- -
- Problem of representativeness of the “new” specimens: there are also possible differences in the compaction energy, the manufacturing water content between the “old” walls and the “new” specimens. Although the walls and the new specimens were all manufactured by the rammed earth professionals, a difference is not evitable. However, in our opinion, this difference cannot be the only factor which can cause a significant difference in the dry density.
- -
- Propagation of micro-cracks under weathering loadings: there are changes at the micro-structure of the material: micro-pores increase which lead to a decrease of dry density.
6. Conclusions and Outlook
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bui, Q.B.; Morel, J.C.; Hans, S.; Meunier, N. Compression behaviour of nonindustrial materials in civil engineering by three scale experiments: The case of rammed earth. Mater. Struct. 2009, 42, 1101–1116. [Google Scholar] [CrossRef]
- Walker, P.; Keable, R.; Martin, J.; Maniatidis, V. Rammed Earth-Design and Construction Guidelines; BRE Bookshop: Watford, UK, 2005. [Google Scholar]
- Habert, G.; Castillo, E.; Vincens, E.; Morel, J.C. Power: A new paradigm for energy use in sustainable construction. Ecol. Indic. 2012, 23, 109–115. [Google Scholar] [CrossRef]
- Allinson, D.; Hall, M. Hygrothermal analysis of a stabilised rammed earth test building in the UK. Energy Build. 2010, 42, 845–852. [Google Scholar] [CrossRef]
- Bui, Q.B.; Morel, J.C.; Reddy, B.V.V.; Ghayad, W. Durability of rammed earth walls exposed for 20 years to natural weathering. Build. Environ. 2009, 44, 912–919. [Google Scholar] [CrossRef]
- Fodde, E. Traditional earthen building techniques in Central Asia. Int. J. Archit. Herit. 2009, 3, 145–168. [Google Scholar] [CrossRef] [Green Version]
- Bui, Q.B.; Morel, J.C.; Hans, S.; Walker, P. Effect of moisture content on the mechanical characteristics of rammed earth. Constr. Build. Mater. 2014, 54, 163–169. [Google Scholar] [CrossRef]
- Hall, M.; Djerbib, Y. Moisture ingress in rammed earth: Part 1-the effect of soil particle—Size distribution on the rate of capillary suction. Constr. Build. Mater. 2004, 18, 269–280. [Google Scholar] [CrossRef]
- Bui, Q.B.; Morel, J.C. Assessing the anisotropy of rammed earth. Constr. Build. Mater. 2009, 23, 3005–3011. [Google Scholar] [CrossRef]
- Bui, T.T.; Bui, Q.B.; Limam, A.; Morel, J.C. Modelling rammed earth wall by discrete element method. In Proceeding of the ICREC 2015, Perth, Australia, 11–13 February 2015.
- Maniatidis, V.; Walker, P. Structural capacity of rammed earth in compression. J. Mater. Civ. Eng. 2008, 20, 230–238. [Google Scholar] [CrossRef]
- Walker, P.; Dobson, S. Pullout tests on deformed and plain rebars in cement stabilized rammed earth. J. Mater. Civ. Eng. 2001, 13, 291–297. [Google Scholar] [CrossRef]
- Bui, T.T.; Bui, Q.B.; Limam, A.; Maximilien, S. Failure of rammed earth walls: From observations to quantifications. Constr. Build. Mater. 2014, 51, 295–302. [Google Scholar] [CrossRef]
- Cheah, J.S.J.; Walker, P.; Heath, A.; Morgan, T.K.K.B. Evaluating shear test methods for stabilised rammed earth. Constr. Mater. 2012, 165, 325–334. [Google Scholar] [CrossRef] [Green Version]
- Silva, R.A.; Oliveira, D.V.; Miranda, T.; Cristelo, N.; Escobar, M.C.; Soares, E. Rammed earth construction with granitic residual soils: The case study of northern Portugal. Constr. Build. Mater. 2013, 47, 181–191. [Google Scholar] [CrossRef] [Green Version]
- Bui, Q.B.; Morel, J.C.; Hans, S.; Do, A.-P. First exploratory study on dynamic characteristics of rammed earth buildings. Eng. Struct. 2011, 33, 3690–3695. [Google Scholar] [CrossRef]
- Gomes, M.I.; Lopes, M.; Brito, J. Seismic resistance of earth construction in Portugal. Eng. Struct. 2011, 33, 932–941. [Google Scholar] [CrossRef]
- Ciancio, D.; Augarde, C. Capacity of unreinforced rammed earth walls subject to lateral wind force: Elastic analysis versus ultimate strength analysis. Mater. Struct. 2013, 46, 1569–1585. [Google Scholar] [CrossRef] [Green Version]
- Standards New Zealand. NZS 4297:1998, Engineering Design of Earth Buildings; Standards New Zealand: Wellington, New Zealand, 1998. [Google Scholar]
- Taylor, P.; Fuller, R.J.; Luther, M.B. Energy use and thermal comfort in a rammed earth office building. Energy Build. 2008, 40, 793–800. [Google Scholar] [CrossRef]
- Taylor, P.; Luther, M.B. Evaluating rammed earth walls: A case study. Sol. Energy 2004, 76, 79–84. [Google Scholar] [CrossRef]
- Chabriac, P.A.; Fabbri, A.; Morel, J.C.; Laurent, J.P.; Blanc-Gonnet, J. A procedure to measure the in-situ hygrothermal behavior of earth walls. Materials 2014, 7, 3002–3020. [Google Scholar] [CrossRef]
- Paul, W.L.; Taylor, P.A. A comparison of occupant comfort and satisfaction between a green building and a conventional building. Build. Environ. 2008, 43, 1858–1870. [Google Scholar] [CrossRef]
- EN 1992-1-1, Eurocode 2. Design of Concrete Structures—Part 1–1: General Rules and Rules for Buildings, 2005.
- Aubert, J.E.; Gasc-Barbier, M. Hardening of clayey soil blocks during freezing and thawing cycles. Appl. Clay Sci. 2012, 65–66, 1–5. [Google Scholar] [CrossRef]
- Grossein, O. Modélisation et Simulation Numérique des Transferts Couplés d’eau, de Chaleur et de Solutés Dans le Patrimoine Architectural en Terre, en Relation Avec sa Dégradation. Ph.D. Thesis, Université Joseph Fourier, Grenoble, France, 2009. [Google Scholar]
- Morel, J.C.; Pkla, A.; Walker, P. Compressive strength testing of compressed earth blocks. Constr Build. Mater. 2007, 21, 303–309. [Google Scholar] [CrossRef]
- Lombillo, I.; Villegas, L.; Fodde, E.; Thomas, C. In situ mechanical investigation of rammed earth: Calibration of minor destructive testing. Constr. Build. Mater. 2014, 51, 451–460. [Google Scholar] [CrossRef]
- Rossi, P.; Charron, J.P.; Bastien-Masse, M.; Tailhan, J.L.; le Maou, F.; Ramanich, S. Tensile basic creep versus compressive basic creep at early ages: Comparison between normal strength concrete and a very high strength fibre reinforced concrete. Mater. Struct. 2014, 47, 1773–1785. [Google Scholar]
- Wang, H.; Li, Q. Prediction of elastic modulus and Poisson’s ratio for unsaturated concrete. Int. J. Solids Struct. 2007, 44, 1370–1379. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bui, Q.-B.; Morel, J.-C. First Exploratory Study on the Ageing of Rammed Earth Material. Materials 2015, 8, 1-15. https://doi.org/10.3390/ma8010001
Bui Q-B, Morel J-C. First Exploratory Study on the Ageing of Rammed Earth Material. Materials. 2015; 8(1):1-15. https://doi.org/10.3390/ma8010001
Chicago/Turabian StyleBui, Quoc-Bao, and Jean-Claude Morel. 2015. "First Exploratory Study on the Ageing of Rammed Earth Material" Materials 8, no. 1: 1-15. https://doi.org/10.3390/ma8010001
APA StyleBui, Q.-B., & Morel, J.-C. (2015). First Exploratory Study on the Ageing of Rammed Earth Material. Materials, 8(1), 1-15. https://doi.org/10.3390/ma8010001






