Dynamic Initiation and Propagation of Multiple Cracks in Brittle Materials
Abstract
:1. Introduction
2. Mechanical Modeling
2.1. Fracture Initiation and Multiple Cracking


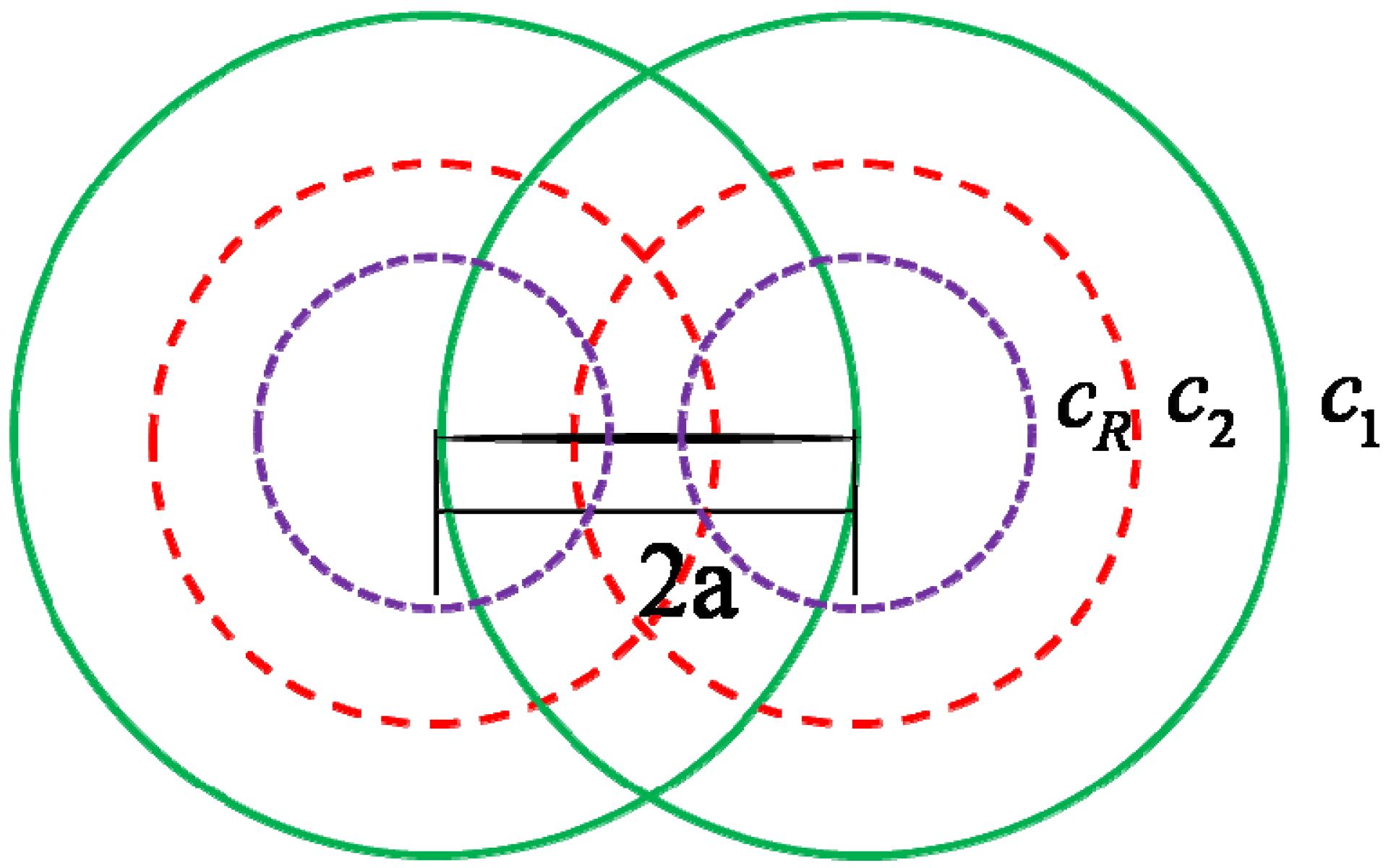


2.2. Multiple Dynamic Fracture model
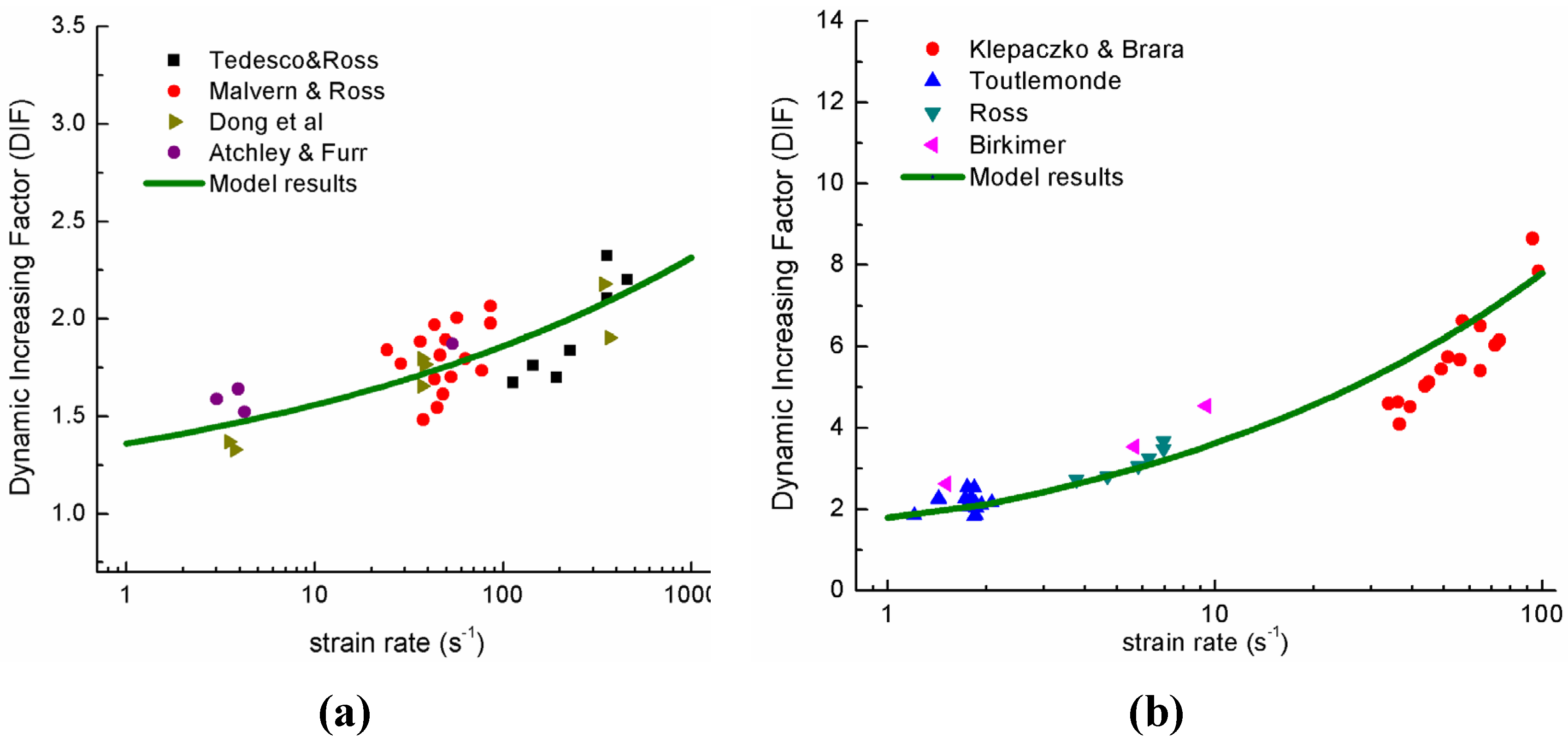
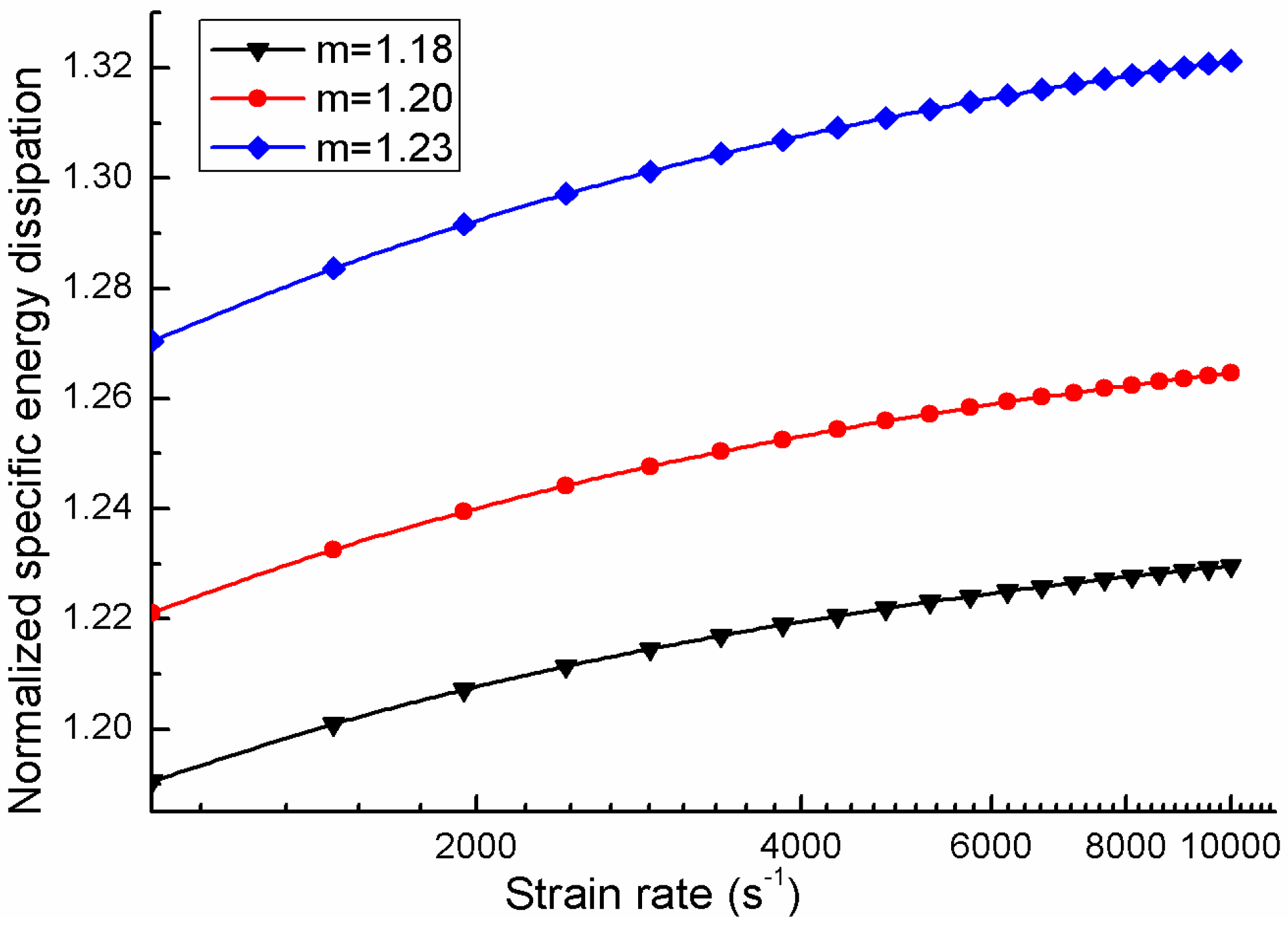
3. Numerical Implementation and Results
| E(GPa) | υ | ρ (Kg/m3) | KIC (MPa ) | c2 (km/s) |
|---|---|---|---|---|
| 30.0 | 0.2 | 2500 | 0.63 | 1.74 |
| λt0 | mt | λc0 | mc | |
| 0.911 | 4500 | 22.0 | 3000 | 4.3 |
4. Conclusions
Acknowledgments
Conflict of Interest
References
- Goldman, T.; Livne, A.; Fineberg, J. Acquisition of inertia by a moving crack. Phys. Rev. Lett. 2010, 104, 114301:1–114301:4. [Google Scholar] [CrossRef]
- Gao, H.J. A theory of local limiting speed in dynamic fracture. Mech. Phys. Solids 1996, 44, 1453–1474. [Google Scholar] [CrossRef]
- Cramer, T.; Wanner, A.; Gumbsch, P. Energy dissipation and path instabilities in dynamic fracture of silicon single crystals. Phys. Rev. Lett. 2000, 85, 788–791. [Google Scholar] [CrossRef] [PubMed]
- Bouchbinder, E. Dynamic crack tip equation of motion: high-speed oscillatory instability. Phys. Rev. Lett. 2009, 103, 164301:1–164301:4. [Google Scholar] [CrossRef]
- Daphalapurkar, N.P.; Ramesh, K.T.; Graham-Brady, L.; Molinari, J.F. Predicting variability in the dynamic failure strength of brittle materials considering pre-existing flaws. J. Mech. Phys. Solids 2011, 59, 297–319. [Google Scholar] [CrossRef]
- Grady, D.E.; Kipp, M.E. Continuum modelling of explosive fracture in oil shale. Int. J. Rock Mech. Min. Sci. 1980, 17, 147–157. [Google Scholar] [CrossRef]
- Grady, D.E. Local inertial effects in dynamic fragmentation. J. Appl. Phys. 1982, 53, 322–325. [Google Scholar] [CrossRef]
- Meyers, M.A. Dynamic Behavior of Materials; John Wiley & Sons: New York, NY, USA, 1994; pp. 488–535. [Google Scholar]
- Ravi-Chandar, K.; Knauss, W.G. An experimental investigation into dynamic fracture: II. Microstructural aspects. Int. J. Fract. 1984, 5, 247–262. [Google Scholar] [CrossRef]
- Escobedo, J.P.; Brown, E.N.; Trujillo, C.P.; Cerreta, E.K.; Gray, G.T.J., III. The effect of shock-wave profile on dynamic brittle failure. Appl. Phys. 2013, 60, 113–124. [Google Scholar]
- Buehler, M.J.; Tang, H.; van Duin, A.C.T.; Goddard, W.A., III. Threshold crack speed controls dynamical fracture of silicon single crystals. Phys. Rev. Lett. 2007, 99, 165502:1–165502:4. [Google Scholar] [CrossRef]
- Livne, A.; Bouchbinder, E.; Fineberg, J. Breakdown of linear elastic fracture mechanics near the tip of a rapid crack. Phys. Rev. Lett. 2008, 101, 264301:1–264301:4. [Google Scholar] [CrossRef]
- Xia, K.W.; Chalivendra, V.B.; Rosakis, A.J. Observing ideal “self-similar” crack growth in experiments. Eng. Fract. Mech. 2006, 73, 2748–2755. [Google Scholar] [CrossRef]
- Zhou, S.J.; Lomdahl, P.S.; Thomson, R.; Holian, B.L. Dynamic crack processes via molecular dynamics. Phys. Rev. Lett. 1996, 76, 2318–2321. [Google Scholar] [CrossRef] [PubMed]
- Zhou, F.; Molinari, J.F.; Ramesh, K.T. A cohesive model based fragmentation analysis: effects of strain rate and initial defects distribution. Int. J. Solids Struct. 2005, 42, 5181–5207. [Google Scholar] [CrossRef]
- Zhou, F.; Molinari, J.F.; Ramesh, K.T. Characteristic fragment size distributions in dynamic fragmentation. Appl. Phys. Lett. 2006, 88, 261918:1–261918:3. [Google Scholar]
- Mott, N.F. Fragmentation of shell cases. Proc. R. Soc. 1947, 189, 300–308. [Google Scholar] [CrossRef]
- Kostrov, B.V.J. Unsteady propagation of longitudinal shear cracks. Appl. Math. Mech. 1966, 30, 1241–1248. [Google Scholar] [CrossRef]
- Freund, L.B.J. Crack propagation in an elastic solid subjected to general loading—III. Stress wave loading. Mech. Phys. Solids. 1973, 21, 47–61. [Google Scholar] [CrossRef]
- Freund, L.B. Dynamic Fracture Mechanics; Cambridge University Press: Cambridge, UK, 1998; pp. 104–151. [Google Scholar]
- Bažant, Z.P.; Planas, J. Fracture and Size Effect. In Concrete and Other Quasibrittle Materials; CRC Press: Boston, MA, USA, 1998; pp. 383–435. [Google Scholar]
- Denoual, C.; Hild, F. Dynamic fragmentation of brittle solids: a multi-scale model. Eur. J. Mech. A. Solids 2002, 21, 105–120. [Google Scholar] [CrossRef]
- Sih, G.C.; Loeber, J.F. Wave propagation in an elastic solid with a line of discontinuity or finite crack. Quart. Appl. Math. 1969, 27, 193–213. [Google Scholar]
- Chen, E.P.; Sih, G.C. Elastodynamic Crack Problems; Sih, G.C., Ed.; Noordhoff: Leyden, The Netherlands, 1977; pp. 1–58. [Google Scholar]
- Kipp, M.E.; Grady, D.E.; Chen, E.P. Strain-rate dependent fracture initiation. Int. J. Fract. 1980, 16, 471–478. [Google Scholar] [CrossRef]
- Gilvarry, J.J.; Bergstrom, B.H.J. Fracture of brittle solids. I. Distribution function for fragment size in single fracture (theoretical). Appl. Phys. 1961, 32, 400–410. [Google Scholar] [CrossRef]
- Hayakawa, Y. Impact fragmentation of an ideal brittle crystal. Phys. Rev. B. 1996, 53, 14828–14833. [Google Scholar] [CrossRef]
- Carpinteri, A.; Spagnoli, A.; Vantadori, S. A multifractal analysis of fatigue crack growth and its application to concrete. Eng. Fract. Mech. 2010, 77, 974–984. [Google Scholar] [CrossRef]
- Pla, O.; Guinea, F.; Louis, E.; Li, G.; Sander, L.M.; Yan, H.; Meakin, P. Crossover between different growth regimes in crack formation. Phys. Rev. A. 1990, 42, 3670–3673. [Google Scholar] [CrossRef] [PubMed]
- Herrman, H.J. Patterns and scaling in fracture. Phys. Scr. 1991, 38, 13–21. [Google Scholar] [CrossRef]
- Turcotte, D.L. Fractals and fragmentation. J. Geophys. Res. B. 1986, 91, 1921–1926. [Google Scholar] [CrossRef]
- Grady, D.E. Fragment size distributions from the dynamic fragmentation of brittle solids. Int. J. Impact Eng. 2008, 35, 1557–1562. [Google Scholar] [CrossRef]
- Xie, H.P. Introduction to Fractal–Rock Mechanics; [in Chinese]; Science Press: Beijing, China, 1996; pp. 129–167. [Google Scholar]
- Oddershede, L.; Dimon, P.; Bohr, J. Self-organized criticality in fragmenting. Phys. Rev. Lett. 1993, 71, 3107–3110. [Google Scholar] [CrossRef] [PubMed]
- Hogan, J.D.; Spray, J.G.; Rogers, R.J.; Boonsue, S.; Vincent, G.; Schneider, M. Micro-scale energy dissipation mechanisms during dynamic fracture in natural polyphase ceramic blocks. Int. J. Impact Eng. 2011, 38, 931–939. [Google Scholar] [CrossRef]
- Scheibert, J.; Guerra, C.; Celarie, F.; Dalmas, D.; Bonamy, D.J. Brittle-quasibrittle transition in dynamic fracture: An energetic signature. Phys. Rev. Lett. 2010, 104, 045501:1–045501:4. [Google Scholar] [CrossRef]
- Ren, X.D.; Li, J. Dynamic fracture in irregularly structured systems. Phys. Rev. E. 2012, 85, 055102:1–055102:3. [Google Scholar]
- Huang, Q.P. Dynamic Damage Mechanism and Stochastic Dynamic Damage Constitutive Model for Concrete. Ph.D. Thesis, Tongji University, Shanghai, China, 2011. [Google Scholar]
- Klepaczko, J.R.; Brara, A. An experimental method for dynamic tensile testing of concrete by spalling. Int. J. Impact Eng. 2001, 25, 387–409. [Google Scholar] [CrossRef]
- Toutlemonde, F. Shock Strength of Concrete Structures: From Material Behaviour to Structure Design. Ph.D. Thesis, E.N.P.C(Ecole Nationale des Ponts et Chaussees), Paris, France, 1994. [Google Scholar]
- Ross, C.A.; Tedesco, J.W.; Kuenen, S.T. Effects of strain-rate on concrete strength. ACI Mater. J. 1995, 92, 37–47. [Google Scholar]
- Birkimer, D.L. Critical Normal Fracture Strain of Cement Portland Concrete. Ph.D. Thesis, University of Cincinnati, Cincinnati, OH, USA, 1968. [Google Scholar]
- Barpi, F. Impact behaviour of concrete: A computational approach. Eng. Fract. Mech. 2004, 71, 2197–2213. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Li, J.; Huang, Q.; Ren, X. Dynamic Initiation and Propagation of Multiple Cracks in Brittle Materials. Materials 2013, 6, 3241-3253. https://doi.org/10.3390/ma6083241
Li J, Huang Q, Ren X. Dynamic Initiation and Propagation of Multiple Cracks in Brittle Materials. Materials. 2013; 6(8):3241-3253. https://doi.org/10.3390/ma6083241
Chicago/Turabian StyleLi, Jie, Qiaoping Huang, and Xiaodan Ren. 2013. "Dynamic Initiation and Propagation of Multiple Cracks in Brittle Materials" Materials 6, no. 8: 3241-3253. https://doi.org/10.3390/ma6083241