Geometrical Description in Binary Composites and Spectral Density Representation
Abstract
:1. Introduction
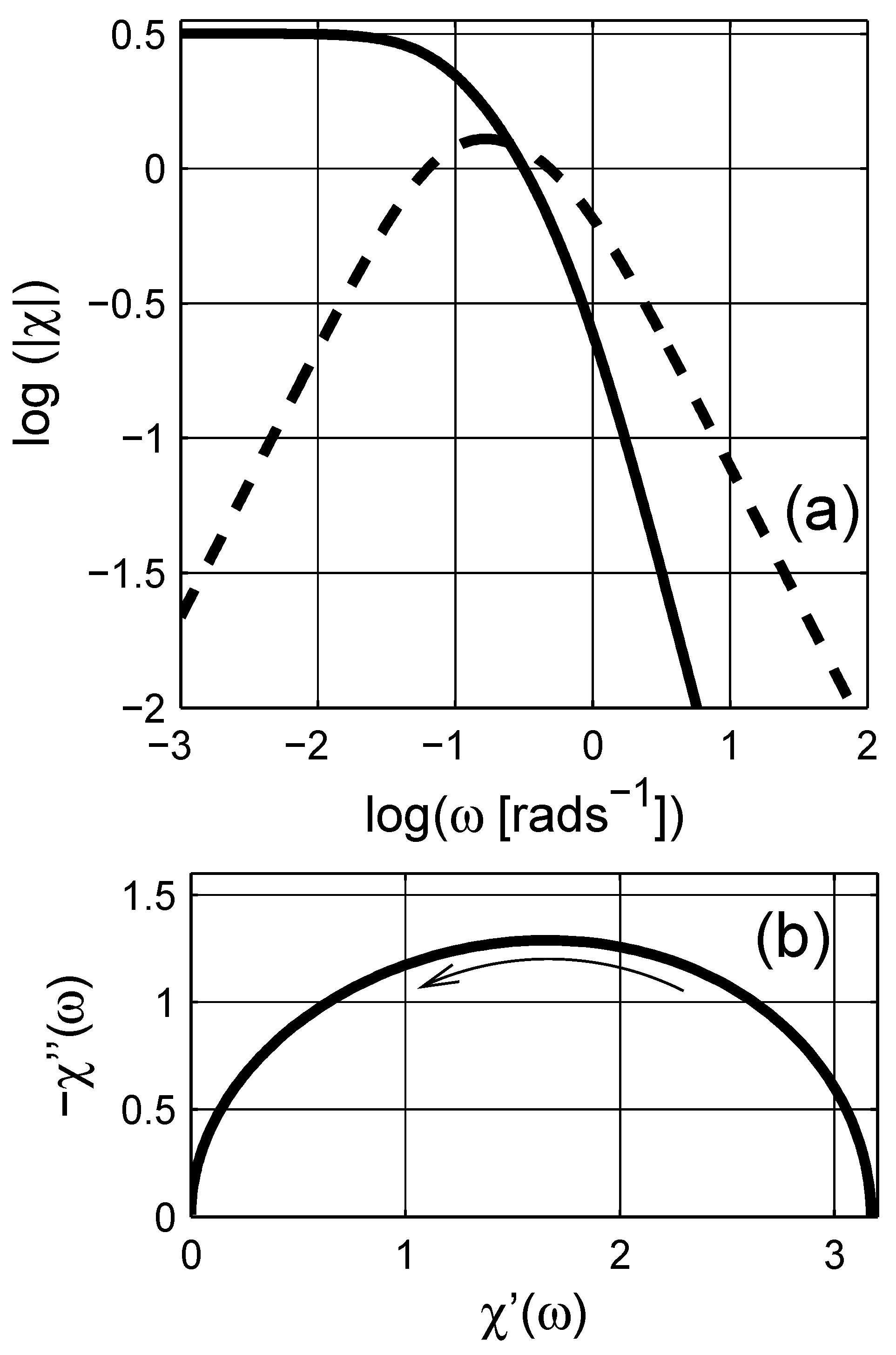
2. Spectral Density Representation
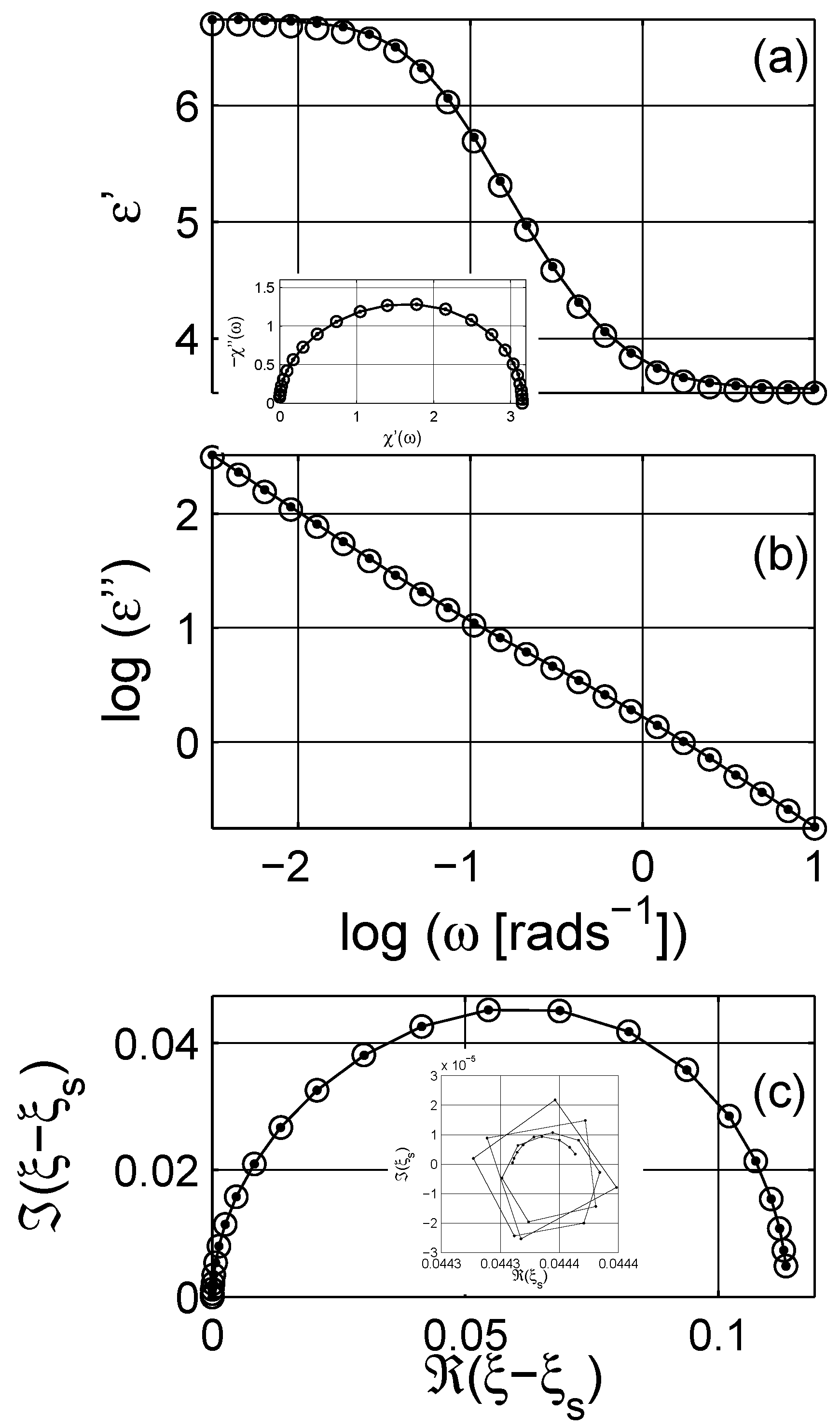
3. Representation of Dielectric Data
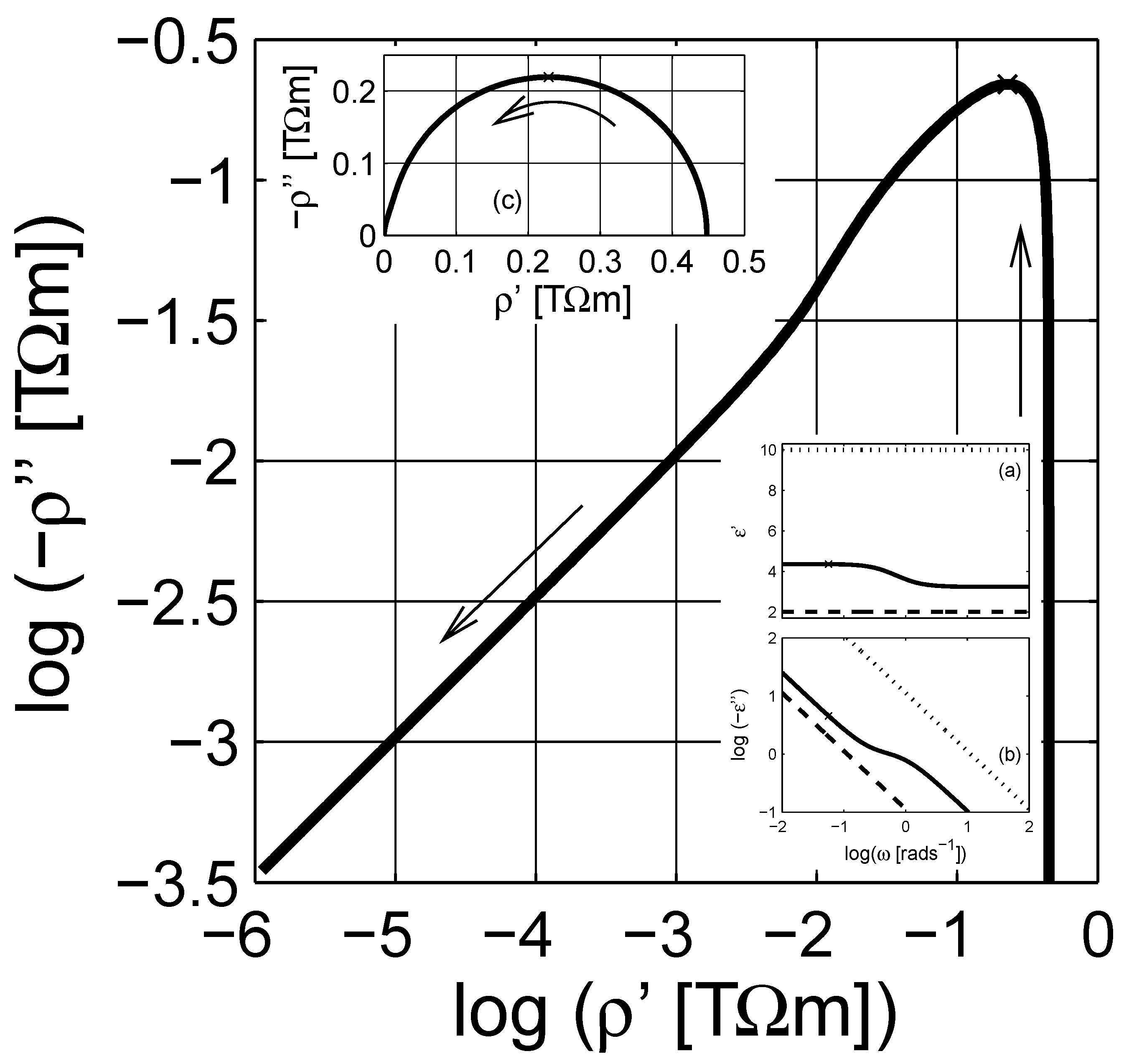

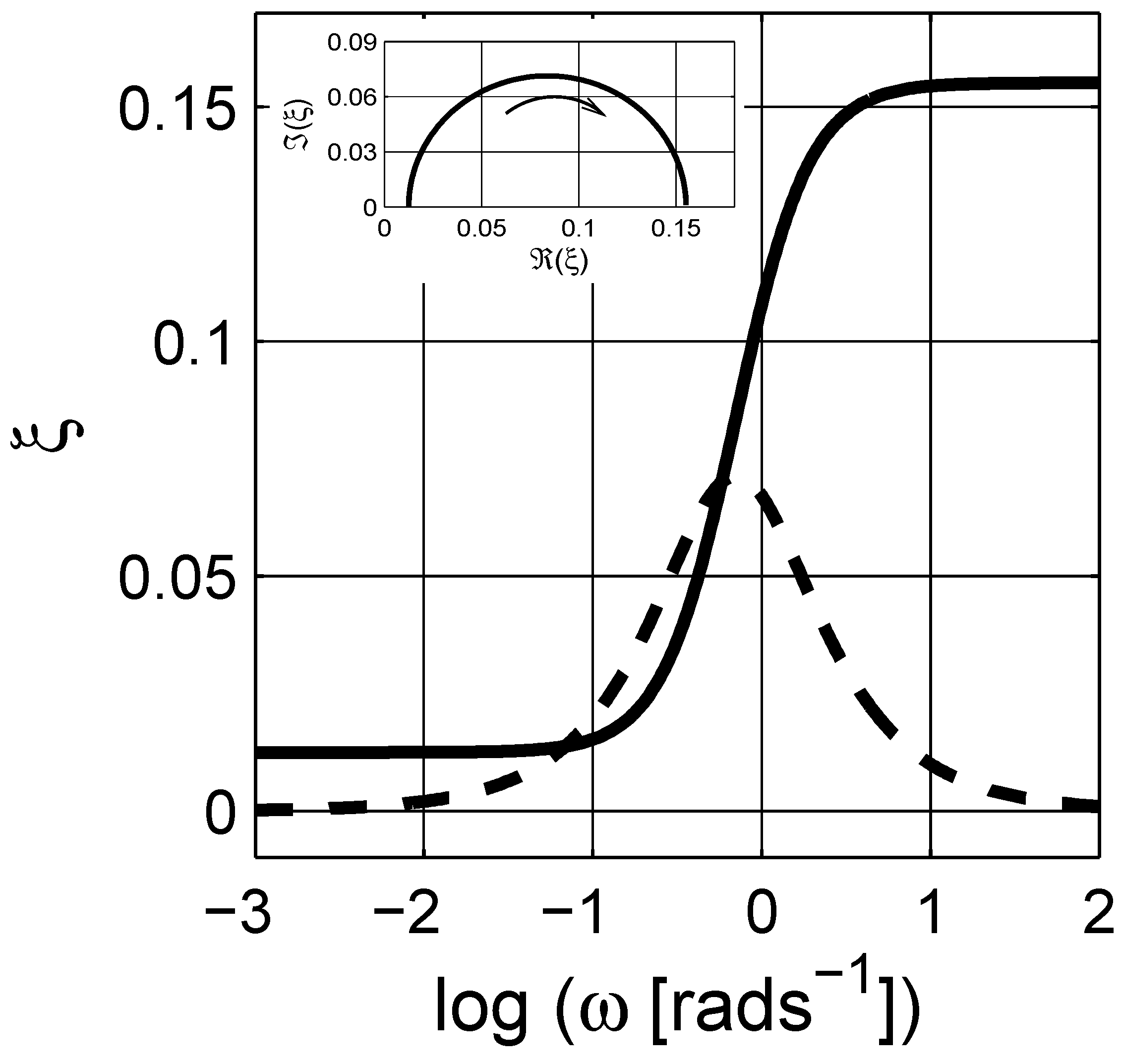
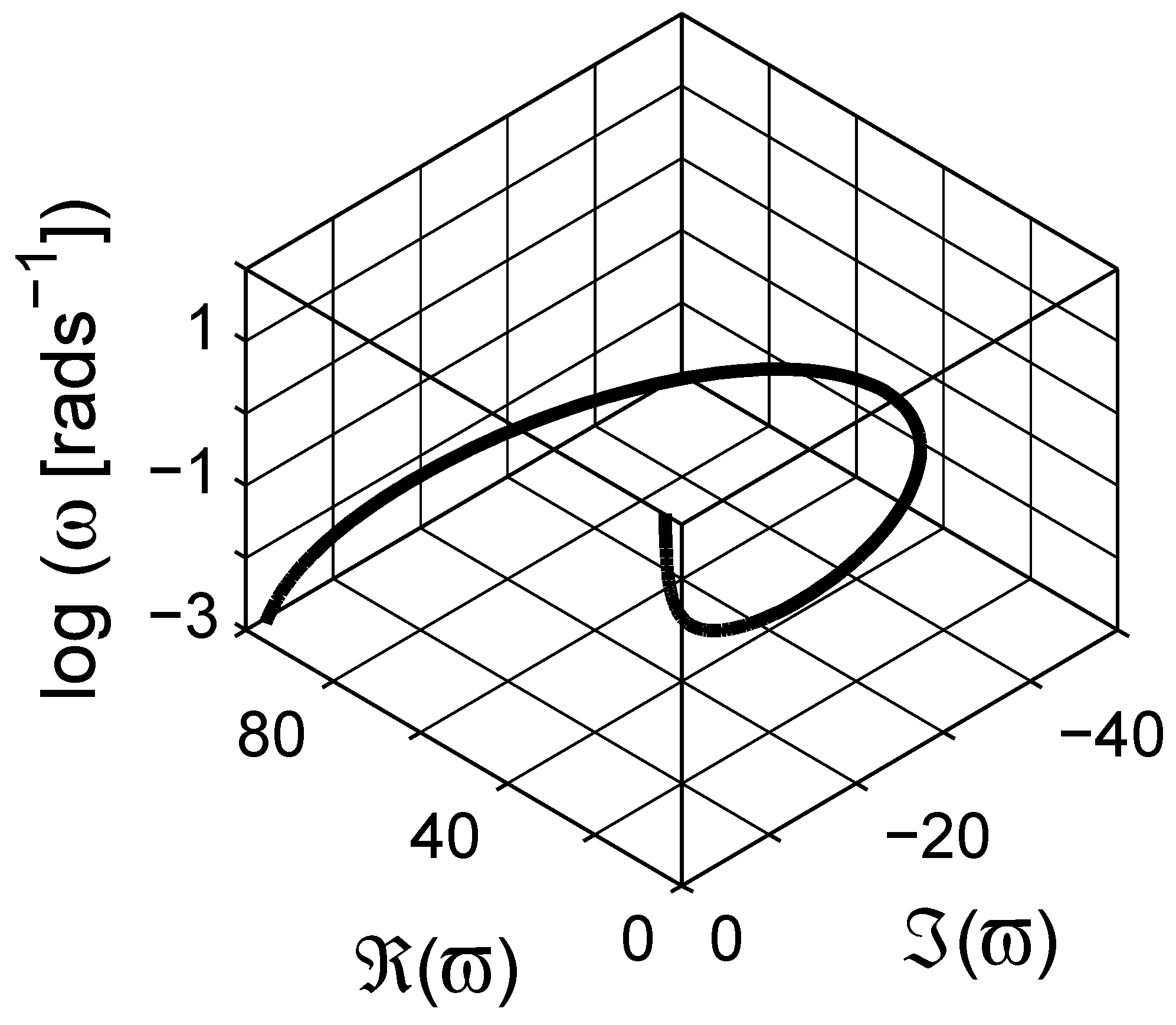
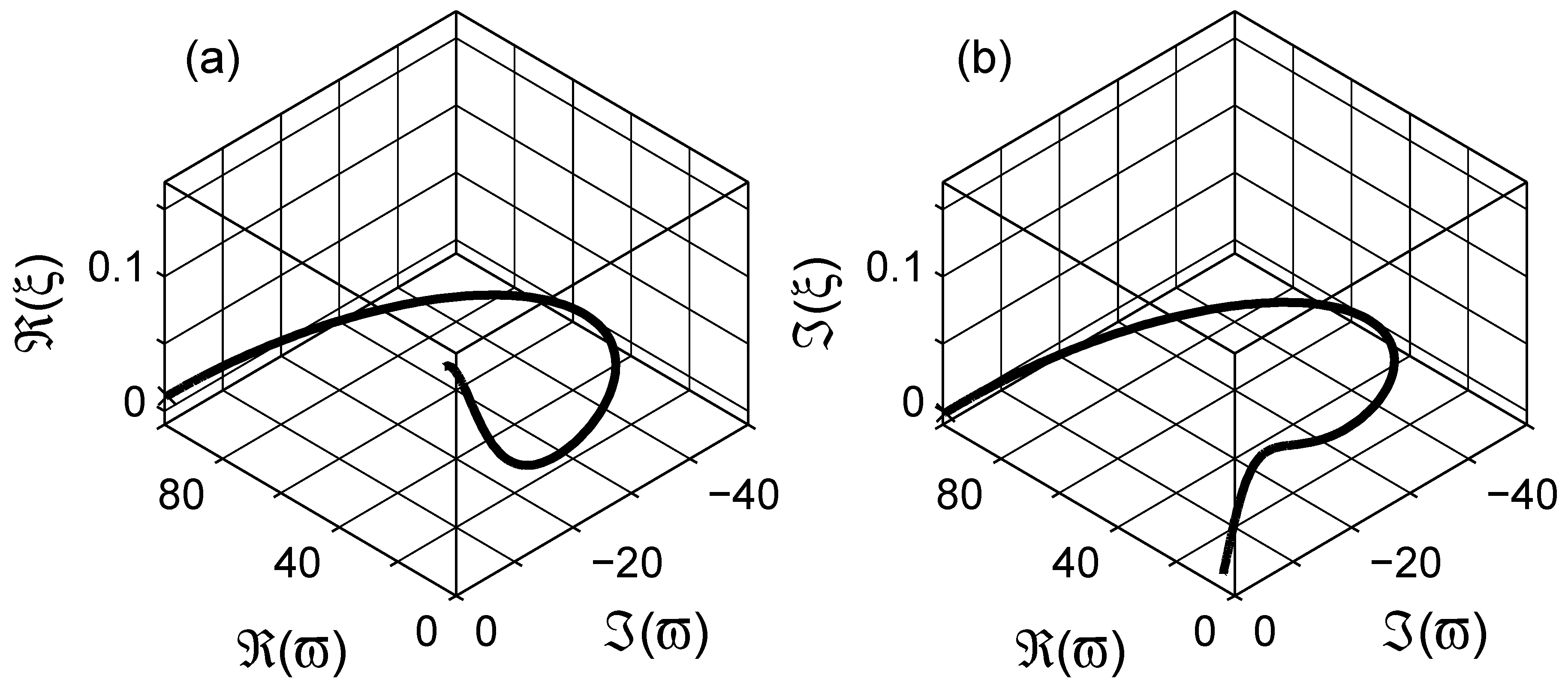
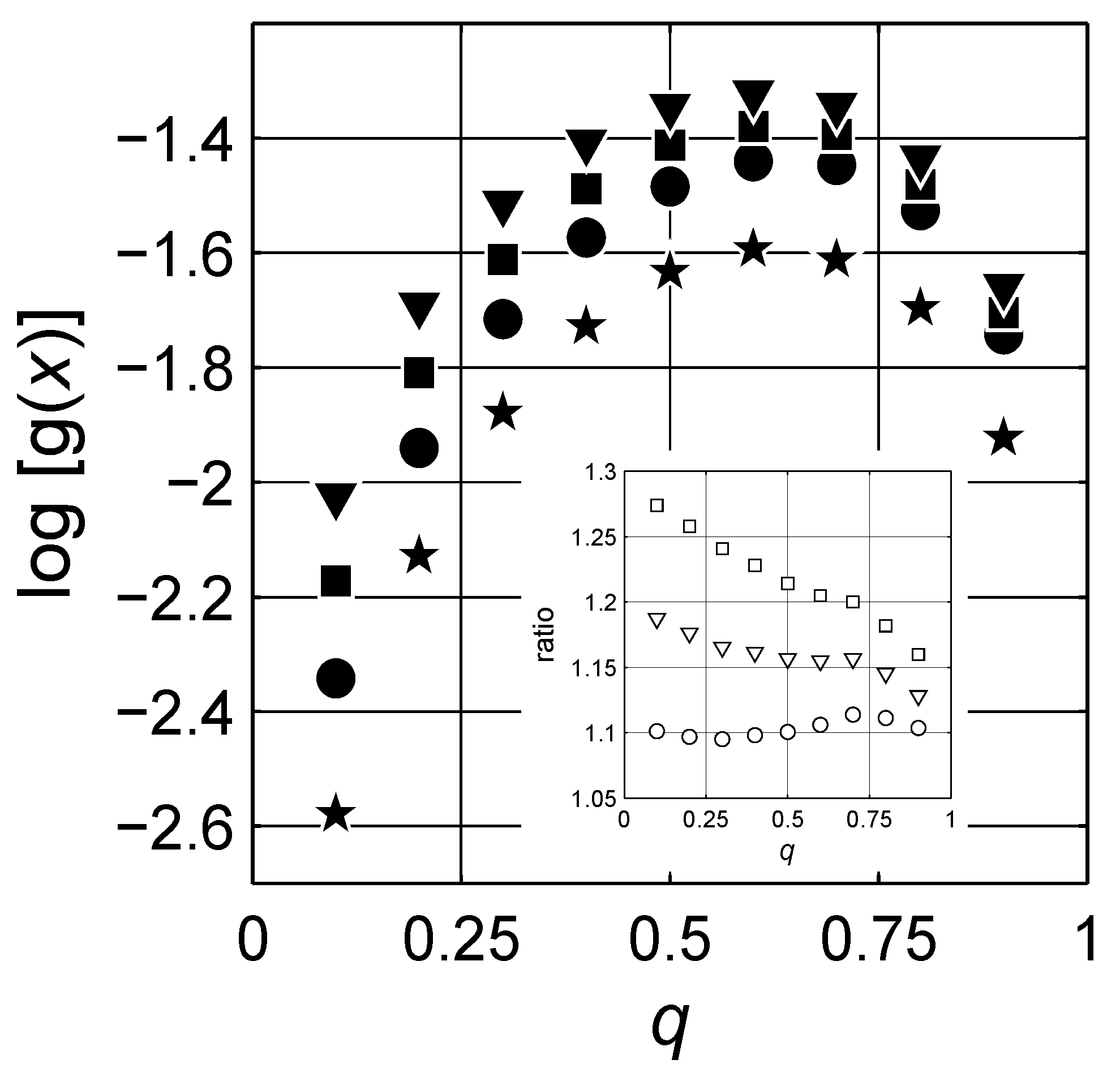
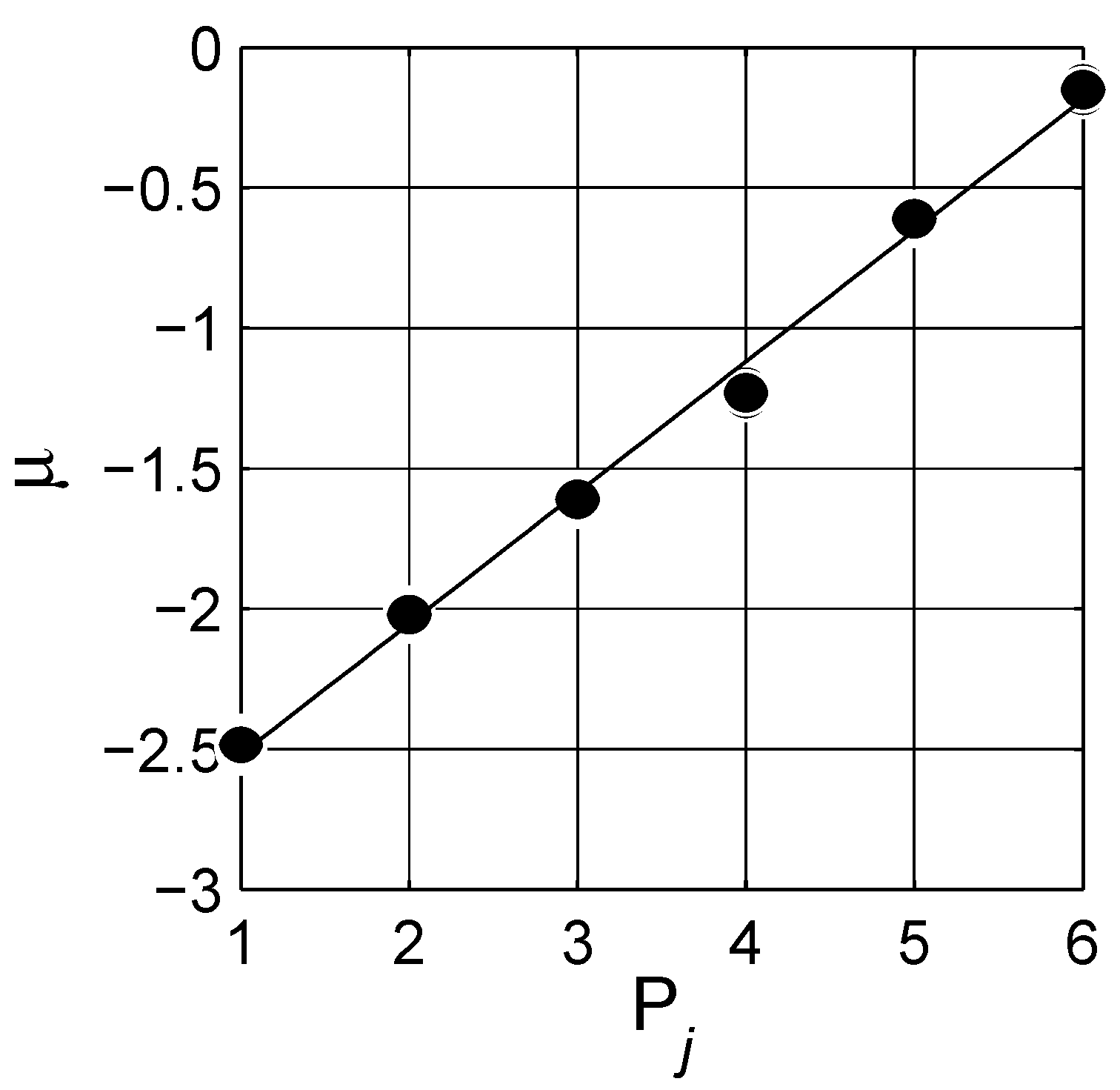
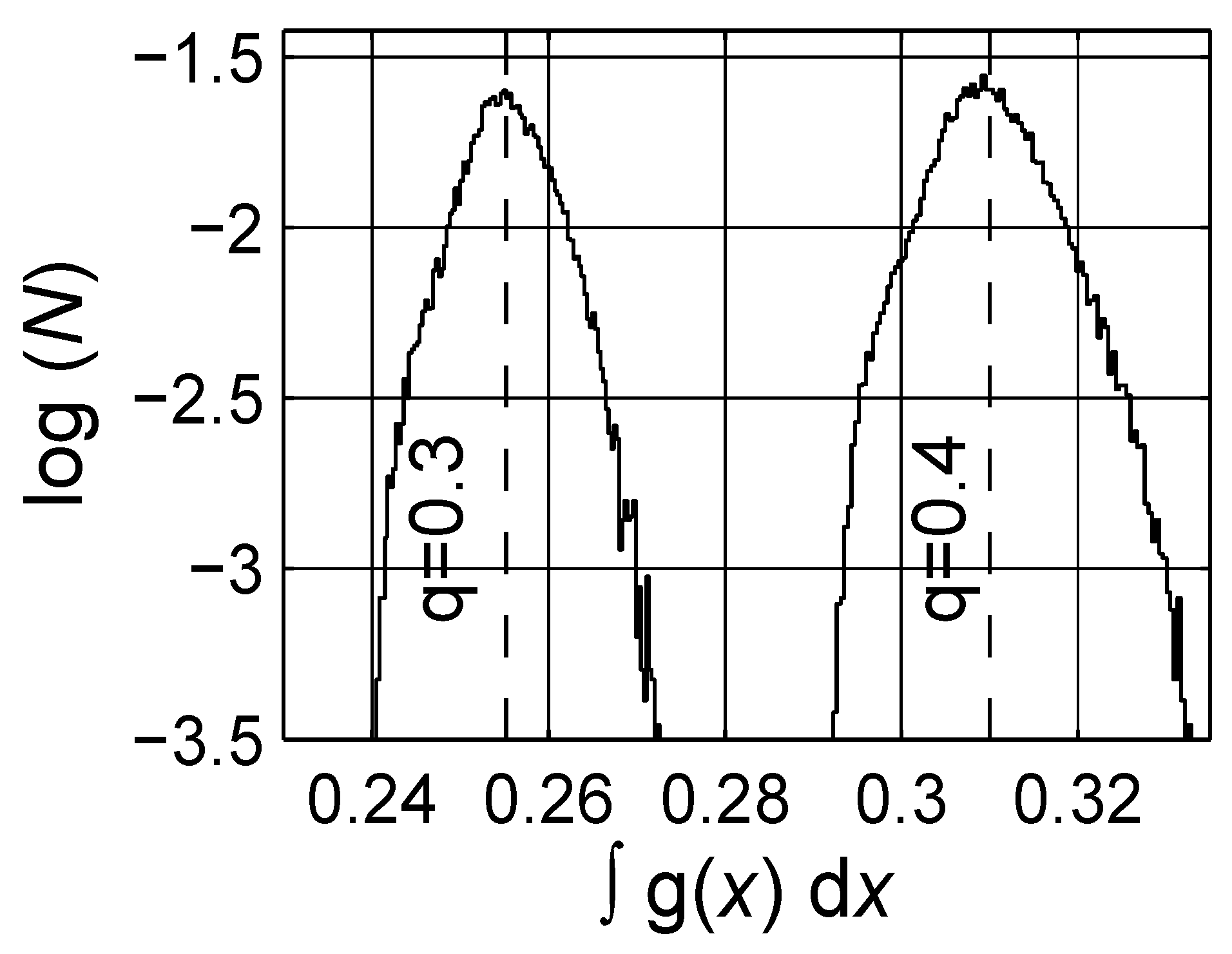
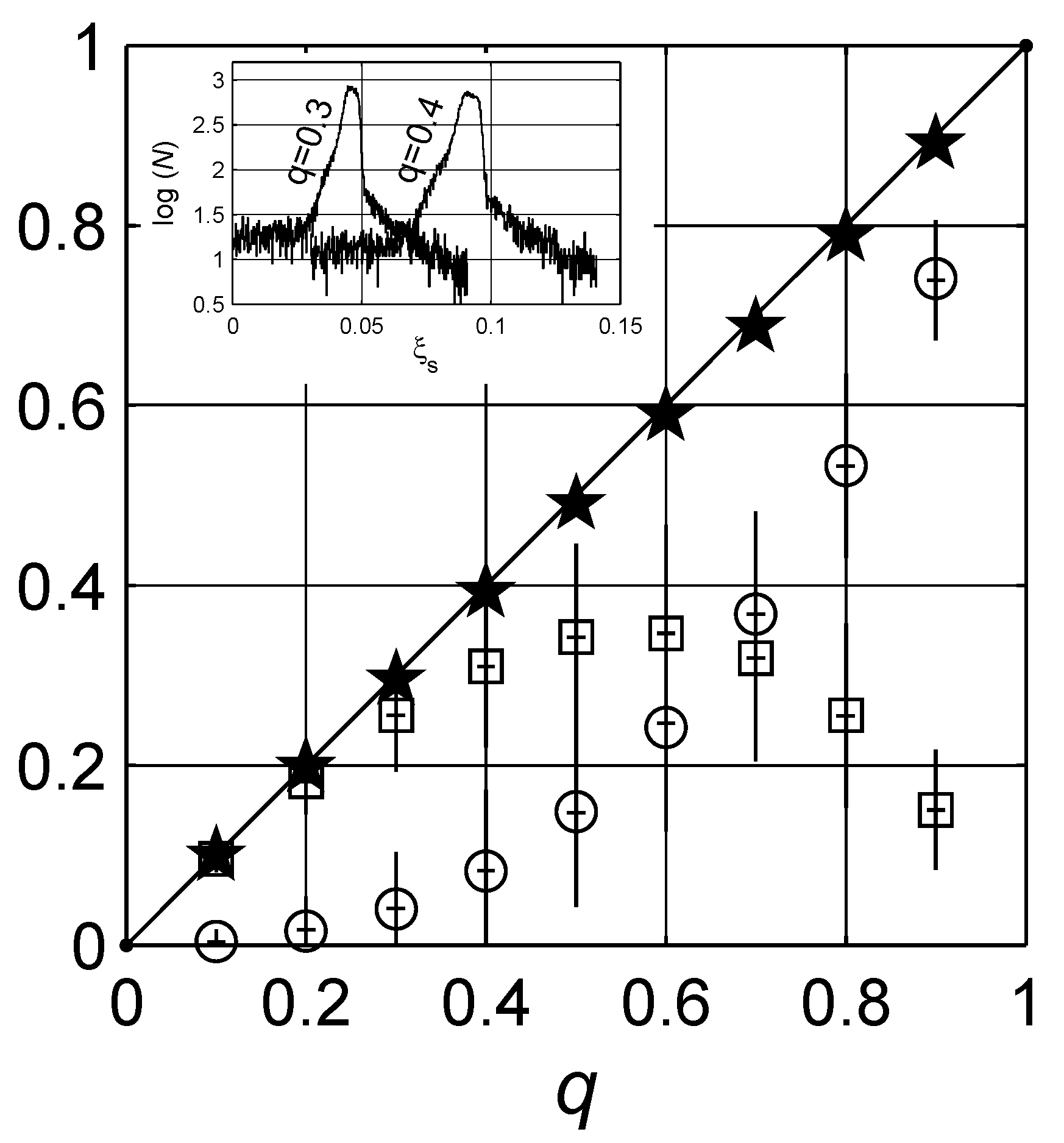
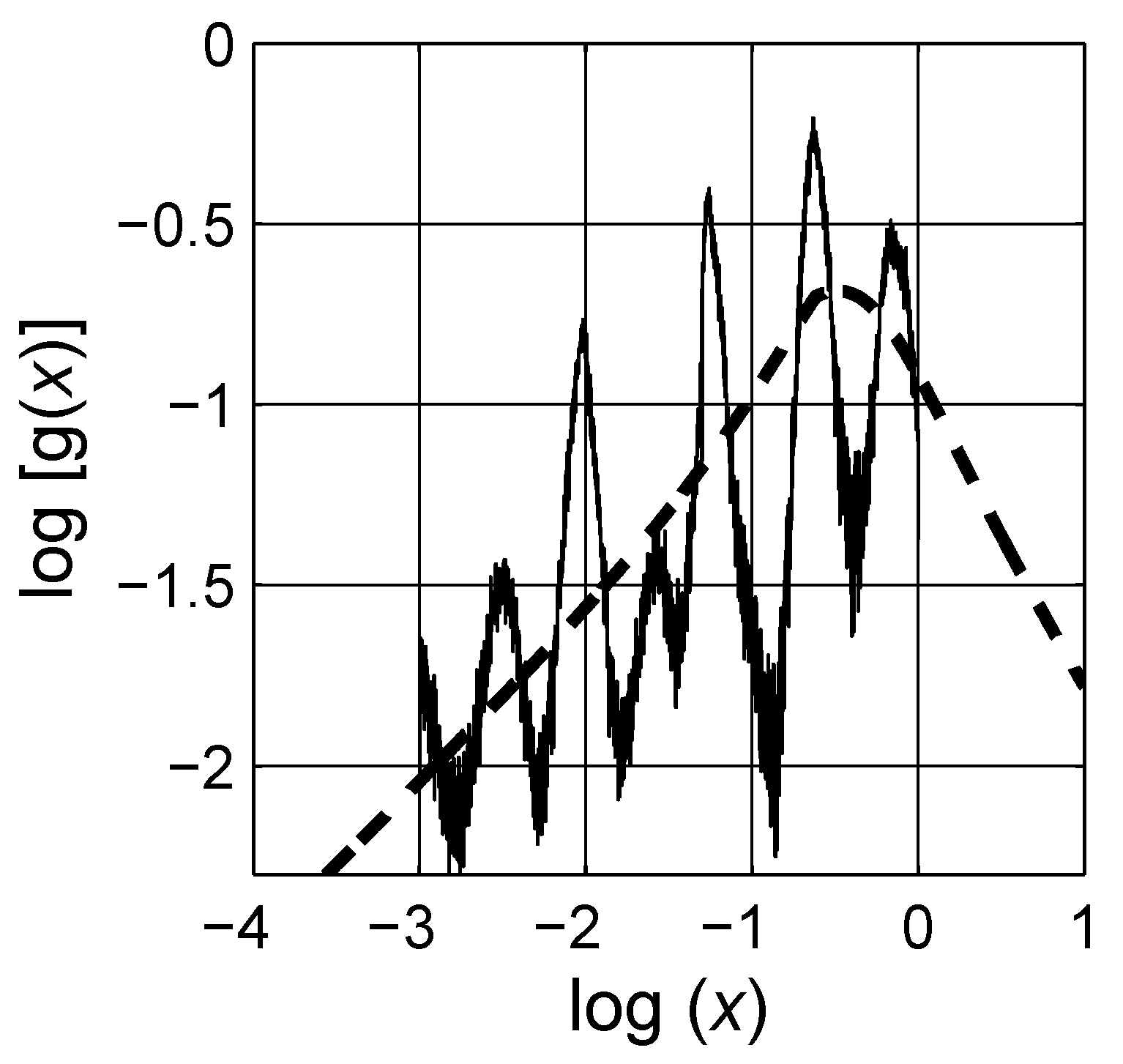
4. Numerical Estimation of Spectral Density Function
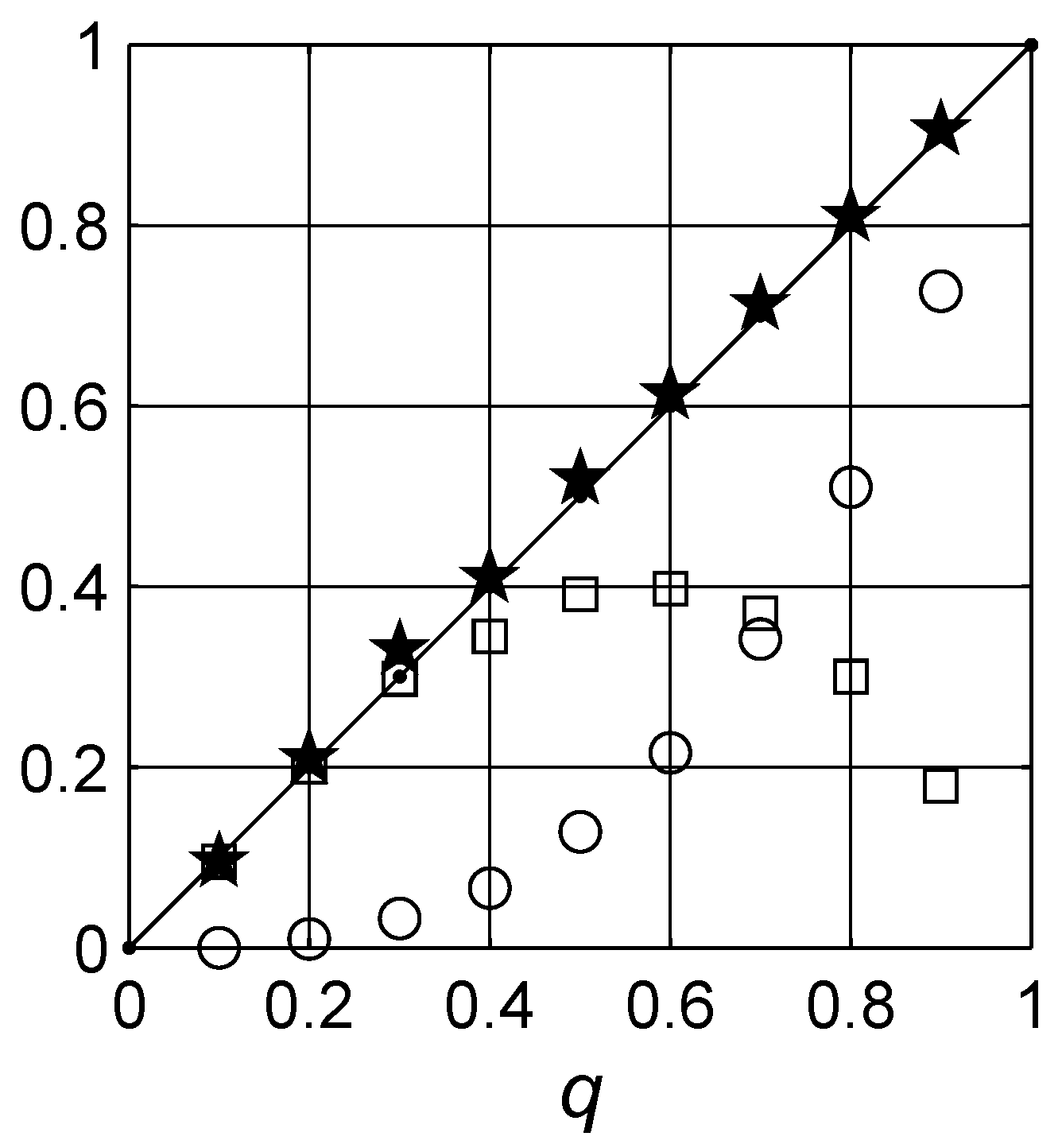
5. Landau-Lifshitz/Looyenga Expression


| Peak | q | μ | γ | ζ | Peak | q | μ | γ | ζ | ||
| 1 | 0.1 | 0.01 | -2.47 | 1.58 | 6.18 | 2 | 0.1 | 0.06 | -2.01 | 0.89 | 15.84 |
| 0.2 | 0.02 | -2.49 | 1.71 | 6.57 | 0.2 | 0.11 | -2.02 | 1.10 | 12.74 | ||
| 0.3 | 0.03 | -2.50 | 1.66 | 7.29 | 0.3 | 0.18 | -2.02 | 1.09 | 12.83 | ||
| 0.4 | 0.04 | -2.50 | 1.75 | 7.83 | 0.4 | 0.22 | -2.02 | 1.20 | 11.81 | ||
| 0.5 | 0.04 | -2.50 | 1.94 | 7.53 | 0.5 | 0.26 | -2.03 | 1.30 | 11.43 | ||
| 0.6 | 0.04 | -2.49 | 2.06 | 7.81 | 0.6 | 0.28 | -2.03 | 1.33 | 11.46 | ||
| 0.7 | 0.04 | -2.49 | 1.98 | 7.86 | 0.7 | 0.28 | -2.03 | 1.22 | 11.84 | ||
| 0.8 | 0.04 | -2.48 | 2.09 | 7.59 | 0.8 | 0.24 | -2.03 | 1.26 | 11.63 | ||
| 0.9 | 0.03 | -2.48 | 1.79 | 7.20 | 0.9 | 0.16 | -2.02 | 1.15 | 11.54 | ||
| 3 | 0.1 | 0.01 | -1.62 | 2.97 | 8.23 | 4 | 0.1 | 0.23 | -1.22 | 0.58 | 35.98 |
| 0.2 | 0.02 | -1.62 | 2.70 | 8.26 | 0.2 | 0.54 | -1.24 | 0.52 | 49.50 | ||
| 0.3 | 0.03 | -1.61 | 2.21 | 9.34 | 0.3 | 0.82 | -1.24 | 0.52 | 53.04 | ||
| 0.4 | 0.03 | -1.61 | 2.27 | 9.10 | 0.4 | 1.04 | -1.24 | 0.56 | 49.16 | ||
| 0.5 | 0.04 | -1.61 | 2.51 | 8.84 | 0.5 | 1.20 | -1.24 | 0.57 | 48.10 | ||
| 0.6 | 0.04 | -1.60 | 2.22 | 9.05 | 0.6 | 1.30 | -1.24 | 0.60 | 47.57 | ||
| 0.7 | 0.03 | -1.61 | 2.58 | 8.91 | 0.7 | 1.26 | -1.24 | 0.60 | 48.15 | ||
| 0.8 | 0.02 | -1.61 | 2.34 | 8.69 | 0.8 | 1.05 | -1.24 | 0.62 | 45.98 | ||
| 0.9 | 0.01 | -1.62 | 2.43 | 8.32 | 0.9 | 0.58 | -1.24 | 0.62 | 41.94 | ||
| 5 | 0.1 | 0.20 | -0.62 | 1.85 | 10.89 | 6 | 0.1 | 0.22 | -0.16 | 0.67 | 15.10 |
| 0.2 | 0.36 | -0.62 | 1.90 | 10.51 | 0.2 | 0.31 | -0.14 | 0.77 | 10.98 | ||
| 0.3 | 0.54 | -0.62 | 1.70 | 11.15 | 0.3 | 0.38 | -0.14 | 0.81 | 10.58 | ||
| 0.4 | 0.62 | -0.62 | 1.72 | 10.89 | 0.4 | 0.40 | -0.14 | 0.80 | 9.84 | ||
| 0.5 | 0.69 | -0.61 | 1.58 | 10.90 | 0.5 | 0.37 | -0.14 | 0.97 | 9.08 | ||
| 0.6 | 0.65 | -0.61 | 1.63 | 10.25 | 0.6 | 0.33 | -0.14 | 1.02 | 8.87 | ||
| 0.7 | 0.56 | -0.61 | 1.66 | 9.57 | 0.7 | 0.28 | -0.14 | 1.08 | 8.93 | ||
| 0.8 | 0.39 | -0.60 | 1.80 | 8.46 | 0.8 | 0.18 | -0.14 | 1.33 | 8.22 | ||
| 0.9 | 0.26 | -0.60 | 1.50 | 9.33 | 0.9 | 0.10 | -0.14 | 1.34 | 8.45 |

6. Application of the Havriliak-Negami Expression
| q | α | β | ||||
| 0.1 | 1.034 | 0.438 | 0.536 | 0.095 | 0.000 | 1.19 |
| 0.2 | 0.822 | 0.555 | 0.514 | 0.200 | 0.009 | 7.28 |
| 0.3 | 0.716 | 0.635 | 0.464 | 0.297 | 0.032 | 2.45 |
| 0.4 | 0.850 | 0.454 | 0.522 | 0.345 | 0.066 | 4.27 |
| 0.5 | 0.800 | 0.470 | 0.494 | 0.391 | 0.128 | 2.06 |
| 0.6 | 0.828 | 0.422 | 0.493 | 0.397 | 0.216 | 4.08 |
| 0.7 | 0.822 | 0.409 | 0.475 | 0.371 | 0.342 | 5.20 |
| 0.8 | 0.815 | 0.399 | 0.456 | 0.300 | 0.510 | 6.41 |
| 0.9 | 0.810 | 0.390 | 0.438 | 0.179 | 0.727 | 7.60 |
7. Conclusions

Acknowledgements
References
- Lowry, H.H. Significance of the dielectric constant of a mixture. J. Franklin Inst. 1927, 203, 413–439. [Google Scholar] [CrossRef]
- Landauer, R. Electrical conductivity in inhomogeneous media. In Electrical Transport and Optical Properties of Inhomogeneous Media; Garland, J.C., Tanner, D.B., Eds.; American Institute of Physics: New York, NY, USA, 1978; Volume 40, AIP Conference Proceedings; pp. 2–43. [Google Scholar]
- Priou, A. (Ed.) Dielectric Properties of Heterogeneous Materials. In Progress in Electromagnetics Research; Elsevier: New York, NY, USA, 1992.
- Torquato, S. Random Heterogeneous Materials: Microstructure and Macroscopic Properties; Springer-Verlag: Berlin, Germany, 2001; Volume 16. [Google Scholar]
- Sahimi, M. Heterogeneous Materials I: Linear Transport and Optical Properties; Springer-Verlag: Berlin, Germany, 2003; Volume 22. [Google Scholar]
- Tuncer, E.; Serdyuk, Y.V.; Gubanski, S.M. Dielectric mixtures: Electrical properties and modeling. IEEE Trans. Dielect. Elect. Insul. 2002, 9, 809–828. [Google Scholar] [CrossRef]
- Bergman, D.J.; Stroud, D. The Physical Properties of Macroscopically Inhomogeneous Media. Solid State Phys. 1992, 46, 147. [Google Scholar]
- Sihvola, A. Electromagnetic Mixing Formulas and Applications; The Institute of Electrical Engineers: London, UK, 1999; Volume 47, IEE Electromagnetic Waves Series. [Google Scholar]
- Tuncer, E.; Gubański, S.M.; Nettelblad, B. Dielectric relaxation in dielectric mixtures: Application of the Finite Element Method and its comparison with mixture formulas. J. Appl. Phys. 2001, 89, 8092–8100. [Google Scholar] [CrossRef]
- Keldysh, L.V.; Kirzhnitz, D.A.; Maradudin, A.A. (Eds.) The Dielectric Function of Condensed Systems; Elsevier Science Publisher B.V.: Amsterdam, The Netherlands, 1989.
- Brosseau, C.; Beroual, A. Computational Electromagnetics and the rational design of new dielectric heterostructures. Prog. Mater. Sci. 2003, 48, 373–456. [Google Scholar] [CrossRef]
- Gunnar, G.A.; Granqvist, C.G. Optical properties and solar selectivity of coevaporated Co-Al2O3 composite films. J. Appl. Phys. 1984, 55, 3382–3410. [Google Scholar]
- Tinga, W.R.; Voss, W.A.G.; Blossey, D.F. Generalized approach to multiphase dielectric mixture theory. J. Appl. Phys. 1973, 44, 3897–3902. [Google Scholar] [CrossRef]
- Granqvist, C.G. Optical properties of ultrafine gold particles. In Electrical Transport and Optical Properties of Inhomogeneous Media; Garland, J.C., Tanner, D.B., Eds.; American Institute of Physics: New York, NY, USA, 1978; Volume 40, AIP Conference Proceedings; pp. 196–219. [Google Scholar]
- McPhedran, R.C.; McKenzie, D.R. Exact solutions for tranport properties of arrays of spheres. In The Physics of Submicron Structures; Grubin, H., Hess, K., Iafrate, G., Ferry, D., Eds.; American Institute of Physics: New York, NY, USA, 1984; pp. 294–299. [Google Scholar]
- Milton, G.; McPhedran, R.; McKenzie, D. Transport properties of arrays of intersecting cylinders. Appl. Phys. 1981, 25, 23–40. [Google Scholar] [CrossRef]
- Perrins, W.T.; Kenzie, D.R.M.; McPhedran, R.C. Transport properties of regular arrays of cylinders. Proc. R. Soc. London A 1979, 369, 207–225. [Google Scholar] [CrossRef]
- McPhedran, R.C.; McKenzie, D.R. The conductivity of lattices of spheres: I. The simple cubic lattice. Proc. R. Soc. London A. 1978, 359, 45–63. [Google Scholar] [CrossRef]
- Tuncer, E. Extracting spectral density function of a binary composite without a-priori assumption. Phys. Rev. B 2005, 71, 012101. [Google Scholar] [CrossRef]
- Tuncer, E. Structure/property relationship in dielectric mixtures: Application of the spectral density theory. J. Phys. D: Appl. Phys. 2005, 38, 223–234. [Google Scholar] [CrossRef]
- Tuncer, E. Analogy between dielectric relation and dielectric mixtures: Application of the spectral density representation. J. Phys.: Condens. Matter 2005, 17, L125–L128. [Google Scholar]
- Fuchs, R. Theory of the optical properties of ionic crystal cubes. Phys. Rev. 1975, B11, 1732. [Google Scholar] [CrossRef]
- Fuchs, R. Optical properties of small metal particles. In Electrical Transport and Optical properties of Inhomogeneous Media; Garland, J.C., Tanner, D.B., Eds.; American Institute of Physics: New York, NY, USA, 1978; Volume 40, AIP Conference Proceedings; pp. 276–281. [Google Scholar]
- Bergman, D.J. Rigorous Bounds for Complex Dielectric Constant of a Two-Component Composite. Ann. Phys. 1982, 138, 78–114. [Google Scholar] [CrossRef]
- Bergman, D.J. Exactly solvable microscopic geometries and rigorous bounds for the complex dielectric constant of a two-component composite material. Phys. Rev. Lett. 1980, 44, 1285–1287. [Google Scholar] [CrossRef]
- Bergman, D.J. The dielectric constant of a composite material—A problem in classical physics. Phys. Rep. 1978, 43, 377–407. [Google Scholar] [CrossRef]
- Milton, G.W. Bounds on the complex permittivity of a two-component composite material. J. Appl. Phys. 1981, 52, 5286–5293. [Google Scholar] [CrossRef]
- Milton, G.W. Bounds on the transport and optical properties of a two-component composite material. J. Appl. Phys. 1981, 52, 5294–5304. [Google Scholar] [CrossRef]
- Milton, G.W. Bounds on the electromagnetic, elastic, and other properties of two-component composites. Phys. Rev. Lett. 1981, 46, 542–545. [Google Scholar] [CrossRef]
- Golden, K.; Papanicolaou, G. Bounds on effective parameters of heterogeneous media by analytic continuation. Commun. Math. Phys. 1983, 90, 473–491. [Google Scholar] [CrossRef]
- Golden, K.; Papanicolaou, G. Bounds for effective parameters of multicomponent media by analytical continuation. J. Stat. Phys. 1985, 40, 655–667. [Google Scholar] [CrossRef]
- Fuchs, R.; Claro, F. Spectral representation for the polarizability of a collection of dielectric spheres. Phys. Rev. B 1989, 39, 3875–3878. [Google Scholar] [CrossRef]
- Ghosh, K.; Fuchs, R. Spectral theory of two-component porous media. Phys. Rev. B 1988, 38, 5222–5236. [Google Scholar] [CrossRef]
- Tuncer, E. A formula for dielectric mixtures. Phil. Mag. Lett. 2005, 85, 269–275. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; Freeman: San Francisco, CA, USA, 1982. [Google Scholar]
- Clerc, J.P.; Giraud, G.; Laugier, J.M.; Luck, J.M. The electrical conductivity of binary disordered systems, percolation clusters, fractals and related models. Adv. Phys. 1990, 39, 191–308. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Fractals: Form, Chance and Dimensions; Freeman: San Francisco, CA, USA, 1977. [Google Scholar]
- Aharony, A. Percolation. In Directions in Condensed Matter Physics; Grinstein, G., Mazenko, G., Eds.; World Scientific: Singapore, 1986. [Google Scholar]
- Ahanory, A.; Feder, J. (Eds.) Proc. Inter. Conf. Honouring Benoit B. Mandelbrot; North-Holland: Amsterdam, The Netherlands, 1989.
- Pietronero, L.; Tosatti, E. Proc. Sixth Trieste Inter. Symp. on Fractals in Physics; North-Holland: Amsterdam, The Netherlands, 1985. [Google Scholar]
- Niklasson, G.A. Fractals and the AC conductivity of disordered materials. In Proc. Inter. Conf. Honouring Benoit B. Mandelbrot; Ahanory, A., Feder, J., Eds.; North-Holland: Amsterdam, The Netherlands, 1989; pp. 260–265. [Google Scholar]
- Niklasson, G.A. A fractal description of the dielectric response in disordered materials. J. Phys.: Condens. Matter 1993, 5, 4233–4242. [Google Scholar] [CrossRef]
- Sotelo, J.A.; Pustovit, V.N.; Niklasson, G.A. Optical constants of gold blacks: Fractal network models and experimental data. Phys. Rev. B 2002, 65, 245113. [Google Scholar] [CrossRef]
- Zabel, I.; Stroud, D. Metal clusters and model rocks: Electromagnetic properties of conducting fractal aggregates. Phys. Rev. B 1992, 46, 8132–8138. [Google Scholar] [CrossRef]
- Hui, P.M.; Stroud, D. Complex dielectric response of metal-particle clusters. Phys. Rev. B 1986, 33, 2163–2169. [Google Scholar] [CrossRef]
- Niklasson, G.A.; Yatsuya, S.; Granqvist, C.G. Far-infrared absorbtion in gas-evaporated Al particles: Effects of a fractal structure. Solid State Commun. 1986, 59, 579–582. [Google Scholar] [CrossRef]
- Clerc, J.P.; Giraud, G.; Luck, J.M.; Robin, T. Dielectric resonances of lattice animals and other fractal clusters. J. Phys. A: Math. Gen. 1996, 29, 4781–4801. [Google Scholar] [CrossRef]
- Brouers, F.; Rauw, D.; Clerc, J.P.; Giraud, G. Self-similar properties of the far-infrared and optical absorbtion of fractal metallic clusters. Phys. Rev. B 1994, 49, 14582–14588. [Google Scholar] [CrossRef]
- Tuncer, E.; Niklasson, G.A. Optical properties of non-dilute metal-insulator composites. Opt. Commun. 2008, 281, 4374–4379. [Google Scholar] [CrossRef]
- Sillars, R. The properties of a dielectric containing semiconducting particles of various shapes. J. Inst. Electr, Eng. 1937, 80, 378–394. [Google Scholar]
- Wiener, O. Die Theorie des Mischkörpers für das Feld der Statonären Strömung I. Die Mittelwertsätze für Kraft, Polarisation und Energie. Abh. Math.-Phys. Kl. Königl. Sachsischen Ges. Wiss. 1912, 32, 509–604. [Google Scholar]
- Landau, L.; Lifshitz, E. Electrodynamics of Continuous Media, 2nd ed.; Perganom Press: New York, NY, USA, 1982; Volume 8, Course of Theoretical Physics. [Google Scholar]
- Looyenga, H. Dielectric constants of heterogeneous mixtures. Physica 1965, 31, 401–406. [Google Scholar] [CrossRef]
- Spanier, J.E.; Herman, I.P. Using of hybrid phenomenological and statistical effective-medium theories of dielectric functions to model the infrared reflectance of porous SiC films. Phys. Rev. B 2000, 61, 10437–10450. [Google Scholar] [CrossRef]
- Marquardt, P.; Nimtz, G. Size-governed electromagnetic absorbtion by metal particles. Phys. Rev. B 1989, 40, 7996–7998. [Google Scholar] [CrossRef]
- Nelson, S.O. Estimation of permittivities of solids from measurements on pulverized or granular materials. In Dielectric Properties of Heterogeneous Materials; Elsevier: Amsterdam, The Netherlands, 1992; Volume 6, Progress in Electromagnetic Research, Chapter 1; pp. 231–271. [Google Scholar]
- Dua, H.; Chenb, H.; Gonga, J.; Wanga, T.G.; Suna, C.; Leeb, S.W.; Wena, L.S. Use of effective medium theory to model the effect of the microstructure on dc conductivity of nano-titanium films. Appl. Surf. Sci. 2004, 233, 99–104. [Google Scholar] [CrossRef]
- Kolokolova, L.; Gustafson, B.A.S. Scattering by inhomogeneous particles: Microwave analog experiments and comparison to e+ective medium theories. J. Quant. Spect. Rad. Transf. 2001, 70, 611–625. [Google Scholar] [CrossRef]
- Bordi, F.; Cametti, C.; Gili, T. Dielectric spectroscopy of erythrocyte cell suspensions. A comparison between Looyenga and Maxwell-Wagner-Hanai effective medium theory formulations. J. Non-Cryst. Solids 2002, 305, 278–284. [Google Scholar] [CrossRef]
- Bonincontro, A.; Briganti, G.; Giansanti, A.; Pedone, F.; Risuleo, G. Electrical conductivity and dielectric dispersion of E. coli 70S ribosomes and of 30S and 50S subunits: Effects of magnesium ions. Coll. Surf. B: Biointerfaces 1996, 6, 219–226. [Google Scholar] [CrossRef]
- Bordi, F.; Cametti, C.; Biasio, A.D. Conductometric study of poly(ethylene oxide)-water interactions in electrolyte solutions. Coll. Surf. 1989, 35, 337–342. [Google Scholar] [CrossRef]
- Trabelsi, S.; Nelson, S.O. Free-space measurement of dielectric properties of cereal grain and oilseed at microwave frequencies. Meas. Sci. Tech. 2003, 14, 589–600. [Google Scholar] [CrossRef]
- Nelson, S.O.; You, T.S. Relationships between microwave permittivities of solid and pulverised plastics. J. Phys. D: Appl. Phys. 1990, 23, 346–353. [Google Scholar] [CrossRef]
- Neelakantaswamy, P.S.; Chowdari, B.V.R.; Rajaratnam, A. Estimation of permittivity of a compact crystal by dielectric measurements on its powder: A stochastic mixture model for the powder-dielectric. J. Phys. D: Appl. Phys. 1983, 16, 1785–1799. [Google Scholar] [CrossRef]
- Benadda, M.D.; Carru, J.C.; Amoureux, J.P.; Castelain, M.; Chapoton, A. Experimental and theoretical study of the dielectric properties of 1-cyanoadamantane; spectrum of the compact crystal from measurements on powder. J. Phys. D: Appl. Phys. 1982, 15, 1477–1489. [Google Scholar] [CrossRef]
- Davies, W.E.A. The dielectric constants of axially isotropic composite materials. J Phys. D: Appl. Phys. 1974, 7, 1016–1029. [Google Scholar] [CrossRef]
- Lal, K.; Parshad, R. Test and utilization of the Fricke and Pearce equations for dielectric correlation between powder and bulk. J Phys. D: Appl. Phys. 1974, 7, 455–461. [Google Scholar] [CrossRef]
- Levy, O.; Stroud, D. Maxwell Garnett theory for mixtures of anisotropic inclusions: Application to conducting polymers. Phys. Rev. B 1997, 56, 8035–8046. [Google Scholar] [CrossRef]
- Garnett, J.C.M. Colours in metal glasses and in metallic films. Phil. Trans. R. Soc. London A 1904, 203, 385–420. [Google Scholar] [CrossRef]
- Bruggeman, D.A.G. Berechnung verschiedener physikalischer Konstanten von heterogenen Substanzen. Ann. Phys. 1935, 24, 636–679. [Google Scholar] [CrossRef]
- Jonscher, A.K. Dielectric Relaxation in Solids; Chelsea Dielectric: London, UK, 1983. [Google Scholar]
- Tuncer, E.; Macdonald, J.R. Comparison of methods for estimating continuous distributions of relaxation times. unpublished work.
- Tuncer, E.; Gubański, S.M. On dielectric data analysis: Introduction of the Monte Carlo Method to obtain distributions of relaxation times and a comparison with a functional approach. IEEE Trans. Dielect. Elect. Insul. 2001, 8, 310–320. [Google Scholar] [CrossRef]
- Macdonald, J.R. (Ed.) Impedance Spectroscopy; John Wiley & Sons: New York, NY, USA, 1987.
- Macdonald, J.R.; Potter, L.D.J. A flexible procedure for analyzing impedance spectroscopy results: Description and illustrations. Solid State Ionics 1987, 24, 61–79, The latest version of the LEVM fitting program, V. 8.0, may be obtained at no cost from http//www.physics.unc.edu/~macd/ where more details about the program appear. An extensive manual, source code, and executable code are included. [Google Scholar] [CrossRef]
- Tuncer, E. Dielectric properties of composite structures and filled polymeric composite materials. Licenciate thesis–Tech. rep. 338 L, Department of Electric Power Eng., Chalmers University of Technology, Gothenburg, Sweden, 2000; pp. 63–83. [Google Scholar]
- Tuncer, E.; Lang, S.B. Numerical extraction of distributions of space-charge and polarization from laser intensity modulation method. Appl. Phys. Lett. 2005, 86, 071107. [Google Scholar] [CrossRef]
- Goncharenko, A.V.; Lozovski, V.Z.; Venger, E.F. Lichtenecker’s equation: Applicability and limitations. Opt. Commun. 2000, 174, 19–32. [Google Scholar] [CrossRef]
- Goncharenko, A.V. Generalizations of the Bruggeman equation and a concept of shape-distributed particle composites. Phys. Rev. E 2003, 68, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Day, A.R.; Thorpe, M.F. The spectral fuction of composites. J. Phys.: Condens. Matter 1999, 11, 2551–2568. [Google Scholar]
- Stroud, D.; Milton, G.W.; De, B.R. Analytical model for the dielectric response of brine-saturated rocks. Phys. Rev. B 1986, 34, 5145–5153. [Google Scholar] [CrossRef]
- Böttcher, C.J.F.; Bordewijk, P. (Eds.) Theory of Electric Polarization; Elsevier: Amsterdam, The Netherlands, 1996; Chapter IX; pp. 45–137.
- Macdonald, J.R. Dispersed electrical-relaxation response: discrimination between conductive and dielectric relaxation processes. Brazil. J. Phys. 1999, 29, 332–346. [Google Scholar] [CrossRef]
- McCrum, N.G.; Read, B.E.; Williams, G. Anelastic and Dielectric Effects in Polymeric Solids, Dover ed.; John Wiley & Sons Ltd.: London, UK, 1967; pp. 127–136. [Google Scholar]
- Macdonald, J.R. Comparison of parametric and nonparametric methods for the analysis and inversion of immittance data: Critique of earlier work. J. Comp. Phys. 2000, 157, 280–301. [Google Scholar] [CrossRef]
- Macdonald, J.R. On relaxation-spectrum estimation for decades of data: accuracy and sampling-localization considerations. Inv. Problems 2000, 16, 1561–1583. [Google Scholar] [CrossRef]
- Macdonald, J.R. Exact and approximate nonlinear least-squares inversion of dielectric relaxation spectra. J. Chem. Phys. 1995, 102, 6241–6250. [Google Scholar] [CrossRef]
- Dias, C.J. Determination of a distribution of relaxation frequencies based on experimental relaxation data. Phys. Rev. B 1996, 53, 14212–14222. [Google Scholar] [CrossRef]
- Tuncer, E.; Furlani, M.; Mellander, B.E. Resolving distribution of relaxation times in poly(propylene glycol) on the crossover region. J. Appl. Phys. 2004, 95, 3131–3140. [Google Scholar] [CrossRef]
- Havriliak, S.; Negami, S. A complex plane analysis of α—dispersion in some polymer systems. J. Polym. Sci. C 1966, 14, 99–117. [Google Scholar] [CrossRef]
- Debye, P. Polar Molecules; Dover Publications: New York, NY, USA, 1945. [Google Scholar]
- Davidson, D.W.; Cole, R.H. Dielectric relaxation in glycole, propylene glycol, and n-propanol. J. Chem. Phys. 1951, 19, 1484–1490. [Google Scholar] [CrossRef]
- Cole, K.S.; Cole, R.H. Dispersion and adsorption in dielectrics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef]
- Nigmatullin, R.R.; Jafar, M.M.A.G.; Shinyashiki, N.; Sudo, S.; Yagihara, S. Recognition of a new permittivity function for glycerol by the use of the eigen-coordinates method. J. Non-Cryst. Solids 2002, 305, 96–111. [Google Scholar] [CrossRef]
- Nigmatullin, R.R.; Osokin, S.I.; Smith, G. The justified data-curve fitting approach: recognition of the new type of kinetic equations in fractional derivatives from analysis of raw dielectric data. J. Phys. D: Appl. Phys. 2003, 36, 2281–2294. [Google Scholar] [CrossRef]
- Nigmatullin, R.R.; Osokin, S.I.; Smith, G. New approach in the description of dielectric relaxation phenomenon: correct deduction and interpretation of the Vogel-Fulcher-Tamman equation. J. Phys.: Condens. Matter 2003, 15, 3481–3503. [Google Scholar] [CrossRef]
- Volterra, V. Sulla inversione degli integrali definiti. Rend. Accad. Lincei 1896, 5, 177–185. [Google Scholar]
- Fredholm, I. Sur une nouvelle méthode pour la résolution du probléme de Dirichlet. Kong. Vetenskaps-Akademiens Förh. Stockholm 1900, 57, 39–46. [Google Scholar]
- Day, A.R.; Thorpe, M.F.; Grant, A.G.; Sievers, A.J. The spectral function of a composite from reflectance data. Physica B 2000, 279, 17–20. [Google Scholar] [CrossRef]
- Day, A.R.; Grant, A.R.; Sievers, A.J.; Thorpe, M.F. Spectral function of composites from reflectivity measurements. Phys. Rev. Lett. 2000, 84, 1978–1981. [Google Scholar] [CrossRef] [PubMed]
- Cherkaev, E.; Zhang, D. Coupling of the efective properties of a random mixture through the reconsructed spectral representation. Physica B 2003, 338, 16–23. [Google Scholar] [CrossRef]
- Barabash, S.; Stroud, D. Spectral representation for the effective macroscopic response of a polycrystal: application to third-order non-linear susceptibility. J. Phys.: Condens. Matter 1999, 11, 10323–10334. [Google Scholar] [CrossRef]
- Butkov, E. Mathematical Physics; Addison-Wesley Publishing Company: Menlo Park, CA, USA, 1968; Addison-Wesley Series in Advanced Physics. [Google Scholar]
- Breiman, L. Probability; Addison-Wesley Publishing Company, Inc.: Reading, PA, USA, 1968; Addison-Wesley Series in Statistics. [Google Scholar]
- Loéve, M. Probability Theory I, 4th ed.; Spreinger-Verlag: Berlin, Germany, 1977; Number 45 in Graduate Texts in Mathematics. [Google Scholar]
- Walter, C. Lévy-stability-under-addition and fractal structure of markets: Implications for the investment management industry and emphasized examination of MATIF notional contract. Math. Comput. Model. 1999, 29, 37–56. [Google Scholar] [CrossRef]
- Donth, E. Dynamic or configurational approach to the glass transition. J. Non-Cryst. Solids 2002, 307-310, 364–375. [Google Scholar] [CrossRef]
- Feller, W. An Introduction to Probability Theory and Its Applications; John Wiley and Sons: New York, NY, USA, 1970; Volume 2. [Google Scholar]
- Barkai, E.; Silbey, R.; Zumofen, G. Lévy distribution of single molecule line shape cumulants in glasses. Phys. Rev. Lett. 2000, 84, 5339–5342. [Google Scholar] [CrossRef] [PubMed]
- Barkai, E.; Silbey, R.; Zumofen, G. Lévy statistics for random single-molecule line shapes in a glass. Phys. Rev. Lett. 2002, 91, 0755021. [Google Scholar] [CrossRef] [PubMed]
- Furukawa, Y.; Nakai, Y.; Kunitomi, N. Stable distribution analysis of internal field distribution in Au(Fe) spin glass system. I Variation of the distribution with concentration. J. Phys. Soc. Jpn. 1993, 62, 306. [Google Scholar] [CrossRef]
- Stoneham, A.M. Shapes of inhomogeneously broadened resonance lines of solids. Rev. Mod. Phys. 1969, 41, 82–108. [Google Scholar] [CrossRef]
- Ghosh, K.; Fuchs, R. Critical behavior in the dielectric properties of random self-similar composites. Phys. Rev. B 1991, 44, 7330–7343. [Google Scholar] [CrossRef]
- Havriliak, S.; Negami, S. A complex plane representation of dielectric and mechanical relaxation processes in some polymers. Polymer 1967, 8, 161–210. [Google Scholar] [CrossRef]
Appendix A. Derivation of the Simple Form
Appendix B. Havriliak-Negami Distribution Function
© 2010 by the author; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license http://creativecommons.org/licenses/by/3.0/.
Share and Cite
Tuncer, E. Geometrical Description in Binary Composites and Spectral Density Representation. Materials 2010, 3, 585-613. https://doi.org/10.3390/ma3010585
Tuncer E. Geometrical Description in Binary Composites and Spectral Density Representation. Materials. 2010; 3(1):585-613. https://doi.org/10.3390/ma3010585
Chicago/Turabian StyleTuncer, Enis. 2010. "Geometrical Description in Binary Composites and Spectral Density Representation" Materials 3, no. 1: 585-613. https://doi.org/10.3390/ma3010585




