FRCM Confinement of Masonry: Strain Model Assessment and New Proposals
Abstract
:1. Introduction and Background of this Study
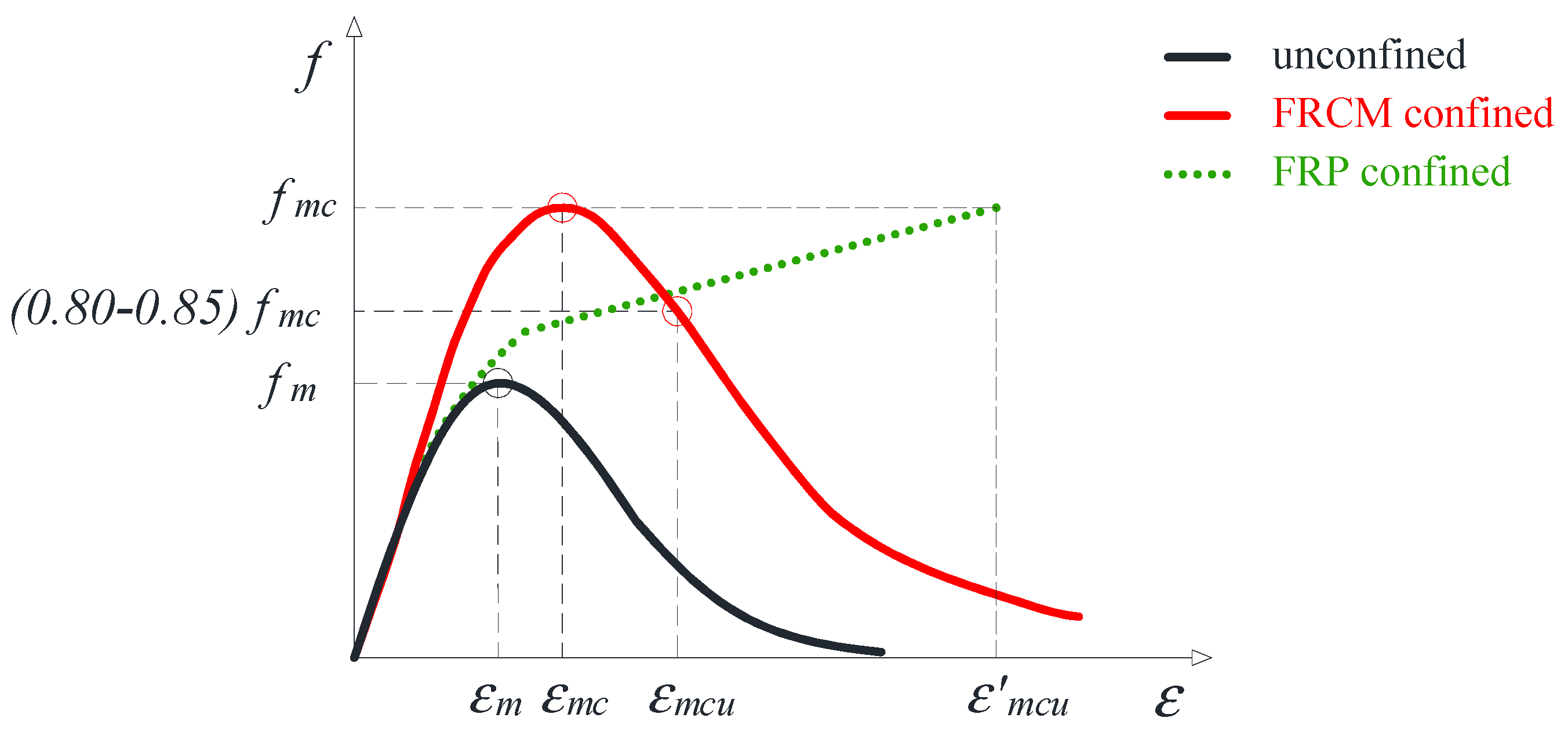
2. Structural Behavior of FRCM-Confined Masonry
- For unconfined masonry, is the compressive strength and , the corresponding strain.
- For FRP-confined masonry, is the compressive strength and , the corresponding strain that, in the case of an ascending stress–strain response, coincides with the ultimate one (i.e., the strain attained at jacket failure).
- For FRCM-confined masonry, is, again, the compressive strength while is the corresponding strain; is the conventional ultimate strain that, according to [19], is assumed to be in the range 80–85% of the peak axial stress, identified at the post-peak branch since, at that stage, the member’s structural capacity is believed to be rather compromised.
3. Overview of the Existing Strain Models
- = is the confinement efficiency factor, with (≤1) and (≤1) being the horizontal and vertical confinement efficiency factors, respectively, estimated by the various models.
- is the lateral confining pressure given bywhere
- is the geometric strengthening ratio related to the FRCM system, which is dependent on both the equivalent thickness of the single FRCM layer () multiplied by the number of FRCM layers (), i.e., , and the cross-section geometry of the confined member;
- and are the elastic modulus and the ultimate tensile strain of the dry strengthening sheet, respectively;
- (≤1) is the strain efficiency factor defined as the ratio between the ultimate hoop strain experimentally measured in the FRCM jacket (εj,u) and the ultimate strain found from fiber coupon tensile tests (εf,u).
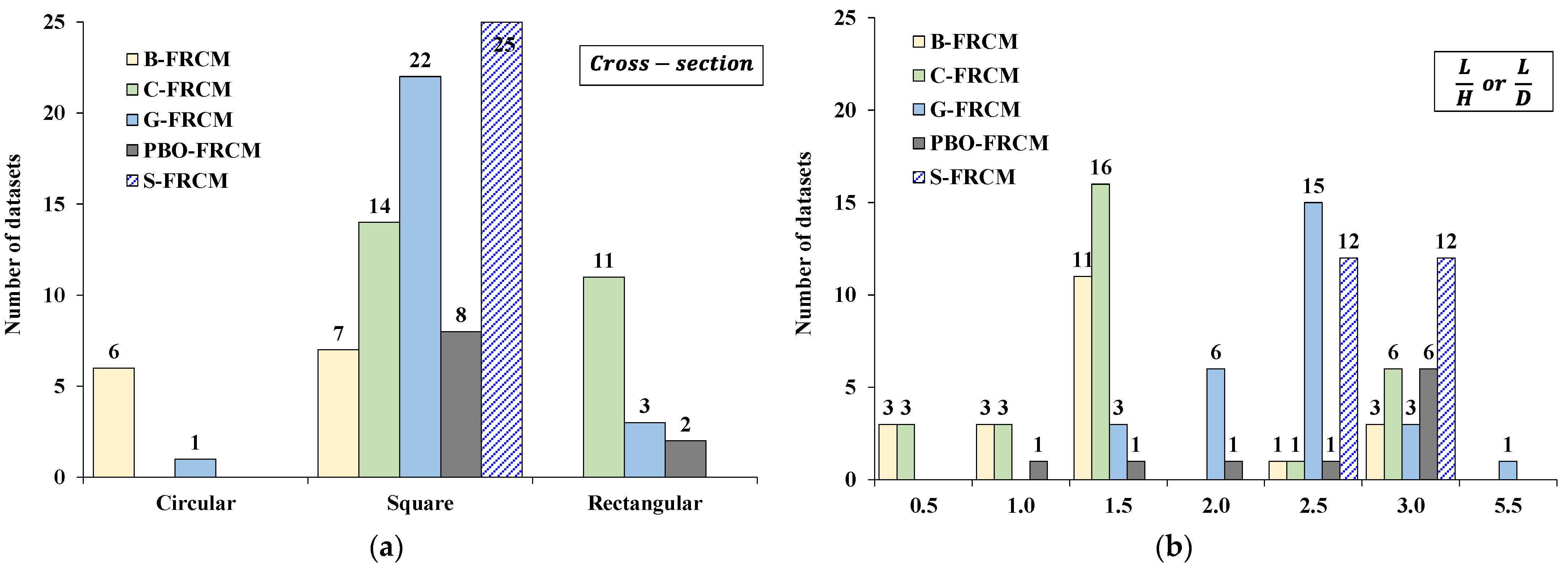
4. Collection of Experimental Datasets
- material and masonry arrangement;
- specimen size;
- geometry, typology of the FRCM system, and confinement layout;
- mechanical properties of the fiber mesh;
- thickness and mechanical properties of the inorganic matrix employed in the FRCM system;
- compressive strength of the unconfined masonry.
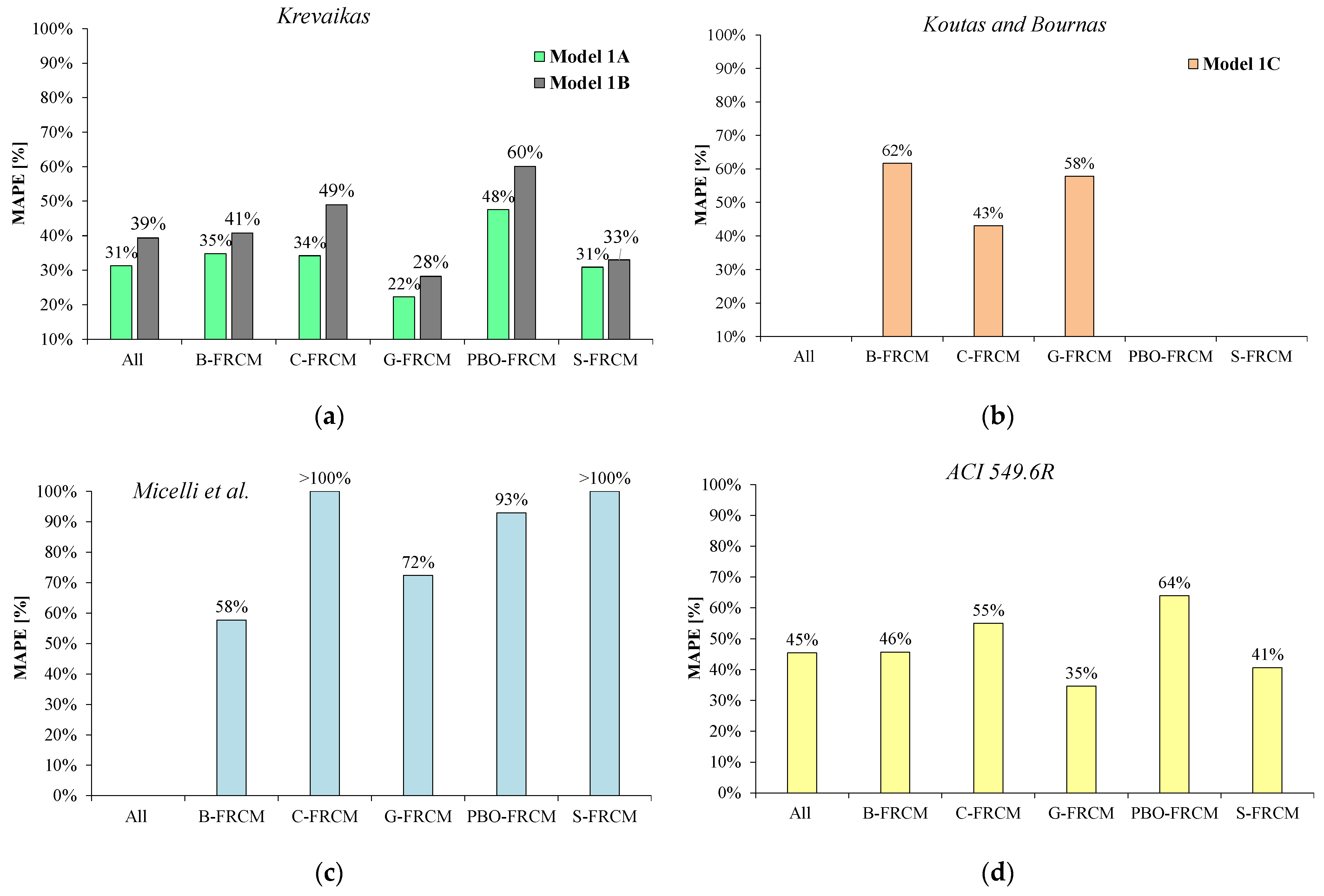
5. Assessment of the Existing Strain Models
- the subscript “i” stands for the i-th datasets;
- and are the i-th experimental values of the axial strain at the peak and ultimate, respectively, and and are the corresponding theoretical values estimated according to the models.
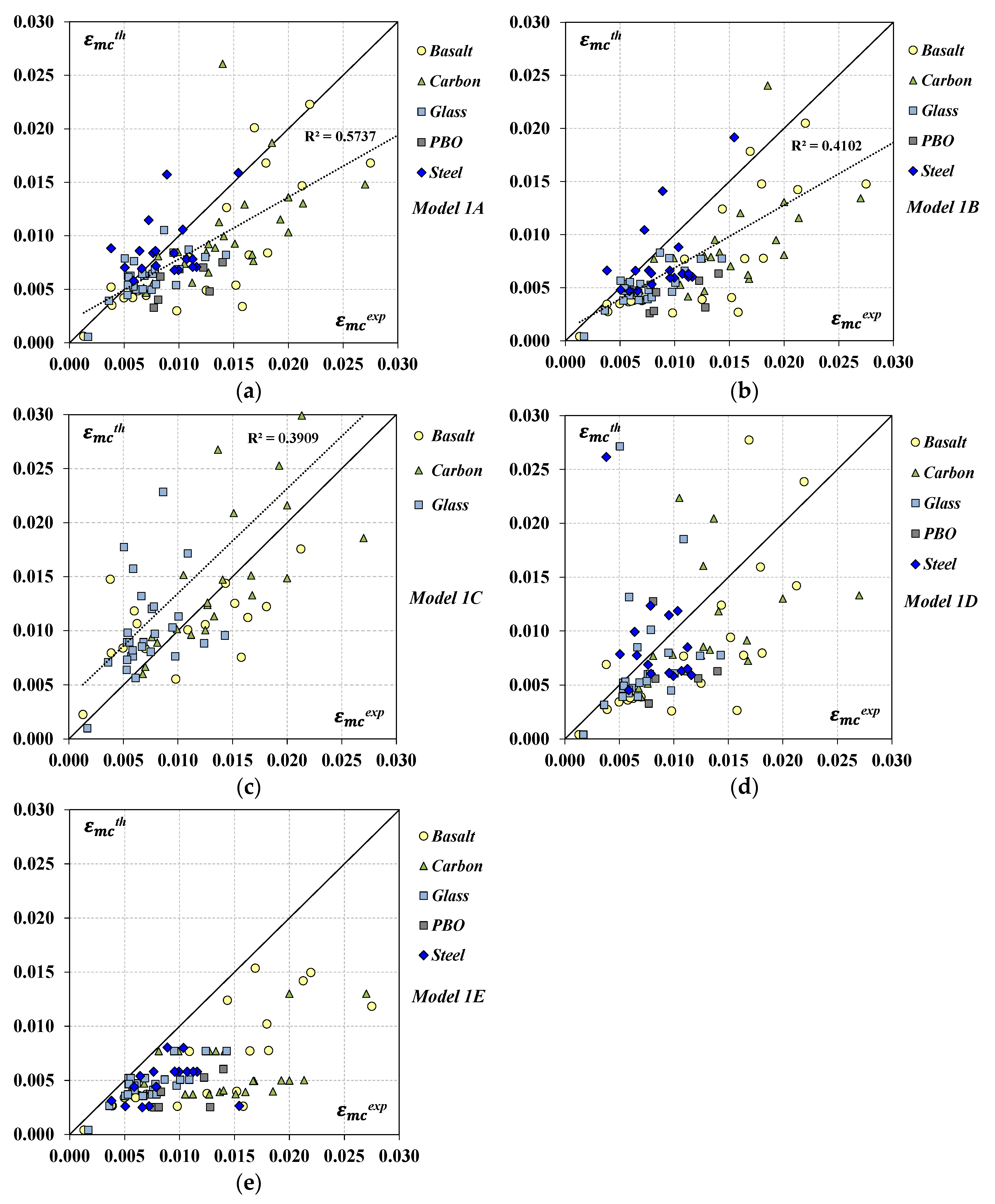
5.1. Prediction of the Peak Axial Strain
5.2. Prediction of the Ultimate Axial Strain
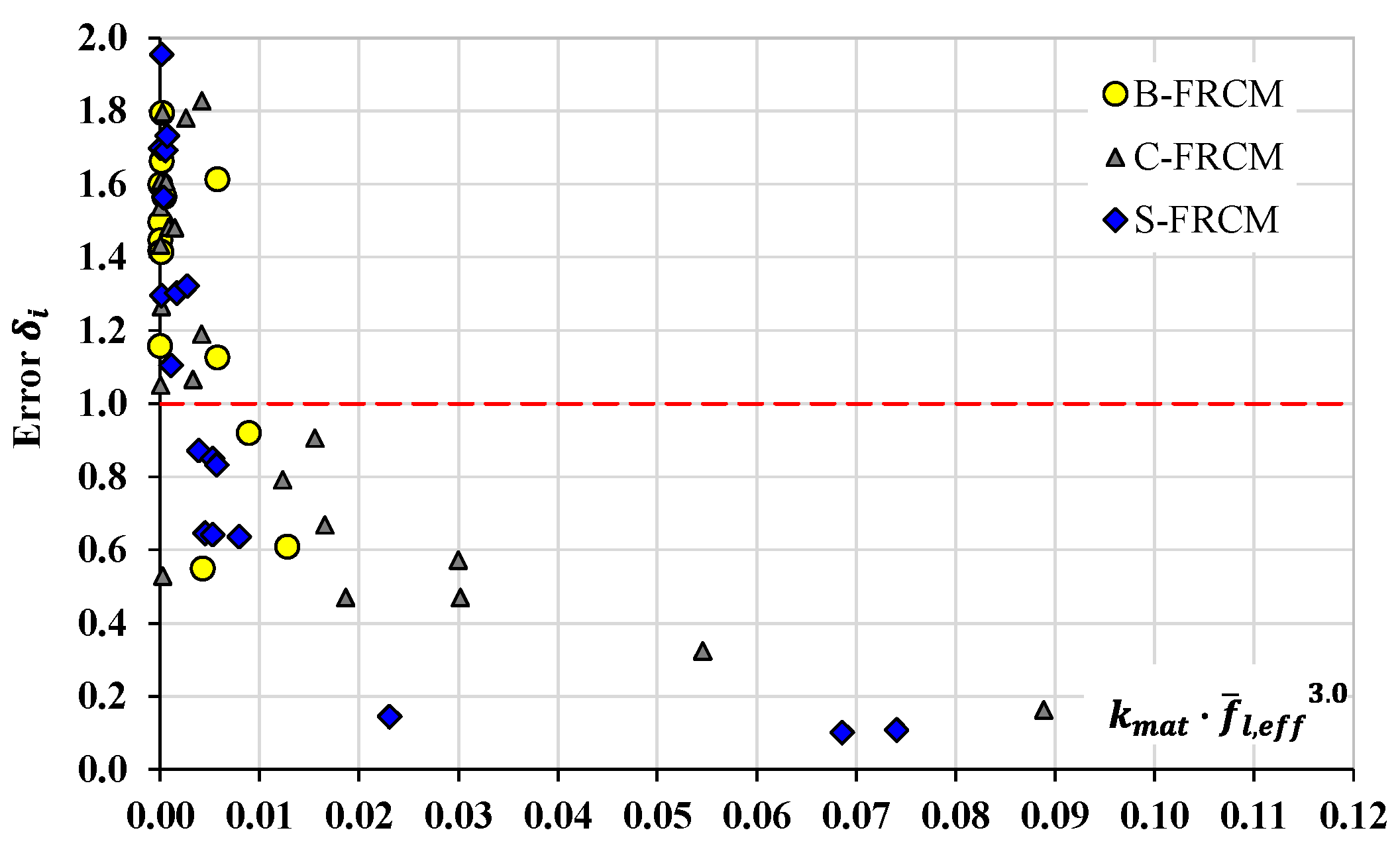
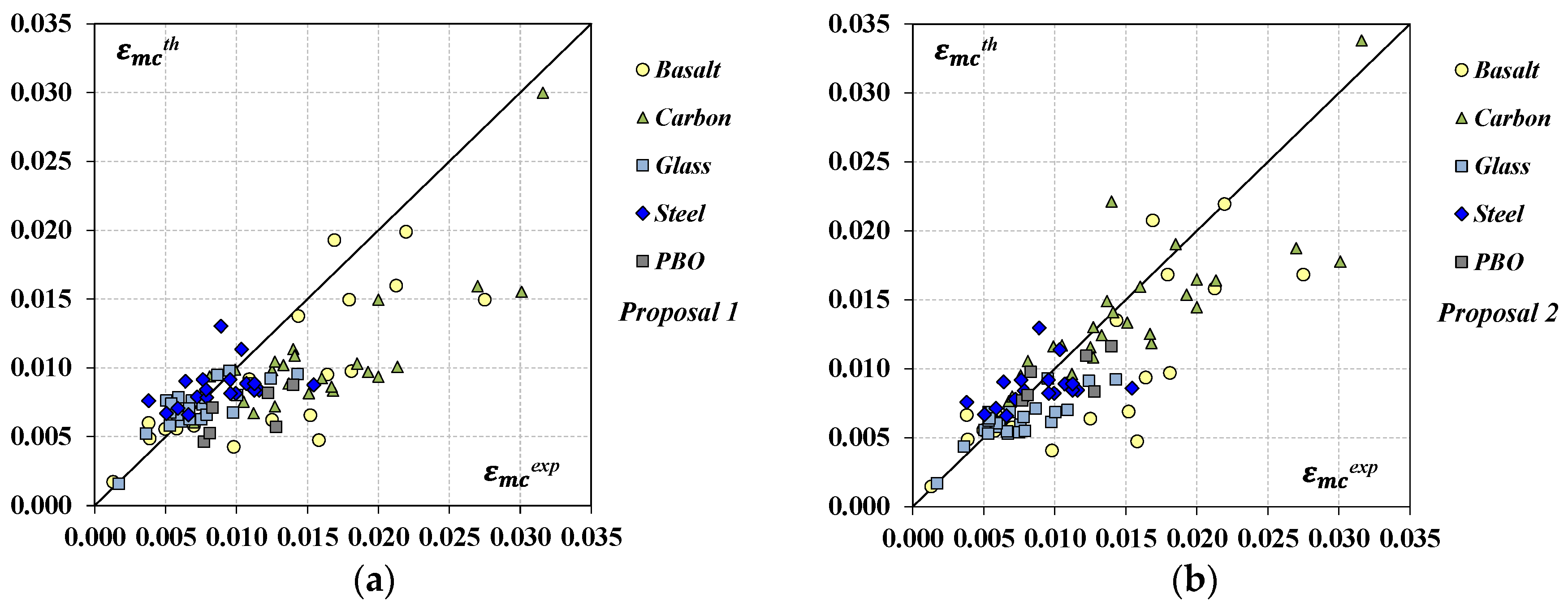
6. New Proposals
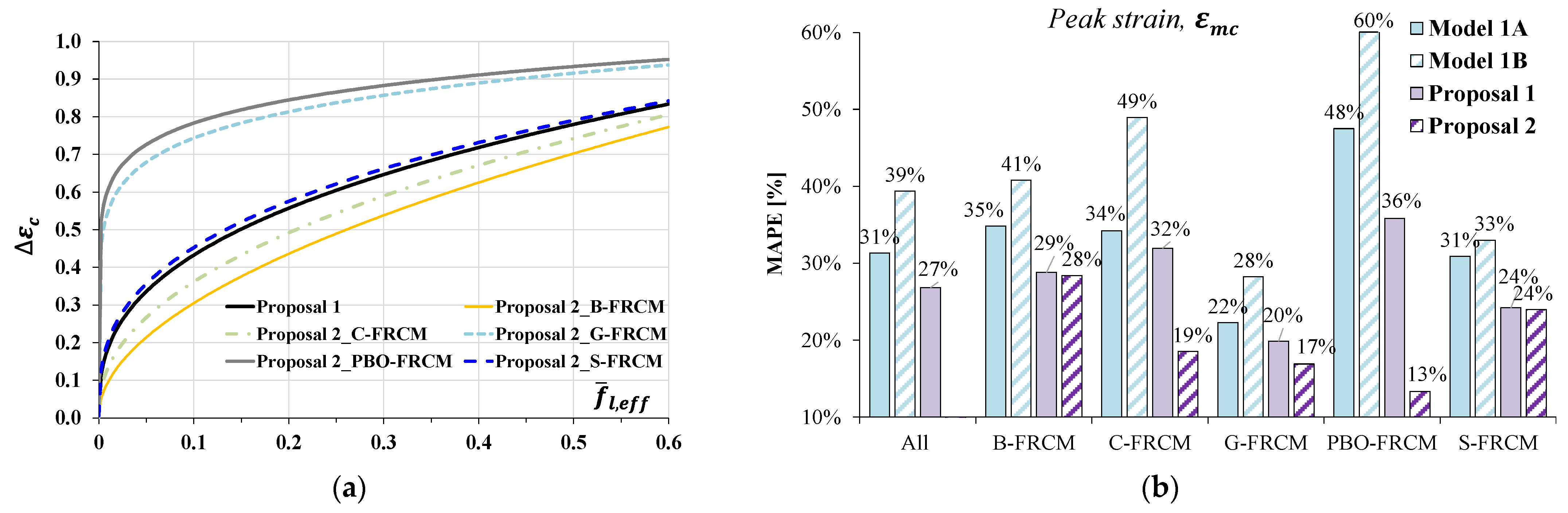
6.1. Proposal for the Prediction of the Peak Axial Strain
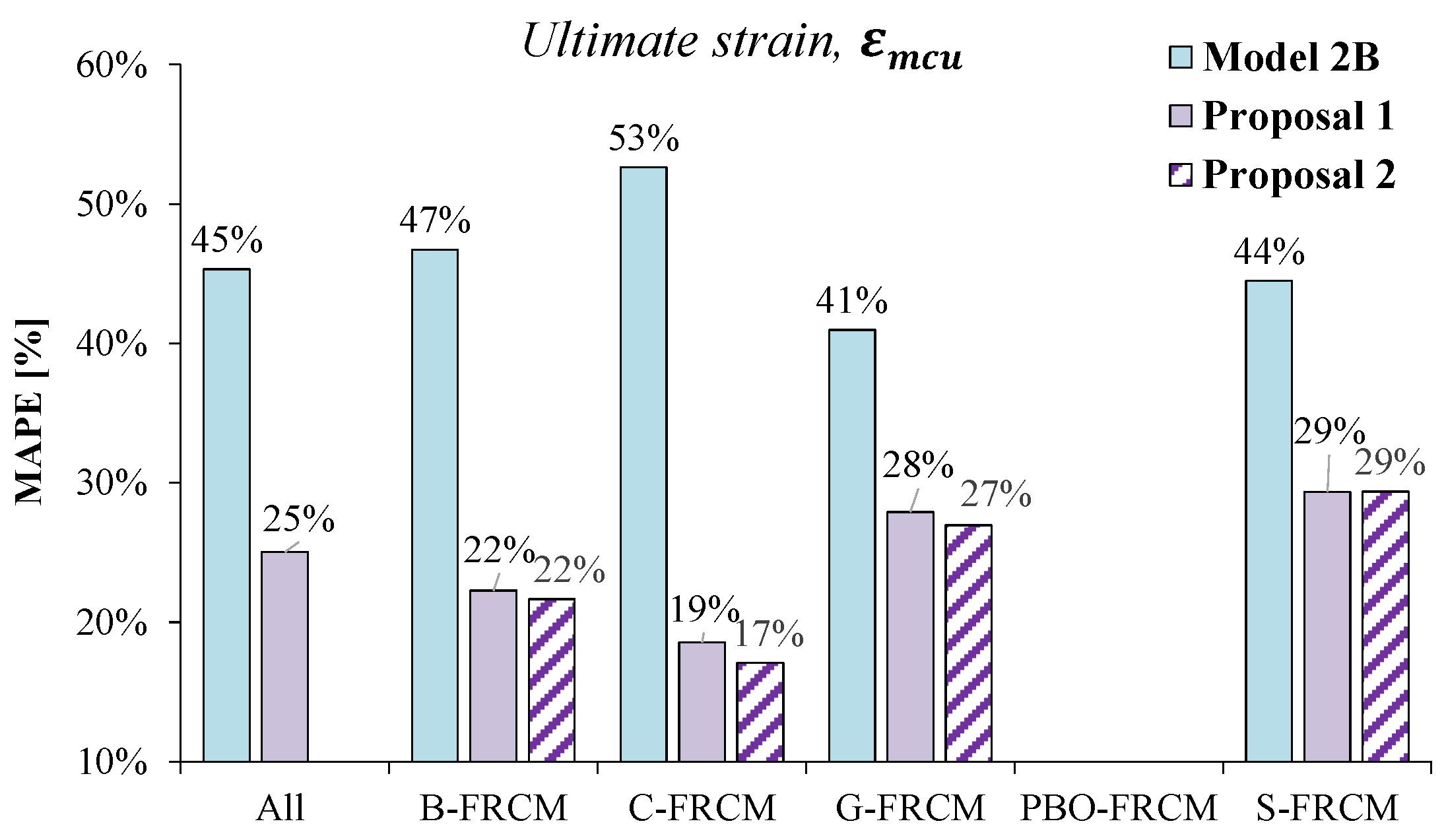
6.2. Proposal for the Prediction of the Ultimate Axial Strain
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Database Collection
- the reference to the manuscript (“source”) from which the experimental data were obtained;
- the nature of the masonry (type) and its mass density ;
- the label of each single dataset (ID);
- the number of specimens per dataset (N);
- the shape of the column cross-section (R = rectangular, S = square, C = circular);
- the width (B), depth (H), or diameter (D) of the cross-section and the height (H) of the column;
- the corner radius () of the column cross-section in the cases of S and R specimens;
- the compressive strength of the unconfined masonry (), corresponding axial strain , and ultimate one ;
- the elastic modulus in compression (, compressive strength (), and bending strength () of the inorganic matrix;
- the overall thickness of the FRCM jacket ();
- the density tensile strength , elastic modulus , and ultimate strain of the dry strengthening sheet ( and the equivalent thickness of the single layer (;
- the number and the overlapping length of the FRCM layers;
- the confinement layout (F-W = full-wrapping, DIS-W = discontinuous wrapping);
- the ratio between the compressive strength of the confined masonry and the strength of the unconfined masonry ;
- the ratio between the compressive strain at the peak strength of the confined masonry and the corresponding peak strain of the unconfined masonry ;
- the ratio between the conventional ultimate strain—at 15–20% strength decay in the softening branch—( and ;
- the dominant failure mode (FM) exhibited by test specimens (i.e., JF = jacket failure, DB = debonding of the reinforcement at the overlap region, S = fiber–matrix slippage (S)).
- Concerning the masonry mass density, it is noted that when it was not found in the literature, a typical average value of for that type of masonry was assumed and is indicated in the tables (in these cases, the values are reported in italics).
| Source | Masonry | Specimens | Strengthening | Results | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Matrix’s Properties | Fabric Mesh’s Properties | Jacket | ||||||||||||||||||||||||||
| Type | gm1 | Dataset ID | N | Shape | B | H | L | rc | fm | εm | εm,u | fmat,c | fmat,b | Emat | tmat | γf | ff,u | Ef | εf,u | tf,j | nf | Lb | Layout | fmc/fm | εmc/εm | εmcu/εm | FM | |
| [kg/m3] | [-] | [-] | [mm] | [mm] | [mm] | [mm] | [MPa] | [-] | [-] | [MPa] | [MPa] | [GPa] | [mm] | [g/m2] | [MPa] | [GPa] | [%] | [mm] | [-] | [mm] | [-] | [MPa] | [-] | [-] | ||||
| [23] | CB | 1700 | M1_BF_1,2 | 2 | S | 230 | 230 | 960 | 20 | 4.68 | 0.01420 | 0.01680 | 0.55 | 0.44 | - | 10 | 250 | 1542 | 89.00 | 1.80 | 0.039 | 1 | 460 | F-W | 1.74 | 1.50 | 1.75 | JF |
| M3_BF_1,2 | 2 | S | 9.42 | 0.01240 | 0.01390 | 4.54 | 3.13 | - | 10 | 1 | 460 | F-W | 1.14 | 1.16 | 1.29 | JF | ||||||||||||
| [24] | CB | 1700 | S-2B-L (1), (2) | 2 | S | 360 | 360 | 900 | 12 | 1.61 | 0.01020 | 0.01180 | 0.87 | - | - | 18 | 170 | - | 370.00 | 1.62 | 0.046 | 2 | 360 | F-W | 1.10 | 1.76 | 2.43 | JF |
| S-2B-F (1), (2) | 2 | S | 9.83 | - | - | 18 | 2 | 360 | F-W | 1.04 | 2.70 | 3.24 | JF | |||||||||||||||
| R-2B-L (1), (2) | 2 | R | 360 | 630 | 900 | 12 | 1.45 | 0.01495 | 0.01830 | 0.87 | - | - | 18 | 2 | 360 | F-W | 0.99 | 1.47 | 1.90 | JF | ||||||||
| R-2B-F (1), (2) | 2 | R | 9.83 | - | - | 18 | 2 | 360 | F-W | 1.00 | 1.13 | 1.57 | JF | |||||||||||||||
| [25] | LS | 1600 | S_Bgrid | 1 | S | 400 | 400 | 2100 | 20 | 4.78 | 0.00040 | 0.00050 | 13.61 | 15.54 | - | 15 | 250 | 1602 | 89.00 | 1.80 | 0.039 | 1 | 100 | F-W | 1.68 | 3.25 | 4.75 | DB |
| [26] | CB | 1700 | C-B-1 | 1 | S | 250 | 250 | 770 | 20 | 5.35 | 0.00260 | - | 12.85 | 2.65 | - | 6 | - | 930 | 70.30 | 1.40 | 0.064 | 1 | - | F-W | 1.44 | 3.77 | 7.31 | DB-JF |
| C-B-2 | 1 | S | 9 | 2 | - | F-W | 1.29 | 6.08 | 10.00 | DB-JF | ||||||||||||||||||
| [21] | CB | 1700 | A_B3 | 1 | S | 215 | 215 | 670 | 20 | 9.97 | 0.00370 | 0.00510 | 37.80 | 9.30 | - | 20 a | 220 | - | 89.00 | - | 0.037 | 3 | 195 | F-W | 1.15 | 1.89 | 2.38 | JF |
| A_B5 | 1 | S | 30 a | 5 | 195 | F-W | 1.31 | 3.38 | 3.57 | JF | ||||||||||||||||||
| A_B7 | 1 | S | 40 a | 7 | 195 | F-W | 1.44 | 4.11 | 4.35 | JF | ||||||||||||||||||
| B_B3 | 1 | R | 215 | 440 | 670 | 20 | 8.79 | 0.00770 | 0.01350 | 20 a | 3 | 195 | F-W | 1.03 | 1.42 | 1.95 | JF | |||||||||||
| B_B5 | 1 | R | 30 a | 5 | 195 | F-W | 1.11 | 2.13 | 2.34 | JF | ||||||||||||||||||
| B_B7 | 1 | R | 40 a | 7 | 195 | F-W | 1.17 | 2.35 | - | JF | ||||||||||||||||||
| [27] | LS | 2000 | BG.01.01, 02, 03, 04 | 4 | C | 83 | 218 | - | 20.79 | 0.00264 | - | 28.00 | 10.00 | 11.00 | 7 | 250 | 1542 | 89.00 | 1.80 | 0.039 | 1 | 130 | F-W | 1.21 | 1.47 | 2.28 | - | |
| BG.03.01, 02, 03, 04 | 4 | C | 10 | 3 | 130 | F-W | 1.24 | 1.44 | 6.38 | JF | ||||||||||||||||||
| [28] | CB | 1700 | C1, 2, 3, 4M_W1L | 4 | C | 94 | 190 | - | 25.19 | 0.00360 | 0.00380 | 25.00 | 8.00 | 10.00 | 4 | 250 | 1542 | 89.00 | 1.80 | 0.039 | 1 | 100 | F-W | 1.27 | 1.60 | 2.06 | JF | |
| C1, 2, 3M_W2L | 3 | C | 6 | 2 | 100 | F-W | 1.38 | 1.74 | 2.36 | JF | ||||||||||||||||||
| C1, 2, 3M_C1L | 3 | C | 19.85 | 0.00340 | 0.00380 | 4 | 1 | 100 | F-W | 1.66 | 1.46 | 2.22 | JF | |||||||||||||||
| C1, 2M_C2L | 2 | C | 6 | 2 | 100 | F-W | 1.85 | 1.76 | 2.49 | JF | ||||||||||||||||||
| Source | Masonry | Specimens | Strengthening | Results | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Matrix’s Properties | Fabric Mesh’s Properties | Jacket | ||||||||||||||||||||||||||
| Type | gm1 | Dataset ID | N | Shape | B | H | L | rc | fm | εm | εmu | fmat,c | fmat,b | Emat | tmat | γf | ff,u | Ef | εf,u | tf,j | nf | Lb | Layout | fmc/fm | εmc/εm | εmcu/εm | FM | |
| [kg/m3] | [-] | [-] | [mm] | [mm] | [mm] | [mm] | [MPa] | [-] | [-] | [MPa] | [MPa] | [GPa] | [mm] | [g/m2] | [MPa] | [GPa] | [%] | [mm] | [-] | [mm] | [-] | [MPa] | [-] | [-] | ||||
| [8] | CB | 1700 | C1_1_R20 | 3 | S | 240 | 240 | 300 | 20 | 1.19 | 0.00390 | 0.01350 | 5.27 | - | - | 5 | 220 | 4800 | 220.00 | 2.20 | 0.047 | 1 | 100 | F-W | 1.74 | 4.10 | 5.09 | JF |
| C1_1_R10 | 3 | S | 240 | 240 | 300 | 10 | 1 | 100 | F-W | 2.86 | 3.50 | 6.02 | JF | |||||||||||||||
| C2_1_R10 | 3 | S | 10 | 2 | 100 | F-W | 3.87 | 4.74 | 6.62 | JF | ||||||||||||||||||
| C3_1_R10 | 3 | S | 15 | 3 | 100 | F-W | 5.07 | 3.59 | 4.69 | JF | ||||||||||||||||||
| C1_1_R10 | 3 | S | 240 | 240 | 310 | 10 | 4.07 | 0.00495 | - | 35.00 | - | - | 6 | 270 | 3800 | 230.00 | 1.65 | 0.075 | 1 | 120 | F-W | 1.05 | 3.39 | - | DB-JF | |||
| C2_1_R10 | 3 | S | 9 | 2 | 120 | F-W | 1.28 | 4.04 | - | DB-JF | ||||||||||||||||||
| C3_1_R10 | 3 | S | 12 | 3 | 120 | F-W | 1.57 | 4.31 | - | DB-JF | ||||||||||||||||||
| C1_1_R20 | 3 | S | 240 | 240 | 310 | 20 | 6 | 1 | 120 | F-W | 0.87 | 3.37 | - | DB-JF | ||||||||||||||
| C2_1_R20 | 3 | S | 9 | 2 | 120 | F-W | 1.89 | 3.89 | - | DB-JF | ||||||||||||||||||
| C3_1_R20 | 3 | S | 12 | 3 | 120 | F-W | 2.22 | 7.27 | - | DB-JF | ||||||||||||||||||
| C1_1.5_R10 | 3 | R | 240 | 360 | 310 | 10 | 4.76 | 0.02640 | - | 6 | 1 | 180 | F-W | 1.08 | * | - | DB-JF | |||||||||||
| C2_1.5_R10 | 3 | R | 9 | 2 | 180 | F-W | 1.28 | 1.20 | - | DB-JF | ||||||||||||||||||
| C3_1.5_R10 | 3 | R | 12 | 3 | 180 | F-W | 1.55 | 1.44 | - | DB-JF | ||||||||||||||||||
| C1_2_R10 | 3 | R | 240 | 480 | 310 | 10 | 7.38 | 0.01300 | - | 6 | 1 | 240 | F-W | 0.96 | 1.54 | - | DB-JF | |||||||||||
| C2_2_R10 | 3 | R | 9 | 2 | 240 | F-W | 1.18 | 2.32 | - | DB-JF | ||||||||||||||||||
| C3_2_R10 | 3 | R | 12 | 3 | 240 | F-W | 1.23 | 2.08 | - | DB-JF | ||||||||||||||||||
| [9,29] | CB | 1700 | CP_RC170_01,02 | 2 | S | 380 | 380 | 1000 | 20 | 12.63 | 0.00472 | 6.52 | - | 5.90 | 7 | 170 | 2363 | 220.36 | 1.80 | 0.047 | 2 | 250 | F-W | 1.04 | 1.43 | - | JF | |
| [21] | CB | 1700 | A_CH1 | 1 | S | 215 | 215 | 670 | 20 | 9.97 | 0.00370 | 0.00500 | 37.80 | 9.30 | - | 10 a | 348 | 4800 | 225.00 | 2.13 | 0.095 | 1 | 195 | F-W | 1.13 | 2.05 | 2.36 | JF |
| A_CH2 | 1 | S | 215 | 215 | 670 | 20 | 37.80 | 9.30 | - | 15 a | 348 | 4800 | 225.00 | 2.13 | 0.095 | 2 | 195 | F-W | 1.47 | 2.84 | 3.76 | JF | ||||||
| A_CH3 | 1 | S | 20 a | 3 | 195 | F-W | 1.61 | 4.08 | 4.24 | JF | ||||||||||||||||||
| B_CH1 | 1 | R | 215 | 440 | 670 | 20 | 8.79 | 0.00770 | 0.00139 | 10 a | 1 | 195 | F-W | 1.18 | 1.62 | 2.38 | JF | |||||||||||
| B_CH2 | 1 | R | 15 a | 2 | 195 | F-W | 1.35 | 1.65 | - | JF | ||||||||||||||||||
| B_CH3 | 1 | R | 20 a | 3 | 195 | F-W | 1.37 | 1.83 | - | JF | ||||||||||||||||||
| A_CL1 | 1 | S | 215 | 215 | 670 | 20 | 9.97 | 0.00370 | 0.00500 | 10 a | 220 | 3800 | 225.00 | 1.69 | 0.062 | 1 | 195 | F-W | 1.07 | 1.89 | 1.98 | JF | ||||||
| A_CL2 | 1 | S | 15 a | 2 | 195 | F-W | 1.40 | 3.03 | - | JF | ||||||||||||||||||
| A_CL3 | 1 | S | 20 a | 3 | 195 | F-W | 1.45 | 3.43 | - | JF | ||||||||||||||||||
| B_CL1 | 1 | R | 215 | 440 | 670 | 20 | 8.79 | 0.00770 | 0.00139 | 10 a | 1 | 195 | F-W | 1.09 | 1.05 | 1.25 | JF | |||||||||||
| B_CL2 | 1 | R | 15 a | 2 | 195 | F-W | 1.19 | 1.29 | 1.76 | JF | ||||||||||||||||||
| B_CL3 | 1 | R | 20 a | 3 | 195 | F-W | 1.52 | 1.73 | - | JF | ||||||||||||||||||
| Source | Masonry | Specimens | Strengthening | Results | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Matrix’s Properties | Fabric Mesh’s Properties | Jacket | ||||||||||||||||||||||||||
| Type | gm1 | Dataset ID | N | Shape | B | H | L | rc | fm | εm | εmu | fmat,c | fmat,b | Emat | tmat | γf | ff,u | Ef | εf,u | tf,j | nf | Lb | Layout | fmc/fm | εmc/εm | εmcu/εm | FM | |
| [kg/m3] | [-] | [-] | [mm] | [mm] | [mm] | [mm] | [MPa] | [-] | [-] | [MPa] | [MPa] | [GPa] | [mm] | [g/m2] | [MPa] | [GPa] | [%] | [mm] | [-] | [mm] | [-] | [MPa] | [-] | [-] | ||||
| [25] | LS | 1600 | S_Grid | 1 | S | 400 | 400 | 2100 | 20 | 4.78 | 0.00040 | 0.00050 | 13.61 | 5.54 | - | 15 | 225 | 1296 | 72.00 | 1.80 | 0.035 | 1 | 100 | F-W | 1.50 | 4.25 | 5.25 | DB |
| [29] | CB | 1700 | CP_RV320_01, 02 | 2 | S | 380 | 380 | 1000 | 20 | 12.63 | 0.00472 | - | 6.52 | - | 5.90 | 7 | 300 | 1200 | 60.00 | 2.00 | 0.064 | 2 | 250 | F-W | 1.07 | 1.30 | - | JF |
| [30] | LS | 1530 | FRCM_M4_1, 2, 3 | 3 | S | 250 | 250 | 500 | 30 | 7.61 | 0.00520 | 0.01800 | 4.15 | - | - | 10 | 120 | 742.4 | 37.12 | 2.00 | 0.250 | 1 | 250 | F-W | 1.06 | 1.03 | 1.86 | DB-JF-S |
| FRCM_M7_1, 2, 3 | 3 | S | 7.26 | - | - | 10 | 1 | 250 | F-W | 1.31 | 1.32 | 2.24 | JF | |||||||||||||||
| FRCM_M23_1, 2, 3 | 3 | S | 250 | 250 | 500 | 30 | 22.93 | - | - | 10 | 1 | 250 | F-W | 1.87 | 1.07 | 1.47 | JF | |||||||||||
| [31] | LS | 1800 | CM8-1, 2, 3 | 3 | S | 250 | 250 | 500 | 20 | 5.23 | 0.00450 | 0.00962 | 1.67 | 0.79 | - | 10 | 220 | 1400 | 70.00 | 2.00 | 0.088 | 1 | 250 | F-W | 1.17 | 2.17 | 3.55 | JF |
| CM13-1, 2, 3 | 3 | S | 2.16 | 0.95 | - | 10 | 1 | 250 | F-W | 1.11 | 1.27 | 3.57 | JF | |||||||||||||||
| CC25-1, 2, 3 | 3 | S | 16.84 | 4.78 | - | 10 | 1 | 250 | F-W | 1.14 | 1.31 | 2.80 | JF | |||||||||||||||
| [21] | CB | 1700 | A_G3 | 1 | S | 215 | 215 | 670 | 20 | 9.97 | 0.00370 | 0.00500 | 37.80 | 9.30 | - | 20 a | 220 | 1400 | 74.00 | 1.89 | 0.044 | 3 | 195 | F-W | 1.28 | 1.43 | 1.59 | JF |
| A_G5 | 1 | S | 30 a | 5 | 195 | F-W | 1.35 | 2.03 | - | JF | ||||||||||||||||||
| A_G7 | 1 | S | 40 a | 7 | 195 | F-W | 1.49 | 2.14 | - | JF | ||||||||||||||||||
| B_G3 | 1 | R | 215 | 440 | 670 | 20 | 8.79 | 0.00770 | 0.00139 | 20 a | 3 | 195 | F-W | 1.02 | 1.61 | - | JF | |||||||||||
| B_G5 | 1 | R | 30 a | 5 | 195 | F-W | 1.08 | 1.86 | - | JF | ||||||||||||||||||
| B_G7 | 1 | R | 40 a | 7 | 195 | F-W | 1.12 | 1.23 | - | JF | ||||||||||||||||||
| [32] | TU | 1400 | 3, 4_RM—UniSal | 2 | S | 250 | 250 | 615 | 20 | 2.25 | 0.00505 | 0.00635 | 9.10 | - | - | 10 | 300 | 1929 | 108.00 | 1.80 | 0.060 | 1 | 250 | F-W | 1.10 | 1.99 | 3.80 | JF |
| 5, 6_RM—UniSal | 2 | S | 15 | 2 | 250 | F-W | 1.66 | 2.16 | 3.91 | JF | ||||||||||||||||||
| 7, 8_RM—UniSal | 2 | S | 20 | 3 | 250 | F-W | 2.08 | 1.71 | 2.84 | JF | ||||||||||||||||||
| TU | 1400 | 3, 4_RM—UniPa | 2 | S | 250 | 250 | 615 | 20 | 2.85 | 0.00355 | 0.00455 | 9.10 | - | - | 10 | 300 | 1929 | 108.00 | 1.80 | 0.060 | 1 | 250 | F-W | 1.00 | 1.89 | 4.25 | JF | |
| 5, 6_RM—UniPa | 2 | S | 15 | 2 | 250 | F-W | 1.10 | 1.87 | 3.62 | JF | ||||||||||||||||||
| 7, 8_RM—UniPa | 2 | S | 20 | 3 | 250 | F-W | 1.52 | 1.42 | 3.68 | JF | ||||||||||||||||||
| CB | 1600 | 3, 4_RM—UniCal | 2 | S | 250 | 250 | 575 | 20 | 3.58 | 0.00410 | 0.00540 | 9.10 | - | - | 10 | 300 | 1929 | 108.00 | 1.80 | 0.060 | 1 | 250 | F-W | 1.59 | 1.43 | 1.79 | JF | |
| 5, 6_RM—UniCal | 2 | S | 15 | 2 | 250 | F-W | 2.27 | 1.85 | 1.79 | JF | ||||||||||||||||||
| 7, 8_RM—UniCal | 2 | S | 20 | 3 | 250 | F-W | 2.32 | 1.44 | 1.80 | JF | ||||||||||||||||||
| CB | 1600 | 3, 4_RM—UniNa | 2 | S | 250 | 250 | 575 | 20 | 5.62 | 0.00465 | 0.00615 | 9.10 | - | - | 10 | 300 | 1929 | 108.00 | 1.80 | 0.060 | 1 | 250 | F-W | 1.18 | 1.15 | 1.63 | JF | |
| 5, 6_RM—UniNa | 2 | S | 15 | 2 | 250 | F-W | 1.05 | 1.16 | 1.41 | JF | ||||||||||||||||||
| 7, 8_RM—UniNa | 2 | S | 20 | 3 | 250 | F-W | 1.37 | 1.68 | 2.25 | JF | ||||||||||||||||||
| [27] | LS | 2000 | GG.01.01, 02, 03, 04 | 4 | C | 81 | 218 | - | 20.79 | 0.00264 | - | 28.00 | 10.00 | 11.00 | 7 | 125 | 1276 | 72.00 | 1.80 | 0.024 | 1 | 130 | F-W | 1.01 | * | 1.66 | JF | |
| GG.03.01, 02, 03, 04 | 4 | C | 10 | 3 | 130 | F-W | 1.26 | 1.37 | 2.21 | JF | ||||||||||||||||||
| Source | Masonry | Specimens | Strengthening | Results | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Matrix’s Properties | Fabric Mesh’s Properties | Jacket | ||||||||||||||||||||||||||
| Type | gm 1 | Dataset ID | N | Shape | B | H | L | rc | fm | εm | εmu | fmat,c | fmat,b | Emat | tmat | γf | ff,u | Ef | εf,u | tf,j | nf | Lb | Layout | fmc/fm | εmc/εm | εmcu/εm | FM | |
| [kg/m3] | [-] | [-] | [mm] | [mm] | [mm] | [mm] | [MPa] | [-] | [-] | [MPa] | [MPa] | [GPa] | [mm] | [g/m2] | [MPa] | [GPa] | [%] | [mm] | [-] | [mm] | [-] | [MPa] | [-] | [-] | ||||
| [10] | CB | 1700 | W_C-1, 2, 3 | 3 | R | 90 | 200 | 380 | 10 | 36.33 | 0.00557 | - | 28.40 | - | - | 8 | - | 5800 | 270.00 | 2.15 | 0.092 | 1 | 100 | F-W | 1.16 | * | - | S |
| SQ_C-1, 2, 3 | 3 | S | 102 | 100 | 240 | 10 | 29.07 | 0.00527 | - | 1 | 100 | F-W | 1.29 | 2.32 | - | S | ||||||||||||
| RECT_1_C-1, 2, 3 | 3 | R | 102 | 152 | 240 | 10 | 22.00 | 0.00603 | - | 1 | 100 | F-W | 1.72 | 2.32 | - | S | ||||||||||||
| RECT_2_C-1, 2 | 2 | R | 102 | 204 | 240 | 10 | 8.90 | 0.00393 | - | 1 | 100 | F-W | 3.97 | 1.59 | - | S | ||||||||||||
| [26] | CB | 1700 | C-P-1 | 1 | S | 250 | 250 | 770 | 20 | 5.35 | 0.00260 | - | 36.16 | 5.50 | - | 6 | - | 3400 | 211.40 | 2.50 | 0.046 | 1 | - | F-W | 1.98 | 10.12 ** | - | JF |
| C-P-2 | 1 | S | 0.00260 | - | 9 | 2 | - | F-W | 2.54 | 9.23 ** | - | DB | ||||||||||||||||
| C-P-3 | 1 | S | 0.00260 | - | 12 | 3 | - | F-W | 2.85 | 10.73 ** | - | DB | ||||||||||||||||
| [33] | CB | 1700 | C-D-P-1L | 1 | S | 250 | 250 | 770 | 20 | 5.19 | 0.00250 | - | 36.16 | 5.50 | - | 6 | - | 3400 | 211.40 | 2.59 | 0.046 | 1 | - | DIS-W | 1.34 | 3.08 | - | DB |
| C-D-P-2L | 1 | S | 0.00250 | - | 9 | 2 | - | DIS-W | 1.43 | 3.24 | - | DB | ||||||||||||||||
| C-D-P-3L | 1 | S | 0.00250 | - | 12 | 3 | - | DIS-W | 1.93 | 5.12 | - | DB | ||||||||||||||||
| Source | Masonry | Specimens | Strengthening | Strengthening | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Matrix’s Properties | Fabric Mesh’s Properties | Jacket | |||||||||||||||||||||||||||
| Type | gm1 | Dataset ID | N | Shape | B | H | L | rc | fm | εm | εmu | fmat,c | fmat,b | Emat | tmat | γf | ff,u | Ef | εf,u | tf,j | nf | Lb | kV | kH | fmc/fm | εmc/εm | εmcu/εm | FM | |
| [kg/m3] | [-] | [-] | [mm] | [mm] | [mm] | [mm] | [MPa] | [-] | [-] | [-] | [MPa] | [GPa] | [mm] | [g/m2] | [MPa] | [GPa] | [%] | [mm] | [-] | [mm] | [-] | [-] | [MPa] | [-] | [-] | ||||
| [34,35] | CB | 1700 | C-1-6-0-1, 2, 3, 4 | 4 | S | 250 | 250 | 720 | 0 | 7.38 | 0.00580 | 0.00857 | 15.00 | 5.00 | 9.00 | 8 | 670 | 2900 | 205.00 | 2.00 | 0.084 | 1 | 250 | 1.00 | 0.33 | 1.27 | 1.72 | 2.19 | DB |
| C-1-6-9-1, 2, 3 | 3 | S | 250 | 250 | 720 | 9.5 | 0.00580 | 0.00857 | 0.084 | 1 | 250 | 1.00 | 0.43 | 1.28 | 2.00 | 2.48 | DB | ||||||||||||
| C-1-6-38-1, 2, 3, 4 | 4 | S | 250 | 250 | 720 | 38.1 | 0.00580 | 0.00857 | 0.084 | 1 | 250 | 1.00 | 0.68 | 1.41 | 1.84 | 2.39 | DB | ||||||||||||
| C-1-12-9-1, 2, 3, 4 | 4 | S | 250 | 250 | 720 | 9.5 | 0.00580 | 0.00857 | 1200 | 0.169 | 1 | 250 | 1.00 | 0.43 | 1.35 | 1.31 | 1.58 | DB | |||||||||||
| [35] | CB | 1700 | C-2-6-0-1, 2, 3, 4 | 4 | S | 250 | 250 | 720 | 0 | 7.38 | 0.00580 | 0.00857 | 47.10 | 4.40 | - | 10 | 670 | 2900 | 205.00 | 2.00 | 0.084 | 1 | 240 | 1.00 | 0.33 | 1.26 | 1.65 | 1.96 | DB/JF |
| C-2-6-9-1, 2, 3, 4 | 4 | S | 250 | 250 | 720 | 9.5 | 0.00580 | 0.00857 | 0.084 | 1 | 200 | 1.00 | 0.43 | 1.33 | 1.94 | 2.85 | DB | ||||||||||||
| C-2-6-38-1, 2, 3, 4 | 4 | S | 250 | 250 | 720 | 38.1 | 0.00580 | 0.00857 | 0.084 | 1 | 200 | 1.00 | 0.68 | 1.39 | 1.94 | 3.42 | DB/JF | ||||||||||||
| C-2-12-9-1, 2, 3, 4 | 4 | S | 250 | 250 | 720 | 9.5 | 0.00580 | 0.00857 | 1200 | 0.169 | 1 | 200 | 1.00 | 0.43 | 1.42 | 1.65 | 2.00 | DB | |||||||||||
| [36] | CB | 1700 | C-12-1-1-0 | 1 | S | 250 | 250 | 770 | 20 | 5.19 | 0.00260 | - | 12.85 | 2.65 | - | 6 | 1200 | 2900 | 205.00 | 2.00 | 0.169 | 1 | 250 | 1.00 | 0.53 | 2.13 | 1.94 | - | DB |
| C-12-2-1-0 | 1 | S | 0.00260 | - | 9 | 2 | 250 | 1.00 | 0.53 | 1.96 | 2.78 | - | DB | ||||||||||||||||
| C-12-3-1-0 | 1 | S | 0.00260 | - | 12 | 3 | 250 | 1.00 | 0.53 | 2.91 | 5.94 | - | DB | ||||||||||||||||
| [26] | CB | 1700 | C-S-1, 2 | 1 | S | 250 | 250 | 770 | 20 | 5.19 | 0.00250 | - | 12.85 | 2.65 | - | 6 | 1200 | 2900 | 205.00 | 2.00 | 0.169 | 1 | 250 | 1.00 | 0.53 | 1.82 | 2.64 | - | DB |
| [31] | TU | 1400 | 2, 3, 4_RM—UniSa | 3 | S | 250 | 250 | 615 | 20 | 3.89 | 0.00540 | 0.00730 | 13.40 | - | - | 10 | 670 | 3080 | 193.40 | 2.17 | 0.084 | 1 | 375 | 1.00 | 0.53 | 1.28 | 1.19 | - | DB |
| 5, 6_RM—UniSa | 2 | S | 0.00540 | 0.00730 | 15 | 2 | 375 | 1.00 | 0.53 | 1.48 | * | - | DB | ||||||||||||||||
| 7, 8_RM—UniSa | 2 | S | 0.00540 | 0.00730 | 20 | 3 | 375 | 1.00 | 0.53 | 1.60 | * | - | DB | ||||||||||||||||
| TU | 1400 | 2, 3, 4_RM—UniFi | 3 | S | 250 | 250 | 615 | 20 | 4.33 | 0.00310 | 0.00360 | 13.40 | - | - | 10 | 670 | 3080 | 193.40 | 2.17 | 0.084 | 1 | 375 | 1.00 | 0.53 | 1.12 | 1.23 | 13.17 | DB | |
| 5, 6_RM—UniFi | 2 | S | 0.00310 | 0.00360 | 15 | 2 | 375 | 1.00 | 0.53 | 1.23 | 13.10 ** | - | DB | ||||||||||||||||
| 7, 8_RM—UniFi | 2 | S | 0.00310 | 0.00360 | 20 | 3 | 375 | 1.00 | 0.53 | 1.26 | 15.35 ** | - | DB | ||||||||||||||||
| CB | 1600 | 2, 3, 4_RM—UniBo | 3 | S | 250 | 250 | 575 | 20 | 9.09 | 0.00440 | 0.00690 | 13.40 | - | - | 10 | 670 | 3080 | 193.40 | 2.17 | 0.084 | 1 | 375 | 1.00 | 0.53 | 1.15 | 1.33 | 2.26 | DB | |
| 5, 6_RM—UniBo | 2 | S | 0.00440 | 0.00690 | 15 | 2 | 375 | 1.00 | 0.53 | 1.28 | 1.80 | 3.58 | DB | ||||||||||||||||
| 7, 8_RM—UniBo | 2 | S | 0.00440 | 0.00690 | 20 | 3 | 375 | 1.00 | 0.53 | 1.38 | 1.78 | 7.18 | DB | ||||||||||||||||
| CB | 1600 | 2, 3, 4_RM—PoliMi | 3 | S | 250 | 250 | 575 | 20 | 4.92 | 0.00800 | - | 13.40 | - | - | 10 | 670 | 3080 | 193.40 | 2.17 | 0.084 | 1 | 375 | 1.00 | 0.53 | 2.07 | * | 1.29 | DB | |
| 5, 6_RM—PoliMi | 2 | S | 0.00800 | - | 15 | 2 | 375 | 1.00 | 0.53 | 2.24 | 1.11 | 2.10 | DB | ||||||||||||||||
| 7, 8_RM—PoliMi | 1 | S | 0.00800 | - | 20 | 3 | 375 | 1.00 | 0.53 | 2.52 | 1.29 | 2.26 | DB | ||||||||||||||||
References
- Mercuri, M.; Vailati, M.; Gregori, A. Lime-based mortar reinforced with randomly oriented polyvinyl-alcohol (PVA) fibers for strengthening historical masonry structures. Dev. Built Environ. 2023, 14, 100152. [Google Scholar] [CrossRef]
- Kouris, L.A.S.; Triantafillou, T.C. State-of-the-art on strengthening of masonry structures with textile reinforced mortar (TRM). Constr. Build. Mater. 2018, 188, 1221–1233. [Google Scholar] [CrossRef]
- Irandegani, M.A.; Zhang, D.; Shadabfar, M.; Kontoni, D.-P.N.; Iqbal, M. Failure Modes of RC Structural Elements and Masonry Members Retrofitted with Fabric-Reinforced Cementitious Matrix (FRCM) System: A Review. Buildings 2022, 12, 653. [Google Scholar] [CrossRef]
- CNR-DT 215/2018; Guide for the Design and Construction of Externally Bonded Fibre Reinforced Inorganic Matrix Systems for Strengthening Existing Structures. National Research Council (CNR): Rome, Italy, 2018.
- ACI 549.6R 2020; Guide to Design and Construction of Externally Bonded Fabric-Reinforced Cementitious Matrix (FRCM) and Steel-Reinforced Grout (SRG) Systems for Repair and Strengthening Masonry Structures. American Concrete Institute (ACI): Farmington Hills, MI, USA, 2020.
- CNR-DT200 R1/2013; Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Existing Structures. National Research Council (CNR): Rome, Italy, 2013.
- ACI 440.2R 2017; Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures. American Concrete Institute (ACI): Farmington Hills, MI, USA, 2017.
- Krevaikas, T. Textile Reinforced Mortar System as a means for confinement of masonry structures. In Proceedings of the 12th International Symposium on Fiber Reinforced Polymers for Reinforced Concrete Structures (FRPRCS-12) and 5th Asia-Pacific Conference on Fiber Reinforced Polymers in Structures (APFIS-2015), Nanjing, China, 14–16 December 2015. [Google Scholar]
- Incerti, A.; Vasiliu, A.; Ferracuti, B.; Mazzotti, C. Uni-axial Compressive tests on masonry columns confined by FRP and FRCM. In Proceedings of the 12th International Symposium on Fiber Reinforced Polymers for Reinforced Concrete Structures (FRPRCS-12) and 5th Asia-Pacific Conference on Fiber Reinforced Polymers in Structures (APFIS-2015), Nanjing, China, 14–16 December 2015. [Google Scholar]
- Carloni, C.; Mazzotti, C.; Savoia, M.; Subramaniam, K.V. Confinement of Masonry Columns with PBO FRCM Composites. Key Eng. Mater. 2015, 624, 644–651. [Google Scholar] [CrossRef]
- Yan, L.B.; Chouw, N.; Jayaraman, K. Flax fibre and its composites—A review. Compos. Part. B 2014, 56, 296–317. [Google Scholar] [CrossRef]
- Dittenber, D.B.; GangaRao, H.V.S. Critical review of recent publications on use of natural composites in infrastructure. Compos. Part. A 2012, 43, 1419–1429. [Google Scholar] [CrossRef]
- Napoli, A.; Realfonzo, R. Compressive Behavior of Masonry Columns Confined with FRCM Systems: Research Overview and Analytical Proposals. J. Compos. Constr. 2022, 26, 04022019. [Google Scholar] [CrossRef]
- Napoli, A.; Realfonzo, R. Confinement of Masonry with FRCM Composites: Strength Predictive Models. Compos. Struct. 2024, 331, 117864. [Google Scholar] [CrossRef]
- Bilotta, A.; Ceroni, F.; Nigro, E.; Pecce, M.R. Experimental tests on FRCM strengthening systems for tuff masonry elements. Constr. Build. Mater. 2017, 138, 114–133. [Google Scholar] [CrossRef]
- De Santis, S.; Ceroni, F.; de Felice, G.; Fagone, M.; Ghiassi, B.; Kwiecień, A.; Lignola, G.P.; Morganti, M.; Santandrea, M.; Valluzzi, M.R.; et al. Round Robin Test on tensile and bond behaviour of Steel Reinforced Grout systems. Compos. B. Eng. 2017, 127, 100–120. [Google Scholar] [CrossRef]
- Napoli, A.; Realfonzo, R. Compressive strength of concrete confined with fabric reinforced cementitious matrix (FRCM): Analytical models. Compos. C. Open Access 2020, 2, 100032. [Google Scholar] [CrossRef]
- Micelli, F.; Maddaloni, G.; Longo, F.; Prota, A. Axial Stress–Strain Model for FRCM Confinement of Masonry Columns. J. Compos. Constr. 2021, 25, 04020078. [Google Scholar] [CrossRef]
- EN1998-3 2005; Eurocode 8: Design of Structures for Earthquake Resistance Resistance—Part 3: Assessment and Retrofitting of Buildings. CEN, European Committee for Standardization: Brussels, Belgium, 2005.
- Lam, L.; Teng, J.G. Design-oriented stress–strain model for FRP-confined concrete. Constr. Build. Mater. 2003, 17, 471–489. [Google Scholar] [CrossRef]
- Koutas, L.N.; Bournas, D.A. Confinement of masonry columns with textile-reinforced mortar jackets. Constr. Build. Mater. 2020, 258, 120343. [Google Scholar] [CrossRef]
- Krevaikas, T.D. Experimental study on carbon fiber textile reinforced mortar system as a means for confinement of masonry columns. Constr. Build. Mater. 2019, 208, 723–733. [Google Scholar] [CrossRef]
- Fossetti, M.; Minafò, G. Strengthening of Masonry Columns with BFRCM or with Steel Wires: An Experimental Study. Fibers 2016, 4, 15. [Google Scholar] [CrossRef]
- Mezrea, P.E.; Ispir, M.; Binbir, E.; Bal, I.E.; Ilki, A. External jacketing of unreinforced historical masonry piers with open-grid basalt-reinforced mortar. J. Compos. Constr. 2017, 21, 04016110. [Google Scholar] [CrossRef]
- Maddaloni, G.; Cascardi, A.; Balsamo, A.; Di Ludovico, M.; Micelli, F.; Aiello, M.A.; Prota, A. Confinement of Full-Scale Masonry Columns with FRCM Systems. Key Eng. Mater. 2017, 747, 374–381. [Google Scholar] [CrossRef]
- Ombres, L.; Iorfida, A.; Verre, S. Confinement of Masonry Columns with PBO and Basalt FRCM Composites. Key Eng. Mater. 2019, 817, 392–397. [Google Scholar] [CrossRef]
- Estevan, L.; Baeza, F.J.; Bru, D.; Ivorra, S. Stone masonry confinement with FRP and FRCM composites. Constr. Build. Mater. 2020, 237, 117612. [Google Scholar] [CrossRef]
- D’Anna, J.; Amato, G.; Chen, J.F.; Minafò, G.; La Mendola, L. Experimental investigation on BFRCM confinement of masonry cylinders and comparison with BFRP system. Constr. Build. Mater. 2021, 297, 123671. [Google Scholar] [CrossRef]
- Murgo, F.S.; Mazzotti, C. Masonry columns strengthened with FRCM system: Numerical and experimental evaluation. Constr. Build. Mater. 2019, 202, 208–222. [Google Scholar] [CrossRef]
- Cascardi, A.; Micelli, F.; Aiello, M.A. FRCM-confined masonry columns: Experimental investigation on the effect of the inorganic matrix properties. Constr. Build. Mater. 2018, 186, 811–825. [Google Scholar] [CrossRef]
- Minafò, G.; La Mendola, L. Experimental investigation on the effect of mortar grade on the compressive behaviour of FRCM confined masonry columns. Compos. B. Eng. 2018, 146, 1–12. [Google Scholar] [CrossRef]
- Aiello, M.A.; Bencardino, F.; Cascardi, A.; D’Antino, T.; Fagone, M.; Frana, I.; La Mendola, L.; Lignola, G.P.; Mazzotti, C.; Micelli, F.; et al. Masonry columns confined with fabric reinforced cementitious matrix systems: A round robin test. Constr. Build. Mater. 2021, 298, 123816. [Google Scholar] [CrossRef]
- Aiello, M.A.; Cascardi, A.; Ombres, L.; Verre, S. Confinement of Masonry Columns with the FRCM-System: Theoretical and Experimental Investigation. Infrastructures 2020, 5, 101. [Google Scholar] [CrossRef]
- Sneed, L.H.; Carloni, C.; Baietti, G.; Fraioli, G. Confinement of clay masonry columns with SRG. Key Eng. Mater. 2017, 747, 350–357. [Google Scholar] [CrossRef]
- Sneed, L.H.; Baietti, G.; Fraioli, G.; Carloni, C. Compressive Behavior of Brick Masonry Columns Confined with Steel-Reinforced Grout Jackets. J. Compos. Constr. 2019, 23, 04019037. [Google Scholar] [CrossRef]
- Ombres, L.; Verre, S. Masonry columns strengthened with Steel Fabric Reinforced Cementitious Matrix (S-FRCM) jackets: Experimental and numerical analysis. Measurement 2018, 127, 238–245. [Google Scholar] [CrossRef]
- EN 1990:2002; Eurocode 0: Basis of Structural Design. CEN, European Committee for Standardization: Brussels, Belgium, 2002.
- Realfonzo, R.; Napoli, A. Confining concrete members with FRP systems: Predictive vs. design strain models. Compos. Struct. 2013, 104, 304–319. [Google Scholar] [CrossRef]



| Ref. | ID | Model | kH | kV | ||
|---|---|---|---|---|---|---|
| (a) | ||||||
| Krevaikas [22] | 1A | 0.85 | ||||
| 1B | ||||||
| Koutas and Bournas [21] | 1C | 0.85 | ||||
| Micelli et al. [18] | 1D | 1.00 | ||||
| ACI 549.6R [5] European approach | 1E | 1.00 | ||||
| (b) | ||||||
| ACI 549.6R [5] ACI approach | 2A | 1.00 | ||||
| Micelli et al. [18] | 2B | 1.00 | ||||
| Strain Data | ALL | B-FRCM | C-FRCM | G-FRCM | PBO-FRCM | S-FRCM | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N. Specimens | n. Datasets | N. Specimens | n. Datasets | N. Specimens | n. Datasets | N. Specimens | n. Datasets | N. Specimens | n. Datasets | N. Specimens | n. Datasets | |
| 243 | 112 | 41 | 21 | 62 | 29 | 59 | 28 | 17 | 10 | 6 | 24 | |
| 160 | 68 | 40 | 20 | 19 | 11 | 53 | 22 | – | – | 48 | 15 | |
| Strain Data | ALL | B-FRCM | C-FRCM | G-FRCM | PBO-FRCM | S-FRCM | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AM | NM | AM | NM | AM | NM | AM | NM | AM | NM | AM | NM | |
| 88 | 24 | 18 | 3 | 29 | – | 13 | 15 | 10 | – | 18 | 6 | |
| 49 | 19 | 17 | 3 | 11 | – | 7 | 15 | – | – | 14 | 1 | |
| (a) | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FRCM | n | Model 1A | Model 1B | Model 1C | ||||||||||||
| [-] | [-] | [-] | [-] | [-] | [-] | [-] | [-] | [-] | [%] | [-] | [-] | [-] | [-] | [%] | ||
| ALL | 101 | 1.34 | 1.43 | 0.63 | 1.30 | 1.30 | 1.59 | 1.74 | 0.84 | 1.97 | 0.465 | - | - | - | - | - |
| B-FRCM | 21 | 1.37 | 1.74 | 0.95 | 1.57 | 1.83 | 1.61 | 2.09 | 1.22 | 1.80 | 0.087 | 0.79 | 0.92 | 0.48 | 0.88 | 0.144 |
| C-FRCM | 28 | 1.47 | 1.52 | 0.42 | 1.13 | 1.09 | 1.76 | 1.79 | 0.62 | -0.17 | 0.310 | 0.97 | 0.95 | 0.34 | 0.03 | 0.531 |
| G-FRCM | 27 | 1.13 | 1.23 | 0.47 | 1.27 | 1.28 | 1.36 | 1.52 | 0.63 | 3.15 | 0.020 | 0.75 | 0.80 | 0.34 | 1.10 | 0.071 |
| PBO-FRCM | 6 | 1.94 | 2.00 | 0.47 | 1.83 | 1.52 | 2.55 | 2.69 | 0.81 | 0.99 | 0.026 | - | - | - | - | - |
| S-FRCM | 19 | 0.98 | 1.05 | 0.35 | 0.87 | 0.98 | 1.26 | 1.29 | 0.42 | -0.21 | 0.022 | - | - | - | - | - |
| (b) | ||||||||||||||||
| FRCM | n | Model 1D | Model 1E | |||||||||||||
| [-] | [-] | [-] | [-] | [-] | [-] | [-] | [-] | [-] | [-] | |||||||
| ALL | 101 | 1.30 | 1.30 | 1.30 | 1.30 | 1.30 | 1.30 | 1.30 | 1.30 | 1.30 | 1.30 | |||||
| B-FRCM | 21 | 1.57 | 1.83 | 1.57 | 1.83 | 1.57 | 1.83 | 1.57 | 1.83 | 1.57 | 1.83 | |||||
| C-FRCM | 28 | 1.13 | 1.09 | 1.13 | 1.09 | 1.13 | 1.09 | 1.13 | 1.09 | 1.13 | 1.09 | |||||
| G-FRCM | 27 | 1.27 | 1.28 | 1.27 | 1.28 | 1.27 | 1.28 | 1.27 | 1.28 | 1.27 | 1.28 | |||||
| PBO-FRCM | 6 | 1.83 | 1.52 | 1.83 | 1.52 | 1.83 | 1.52 | 1.83 | 1.52 | 1.83 | 1.52 | |||||
| S-FRCM | 19 | 0.87 | 0.98 | 0.87 | 0.98 | 0.87 | 0.98 | 0.87 | 0.98 | 0.87 | 0.98 | |||||
| FRCM | n | Model 2B | ||||
|---|---|---|---|---|---|---|
| [-] | [-] | [-] | [-] | [%] | ||
| ALL | 68 | 1.74 | 2.33 | 1.53 | 2.51 | 0.718 |
| B-FRCM | 20 | 1.74 | 2.45 | 1.64 | 1.89 | 0.184 |
| C-FRCM | 11 | 2.76 | 2.66 | 1.32 | 0.29 | 0.140 |
| G-FRCM | 22 | 1.65 | 1.97 | 0.81 | 0.68 | 0.094 |
| PBO-FRCM | – | – | – | – | – | – |
| S-FRCM | 15 | 1.66 | 2.48 | 2.23 | 2.82 | 0.300 |
| FRCM | n | Proposal 1 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| [-] | [-] | [-] | [-] | [-] | [-] | [-] | [%] | [%] | ||
| ALL | 101 | 0.006 | 0.37 | 1.19 | 1.28 | 0.52 | 1.60 | 0.275 | 27 | |
| B-FRCM | 21 | 1.19 | 1.40 | 0.67 | 1.40 | 0.060 | 29 | |||
| C-FRCM | 28 | 1.47 | 1.58 | 0.52 | 1.64 | 0.182 | 32 | |||
| G-FRCM | 27 | 0.94 | 0.99 | 0.23 | 0.61 | 0.009 | 20 | |||
| PBO-FRCM | 6 | 1.57 | 1.62 | 0.35 | 1.04 | 0.011 | 36 | |||
| S-FRCM | 19 | 1.00 | 1.02 | 0.30 | 0.59 | 0.012 | 24 |
| FRCM | n | Proposal 2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| [-] | [-] | [-] | [-] | [-] | [-] | [-] | [%] | [%] | ||
| B-FRCM | 21 | 0.010 | 0.53 | 21 | 1.07 | 1.38 | 0.67 | 1.47 | 28 | |
| C-FRCM | 28 | 0.015 | 0.46 | 28 | 1.07 | 1.12 | 0.30 | 1.25 | 19 | |
| G-FRCM | 27 | 0.002 | 0.13 | 27 | 1.01 | 1.13 | 0.25 | 0.45 | 17 | |
| PBO-FRCM | 6 | 0.007 | 0.11 | 6 | 1.06 | 1.12 | 0.24 | 1.13 | 13 | |
| S-FRCM | 19 | 0.006 | 0.35 | 19 | 1.00 | 1.02 | 0.30 | 0.71 | 24 |
| FRCM | n | Proposal 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| [-] | [-] | [-] | [-] | [-] | [-] | [-] | [-] | [%] | [%] | ||
| ALL | 68 | 0.64 | 0.53 | 1.00 | 1.07 | 1.24 | 0.66 | 3.06 | 0.369 | 25 | |
| B-FRCM | 20 | 1.14 | 1.49 | 0.96 | 2.52 | 0.094 | 22 | ||||
| C-FRCM | 11 | 1.08 | 1.10 | 0.25 | 0.49 | 0.018 | 19 | ||||
| G-FRCM | 22 | 0.97 | 1.09 | 0.38 | 0.67 | 0.033 | 28 | ||||
| PBO-FRCM | - | - | - | - | - | - | - | ||||
| S-FRCM | 15 | 1.06 | 1.24 | 0.63 | 1.80 | 0.223 | 29 |
| FRCM | n | Proposal 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| [-] | [-] | [-] | [-] | [-] | [-] | [-] | [-] | [%] | [%] | ||
| B-FRCM | 20 | 1.00 | 0.66 | 1.00 | 1.05 | 1.41 | 0.94 | 2.60 | 0.084 | 22 | |
| C-FRCM | 11 | 1.29 | 0.66 | 0.72 | 1.00 | 1.03 | 0.23 | 0.30 | 0.019 | 17 | |
| G-FRCM | 22 | 0.65 | 0.58 | 1.00 | 0.99 | 1.13 | 0.40 | 0.64 | 0.035 | 27 | |
| PBO-FRCM | - | - | - | - | - | - | - | - | - | - | - |
| S-FRCM | 15 | 0.65 | 0.45 | 1.00 | 1.01 | 1.17 | 0.60 | 1.86 | 0.219 | 29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Napoli, A.; Realfonzo, R. FRCM Confinement of Masonry: Strain Model Assessment and New Proposals. Materials 2024, 17, 1159. https://doi.org/10.3390/ma17051159
Napoli A, Realfonzo R. FRCM Confinement of Masonry: Strain Model Assessment and New Proposals. Materials. 2024; 17(5):1159. https://doi.org/10.3390/ma17051159
Chicago/Turabian StyleNapoli, Annalisa, and Roberto Realfonzo. 2024. "FRCM Confinement of Masonry: Strain Model Assessment and New Proposals" Materials 17, no. 5: 1159. https://doi.org/10.3390/ma17051159
APA StyleNapoli, A., & Realfonzo, R. (2024). FRCM Confinement of Masonry: Strain Model Assessment and New Proposals. Materials, 17(5), 1159. https://doi.org/10.3390/ma17051159








