Comprehensive Understanding of the Effect of TGO Growth Modes on Thermal Barrier Coating Failure Based on a Simulation
Abstract
:1. Introduction
2. Numerical Model Development
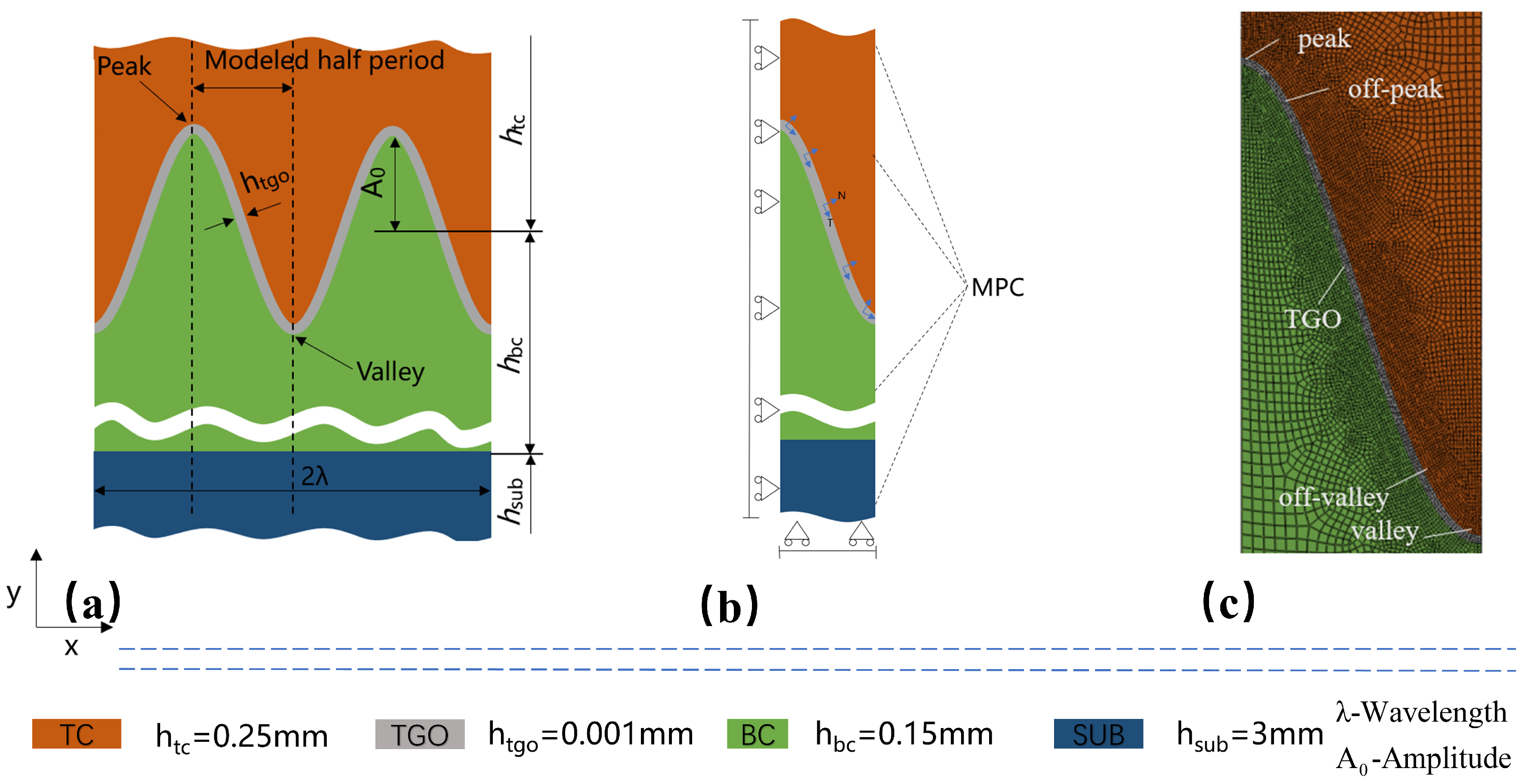
2.1. Geometry and Meshing
2.2. Material Property
2.3. Boundary Condition and Thermal Loading History
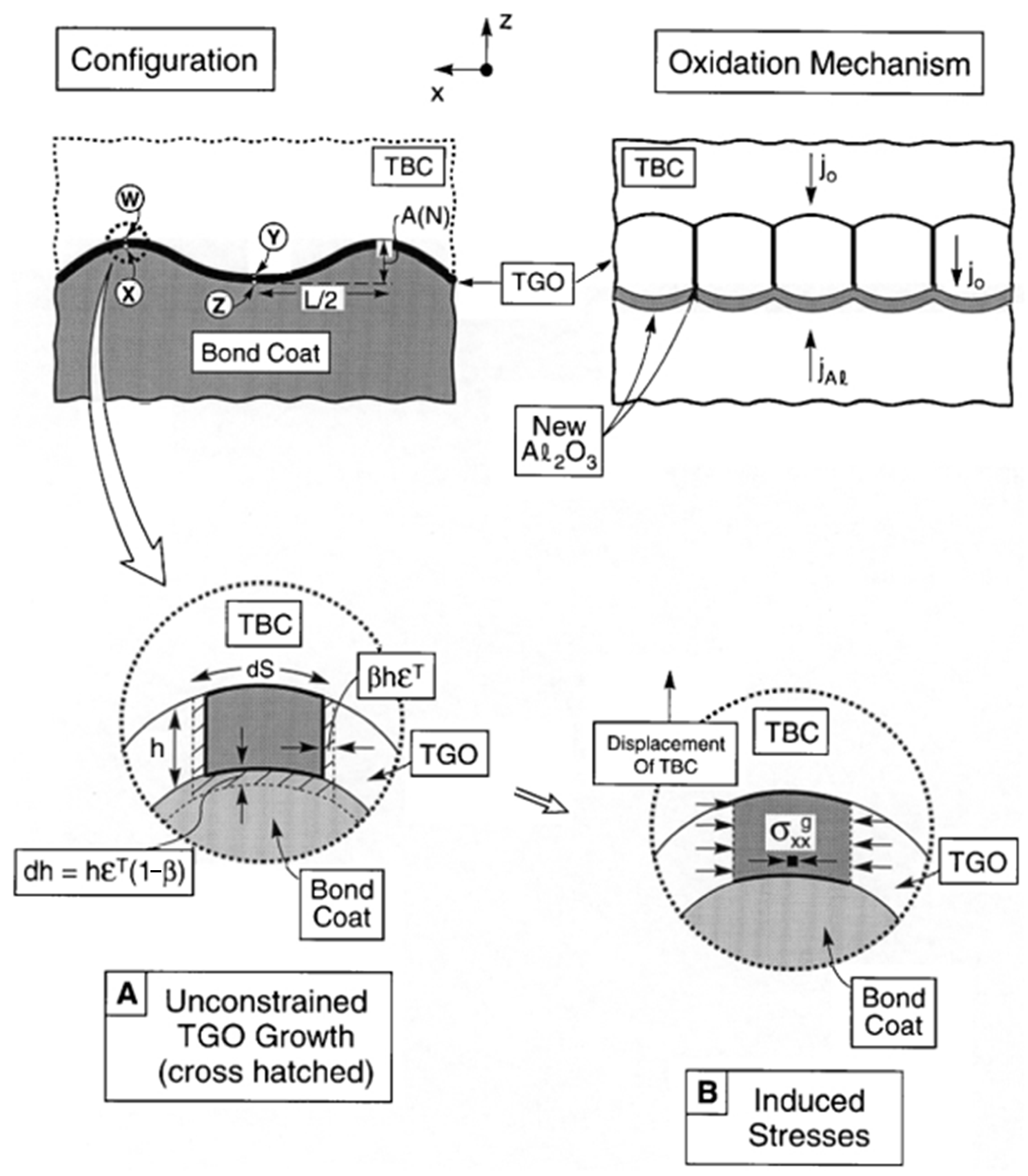
2.4. Dynamic TGO Growth Modeling
2.5. Modeling Tool Used for Crack Initiation and Propagation
3. Results and Discussions
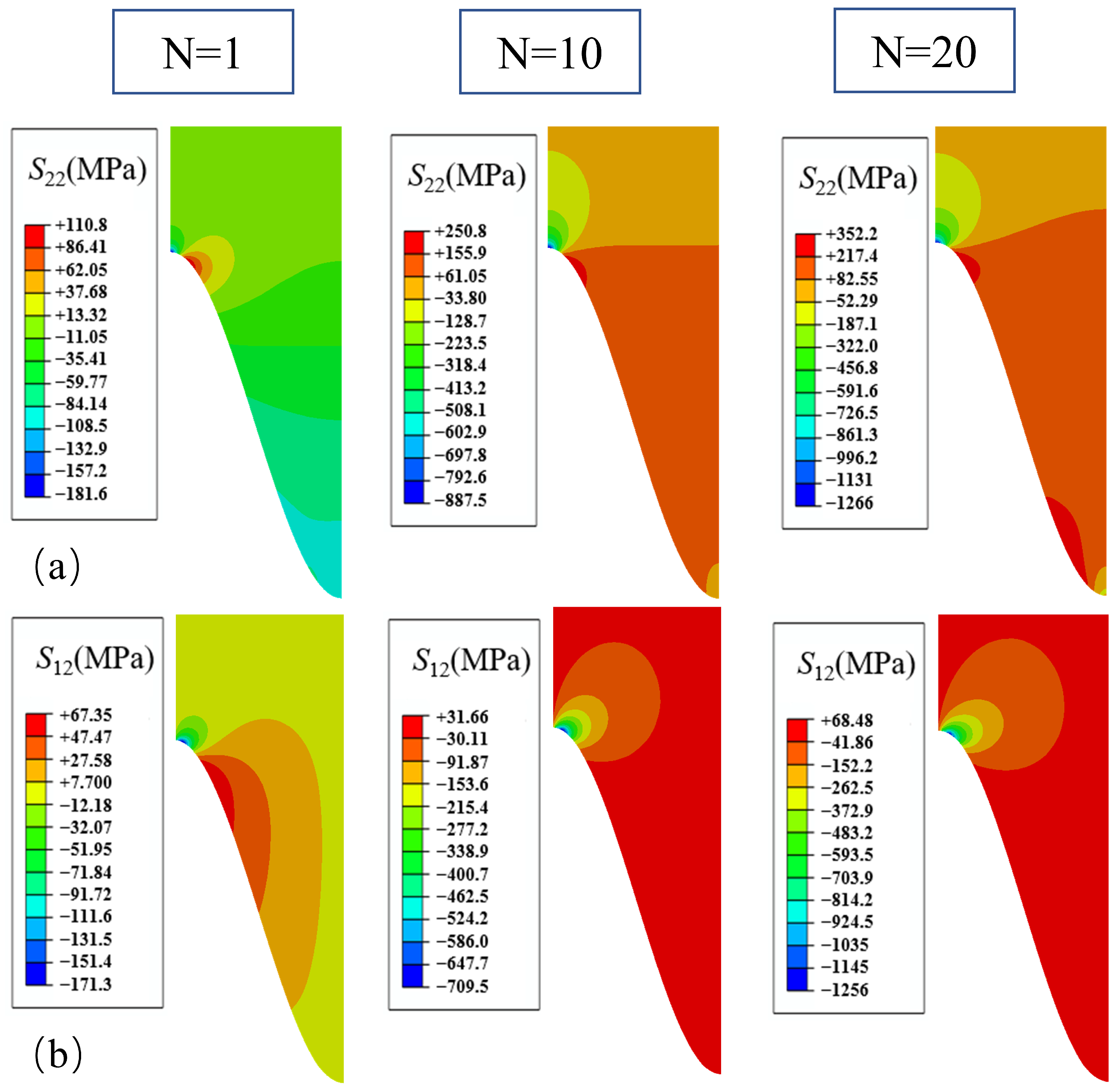
3.1. Stress Distribution for the Uniform TGO
3.1.1. Only the Thickening Growth
3.1.2. Thickening and Lateral Growth
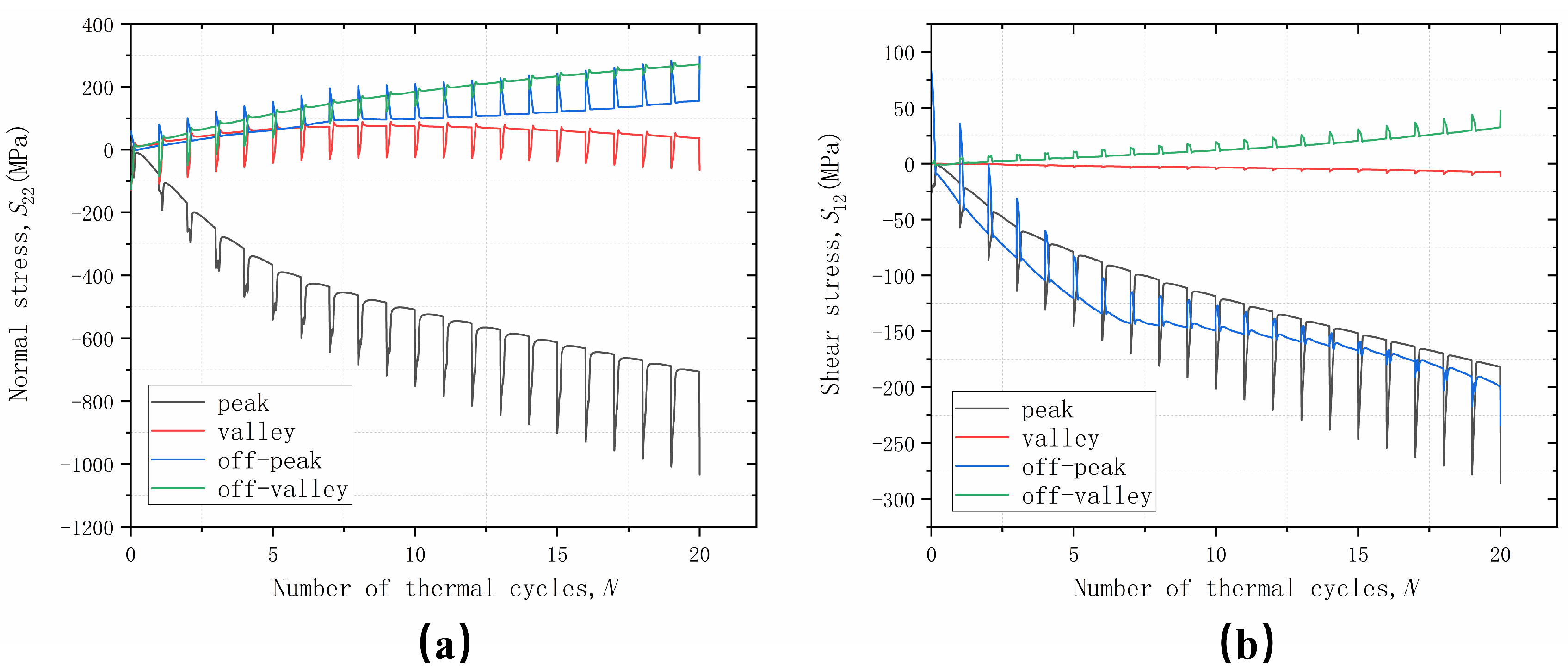
3.2. Stress Distribution for Non-Uniform Growth
3.2.1. Only the Thickening Growth
3.2.2. Thickening and Lateral Growth
3.3. Interfacial Cracking Behavior of TGO under Different Growth Modes
4. Conclusions
- (1)
- When only uniform growth in the direction of TGO thickening is considered, the worst stress conditions are found in the off-peak region. When lateral growth is also considered, tensile separation stresses to the off-valley region will increase. The shear separation stress S12 in the off-peak region will further increase;
- (2)
- When only non-uniform growth in the direction of TGO thickening is considered, the harshness of the stress in the off-peak region is further exacerbated. Lateral growth will increase the tensile separation stress in the off-valley region and decrease the tensile separation stress in the off-peak region. In addition, it greatly increases the shear separation stresses in the off-peak and peak regions and decreases the shear stresses in the off-valley region;
- (3)
- Lateral growth has a greater influence on the interfacial damage and cracking behavior, which will lead to a change in the crack extension mode from the off-valley area as the crack initiation point. The non-uniformity accelerates the occurrence of failure behavior in the off-peak and peak areas, and also leads to destructive behavior in the off-valley area.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Goswami, B.; Ray, A.; Sahay, S. Thermal Barrier Coating System for Gas Turbine Application—A Review. High Temp. Mater. Process. 2004, 23, 73–92. [Google Scholar] [CrossRef]
- Padture, N.P. Advanced structural ceramics in aerospace propulsion. Nat. Mater. 2016, 15, 804–809. [Google Scholar] [CrossRef]
- Ang, A.S.M.; Berndt, C.C. A review of testing methods for thermal spray coatings. Int. Mater. Rev. 2014, 59, 179–223. [Google Scholar] [CrossRef]
- Abdelgawad, A.; Al-Athel, K. Effect of TGO thickness, pores, and creep on the developed residual stresses in thermal barrier coatings under cyclic loading using SEM image-based finite element model. Ceram. Int. 2021, 47, 20064–20076. [Google Scholar] [CrossRef]
- Richards, B.T.; Wadley, H.N.G. Plasma spray deposition of tri-layer environmental barrier coatings. J. Eur. Ceram. Soc. 2014, 34, 3069–3083. [Google Scholar] [CrossRef]
- Seiler, P.; Bäker, M.; Rösler, J. Influence of creep and cyclic oxidation in thermal barrier coatings. Int. J. Mater. Res. 2012, 103, 50–56. [Google Scholar] [CrossRef]
- Soltani, R.; Coyle, T.W.; Mostaghimi, J. Microstructure and creep behavior of plasma-sprayed yttria stabilized zirconia thermal barrier coatings. J. Therm. Spray Technol. 2008, 17, 244–253. [Google Scholar] [CrossRef]
- Beck, T.; Schweda, M.; Singheiser, L. Influence of interface roughness, substrate and oxide-creep on damage evolution and lifetime of plasma sprayed zirconia-based thermal barrier coatings. Procedia Eng. 2013, 55, 191–198. [Google Scholar] [CrossRef]
- Krishnamurthy, R.; Srolovitz, D.J. Sintering and microstructure evolution in columnar thermal barrier coatings. Acta Mater. 2009, 57, 1035–1048. [Google Scholar] [CrossRef]
- Cipitria, A.; Golosnoy, I.O.; Clyne, T.W. A sintering model for plasma-sprayed zirconia thermal barrier coatings. Part II: Coatings bonded to a rigid substrate. Acta Mater. 2009, 57, 993–1003. [Google Scholar] [CrossRef]
- Aranke, O.; Gupta, M.; Markocsan, N.; Li, X.H.; Kjellman, B. Microstructural evolution and sintering of suspension plasma-sprayed columnar thermal barrier coatings. J. Therm. Spray Technol. 2019, 28, 198–211. [Google Scholar] [CrossRef]
- Morelli, S.; Testa, V.; Bolelli, G.; Ligabue, O.; Molinari, E.; Antolotti, N.; Lusvarghi, L. CMAS corrosion of YSZ thermal barrier coatings obtained by different thermal spray processes. J. Eur. Ceram. Soc. 2020, 40, 4084–4100. [Google Scholar] [CrossRef]
- Gámez-Pérez, J.; Velazquez-Infante, J.C.; Franco-Urquiza, E.; Carrasco, F.; Santana, O.O.; Maspoch, M.L. Fracture behavior of quenched poly (lactic acid). Express Polym. Lett. 2011, 5, 82–91. [Google Scholar] [CrossRef]
- Wei, Z.Y.; Cai, H.N.; Feng, R.X.; Zhang, H. The combined effect of creep and TGO growth on the cracking driving force in a plasma-sprayed thermal barrier system. J. Therm. Spray Technol. 2019, 28, 1000–1016. [Google Scholar] [CrossRef]
- Torkashvand, K.; Poursaeidi, E.; Mohammadi, M. Effect of TGO thickness on the thermal barrier coatings life under thermal shock and thermal cycle loading. Ceram. Int. 2018, 44, 9283–9293. [Google Scholar] [CrossRef]
- Izadinia, M.; Soltani, R.; Sohi, M.H. Effect of segmented cracks on TGO growth and life of thick thermal barrier coating under isothermal oxidation conditions. Ceram. Int. 2020, 46, 7475–7481. [Google Scholar] [CrossRef]
- Góral, M.; Swadźba, R.; Kubaszek, T. TEM investigations of TGO formation during cyclic oxidation in two-and three-layered Thermal Barrier Coatings produced using LPPS, CVD and PS-PVD methods. Surf. Coat. Technol. 2020, 394, 125875. [Google Scholar] [CrossRef]
- Padture, N.P.; Gell, M.; Jordan, E.H. Thermal Barrier Coatings for Gas-Turbine Engine Applications. Science 2002, 296, 280–284. [Google Scholar] [CrossRef]
- Beck, T.; Białas, M.; Bednarz, P.; Singheiser, L.; Bobzin, K.; Bagcivan, N.; Daniel Parkot, P.; Kashko, T.; Petković, I.; Hallstedt, B.; et al. Modeling of coating process, phase changes, and damage of plasma sprayed thermal barrier coatings on Ni-base superalloys. Adv. Eng. Mater. 2010, 12, 110–126. [Google Scholar] [CrossRef]
- Trunova, O. Effect of Thermal and Mechanical Loadings on the Degradation and Failure Modes of APS TBCs. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 2006. [Google Scholar]
- Song, J.; Qi, H.; Shi, D.; Yang, X.; Li, S. Effect of non-uniform growth of TGO layer on cracking behaviors in thermal barrier coatings: A numerical study. Surf. Coat. Technol. 2019, 370, 113–124. [Google Scholar] [CrossRef]
- Evans, A.G.; He, M.Y.; Hutchinson, J.W. Mechanics-based scaling laws for the durability of thermal barrier coatings. Prog. Mater. Sci. 2001, 46, 249–271. [Google Scholar] [CrossRef]
- Yu, Q.M.; Zhou, H.L.; Wang, L.B. Influences of interface morphology and thermally grown oxide thickness on residual stress distribution in thermal barrier coating system. Ceram. Int. 2016, 42, 8338–8350. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, H.; Zhao, K.; Jia, W.; Fang, L. Influence of inhomogeneous thermally grown oxide thickness on residual stress distribution in thermal barrier coating system. Ceram. Int. 2018, 44, 16937–16946. [Google Scholar] [CrossRef]
- Song, J.; Li, S.; Yang, X.; Qi, H.; Shi, D. Numerical investigation on the cracking behaviors of thermal barrier coating system under different thermal cycle loading waveforms. Surf. Coat. Technol. 2018, 349, 166–176. [Google Scholar] [CrossRef]
- Wei, Z.Y.; Cai, H.N.; Li, C.J. Comprehensive dynamic failure mechanism of thermal barrier coatings based on a novel crack propagation and TGO growth coupling model. Ceram. Int. 2018, 44, 22556–22566. [Google Scholar] [CrossRef]
- Clarke, D.R. The lateral growth strain accompanying the formation of a thermally grown oxide. Acta Mater. 2003, 51, 1393–1407. [Google Scholar] [CrossRef]
- Burov, A.; Fedorova, E. Modeling of interface failure in a thermal barrier coating system on Ni-based superalloys. Eng. Fail. Anal. 2021, 123, 105320. [Google Scholar] [CrossRef]
- Liu, Y.; Quan, C.B.; Yang, X.G. Effect of non-uniform growth of TGO on stress development and failure mechanism of thermal barrier coatings. J. Aerosp. Power 2020, 35, 1140–1148. [Google Scholar]
- Cen, L.; Qin, W.Y.; Yu, Q.M. Analysis of interface delamination in thermal barrier coating system with axisymmetric structure based on corresponding normal and tangential stresses. Surf. Coat. Technol. 2019, 358, 785–795. [Google Scholar] [CrossRef]
- Białas, M. Finite element analysis of stress distribution in thermal barrier coatings. Surf. Coat. Technol. 2008, 202, 6002–6010. [Google Scholar] [CrossRef]
- Rajabi, M.; Aboutalebi, M.R.; Seyedein, S.H.; Ataie, S.A. Simulation of residual stress in thick thermal barrier coating (TTBC) during thermal shock: A response surface-finite element modeling. Ceram. Int. 2022, 48, 5299–5311. [Google Scholar] [CrossRef]
- Ranjbar-Far, M.; Absi, J.; Shahidi, S.; Mariaux, G. Impact of the non-homogenous temperature distribution and the coatings process modeling on the thermal barrier coatings system. Mater. Des. 2011, 32, 728–735. [Google Scholar] [CrossRef]
- Xu, T.; He, M.Y.; Evans, A.G. A numerical assessment of the durability of thermal barrier systems that fail by ratcheting of the thermally grown oxide. Acta Mater. 2003, 51, 3807–3820. [Google Scholar] [CrossRef]
- Cen, L.; Qin, W.Y.; Yu, Q.M. Finite Element Analysis of Interface Undulation and Interface Delamination in the MCrAlY Coating System Under Thermal Cycling: Considering Oxide Thickness and Top-Coat Effects. J. Therm. Spray Technol. 2020, 29, 597–610. [Google Scholar] [CrossRef]
- Ranjbar-Far, M.; Absi, J.; Mariaux, G.; Dubois, F. Simulation of the effect of material properties and interface roughness on the stress distribution in thermal barrier coatings using finite element method. Mater. Des. 2010, 31, 772–781. [Google Scholar] [CrossRef]
- Ranjbar-Far, M.; Absi, J.; Mariaux, G. Finite Element Modeling of the Different Failure Mechanisms of a Plasma Sprayed Thermal Barrier Coatings System. J. Therm. Spray Technol. 2012, 21, 1234–1244. [Google Scholar] [CrossRef]
- Rösler, J.; Bäker, M.; Aufzug, K. A parametric study of the stress state of thermal barrier coatings Part I: Creep relaxation. Acta Mater. 2004, 52, 4809–4817. [Google Scholar]
- Vaßen, R.; Giesen, S.; Stöver, D. Lifetime of plasma-sprayed thermal barrier coatings: Comparison of numerical and experimental results. J. Therm. Spray Technol. 2009, 18, 835–845. [Google Scholar] [CrossRef]
- Hille, T.S.; Nijdam, T.J.; Suiker, A.S.; Turteltaub, S.; Sloof, W.G. Damage growth triggered by interface irregularities in thermal barrier coatings. Acta Mater. 2009, 57, 2624–2630. [Google Scholar] [CrossRef]
- Deng, H.X.; Shi, H.J.; Yu, H.C.; Zhong, B. Effect of heat treatment at 900 °C on microstructural and mechanical properties of thermal barrier coatings. Surf. Coat. Technol. 2011, 205, 3621–3630. [Google Scholar] [CrossRef]
- Huang, Y.P.; Wei, Z.Y.; Cai, H.N.; Liu, Y.; Han, X.C. The effects of tgo growth stress and creep rate on tc/tgo interface cracking in aps thermal barrier coatings. Ceram. Int. 2021, 47, 24760–24769. [Google Scholar] [CrossRef]













| Material | Temperature/ °C | Elastic Modulus/ GPa | μ | Density/ (g·cm−3) | Thermal Expansion Coeff./ (10−6·K−1) | Thermal Conductivity/ (W·m−1·K−1) | Specific Heat/ (J·kg−1·K−1) |
|---|---|---|---|---|---|---|---|
| TC | 25 | 17.5 | 0.20 | 5.650 | 9.68 | 1.05 | 483 |
| 400 | - | 0.20 | 5.650 | 9.70 | 1.05 | 483 | |
| 800 | - | 0.20 | 5.650 | 9.88 | 1.05 | 483 | |
| 1000 | 12.4 | 0.20 | 5.650 | 10.34 | 1.05 | 483 | |
| TGO | 25 | 380 | 0.27 | 3.978 | 5.10 | 25.2 | 857 |
| 400 | - | 0.27 | 3.978 | - | 25.2 | 857 | |
| 800 | 338 | 0.27 | 3.978 | - | 25.2 | 857 | |
| 1000 | 312 | 0.27 | 3.978 | 9.80 | 25.2 | 857 | |
| BC | 25 | 183 | 0.30 | 7.320 | - | 4.6 | 501 |
| 400 | 152 | 0.30 | 7.320 | 12.50 | 6.4 | 593 | |
| 800 | 109 | 0.30 | 7.320 | 14.30 | 10.2 | 781 | |
| 1000 | - | 0.30 | 7.320 | 16.00 | 16.1 | 764 | |
| DZ411 | 25 | 129.9 | 0.30 | 8.344 | - | 8.6 | 469 |
| 400 | 118 | 0.30 | 8.344 | 12.90 | 15.5 | 501 | |
| 800 | 101 | 0.30 | 8.344 | 14.50 | 21.1 | 547 | |
| 1000 | 86 | 0.30 | 8.344 | 15.60 | 23.1 | 575 |
| Layers | Temperature/°C | Plastic Strain | σy/MPa |
|---|---|---|---|
| TGO | 20 | 0 | 10,000 |
| 900 | 0 | 10,000 | |
| 1000 | 0 | 1000 | |
| BC | 20 | 0 | 1000 |
| 300 | 0 | 1000 | |
| 750 | 0 | 100 | |
| 1000 | 0 | 100 | |
| DZ411 | 20 | 0 | 1280 |
| 650 | 0 | 1255 | |
| 700 | 0 | 1185 | |
| 800 | 0 | 955 | |
| 900 | 0 | 655 | |
| 980 | 0 | 595 | |
| 1000 | 0 | 356 |
| Layers | B (s−1·MPa−n) | n | T (°C) |
|---|---|---|---|
| TC | 1.8 × 10−9 | 1 | 1000 |
| TGO | 7.3 × 10−9 | 1 | 1000 |
| BC | 6.54 × 10−19 | 4.57 | ≤600 |
| 2.20 × 10−12 | 2.99 | 700 | |
| 1.84 × 10−7 | 1.55 | 800 | |
| 2.15 × 10−8 | 2.45 | ≥850 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, D.; Man, J.; Yan, W.; Xue, B.; Bian, X.; Zeng, W. Comprehensive Understanding of the Effect of TGO Growth Modes on Thermal Barrier Coating Failure Based on a Simulation. Materials 2024, 17, 180. https://doi.org/10.3390/ma17010180
Qiao D, Man J, Yan W, Xue B, Bian X, Zeng W. Comprehensive Understanding of the Effect of TGO Growth Modes on Thermal Barrier Coating Failure Based on a Simulation. Materials. 2024; 17(1):180. https://doi.org/10.3390/ma17010180
Chicago/Turabian StyleQiao, Da, Jixin Man, Wengao Yan, Beirao Xue, Xiangde Bian, and Wu Zeng. 2024. "Comprehensive Understanding of the Effect of TGO Growth Modes on Thermal Barrier Coating Failure Based on a Simulation" Materials 17, no. 1: 180. https://doi.org/10.3390/ma17010180





