Inverse Design of Micro Phononic Beams Incorporating Size Effects via Tandem Neural Network
Abstract
:1. Introduction
2. Theoretical Formulations and Methods
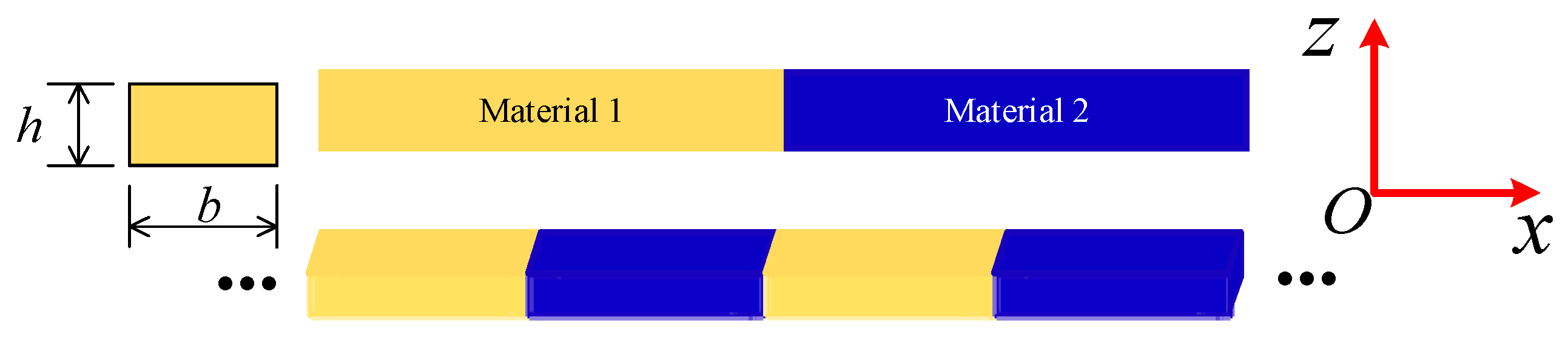
2.1. Model Descriptions of PnC Beam Incorporating Size Effects
2.2. Dispersion Analysis using the Transfer Matrix Method
2.3. The Neural Network Model
2.3.1. Basis of Artificial Neural Networks
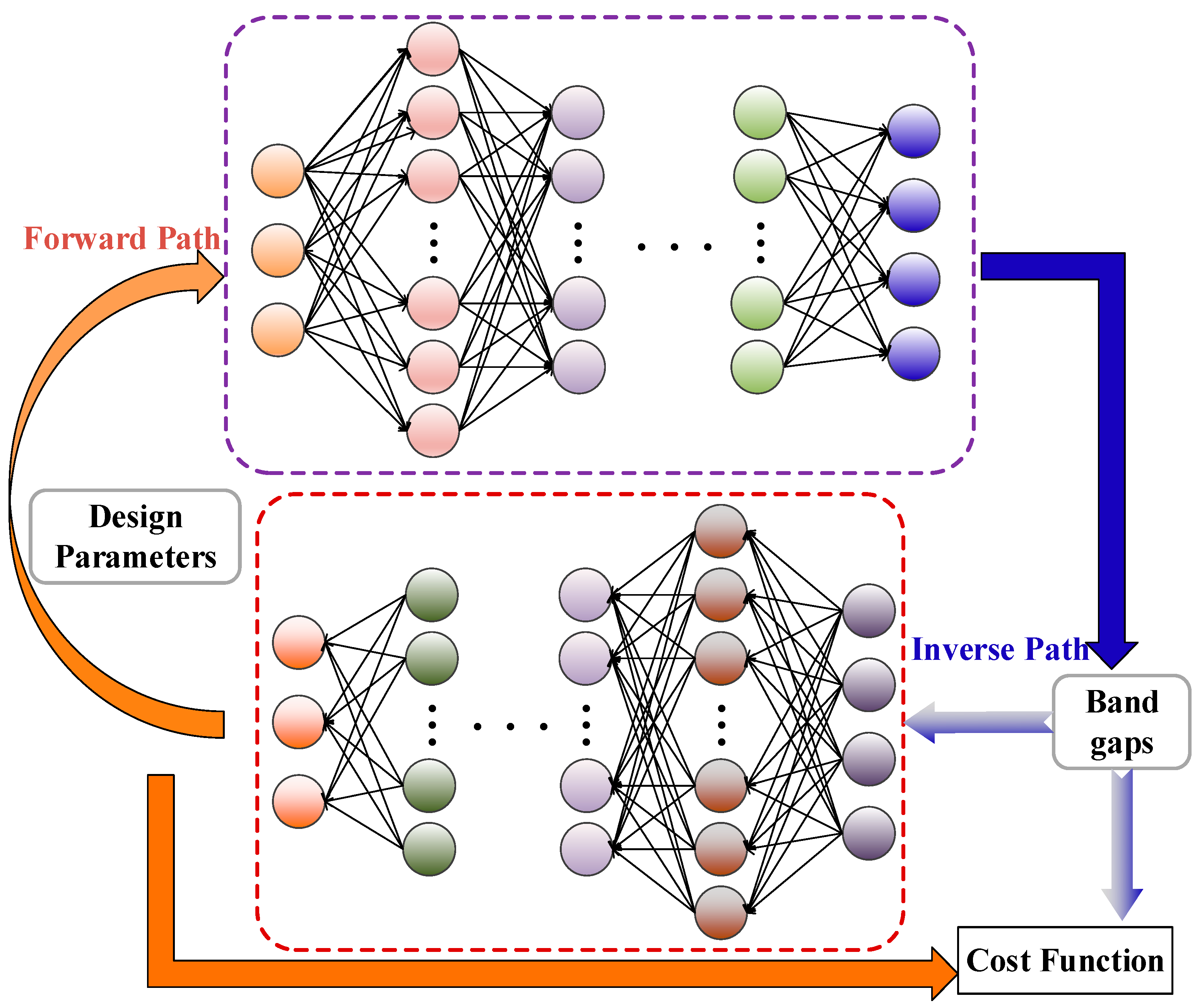
2.3.2. The Tandem Framework for Inverse Design
3. Results and Discussions
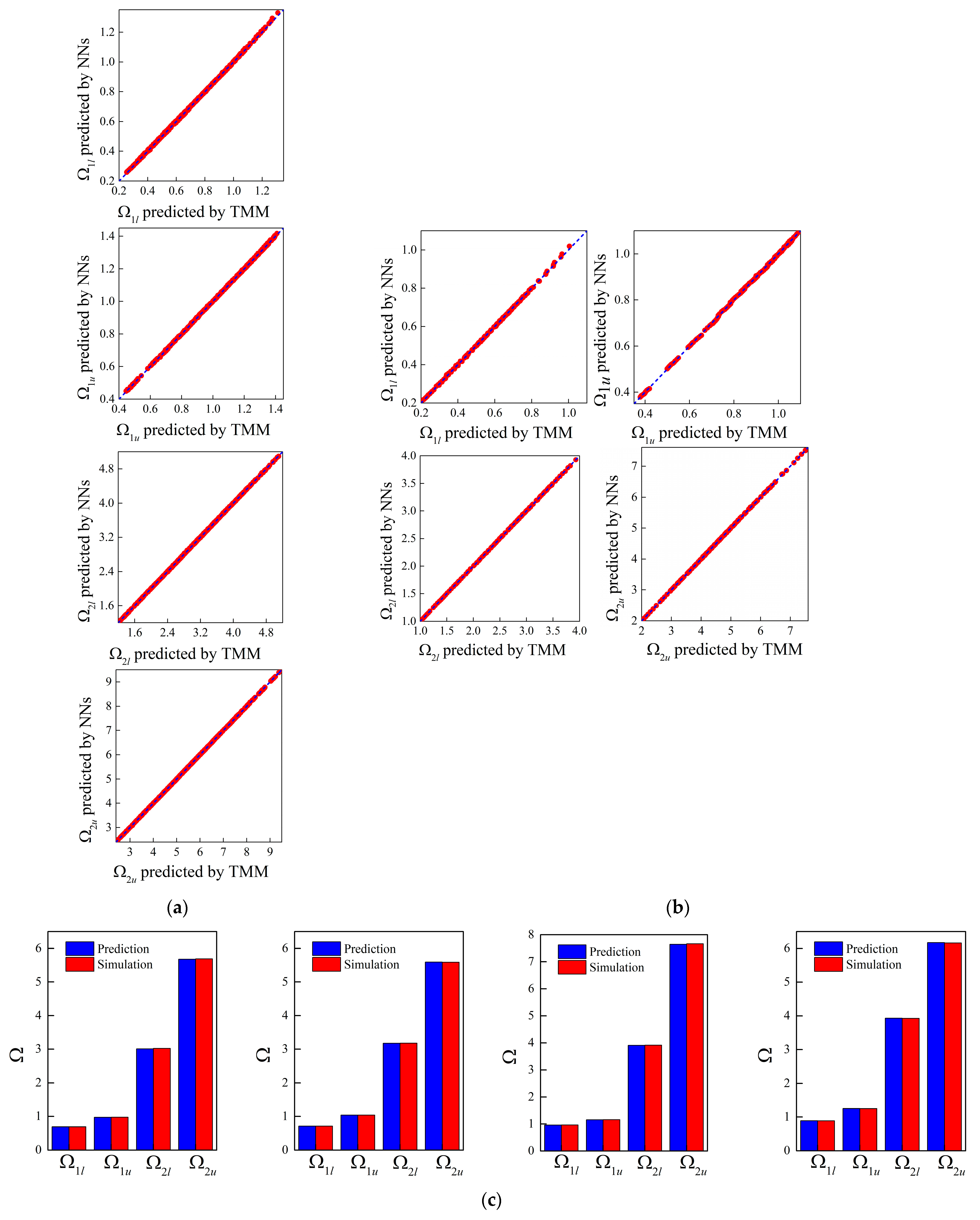
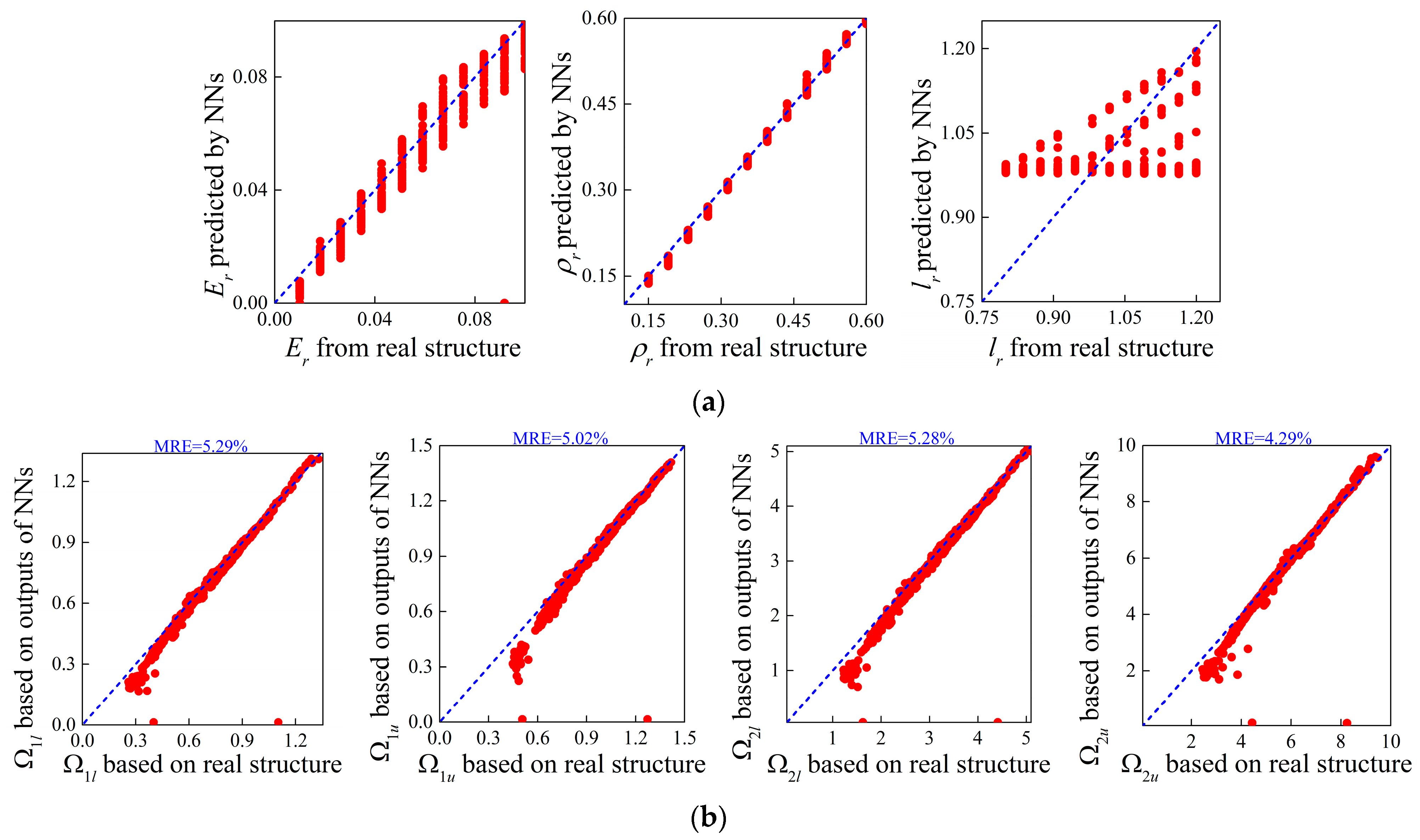
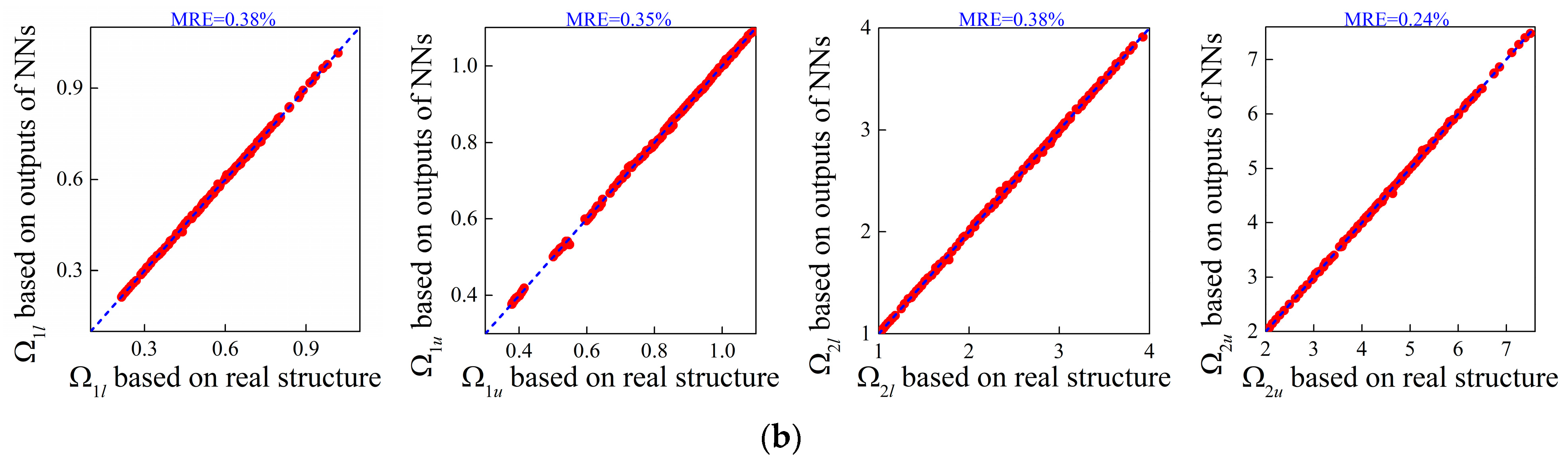
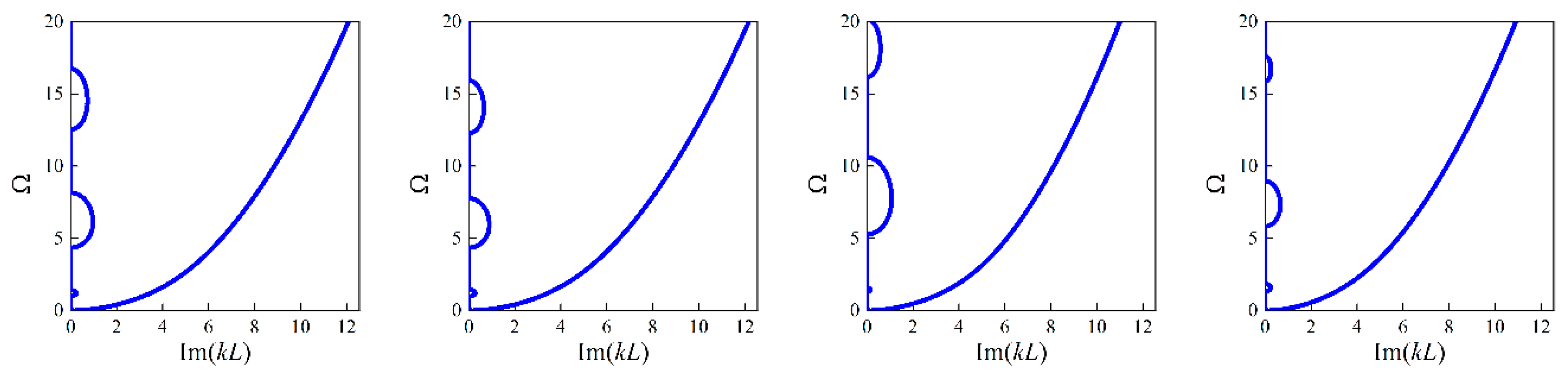
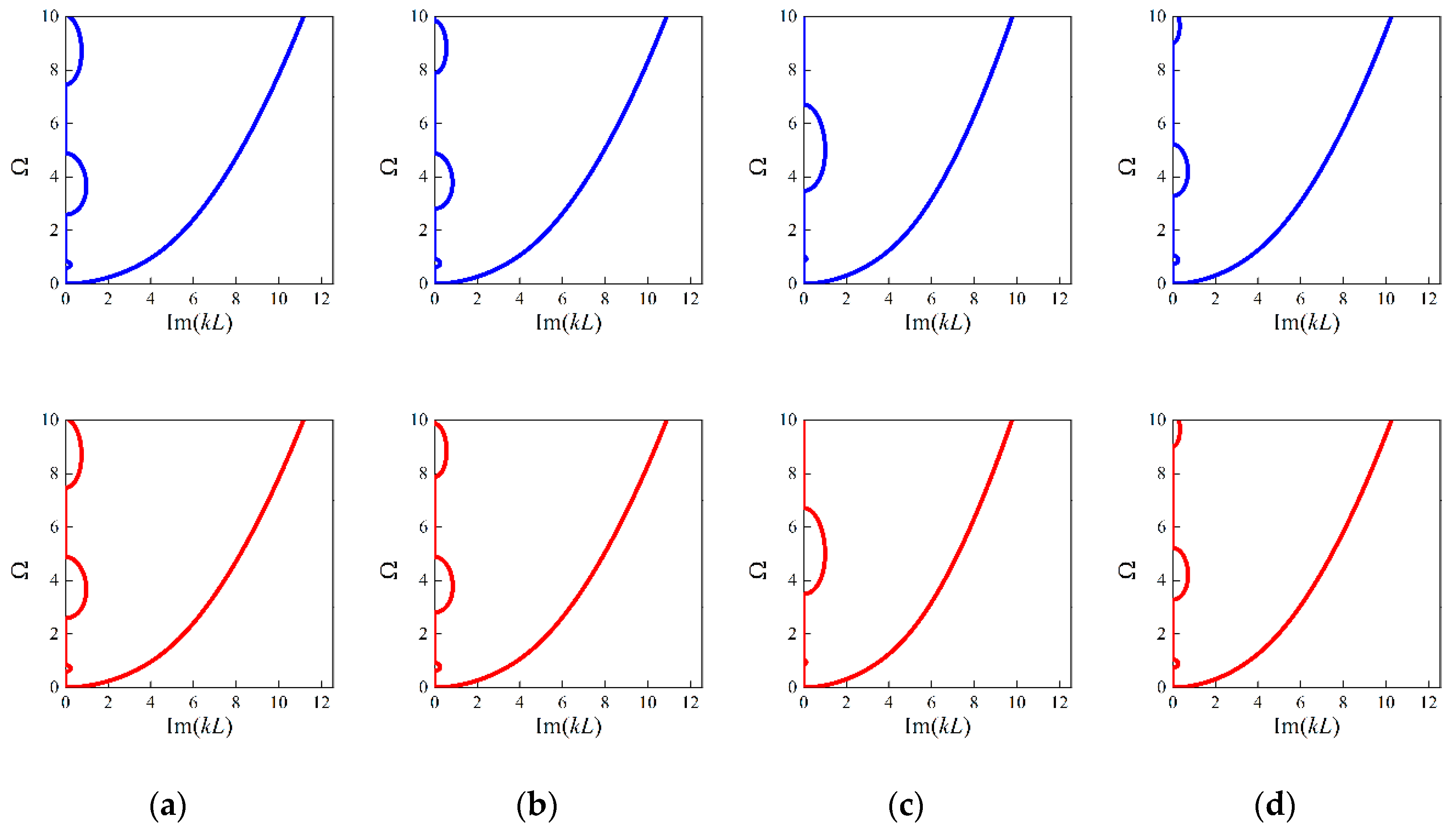
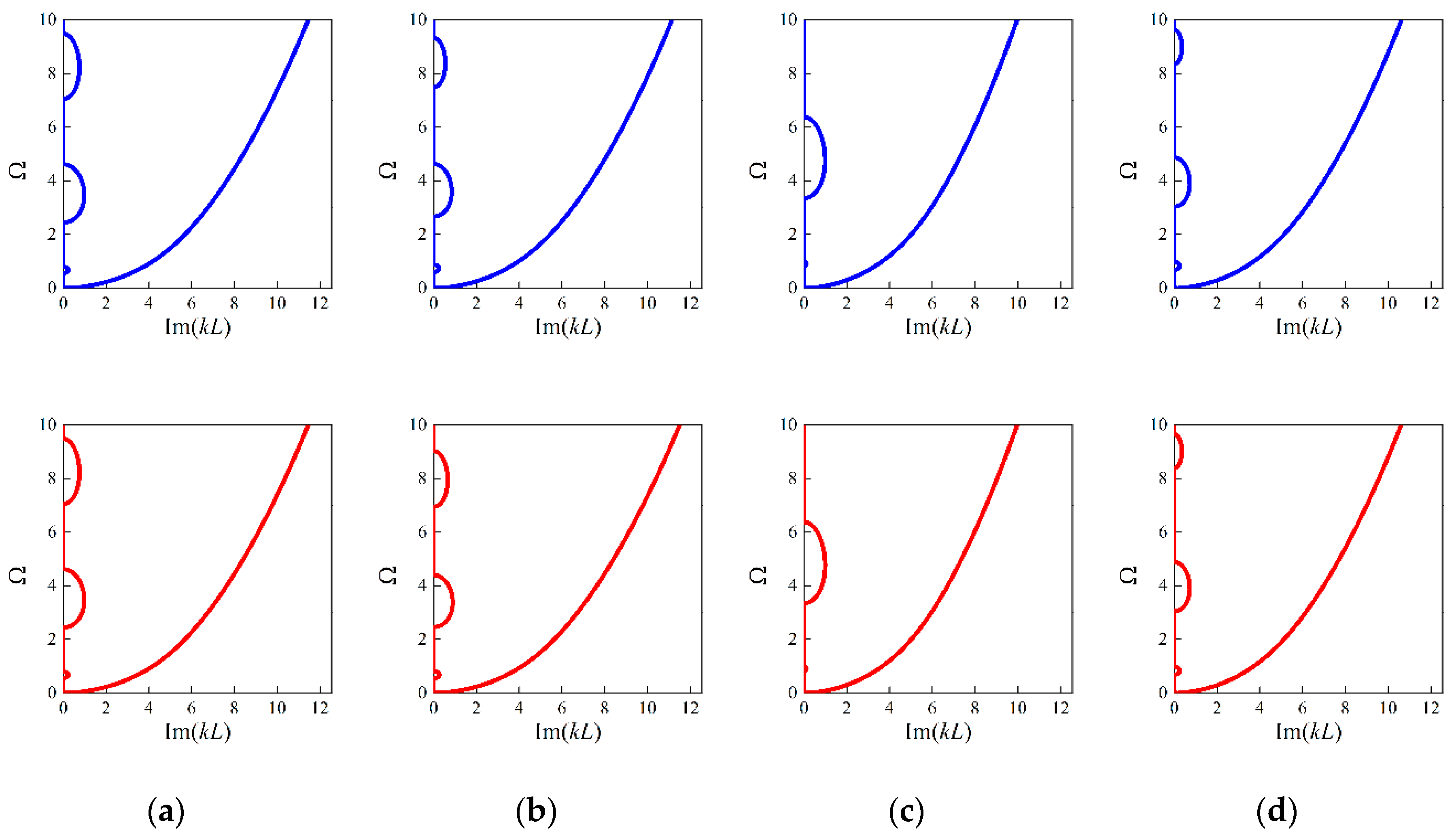
3.1. Forward Design of Micro-PnC Beams
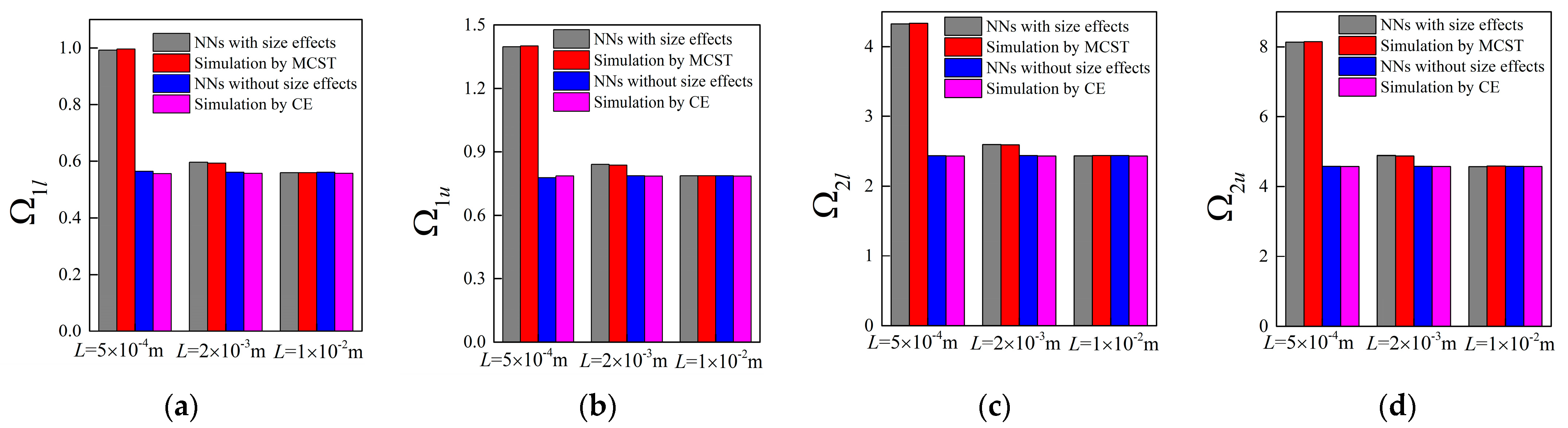
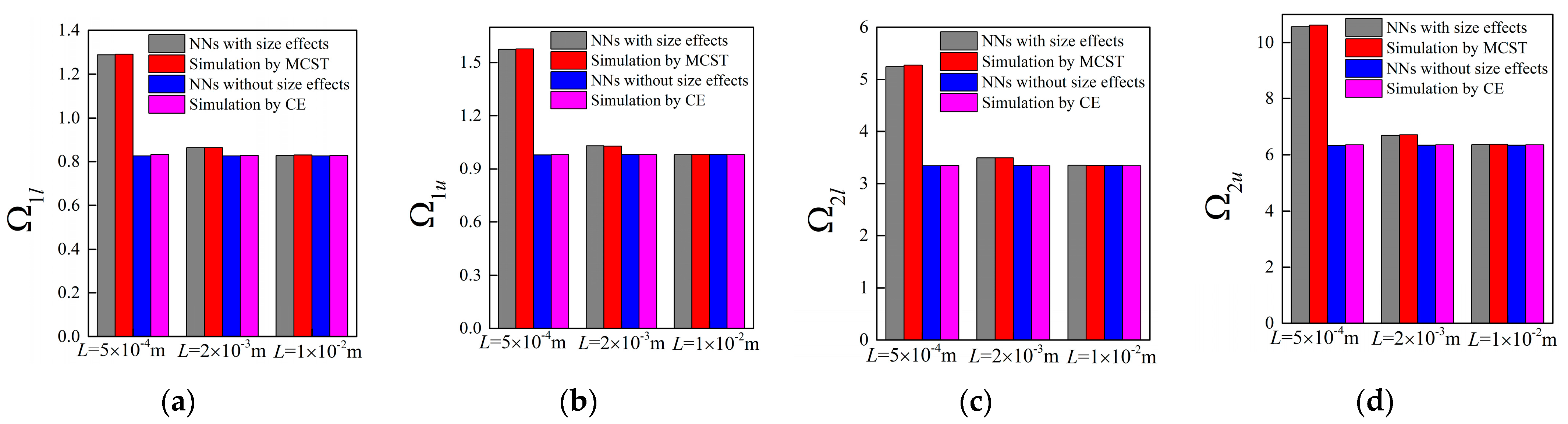
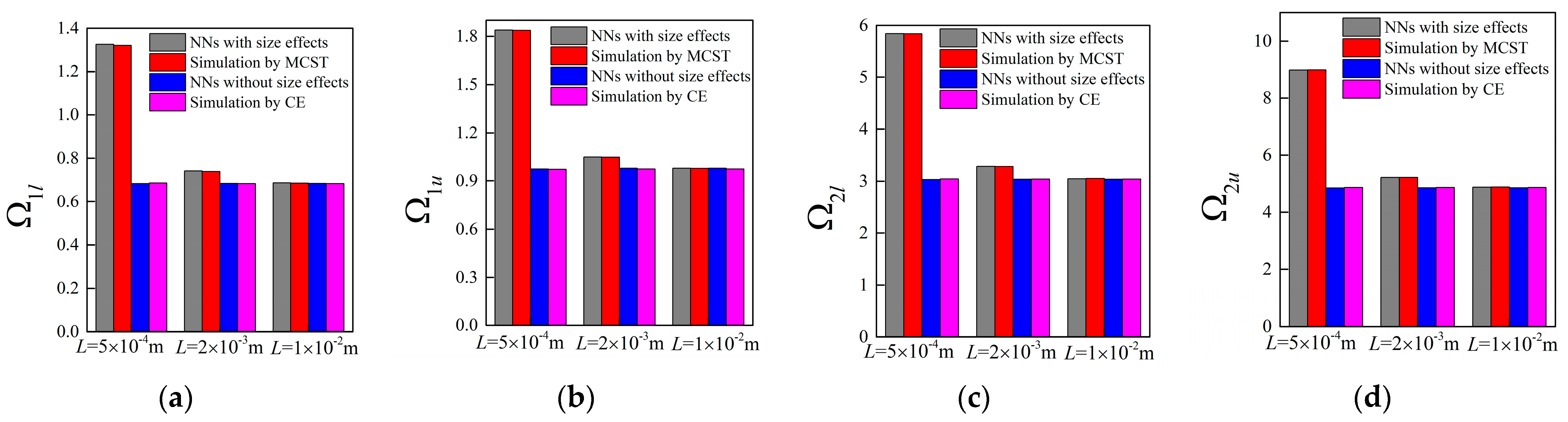
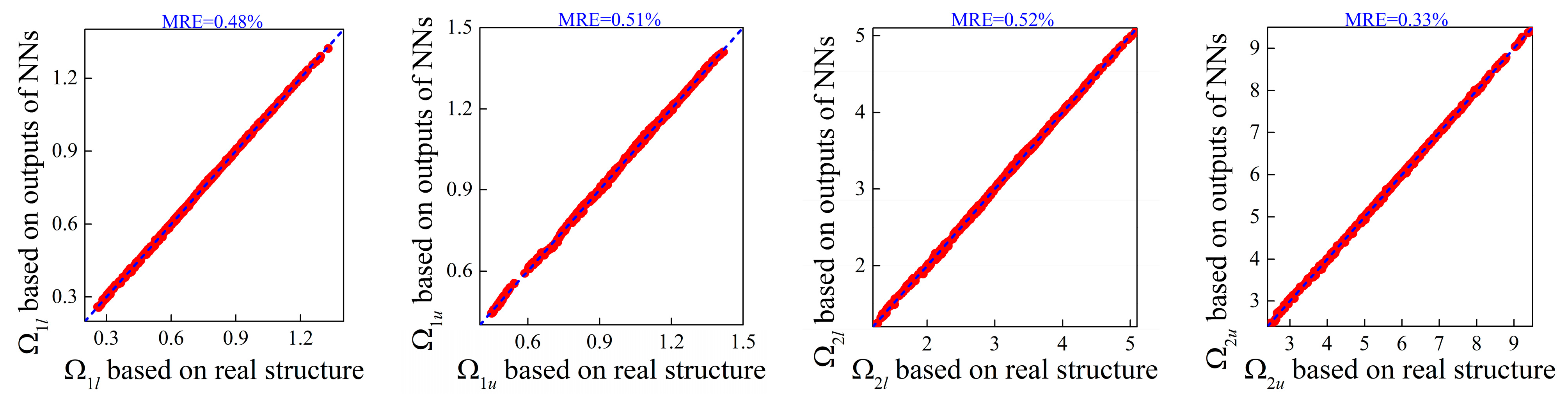
3.2. Forward Network with Different Unit Cell Lengths
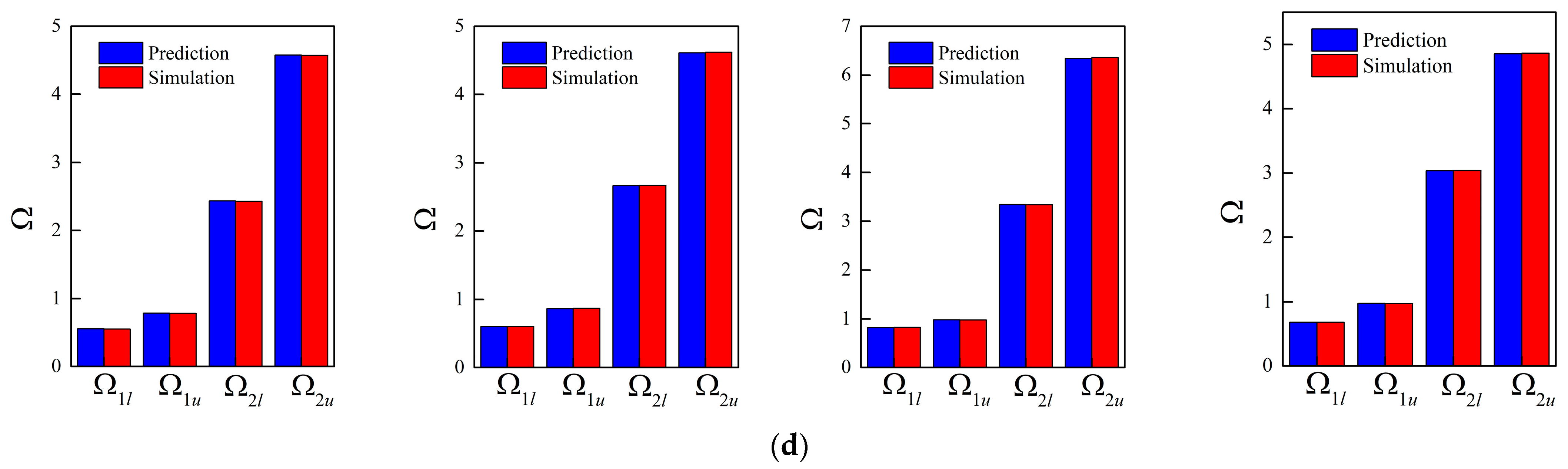
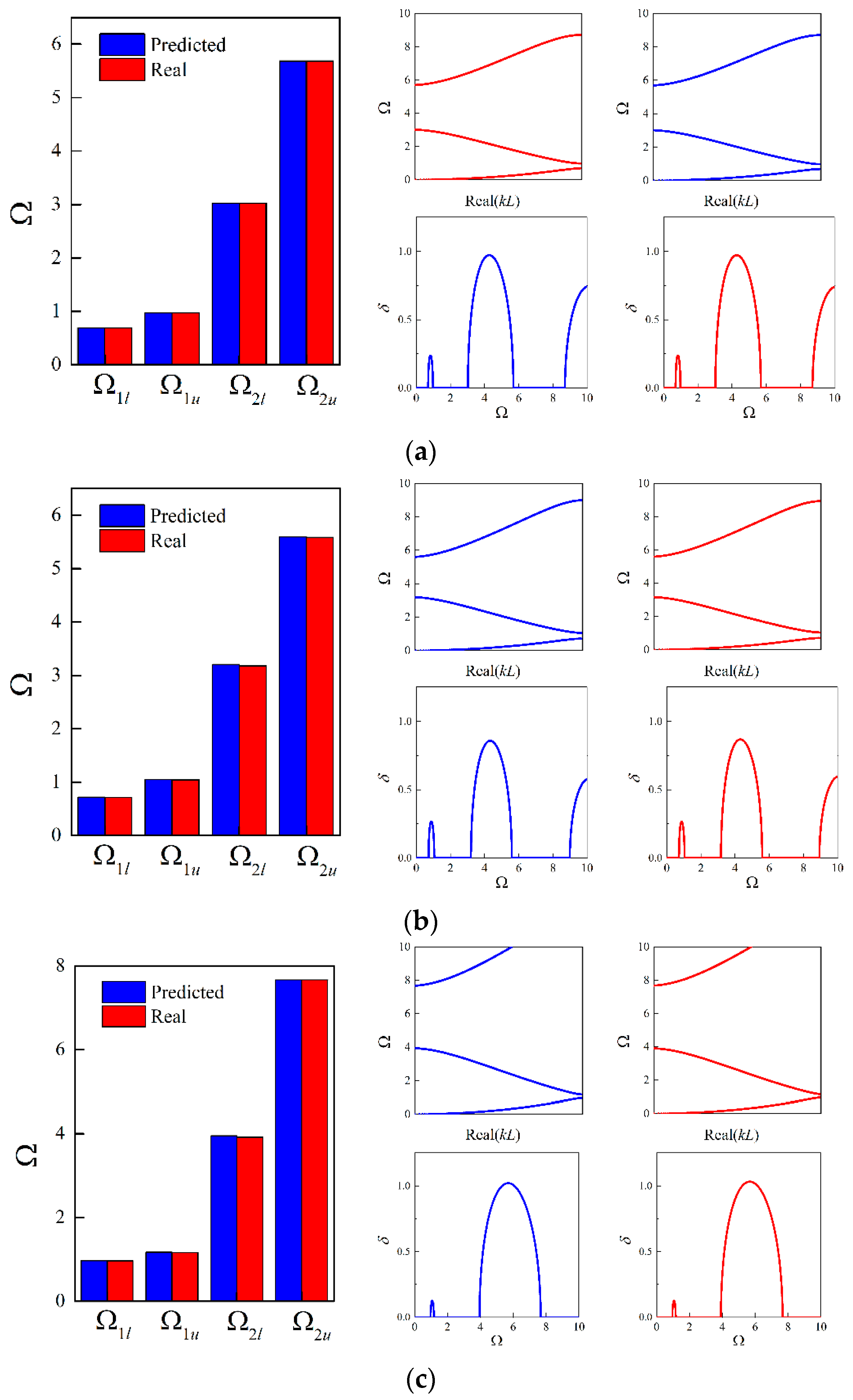
3.3. Inverse Design of Micro-PnC Beams
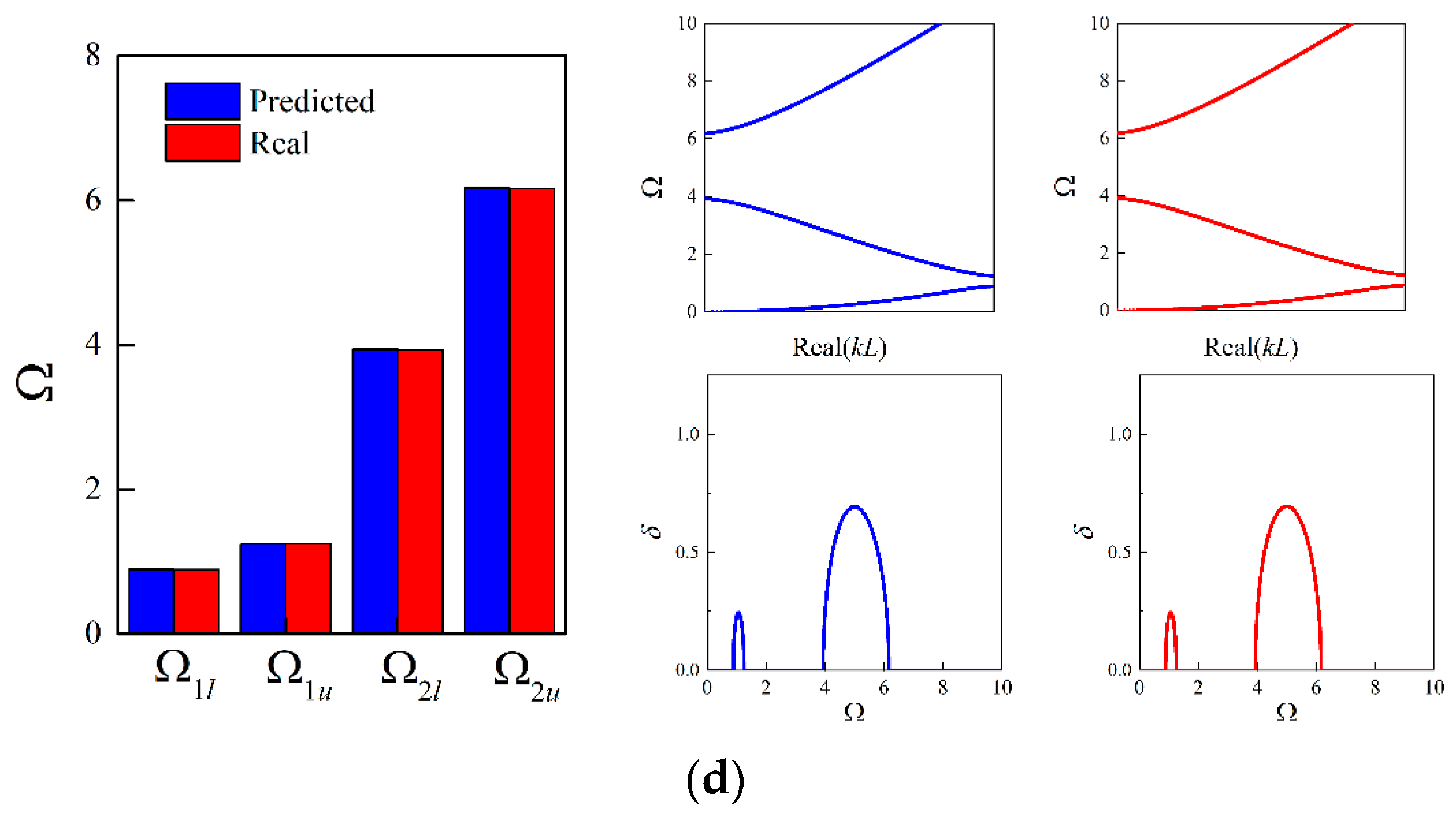
3.4. Inverse Design with Different Unit Cell Lengths
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lim, C.W. Elastic waves propagation in thin plate metamaterials and evidence of low frequency pseudo and local resonance bandgaps. Phys. Lett. A 2019, 383, 2789–2796. [Google Scholar] [CrossRef]
- Li, Y.; Xiao, Y.; Guo, J.; Zhu, Z.; Wen, J. Single-phase metabeam for three-directional broadband vibration suppression. Int. J. Mech. Sci. 2022, 234, 107683. [Google Scholar] [CrossRef]
- Guo, Z.; Chen, S.; Wang, C.; Hao, C. Subwavelength bandgap phononic crystals with mixed resonant modes. Phys. Lett. A 2022, 438, 128109. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, Q.; Zhou, L.; Zhu, L.; Guo, K. Flexural wave band gaps and vibration attenuation characteristics in periodic bi-directionally orthogonal stiffened plates. Ocean Eng. 2019, 178, 95–103. [Google Scholar] [CrossRef]
- Acar, G.; Yilmaz, C. Experimental and numerical evidence for the existence of wide and deep phononic gaps induced by inertial amplification in two-dimensional solid structures. J. Sound Vib. 2013, 332, 6389–6404. [Google Scholar] [CrossRef]
- Goto, A.M.; Nóbrega, E.D.; Pereira, F.N.; Dos Santos, J.M.C. Numerical and experimental investigation of phononic crystals via wave-based higher-order rod models. Int. J. Mech. Sci. 2020, 181, 105776. [Google Scholar] [CrossRef]
- Park, S.; Jeon, W. Ultra-wide low-frequency band gap in a tapered phononic beam. J. Sound Vib. 2021, 499, 115977. [Google Scholar] [CrossRef]
- Miao, Z.; Li, J.; Li, S.; Ma, Q. Complex Band Structure of 2D Piezoelectric Local Resonant Phononic Crystal with Finite Out-Of Plane Extension. Appl. Sci. 2022, 12, 7021. [Google Scholar] [CrossRef]
- Muhammad; Lim, C.W.; Yaw, Z.; Chen, Z. Periodic and aperiodic 3-D composite metastructures with ultrawide bandgap for vibration and noise control. Compos. Struct. 2022, 287, 115324. [Google Scholar] [CrossRef]
- Li, J.; Yang, P.; Li, S. Multiple band gaps for efficient wave attenuation by inertial amplification in periodic functionally graded beams. Compos. Struct. 2021, 271, 114130. [Google Scholar] [CrossRef]
- Zhou, J.; Dou, L.; Wang, K.; Xu, D.; Ouyang, H. A nonlinear resonator with inertial amplification for very low-frequency flexural wave attenuations in beams. Nonlinear. Dyn. 2019, 96, 647–665. [Google Scholar] [CrossRef]
- Wang, T.-T.; Wang, Y.-F.; Deng, Z.-C.; Laude, V.; Wang, Y.-S. Reconfigurable coupled-resonator acoustoelastic waveguides in fluid-filled phononic metaplates. Compos. Struct. 2023, 303, 116355. [Google Scholar] [CrossRef]
- Sepehri, S.; Mashhadi, M.M.; Seyyed Fakhrabadi, M.M. Active/passive tuning of wave propagation in phononic microbeams via piezoelectric patches. Mech. Mater. 2022, 167, 104249. [Google Scholar] [CrossRef]
- Xiao, S.-H.; Zhang, C.; Qin, Q.-H.; Wang, H. A novel planar auxetic phononic crystal with periodic cookie-shaped cellular microstructures. Mech. Adv. Mater. Struct. 2022, 29, 3345–3358. [Google Scholar] [CrossRef]
- Li, Y.; Luo, Y.; Zhang, X. Topological design of phononic crystals for multiple wide band gaps. J. Sound Vib. 2022, 529, 116962. [Google Scholar] [CrossRef]
- Han, X.K.; Zhang, Z. Topological Optimization of Phononic Crystal Thin Plate by a Genetic Algorithm. Sci. Rep. 2019, 9, 8331. [Google Scholar] [CrossRef]
- Li, W.; Meng, F.; Li, Y.F.; Huang, X. Topological design of 3D phononic crystals for ultra-wide omnidirectional bandgaps. Struct. Multidisc. Optim. 2019, 60, 2405–2415. [Google Scholar] [CrossRef]
- Christiansen, R.E.; Sigmund, O. Designing meta material slabs exhibiting negative refraction using topology optimization. Struct. Multidisc. Optim. 2016, 54, 469–482. [Google Scholar] [CrossRef]
- Dong, H.-W.; Zhao, S.-D.; Wang, Y.-S.; Zhang, C. Topology optimization of anisotropic broadband double-negative elastic metamaterials. J. Mech. Phys. Solids 2017, 105, 54–80. [Google Scholar] [CrossRef]
- Zhang, W.; Qin, L.; Wang, J.; Xu, W. A pixel design method for mechanical metamaterials based on topology optimization. Mech. Adv. Mater. Struct. 2022, 1–9. [Google Scholar] [CrossRef]
- Han, Z.; Wang, Z.; Wei, K. Shape morphing structures inspired by multi-material topology optimized bi-functional metamaterials. Compos. Struct. 2022, 300, 116135. [Google Scholar] [CrossRef]
- Sharma, A.K.; Joglekar, M.M.; Joglekar, D.M.; Alam, Z. Topology optimization of soft compressible phononic laminates for widening the mechanically tunable band gaps. Compos. Struct. 2022, 289, 115389. [Google Scholar] [CrossRef]
- Sun, P.; Zhang, Z.; Guo, H.; Liu, N.; Jin, W.; Yuan, T.; Wang, Y. Topological optimization of hierarchical honeycomb acoustic metamaterials for low-frequency extreme broad band gaps. Appl. Acoust. 2022, 188, 108579. [Google Scholar] [CrossRef]
- Liu, Z.; Dong, H.-W.; Yu, G.-L.; Cheng, L. Achieving ultra-broadband and ultra-low-frequency surface wave bandgaps in seismic metamaterials through topology optimization. Compos. Struct. 2022, 295, 115863. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.-W. A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Hinton, G.; Deng, L.; Yu, D.; Dahl, G.E.; Mohamed, A.; Jaitly, N.; Senior, A.; Vanhoucke, V.; Nguyen, P.; Sainath, T.N.; et al. Deep Neural Networks for Acoustic Modeling in Speech Recognition: The Shared Views of Four Research Groups. IEEE Signal Process. Mag. 2012, 29, 82–97. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; van den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef]
- Peurifoy, J.; Shen, Y.; Jing, L.; Yang, Y.; Cano-Renteria, F.; DeLacy, B.G.; Joannopoulos, J.D.; Tegmark, M.; Soljačić, M. Nanophotonic particle simulation and inverse design using artificial neural networks. Sci. Adv. 2018, 4, eaar4206. [Google Scholar] [CrossRef]
- Lu, F.; Wang, J.; Li, H.; Qing, C.; Lei, T.; Xiang, T.; Hu, S. Inverse Design of Metamaterials via Deep Learning for Electromagnetically Induced Transparency. J. Phys. Conf. Ser. 2022, 2384, 012045. [Google Scholar] [CrossRef]
- Ji, G.; Li, F.; Li, Q.; Li, H.; Li, Z. A comparative study on Arrhenius-type constitutive model and artificial neural network model to predict high-temperature deformation behaviour in Aermet100 steel. Mater. Sci. Eng. A 2011, 528, 4774–4782. [Google Scholar] [CrossRef]
- Sun, X.; Jia, H.; Yang, Y.; Zhao, H.; Bi, Y.; Sun, Z.; Yang, J. Acoustic Structure Inverse Design and Optimization Using Deep Learning 2021. arXiv 2021, arXiv:2102.02063. [Google Scholar] [CrossRef]
- Long, Y.; Ren, J.; Li, Y.; Chen, H. Inverse design of photonic topological state via machine learning. Appl. Phys. Lett. 2019, 114, 181105. [Google Scholar] [CrossRef]
- Muhammad; Ogun, O.; Kennedy, J. Inverse design of a topological phononic beam with interface modes. J. Phys. D Appl. Phys. 2022, 56, 015106. [Google Scholar] [CrossRef]
- So, S.; Mun, J.; Rho, J. Simultaneous Inverse Design of Materials and Structures via Deep Learning: Demonstration of Dipole Resonance Engineering Using Core–Shell Nanoparticles. ACS Appl. Mater. Interfaces 2019, 11, 24264–24268. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.-X.; Yu, G.-L.; Zhao, G.-Y. Neural networks for inverse design of phononic crystals. AIP Adv. 2019, 9, 085223. [Google Scholar] [CrossRef]
- Chen, J.; Chen, Y.; Xu, X.; Zhou, W.; Huang, G. A physics-guided machine learning for multifunctional wave control in active metabeams. Extrem. Mech. Lett. 2022, 55, 101827. [Google Scholar] [CrossRef]
- Finol, D.; Lu, Y.; Mahadevan, V.; Srivastava, A. Deep convolutional neural networks for eigenvalue problems in mechanics. Int. J. Numer. Methods Eng. 2019, 118, 258–275. [Google Scholar] [CrossRef]
- Goodfellow, I. NIPS 2016 Tutorial: Generative Adversarial Networks. arXiv 2016, arXiv:1701.00160. [Google Scholar] [CrossRef]
- Kiarashinejad, Y.; Abdollahramezani, S.; Zandehshahvar, M.; Hemmatyar, O.; Adibi, A. Deep Learning Reveals Underlying Physics of Light–Matter Interactions in Nanophotonic Devices. Adv. Theory Simul. 2019, 2, 1900088. [Google Scholar] [CrossRef]
- Li, X.; Ning, S.; Liu, Z.; Yan, Z.; Luo, C.; Zhuang, Z. Designing phononic crystal with anticipated band gap through a deep learning based data-driven method. Comput. Methods Appl. Mech. Eng. 2020, 361, 112737. [Google Scholar] [CrossRef]
- Jiang, W.; Zhu, Y.; Yin, G.; Lu, H.; Xie, L.; Yin, M. Dispersion relation prediction and structure inverse design of elastic metamaterials via deep learning. Mater. Today Phys. 2022, 22, 100616. [Google Scholar] [CrossRef]
- Gurbuz, C.; Kronowetter, F.; Dietz, C.; Eser, M.; Schmid, J.; Marburg, S. Generative adversarial networks for the design of acoustic metamaterials. J. Acoust. Soc. Am. 2021, 149, 1162–1174. [Google Scholar] [CrossRef] [PubMed]
- Zhao, B.; Chen, J.; Liu, T.; Song, W.; Zhang, J. A new Timoshenko beam model based on modified gradient elasticity: Shearing effect and size effect of micro-beam. Compos. Struct. 2019, 223, 110946. [Google Scholar] [CrossRef]
- Polizzotto, C. A hierarchy of simplified constitutive models within isotropic strain gradient elasticity. Eur. J. Mech. A/Solids 2017, 61, 92–109. [Google Scholar] [CrossRef]
- Park, S.K.; Gao, X.-L. Variational formulation of a modified couple stress theory and its application to a simple shear problem. Z. Angew. Math. Phys. 2008, 59, 904–917. [Google Scholar] [CrossRef]
- Yang, F.; Chong, A.C.M.; Lam, D.C.C.; Tong, P. Couple stress based strain gradient theory for elasticity. Int. J. Solids Struct. 2002, 39, 2731–2743. [Google Scholar] [CrossRef]
- Zhang, G.Y.; Gao, X.-L.; Bishop, J.E.; Fang, H.E. Band gaps for elastic wave propagation in a periodic composite beam structure incorporating microstructure and surface energy effects. Compos. Struct. 2018, 189, 263–272. [Google Scholar] [CrossRef]
- Sepehri, S.; Jafari, H.; Mashhadi, M.M.; Yazdi, M.R.H.; Fakhrabadi, M.M.S. Small-scale effects on wave propagation in planar micro-lattices. J. Sound Vib. 2021, 494, 115894. [Google Scholar] [CrossRef]
- Li, J.; Li, S.; Lin, W. Actively controllable size-dependent elastic wave band gaps in planar functionally graded micro-lattice. Mech. Adv. Mater. Struct. 2022, 1–21. [Google Scholar] [CrossRef]
- Zhang, G.Y.; Gao, X.-L. Band gaps for wave propagation in 2-D periodic three-phase composites with coated star-shaped inclusions and an orthotropic matrix. Compos. Part B Eng. 2020, 182, 107319. [Google Scholar] [CrossRef]
- Zhang, G.Y.; Gao, X.-L. Elastic wave propagation in 3-D periodic composites: Band gaps incorporating microstructure effects. Compos. Struct. 2018, 204, 920–932. [Google Scholar] [CrossRef]
- Liu, C.-X.; Yu, G.-L. Intelligent design of engineered metabarrier based on deep learning. Compos. Struct. 2022, 280, 114911. [Google Scholar] [CrossRef]
- Liu, C.-X.; Yu, G.-L. A deep learning model for the topological design of 2D periodic wave barriers. Comput. Aided Civ. Infrastruct. Eng. 2022, 37, 451–469. [Google Scholar] [CrossRef]




| Parameters | Descriptions | Value |
|---|---|---|
| L (mm) | The unit cell length | 1 |
| h (mm) | The thickness of microbeam | L/50 |
| b (mm) | The width of the rectangular section | 2h |
| Vf | The volume fraction of material 1 | 0.5 |
| Er | ρr | lr |
|---|---|---|
| 0.0100 | 0.1500 | 0.8000 |
| 0.0182 | 0.1909 | 0.8364 |
| 0.0264 | 0.2318 | 0.8727 |
| 0.0345 | 0.2727 | 0.9091 |
| 0.0427 | 0.3136 | 0.9455 |
| 0.0509 | 0.3545 | 0.9818 |
| 0.0591 | 0.3955 | 1.0182 |
| 0.0673 | 0.4364 | 1.0545 |
| 0.0755 | 0.4773 | 1.0909 |
| 0.0836 | 0.5182 | 1.1273 |
| 0.0918 | 0.5591 | 1.1636 |
| 0.1000 | 0.6000 | 1.2000 |
| Material Features | Example 1 | Example 2 | Example 3 | Example 4 |
|---|---|---|---|---|
| Er | 0.045 | 0.06 | 0.75 | 0.0822 |
| ρr | 0.33 | 0.4 | 0.2 | 0.433 |
| lr | 0.99 | 0.85 | 0.8 | 1.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Miao, Z.; Li, S.; Ma, Q. Inverse Design of Micro Phononic Beams Incorporating Size Effects via Tandem Neural Network. Materials 2023, 16, 1518. https://doi.org/10.3390/ma16041518
Li J, Miao Z, Li S, Ma Q. Inverse Design of Micro Phononic Beams Incorporating Size Effects via Tandem Neural Network. Materials. 2023; 16(4):1518. https://doi.org/10.3390/ma16041518
Chicago/Turabian StyleLi, Jingru, Zhongjian Miao, Sheng Li, and Qingfen Ma. 2023. "Inverse Design of Micro Phononic Beams Incorporating Size Effects via Tandem Neural Network" Materials 16, no. 4: 1518. https://doi.org/10.3390/ma16041518




