Understanding Effects of Ultrasonic Vibration on Microstructure Evolution in Hot Forming Process via Cellular Automata Method
Abstract
:1. Introduction
2. CA Model
2.1. Grain Growth
- (1)
- Thermodynamic energy mechanism. The normal grain growth process is essentially a process of thermal activation. Grain boundary migration can occur only when grain boundary atoms overcome certain energy barriers. When the thermal energy of the cell at the grain boundary is greater than the activation energy of thermal diffusion, its state can change. According to statistical thermodynamic theory, the probability that the thermal energy of the cell at the grain boundary is greater than the activation energy of thermal diffusion can be calculated as follows [17]:
- (2)
- Curvature drive mechanism. According to the orientation relationship and grain boundary type of neighbor cells, the current judging cell is regarded as the central cell. If four or more neighbor cells have the same state “A”, while the central cell state is different from them, the central cell state will change into “A” state at the next time step.
- (3)
- The principle of least energy. According to the principle of energy dissipation, normal grain growth is a process in which the grain boundary expands outward and the grain boundary energy decreases. Since hexagonal cellular can simulate isotropy well, the calculated grain boundary energy also has isotropy, and the Hamiltonian function is used to represent the grain boundary energy [18]:
2.2. Dynamic Recrystallization with Ultrasound
2.2.1. Dislocation Density Model
2.2.2. Dynamic Recrystallization Nucleation and Growth Model
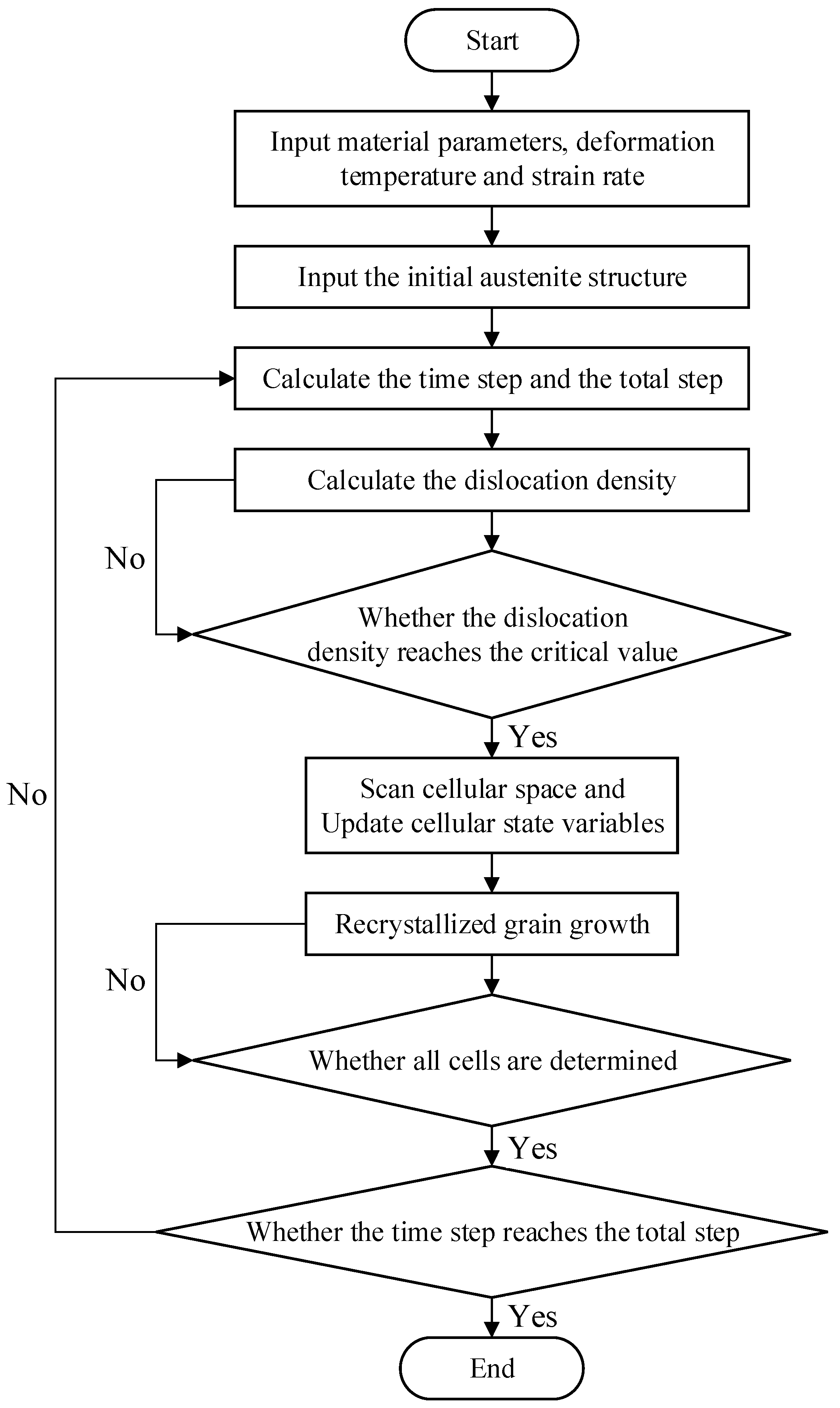
2.3. Program Flow Chart
3. Experiment
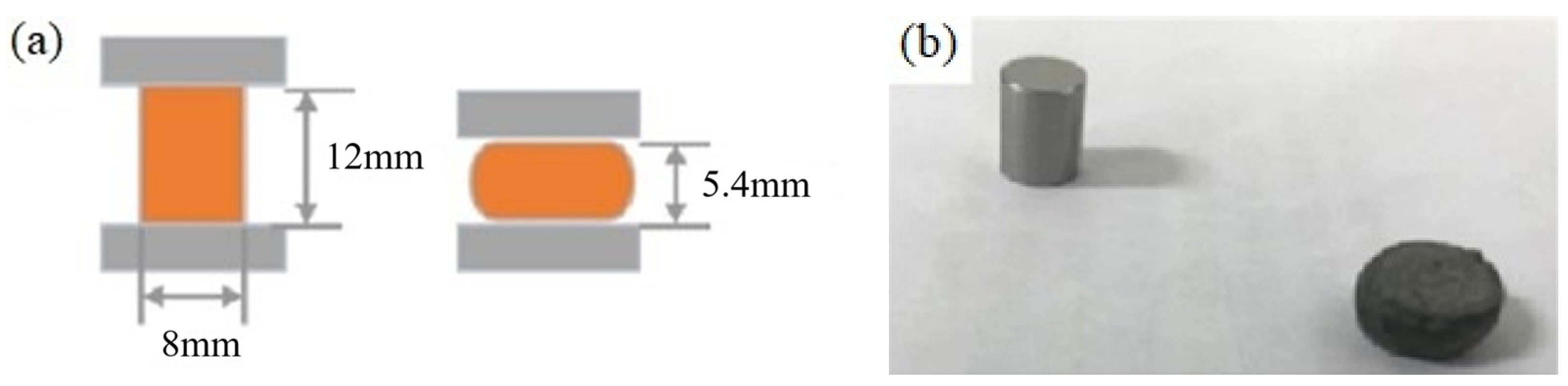
3.1. Hot Compression Experiment
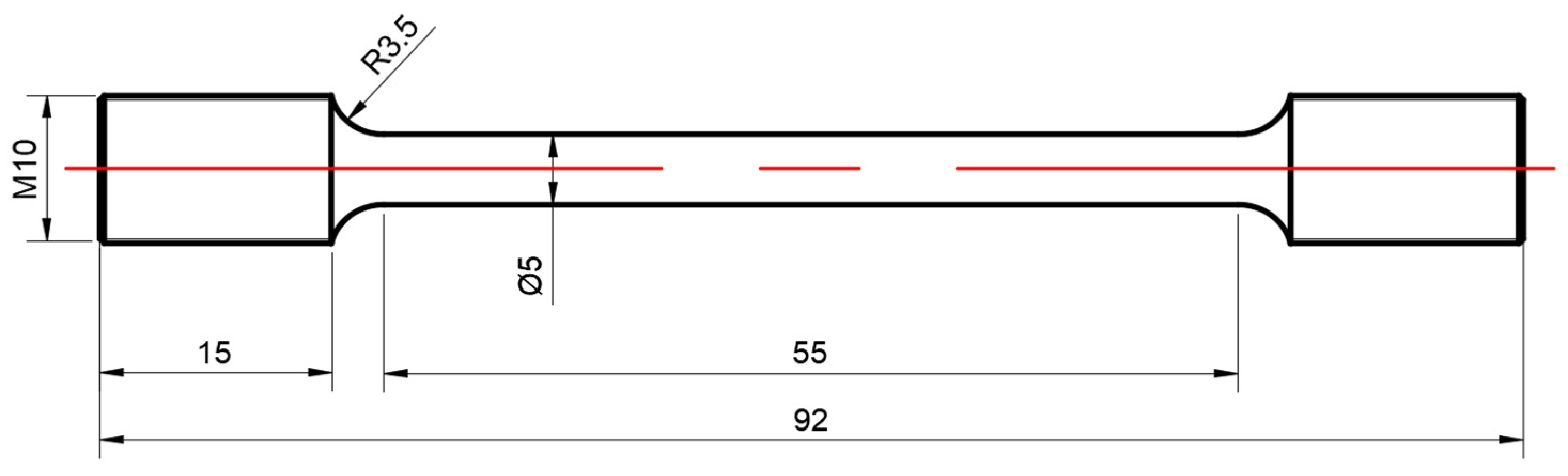
3.2. Ultrasonic-Assisted Tensile Experiments
4. Results and Discussion
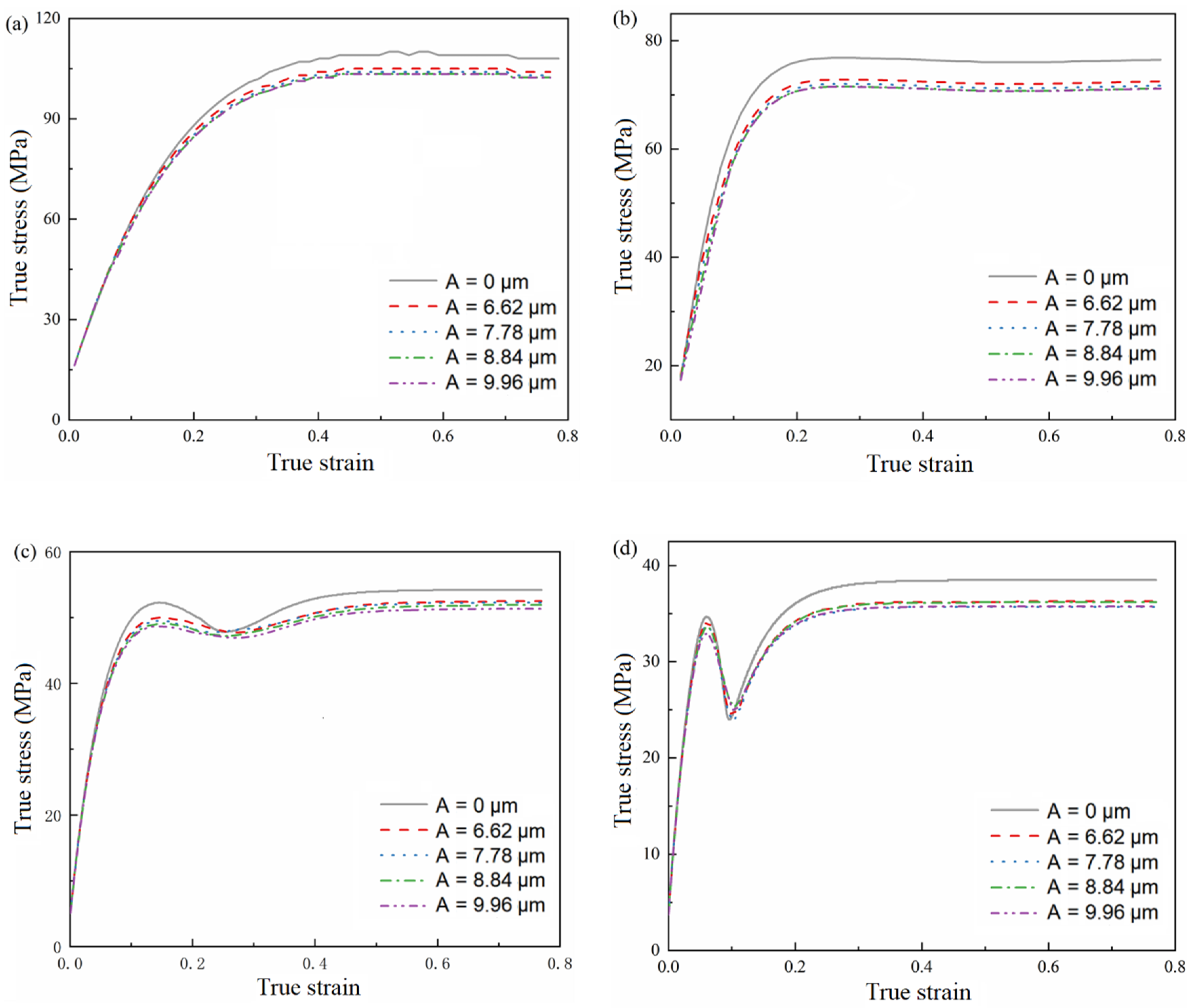
4.1. Hot Compression Experimental Results
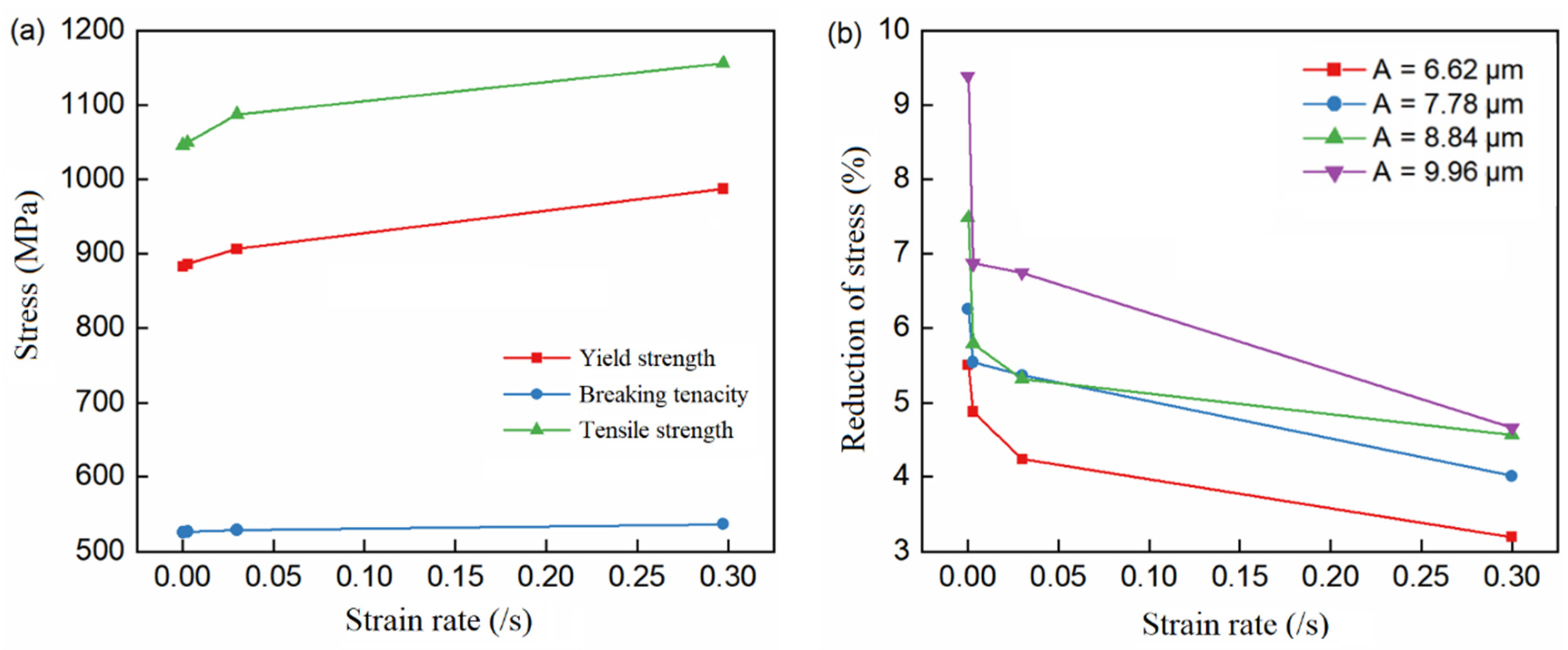
4.2. Ultrasonic-Assisted Tensile Experiment Results
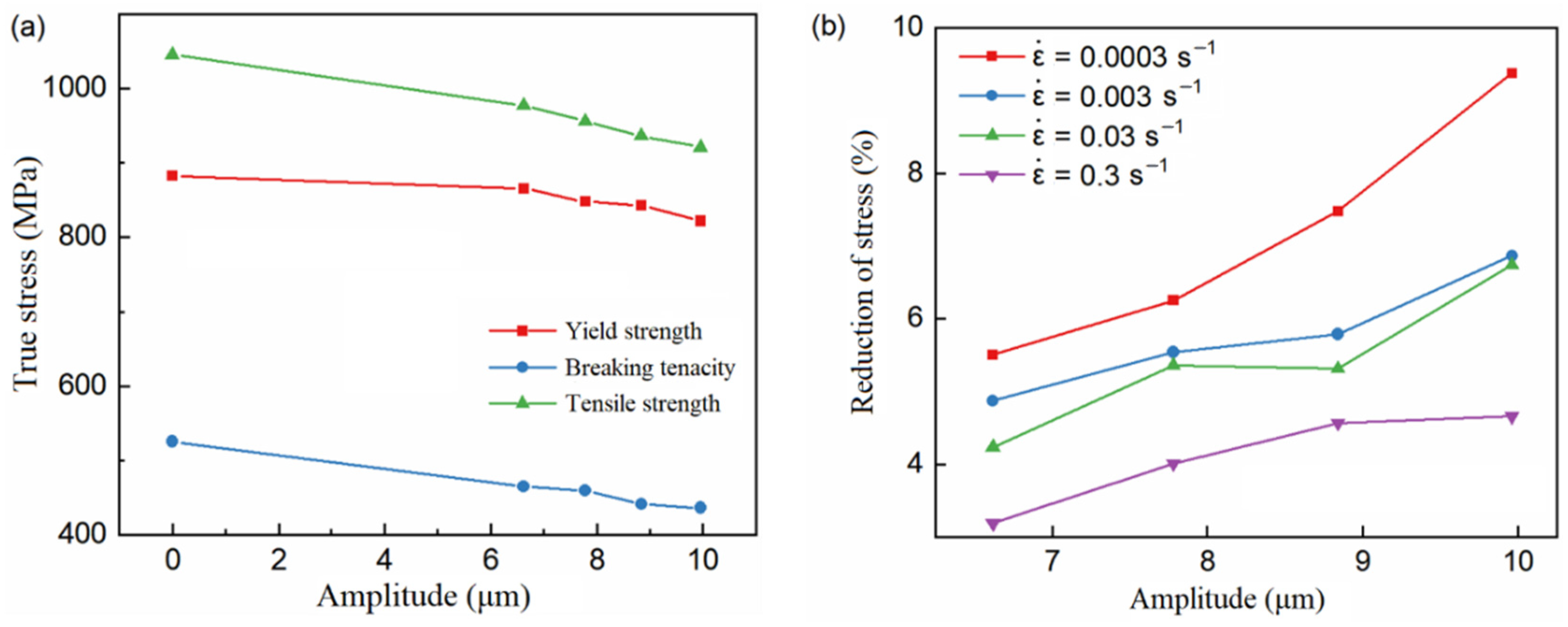
4.3. Stress Reduction Amplitude
4.4. CA Simulation Results
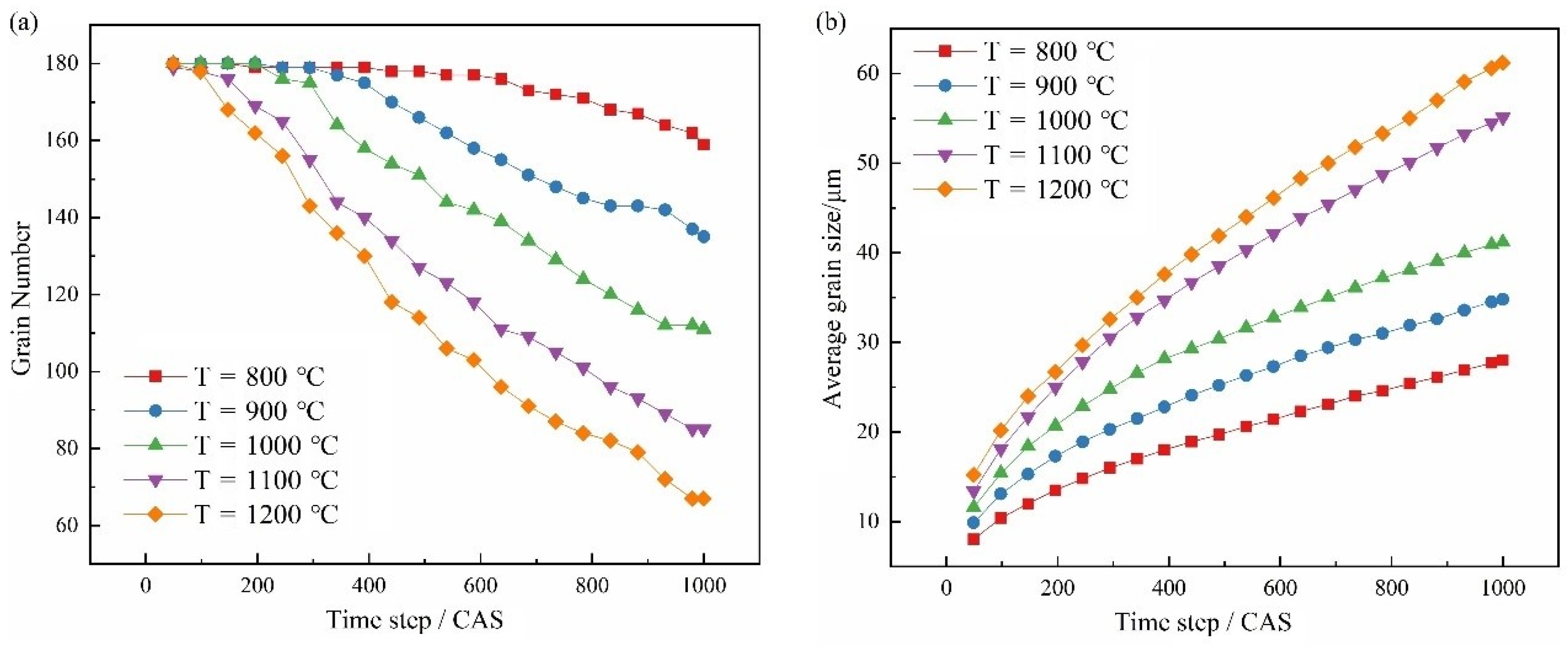
4.4.1. Grain Growth Results
4.4.2. Effect of Initial Grain Size
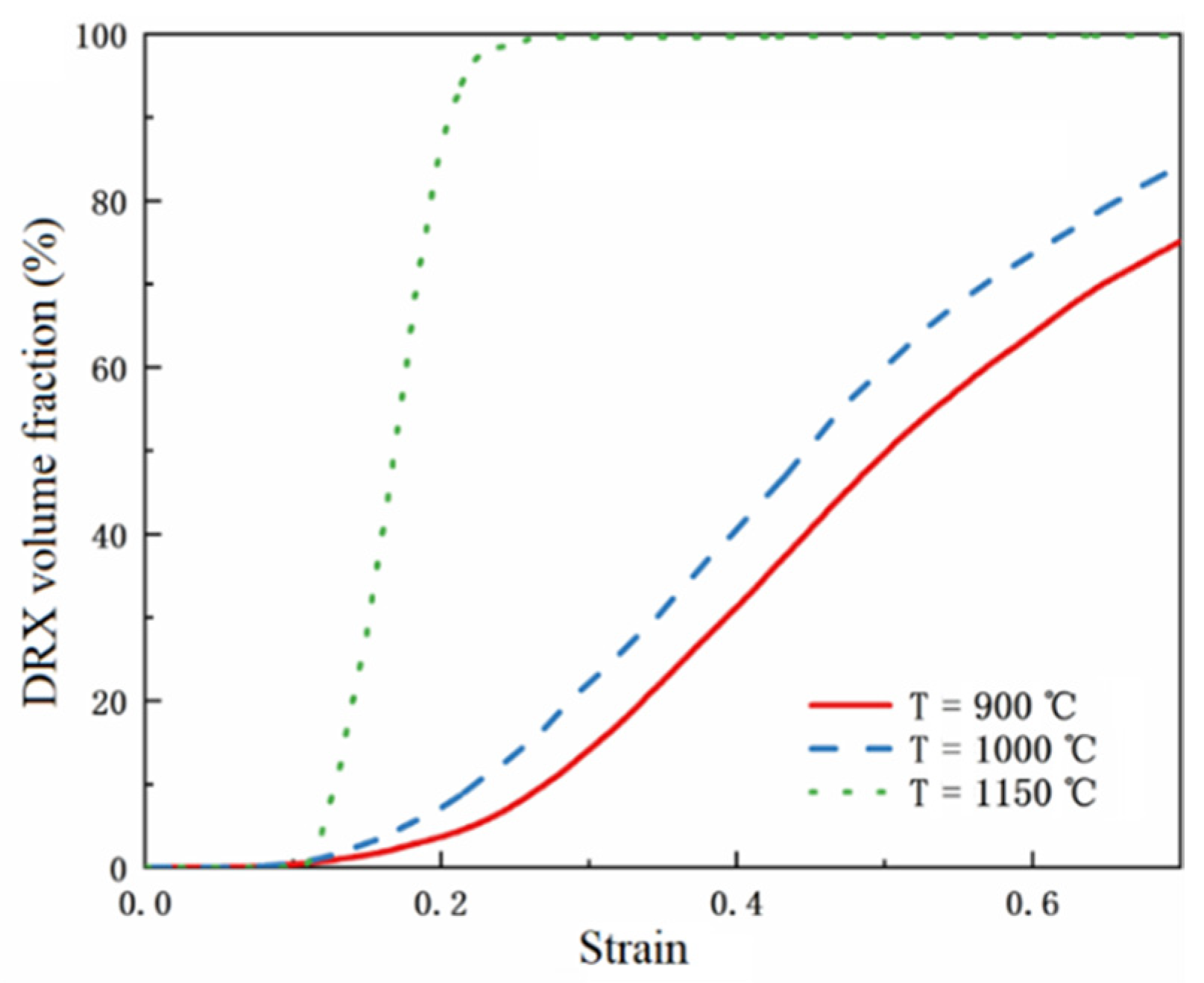
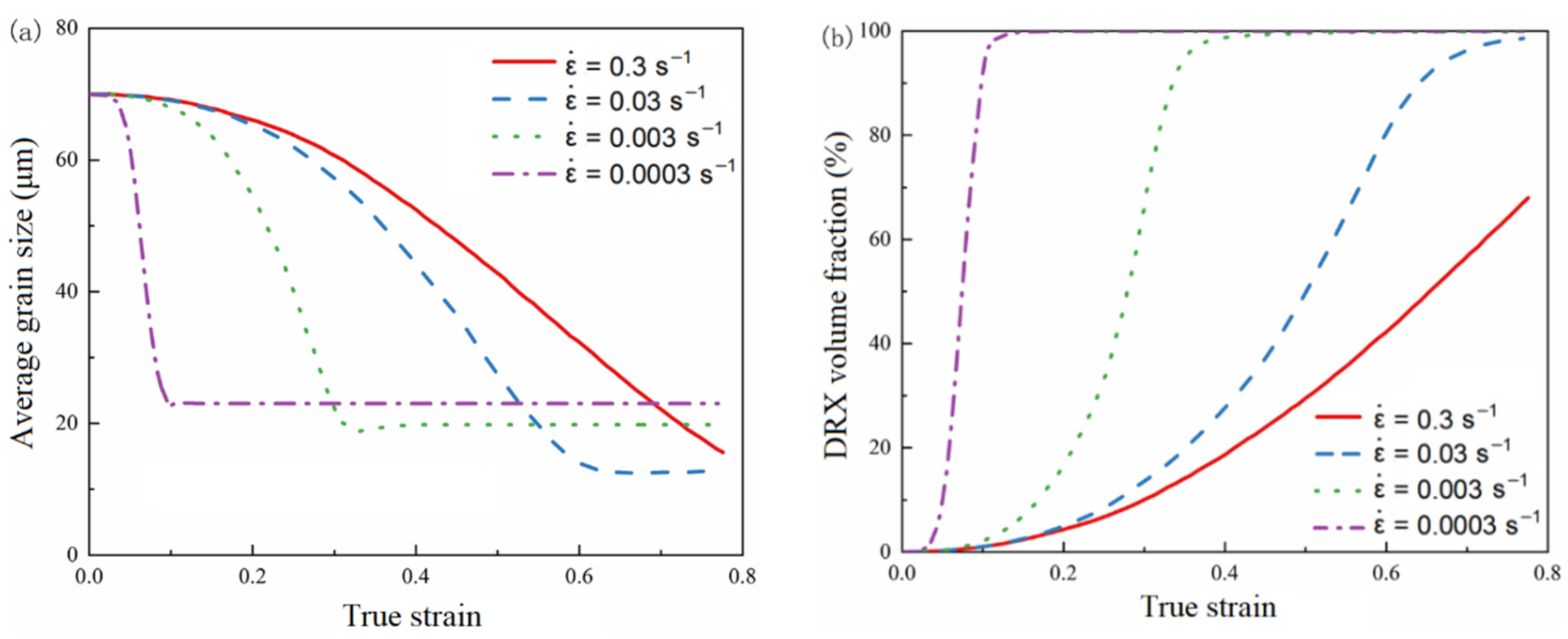
4.4.3. Effects of Temperature and Strain Rate
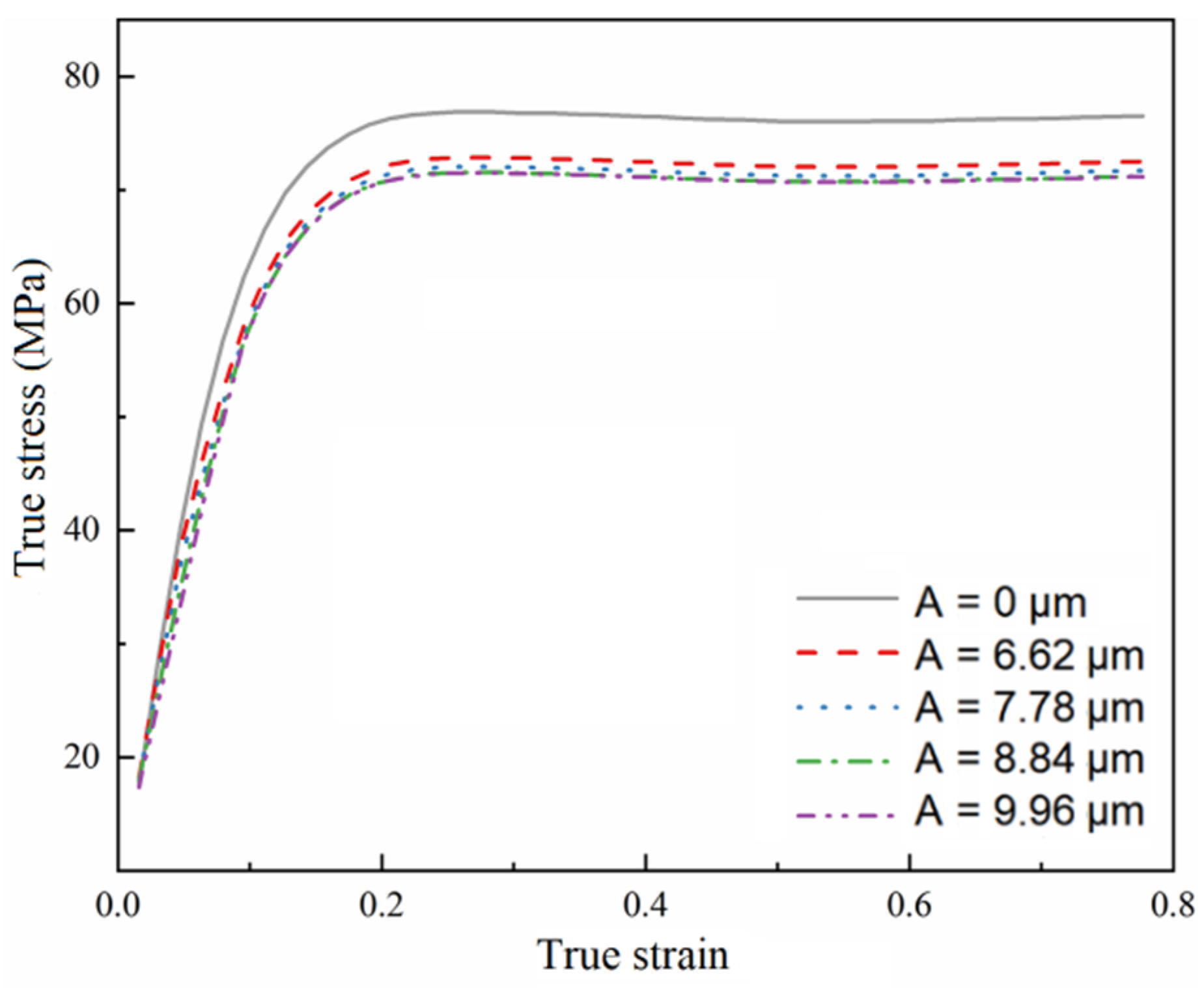
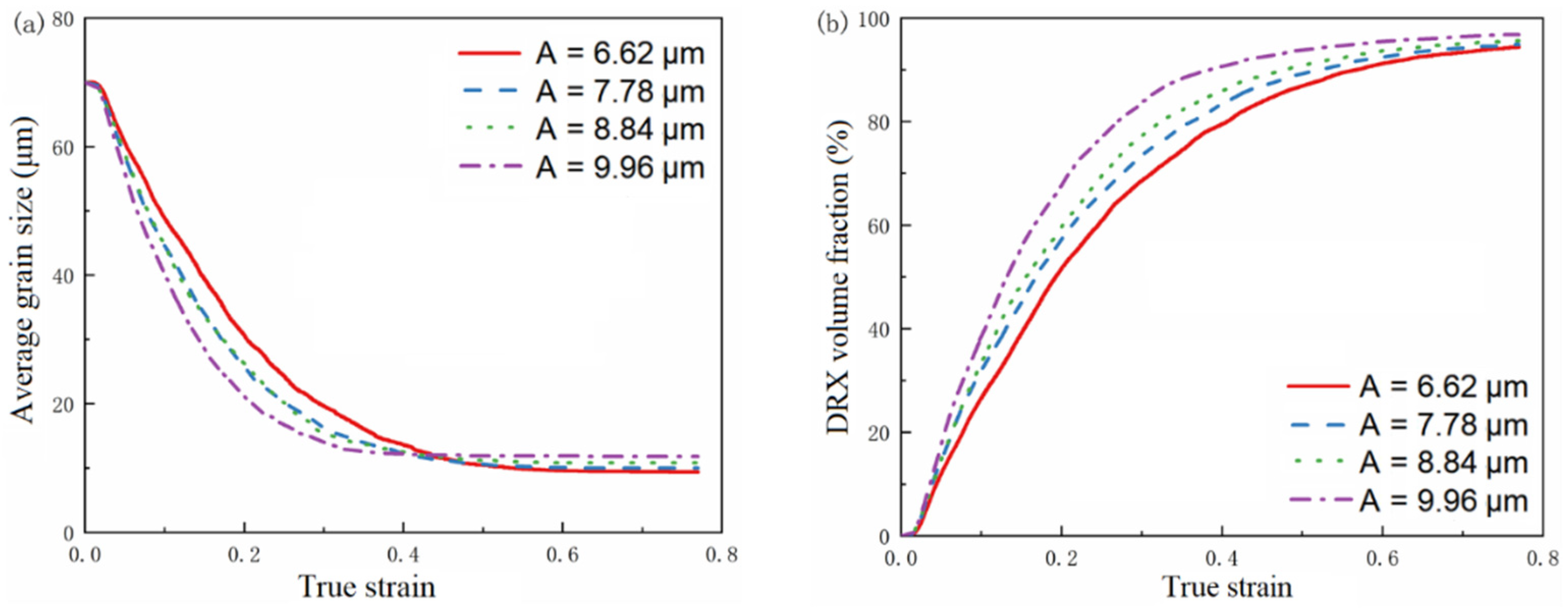
4.4.4. Effect of Ultrasonic Vibration Amplitude
5. Conclusions
- (1)
- Based on the dislocation density model, grain growth model, and dynamic recrystallization rule, ultrasonic energy was introduced to modify the thermal activation energy and dynamic recovery coefficient, and the CA model of microstructure simulation of the ultrasonic-assisted thermal forming process was established.
- (2)
- Stress reduction occurs in the process of compression and tension under the action of ultrasound, and the stress reduction amplitude is similar under the same ultrasonic amplitude.
- (3)
- The stress curves at different temperatures and strain rates were obtained by hot compression experiments, and it was found that the true stress–strain curves had the characteristics of peak stress, strain softening, and steady flow. At high temperatures and low strain rates, the softening phenomenon is more significant.
- (4)
- After applying ultrasonic vibration, the introduction of ultrasonic energy reduces the activation energy of dislocation movement, promotes the occurrence of dynamic recrystallization, and finally leads to the reduction of flow stress and material softening. The softening effect is enhanced with an increase in ultrasonic vibration amplitude.
- (5)
- Decreasing the strain rate and increasing the temperature or vibration amplitude will lead to a faster increase in the recrystallization volume fraction, and an increase in the dynamic recrystallization volume fraction and the average grain size.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Description | Symbol | Description |
| Cell size | Orientation angle of large Angle grains | ||
| A | Material parameter | Orientation difference | |
| T | Temperature | Berkovian vector | |
| Qb | Thermal diffusion activation energy | Activation energy after applying ultrasonic vibration | |
| R | Molar gas constant | ||
| Grain boundary energy of austenite | Correction coefficient of ultrasonic energy | ||
| J | Grain boundary energy coefficient | A | Ultrasonic energy Ultrasonic vibration amplitude |
| N | Number of neighbors of the cellular | ||
| K | Neighbor of the current judged cell | ω | Vibration circle frequency |
| δ | Kronecher symbol | Ultrasonic vibration frequency | |
| Current orientation of the cell | Density | ||
| Orientation value of the neighbor cell of the current judgment cell | Grain boundary migration energy under ultrasonic vibration | ||
| Dislocation density | Dislocation extinction coefficient under ultrasonic vibration | ||
| Dislocation increment coefficient | |||
| Dislocation extinction coefficient | Correlation coefficient of dislocation extinction coefficient under ultrasonic vibration | ||
| C | Hardening index | ||
| Flow stress | Exponent of the ultrasonic vibration amplitude Saturation dislocation density | ||
| Material constant of flow stress | |||
| Shear modulus | Nucleation probability Grain boundary nucleation rate | ||
| Average dislocation density | |||
| Initial dislocation density | L | Growth distance | |
| Initial yield stress | V | Growth rate | |
| Time step | P | Driving force | |
| Strain rate | Dislocation density of adjacent cells | ||
| Grain boundary energy of recrystallization | Dislocation density of recrystallized grains respectively | ||
| M | Grain boundary migration energy | ||
| Dislocation line energy | Radius of the recrystallization grain | ||
| Self-diffusion coefficient | Maximum growth distance | ||
| Grain boundary energy of large angle grains |
References
- Xie, J.; Zhou, T.; Liu, Y.; Kuriyagawa, T.; Wang, X. Mechanism study on microgroove forming by ultrasonic vibration assisted hot pressing. Precis. Eng. 2016, 46, 270–277. [Google Scholar] [CrossRef]
- Yang, B.; Ming, Y. Investigation on mechanism of metal foil surface finishing with vibration-assisted micro-forging. J. Mater. Process. Technol. 2013, 213, 330–336. [Google Scholar]
- Zhou, W.; Tang, J.; Shao, W.; Wen, J. Towards understanding the ploughing friction mechanism in ultrasonic assisted grinding with single grain. Int. J. Mech. Sci. 2022, 222, 107248. [Google Scholar] [CrossRef]
- Hu, J.; Shimizu, T.; Yoshino, T.; Shiratori, T.; Yang, M. Evolution of acoustic softening effect on ultrasonic-assisted micro/meso-compression behavior and microstructure. Ultrasonics 2020, 107, 106107. [Google Scholar] [CrossRef] [PubMed]
- Mao, Q.; Coutris, N.; Rack, H.; Fadela, G.; Gibertc, J. Investigating ultrasound-induced acoustic softening in aluminum and its alloys. Ultrasonics 2020, 102, 106005. [Google Scholar] [CrossRef] [PubMed]
- Wen, T.; Wei, L.; Chen, X.; Pei, C.L. Effects of ultrasonic vibration on plastic deformation of AZ31 during the tensile process. Int. J. Miner. Metall. Mater. 2011, 18, 70–76. [Google Scholar] [CrossRef]
- Zhou, H.; Cui, H.; Qin, Q.H. Influence of ultrasonic vibration on the plasticity of metals during compression process. J. Mater. Process. Technol. 2018, 251, 146–159. [Google Scholar] [CrossRef]
- Zhou, H.; Cui, H.; Qin, Q.H.; Wang, H.; Shen, Y. A comparative study of mechanical and microstructural characteristics of aluminium and titanium undergoing ultrasonic assisted compression testing. Mater. Sci. Eng. A 2017, 682, 376–388. [Google Scholar] [CrossRef]
- Liu, T.; Lin, J.; Guan, Y.; Xie, Z.; Zhai, J. Effects of ultrasonic vibration on the compression of pure titanium. Ultrasonics 2018, 89, 26–33. [Google Scholar] [CrossRef] [PubMed]
- Hung, J.-C.; Lin, C.-C. Investigations on the material property changes of ultrasonic-vibration assisted aluminum alloy upsetting. Mater. Des. 2013, 45, 412–420. [Google Scholar] [CrossRef]
- Hung, J.-C.; Tsai, Y.-C. Investigation of the effects of ultrasonic vibration-assisted micro-upsetting on brass. Mater. Sci. Eng. A 2013, 580, 125–132. [Google Scholar] [CrossRef]
- Zhao, X.; Zhao, S.; Han, Q. Effects of vibration direction on the mechanical behavior and microstructure of a metal sheet undergoing vibration-assisted uniaxial tension. Mater. Sci. Eng. A 2019, 743, 472–481. [Google Scholar]
- Liu, Y.; Suslov, S.; Han, Q.; Xu, C.; Hua, L. Microstructure of the pure copper produced by upsetting with ultrasonic vibration. Mater. Lett. 2012, 67, 52–55. [Google Scholar] [CrossRef]
- Wang, X.; Qi, Z.; Chen, W. Investigation of mechanical and microstructural characteristics of Ti–45Nb undergoing transversal ultrasonic vibration-assisted upsetting. Mater. Sci. Eng. A 2021, 813, 141169. [Google Scholar] [CrossRef]
- Wang, X.; Qi, Z.; Chen, W. Investigation of Ti–45Nb alloy’s mechanical and microscopic behaviors under transverse ultrasonic vibration-assisted compression. Mater. Sci. Eng. A 2022, 832, 142401. [Google Scholar] [CrossRef]
- Von Neumann, J. Papers of John Von Neumann on Computing and Computer Theory; MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Humphreys, F.J.; Hatherly, M. Recryatailization and Related Annealing Phenomena; Pergamon Press: Oxford, UK, 1995. [Google Scholar]
- Duan, C.; Zhang, F.; Qin, S.; Sun, W.; Wang, M. Modeling of dynamic recrystallization in white layer in dry hard cutting by finite element—Cellular automaton method. J. Mech. Sci. Technol. 2018, 32, 4299–4312. [Google Scholar] [CrossRef]
- Mecking, H.; Kocks, U.F. Kinetics of flow and strain-harding. Acta Metall. 1981, 29, 1865–1875. [Google Scholar] [CrossRef]
- Zhang, T.; Lu, S.; Wu, Y.; Gong, H. Optimization of deformation parameters of dynamic recrystallization for 7055 aluminum alloy by cellular automaton. Trans. Nonferrous Met. Soc. China 2017, 27, 1327–1337. [Google Scholar] [CrossRef]
- Yazdipour, N.; Davies, C.H.J.; Hodgson, P.D. Microstructural modeling of dynamic recrystallization using irregular cellular automata. Comput. Mater. Sci. 2008, 44, 566–576. [Google Scholar] [CrossRef]
- Wang, S.; Xu, W.; Wu, H.; Yuan, R.; Jin, X.; Shan, D. Simulation of dynamic recrystallization of a magnesium alloy with a cellular automaton method coupled with adaptive activation energy and matrix deformation topology. Manuf. Rev. 2021, 8, 11. [Google Scholar] [CrossRef]









| C | Si | Mn | S | P | Cr | Ni | Mo | Cu |
|---|---|---|---|---|---|---|---|---|
| 0.08 | 0.20 | 0.58 | <0.015 | 0.0026 | 1.31 | 3.33 | 0.10 | 0.015 |
| Ultrasound Amplitude/μm | 6.62 | 7.78 | 8.84 | 9.96 |
|---|---|---|---|---|
| Strain rate/s−1 | 0.0003 | 0.003 | 0.03 | 0.3 |
| Strain Rate (s−1). | Ultrasound Amplitude (μm). | Experimental Value (%) | Simulated Value (%) | Relative Error (%) |
|---|---|---|---|---|
| 0.0003 | 6.62 | 5.51 | 5.20 | 5.57 |
| 0.0003 | 7.78 | 6.25 | 6.21 | 0.73 |
| 0.0003 | 8.84 | 7.48 | 7.04 | 5.97 |
| 0.0003 | 9.96 | 9.38 | 9.10 | 2.99 |
| 0.003 | 6.62 | 4.88 | 4.79 | 1.88 |
| 0.003 | 7.78 | 5.54 | 5.24 | 5.33 |
| 0.003 | 8.84 | 5.79 | 5.90 | 1.79 |
| 0.003 | 9.96 | 6.87 | 6.35 | 7.53 |
| 0.03 | 6.62 | 4.24 | 4.22 | 0.48 |
| 0.03 | 7.78 | 5.37 | 5.07 | 5.53 |
| 0.03 | 8.84 | 5.32 | 5.30 | 0.34 |
| 0.03 | 9.96 | 6.74 | 5.96 | 11.60 |
| 0.3 | 6.62 | 3.19 | 3.55 | 11.07 |
| 0.3 | 7.78 | 4.01 | 4.45 | 11.04 |
| 0.3 | 8.84 | 4.57 | 5.00 | 9.50 |
| 0.3 | 9.96 | 4.66 | 5.09 | 9.22 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zhou, W.; Tang, J.; He, Y. Understanding Effects of Ultrasonic Vibration on Microstructure Evolution in Hot Forming Process via Cellular Automata Method. Materials 2022, 15, 7359. https://doi.org/10.3390/ma15207359
Zhang Y, Zhou W, Tang J, He Y. Understanding Effects of Ultrasonic Vibration on Microstructure Evolution in Hot Forming Process via Cellular Automata Method. Materials. 2022; 15(20):7359. https://doi.org/10.3390/ma15207359
Chicago/Turabian StyleZhang, Yutong, Weihua Zhou, Jinyuan Tang, and Yuhui He. 2022. "Understanding Effects of Ultrasonic Vibration on Microstructure Evolution in Hot Forming Process via Cellular Automata Method" Materials 15, no. 20: 7359. https://doi.org/10.3390/ma15207359




