Predicting Surface Residual Stress for Multi-Axis Milling of Ti-6Al-4V Titanium Alloy in Combined Simulation and Experiments
Abstract
:1. Introduction
2. Numerical Model for Residual Stress Induced by Multi-Axis Milling
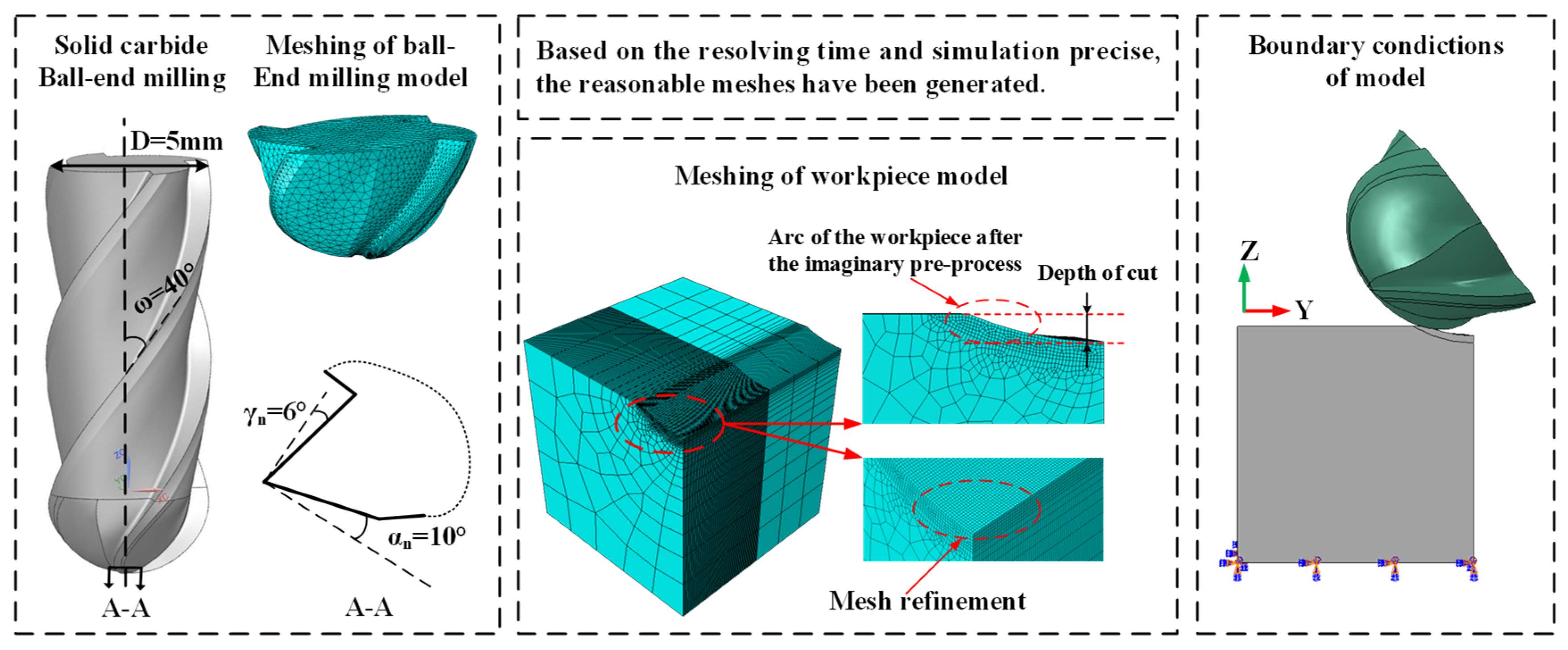
2.1. Simulation Details
2.2. Governing Equations
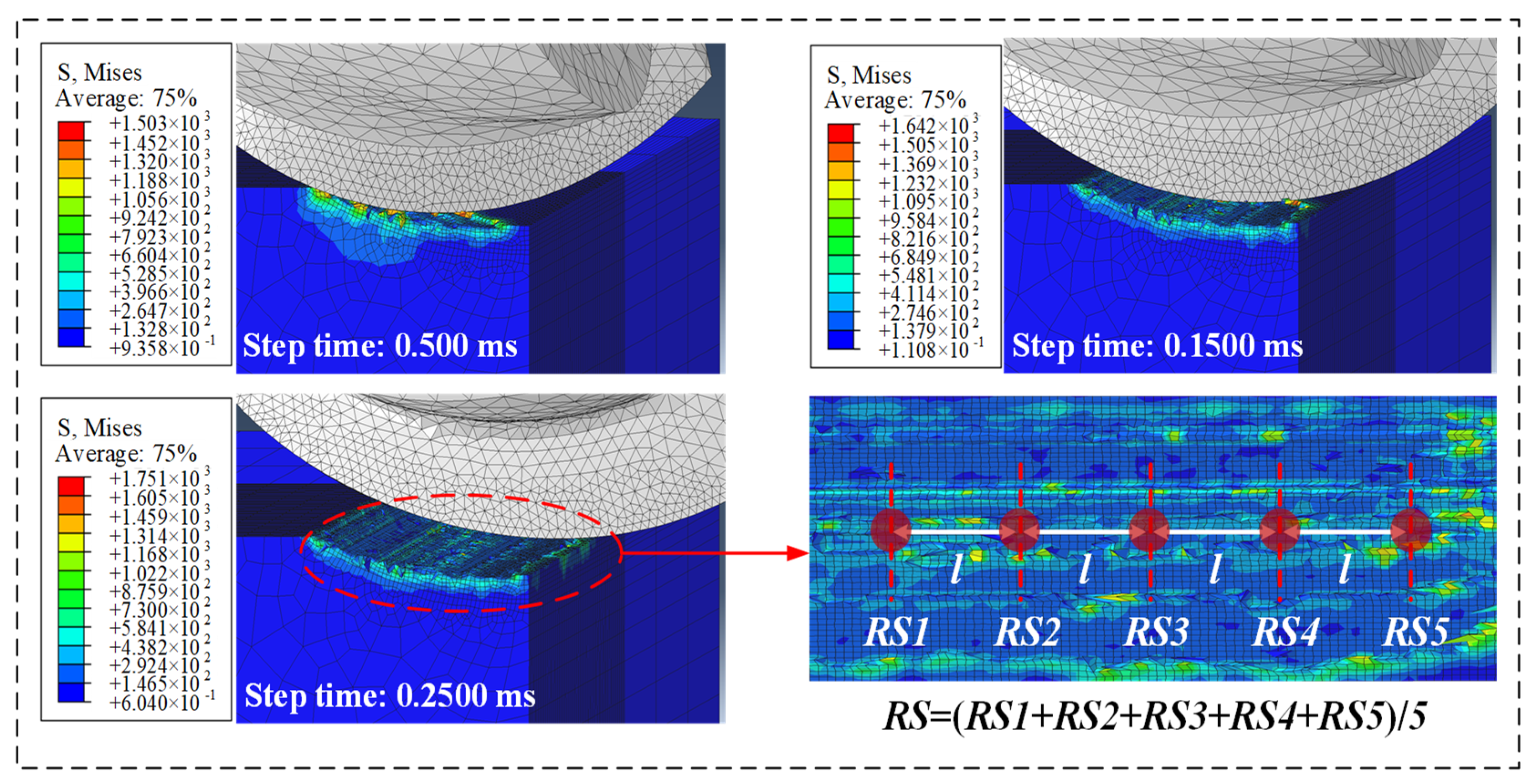
2.3. Data Extraction of Simulated Residual Stress
2.4. Verification Experiment
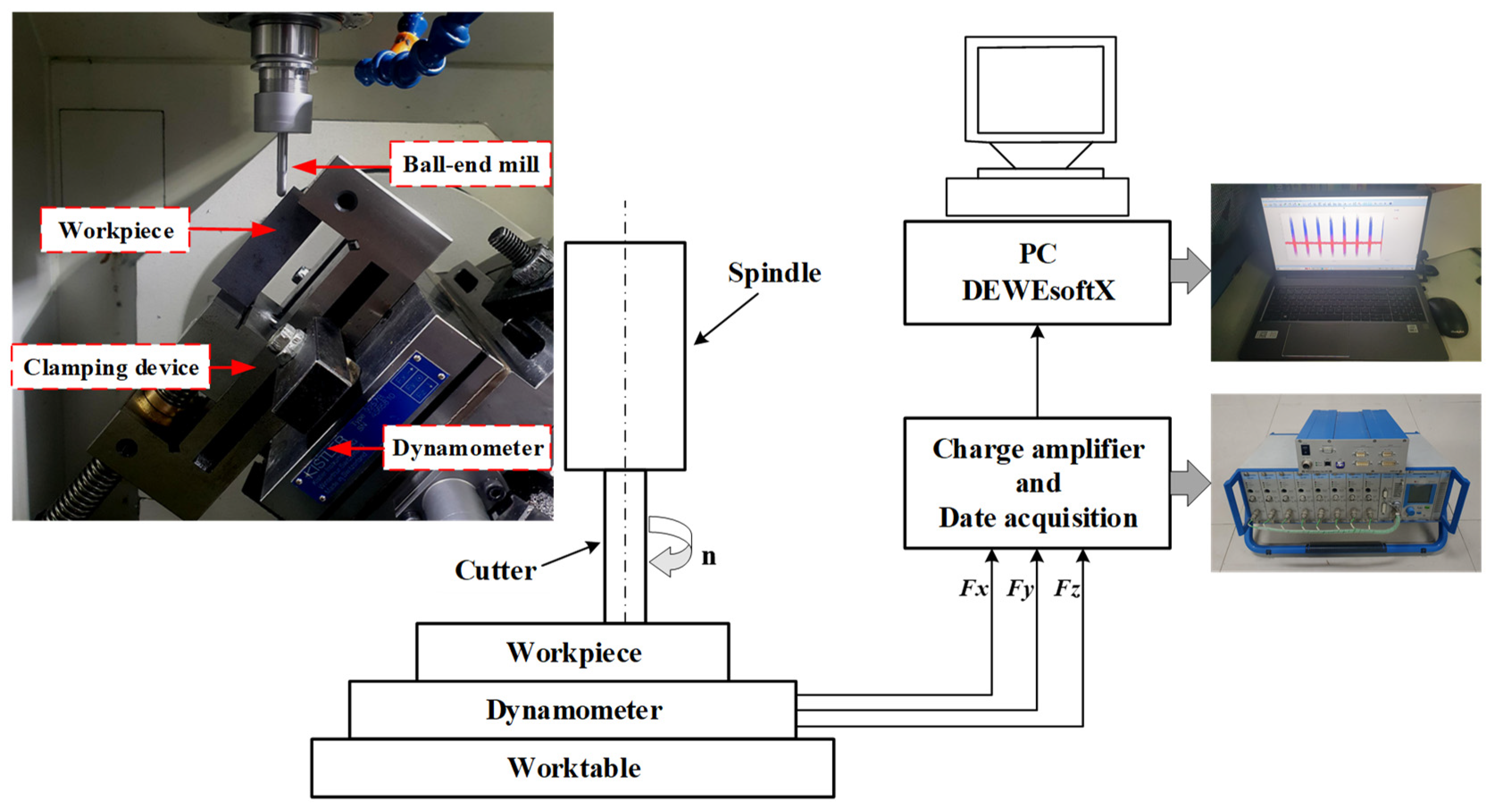
2.4.1. Machining Experiment
2.4.2. Residual Stress Measurement
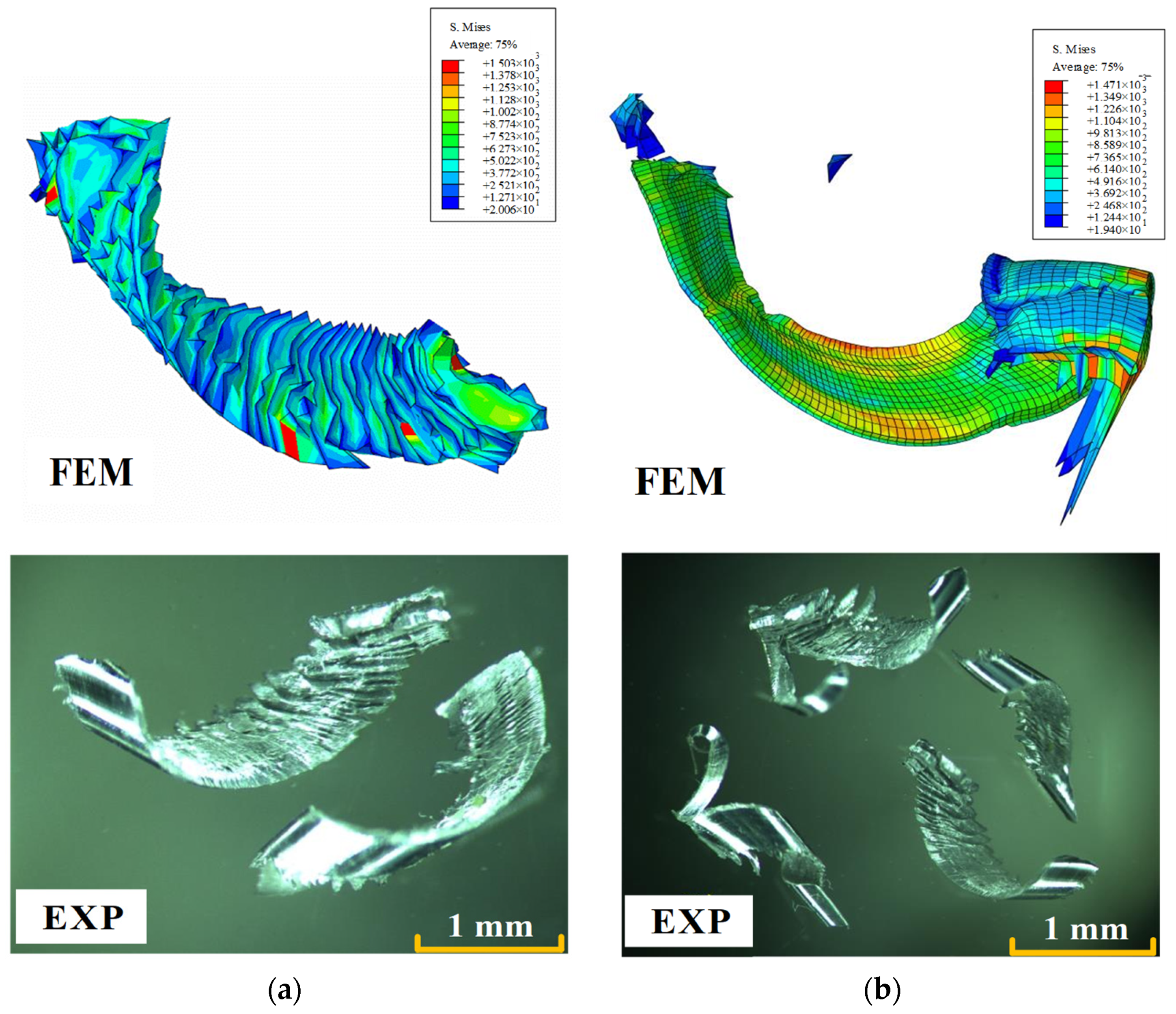
2.4.3. Simulated and Measured Cutting Forces and Chip Morphology
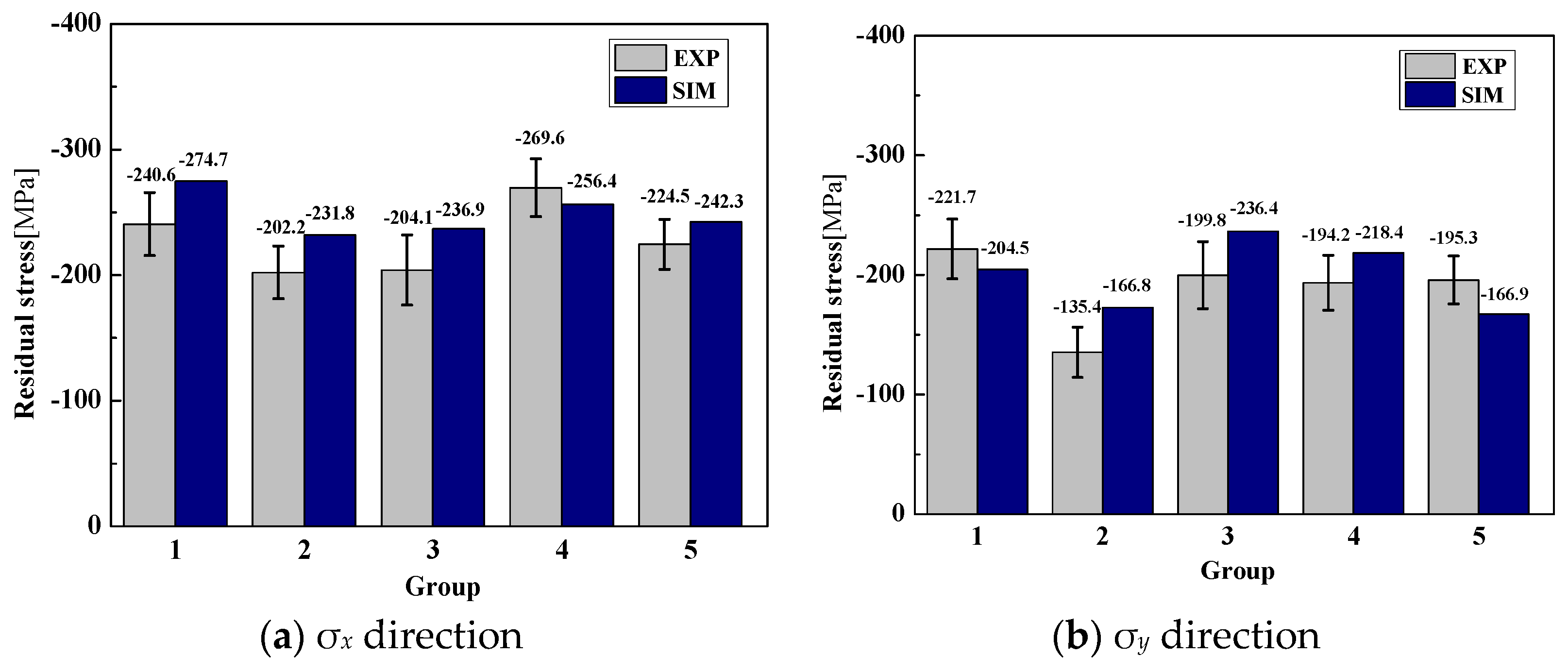
2.4.4. Simulated and Measured Surface Residual Stress
3. RBF Neural Network Model of Surface Residual Stress
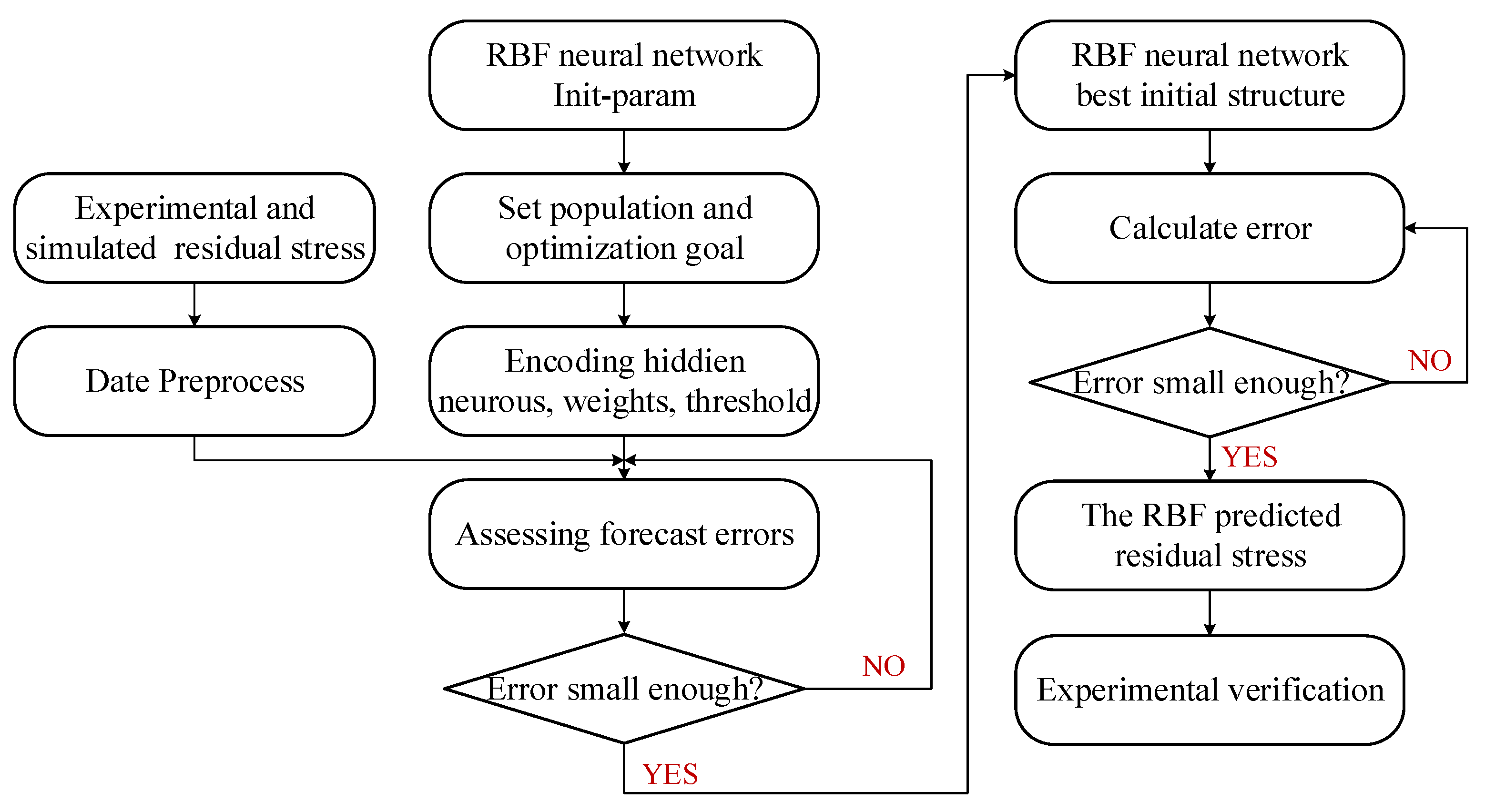
3.1. RBF Neural Network
3.2. Prediction Model of Surface Residual Stress
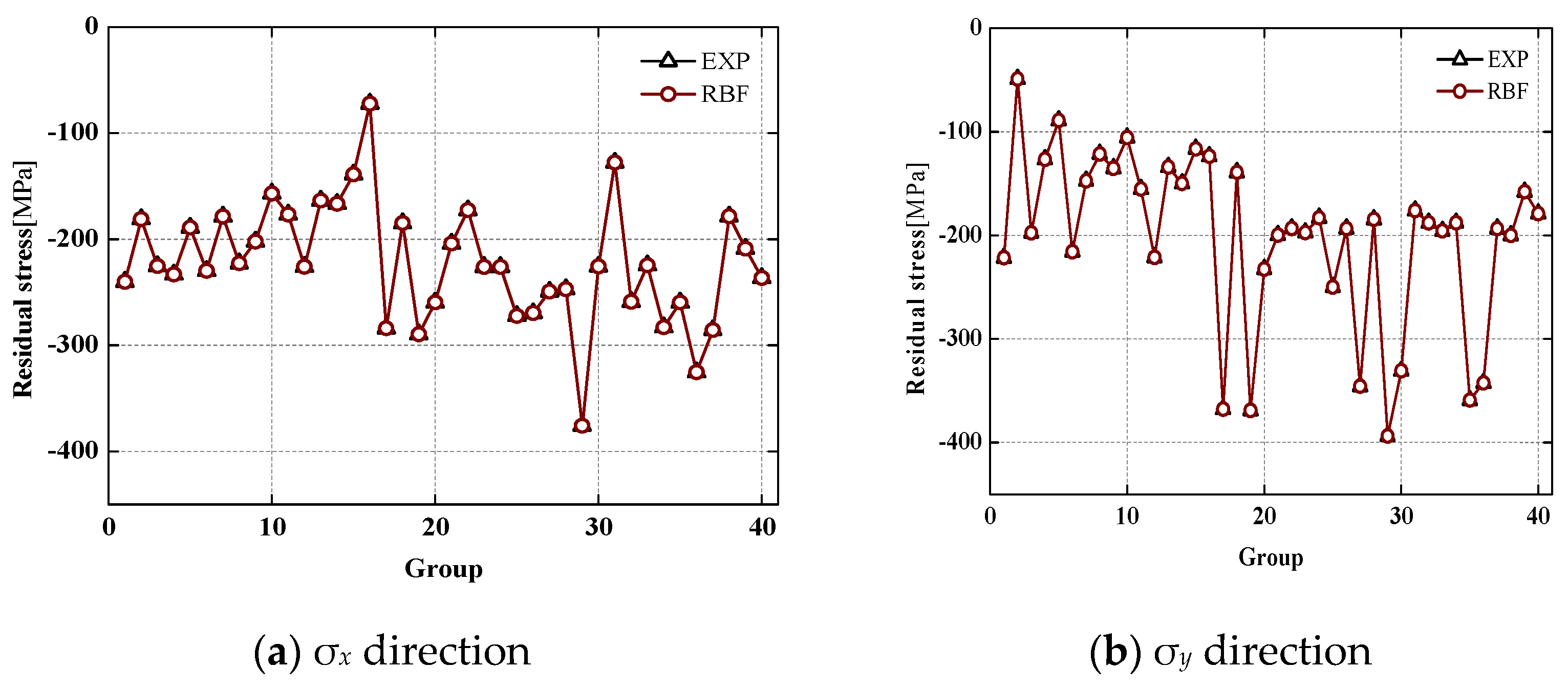
3.3. Verification of Residual Stress
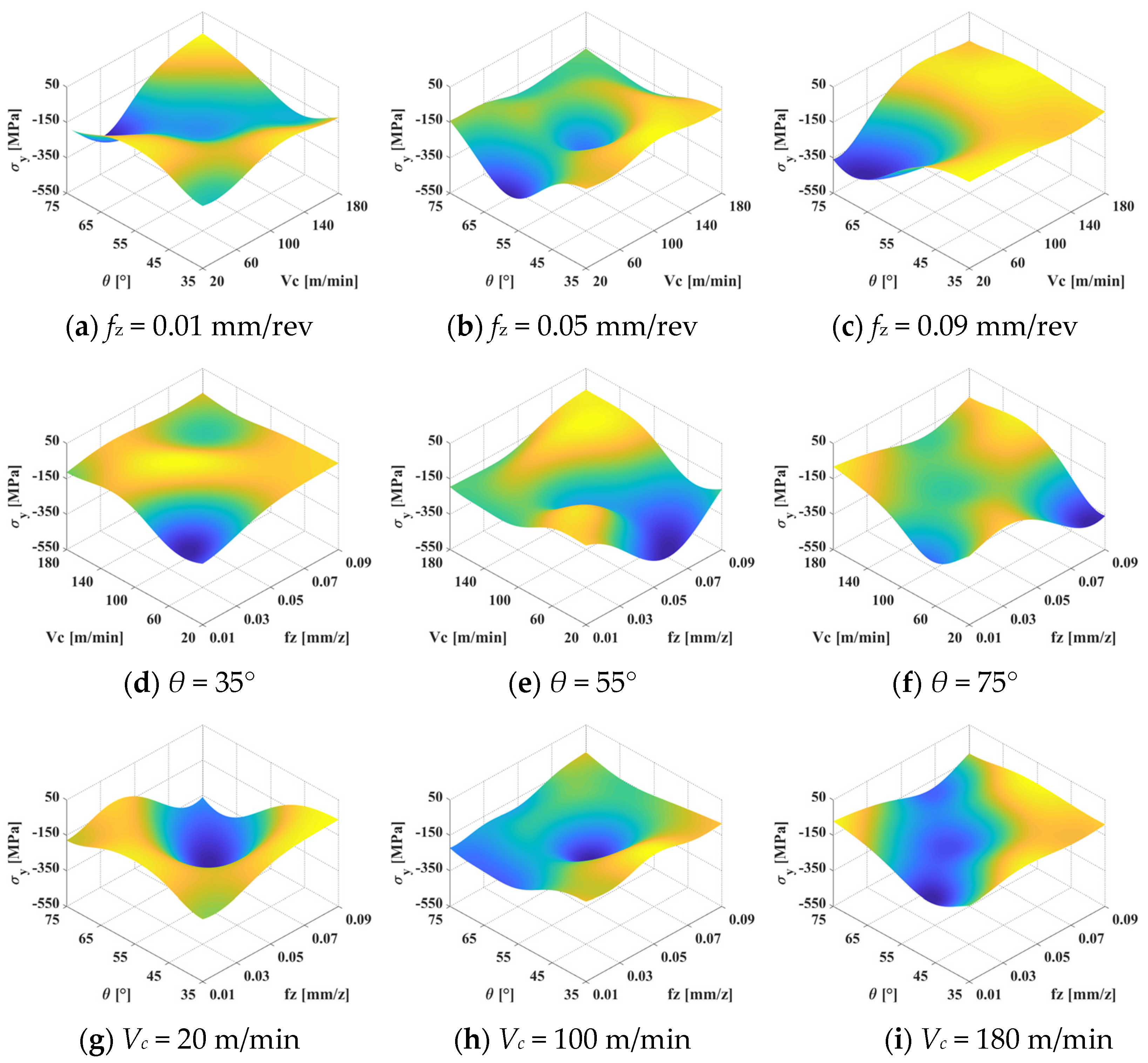
4. Influence of Machining Parameters
5. Conclusions
- (1)
- A 3D numerical model was established to predict the surface residual stress induced by multi-axis milling of Ti-6Al-4V titanium alloy. The simulated and experimental values followed a similar trend and gave good agreement between them. The total average prediction error rate of surface residual stress was 11.6% and 15.2% in the σx and σy directions, respectively.
- (2)
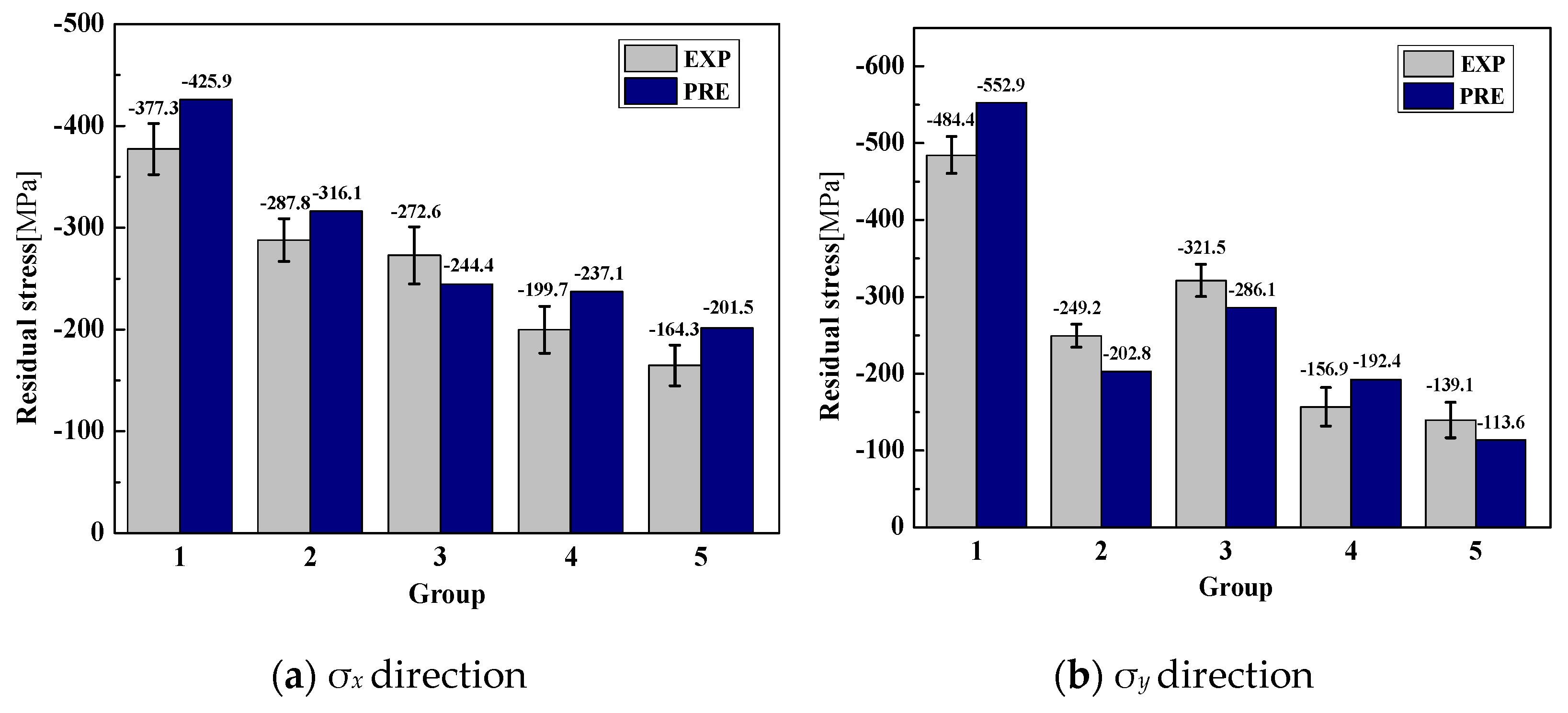
- The verification shows that the surface residual stress can be well predicted by using the modeling method based on the RBF neural network presented in this paper. Within the thresholds of cutting speed of 20~180 m/min, feed rate of 0.01~0.09 mm/rev, and roll angle of 35~75°, the prediction error ranges from 28.2 MPa to 48.6 MPa in the σx direction, and from 25.5 MPa to 68.5 MPa in the σy directions. The average prediction error rates of surface residual stress in the two directions are 14.4% and 17.2%, respectively. The proposed prediction model in this paper, based on experimentation and simulation, can effectively predict the surface residual stress induced by multi-axis milling of Ti-6Al-4V titanium alloy.
- (3)
- The inclination angle, cutting speed, and feed rate have a strong nonlinear relationship with the surface residual stress. Parameters that are too large or too small will lead to the transformation of the surface residual stress form from compression to tension.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mirzendehdel, A.M.; Behandish, M.; Nelaturi, S. Topology optimization with accessibility constraint for multi-axis machining. Comput.-Aided Des. 2020, 122, 102825. [Google Scholar] [CrossRef]
- Wan, M.; Ye, X.-Y.; Wen, D.-Y.; Zhang, W. Modeling of machining-induced residual stresses. J. Mater. Sci. 2019, 54, 1–35. [Google Scholar] [CrossRef]
- Wu, G.; Li, G.; Pan, W.; Raja, I.; Wang, X.; Ding, S. A state-of-art review on chatter and geometric errors in thin-wall machining processes. J. Manuf. Process. 2021, 68, 454–480. [Google Scholar] [CrossRef]
- Yue, C.; Gao, H.; Liu, X.; Liang, S.Y. Part functionality alterations induced by changes of surface integrity in metal milling process: A review. Appl. Sci. 2018, 8, 2550. [Google Scholar] [CrossRef]
- Li, B.; Deng, H.; Hui, D.; Hu, Z.; Zhang, W. A semi-analytical model for predicting the machining deformation of thin-walled parts considering machining-induced and blank initial residual stress. Int. J. Adv. Manuf. Technol. 2020, 110, 139–161. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, Y.; Wu, Q.; Li, B. Investigation on influences of initial residual stress on thin-walled part machining deformation based on a semi-analytical model. J. Mater. Process. Technol. 2018, 262, 437–448. [Google Scholar] [CrossRef]
- Liang, X.; Liu, Z.; Wang, B.; Song, Q.; Cai, Y.; Wan, Y. Prediction of residual stress with multi-physics model for orthogonal cutting Ti-6Al-4V under various tool wear morphologies. J. Mater. Process. Technol. 2021, 288, 116908. [Google Scholar] [CrossRef]
- Ji, X.; Liang, S.Y. Model-based sensitivity analysis of machining-induced residual stress under minimum quantity lubrication. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2017, 231, 1528–1541. [Google Scholar] [CrossRef]
- Ji, X.; Zhang, X.; Liang, S.Y. Predictive modeling of residual stress in minimum quantity lubrication machining. Int. J. Adv. Manuf. Technol. 2014, 70, 2159–2168. [Google Scholar] [CrossRef]
- Outeiro, J.; Umbrello, D.; M’saoubi, R. Experimental and numerical modelling of the residual stresses induced in orthogonal cutting of AISI 316L steel. Int. J. Mach. Tools Manuf. 2006, 46, 1786–1794. [Google Scholar] [CrossRef]
- Arrazola, P.J.; Kortabarria, A.; Madariaga, A.; Esnaola, J.; Fernandez, E.; Cappellini, C.; Ulutan, D.; Özel, T. On the machining induced residual stresses in IN718 nickel-based alloy: Experiments and predictions with finite element simulation. Simul. Model. Pract. Theory 2014, 41, 87–103. [Google Scholar] [CrossRef]
- Xin, H.; Shi, Y.; Ning, L.; Zhao, T. Residual stress and affected layer in disc milling of titanium alloy. Mater. Manuf. Process. 2016, 31, 1645–1653. [Google Scholar] [CrossRef]
- Sahu, N.K.; Andhare, A.B. Prediction of residual stress using RSM during turning of Ti–6Al–4V with the 3D FEM assist and experiments. SN Appl. Sci. 2019, 1, 891. [Google Scholar] [CrossRef]
- Özel, T.; Ulutan, D. Prediction of machining induced residual stresses in turning of titanium and nickel based alloys with experiments and finite element simulations. CIRP Ann. 2012, 61, 547–550. [Google Scholar] [CrossRef]
- Mishra, S.K.; Ghosh, S.; Aravindan, S. Finite element investigations on temperature and residual stresses during machining Ti6Al4V alloy using TiAlN coated plain and textured tools. In Proceedings of the International Conference on Precision, Meso, Micro and Nano Engineering, COPEN, Chennai, India, 6–9 December 2017; Volume 10, pp. 979–982. [Google Scholar]
- Ayeb, M.; Frija, M.; Fathallah, R. Prediction of residual stress profile and optimization of surface conditions induced by laser shock peening process using artificial neural networks. Int. J. Adv. Manuf. Technol. 2019, 100, 2455–2471. [Google Scholar] [CrossRef]
- Cheng, M.; Jiao, L.; Yan, P.; Feng, L.; Qiu, T.; Wang, X.; Zhang, B. Prediction of surface residual stress in end milling with Gaussian process regression. Measurement 2021, 178, 109333. [Google Scholar] [CrossRef]
- Elsheikh, A.H.; Muthuramalingam, T.; Shanmugan, S.; Ibrahim, A.M.M.; Ramesh, B.; Khoshaim, A.B.; Moustafa, E.B.; Bedairi, B.; Panchal, H.; Sathyamurthy, R. Fine-tuned artificial intelligence model using pigeon optimizer for prediction of residual stresses during turning of Inconel 718. J. Mater. Res. Technol. 2021, 15, 3622–3634. [Google Scholar] [CrossRef]
- Jafarian, F.; Amirabadi, H.; Fattahi, M. Improving surface integrity in finish machining of Inconel 718 alloy using intelligent systems. Int. J. Adv. Manuf. Technol. 2014, 71, 817–827. [Google Scholar] [CrossRef]
- Xu, L.; Huang, C.; Li, C.; Wang, J.; Liu, H.; Wang, X. An improved case based reasoning method and its application in estimation of surface quality toward intelligent machining. J. Intell. Manuf. 2021, 32, 313–327. [Google Scholar] [CrossRef]
- Ullah, I.; Zhang, S.; Waqar, S. Numerical and experimental investigation on thermo-mechanically induced residual stress in high-speed milling of Ti-6Al-4V alloy. J. Manuf. Process. 2022, 76, 575–587. [Google Scholar] [CrossRef]
- Ee, K.; Dillon, O., Jr.; Jawahir, I. Finite element modeling of residual stresses in machining induced by cutting using a tool with finite edge radius. Int. J. Mech. Sci. 2005, 47, 1611–1628. [Google Scholar] [CrossRef]
- Ren, J.; Cai, J.; Zhou, J.; Shi, K.; Li, X. Inverse determination of improved constitutive equation for cutting titanium alloy Ti-6Al-4V based on finite element analysis. Int. J. Adv. Manuf. Technol. 2018, 97, 3671–3682. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, Z.; Yang, D.; Mohsan, A.U.H. Metallurgical-based prediction of stress-temperature induced rapid heating and cooling phase transformations for high speed machining Ti-6Al-4V alloy. Mater. Des. 2017, 119, 208–218. [Google Scholar] [CrossRef]
- Pan, Z.; Liang, S.Y.; Garmestani, H.; Shih, D.; Hoar, E. Residual stress prediction based on MTS model during machining of Ti-6Al-4V. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 3743–3750. [Google Scholar] [CrossRef]
- Vahabli, E.; Rahmati, S. Application of an RBF neural network for FDM parts’ surface roughness prediction for enhancing surface quality. Int. J. Precis. Eng. Manuf. 2016, 17, 1589–1603. [Google Scholar] [CrossRef]
- Zhou, J.; Ren, J.; Tian, W. Grey-RBF-FA method to optimize surface integrity for inclined end milling Inconel 718. Int. J. Adv. Manuf. Technol. 2017, 91, 2975–2993. [Google Scholar] [CrossRef]
- Marek, A.; Davis, F.M.; Rossi, M.; Pierron, F. Extension of the sensitivity-based virtual fields to large deformation anisotropic plasticity. Int. J. Mater. Form. 2019, 12, 457–476. [Google Scholar] [CrossRef] [Green Version]
- Singh, P.; Pungotra, H.; Kalsi, N.S. On the complexities in machining titanium alloys. In CAD/CAM, Robotics and Factories of the Future; Springer: Heidelberg, Germany, 2016; pp. 499–507. [Google Scholar]




| A | B | C | n | m | |
|---|---|---|---|---|---|
| 782 | 498 | 0.028 | 0.28 | 1 | 0.0001 |
| d1 | d2 | d3 | d4 | d5 |
|---|---|---|---|---|
| −0.09 | 0.25 | −0.5 | 0.014 | 3.87 |
| Elastic Modulus (MPa) | Poisson’s Ratio | Heat Capacity (J/(Kg °C)) | Conductivity (W/(m °C)) | Expansion (μm/(m °C)) |
|---|---|---|---|---|
| 0.7412 T + 113375 | 0.34 | 2.24 e0.0007T | 7.039 e0.0011T | 3 × 10−9 T + 7 × 10−6 |
| No. | θ (°) | Vc (m/min) | fz (mm/rev) | σx (MPa) | σy (MPa) | ||||
|---|---|---|---|---|---|---|---|---|---|
| EXP | SIM | Error | EXP | SIM | Error | ||||
| 1 | 35 | 60 | 0.03 | −240.6 | −274.7 | 14.2% | −221.7 | −204.5 | 7.8% |
| 2 | 45 | 100 | 0.07 | −202.2 | −231.8 | 14.7% | −135.4 | −166.8 | 23.2% |
| 3 | 55 | 180 | 0.05 | −204.1 | −236.9 | 16.1% | −199.8 | −236.4 | 18.3% |
| 4 | 65 | 140 | 0.03 | −269.6 | −256.4 | 4.9% | −194.2 | −218.4 | 12.5% |
| 5 | 75 | 100 | 0.03 | −224.5 | −242.3 | 8.1% | −195.3 | −166.9 | 14.4% |
| No. | θ (°) | Vc (m/min) | fz (mm/rev) | σx (MPa) | σy (MPa) | Source |
|---|---|---|---|---|---|---|
| 1 | 35 | 60 | 0.03 | −240.16 | −221.7 | EXP |
| 2 | 35 | 100 | 0.05 | −181.1 | −49.1 | EXP |
| 3 | 35 | 20 | 0.01 | −225.3 | −197.6 | SIM |
| 4 | 35 | 140 | 0.07 | −233.1 | −126.8 | SIM |
| 5 | 35 | 180 | 0.09 | −189 | −89.1 | SIM |
| 6 | 35 | 60 | 0.07 | −229.7 | −215.9 | SIM |
| 7 | 35 | 100 | 0.03 | −178.6 | −147.5 | SIM |
| 8 | 35 | 140 | 0.03 | −222.7 | −121.6 | SIM |
| 9 | 45 | 100 | 0.07 | −202.2 | −135.4 | EXP |
| 10 | 45 | 140 | 0.09 | −157 | −105.6 | EXP |
| 11 | 45 | 20 | 0.03 | −176.61 | −155.3 | SIM |
| 12 | 45 | 180 | 0.01 | −226 | −221.3 | SIM |
| 13 | 45 | 100 | 0.05 | −163.5 | −134.1 | SIM |
| 14 | 45 | 20 | 0.07 | −166.6 | −149.9 | SIM |
| 15 | 45 | 60 | 0.09 | −138.9 | −116.6 | SIM |
| 16 | 45 | 100 | 0.01 | −72.1 | −123.7 | SIM |
| 17 | 55 | 60 | 0.07 | −284 | −367.7 | EXP |
| 18 | 55 | 100 | 0.09 | −184.7 | −139.1 | EXP |
| 19 | 55 | 20 | 0.05 | −289.5 | −369 | SIM |
| 20 | 55 | 140 | 0.01 | −259.6 | −232.6 | SIM |
| 21 | 55 | 180 | 0.03 | −204.1 | −199.8 | SIM |
| 22 | 55 | 180 | 0.05 | −172.6 | −193.4 | SIM |
| 23 | 55 | 100 | 0.07 | −226.1 | −197.4 | SIM |
| 24 | 55 | 100 | 0.03 | −226.1 | −183.1 | SIM |
| 25 | 65 | 100 | 0.01 | −272.3 | −250 | EXP |
| 26 | 65 | 140 | 0.03 | −269.6 | −193.5 | EXP |
| 27 | 65 | 60 | 0.09 | −249.3 | −345.6 | SIM |
| 28 | 65 | 180 | 0.05 | −247 | −184.6 | SIM |
| 29 | 65 | 20 | 0.03 | −375.8 | −393.7 | SIM |
| 30 | 65 | 60 | 0.03 | −225.7 | −330.7 | SIM |
| 31 | 65 | 100 | 0.09 | −127.8 | −176.2 | SIM |
| 32 | 65 | 140 | 0.07 | −258.9 | −187.9 | SIM |
| 33 | 75 | 100 | 0.03 | −224.5 | −195.8 | EXP |
| 34 | 75 | 140 | 0.05 | −283 | −187.9 | EXP |
| 35 | 75 | 20 | 0.09 | −259.5 | −359 | SIM |
| 36 | 75 | 60 | 0.01 | −325.3 | −342.4 | SIM |
| 37 | 75 | 180 | 0.07 | −285.6 | −193.5 | SIM |
| 38 | 75 | 100 | 0.05 | −178.4 | −200.1 | SIM |
| 39 | 75 | 140 | 0.03 | −208.9 | −157.9 | SIM |
| 40 | 75 | 180 | 0.07 | −236.5 | −179.1 | SIM |
| No. | θ (°) | Vc (m/min) | fz (mm/rev) | σx (MPa) | σy (MPa) | ||||
|---|---|---|---|---|---|---|---|---|---|
| EXP | PRE | Error | EXP | PRE | Error | ||||
| 1 | 65 | 20 | 0.07 | −377.3 | −425.9 | 12.9% | −484.4 | −552.9 | 14.2% |
| 2 | 55 | 100 | 0.01 | −287.8 | −316.1 | 9.8% | −249.2 | −202.8 | 18.7% |
| 3 | 55 | 100 | 0.05 | −272.6 | −244.4 | 10.4% | −321.5 | −286.1 | 11.1% |
| 4 | 65 | 100 | 0.05 | −199.7 | −232.1 | 16.2% | −156.9 | −192.4 | 22.6% |
| 5 | 45 | 60 | 0.05 | −164.3 | −201.5 | 22.7% | −139.1 | −113.6 | 19.3% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Zhou, J.; Ren, J.; Shu, A. Predicting Surface Residual Stress for Multi-Axis Milling of Ti-6Al-4V Titanium Alloy in Combined Simulation and Experiments. Materials 2022, 15, 6471. https://doi.org/10.3390/ma15186471
Wang Z, Zhou J, Ren J, Shu A. Predicting Surface Residual Stress for Multi-Axis Milling of Ti-6Al-4V Titanium Alloy in Combined Simulation and Experiments. Materials. 2022; 15(18):6471. https://doi.org/10.3390/ma15186471
Chicago/Turabian StyleWang, Zongyuan, Jinhua Zhou, Junxue Ren, and Ailing Shu. 2022. "Predicting Surface Residual Stress for Multi-Axis Milling of Ti-6Al-4V Titanium Alloy in Combined Simulation and Experiments" Materials 15, no. 18: 6471. https://doi.org/10.3390/ma15186471





