Moisture Transport of Axial-Compression-Damaged Mortar and Concrete in Atmospheric Environment
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Pore Size Distribution by MIP
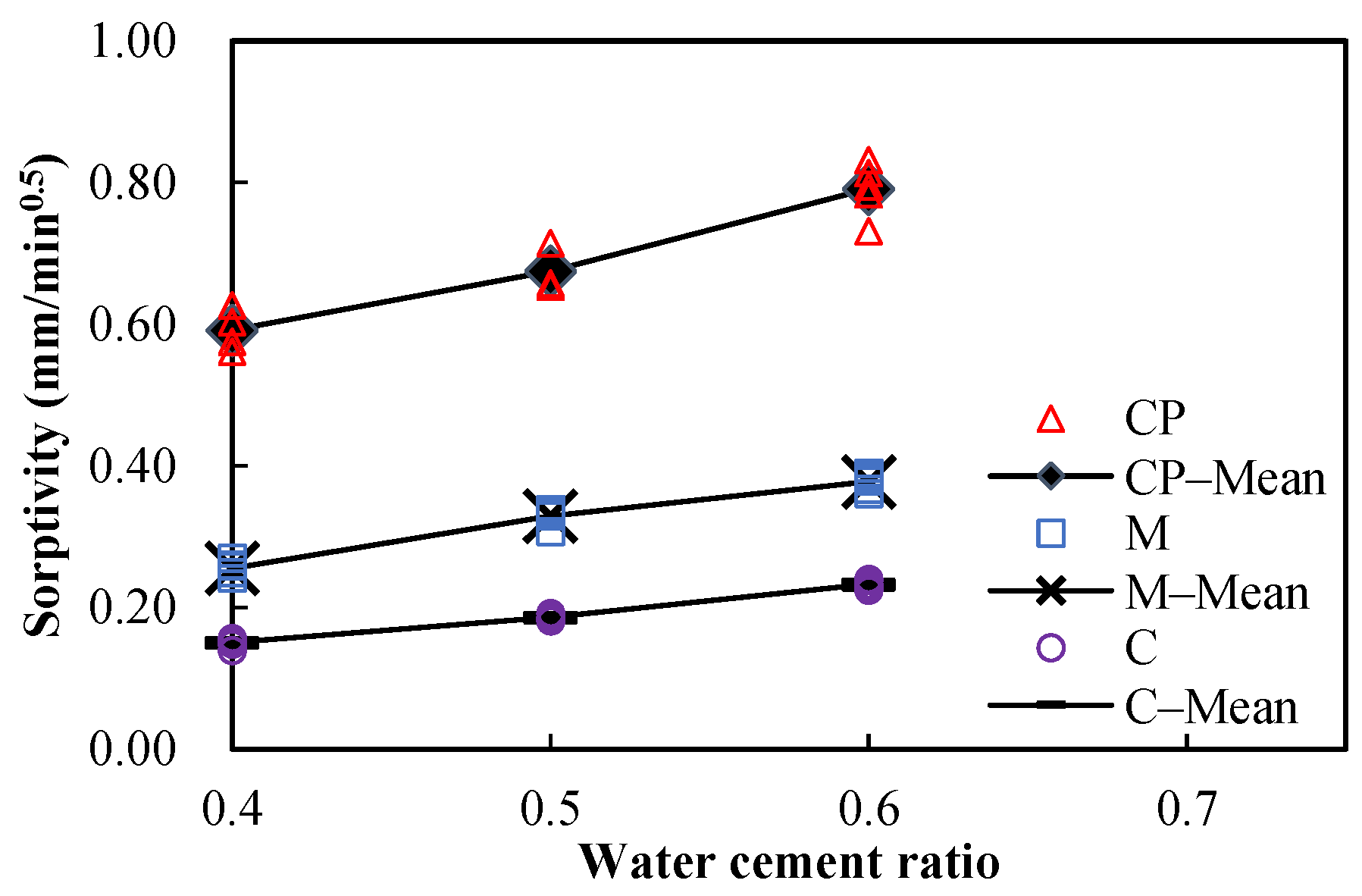
3.2. Porosities and Sorptivities of Undamaged Specimens
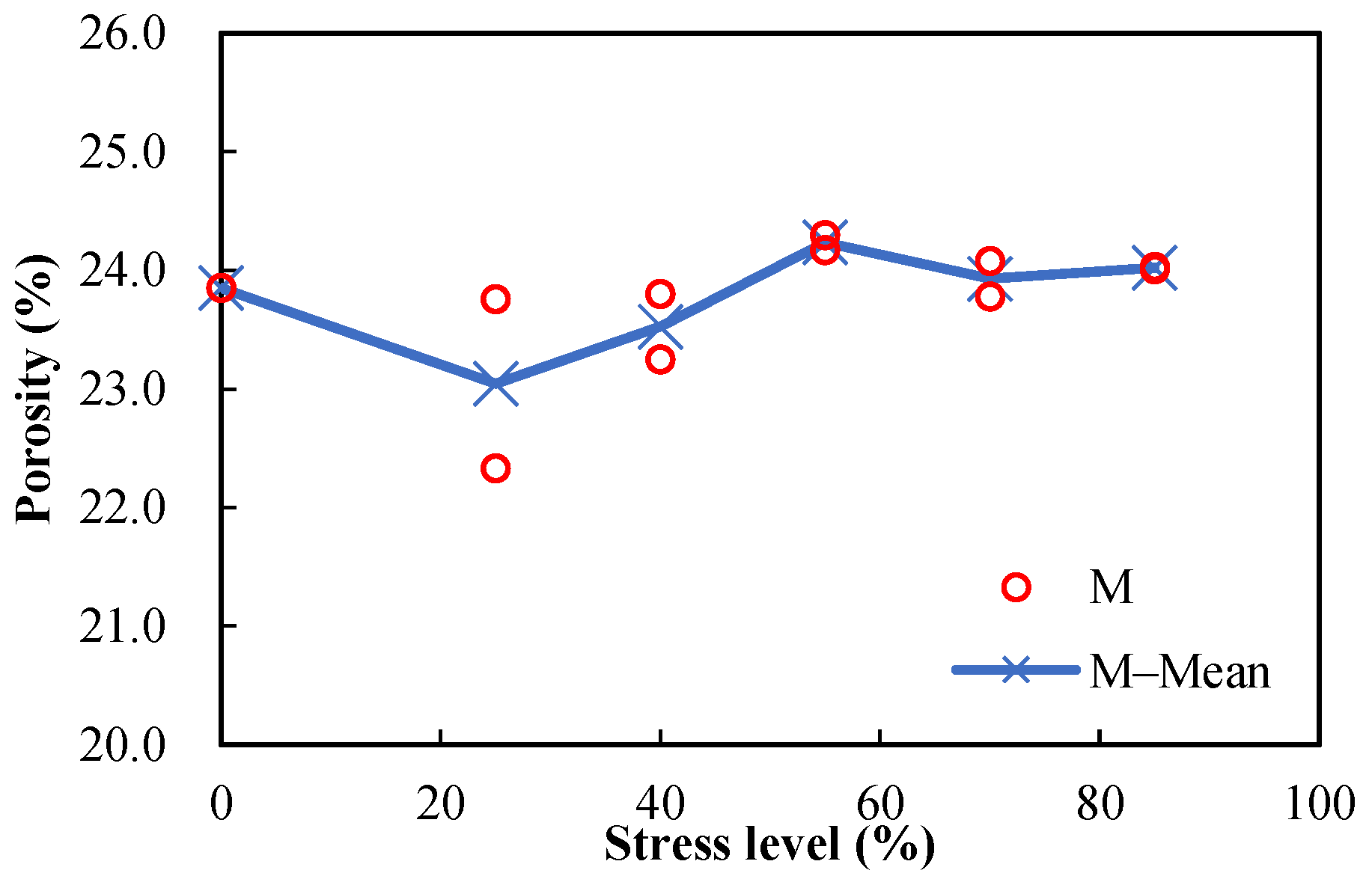
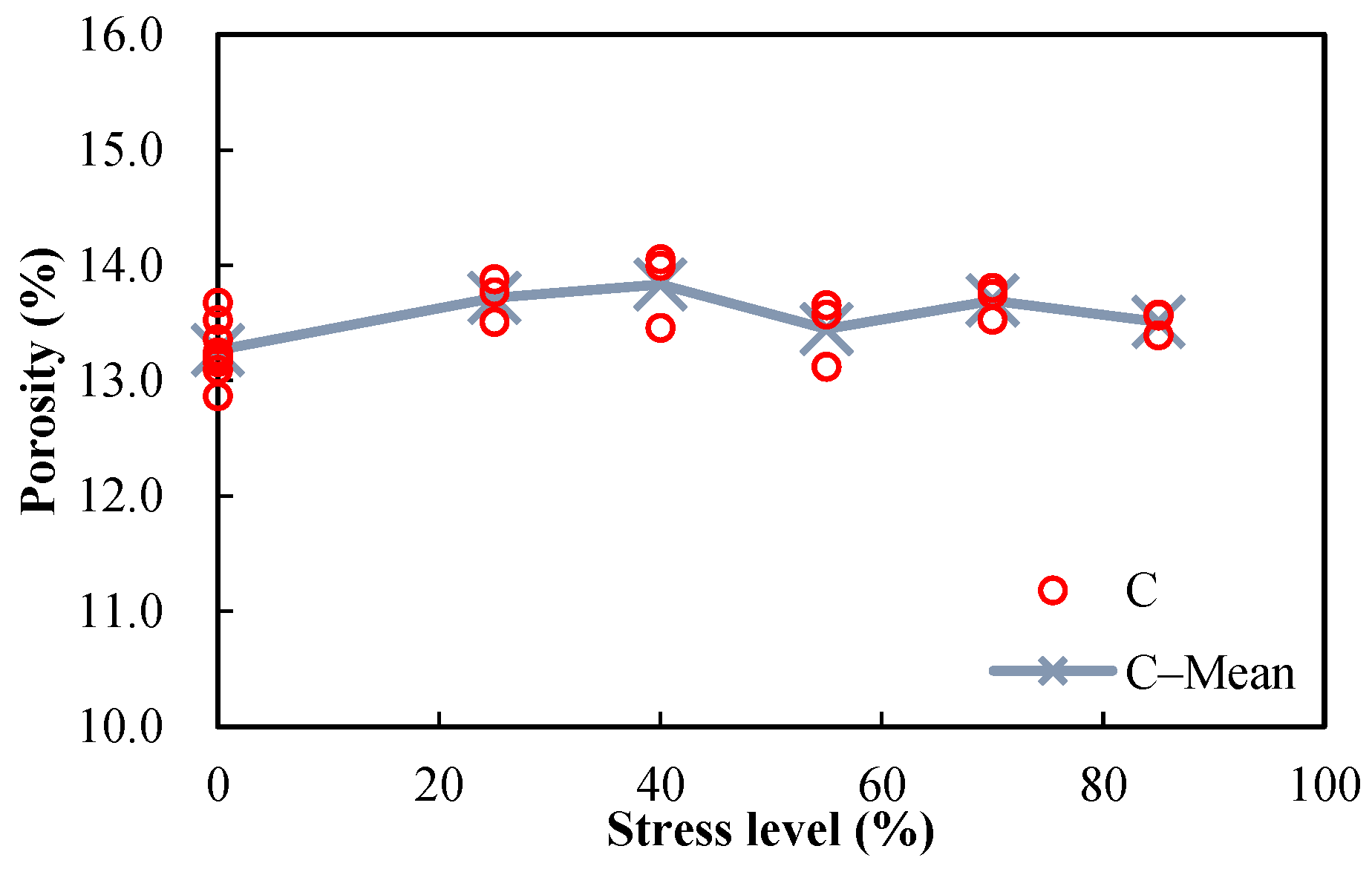
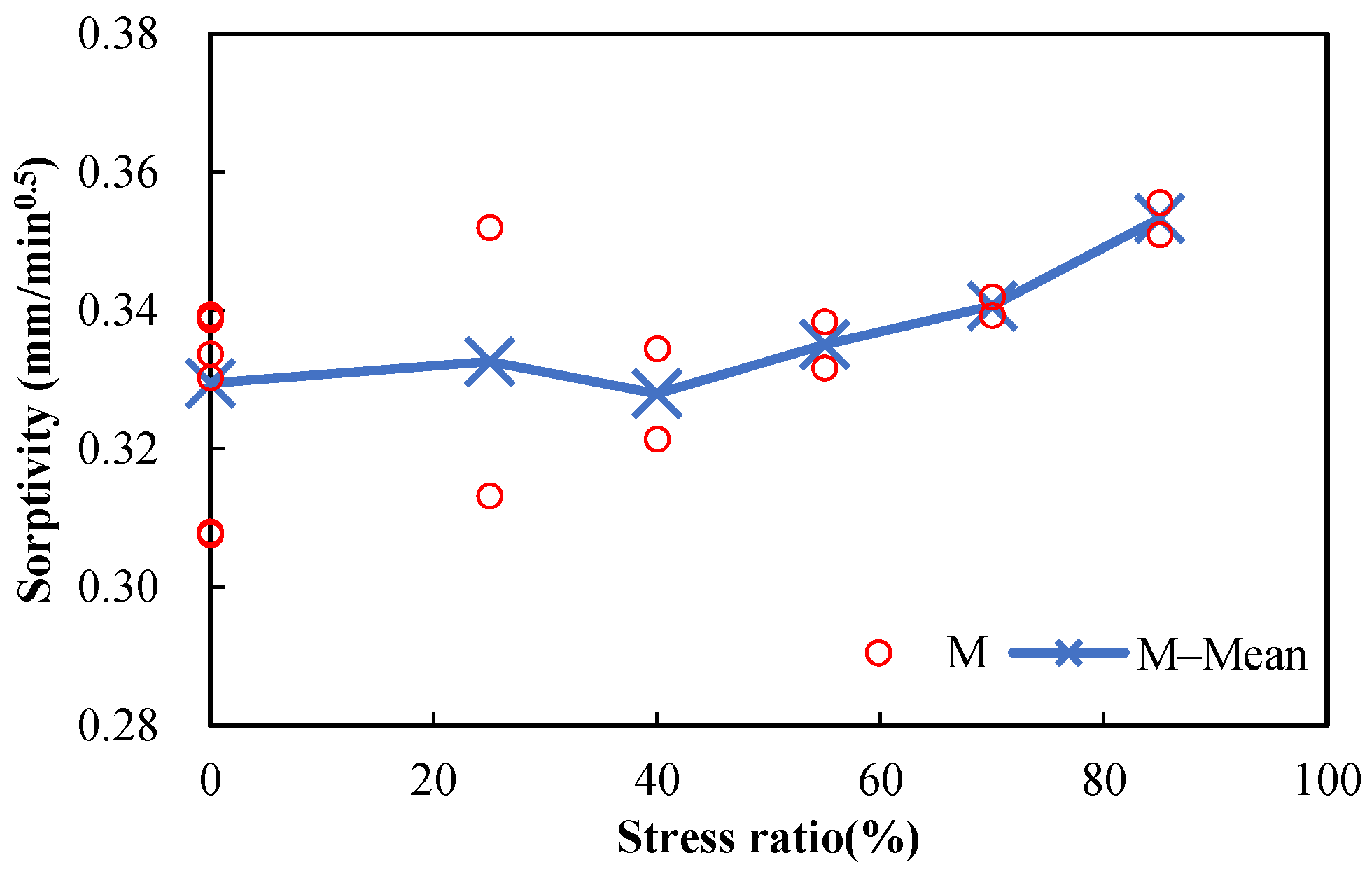
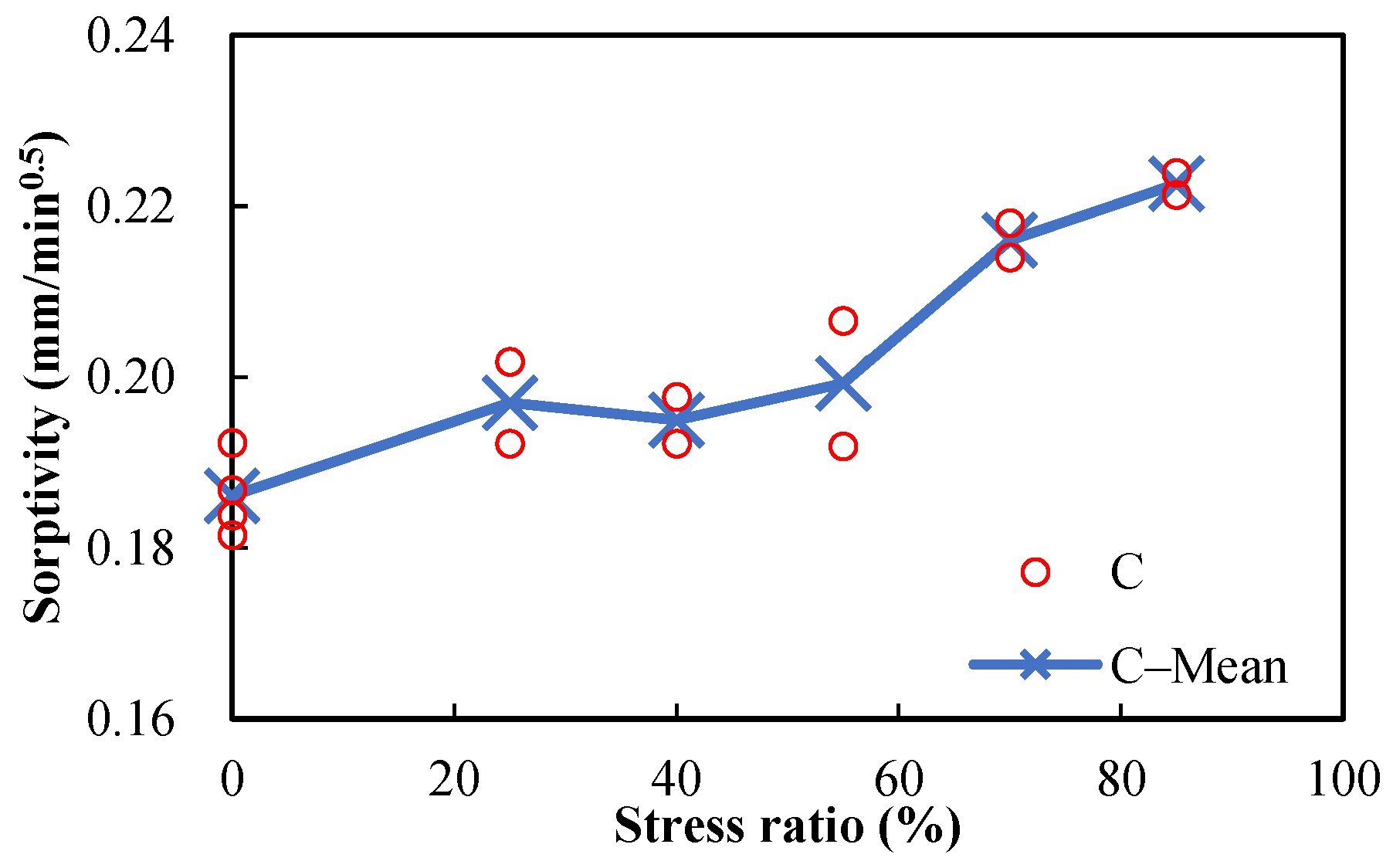
3.3. Porosities and Sorptivities of Damaged Specimens
4. Analytical Analysis
4.1. Analytical Model of Sorptivity
4.2. Damage-Representative Radius
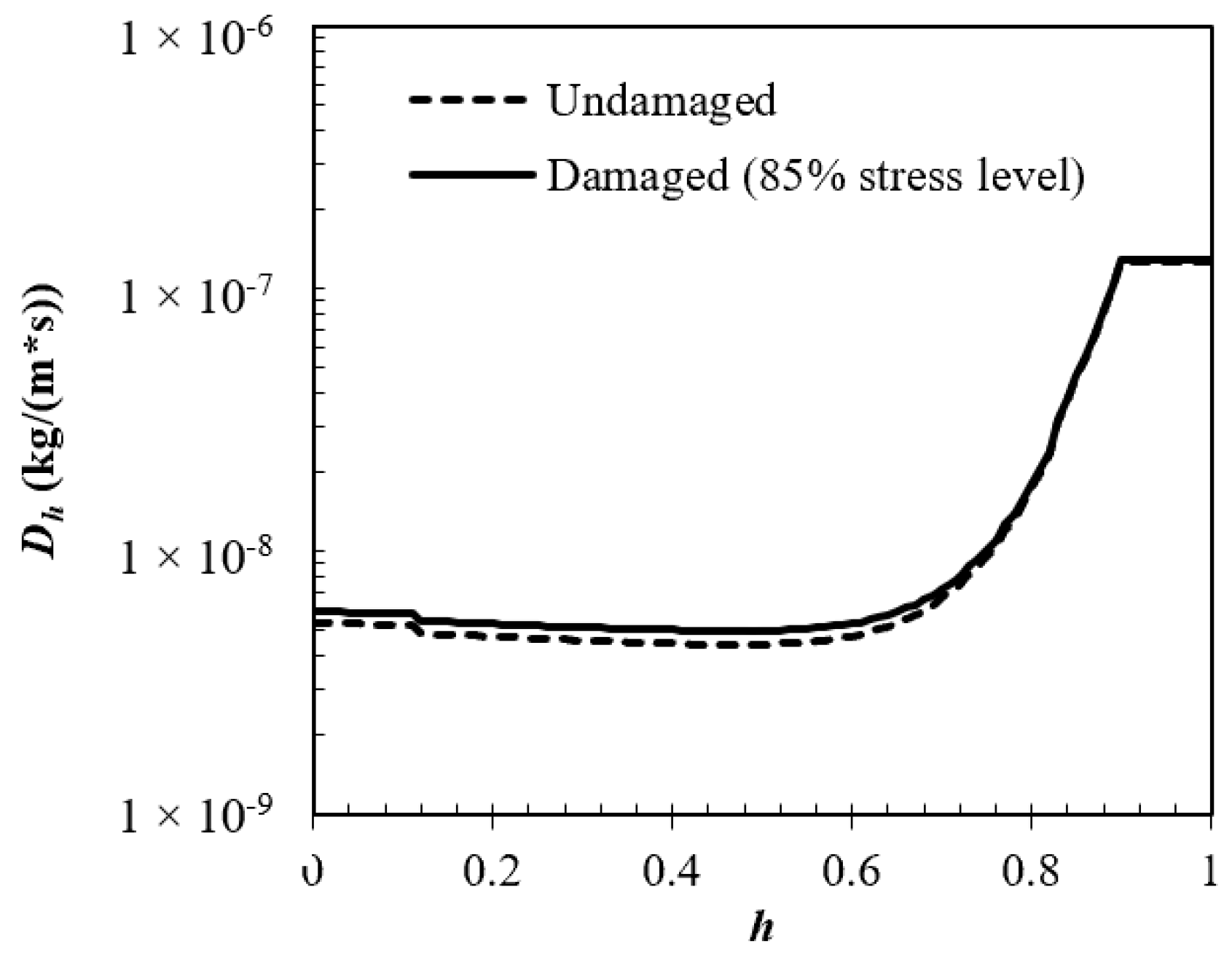
4.3. Moisture Diffusivity for Damaged Concrete Based on the Damage-Representative Radius
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bažant, Z.P.; Najjar, L.J. Nonlinear water diffusion in nonsaturated concrete. Matériaux Constr. 1972, 5, 3–20. [Google Scholar] [CrossRef]
- Sakata, K. A Study on Moisture Diffusion in Drying and Drying Shrinkage of Concrete. Cem. Concr. Res. 1983, 13, 216–224. [Google Scholar] [CrossRef]
- Xi, Y.P.; Bazant, Z.P.; Molina, L.; Jennings, H.M. Moisture Diffusion in Cementitious Materials—Moisture Capacity and Diffusivity. Adv. Cem. Based Mater. 1994, 1, 258–266. [Google Scholar] [CrossRef]
- Garrabrants, A.C.; Kosson, D.S. Modeling moisture transport from a Portland cement-based material during storage in reactive and inert atmospheres. Dry. Technol. 2003, 21, 775–805. [Google Scholar] [CrossRef]
- Leech, C.; Lockington, D.; Dux, P. Unsaturated diffusivity functions for concrete derived from NMR images. Mater. Struct. 2003, 36, 413–418. [Google Scholar] [CrossRef]
- Daian, J.F. Condensation and Isothermal Water Transfer in Cement Mortar Part I. Pore-Size Distribution, Equilibrium Water Condensation and Imbibition. Transp. Porous Media 1988, 3, 563–589. [Google Scholar] [CrossRef]
- Zhang, Q.Z.; Gu, X.L.; Jiang, Z.L.; Zhang, W.P. Similarities in Accelerated Chloride Ion Transport Tests for Concrete in Tidal Zones. Mater. J. 2018, 115, 499–507. [Google Scholar] [CrossRef]
- Maekawa, K.; Ishida, T.; Kishi, T. Multi-Scale Modeling of Structural Concrete; Taylor & Francis: London, UK, 2009. [Google Scholar]
- Ishida, T.; Maekawa, K.; Kishi, T. Enhanced modeling of moisture equilibrium and transport in cementitious materials under arbitrary temperature and relative humidity history. Cem. Concr. Res. 2007, 37, 565–578. [Google Scholar] [CrossRef]
- Huang, Q.; Jiang, Z.; Gu, X.; Zhang, W.; Guo, B. Numerical simulation of moisture transport in concrete based on a pore size distribution model. Cem. Concr. Res. 2015, 67, 31–43. [Google Scholar] [CrossRef]
- Joyner, L.G.; Barrett, E.P.; Skold, R.V. The Determination of Pore Volume and Area Distributions in Porous Substances. II. Comparison between Nitrogen Isotherm and Mercury Porosimeter Methods. J. Am. Chem. Soc. 1951, 73, 3155–3158. [Google Scholar] [CrossRef]
- Zhang, W.P.; Tong, F.; Gu, X.L.; Xi, Y.P. Study on moisture transport in concrete in atmospheric environment. Comput. Concr. 2015, 16, 775–793. [Google Scholar] [CrossRef]
- Ghasemzadeh, F.; Pour-Ghaz, M. Effect of Damage on Moisture Transport in Concrete. J. Mater. Civ. Eng. 2015, 27, 04014242. [Google Scholar] [CrossRef]
- Wang, L.C.; Zhang, Q.Y. Investigation on water absorption in concrete after subjected to compressive fatigue loading. Constr. Build. Mater. 2021, 299, 123897. [Google Scholar] [CrossRef]
- Gerard, B.; Breysse, D.; Ammouche, A.; Houdusse, O.; Didry, O. Cracking and permeability of concrete under tension. Mater. Struct. 1996, 29, 141–151. [Google Scholar] [CrossRef]
- Yang, Z.F.; Weiss, W.J.; Olek, J. Water transport in concrete damaged by tensile loading and freeze-thaw cycling. J. Mater. Civ. Eng. 2006, 18, 424–434. [Google Scholar] [CrossRef]
- Wang, L.; Li, S. Capillary absorption of concrete after mechanical loading. Mag. Concr. Res. 2014, 66, 420–431. [Google Scholar] [CrossRef]
- Wang, R.; Gao, X.; Li, Q.; Yang, Y. Influence of splitting load on transport properties of ultra-high performance concrete. Constr. Build. Mater. 2018, 171, 708–718. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Q.; Gu, C.; Su, H.; Li, V.C. Influence of micro-cracking on the permeability of engineered cementitious composites. Cem. Concr. Compos. 2016, 72, 104–113. [Google Scholar] [CrossRef]
- Kermani, A. Steady-State method of measuring permeability of hardened concrete studies in relation to the change in structure of concrete under various short-term stress levels. Build. Res. Inf. 1991, 19, 360–366. [Google Scholar] [CrossRef]
- Banthia, N.; Biparva, A.; Mindess, S. Permeability of concrete under stress. Cem. Concr. Res. 2005, 35, 1651–1655. [Google Scholar] [CrossRef]
- Hearn, N.; Mills, R.H. A Simple Permeameter for Water or Gas-Flow. Cem. Concr. Res. 1991, 21, 257–261. [Google Scholar] [CrossRef]
- Sugiyama, T.; Bremner, T.W.; Holm, T.A. Effect of stress on gas permeability in concrete. Mater. J. 1996, 93, 443–450. [Google Scholar]
- Picandet, V.; Khelidj, A.; Bastian, G. Effect of axial compressive damage on gas permeability of ordinary and high-performance concrete. Cem. Concr. Res. 2001, 31, 1525–1532. [Google Scholar] [CrossRef] [Green Version]
- Choinska, M.; Khelidj, A.; Chatzigeorgiou, G.; Pijaudier-Cabot, G. Effects and interactions of temperature and stress-level related damage on permeability of concrete. Cem. Concr. Res. 2007, 37, 79–88. [Google Scholar] [CrossRef] [Green Version]
- Samaha, H.R.; Hover, K.C. Influence of Microcracking on the Mass-Transport Properties of Concrete. Mater. J. 1992, 89, 416–424. [Google Scholar]
- Saito, M.; Ishimori, H. Chloride Permeability of Concrete under Static and Repeated Compressive Loading. Cem. Concr. Res. 1995, 25, 803–808. [Google Scholar] [CrossRef]
- Zhou, C.; Li, K.; Pang, X. Geometry of crack network and its impact on transport properties of concrete. Cem. Concr. Res. 2012, 42, 1261–1272. [Google Scholar] [CrossRef]
- Djerbi Tegguer, A.; Bonnet, S.; Khelidj, A.; Baroghel-Bouny, V. Effect of uniaxial compressive loading on gas permeability and chloride diffusion coefficient of concrete and their relationship. Cem. Concr. Res. 2013, 52, 131–139. [Google Scholar] [CrossRef] [Green Version]
- Lim, C.C.; Gowripalan, N.; Sirivivatnanon, V. Microcracking and chloride permeability of concrete under uniaxial compression. Cem. Concr. Compos. 2000, 22, 353–360. [Google Scholar] [CrossRef]
- Tran, T.T.; Pham, D.T.; Vu, M.N.; Truong, V.Q.; Ho, X.B.; Tran, N.L.; Nguyen-Sy, T.; To, Q.D. Relation between water permeability and chloride diffusivity of concrete under compressive stress: Experimental investigation and mesoscale lattice modelling. Constr. Build. Mater. 2021, 267, 121164. [Google Scholar] [CrossRef]
- Ye, H.; Jin, X.; Fu, C.; Jin, N.; Xu, Y.; Huang, T. Chloride penetration in concrete exposed to cyclic drying-wetting and carbonation. Constr. Build. Mater. 2016, 112, 457–463. [Google Scholar] [CrossRef]
- Chung, C.W.; Shon, C.S.; Kim, Y.S. Chloride ion diffusivity of fly ash and silica fume concretes exposed to freeze–thaw cycles. Constr. Build. Mater. 2010, 24, 1739–1745. [Google Scholar] [CrossRef]
- Ghasemzadeh, F.; Rashetnia, R.; Smyl, D.; Pour-Ghaz, M. A comparison of methods to evaluate mass transport in damaged mortar. Cem. Concr. Compos. 2016, 70, 119–129. [Google Scholar] [CrossRef]
- GB/T 14684; Sand for Construction, Standardization Administration of the PRC 2014. China National Standards: Shenzhen, China, 2014.
- Hearn, N. Effect of shrinkage and load-induced cracking on water permeability of concrete. Mater. J. 1999, 96, 234–241. [Google Scholar]
- Galle, C. Effect of drying on cement-based materials pore structure as identified by mercury intrusion porosimetry—A comparative study between oven-, vacuum-, and freeze-drying. Cem. Concr. Res. 2001, 31, 1467–1477. [Google Scholar] [CrossRef]
- Sahmaran, M.; Li, V.C. Influence of microcracking on water absorption and sorptivity of ECC. Mater. Struct. 2009, 42, 593–603. [Google Scholar] [CrossRef]
- ASTM C1585-13; Standard Test Method for Measurement of Rate of Absorption of Water by Hydraulic-Cement Concretes 2013. ASTM International: West Conshohocken, PA, USA, 2013.
- Winslow, D.; Liu, D. The Pore Structure of Paste in Concrete. Cem. Concr. Res. 1990, 20, 227–235. [Google Scholar] [CrossRef]
- Grassl, P.; Wong, H.S.; Buenfeld, N.R. Influence of aggregate size and volume fraction on shrinkage induced micro-cracking of concrete and mortar. Cem. Concr. Res. 2010, 40, 85–93. [Google Scholar] [CrossRef] [Green Version]
- Wong, H.S.; Zobel, M.; Buenfeld, N.R.; Zimmerman, R.W. Influence of the interfacial transition zone and microcracking on the diffusivity, permeability and sorptivity of cement-based materials after drying. Mag. Concr. Res. 2009, 61, 571–589. [Google Scholar] [CrossRef] [Green Version]
- Washburn, E.W. The dynamic of capillary flow. Phys. Rev. 1921, 17, 273–283. [Google Scholar] [CrossRef]
- Yan, Y. Transportation of Chloride Ions in Damaged and Cracked Concrete and Its Action. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2011. [Google Scholar]
- Hillerborg, A. A modified absorption theory. Cem. Concr. Res. 1985, 15, 809–816. [Google Scholar] [CrossRef]
- Ababneh, A.; Benboudjema, F.; Xi, Y.P. Chloride penetration in nonsaturated concrete. J. Mater. Civ. Eng. 2003, 15, 183–191. [Google Scholar] [CrossRef]
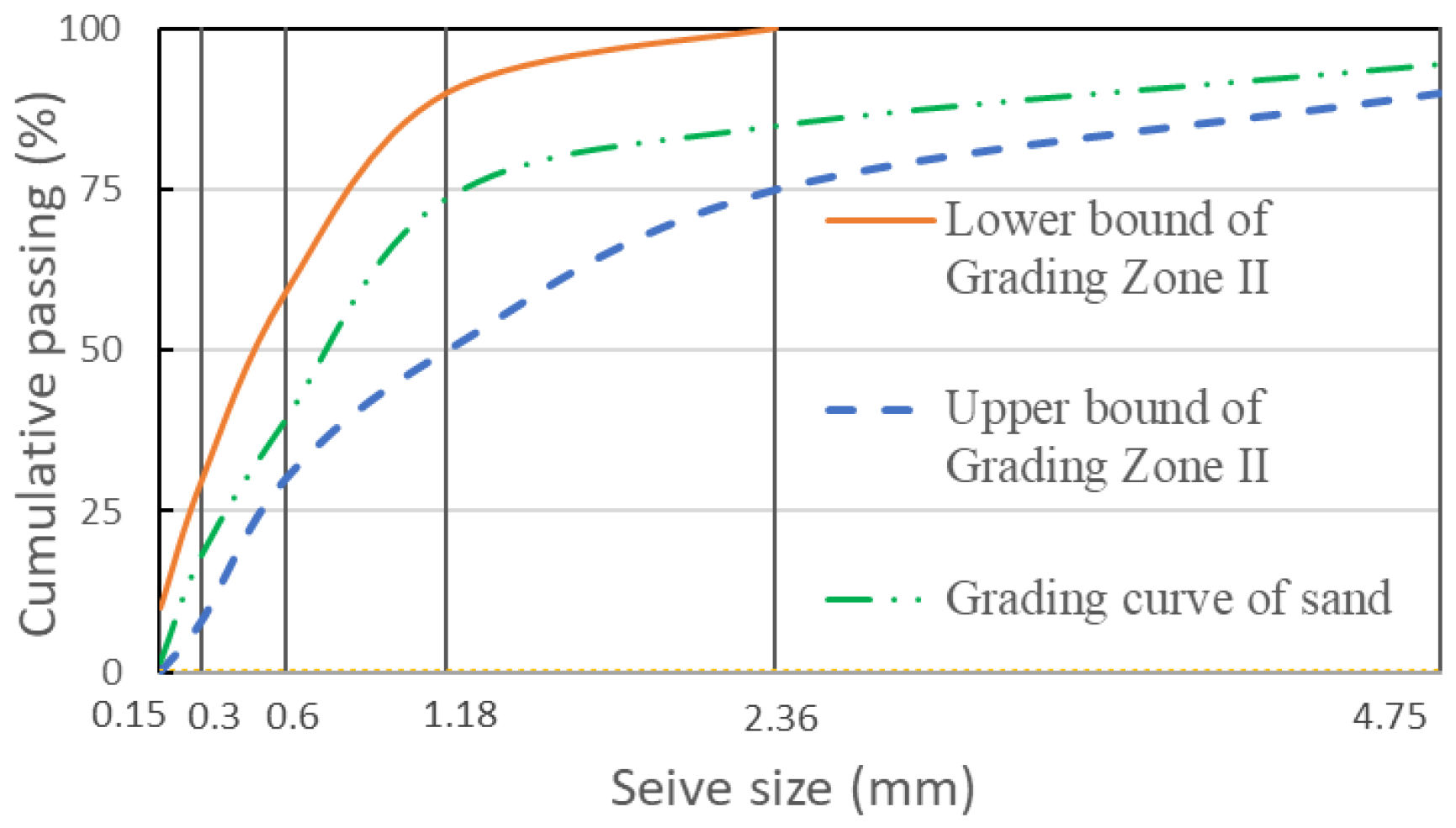

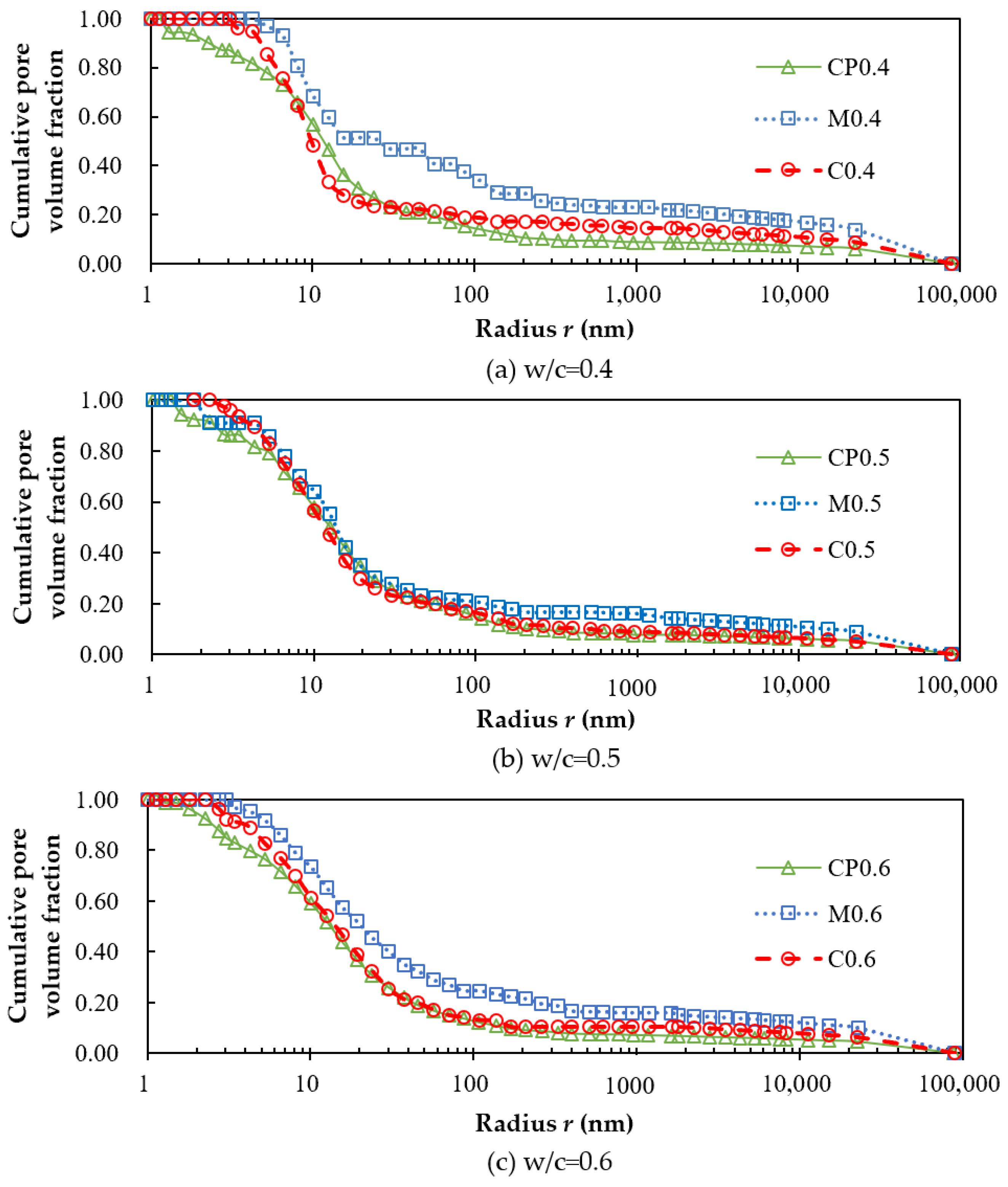
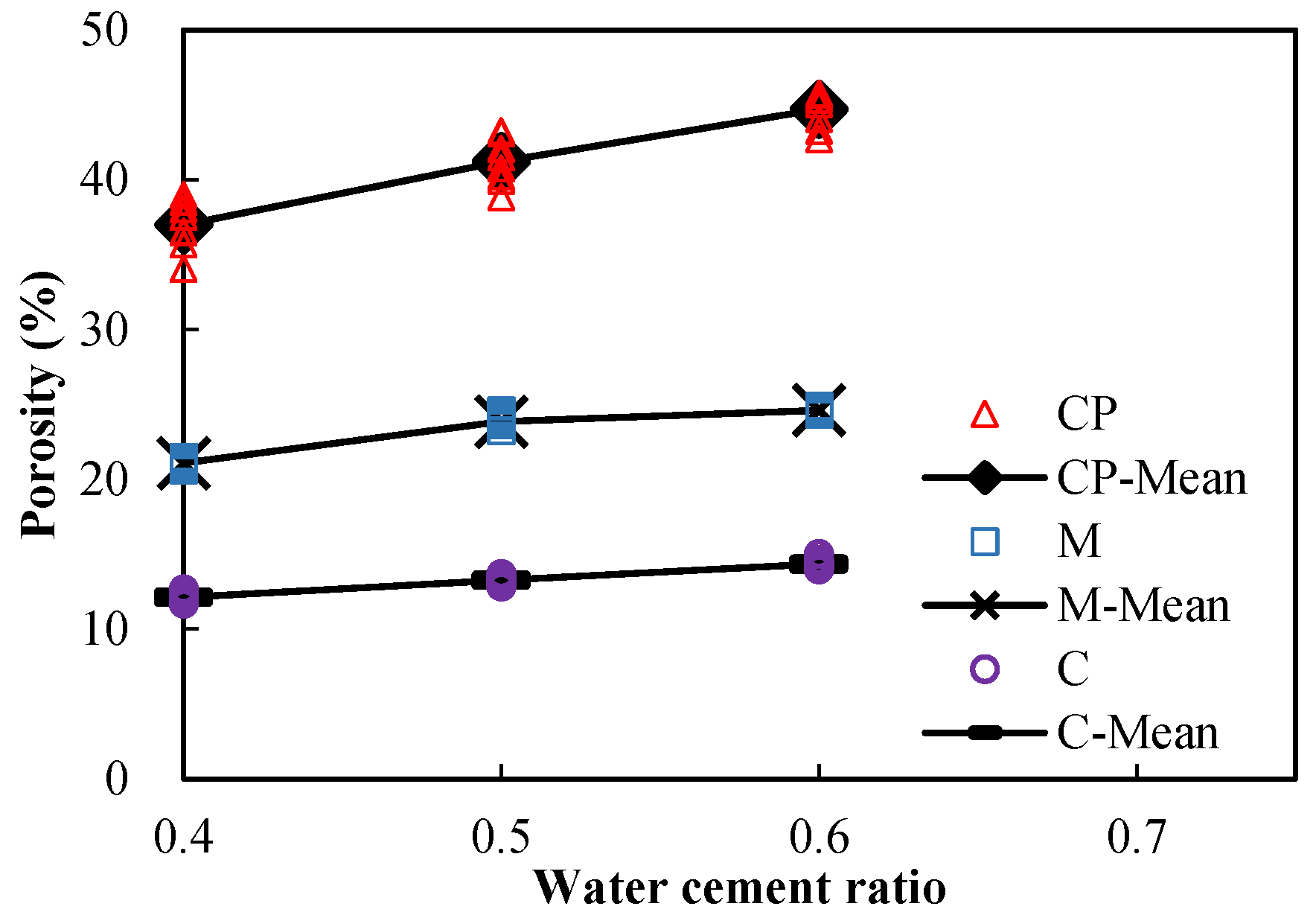
| Type | No. | Mixture Proportions (kg/m3) | Number of Specimens | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| W 1 | C 2 | S 3 | CA 4 | MIP | AC 5 | Porosity and Sorptivity | Total | |||
| U 6 | D 7 | |||||||||
| Cement paste | CP0.4 | 552 | 1379 | / | / | 1 | / | 3 | / | 4 |
| CP0.5 | 606 | 1212 | / | / | 1 | / | 3 | / | 4 | |
| CP0.6 | 649 | 1081 | / | / | 1 | / | 3 | / | 4 | |
| Mortar | M0.4 | 331 | 827 | 1023 | / | 1 | / | 3 | / | 4 |
| M0.5 | 363 | 727 | 1023 | / | 1 | 3 | 4 | 5 | 13 | |
| M0.6 | 389 | 647 | 1023 | / | 1 | / | 3 | / | 4 | |
| Concrete | C0.4 | 191 | 478 | 591 | 1098 | 1 | / | 4 | / | 5 |
| C0.5 | 210 | 420 | 591 | 1098 | 1 | 3 | 3 | 5 | 12 | |
| C0.6 | 225 | 375 | 591 | 1098 | 1 | / | 4 | / | 5 | |
| Type | No. | SM 1 | PM 2 (%) | Cement Paste Phase | Mortar Phase | ||||
|---|---|---|---|---|---|---|---|---|---|
| VF 3 | CP 4 (%) | Error 5 (%) | VF3 | CP 4 (%) | Error 5 (%) | ||||
| Cement paste | CP0.4 | 0.5917 | 36.9925 | 1 | / | / | / | / | / |
| CP0.5 | 0.6753 | 41.2243 | 1 | / | / | / | / | / | |
| CP0.6 | 0.7913 | 44.7143 | 1 | / | / | / | / | / | |
| Mortar | M0.4 | 0.2554 | 21.0931 | 0.5998 | 35.1687 | −4.93 | 1 | / | / |
| M0.5 | 0.3295 | 23.8516 | 0.5993 | 39.8012 | −3.45 | 1 | / | / | |
| M0.6 | 0.3779 | 24.6051 | 0.5993 | 41.0585 | −8.18 | 1 | / | / | |
| Concrete | C0.4 | 0.1508 | 12.1200 | 0.3463 | 34.9940 | −5.40 | 0.5733 | 21.1407 | 0.23 |
| C0.5 | 0.1861 | 13.2644 | 0.3465 | 38.2815 | −7.14 | 0.5735 | 23.1307 | −3.02 | |
| C0.6 | 0.2331 | 14.3544 | 0.3469 | 41.3825 | −7.45 | 0.5738 | 25.0151 | 1.67 | |
| Stress Level (%) | No. | Porosity (%) | Sorptivity (mm/min0.5) | ||||
|---|---|---|---|---|---|---|---|
| Measured | Mean | Error (%) | Measured | Mean | Error (%) | ||
| 25 | * M0.5−11−1 | 23.7563 | 23.0435 | 3.0931 | 0.3520 | 0.3326 | 5.8328 |
| * M0.5−11−2 | 22.3308 | −3.0931 | 0.3132 | −5.8328 | |||
| 40 | * M0.5−14−1 | 23.2492 | 23.5260 | −1.1767 | 0.3214 | 0.3280 | −1.9973 |
| * M0.5−14−2 | 23.8029 | 1.1767 | 0.3345 | 1.9973 | |||
| 55 | * M0.5−17−1 | 24.1703 | 24.2343 | −0.2642 | 0.3317 | 0.3351 | −0.9999 |
| * M0.5−17−2 | 24.2984 | 0.2642 | 0.3384 | 0.9999 | |||
| 70 | * M0.5−10−1 | 23.7798 | 23.9300 | −0.6277 | 0.3393 | 0.3407 | −0.3963 |
| * M0.5−10−2 | 24.0802 | 0.6277 | 0.3420 | 0.3963 | |||
| 85 | * M0.5−23−1 | 24.0097 | 24.0194 | −0.0406 | 0.3510 | 0.3533 | −0.6510 |
| * M0.5−23−2 | 24.0292 | 0.0406 | 0.3556 | 0.6510 | |||
| Stress Level (%) | No. | Porosity (%) | Sorptivity (mm/min0.5) | ||||
|---|---|---|---|---|---|---|---|
| Measured | Mean | Error (%) | Measured | Mean | Error (%) | ||
| 25 | * C0.5−11−1 | 13.8774 | 13.7172 | 1.1682 | 0.2018 | 0.1970 | 2.4365 |
| * C0.5−11−2 | 13.7666 | 0.3598 | 0.1922 | −2.4365 | |||
| C0.5−11−3 | 13.5076 | −1.5279 | / | / | |||
| 40 | * C0.5−13−1 | 13.4556 | 13.8339 | −2.7347 | 0.1922 | 0.1950 | −1.4106 |
| * C0.5−13−2 | 14.0514 | 1.5727 | 0.1977 | 1.4106 | |||
| C0.5−13−3 | 13.9946 | 1.1620 | / | / | |||
| 55 | * C0.5−15−1 | 13.6523 | 13.4471 | 1.5255 | 0.1919 | 0.1993 | −3.6888 |
| * C0.5−15−2 | 13.5717 | 0.9262 | 0.2066 | 3.6888 | |||
| C0.5−15−3 | 13.1175 | −2.4517 | / | / | |||
| 70 | * C0.5−17−1 | 13.7497 | 13.6934 | 0.4114 | 0.2140 | 0.2160 | −0.9259 |
| * C0.5−17−2 | 13.8042 | 0.8096 | 0.2180 | 0.9259 | |||
| C0.5−17−3 | 13.5262 | −1.2210 | / | / | |||
| 85 | * C0.5−20−1 | 13.5719 | 13.5080 | 0.4734 | 0.2239 | 0.2226 | 0.5840 |
| * C0.5−20−2 | 13.3907 | −0.8683 | 0.2213 | −0.5840 | |||
| C0.5−20−3 | 13.5613 | 0.3948 | / | / | |||
| Type | w/c | Φ–Mean (%) | Error (%) | ||
|---|---|---|---|---|---|
| Measured–Mean | Calculated | ||||
| Cement paste | 0.4 | 36.9925 | 0.5917 | 0.5261 | –11.0884 |
| 0.5 | 41.2243 | 0.6753 | 0.6038 | –10.5820 | |
| 0.6 | 44.7143 | 0.7913 | 0.7133 | –9.8572 | |
| Mortar | 0.4 | 21.0931 | 0.2554 | 0.2550 | –0.1488 |
| 0.5 | 23.8516 | 0.3295 | 0.3523 | 6.9074 | |
| 0.6 | 24.6051 | 0.3779 | 0.3833 | 1.4184 | |
| Concrete | 0.4 | 12.1200 | 0.1508 | 0.1619 | 7.3276 |
| 0.5 | 13.2644 | 0.1861 | 0.1950 | 4.7985 | |
| 0.6 | 14.3544 | 0.2331 | 0.2394 | 2.6941 | |
| Type | So | Φ (%) | Stress Level (%) | SoD | ΦD (%) | ΔSo | ∆Φ (%) | rD (nm) |
|---|---|---|---|---|---|---|---|---|
| Mortar | 0.3295 | 23.7586 | 0 | 0.3295 | 23.7586 | 0 | 0 | 0 |
| 25 | 0.3326 | 23.0435 | 0.0031 | –0.0072 | 0 | |||
| 40 | 0.3280 | 23.5260 | –0.0015 | –0.0023 | 0 | |||
| 55 | 0.3351 | 24.2343 | 0.0056 | 0.0048 | 3.8592 | |||
| 70 | 0.3407 | 23.9300 | 0.0112 | 0.0017 | 119.1993 | |||
| 85 | 0.3533 | 24.0194 | 0.0238 | 0.0026 | 233.6647 | |||
| Concrete | 0.1861 | 13.0793 | 0 | 0.1861 | 13.0793 | 0 | 0 | 0 |
| 25 | 0.1970 | 13.8220 | 0.0109 | 0.0074 | 6.0256 | |||
| 40 | 0.1950 | 13.7535 | 0.0089 | 0.0067 | 4.8204 | |||
| 55 | 0.1993 | 13.6120 | 0.0132 | 0.0053 | 17.0482 | |||
| 70 | 0.2160 | 13.7770 | 0.0299 | 0.0070 | 51.3804 | |||
| 85 | 0.2226 | 13.4813 | 0.0365 | 0.0040 | 230.5896 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Zhang, W.; Tong, F.; Gu, X. Moisture Transport of Axial-Compression-Damaged Mortar and Concrete in Atmospheric Environment. Materials 2022, 15, 5498. https://doi.org/10.3390/ma15165498
Zhou Y, Zhang W, Tong F, Gu X. Moisture Transport of Axial-Compression-Damaged Mortar and Concrete in Atmospheric Environment. Materials. 2022; 15(16):5498. https://doi.org/10.3390/ma15165498
Chicago/Turabian StyleZhou, Yong, Weiping Zhang, Fei Tong, and Xianglin Gu. 2022. "Moisture Transport of Axial-Compression-Damaged Mortar and Concrete in Atmospheric Environment" Materials 15, no. 16: 5498. https://doi.org/10.3390/ma15165498






