Fatigue Cracking Evolution and Model of Cold Recycled Asphalt Mixtures during Different Curing Times
Abstract
:1. Introduction
2. Materials and Experiments
2.1. Materials
2.1.1. RAP Materials
2.1.2. Asphalt Emulsion
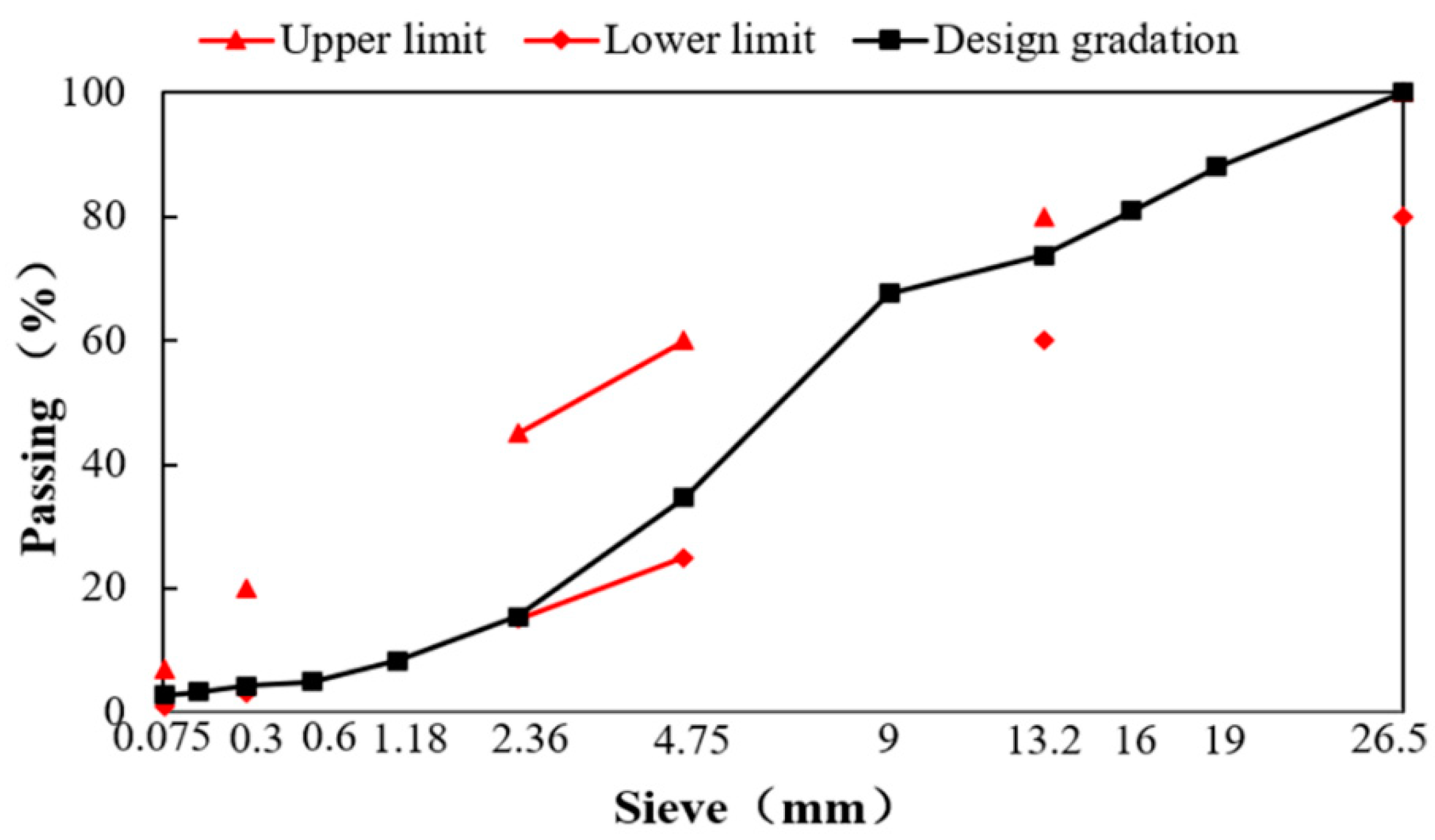
2.1.3. The Gradation of Mixtures
2.2. Material Preparation
2.3. Experiments
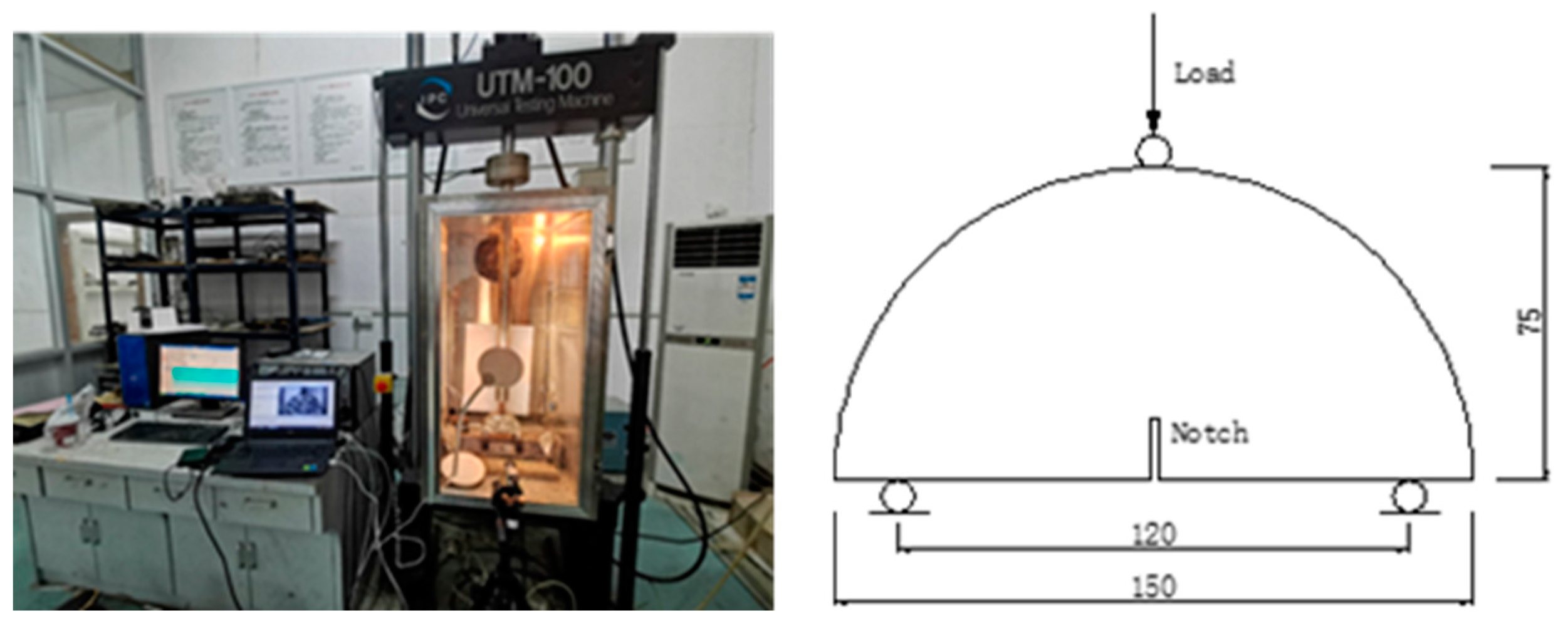
2.3.1. SCB Strength Test
2.3.2. SCB Fatigue Test
3. Result and Discussion
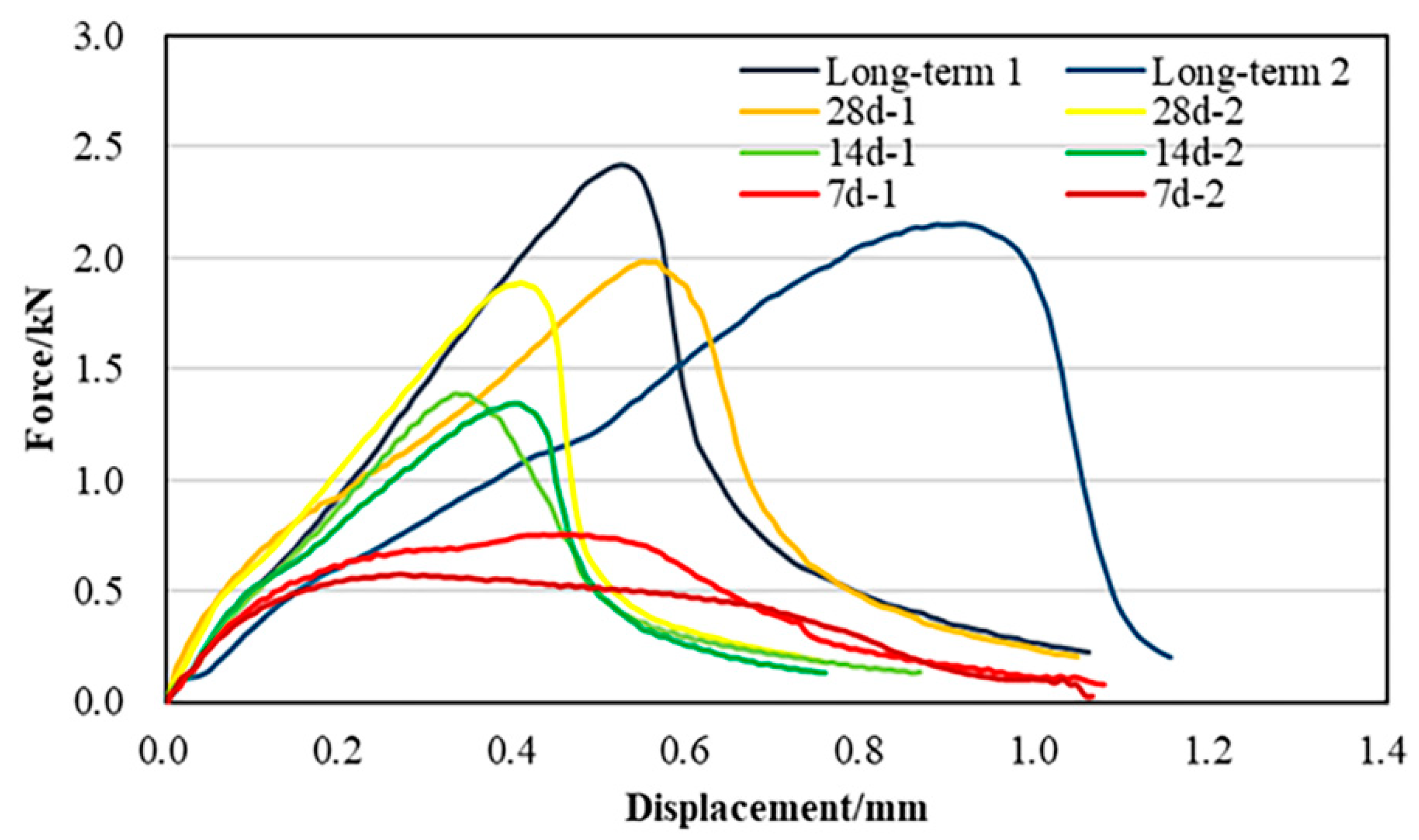
3.1. SCB Strength
3.2. Fatigue Life and Fatigue Equation
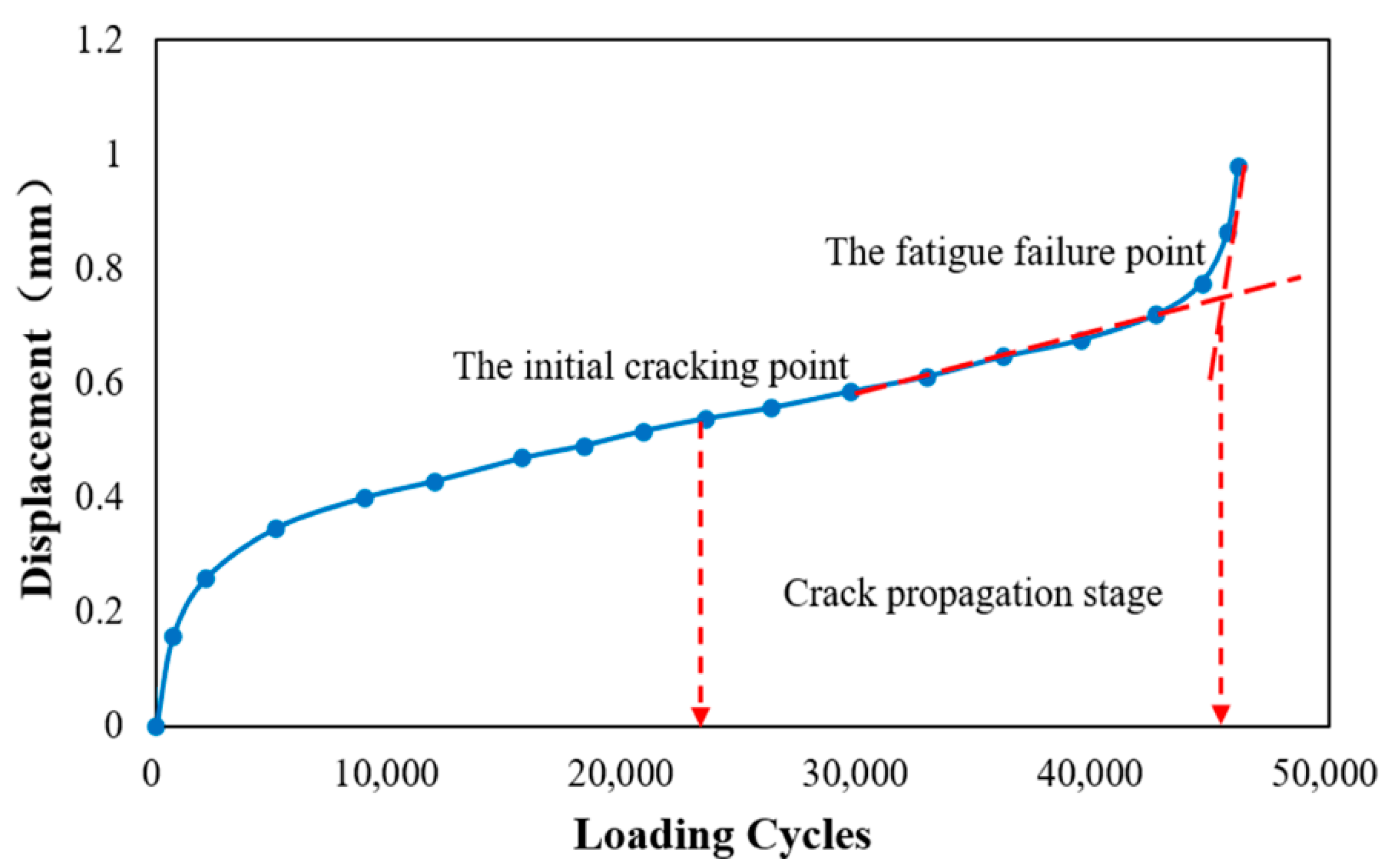
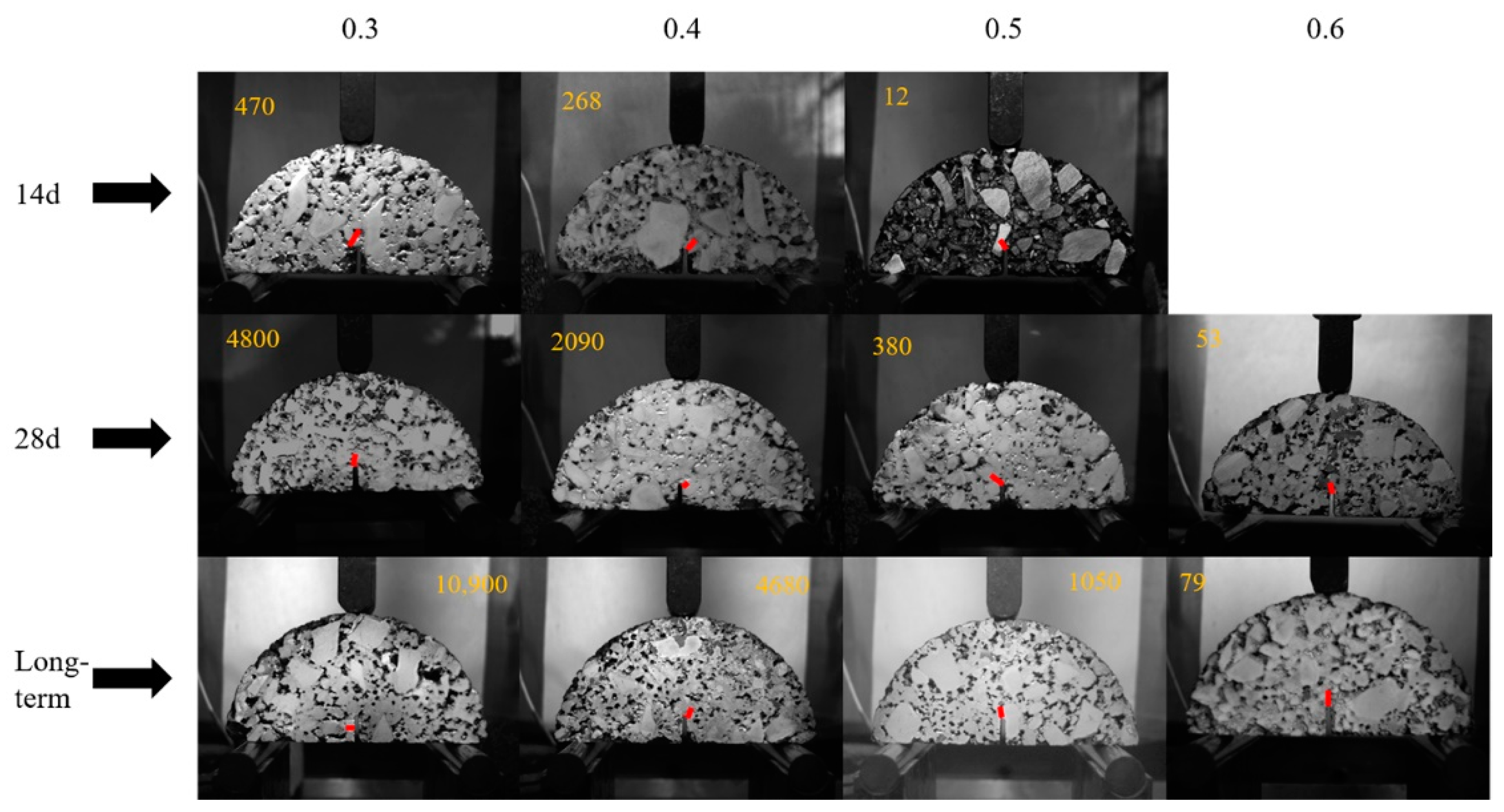
3.3. Fatigue Cracking Point Analysis
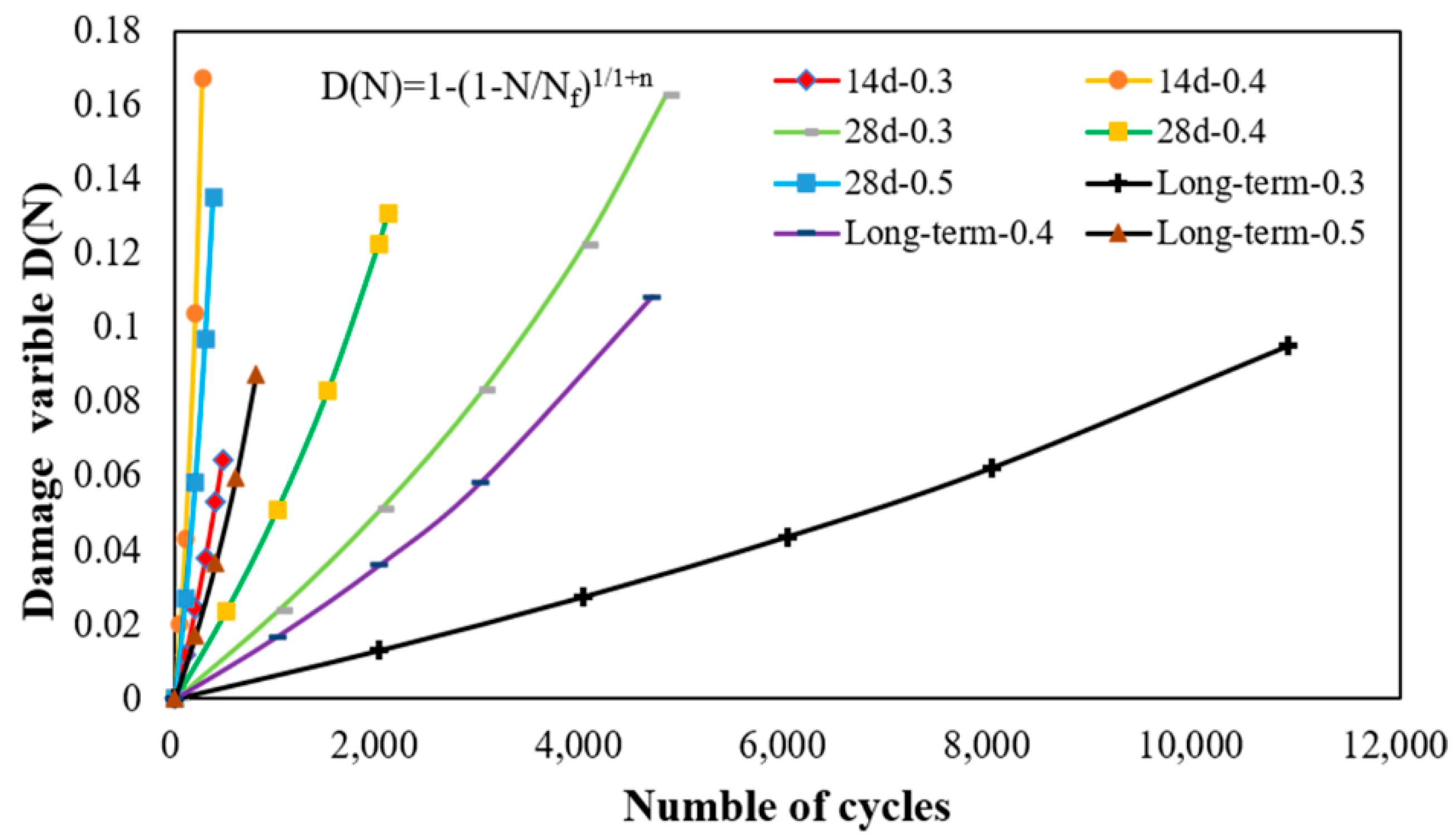
3.4. Fatigue Damage Model Based on Damage Mechanics
3.5. Fatigue Damage Model Based on Fracture Mechanics
3.6. Microscopic Morphology of Fracture Point
4. Conclusions
- (1)
- The fracture toughness is used to characterize the crack resistance of CRME. CRME has a poor cracking resistance in the early time, and it gradually increases with the increase of the curing time.
- (2)
- The fatigue equation of cold recycled mixtures is obtained by fitting the regression equation of , and the value of coefficient k is used to reflect the fatigue cracking resistance. The value of k gradually increases with the increase of the curing time, which indicates that the fatigue performance is gradually improved with the increase of the curing time.
- (3)
- The ratio of the “initial cracking point/fatigue life” under the same curing time increases as the stress ratio increases. In addition, under the same stress ratio, the ratio shows a decreasing trend with the increase of the curing time. The initial fatigue cracking on the surface of the sample appears at around 60% of the fatigue life.
- (4)
- The fatigue damage model based on damage mechanics and the fatigue loading equation of the CRME is established. The damage variable is only between 0.06–0.17 when the initial fatigue cracks begin to start during the loading process.
- (5)
- The Paris formula based on fracture mechanics reflects the relationships between the crack growth rate and stress intensity factor. The crack length “a” has a greater impact on the crack growth rate under high-stress levels at the early stage. In contrast, crack growth at the 28-day and long-term curing is controlled by the cooperation effect of parameters C and m.
- (6)
- The degree of cement hydration and demulsification of asphalt emulsion in CRME is gradually increased, and a denser spatial structure is gradually formed during the curing times, which provides higher fatigue cracking resistance of CRME.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chang, X.W.; Zhang, R.H.; Xiao, Y.; Chen, X.Y.; Zhang, X.S.; Liu, G. Mapping of publications on asphalt pavement and bitumen materials: A bibliometric review. Constr. Build. Mater. 2020, 234, 117370. [Google Scholar] [CrossRef]
- Chen, S.H.; Zheng, W.Y.; Paramitha, P.A. Evaluation of Innovative Cold Mix Recycled Asphalt Concrete as Backfill Material in Pipeline Maintenance. J. Test. Eval. 2019, 47, 1864–1875. [Google Scholar] [CrossRef]
- Grilli, A.; Graziani, A.; Bocci, E.; Bocci, M. Volumetric properties and influence of water content on the compactability of cold recycled mixtures. Mater. Struct. 2016, 49, 4349–4362. [Google Scholar] [CrossRef]
- Leandri, P.; Losa, M.; Natale, A.D. Field validation of recycled cold mixes viscoelastic properties. Constr. Build. Mater. 2015, 75, 275–282. [Google Scholar] [CrossRef]
- Yan, J.H.; Ni, F.J.; Yang, M.K.; Li, J. An experimental study on fatigue properties of emulsion and foam cold recycled mixes. Constr. Build. Mater. 2010, 24, 2151–2156. [Google Scholar] [CrossRef]
- Lin, J.T.; Hong, J.X.; Xiao, Y. Dynamic characteristics of 100% cold recycled asphalt mixture using asphalt emulsion and cement. J. Clean. Prod. 2017, 156, 337–344. [Google Scholar] [CrossRef]
- Wang, D.C.; Hao, P.W.; Wei, L.X. Fatigue performance and influencing factors of emulsified asphalt cold recycled mixture. J. Beijing Univ. Technol. 2016, 42, 541–546. [Google Scholar]
- Zhao, Z.D.; Wang, S.Y.; Ren, J.T.; Wang, W.; Wang, C.G. Fatigue characteristics and prediction of cement-stabilized cold recycled mixture with road-milling materials considering recycled aggregate composition. Constr. Build. Mater. 2021, 301, 124122. [Google Scholar] [CrossRef]
- Gao, L.; Ni, F.J.; Ling, C.; Yan, J.H. Evaluation of fatigue behavior in cold recycled mixture using digital image correlation method. Constr. Build. Mater. 2016, 102, 393–402. [Google Scholar] [CrossRef]
- Jiang, Y.J.; Lin, H.W.; Han, Z.C.; Deng, C.Q. Fatigue Properties of Cold-Recycled Emulsified Asphalt Mixtures Fabricated by Different Compaction Methods. Sustainability 2019, 11, 3483. [Google Scholar] [CrossRef] [Green Version]
- Chelelgo, K.; Zachary, C.; Gariy, A.; Stanley, M.S. Modeling of fatigue-strength development in cold-emulsion asphalt mixtures using maturity method. Appl. Sci. 2019, 9, 2694. [Google Scholar] [CrossRef] [Green Version]
- Kavussi, A.; Nejad, F.M.; Modarres, A. Laboratory fatigue models for recycled mixes with pozzolanic cement and bitumen emulsion. J. Civ. Eng. Manag. 2011, 17, 98–107. [Google Scholar] [CrossRef]
- JTG E20-2011; Standard Test Methods of Bituminous Mixtures for Highway Engineering. China Communication Press: Beijing, China, 2011.
- JTG/T 5521; Technical Specification for Highway Asphalt Pavement Recycling. China Communication Press: Beijing, China, 2019.
- Wang, X.W.; Ren, J.X.; Hu, X.Y.; Gu, X.Y.; Li, N. Determining Optimum Number of Gyrations for Porous Asphalt Mixtures Using Superpave Gyratory Compactor. KSCE J. Civ. Eng. 2021, 25, 1–10. [Google Scholar] [CrossRef]
- Ferrotti, G.; Grilli, A.; Mignini, C.; Graziani, A. Comparing the Field and Laboratory Curing Behaviour of Cold Recycled Asphalt Mixtures for Binder Courses. Materials 2020, 13, 4697. [Google Scholar] [CrossRef] [PubMed]
- Saha, G.; Biligiri, K.P. Fracture properties of asphalt mixtures using semi-circular bending test: A state-of-the-art review and future research. Constr. Build. Mater. 2016, 105, 103–112. [Google Scholar] [CrossRef]
- Huang, B.S.; Shu, X.; Zuo, G. Using notched semi-circular bending fatigue test to characterize fracture resistance of asphalt mixtures. Eng. Fract. Mech. 2013, 109, 78–88. [Google Scholar] [CrossRef]
- Yang, D.T.; Zhu, H.Z. Contrast test of semicircular bending tension and small beam three-point bending tension of asphalt mixture. J. Wuhan Univ. Technol. (Transp. Sci. Eng. Ed.) 2010, 34, 1224–1226. [Google Scholar]
- UNE-EN 12697-44; Bituminous Mixtures-Test Methods-Part 44: Crack Propagation by Semi-Circular Bending Test. BSI Standards Limited: London, UK, 2019.
- Hasan, O.; Lmad, L.; Qadi, L.; John, E.K.; Ahmad, S.P.; Berangere, D. Development of the fracture-based flexibility index for asphalt concrete cracking potential using modified semi-circle bending test parameters. Constr. Build. Mater. 2016, 115, 390–401. [Google Scholar]
- Kaseer, F.; Fan, Y.; Edith, A.M.; Martin, A.E.; Daniel, J.S.; Salari, S. Development of an index to evaluate the cracking potential of asphalt mixtures using the semi-circular bending test. Constr. Build. Mater. 2018, 167, 286–298. [Google Scholar] [CrossRef]
- Lim, I.L.; Johnston, I.W.; Choi, S.K. Stress intensity factors for semi-circular specimens under three-point bending. Eng. Fract. Mech. 1993, 44, 363–382. [Google Scholar] [CrossRef]
- Li, X.; Marasteanu, M. Evaluation of the low temperature fracture resistance of asphalt mixtures using the semi circular bend test. Asph. Paving Technol. Assoc. Asph. Paving Technol.-Proc. Technol. Sess. 2004, 73, 401–426. [Google Scholar]
- Cheng, H.L.; Sun, L.J.; Liu, L.P.; Li, H. Fatigue characteristics of in-service cold recycling mixture with asphalt emulsion and HMA mixture. Constr. Build. Mater. 2018, 192, 704–714. [Google Scholar] [CrossRef]
- Sun, Y.Z.; Fang, C.Z.; Fan, D.; Wang, J.; Yuan, X.Z. A Research on Fatigue Damage Constitutive Equation of Asphalt Mixture. Math. Probl. Eng. 2018, 2018, 3489082. [Google Scholar] [CrossRef] [Green Version]
- Lucon, E. An assessment of different approaches for measuring crack sizes in fatigue and fracture mechanics specimens. Theor. Appl. Fract. Mech. 2021, 116, 103119. [Google Scholar] [CrossRef]
- Jasztal, M.; Kocanda, D.; Tomaszek, H. Predicting fatigue crack growth and fatigue life under variable amplitude loading. Fatigue Aircr. Struct. 2010, 2010, 37–51. [Google Scholar] [CrossRef]





| Sieve (mm) | 26.5 | 19 | 16 | 13.2 | 9 | 4.75 | 2.36 | 1.18 | 0.6 | 0.3 | 0.15 | 0.075 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RAP 10–20 | 100 | 90.9 | 58.6 | 25.7 | 7.0 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
| RAP 5–10 | 100 | 100 | 100 | 100 | 94.7 | 7.2 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| RAP 0–5 | 100 | 100 | 100 | 100 | 100 | 99.8 | 37.4 | 15.3 | 6.6 | 4.8 | 2.4 | 1.8 |
| Property | Unit | Value | Technical Requirements |
|---|---|---|---|
| Demulsification speed | - | Slow-breaking | Slow-breaking |
| Particle charge | - | Cation (+) | Cation (+) |
| Residue on sieve (1.18 mm) | % | 0.02 | ≤0.1 |
| Enguera Viscosity E25 | - | 5.9 | 2–30 |
| Residue by distillation | % | 62.5 | ≥60 |
| Penetration of residue, 25 °C | 0.1 mm | 58.2 | 50–130 |
| Ductility of residue, 15 °C | cm | 69.5 | ≥40 |
| Softening point of residue | °C | 51.3 | ≥46 |
| Adhesion with coarse aggregate, coating area | - | ≥2/3 | ≥2/3 |
| Storage stability at 1 day | % | 0.1 | ≤1 |
| Storage stability at 5 days | % | 0.9 | ≤5 |
| New Aggregate 19–26.5 | RAP 10–20 | RAP 5–10 | RAP 0–5 | New Aggregates 0–5 | Filler |
|---|---|---|---|---|---|
| 10% | 22% | 36% | 24% | 6% | 2% |
| Curing Time (d) | Groups | Fmax (kN) | (MPa·mm1/2) | Gf (J/m2) | FI | CRI (m−1) | |
|---|---|---|---|---|---|---|---|
| 7 | 1 | 0.75 | 0.48 | 17.41 | 198.96 | 0.94 | 0.26 |
| 2 | 0.58 | 0.37 | 13.46 | 167.50 | 1.05 | 0.29 | |
| 14 | 1 | 1.39 | 0.89 | 32.26 | 210.25 | 0.25 | 0.15 |
| 2 | 1.35 | 0.86 | 31.33 | 196.71 | 0.11 | 0.15 | |
| 28 | 1 | 1.98 | 1.27 | 45.95 | 412.75 | 0.32 | 0.21 |
| 2 | 1.89 | 1.21 | 43.86 | 264.17 | 0.07 | 0.14 | |
| Long term | 1 | 2.42 | 1.55 | 56.16 | 440.46 | 0.20 | 0.18 |
| 2 | 2.15 | 1.38 | 49.90 | 579.79 | 0.28 | 0.27 |
| Curing Time (d) | Stress Ratios | Stress (MPa) | Fatigue Life |
|---|---|---|---|
| 14 | 0.2 | 0.17 | 15,630 |
| 0.3 | 0.26 | 1230 | |
| 0.4 | 0.35 | 365 | |
| 0.5 | 0.44 | 29 | |
| 28 | 0.2 | 0.25 | 45,300 |
| 0.3 | 0.37 | 7120 | |
| 0.4 | 0.50 | 3555 | |
| 0.5 | 0.62 | 632 | |
| 0.6 | 0.74 | 93 | |
| Long-term | 0.3 | 0.44 | 19,300 |
| 0.4 | 0.58 | 7610 | |
| 0.5 | 0.73 | 1500 | |
| 0.6 | 0.88 | 94 |
| Curing Time | Fatigue Equation | n | k | R2 |
|---|---|---|---|---|
| 14-day | 6.27 | 0.27 | 0.99 | |
| 28-day | 5.35 | 37.37 | 0.99 | |
| Long-term | 7.33 | 78.92 | 0.92 |
| Curing Time (d) | Stress Ratio | Initial Cracking Point | Fatigue Life | Initial Cracking Point/Fatigue Life |
|---|---|---|---|---|
| 14 | 0.3 | 470 | 1230 | 0.38 |
| 0.4 | 268 | 365 | 0.73 | |
| 0.5 | 12 | 29 | 0.41 | |
| 28 | 0.2 | 23,500 | 45,300 | 0.52 |
| 0.3 | 4800 | 7120 | 0.67 | |
| 0.4 | 2090 | 3555 | 0.59 | |
| 0.5 | 380 | 632 | 0.60 | |
| 0.6 | 53 | 93 | 0.57 | |
| Long-term | 0.3 | 10,900 | 19,300 | 0.56 |
| 0.4 | 4680 | 7610 | 0.62 | |
| 0.5 | 1050 | 1500 | 0.70 | |
| 0.6 | 79 | 94 | 0.84 |
| Curing Time (d) | Stress Ratio | N/Nf | n | D(N) |
|---|---|---|---|---|
| 14 | 0.3 | 0.38 | 6.27 | 0.06 |
| 0.4 | 0.73 | 0.17 | ||
| 28 | 0.3 | 0.67 | 0.16 | |
| 0.4 | 0.59 | 5.35 | 0.13 | |
| 0.5 | 0.60 | 0.13 | ||
| Long-term | 0.3 | 0.56 | 0.09 | |
| 0.4 | 0.62 | 7.33 | 0.11 | |
| 0.5 | 0.70 | 0.13 |
| Curing Time (d) | Stress Ratio | Paris Formula |
|---|---|---|
| 14 | 0.3 | |
| 0.4 | ||
| 0.5 | ||
| 28 | 0.2 | |
| 0.3 | ||
| 0.4 | ||
| 0.5 | ||
| 0.6 | ||
| Long term | 0.3 | |
| 0.4 | ||
| 0.5 | ||
| 0.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, Y.; Lin, J.; Chen, Z.; Cai, J.; Hong, J.; Zhu, X. Fatigue Cracking Evolution and Model of Cold Recycled Asphalt Mixtures during Different Curing Times. Materials 2022, 15, 4476. https://doi.org/10.3390/ma15134476
Xia Y, Lin J, Chen Z, Cai J, Hong J, Zhu X. Fatigue Cracking Evolution and Model of Cold Recycled Asphalt Mixtures during Different Curing Times. Materials. 2022; 15(13):4476. https://doi.org/10.3390/ma15134476
Chicago/Turabian StyleXia, Yu, Juntao Lin, Zongwu Chen, Jun Cai, Jinxiang Hong, and Xiaobin Zhu. 2022. "Fatigue Cracking Evolution and Model of Cold Recycled Asphalt Mixtures during Different Curing Times" Materials 15, no. 13: 4476. https://doi.org/10.3390/ma15134476






