Dynamic Behavior of a Precast and Partial Steel Joint under Various Shear Span-to-Depth Ratios
Abstract
:1. Introduction
2. Finite Element Model
2.1. Fundamental Modifications
- (1)
- Under the influence of Poisson’s ratio, concrete will expand laterally under compression. However, the expansion deformation of concrete will be prevented due to the existence of stirrup reinforcements and steel plates, which have a certain constraint effect [28]. If only the constraint effect of stirrup reinforcements on concrete is considered, the theoretical and numerical results are not in good agreement [29,30]. Therefore, in order to reasonably represent the actual mechanical properties of members, the constraint effect of steel plates should also be considered. Based on the above analysis, the constraint effect of stirrup reinforcements and steel plates should be considered to ensure the accuracy of numerical analysis.
- (2)
- At present, the software ABAQUS is adopted by many scholars to simulate the mechanical properties of beam–column joints under cyclic loading. However, no descending segment existed in the obtained hysteretic curves [31,32]. As a result, it is impossible to reflect whether the beam–column joint is invalid through the hysteretic curves. The reason for the above phenomenon is that the strength degradation of the material is not considered in the selected material constitutive model when the numerical analysis is implemented. To solve the above problem, the descending segment of skeleton curve is introduced into the steel constitutive model according to the published papers [33]. Although the accumulative damage fails to be considered, the strength degradation and failure behavior of steel can be described through this method.
- (3)
- Concrete and steels are both rate-sensitive materials, which will exhibit various mechanical behaviors with conditions of various strain rates. The PPSRC beam–column joint is constituted of concrete and steel, so it is also rate-sensitive. When subjected to dynamic loadings, the response characteristics and damage mechanism of the PPSRC beam–column joint will show obvious differences from that subjected to static or quasi-static loadings [34]. However, knowledge of the strain rate effect on the dynamic behavior of the PPSRC beam–column joint is limited, with emphasis primarily placed on the observed material dynamic mechanical properties and less attention paid to changes in the dynamic behavior of the PPSRC beam–column joint. In view of this, it is of great significance to consider the strain rate effect in the finite element analysis.
2.2. Improved Material Constitutive Models
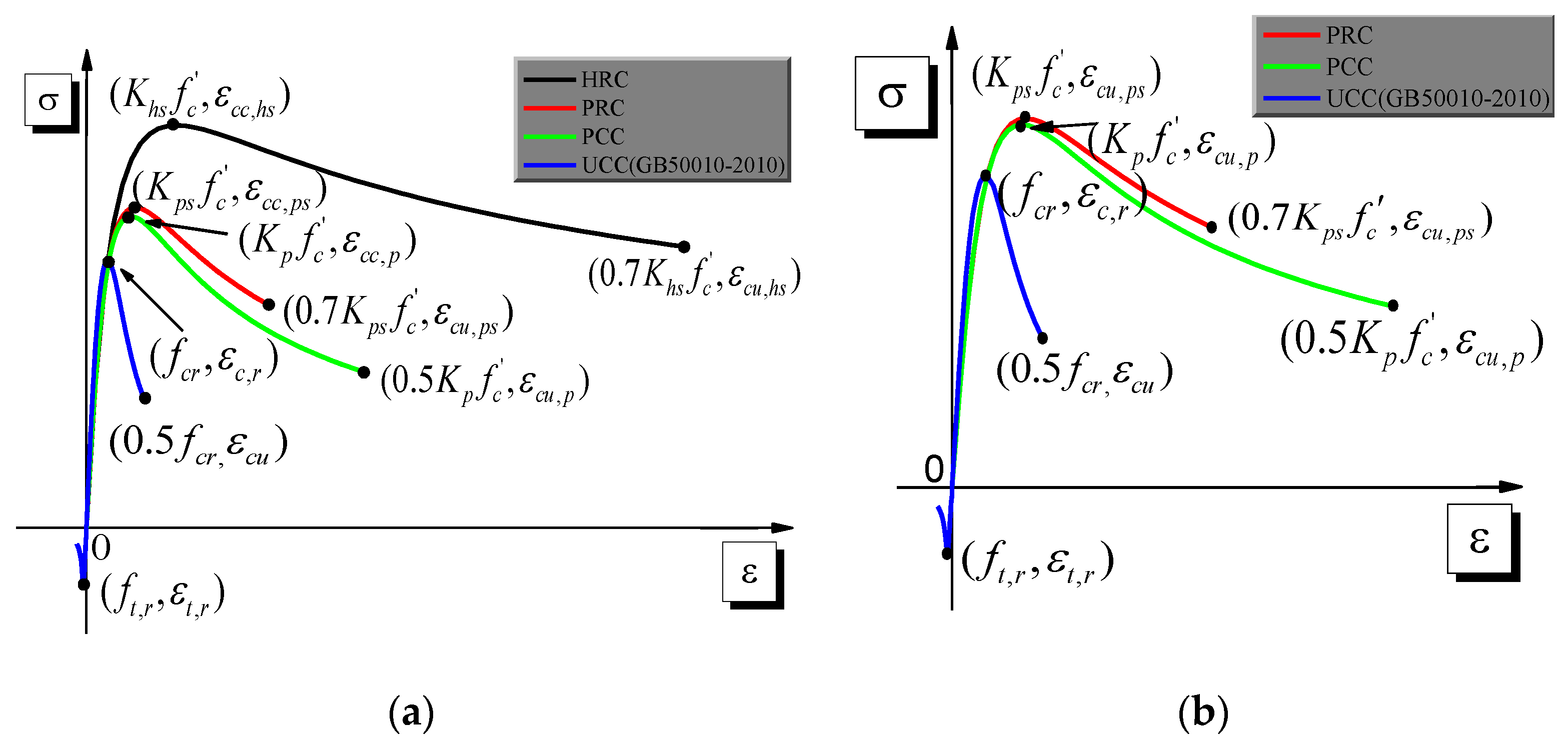
2.2.1. Constraint Effect
- (1)
- Partially restraint concrete (PRC) surrounded by I-steel flanges of the beam. The effective lateral restraint stress of the PRC is the linear superposition of restraint stress provided through steel flanges and stirrup reinforcements. In addition, the effective lateral restraint stress on the PRC can be given by Reference [29].
- (2)
- Highly restraint concrete (HRC) and partially restraint concrete (PRC) surrounded by cross-shaped steel of the column. The effective lateral restraint stress of the HRC and PRC can be calculated by Reference [29].
- (3)
- Partially confined concrete (PCC) surrounded by the stirrup reinforcements. The effective lateral restraint stress of the PCC provided through stirrup reinforcements of beam and column could be calculated as follows [35].
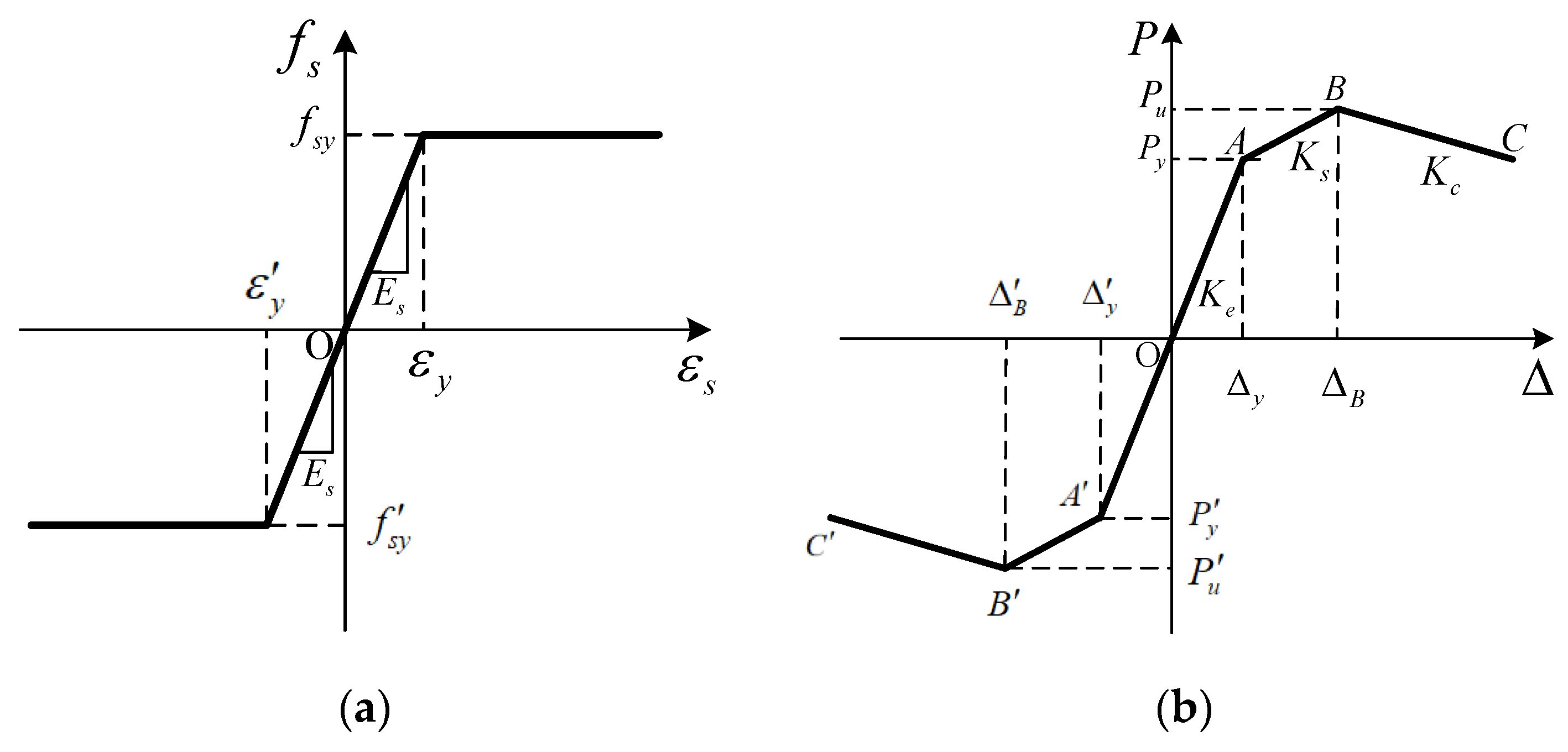
2.2.2. Strength Deterioration
2.2.3. Strain Rate Effect
3. Finite Element Model Verification
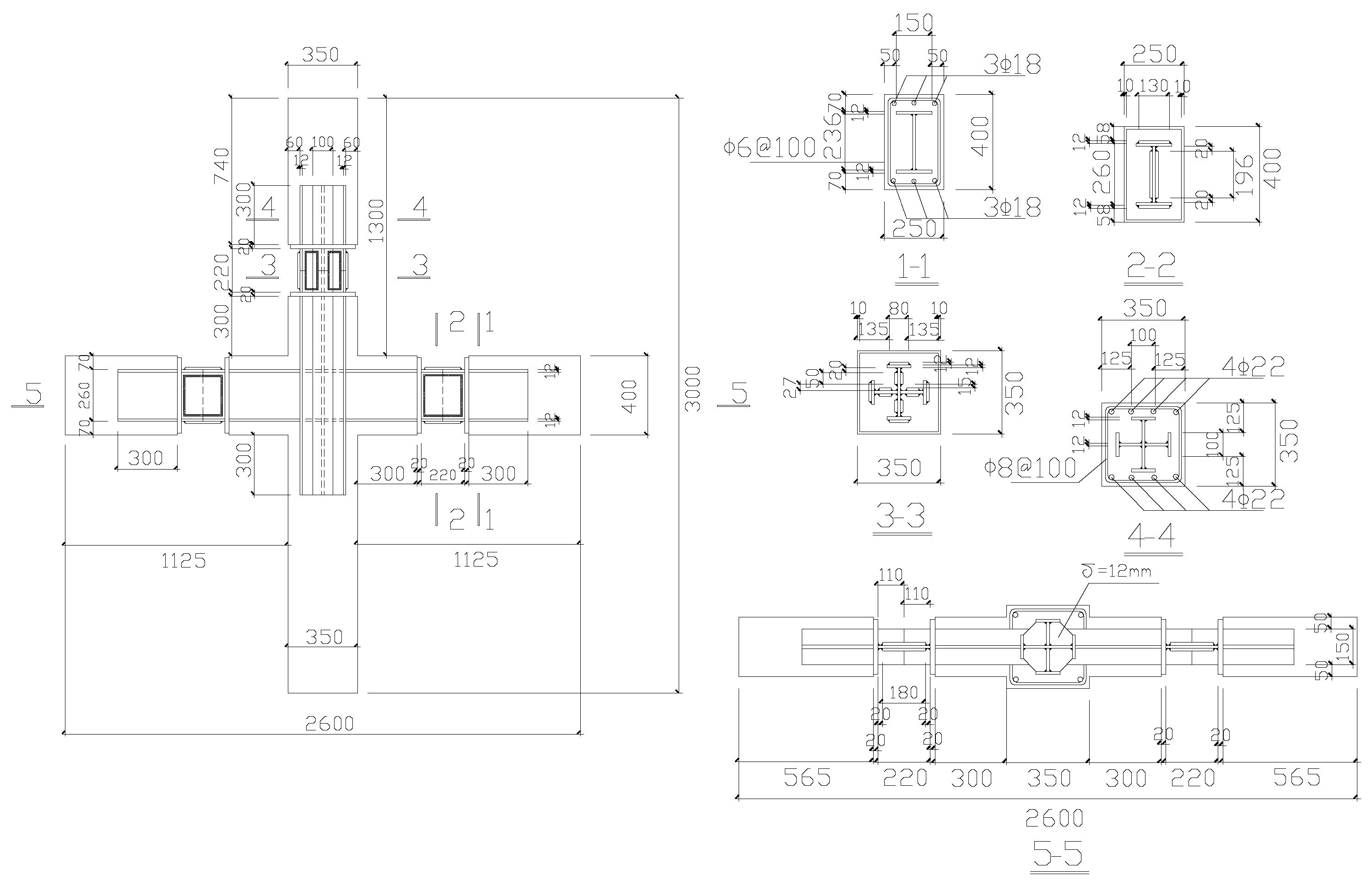
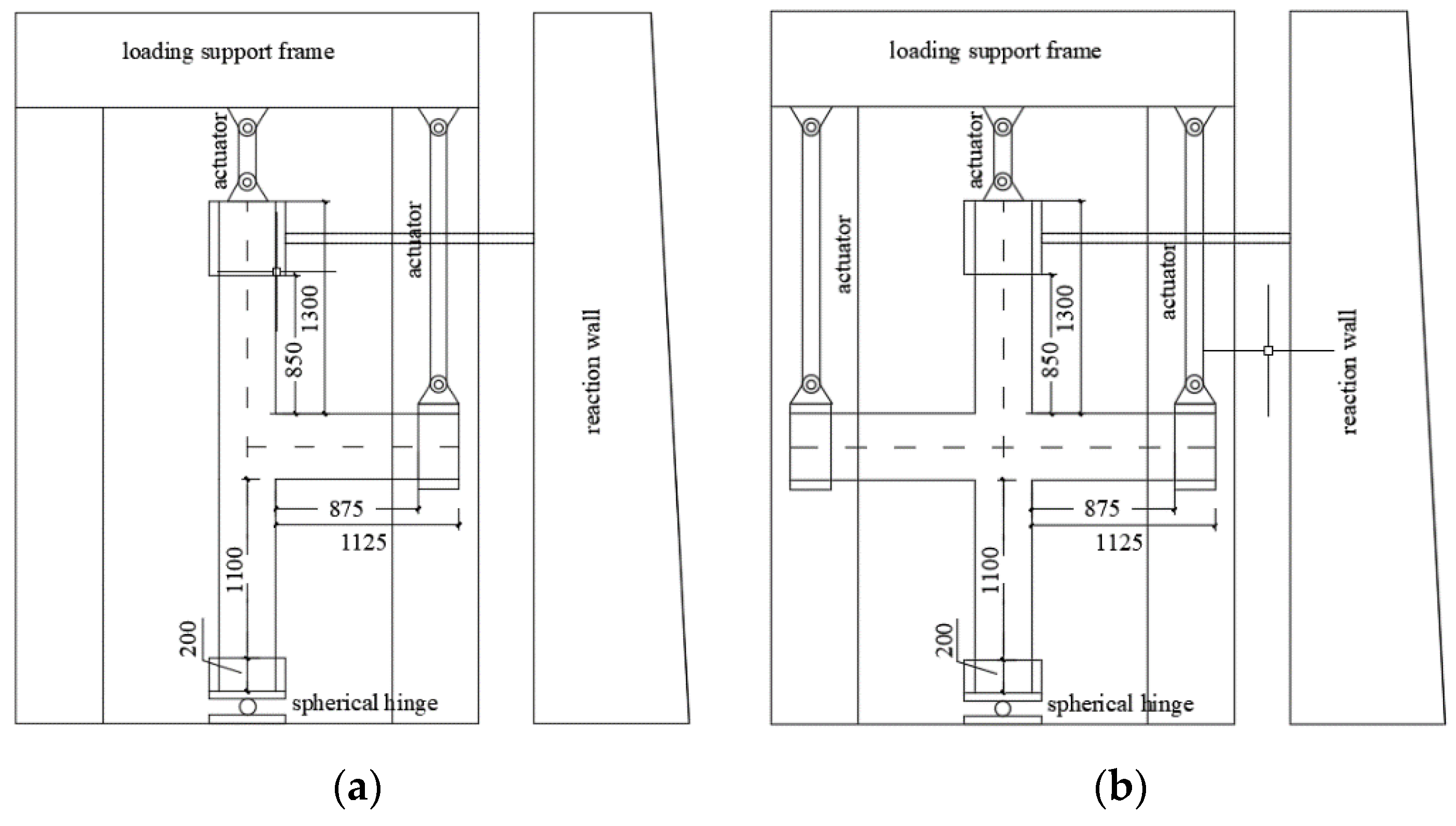
3.1. Experimental Overview
3.2. Information of the Finite Element Model
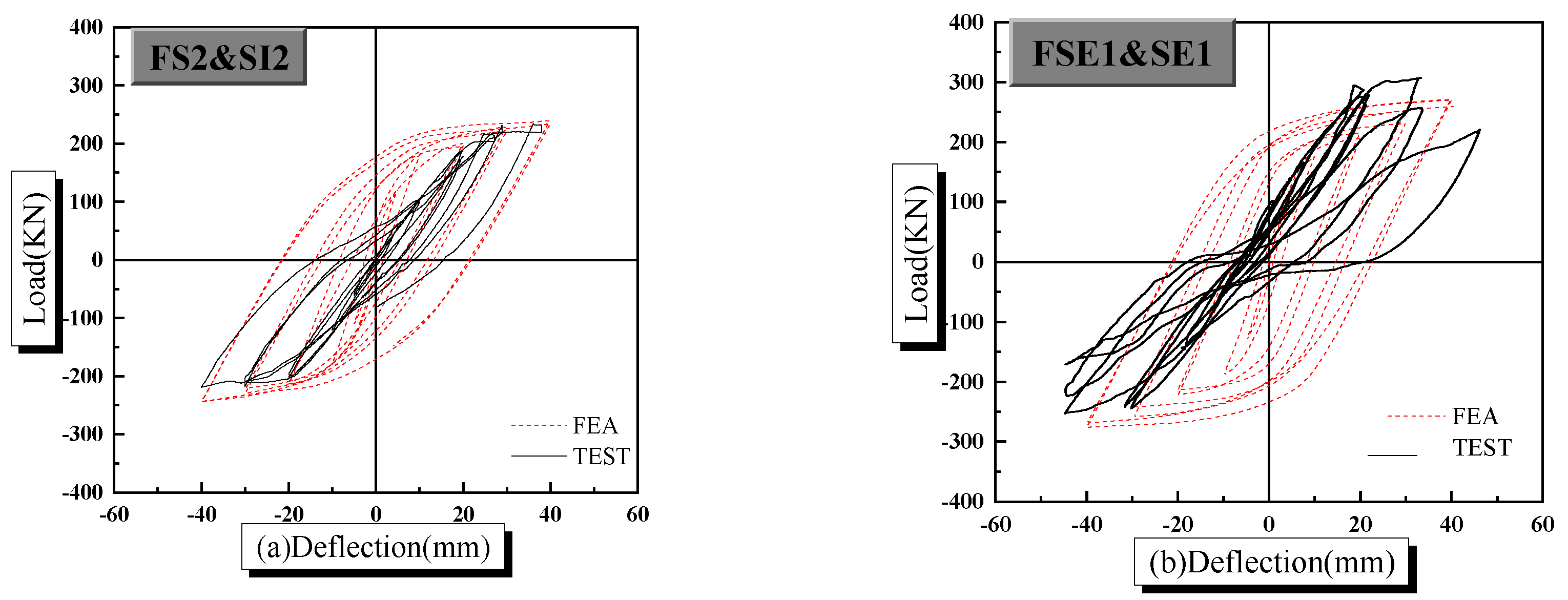
3.3. Verification of the Finite Element Model
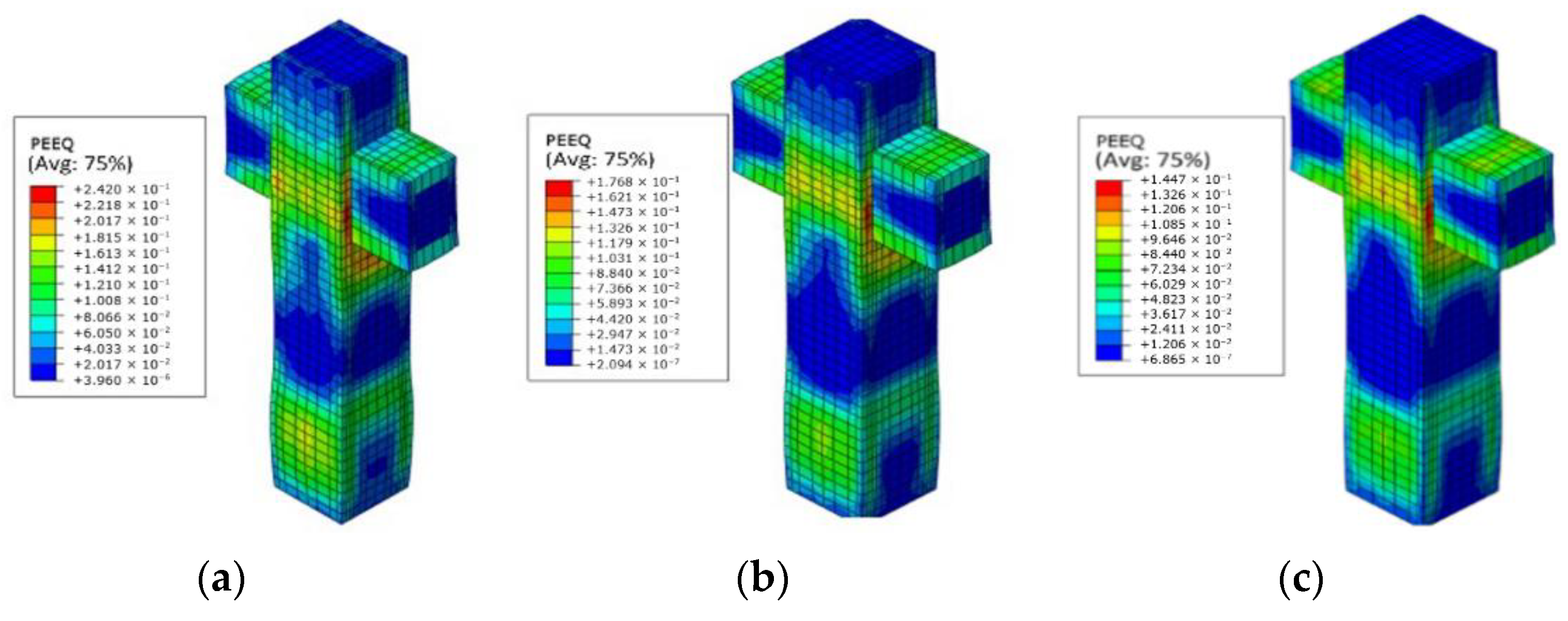
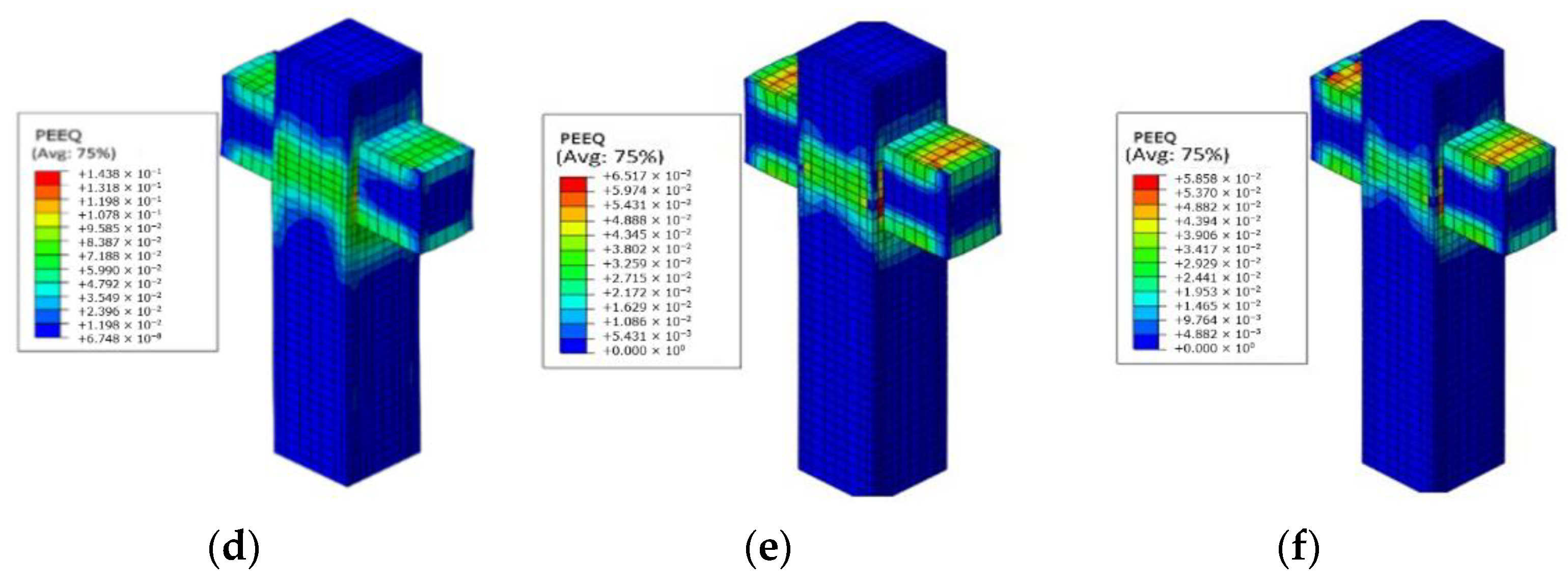
4. Dynamic Behavior of the PPSRC Beam–Column Joint
4.1. Finite Element Models
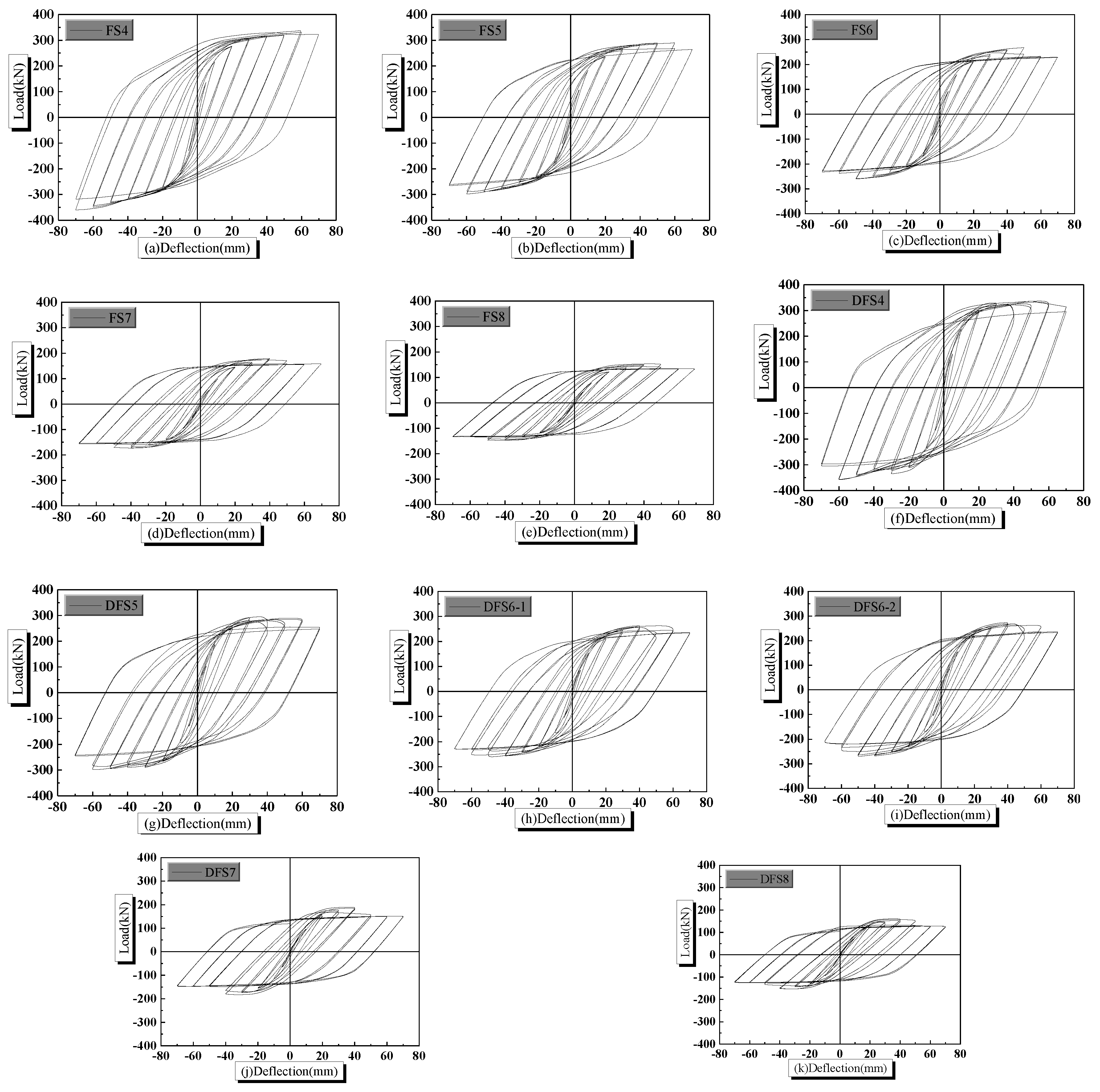
4.2. Hysteretic Curve
4.3. Skeleton Curve
4.4. Subsection
4.5. Ductility Performance
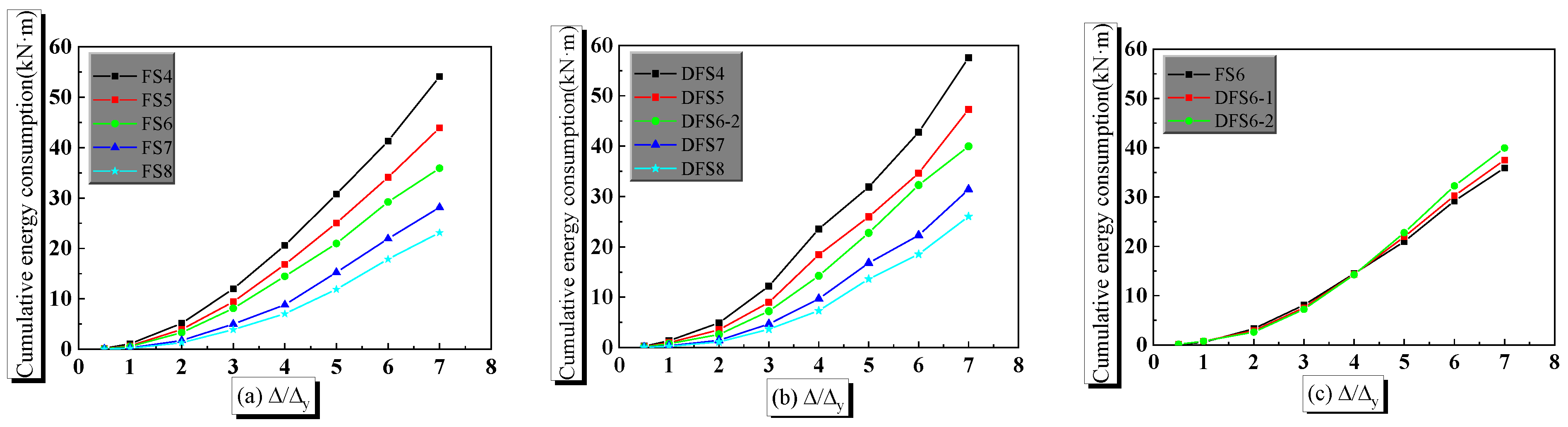
4.6. Energy Consumption
5. Reasonable Extension Length of Partial Steel Plate
6. Discussion and Conclusions
- (1)
- Ultimate bearing capacity and maximum displacement of numerical computation results are almost compatible with of the experimental results. Additionally, the changing trend of load-deflection hysteretic curves of numerical computation results is compatible with that of the experimental results. Moreover, the changing rule of equivalent plastic strain and concrete tensile damage of finite element analysis results is in good agreement with that of experimental results. Hence, the proposed finite element model can be utilized to assess the mechanical properties of the PPSRC beam–column joint.
- (2)
- Both the yield carrying capacity and the ultimate carrying capacity of the PPSRC beam–column joint increase as the strain rate increases. Furthermore, regardless of the strain rate, the ring stiffness of the PPSRC beam–column joint decreases as the shear span-to-depth ratio increases. The ring stiffness under the reverse direction is smaller than that under the forward direction at each displacement level, and the initial stiffness of the PPSRC joint is higher under a larger strain rate. However, stiffness degradation with a higher strain rate is more obvious under a larger displacement level. Moreover, the ductility performance of the PPSRC beam–column joint is rarely affected by strain rate. However, regardless of the strain rate, the displacement ductility factor of the PPSRC beam–column joint increases gradually as the shear span-to-depth ratio increases. Finally, the energy consumption of the PPSRC beam–column joint increases as the strain rate increases. Compared with finite element model FS6, the cumulative energy consumption of finite element models DFS6-1 and DFS6-2 increase by 4.5% and 11.4%, respectively.
- (3)
- Regardless of strain rate, the bearing capacity of the PPSRC beam–column joint decreases as the shear span-to-depth ratio increases. For quasi-static analysis or dynamic analysis, the ultimate bearing capacity of finite element model FS4 (λ = 2.3) is higher than that of finite element model FS8 (λ = 4.0). In addition, initial stiffness and ring stiffness of the PPSRC beam–column joints decrease as the shear span-to-depth ratio increases. However, stiffness degradation of the PPSRC beam–column joint is higher when the shear span-to-depth ratio is reduced. Moreover, the ductility performance of the PPSRC beam–column joint is better when the shear span-to-depth ratio is higher. Finally, the energy consumption of the PPSRC beam–column joint decreases when the shear span-to-depth ratio increases.
- (4)
- The mechanical properties of the PPSRC beam–column joint are affected by the extension length of partial steel plate in the column, and the reasonable extension length of the partial steel plate in the column is related to the shear span-to-depth ratio. When the extension length of the partial steel plate is insufficient, the concrete at the end of the partial steel plate in the column is crushed seriously, but the carrying capacity of the PPSRC beam–column joint does not decrease significantly. When the extension length of the partial steel plate in the column is adequate, the concrete damage in the beam and joint core area is more serious.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| bc | effective section width in x direction |
| DIFfc | dynamic increase factor |
| dc | effective section width in y direction |
| damage evolution coefficient of concrete under uniaxial compression | |
| dt | damage evolution coefficient for concrete under uniaxial tension |
| Ε’ | flow potential eccentricity |
| Ec | elastic modulus for unconfined concrete |
| fc,r | a typical value corresponding to concrete strength under uniaxial compression |
| effective restraint stresses in the x-direction | |
| effective restraint stresses in the y-direction | |
| ft,r | a typical value corresponding to concrete strength under uniaxial tension |
| fx,h | yielding strength supplied by horizontal reinforcement bars |
| fy,h | yielding strength supplied by vertical reinforcement bars |
| HRC | highly restraint concrete |
| h | effective beam height |
| K | increasing factor of strength |
| K1 | second stress invariant ratio of the compression meridian plane to the tension meridian plane |
| Kc | stiffness of the descending stage |
| Ke | stiffness of the elastic stage |
| effective restraint coefficient of stirrup reinforcements | |
| ring stiffness | |
| Ks | stiffness of the post-yielding stage |
| L | shear span length |
| ls | extension length of the partial steel plate in the column |
| n | calculation parameter |
| PPSRC | precast and partial steel reinforced concrete |
| peak load under i cycles | |
| PCC | partially confined concrete |
| PRC | partially restraint concrete |
| Py | yielding strength |
| vertical clear spacing of the spiral reinforcements or hooped reinforcements | |
| UC | unconfined concrete |
| clear spacing of the adjacent longitudinal reinforcements | |
| αf | ultimate stress ratio of biaxial compression to uniaxial compression |
| αc | coefficient corresponding to descending branch of concrete stress–strain curve under uniaxial compression |
| αt | parameter value corresponding to the descending branch of concrete stress–strain curve under uniaxial tension |
| peak displacement under i cycles | |
| ΔB | peak displacement corresponding to the ultimate strength Pu |
| ∆u | ultimate displacement |
| Δy | yielding displacement |
| Δ/Δy | displacement ductility coefficient |
| εc | strain under compression |
| compressive strain corresponding to the concrete compressive strength of HRC | |
| compressive strain corresponding to the concrete compressive strength of PCC | |
| compressive strain corresponding to the concrete compressive strength of PRC | |
| compressive strain corresponding to the concrete compressive strength of UC | |
| εc,r | compressive peak strain corresponding to the typical value of uniaxial compression strength fc,r |
| εt | strain under tension |
| εt,r | tensile peak strain corresponding to the typical value of uniaxial tension strength ft,r |
| λ | shear span-to-depth ratio |
| μ | Poisson ratio |
| μ∆ | displacement ductility factor |
| ν | viscosity parameter |
| ρ | density |
| ρc, | calculation parameter |
| ρcc | longitudinal reinforcement ratio |
| ρt | calculation parameter |
| ρx | reinforcement ratio of the rectangular reinforced concrete member in the horizontal direction |
| ρy | reinforcement ratio of the rectangular reinforced concrete member in the vertical direction |
| σ | concrete stress |
| σc | stress under compression |
| σt | stress under tension |
| calculation parameter | |
| calculation parameter | |
| Ψ | shear dilation angle |
References
- Ye, M.; Jiang, J.; Chen, H.M.; Zhou, H.Y.; Song, D.D. Seismic behavior of an innovative hybrid beam-column connection for precast concrete structures. Eng. Struct. 2021, 227, 111436. [Google Scholar] [CrossRef]
- Arslan, M.H.; Erdoğan, Ö.; Köken, A.; Erkan, İ.H.; Doğan, G. Evaluation of fire performance of prefabricated concrete buildings in Turkey. Mag. Concr. Res. 2017, 69, 389–401. [Google Scholar] [CrossRef]
- Yooprasertchai, E.; Warnitchai, P. An application of precast hybrid moment-resisting frames for seismic improvement. Mag. Concr. Res. 2016, 68, 1051–1069. [Google Scholar] [CrossRef]
- Balineni, H.; Jagarapu, D.C.K.; Eluru, A. Analysis of dry and wet connections in precast beam-column joint using ABAQUS software. Mater. Today Proc. 2020, 33, 287–295. [Google Scholar] [CrossRef]
- Choi, H.K.; Choi, Y.C.; Choi, C.S. Development and testing of precast concrete beam-to-column connections. Eng. Struct. 2013, 56, 1820–1835. [Google Scholar] [CrossRef]
- Fan, G.X.; Song, Y.P. Effect of axial compression ratio on dynamic mechanical properties of RC beam-column joints. Mag. Concr. Res. 2014, 66, 1219–1236. [Google Scholar] [CrossRef]
- Fan, G.X.; Wang, D.B.; Jia, J. Improvement, analytical verification and application of RC frame beam-column joint models. Earthq. Struct. 2018, 14, 273–283. [Google Scholar]
- Li, B.; Leong, C.L. Experimental and numerical investigations of the seismic behavior of high-strength concrete beam-column joints with column axial load. J. Struct. Eng. 2015, 141, 04014220. [Google Scholar] [CrossRef]
- Wang, L.C.; Fan, G.X.; Song, Y.P. Effect of loading velocity on the seismic behavior of RC joints. Earthq. Struct. 2015, 8, 665–679. [Google Scholar] [CrossRef]
- Rashidian, O.; Abbasnia, R.; Ahmadi, R.; Nav, F.M. Progressive collapse of exterior reinforced concrete beam-column sub-assemblages: Considering the effects of a transverse frame. Int. J. Concr. Struct. Mater. 2016, 10, 479–497. [Google Scholar] [CrossRef] [Green Version]
- Fan, G.X.; Song, Y.P.; Wang, L.C. Experimental study on the seismic behavior of reinforced concrete beam-column joints under various strain rates. J. Reinf. Plast. Compos. 2014, 33, 601–618. [Google Scholar] [CrossRef]
- Yang, H.; Guo, Z.X.; Yin, H.; Guan, D.; Yang, S. Development and testing of precast concrete beam-to-column connections with high-strength hooked bars under cyclic loading. Adv. Struct. Eng. 2019, 22, 3042–3054. [Google Scholar] [CrossRef]
- Subramanian, K.; Gopinathan, M.J. Performance and efficiency of joints in precast members. J. Struct. Eng. 2012, 39, 90–95. [Google Scholar]
- Kang, S.B.; Tan, K.H. Behaviour of precast concrete beam–column sub-assemblages subject to column removal. Eng. Struct. 2015, 93, 85–96. [Google Scholar] [CrossRef]
- Shiohara, H.; Watanabe, F. The Japan PRESSS precast concrete connection design. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000. [Google Scholar]
- Liang, X.M.; Parra-Montesinos, G.J. Seismic behavior of reinforced concrete column-steel beam subassemblies and frame systems. J. Struct. Eng. 2004, 130, 310–319. [Google Scholar] [CrossRef]
- Tong, X.D.; Hajjar, J.F.; Schultz, A.E.; Shield, C.K. Cyclic behavior of steel frame structure with composite reinforced concrete infill walls and partially restrained connections. J. Constr. Steel Res. 2005, 61, 531–552. [Google Scholar] [CrossRef]
- Elsanadedy, H.M.; Almusallam, T.H.; Al-Salloum, Y.A.; Abbas, H. Investigation of precast RC beam-column assemblies under column-loss scenario. Constr. Build. Mater. 2017, 142, 552–571. [Google Scholar] [CrossRef]
- Cheng, W.P.; Wang, L.C.; Song, Y.P.; Wang, J. Seismic behaviour of beam-column joints of precast and partial steel reinforced concrete. J. Harbin Inst. Technol. (New Ser.) 2015, 22, 108–117. [Google Scholar]
- China Architecture and Building Press. Code for Seismic Design of Buildings; GB50011-2010; China Architecture and Building Press: Beijing, China, 2010. (In Chinese) [Google Scholar]
- Campione, G.; Minafò, G. Behaviour of concrete deep beams with openings and low shear span-to-depth ratio. Eng. Struct. 2012, 41, 294–306. [Google Scholar] [CrossRef]
- Ghomi, S.K.; El-Salakawy, E. Effect of joint shear stress on seismic behaviour of interior GFRP-RC beam-column joints. Eng. Struct. 2019, 191, 583–597. [Google Scholar] [CrossRef]
- Bousselham, A.; Chaallal, O. Shear strengthening reinforced concrete beams with fiber-reinforced polymer: Assessment of influencing parameters and required research. Struct. J. 2004, 101, 219–227. [Google Scholar]
- Bousselham, A.; Chaallal, O. Effect of transverse steel and shear span on the performance of RC beams strengthened in shear with CFRP. Compos. Part B 2006, 37, 37–46. [Google Scholar] [CrossRef]
- Li, W.W.; Leung, C.K.Y. Effect of shear span-depth ratio on mechanical performance of RC beams strengthened in shear with U-wrapping FRP strips. Compos. Struct. 2017, 177, 141–157. [Google Scholar] [CrossRef]
- Hu, B.; Wu, Y.F. Effect of shear span-to-depth ratio on shear strength components of RC beams. Eng. Struct. 2018, 168, 770–783. [Google Scholar] [CrossRef]
- Zhang, F.B.; Xu, J.; Esther, B.; Lu, H.; Fang, H.; Liu, W. Effect of shear span-to-depth ratio on the mechanical behavior of composite sandwich beams with GFRP ribs and balsa wood core materials. Thin-Walled Struct. 2020, 154, 106799. [Google Scholar] [CrossRef]
- Chen, C.C.; Ko, J.W.; Huang, G.L.; Chang, Y.M. Local buckling and concrete confinement of concrete-filled box columns under axial load. J. Constr. Steel Res. 2012, 78, 8–21. [Google Scholar] [CrossRef]
- Zhao, X.Z.; Wen, F.P.; Chan, T.M.; Cao, S. Theoretical stress-strain model for concrete in steel-reinforced concrete columns. J. Struct. Eng. 2019, 145, 04019009. [Google Scholar] [CrossRef]
- Hu, J.L.; Chen, Y.Y.; Zhao, X.Z.; Wang, D.; Jiang, W.; Bao, L. Study on loading capacity of high steel ratio SRC columns under axial compression. J. Build. Struct. 2008, 29, 24–30. (In Chinese) [Google Scholar]
- Yu, S.J.; Wu, C.L.; Zhou, F.; Wang, P.; Zhao, K.; Liu, J. Experimental study and numerical simulation of a new prefabricated SRC column to steel beam composite joint. Structures 2020, 27, 999–1010. [Google Scholar] [CrossRef]
- Lv, X.Y.; Yu, Z.W.; Shan, Z. Influence of the constraint condition of column ends on seismic performance of a novel prefabricated concrete frame beam-An experimental and numerical investigation. Eng. Struct. 2020, 223, 111173. [Google Scholar] [CrossRef]
- Li, W.; Li, Q.N.; Jiang, W.S. Parameter study on composite frames consisting of steel beams and reinforced concrete columns. J. Constr. Steel Res. 2012, 77, 145–162. [Google Scholar] [CrossRef]
- Leppänen, J.; Johansson, M.; Grassl, P. On the dynamic response of reinforced concrete beams subjected to drop weight impact. Finite Elem. Anal. Des. 2020, 180, 103438. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical stress-strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef] [Green Version]
- China Architecture and Building Press. Code for Design of Concrete Structures; GB50010-2010; China Architecture and Building Press: Beijing, China, 2010. (In Chinese) [Google Scholar]
- Wang, W.D.; Han, L.H. Research on practical resilience model of load versus displacement for concrete filled steel tubular frame. Eng. Mech. 2008, 25, 62–69. [Google Scholar]
- Comtié Euro. International du Betoné. CEB-FIP Model Code 1990; Thomas Telford Ltd.: London, UK, 1993. [Google Scholar]
- Li, M.; Li, H.N. Dynamic test and constitutive model for reinforcing steel. China Civil Eng. J. 2010, 43, 70–75. (In Chinese) [Google Scholar]
- Ding, F.X.; Yin, G.A.; Wang, L.P.; Hu, D.; Chen, G.Q. Seismic performance of a non-through-core concrete between concrete-filled steel tubular columns and reinforced concrete beams. Thin-Walled Struct. 2017, 110, 14–26. [Google Scholar] [CrossRef]
- Cao, W.; Zhang, Y.; Dong, H.; Zhou, Z.; Qiao, Q. Experimental study on the seismic performance of recycled concrete brick walls embedded with vertical reinforcement. Materials 2014, 7, 5934–5958. [Google Scholar] [CrossRef] [PubMed] [Green Version]

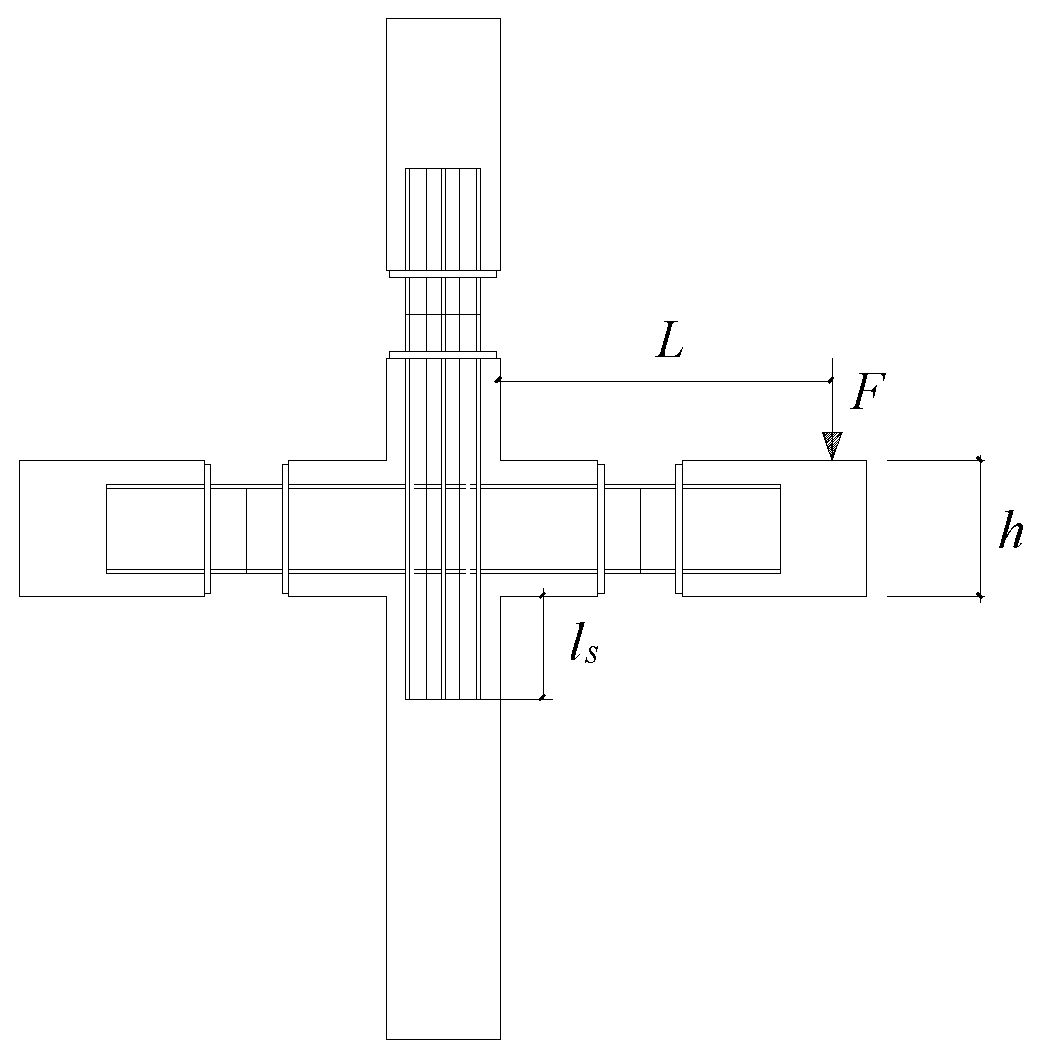




| ρ (kg/m3) | μ | Ψ (°) | Ε’ | αf | K1 | ν |
|---|---|---|---|---|---|---|
| 2400 | 0.2 | 30 | 0.1 | 1.16 | 0.6667 | 0.005 |
| Material | Grade | Yielding Strength (MPa) | Ultimate Strength (MPa) | Elastic Modulus (GPa) |
|---|---|---|---|---|
| steel plate (12 mm) | Q235b | 308 | 440 | 206 |
| steel plate (20 mm) | Q235b | 304 | 440 | 206 |
| longitudinal reinforcement bar (18 mm) | HRB335 | 404 | 623 | 200 |
| longitudinal reinforcement bar (22 mm) | HRB335 | 433 | 593 | 200 |
| stirrup reinforcement (6 mm) | HPB235 | 335 | 475 | 210 |
| stirrup reinforcement (8 mm) | HPB235 | 369 | 526 | 210 |
| concrete | C30 | 22.4 | 31.1 |
| Finite Element Models | Joint Type | Axial Compression Ratio | Shear Span-to-Depth Ratio | Steel Length in Column (mm) |
|---|---|---|---|---|
| FS2 | interior beam–column joint | 0.15 | 2.1 | 370 |
| FSE1 | exterior beam–column joint | 0.1 | 2.3 | 370 |
| Models | Joint Type | Shear Span-to-Depth Ratio | Strain Rate (1/s) | Axial Compression Ratio | Extension Length of Partial Steel Plate (mm) |
|---|---|---|---|---|---|
| FS4 | interior PPSRC beam– column joint | 2.3 | 1.25 × 10−5 | 0.05 | 870 |
| FS5 | 2.6 | ||||
| FS6 | 2.8 | ||||
| FS7 | 3.6 | ||||
| FS8 | 4.0 | ||||
| DFS4 | 2.3 | 1.25 × 10−2 | 0.05 | 870 | |
| DFS5 | 2.6 | ||||
| DFS7 | 3.6 | ||||
| DFS8 | 4.0 | ||||
| DFS6-1 | 2.8 | 1.25 × 10−3 | |||
| DFS6-2 | 2.8 | 1.25 × 10−2 |
| Displacement ductility coefficient | FS4 | FS5 | FS6 | FS7 |
| 2.69 | 2.78 | 2.85 | 3.10 | |
| FS8 | DFS4 | DFS5 | DFS7 | |
| 3.22 | 2.60 | 2.91 | 3.26 | |
| DFS8 | DFS6-1 | DFS6-2 | ||
| 3.47 | 2.81 | 2.99 |
| λ | ≥2.05 | ≥2.3 | ≥2.8 |
|---|---|---|---|
| Reasonable extension length of partial steel plate in the column (mm) | 1070 | 970 | 870 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, G.; Yang, J.; Wang, Y.; Zhang, Q.; Jia, J.; Cheng, W. Dynamic Behavior of a Precast and Partial Steel Joint under Various Shear Span-to-Depth Ratios. Materials 2021, 14, 2162. https://doi.org/10.3390/ma14092162
Fan G, Yang J, Wang Y, Zhang Q, Jia J, Cheng W. Dynamic Behavior of a Precast and Partial Steel Joint under Various Shear Span-to-Depth Ratios. Materials. 2021; 14(9):2162. https://doi.org/10.3390/ma14092162
Chicago/Turabian StyleFan, Guoxi, Jing Yang, Ye Wang, Qiyi Zhang, Jing Jia, and Wanpeng Cheng. 2021. "Dynamic Behavior of a Precast and Partial Steel Joint under Various Shear Span-to-Depth Ratios" Materials 14, no. 9: 2162. https://doi.org/10.3390/ma14092162







