Material Design for Optimal Postbuckling Behaviour of Composite Shells
Abstract
:1. Introduction
2. Mechanical and Numerical Models for Composite Shells
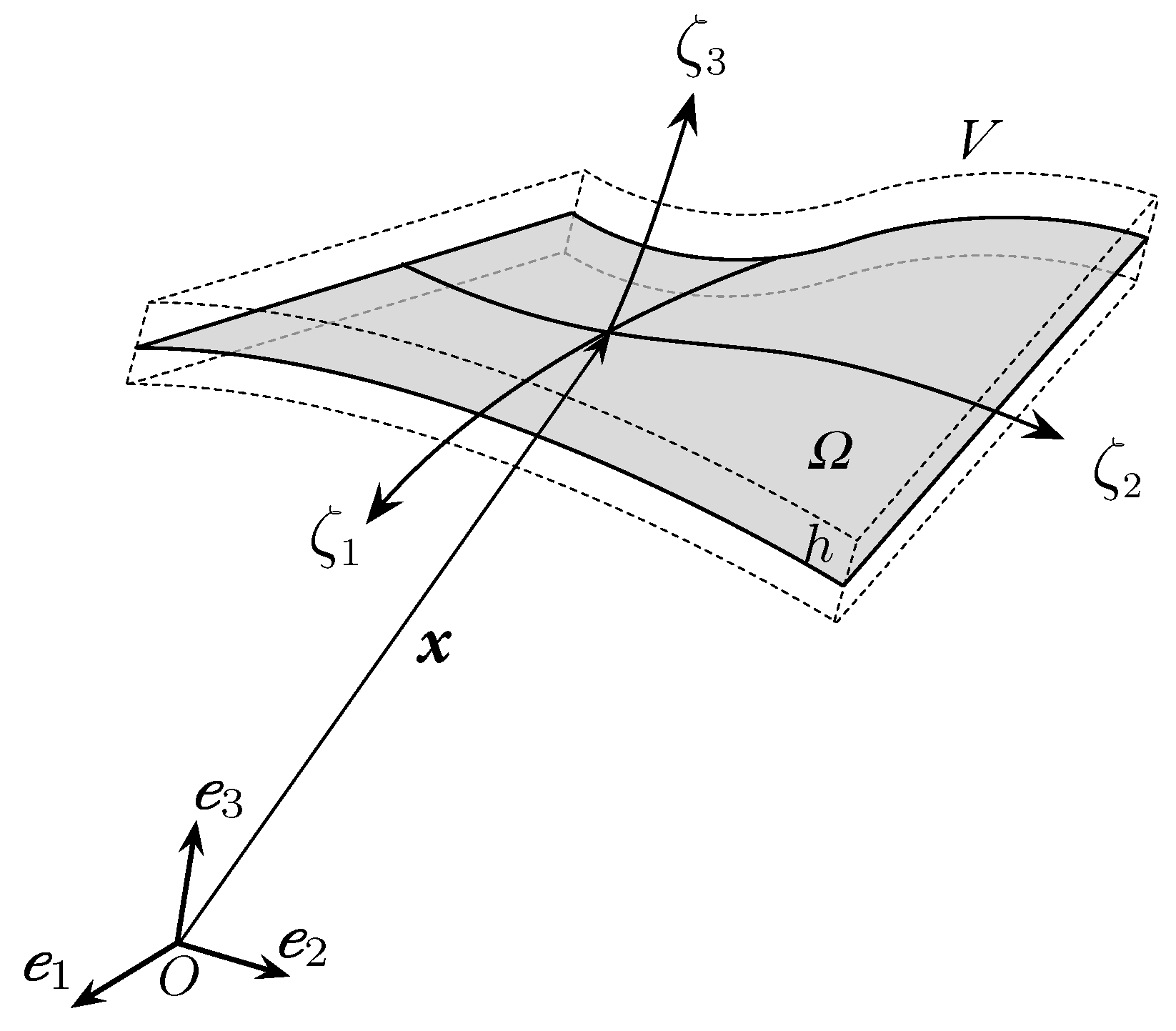
2.1. Kinematics of the Shell from the 3D Continuum
2.2. Constitutive Matrix for the Lamina
2.3. The Strain Energy for the Shell Model in Generalised Quantities
2.4. Discretization Methods
2.4.1. Geometry and Displacement Interpolation
2.4.2. Finite Element Formulation
2.4.3. Isogeometric Formulation
3. Objective Function and Design Variables
3.1. The Objective Function
3.2. Constraints
3.3. Design Variables
3.3.1. Layer-Wise Parameters
3.3.2. Lamination Parameters
4. Equilibrium Path Evaluation
4.1. Path-Following Analysis
4.2. The Mixed Integration Point Strategy
4.3. Koiter Method
4.3.1. The Worst-Case Geometrical Imperfection
4.3.2. Advantages of a TL Solid-Shell Formulation
5. Postbuckling Optimisation Algorithms
5.1. Monte Carlo Random Search with Zoom Steps
5.2. Genetic Algorithm
5.3. Globally Convergent Method of Moving Asymptotes
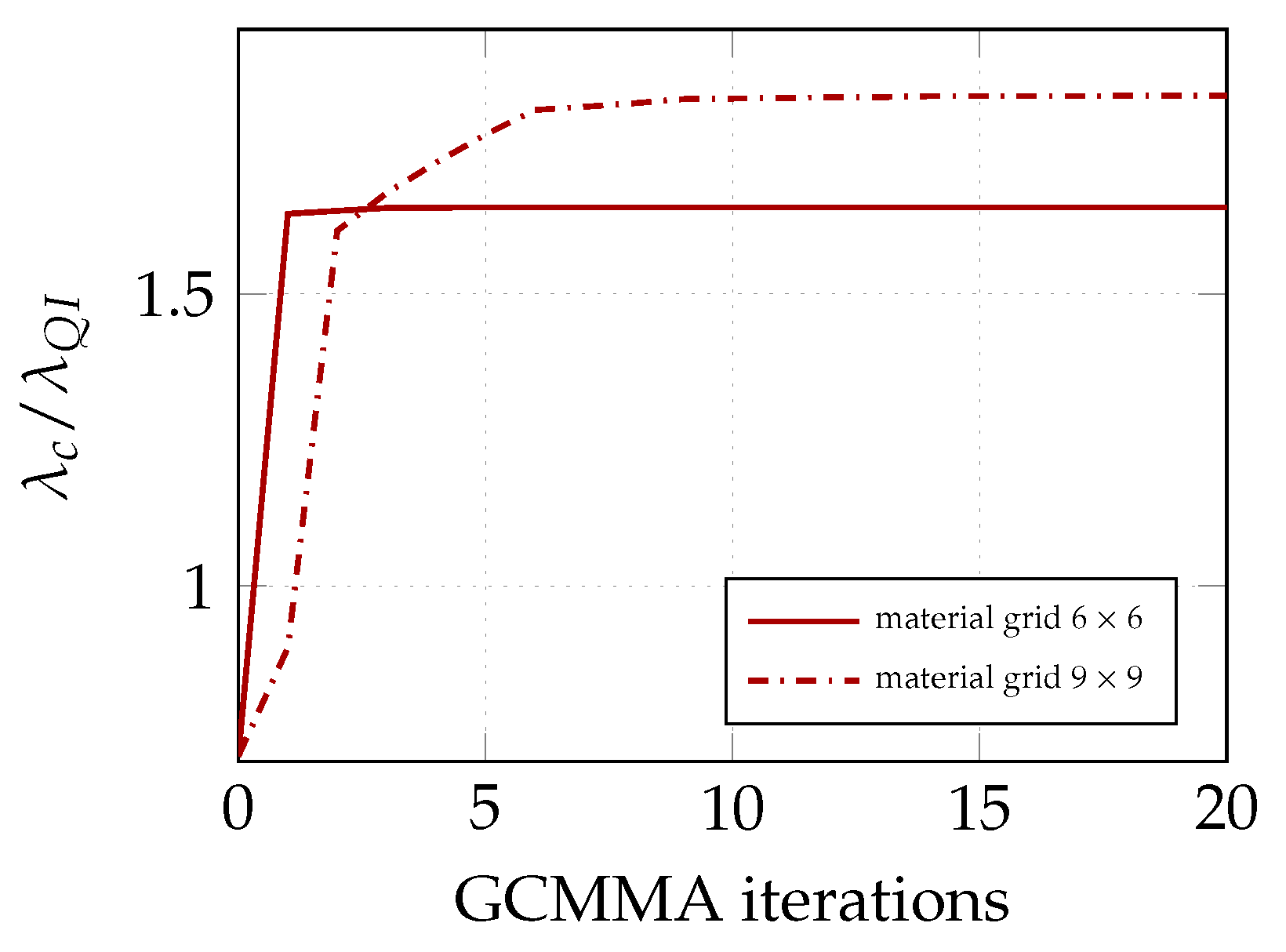
5.4. Comparison of the Optimization Algorithms
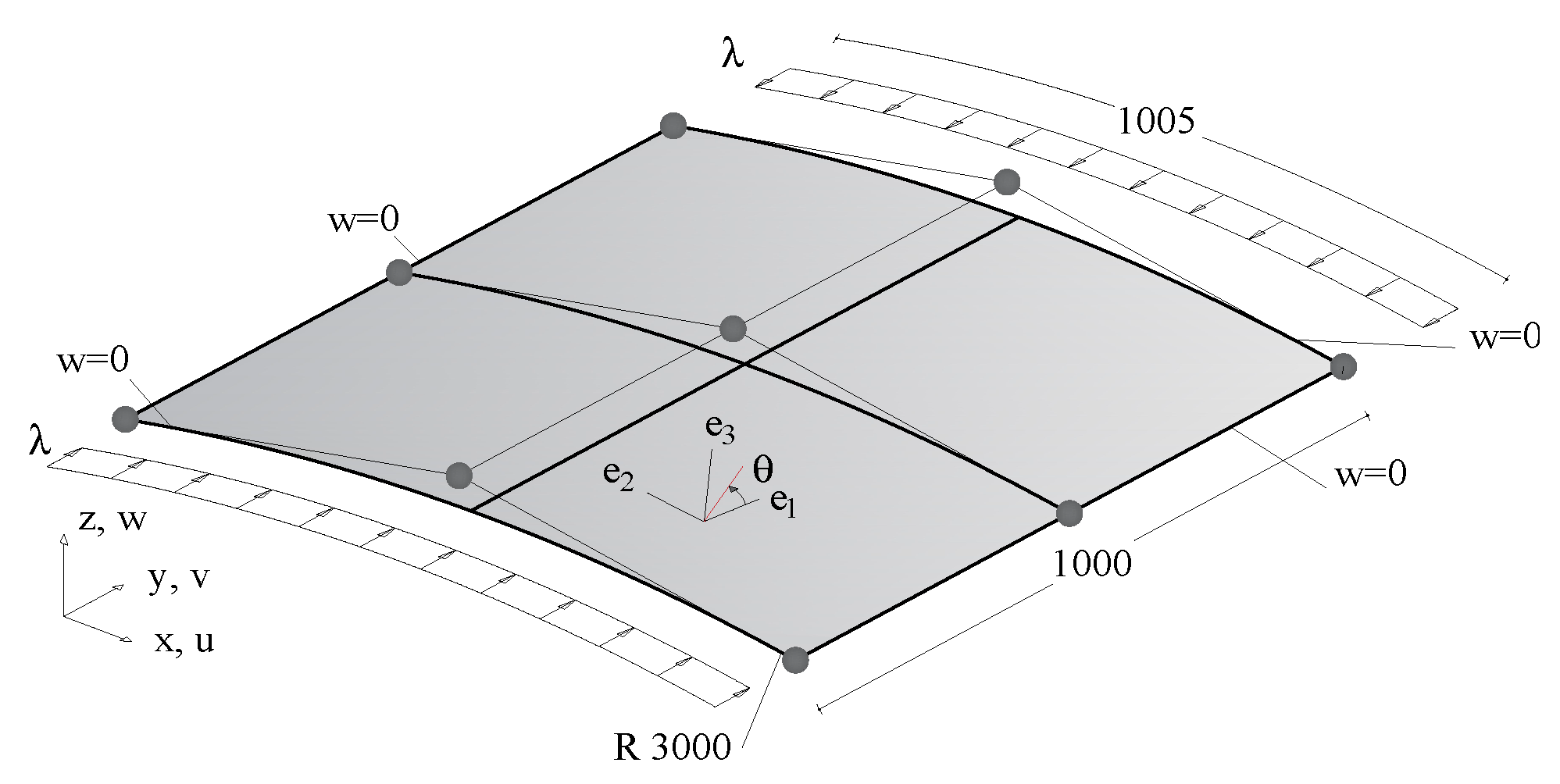
6. Post-Buckling Optimisation of a Cylindrical Panel under Compression
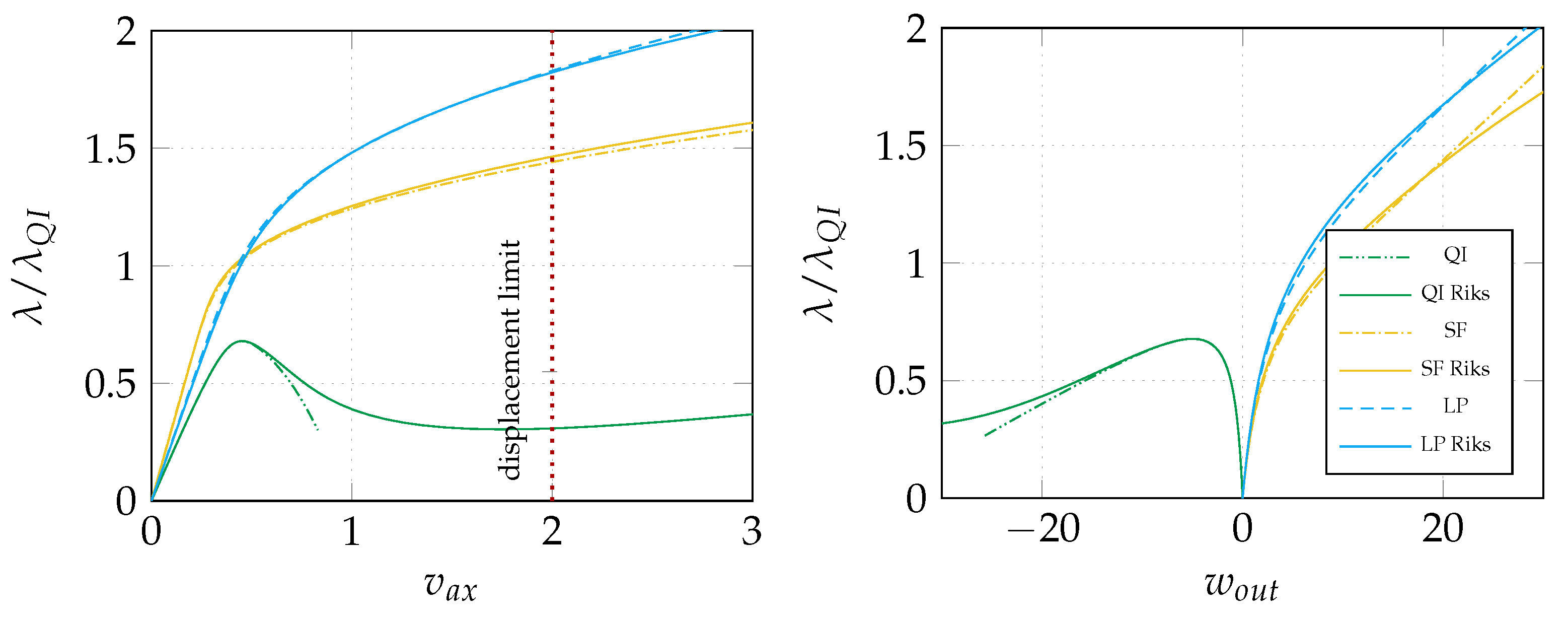
6.1. Stage 1: Determination of the Optimum in Terms of Lamination Parameters
6.2. Stage 2: Recovery of the Lamination Angles
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, B.; Tian, K.; Zhou, C.; Hao, P.; Zheng, Y.; Ma, Y.; Wang, J. Grid-pattern optimization framework of novel hierarchical stiffened shells allowing for imperfection sensitivity. Aerosp. Sci. Technol. 2017, 62, 114–121. [Google Scholar] [CrossRef]
- Wu, Z.; Raju, G.; Weaver, P.M. Optimization of postbuckling behaviour of variable thickness composite panels with variable angle tows: Towards “Buckle-Free” design concept. Int. J. Solids Struct. 2018, 132–133, 66–79. [Google Scholar] [CrossRef]
- Zucco, G.; Groh, R.; Madeo, A.; Weaver, P. Mixed shell element for static and buckling analysis of variable angle tow composite plates. Compos. Struct. 2016, 152, 324–338. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Zhou, Z.; Zhang, F.; Tan, Y.; Tu, Y.; Yang, B. Performance of 3D-Printed Continuous-Carbon-Fiber-Reinforced Plastics with Pressure. Materials 2020, 13, 471. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dickson, A.N.; Abourayana, H.M.; Dowling, D.P. 3D Printing of Fibre-Reinforced Thermoplastic Composites Using Fused Filament Fabrication—A Review. Polymers 2020, 12, 2188. [Google Scholar] [CrossRef]
- Sanei, S.H.R.; Popescu, D. 3D-Printed Carbon Fiber Reinforced Polymer Composites: A Systematic Review. J. Compos. Sci. 2020, 4, 98. [Google Scholar] [CrossRef]
- Odegard, G.; Gates, T.; Wise, K.; Park, C.; Siochi, E. Constitutive modeling of nanotube–reinforced polymer composites. Compos. Sci. Technol. 2003, 63, 1671–1687. [Google Scholar] [CrossRef]
- Talò, M.; Krause, B.; Pionteck, J.; Lanzara, G.; Lacarbonara, W. An updated micromechanical model based on morphological characterization of carbon nanotube nanocomposites. Compos. Part B Eng. 2017, 115, 70–78. [Google Scholar] [CrossRef]
- Ajayan, P.M.; Suhr, J.; Koratkar, N. Utilizing interfaces in carbon nanotube reinforced polymer composites for structural damping. J. Mater. Sci. 2006, 41, 7824–7829. [Google Scholar] [CrossRef]
- Basiricò, L.; Lanzara, G. Moving towards high-power, high-frequency and low-resistance CNT supercapacitors by tuning the CNT length, axial deformation and contact resistance. Nanotechnology 2012, 23, 305–401. [Google Scholar] [CrossRef]
- Formica, G.; Lacarbonara, W. Damage model of carbon nanotubes debonding in nanocomposites. Compos. Struct. 2013, 96, 514–525. [Google Scholar] [CrossRef]
- Sze, K.; Chan, W.; Pian, T. An eight-node hybrid-stress solid-shell element for geometric nonlinear analysis of elastic shells. Int. J. Numer. Methods Eng. 2002, 55, 853–878. [Google Scholar] [CrossRef]
- Leonetti, L.; Liguori, F.; Magisano, D.; Garcea, G. An efficient isogeometric solid-shell formulation for geometrically nonlinear analysis of elastic shells. Comput. Methods Appl. Mech. Eng. 2018, 159–183. [Google Scholar] [CrossRef]
- Cottrell, J.A.; Hughes, T.J.R.; Bazilevs, Y. Isogeometric Analysis: Toward Integration of CAD and FEA; John Wiley & Sons: Hoboken, NJ, USA, 2009; ISBN 978-0-470-74873-2. [Google Scholar]
- Thompson, J. Optimization as a generator of structural instability. Int. J. Mech. Sci. 1972, 14, 627–629. [Google Scholar] [CrossRef]
- Riks, E. An incremental approach to the solution of snapping and buckling problems. Int. J. Solids Struct. 1979, 15, 529–551. [Google Scholar] [CrossRef]
- Magisano, D.; Leonetti, L.; Garcea, G. How to improve efficiency and robustness of the Newton method in geometrically nonlinear structural problem discretized via displacement-based finite elements. Comput. Methods Appl. Mech. Eng. 2017, 986–1005. [Google Scholar] [CrossRef]
- Eriksson, A.; Pacoste, C.; Zdunek, A. Numerical analysis of complex instability behaviour using incremental-iterative strategies. Comput. Methods Appl. Mech. Eng. 1999, 265–305. [Google Scholar] [CrossRef]
- Wunderlich, M.D.W. Direct evaluation of the ‘worst’ imperfection shape in shell buckling. Comput. Methods Appl. Mech. Eng. 1997, 201–222. [Google Scholar] [CrossRef]
- Groh, R.M.J.; Avitabile, D.; Pirrera, A. Generalised path-following for well-behaved nonlinear structures. Comput. Methods Appl. Mech. Eng. 2018, 394–426. [Google Scholar] [CrossRef]
- Lindgaard, E.; Lund, E. Nonlinear buckling optimization of composite structures. Comput. Methods Appl. Mech. Eng. 2010, 2319–2330. [Google Scholar] [CrossRef] [Green Version]
- Lindgaard, E.; Lund, E.; Rasmussen, K. Nonlinear buckling optimization of composite structures considering “worst” shape imperfections. Int. J. Solids Struct. 2010, 3186–3202. [Google Scholar] [CrossRef] [Green Version]
- Henrichsen, S.R.; Lindgaard, E.; Lund, E. Robust buckling optimization of laminated composite structures using discrete material optimization considering “worst” shape imperfections. Thin-Walled Struct. 2015, 624–635. [Google Scholar] [CrossRef]
- Koiter, W. On the Stability of Elastic Equilibrium; Techische Hooge School: Delft, The Netherlands, 1945. [Google Scholar]
- Magisano, D.; Leonetti, L.; Garcea, G. Koiter asymptotic analysis of multilayered composite structures using mixed solid-shell finite elements. Compos. Struct. 2016, 154, 296–308. [Google Scholar] [CrossRef]
- Liguori, F.S.; Madeo, A.; Magisano, D.; Leonetti, L.; Garcea, G. Post-buckling optimisation strategy of imperfection sensitive composite shells using Koiter method and Monte Carlo simulation. Compos. Struct. 2018, 654–670. [Google Scholar] [CrossRef]
- Liguori, F.S.; Zucco, G.; Madeo, A.; Magisano, D.; Leonetti, L.; Garcea, G.; Weaver, P.M. Postbuckling optimisation of a variable angle tow composite wingbox using a multi-modal Koiter approach. Thin-Walled Struct. 2019, 138, 183–198. [Google Scholar] [CrossRef]
- Garcea, G.; Liguori, F.S.; Leonetti, L.; Magisano, D.; Madeo, A. Accurate and efficient a posteriori account of geometrical imperfections in Koiter finite element analysis. Int. J. Numer. Methods Eng. 2017, 112, 1154–1174. [Google Scholar] [CrossRef]
- Liang, K.; Ruess, M.; Abdalla, M. The Koiter-Newton approach using von Karman kinematics for buckling analyses of imperfection sensitive structures. Comput. Methods Appl. Mech. Eng. 2014, 279, 440–468. [Google Scholar] [CrossRef]
- Magisano, D.; Liang, K.; Garcea, G.; Leonetti, L.; Ruess, M. An efficient mixed variational reduced-order model formulation for nonlinear analyses of elastic shells. Int. J. Numer. Methods Eng. 2018, 113, 634–655. [Google Scholar] [CrossRef]
- Barkanov, E.; Ozoliņš, O.; Eglītis, E.; Almeida, F.; Bowering, M.C.; Watson, G. Optimal design of composite lateral wing upper covers. Part I: Linear buckling analysis. Aerosp. Sci. Technol. 2014, 1–8. [Google Scholar] [CrossRef]
- Riche, R.L.; Haftka, R.T. Optimization of laminate stacking sequence for buckling load maximization by genetic algorithm. AIAA J. 1993. [Google Scholar] [CrossRef]
- Svanberg, K. The method of moving asymptotes—A new method for structural optimization. Int. J. Numer. Methods Eng. 1987, 24, 359–373. [Google Scholar] [CrossRef]
- Johansen, L.S.; Lund, E.; Kleist, J. Failure optimization of geometrically linear/nonlinear laminated composite structures using a two-step hierarchical model adaptivity. Comput. Methods Appl. Mech. Eng. 2009, 2421–2438. [Google Scholar] [CrossRef]
- Liguori, F.S.; Zucco, G.; Madeo, A.; Garcea, G.; Leonetti, L.; Weaver, P.M. An isogeometric framework for the optimal design of variable stiffness shells undergoing large deformations. Int. J. Solids Struct. 2021, 210–211, 18–34. [Google Scholar] [CrossRef]
- Leonetti, L.; Magisano, D.; Liguori, F.; Garcea, G. An isogeometric formulation of the Koiter’s theory for buckling and initial post-buckling analysis of composite shells. Comput. Methods Appl. Mech. Eng. 2018, 387–410. [Google Scholar] [CrossRef]
- Hibbit, K.; Sorenson, P. Abaqus Analysis User’s Manual Version 6.7; SIMULIA Worldwide Headquarters: Providence, RI, USA, 2007. [Google Scholar]
- Liguori, F.S.; Magisano, D.; Leonetti, L.; Garcea, G. Nonlinear thermoelastic analysis of shell structures: Solid-shell modelling and high-performing continuation method. Compos. Struct. 2021, 113734. [Google Scholar] [CrossRef]
- Thai, C.H.; Nguyen-Xuan, H.; Bordas, S.P.A.; Nguyen-Thanh, N.; Rabczuk, T. Isogeometric Analysis of Laminated Composite Plates Using the Higher-Order Shear Deformation Theory. Mech. Adv. Mater. Struct. 2015, 22, 451–469. [Google Scholar] [CrossRef]
- Ruess, Y.G.M. A layerwise isogeometric approach for NURBS-derived laminate composite shells. Compos. Struct. 2015, 300–309. [Google Scholar] [CrossRef]
- Dufour, J.E.; Antolin, P.; Sangalli, G.; Auricchio, F.; Reali, A. A cost-effective isogeometric approach for composite plates based on a stress recovery procedure. Compos. Part B Eng. 2018, 12–18. [Google Scholar] [CrossRef] [Green Version]
- Xie, Q.; Sze, K.; Zhou, Y. Drape simulation using solid-shell elements and adaptive mesh subdivision. Finite Elem. Anal. Des. 2015, 106, 85–102. [Google Scholar] [CrossRef] [Green Version]
- Adam, C.; Hughes, T.; Bouabdallah, S.; Zarroug, M.; Maitournam, H. Selective and reduced numerical integrations for NURBS-based isogeometric analysis. Comput. Methods Appl. Mech. Eng. 2015, 284, 732–761. [Google Scholar] [CrossRef]
- Johannessen, K. Optimal quadrature for univariate and tensor product splines. Comput. Methods Appl. Mech. Eng. 2017, 84–99. [Google Scholar] [CrossRef]
- Leonetti, L.; Magisano, D.; Madeo, A.; Garcea, G.; Kiendl, J.; Reali, A. A simplified Kirchhoff–Love large deformation model for elastic shells and its effective isogeometric formulation. Comput. Methods Appl. Mech. Eng. 2019, 354, 369–396. [Google Scholar] [CrossRef]
- Leonetti, L.; Liguori, F.S.; Magisano, D.; Kiendl, J.; Reali, A.; Garcea, G. A robust penalty coupling of non-matching isogeometric Kirchhoff–Love shell patches in large deformations. Comput. Methods Appl. Mech. Eng. 2020, 371, 113289. [Google Scholar] [CrossRef]
- Gurdal, Z.; Olmedo, R. In-plane response of laminates with spatially varying fiber orientations—Variable stiffness concept. AIAA J. 1993, 31, 751–758. [Google Scholar] [CrossRef]
- Catapano, M.M.A. A general B-Spline surfaces theoretical framework for optimisation of variable angle-tow laminates. Compos. Struct. 2019, 561–578. [Google Scholar] [CrossRef]
- Wu, Z.; Raju, G.; Weaver, P.M. Framework for the Buckling Optimization of Variable-Angle Tow Composite Plates. AIAA J. 2015, 53, 3788–3804. [Google Scholar] [CrossRef] [Green Version]
- Tsai, S.; Hahn, H. Introduction to Composite Materials; Technomic Pub Westport, Co.: Westport, CT, USA, 1980. [Google Scholar]
- Raju, G.; Wu, Z.; White, S.; Weaver, P.M. Optimal Postbuckling Design of Variable Angle Tow Composite Plates. AIAA J. 2018, 56, 2045–2061. [Google Scholar] [CrossRef] [Green Version]
- Martins, J.R.R.A.; Sturdza, P.; Alonso, J.J. The Complex-step Derivative Approximation. ACM Trans. Math. Softw. 2003, 29, 245–262. [Google Scholar] [CrossRef] [Green Version]
- Kouhia, R.; Mikkola, M. Tracing the equilibrium path beyond compound critical points. Int. J. Numer. Methods Eng. 1999, 46, 1049–1074. [Google Scholar] [CrossRef]
- Magisano, D.; Leonetti, L.; Garcea, G. Advantages of the mixed format in geometrically nonlinear analysis of beams and shells using solid finite elements. Int. J. Numer. Methods Eng. 2017, 109, 1237–1262. [Google Scholar] [CrossRef]
- Maurin, F.; Greco, F.; Dedoncker, S.; Desmet, W. Isogeometric analysis for nonlinear planar Kirchhoff rods: Weighted residual formulation and collocation of the strong form. Comput. Methods Appl. Mech. Eng. 2018, 1023–1043. [Google Scholar] [CrossRef]
- Maurin, F.; Greco, F.; Desmet, W. Isogeometric analysis for nonlinear planar pantographic lattice: Discrete and continuum models. Contin. Mech. Thermodyn. 2018. [Google Scholar] [CrossRef]
- Pfefferkorn, R.; Bieber, S.; Oesterle, B.; Bischoff, M.; Betsch, P. Improving efficiency and robustness of enhanced assumed strain elements for nonlinear problems. Int. J. Numer. Methods Eng. 2020. [Google Scholar] [CrossRef]
- Cava, D.; Camotim, D.; Dinis, P.B.; Madeo, A. Numerical investigation and direct strength design of cold-formed steel lipped channel columns experiencing local–distortional–global interaction. Thin-Walled Struct. 2016, 231–247. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization & Machine Learning; Addison-Wesley: Boston, MA, USA, 1989. [Google Scholar]
- Zillober, C. A globally convergent version of the method of moving asymptotes. Struct. Optim. 1993, 6, 166–174. [Google Scholar] [CrossRef] [Green Version]
- Bruyneel, M.; Duysinx, P.; Fleury, C. A family of MMA approximations for structural optimization. Struct. Multidiscip. Optim. 2002, 263–276. [Google Scholar] [CrossRef] [Green Version]
- Fleur, M.B.C. Composite structures optimization using sequential convex programming. Adv. Eng. Softw. 2002, 33, 697–711. [Google Scholar]

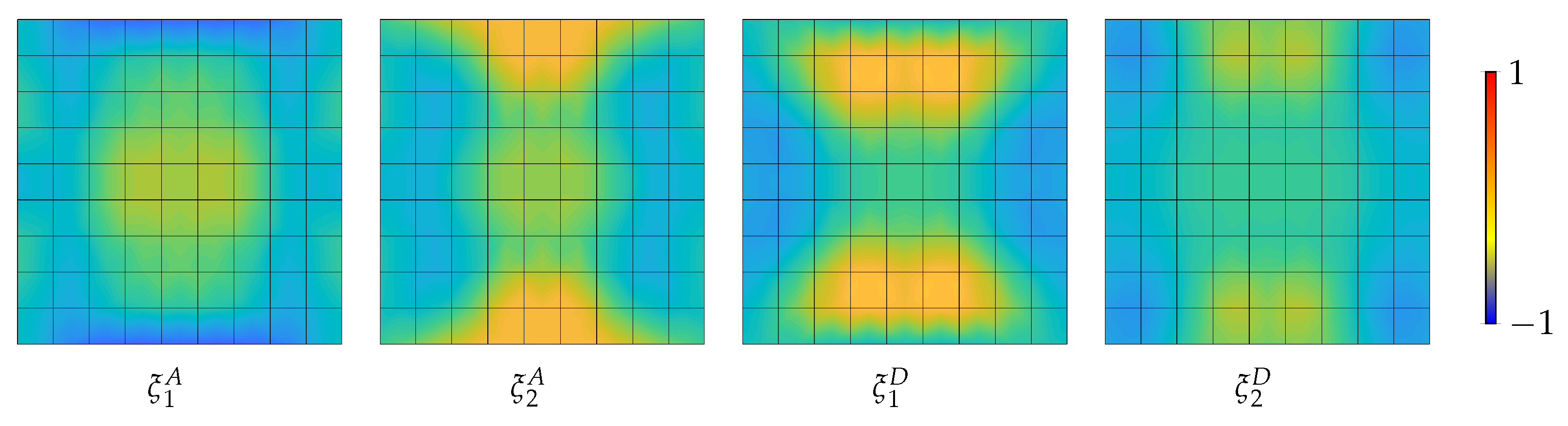
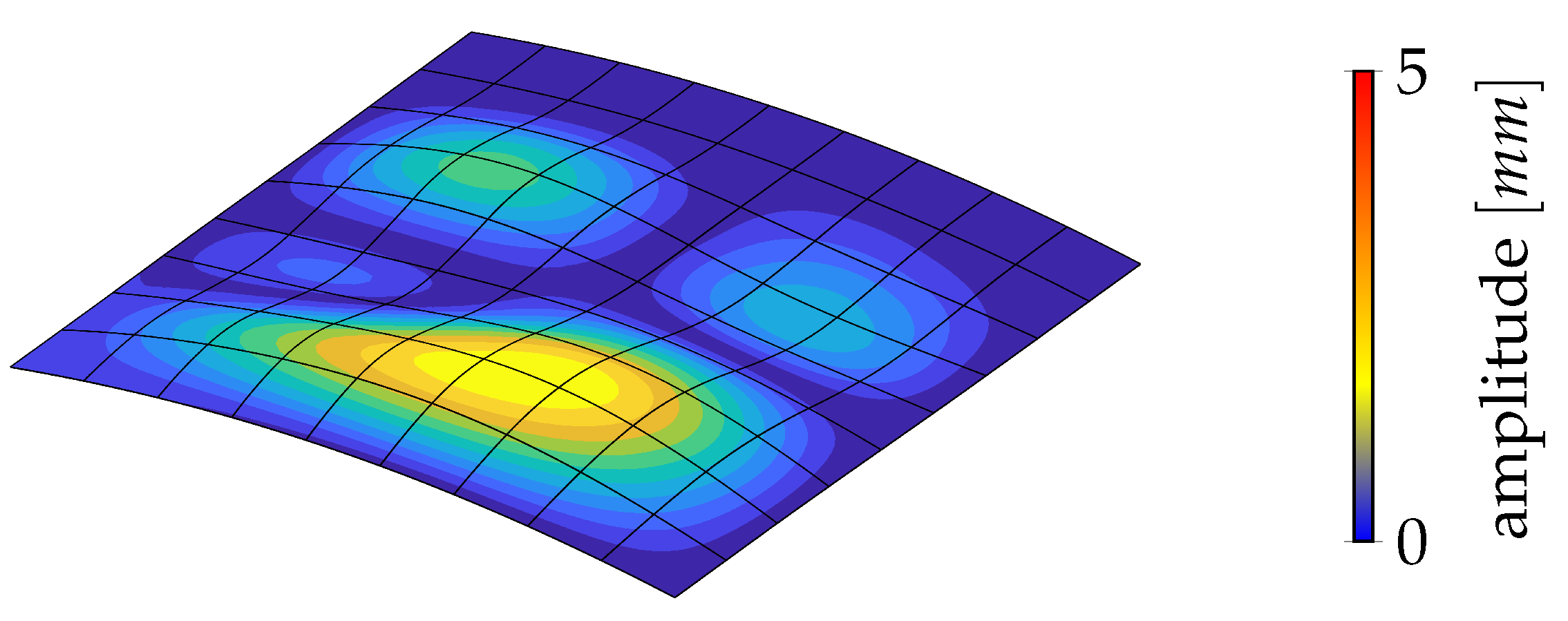
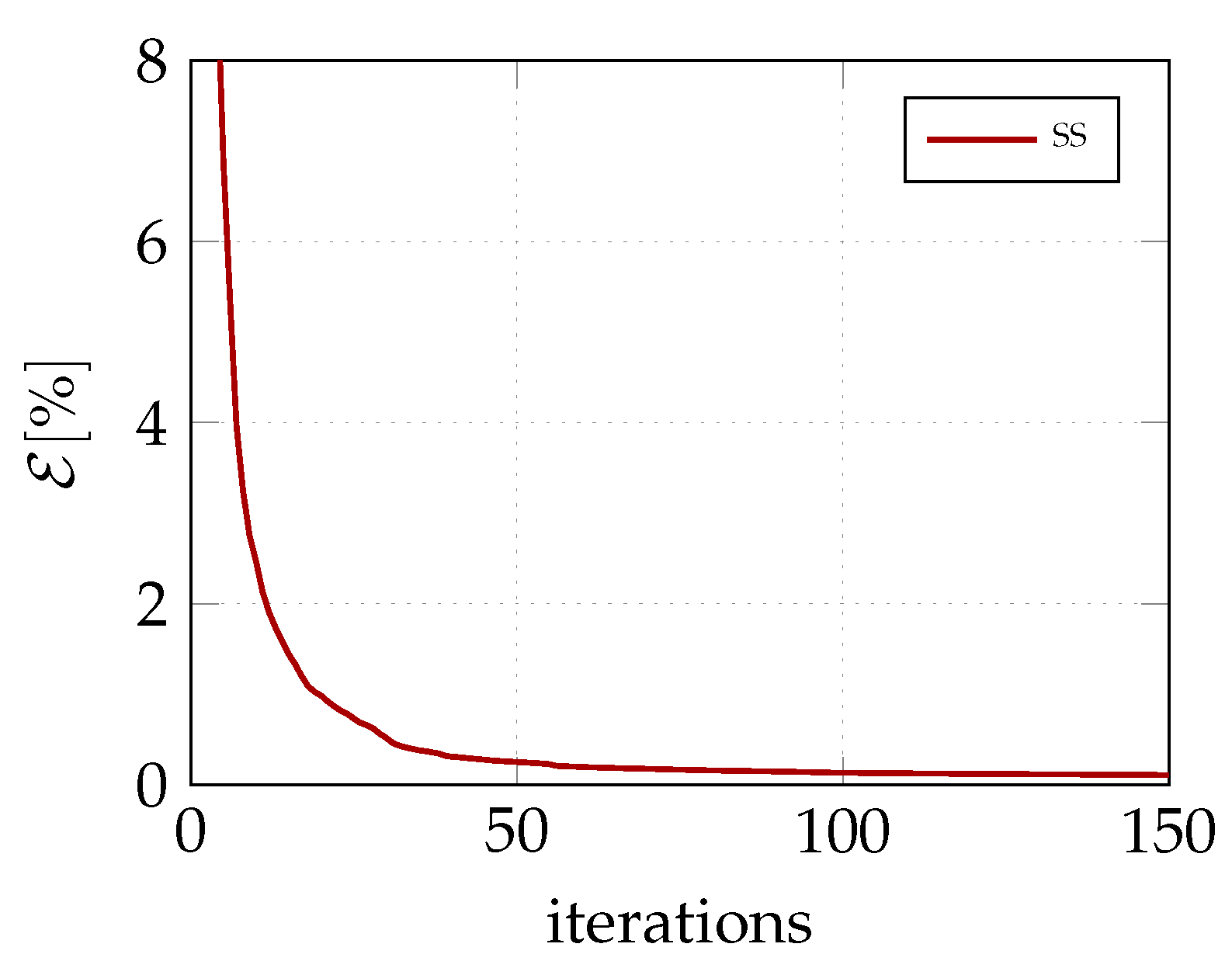
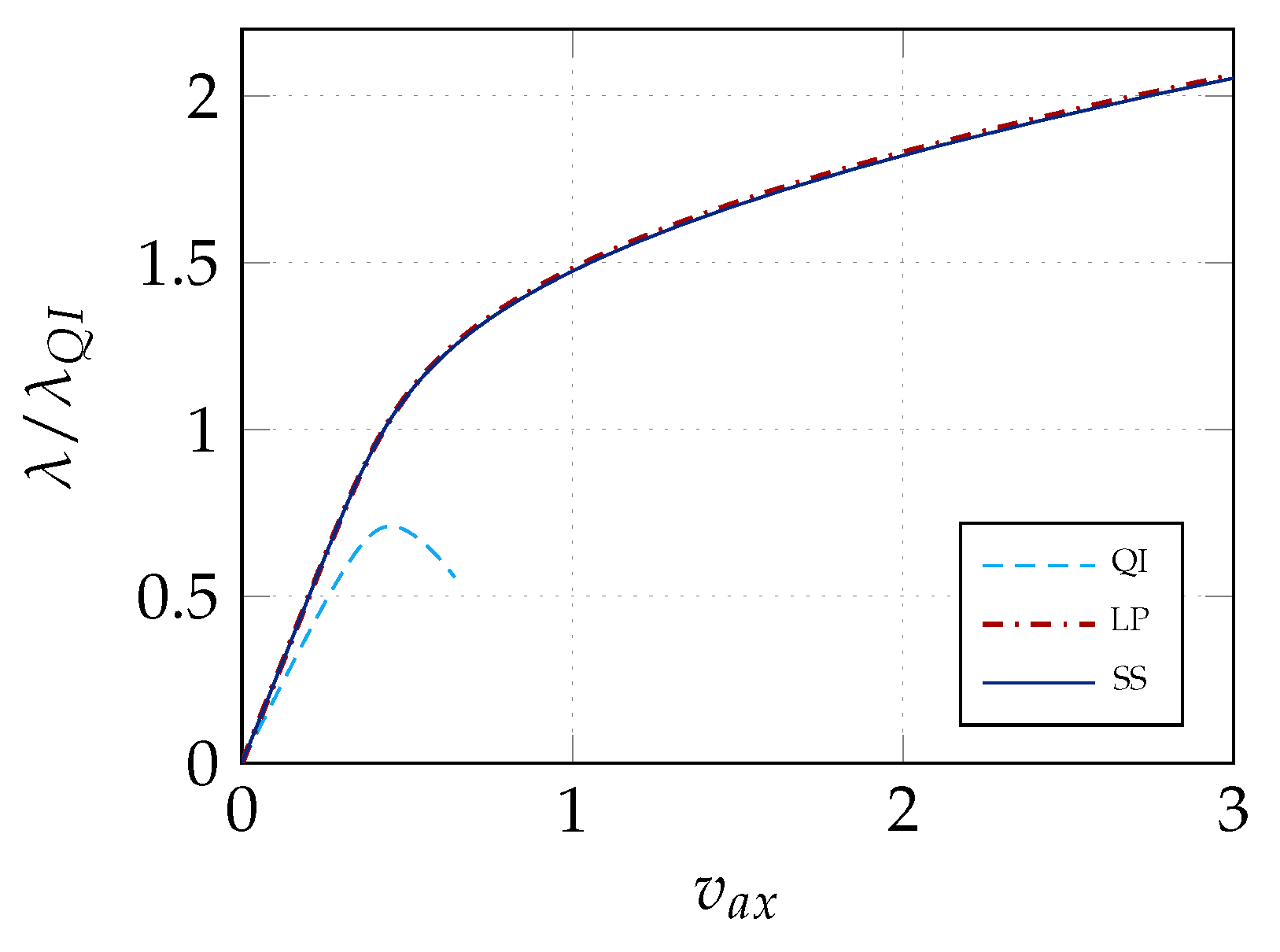

| Case | Match | |||||
|---|---|---|---|---|---|---|
| QI | 0.710 | 1.000 | 1.255 | 1.795 | 1.883 | - |
| LP | 1.830 | 1.177 | 1.489 | 1.840 | 2.100 | - |
| SS | 1.821 | 1.170 | 1.482 | 1.840 | 2.097 | 99.92% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magisano, D.; Liguori, F.; Madeo, A.; Leonetti, L.; Garcea, G. Material Design for Optimal Postbuckling Behaviour of Composite Shells. Materials 2021, 14, 1665. https://doi.org/10.3390/ma14071665
Magisano D, Liguori F, Madeo A, Leonetti L, Garcea G. Material Design for Optimal Postbuckling Behaviour of Composite Shells. Materials. 2021; 14(7):1665. https://doi.org/10.3390/ma14071665
Chicago/Turabian StyleMagisano, Domenico, Francesco Liguori, Antonio Madeo, Leonardo Leonetti, and Giovanni Garcea. 2021. "Material Design for Optimal Postbuckling Behaviour of Composite Shells" Materials 14, no. 7: 1665. https://doi.org/10.3390/ma14071665






