A Generalized Stress State and Temperature Dependent Damage Indicator Framework for Ductile Failure Prediction in Heat-Assisted Forming Operations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material Data
2.2. Plasticity
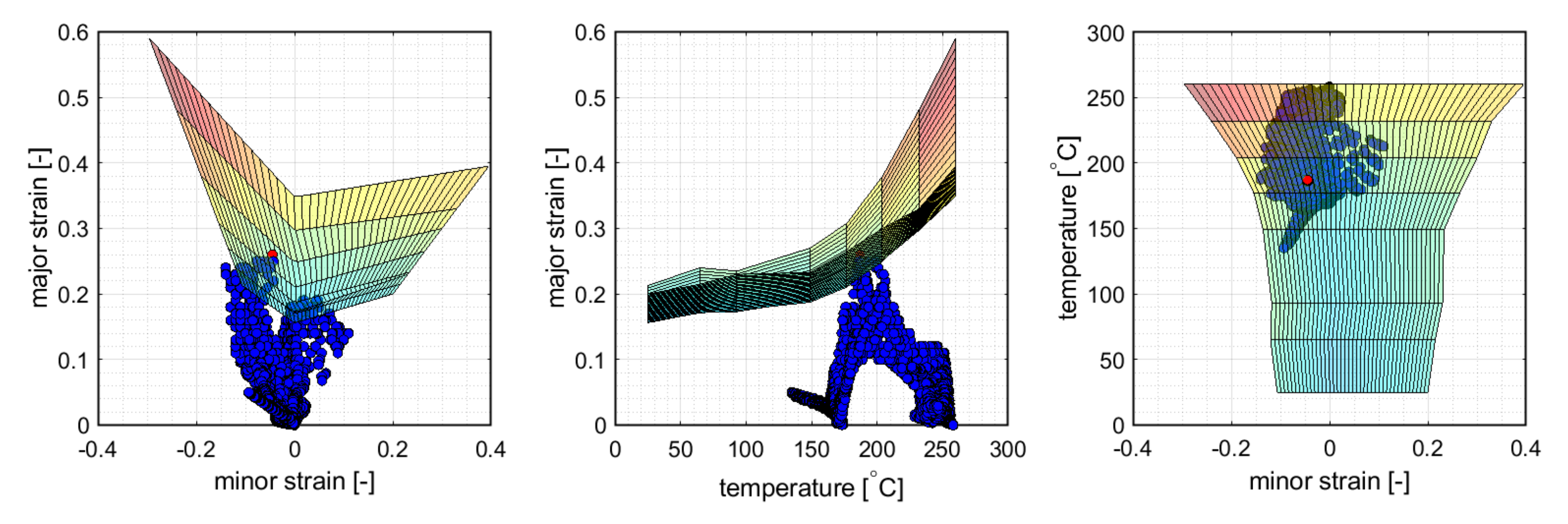
2.3. Forming Limit Curves
3. Damage Indicator Framework with Thermal Effects
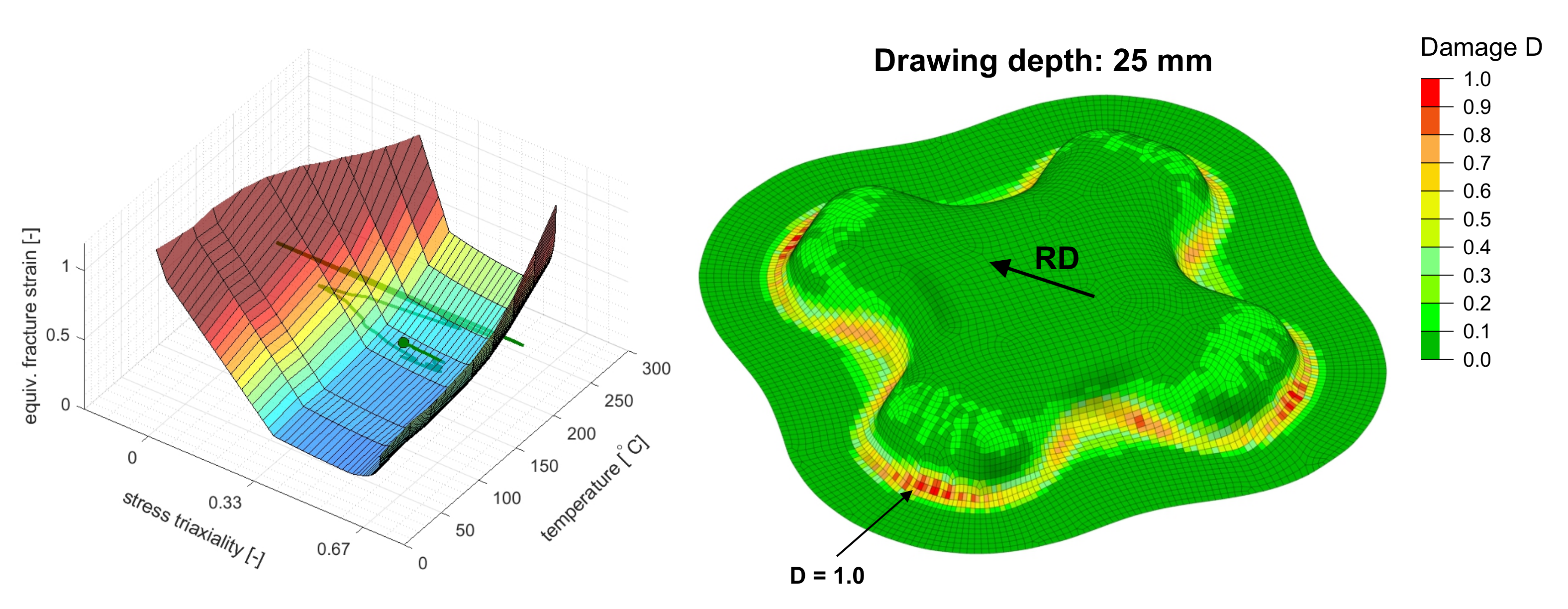
4. Coupled Thermo-Mechanical Finite Element Simulations of Warm Forming
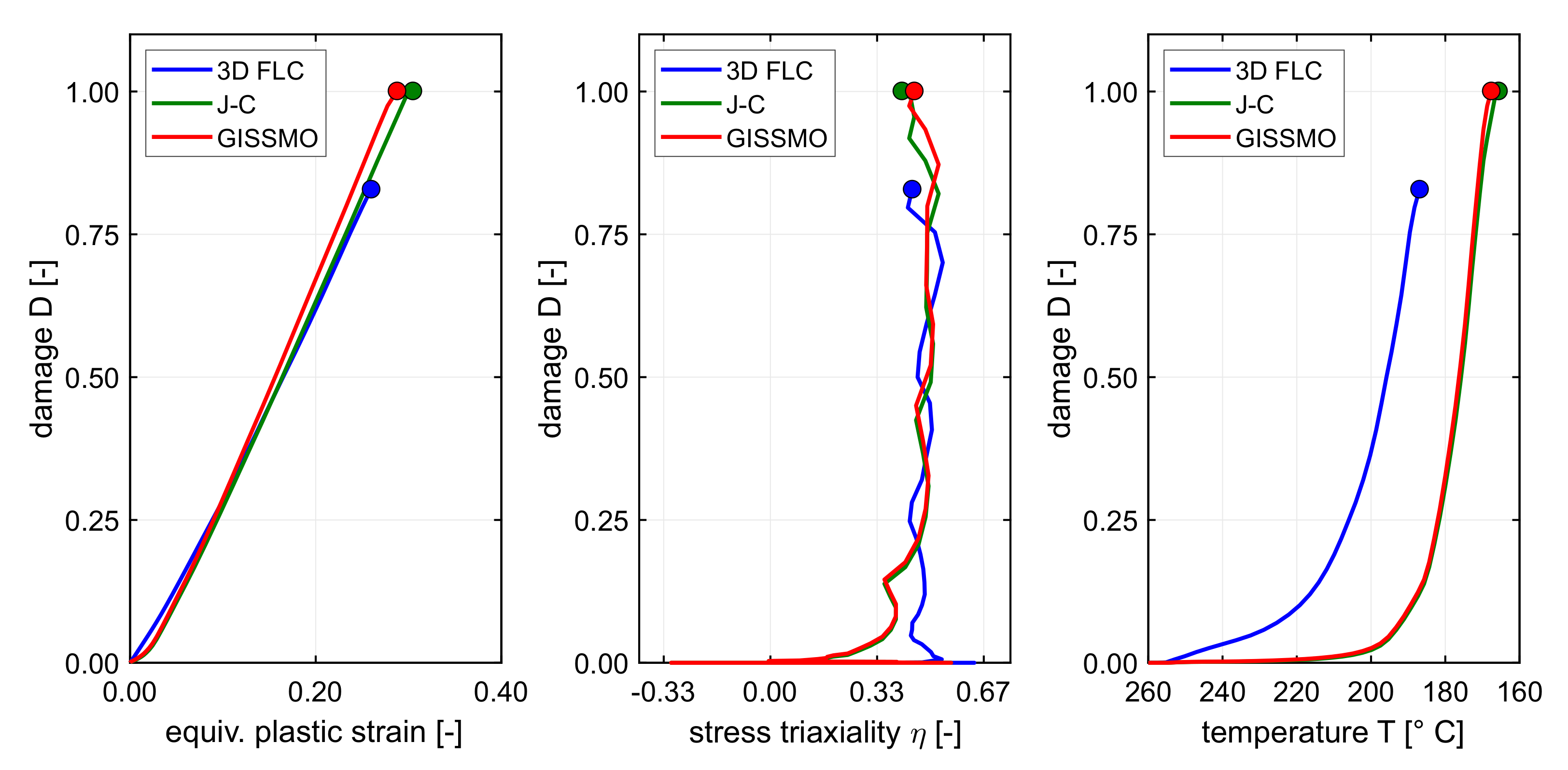
5. Results
5.1. Temperature Dependent 3D Forming Limit Diagram
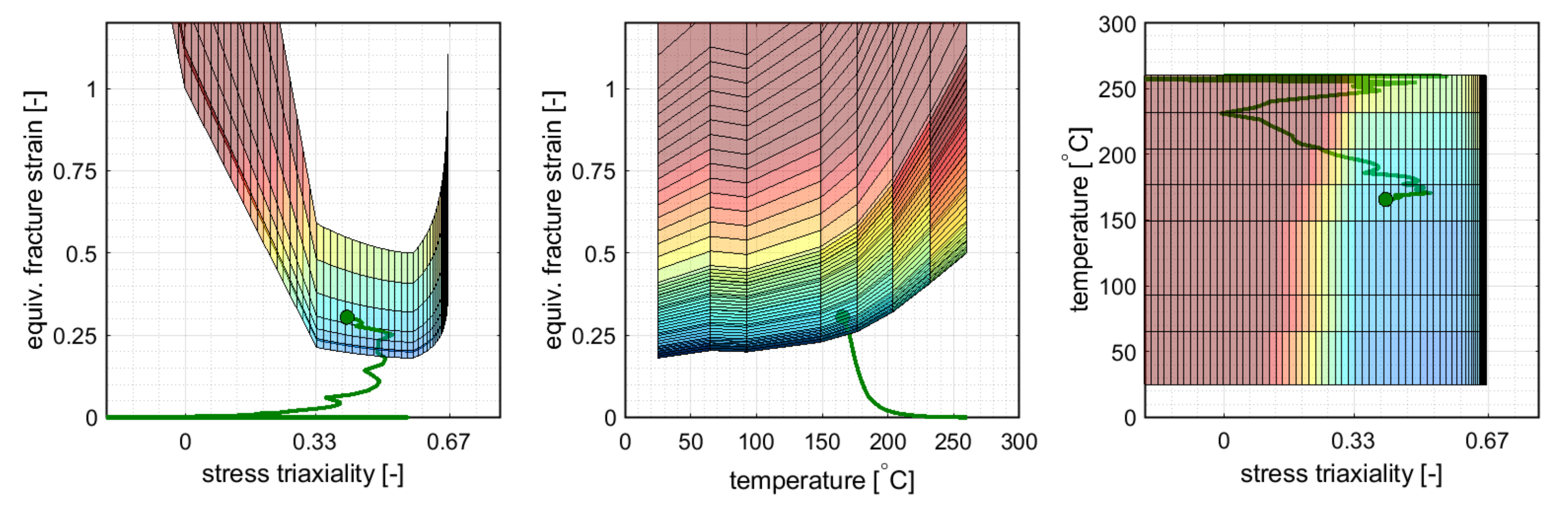
5.2. Johnson–Cook Based Approach
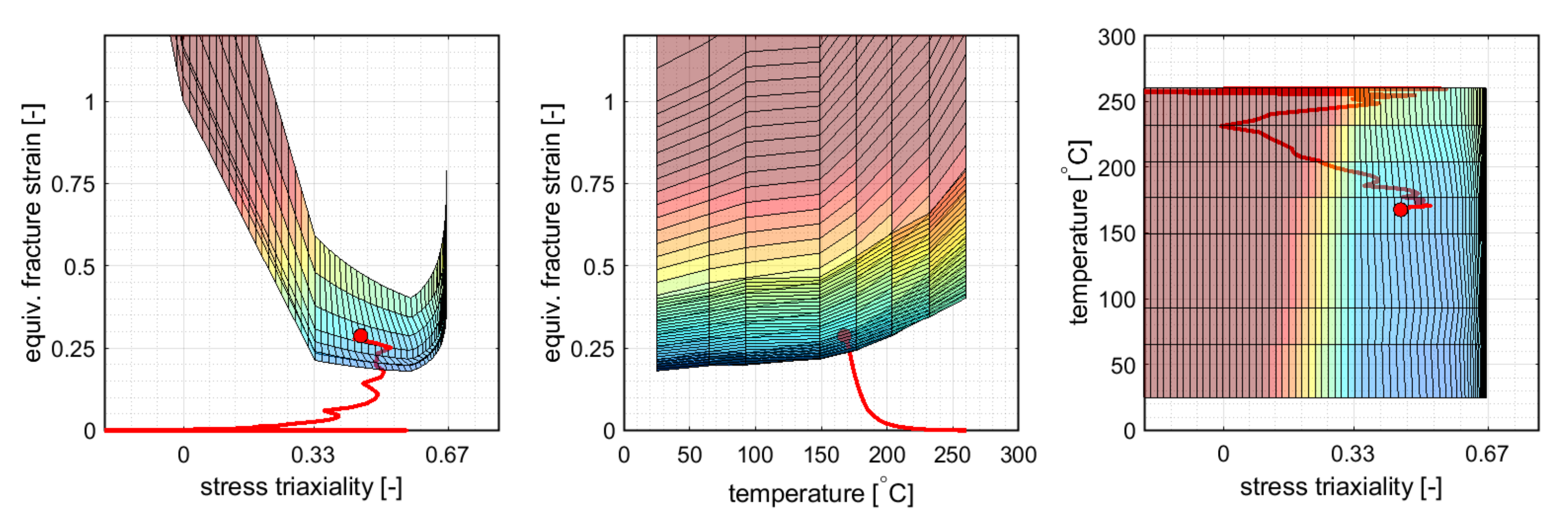
5.3. GISSMO with Temperature Effects
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AA | Aluminum Alloy |
| FLC | Forming Limit Curve |
| FLD | Forming Limit Diagram |
| FE | Finite Element |
| FEA | Finite Element Analysis |
| GISSMO | Generalized Incremental Stress State Dependent Damage Model |
| M-K | Marciniak–Kuczyński Model |
| ISO | International Organization for Standardization |
| CDM | Continuum Damage Mechanics |
| JC | Johnson and Cook Model |
| RD | Rolling Direction |
References
- Serrenho, A.C.; Norman, J.B.; Allwood, J.M. The impact of reducing car weight on global emissions: The future fleet in Great Britain. Philos. Trans. Ser. A Math. Phys. Eng. Sci. 2017, 375. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karbasian, H.; Tekkaya, A.E. A review on hot stamping. J. Mater. Process. Technol. 2010, 210, 2103–2118. [Google Scholar] [CrossRef]
- Zheng, K.; Politis, D.J.; Wang, L.; Lin, J. A review on forming techniques for manufacturing lightweight complex—shaped aluminium panel components. Int. J. Lightweight Mater. Manuf. 2018, 1, 55–80. [Google Scholar] [CrossRef]
- Mori, K.; Bariani, P.F.; Behrens, B.A.; Brosius, A.; Bruschi, S.; Maeno, T.; Merklein, M.; Yanagimoto, J. Hot stamping of ultra-high strength steel parts. CIRP Ann. 2017, 66, 755–777. [Google Scholar] [CrossRef]
- Volk, W.; Groche, P.; Brosius, A.; Ghiotti, A.; Kinsey, B.L.; Liewald, M.; Madej, L.; Min, J.; Yanagimoto, J. Models and modelling for process limits in metal forming. CIRP Ann. 2019, 68, 775–798. [Google Scholar] [CrossRef]
- Nakazima, K.; Kikuma, T.; Hasuka, K. Study on the Formability of Steel Sheets. Yawata Technical Report. 1968, pp. 141–154. Available online: https://www.researchgate.net/publication/284669125_Study_on_the_formability_of_steel_sheets (accessed on 29 August 2021).
- International Organization for Standardization. ISO 12004-2:2021 Metallic Materials—Determination of Forming-Limit Curves for Sheet and Strip—Part 2: Determination of Forming-Limit Curves in the Laboratory; International Organization for Standardization: Geneva, Switzerland, 2021; Volume 2, pp. 1–27. [Google Scholar]
- Banabic, D.; Kami, A.; Comsa, D.S.; Eyckens, P. Developments of the Marciniak-Kuczynski model for sheet metal formability: A review. J. Mater. Process. Technol. 2019, 116446. [Google Scholar] [CrossRef]
- Marciniak, Z. Stability of plastic shells under tension with kinematic boundary condition. Arch. Mech. Stosow. 1965, 17, 577–592. [Google Scholar]
- Merklein, M.; Lechler, J. Investigation of the thermo-mechanical properties of hot stamping steels. J. Mater. Process. Technol. 2006, 177, 452–455. [Google Scholar] [CrossRef]
- Abedrabbo, N.; Pourboghrat, F.; Carsley, J. Forming of AA5182-O and AA5754-O at elevated temperatures using coupled thermo-mechanical finite element models. Int. J. Plast. 2007, 23, 841–875. [Google Scholar] [CrossRef]
- Bariani, P.F.; Bruschi, S.; Ghiotti, A.; Turetta, A. Testing formability in the hot stamping of HSS. CIRP Ann. 2008, 57, 265–268. [Google Scholar] [CrossRef]
- Bariani, P.F.; Bruschi, S.; Ghiotti, A.; Michieletto, F. Hot stamping of AA5083 aluminium alloy sheets. CIRP Ann. 2013, 62, 251–254. [Google Scholar] [CrossRef]
- Jocham, D.; Sunderkötter, C.; Helmholz, R.; Marusch, H.E.; Volk, W. Failure Prediction in direct press hardening through virtual forming limit curves based on measurable material properties. In Proceedings of the 7th Forming Technology Forum, Enschede, The Nederlands, 15–16 September 2014; Hora, P., Ed.; University of Twente, Faculty of Engineering Technology: Enschede, The Netherlands, 2014. [Google Scholar]
- Panicker, S.S.; Singh, H.G.; Panda, S.K.; Dashwood, R. Characterization of Tensile Properties, Limiting Strains, and Deep Drawing Behavior of AA5754-H22 Sheet at Elevated Temperature. J. Mater. Eng. Perform. 2015, 24, 4267–4282. [Google Scholar] [CrossRef]
- Ying, L.; Liu, W.; Wang, D.; Hu, P. Parameter Calibration of GTN Damage Model and Formability Analysis of 22MnB5 in Hot Forming Process. J. Mater. Eng. Perform. 2017, 26, 5155–5165. [Google Scholar] [CrossRef]
- Krauer, J.; Hora, P. Enhanced material models for the process design of the temperature dependent forming behavior of metastable steels. Int. J. Mater. Form. 2012, 5, 361–370. [Google Scholar] [CrossRef]
- Cui, J.; Sun, G.; Xu, J.; Huang, X.; Li, G. A method to evaluate the formability of high-strength steel in hot stamping. Mater. Des. 2015, 77, 95–109. [Google Scholar] [CrossRef]
- Gao, H.; El Fakir, O.; Wang, L.; Politis, D.J.; Li, Z. Forming limit prediction for hot stamping processes featuring non-isothermal and complex loading conditions. Int. J. Mech. Sci. 2017, 131–132, 792–810. [Google Scholar] [CrossRef]
- Gao, H.; Politis, D.J.; Luan, X.; Ji, K.; Zhang, Q.; Zheng, Y.; Gharbi, M.; Wang, L. Forming limit prediction for AA7075 alloys under hot stamping conditions. J. Phys. Conf. Ser. 2017, 896, 012089. [Google Scholar] [CrossRef]
- Andrade, F.X.C.; Feucht, M.; Haufe, A.; Neukamm, F. An incremental stress state dependent damage model for ductile failure prediction. Int. J. Fract. 2016, 200, 127–150. [Google Scholar] [CrossRef]
- Lemaitre, J. A Continuous Damage Mechanics Model for Ductile Fracture. J. Eng. Mater. Technol. 1985, 107, 83–89. [Google Scholar] [CrossRef]
- Heibel, S.; Nester, W.; Clausmeyer, T.; Tekkaya, A.E. Influence of Different Yield Loci on Failure Prediction with Damage Models. J. Phys. Conf. Ser. 2017, 896, 012081. [Google Scholar] [CrossRef]
- Heibel, S.; Nester, W.; Clausmeyer, T.; Tekkaya, A.E. Failure assessment in sheet metal forming using a phenomenological damage model and fracture criterion: Experiments, parameter identification and validation. Procedia Eng. 2017, 207, 2066–2071. [Google Scholar] [CrossRef]
- Pérez Caro, L.; Schill, M.; Haller, K.; Odenberger, E.L.; Oldenburg, M. Damage and fracture during sheet-metal forming of alloy 718. Int. J. Mater. Form. 2020, 13, 15–28. [Google Scholar] [CrossRef] [Green Version]
- Camberg, A.A.; Tröster, T.; Bohner, F.; Tölle, J. Predicting plasticity and fracture of severe pre-strained EN AW-5182 by Yld2000 yield locus and Hosford-Coulomb fracture model in sheet forming applications. IOP Conf. Ser. Mater. Sci. Eng. 2019, 651, 012057. [Google Scholar] [CrossRef]
- Lin, J.; Mohamed, M.; Balint, D.; Dean, T.A. The development of continuum damage mechanics-based theories for predicting forming limit diagrams for hot stamping applications. Int. J. Damage Mech. 2014, 23, 684–701. [Google Scholar] [CrossRef]
- Bai, Q.; Mohamed, M.; Shi, Z.; Lin, J.; Dean, T. Application of a continuum damage mechanics (CDM)-based model for predicting formability of warm formed aluminium alloy. Int. J. Adv. Manuf. Technol. 2017, 88, 3437–3446. [Google Scholar] [CrossRef] [Green Version]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Buyuk, M. Development of A Tabulated Thermo-Viscoplastic Material Model with Regularized Failure for Dynamic Ductile Failure Prediction of Structures under Impact Loading. Ph.D. Thesis, The George Washington University, Ashburn, VA, USA, 2013. [Google Scholar]
- Haight, S.H. An Anisotropic and Asymmetric Material Model for Simulation of Metals Under Dynamic Loading. Ph.D. Thesis, George Mason University, Fairfax, VA, USA, 2016. [Google Scholar]
- Sengoz, K. Development of A Generalized Isotropic Yield Surface for Pressure Insensitive Metal Plasticity Considering Yield Strength Differential Effect in Tension, Compression and Shear Stress States. Ph.D. Thesis, The George Washington University, Washington, DC, USA, 2017. [Google Scholar]
- Roth, C.C.; Mohr, D. Effect of strain rate on ductile fracture initiation in advanced high strength steel sheets: Experiments and modeling. Int. J. Plast. 2014, 56, 19–44. [Google Scholar] [CrossRef]
- Erice, B.; Roth, C.C.; Mohr, D. Stress-state and strain-rate dependent ductile fracture of dual and complex phase steel. Mech. Mater. 2018, 116, 11–32. [Google Scholar] [CrossRef]
- Fras, T.; Roth, C.C.; Mohr, D. Dynamic perforation of ultra-hard high-strength armor steel: Impact experiments and modeling. Int. J. Impact Eng. 2019, 131, 256–271. [Google Scholar] [CrossRef]
- Abedrabbo, N.; Pourboghrat, F.; Carsley, J. Forming of aluminum alloys at elevated temperatures—Part 1: Material characterization. Int. J. Plast. 2006, 22, 314–341. [Google Scholar] [CrossRef]
- Barlat, F.; Lian, K. Plastic behavior and stretchability of sheet metals. Part I: A yield function for orthotropic sheets under plane stress conditions. Int. J. Plast. 1989, 5, 51–66. [Google Scholar] [CrossRef]
- Lee, Y.W. Fracture Prediction in Metal Sheets. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2005. [Google Scholar]
- Rahmaan, T.; Butcher, C.; Abedini, A.; Worswick, M. Effect of strain rate on shear properties and fracture characteristics of DP600 and AA5182-O sheet metal alloys. EPJ Web Conf. 2015, 94, 01033. [Google Scholar] [CrossRef] [Green Version]
- Noder, J.; George, R.; Butcher, C.; Worswick, M.J. Friction characterization and application to warm forming of a high strength 7000-series aluminum sheet. J. Mater. Process. Technol. 2021, 293, 117066. [Google Scholar] [CrossRef]






| T | in MPa | ||
|---|---|---|---|
| ≤93 C | 551.2–0.4623 | 0.3135–0.000363 | |
| >93 C | 641.3–1.829 | 0.3687–0.001065 |
| 25 C | 66 C | 93 C | 121 C | 148 C | 177 C | 204 C | 232 C | 260 C | |
|---|---|---|---|---|---|---|---|---|---|
| 0.8085 | 0.9193 | 0.9719 | 1.1244 | 1.0550 | 1.1315 | 1.1521 | 1.0687 | 1.0687 | |
| 1.0865 | 1.0533 | 1.1359 | 1.1260 | 1.1650 | 1.2576 | 1.1381 | 1.3006 | 1.3412 | |
| 0.9986 | 1.0754 | 1.0634 | 1.2488 | 1.2001 | 1.2377 | 1.2623 | 1.2007 | 1.2340 |
| Contact Pressure p [MPa] | [W/(m K)] |
|---|---|
| 0.5 | 2.6 |
| 2.5 | 3.17 |
| 5.0 | 3.76 |
| 7.5 | 4.24 |
| 10.0 | 4.61 |
| 12.5 | 4.89 |
| 15.0 | 5.09 |
| 17.5 | 5.22 |
| ≥20.0 | 5.23 |
| Property | Blank (AA5182-O) | Tooling (Steel) |
|---|---|---|
| Heat capacity [J/(kg · K)] | 900.0 | 450.0 |
| Thermal conductivity [W/(m · K)] | 130.0 | 30.0 |
| Density [kg/m] | 2780.0 | 7830.0 |
| Initial temperature [C] | 260.0 | 25.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Camberg, A.A.; Erhart, T.; Tröster, T. A Generalized Stress State and Temperature Dependent Damage Indicator Framework for Ductile Failure Prediction in Heat-Assisted Forming Operations. Materials 2021, 14, 5106. https://doi.org/10.3390/ma14175106
Camberg AA, Erhart T, Tröster T. A Generalized Stress State and Temperature Dependent Damage Indicator Framework for Ductile Failure Prediction in Heat-Assisted Forming Operations. Materials. 2021; 14(17):5106. https://doi.org/10.3390/ma14175106
Chicago/Turabian StyleCamberg, Alan A., Tobias Erhart, and Thomas Tröster. 2021. "A Generalized Stress State and Temperature Dependent Damage Indicator Framework for Ductile Failure Prediction in Heat-Assisted Forming Operations" Materials 14, no. 17: 5106. https://doi.org/10.3390/ma14175106






