Characterization of a Disordered above Room Temperature Skyrmion Material Co8Zn8Mn4
Abstract
:1. Introduction
2. Synthesis
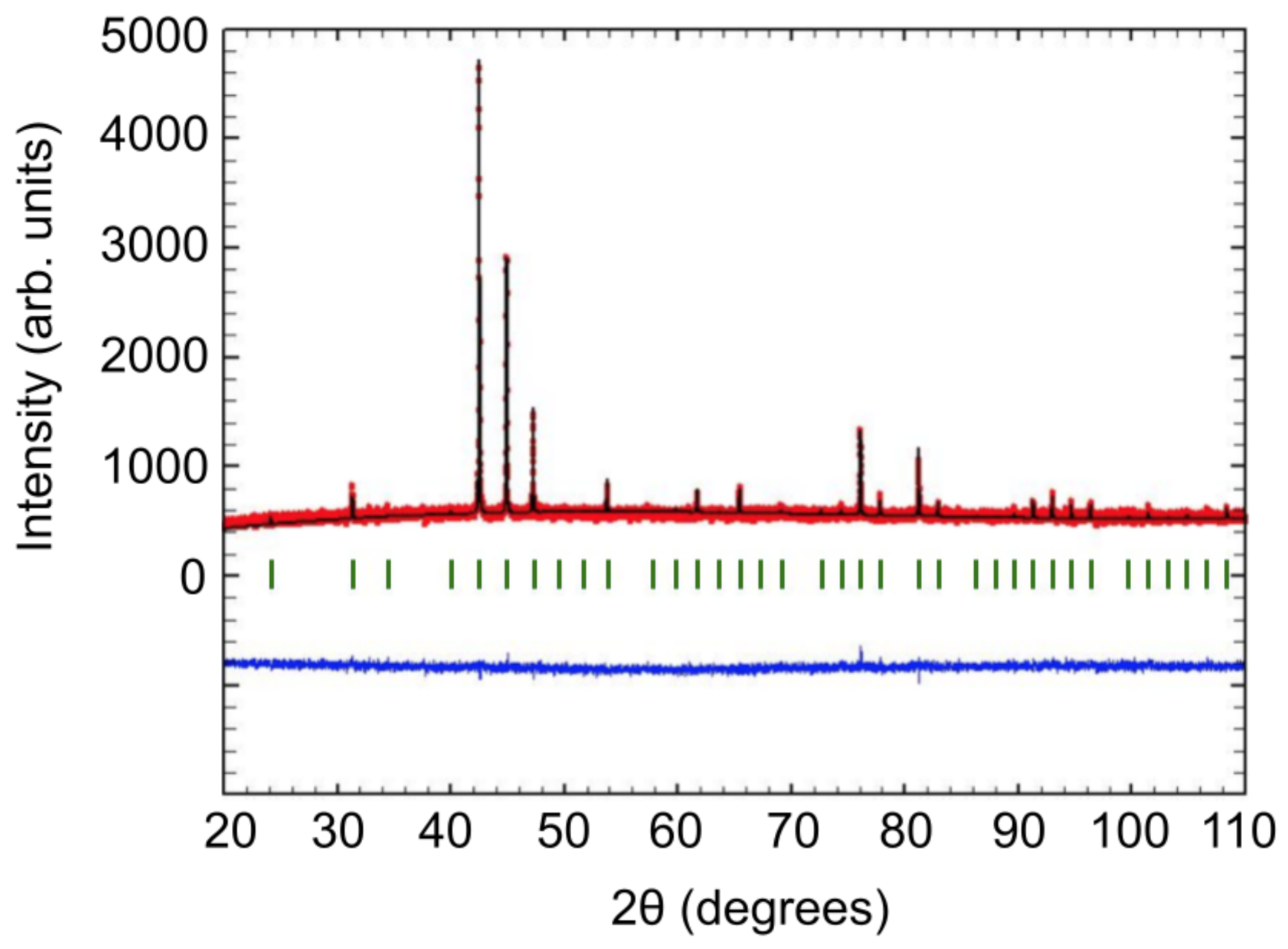
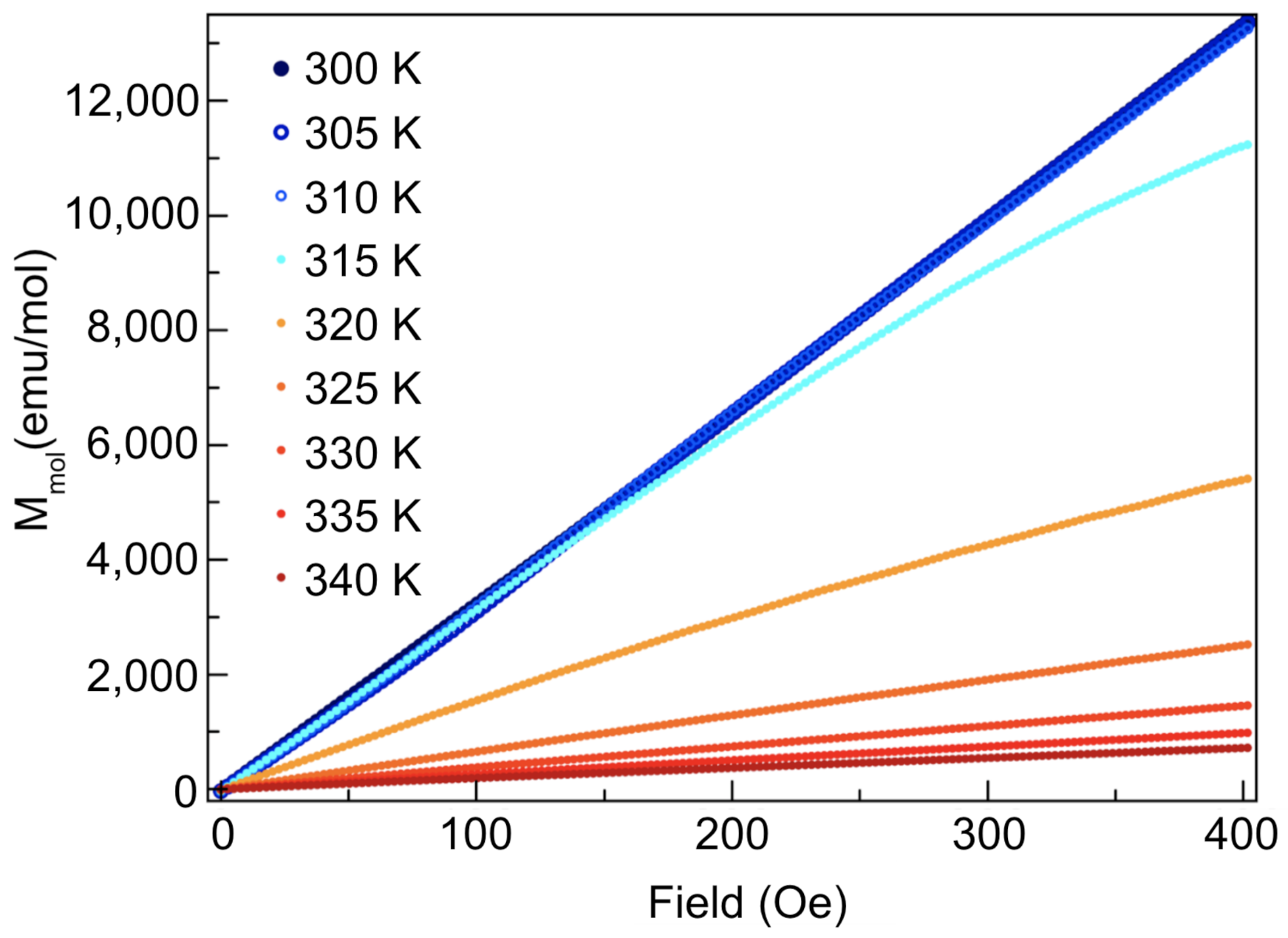
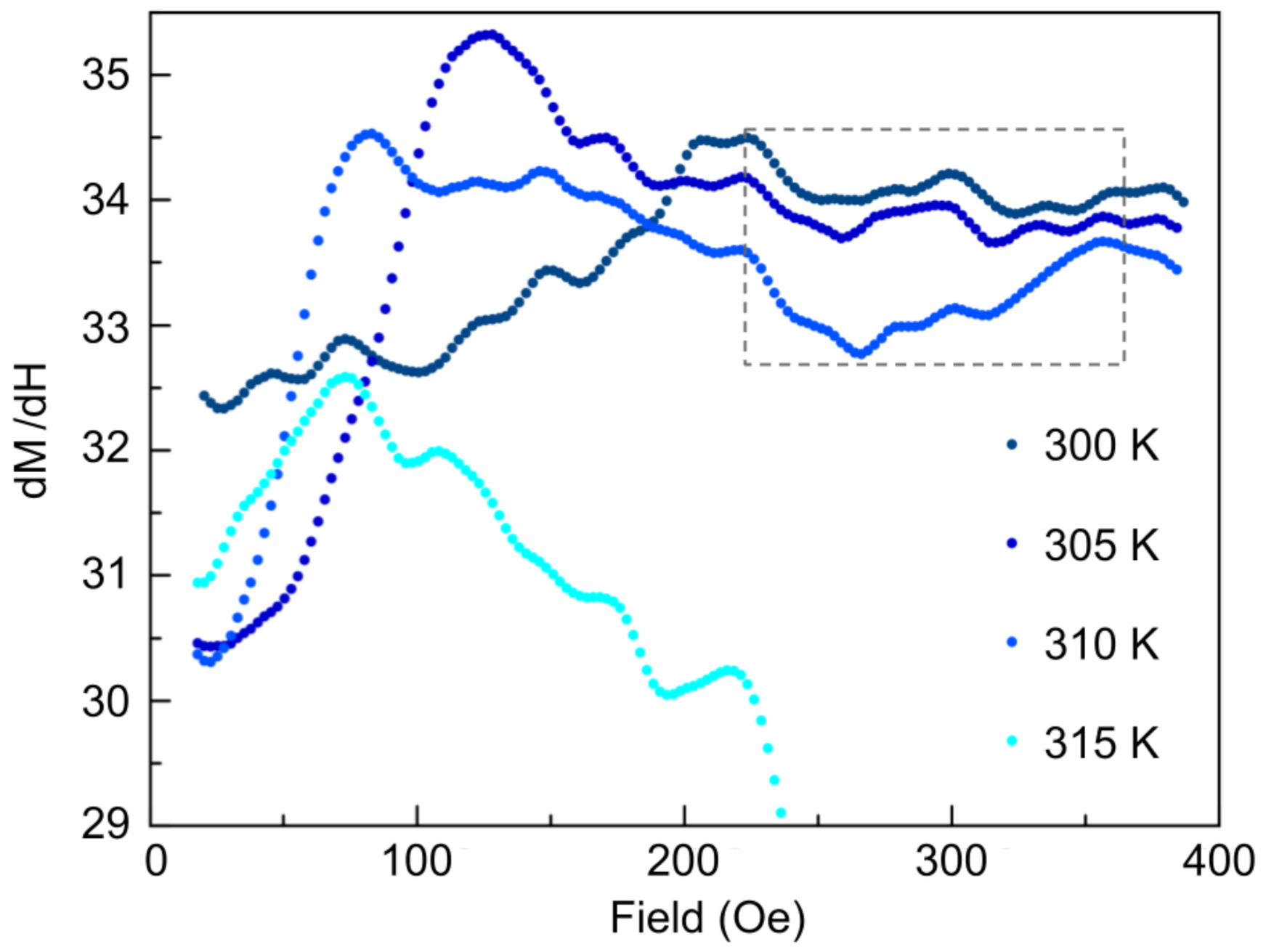
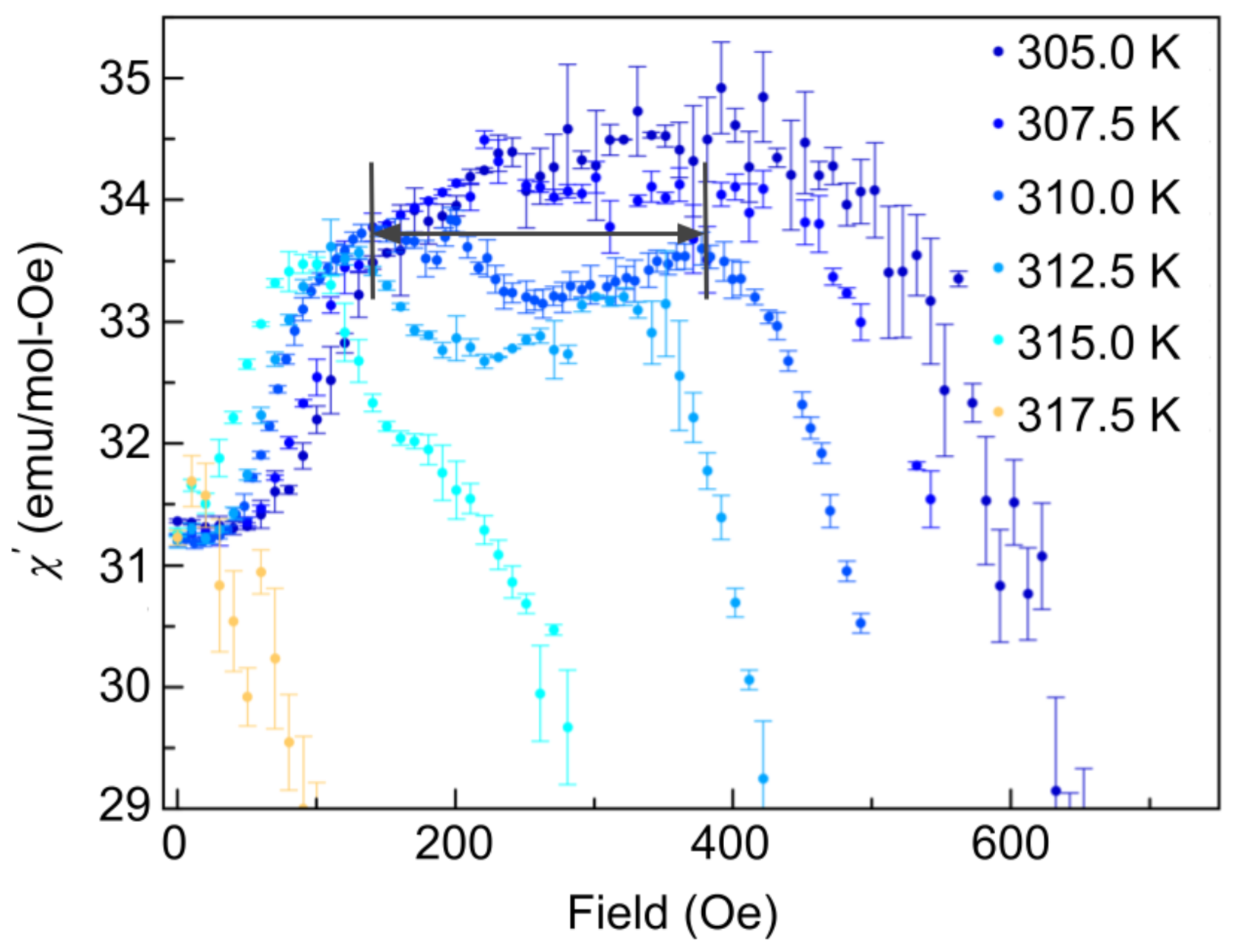
3. Characterization
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| TLA | Three letter acronym |
| LD | Linear dichroism |
References
- Lavrentovich, O.D. Topological defects in dispersed words and worlds around liquid crystals, or liquid crystal drops. Liq. Cryst. 1998, 24, 117–126. [Google Scholar] [CrossRef]
- Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2013 results. XXV. Searches for cosmic strings and other topological defects. Astron Astrophys. 2014, 571, A25. [Google Scholar]
- Mühlbauer, S.; Binz, B.; Jonietz, F.; Pfleiderer, C.; Rosch, A.; Neubauer, A.; Georgii, R.; Böni, P. Skyrmion lattice in a chiral magnet. Science 2009, 323, 915–919. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, X.Z.; Kanazawa, N.; Onose, Y.; Kimoto, K.; Zhang, W.Z.; Ishiwata, S.; Matsui, Y.; Tokura, Y. Near room-temperature formation of a skyrmion crystal in thin-films of the helimagnet FeGe. Nat. Mater. 2011, 10, 106–109. [Google Scholar] [CrossRef] [PubMed]
- Münzer, W.; Neubauer, A.; Adams, T.; Mühlbauer, S.; Franz, C.; Jonietz, F.; Georgii, R.; Böni, P.; Pedersen, B.; Schmidt, M.; et al. Skyrmion lattice in the doped semiconductor Fe1−xCoxSi. Phys. Rev. B 2010, 81, 041203. [Google Scholar] [CrossRef] [Green Version]
- Shibata, K.; Yu, X.Z.; Hara, T.; Morikawa, D.; Kanazawa, N.; Kimoto, K.; Ishiwata, S.; Matsui, Y.; Tokura, Y. Towards control of the size and helicity of skyrmions in helimagnetic alloys by spin–orbit coupling. Nat. Nanotechnol. 2013, 8, 723–728. [Google Scholar] [CrossRef] [Green Version]
- Skyrme, R. Skyrmion Makeover. Nature 2010, 465, 846. [Google Scholar]
- Schulz, T.; Ritz, R.; Bauer, A.; Halder, M.; Wagner, M.; Franz, C.; Pfleiderer, C.; Everschor, K.; Garst, M.; Rosch, A. Emergent electrodynamics of skyrmions in a chiral magnet. Nat. Phys. 2012, 8, 301–304. [Google Scholar] [CrossRef] [Green Version]
- Kanazawa, N.; Onose, Y.; Arima, T.; Okuyama, D.; Ohoyama, K.; Wakimoto, S.; Kakurai, K.; Ishiwata, S.; Tokura, Y. Large Topological Hall Effect in a Short-Period Helimagnet MnGe. Phys. Rev. Lett. 2011, 106, 156603. [Google Scholar] [CrossRef]
- Neubauer, A.; Pfleiderer, C.; Binz, B.; Rosch, A.; Ritz, R.; Niklowitz, P.G.; Böni, P. Topological Hall Effect in the A Phase of MnSi. Phys. Rev. Lett. 2009, 102, 186602. [Google Scholar] [CrossRef] [Green Version]
- Seki, S.; Yu, X.Z.; Ishiwata, S.; Tokura, Y. Observation of Skyrmions in a Multiferroic Material. Science 2012, 336, 198–201. [Google Scholar] [CrossRef] [Green Version]
- White, J.S.; Levatić, I.; Omrani, A.A.; Egetenmeyer, N.; Prša, K.; Živković, I.; Gavilano, J.L.; Kohlbrecher, J.; Bartkowiak, M.; Berger, H.; et al. Electric field control of the skyrmion lattice in Cu2OSeO3. J. Phys. Condens. Matter 2012, 24, 432201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ruff, E.; Widmann, S.; Lunkenheimer, P.; Tsurkan, V.; Bordács, S.; Kézsmárki, I.; Loidl, A. Multiferroicity and skyrmions carrying electric polarization in GaV4S8. J. Sci. Adv. 2015, 1, 1500916. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jonietz, F.; Mühlbauer, S.; Pfleiderer, C.; Neubauer, A.; Munzer, W.; Bauer, A.; Adams, T.; Georgii, R.; Boni, P.; Duine, R.A.; et al. Spin Transfer Torques in MnSi at Ultralow Current Densities. J. Sci. 2010, 330, 1648. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Everschor-Sitte, K.; Sitte, M. Real-space Berry phases: Skyrmion soccer. J. Appl. Phys. 2014, 115, 172602. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Ezawa, M.; Zhou, Y. Magnetic skyrmion logic gates: Conversion, duplication and merging of skyrmions. Sci. Rep. 2015, 5, 9400. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wiesendanger, R. Nanoscale magnetic skyrmions in metallic films and multilayers: A new twist for spintronics. Nat. Rev. Mater. 2016, 1, 16044. [Google Scholar] [CrossRef]
- Yu, X.Z.; Kanazawa, N.; Zhang, W.Z.; Nagai, T.; Hara, T.; Kimoto, K.; Matsui, Y.; Onose, Y.; Tokura, Y. Skyrmion flow near room temperature in an ultralow current density. Nat. Commun. 2012, 3, 988. [Google Scholar] [CrossRef] [Green Version]
- Iwasaki, J.; Mochizuki, M.; Nagaosa, N. Current-induced skyrmion dynamics in constricted geometries. Nat. Nanotechnol. 2013, 8, 742–747. [Google Scholar] [CrossRef] [Green Version]
- Sampaio, J.; Cros, V.; Rohart, S.; Thiaville, A.; Fert, A. Nucleation, stability and current-induced motion of isolated magnetic skyrmions in nanostructures. Nat. Nanotechnol. 2013, 8, 839–844. [Google Scholar] [CrossRef]
- Wilhelm, H.; Baenitz, M.; Schmidt, M.; Rößler, U.K.; Leonov, A.A.; Bogdanov, A.N. Precursor Phenomena at the Magnetic Ordering of the Cubic Helimagnet FeGe. Phys. Rev. Lett. 2011, 107, 127203. [Google Scholar] [CrossRef]
- Nagaosa, N.; Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotechnol. 2013, 8, 899–911. [Google Scholar] [CrossRef]
- Kézsmárki, I.; Bordács, S.; Milde, P.; Neuber, E.; Eng, L.M.; White, J.S.; Ronnow, H.M.; Dewhurst, C.D.; Mochizuki, M.; Yanai, K.; et al. Néel-type skyrmion lattice with confined orientation in the polar magnetic semiconductor GaV4S8. Nat. Mater. 2015, 14, 1116–1122. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tonomura, A.; Yu, X.; Yanagisawa, K.; Matsuda, T.; Onose, Y.; Kanazawa, N.; Park, H.S.; Tokura, Y. Real-Space Observation of Skyrmion Lattice in Helimagnet MnSi Thin Samples. Nano Lett. 2012, 12, 1673–1677. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.Z.; Onose, Y.; Kanazawa, N.; Park, J.H.; Han, J.H.; Matsui, Y.; Nagaosa, N.; Tokura, Y. Real-space observation of a two-dimensional skyrmion crystal. Nature 2010, 465, 901–904. [Google Scholar] [CrossRef]
- Nagase, T.; Komatsu, M.; So, Y.G.; Ishida, T.; Yoshida, H.; Kawaguchi, Y.; Tanaka, Y.; Saitoh, K.; Ikarashi, N.; Kuwahara, M.; et al. Smectic Liquid-Crystalline Structure of Skyrmions in Chiral Magnet Co8.5Zn7.5Mn4(110) Thin Film. Phys. Rev. Lett. 2019, 123, 137203. [Google Scholar] [CrossRef] [PubMed]
- Heinze, S.; von Bergmann, K.; Menzel, M.; Brede, J.; Kubetzka, A.; Wiesendanger, R.; Bihlmayer, G.; Blugel, S. Smectic Spontaneous atomic-scale magnetic skyrmion lattice in two dimensions. Nat. Phys. 2011, 7, 713–718. [Google Scholar] [CrossRef]
- Romming, N.; Hanneken, C.; Menzel, M.; Bickel, J.E.; Wolter, B.; von Bergmann, K.; Kubetzka, A.; Wiesendanger, R. Writing and Deleting Single Magnetic Skyrmions. Science 2013, 341, 636. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dupe, B.; Hoffmann, M.; Paillard, C.; Heinze, S. Tailoring magnetic skyrmions in ultra-thin transition metal films. Nat. Commun. 2014, 5, 4030. [Google Scholar] [CrossRef]
- Woo, S.; Litzius, K.; Krüger, B.; Im, M.Y.; Caretta, L.; Richter, K.; Mann, M.; Krone, A.; Reeve, R.M.; Weigand, M. Observation of room-temperature magnetic skyrmions and their current-driven dynamics in ultrathin metallic ferromagnets. Nat. Mater. 2016, 15, 501. [Google Scholar] [CrossRef]
- Dzyaloshinskii, I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 1958, 4, 241–255. [Google Scholar] [CrossRef]
- Moriya, T. Anisotropic Superexchange Interaction and Weak Ferromagnetism. Phys. Rev. 1960, 120, 91–98. [Google Scholar] [CrossRef]
- Tokunaga, Y.; Yu, X.Z.; White, J.S.; Rønnow, H.M.; Morikawa, D.; Taguchi, Y.; Tokura, Y. A new class of chiral materials hosting magnetic skyrmions beyond room temperature. Nat. Commun. 2015, 6, 7638. [Google Scholar] [CrossRef]
- Karube, K.; White, J.S.; Ukleev, V.; Dewhurst, C.D.; Cubitt, R.; Kikkawa, A.; Tokunaga, Y.; Rønnow, H.M.; Tokura, Y.; Taguchi, Y. Metastable skyrmion lattices governed by magnetic disorder and anisotropy in β-Mn-type chiral magnets. Phys. Rev. B 2020, 102, 064408. [Google Scholar] [CrossRef]
- Karube, K.; White, J.S.; Morikawa, D.; Bartkowiak, M.; Kikkawa, A.; Tokunaga, Y.; Arima, T.; Rønnow, H.M.; Tokura, Y.; Taguchi, Y. Skyrmion formation in a bulk chiral magnet at zero magnetic field and above room temperature. Phys. Rev. Mater. 2017, 1, 074405. [Google Scholar] [CrossRef] [Green Version]
- PreiBinger, M.; Karube, K.; Ehlers, D.; Szigeti, B.; Krug von Nidda, H.-A.; White, J.S.; Ukleev, V.; Rønnow, H.M.; Tokunaga, Y.; Kikkawa, A.; et al. Vital role of magnetocrystalline anisotropy in cubic chiral skyrmion hosts. NPJ Quantum Mater. 2021, 6, 2397–4648. [Google Scholar]
- Karube, K.; White, J.S.; Morikawa, D.; Dewhurst, C.D.; Cubitt, R.; Kikkawa, A.; Yu, X.; Tokunaga, Y.; Arima, T.; Rønnow, H.M.; et al. Disordered skyrmion phase stabilized by magnetic frustration in a chiral magnet. Sci. Adv. 2018, 4, eaar7043. [Google Scholar] [CrossRef] [Green Version]
- Yu, X.Z.; Koshibae, W.; Tokunaga, Y.; Shibata, K.; Taguchi, Y.; Nagaosa, N.; Tokura, Y. Transformation between meron and skyrmion topological spin textures in a chiral magnet. Nature 2018, 564, 95–98. [Google Scholar] [CrossRef]
- Nakajima, T.; Karube, K.; Ishikawa, Y.; Yonemura, M.; Reynolds, N.; White, J.S.; Rønnow, H.M.; Kikkawa, A.; Tokunaga, Y.; Taguchi, Y.; et al. Correlation between site occupancies and spin-glass transition in skyrmion host Co10− Zn10− Mnx. Phys. Rev. B 2019, 100, 064407. [Google Scholar] [CrossRef]
- Gilbert, D.A.; Grutter, A.J.; Neves, P.M.; Shu, G.J.; Zimanyi, G.; Maranville, B.B.; Chou, F.C.; Krycka, K.; Butch, N.P.; Huang, S. Precipitating ordered skyrmion lattices from helical spaghetti and granular powders. Phys. Rev. Mater. 2019, 3, 014408. [Google Scholar] [CrossRef]
- Nagata, S.; Keesom, P.H.; Harrison, H.R.A. Low-dc-field susceptibility of CuMn spin glass. Phys. Rev. B 1979, 19, 1633–1638. [Google Scholar] [CrossRef]
- Glinka, C.J.; Barker, J.G.; Hammouda, B.; Krueger, S.; Moyer, J.J.; Orts, W.J. The 30 m Small-Angle Neutron Scattering Instruments at the National Institute of Standards and Technology. J. Appl. Cryst. 2018, 31, 430–445. [Google Scholar] [CrossRef]
- Kline, S.R. Reduction and analysis of SANS and USANS data using IGOR Pro. J. Appl. Cryst. 2006, 39, 895–900. [Google Scholar] [CrossRef]
- Adams, T.; Mühlbauer, S.; Pfleiderer, C.; Jonietz, F.; Bauer, A.; Neubauer, A.; Georgii, R.; Böni, P.; Keiderling, U.; Everschor, K. Long-range crystalline nature of the skyrmion lattice in MnSi. Phys. Rev. Lett. 2011, 107, 217206. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Heacock, B.; Sarenac, D.; Cory, D.G.; Huber, M.G.; MacLean, J.P.W.; Miao, H.; Wen, H.; Pushin, D.A. Neutron sub-micrometre tomography from scattering data. IUCrJ 2018, 5, 893–900. [Google Scholar] [CrossRef] [PubMed]
- Nsofini, J.; Sarenac, D.; Wood, C.J.; Cory, D.G.; Arif, M.; Clark, C.W.; Huber, M.G.; Pushin, D.A. Spin-orbit states of neutron wave packets. Phys. Rev. A 2016, 94, 013605. [Google Scholar] [CrossRef] [Green Version]
- Sarenac, D.; Kapahi, C.; Wangchun, C.; Clark, C.W.; Corey, D.G.; Huber, M.G.; Taminiau, I.; Zhernenkov, K.; Pushin, D.A. Generation and detection of spin-orbit coupled neutron beams. Proc. Natl. Acad. Sci. USA 2019, 116, 20328–20332. [Google Scholar] [CrossRef] [Green Version]
- Sarenac, D.; Nsofini, J.; Hincks, I.; Arif, M.; Clark, C.W.; Cory, D.G.; Huber, M.G.; Pushin, D.A. Methods for preparation and detection of neutron spin-orbit states. New J. Phys. 2018, 20, 103012. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Henderson, M.E.; Beare, J.; Sharma, S.; Bleuel, M.; Clancy, P.; Cory, D.G.; Huber, M.G.; Marjerrison, C.A.; Pula, M.; Sarenac, D.; et al. Characterization of a Disordered above Room Temperature Skyrmion Material Co8Zn8Mn4. Materials 2021, 14, 4689. https://doi.org/10.3390/ma14164689
Henderson ME, Beare J, Sharma S, Bleuel M, Clancy P, Cory DG, Huber MG, Marjerrison CA, Pula M, Sarenac D, et al. Characterization of a Disordered above Room Temperature Skyrmion Material Co8Zn8Mn4. Materials. 2021; 14(16):4689. https://doi.org/10.3390/ma14164689
Chicago/Turabian StyleHenderson, Melissa E., James Beare, Sudarshan Sharma, Markus Bleuel, Pat Clancy, David G. Cory, Michael G. Huber, Casey A. Marjerrison, Mathew Pula, Dusan Sarenac, and et al. 2021. "Characterization of a Disordered above Room Temperature Skyrmion Material Co8Zn8Mn4" Materials 14, no. 16: 4689. https://doi.org/10.3390/ma14164689





