Characterization of Ultrasonic Bubble Clouds in A Liquid Metal by Synchrotron X-ray High Speed Imaging and Statistical Analysis
Abstract
:1. Introduction
2. Experiments
2.1. Alloy and Sample Preparation
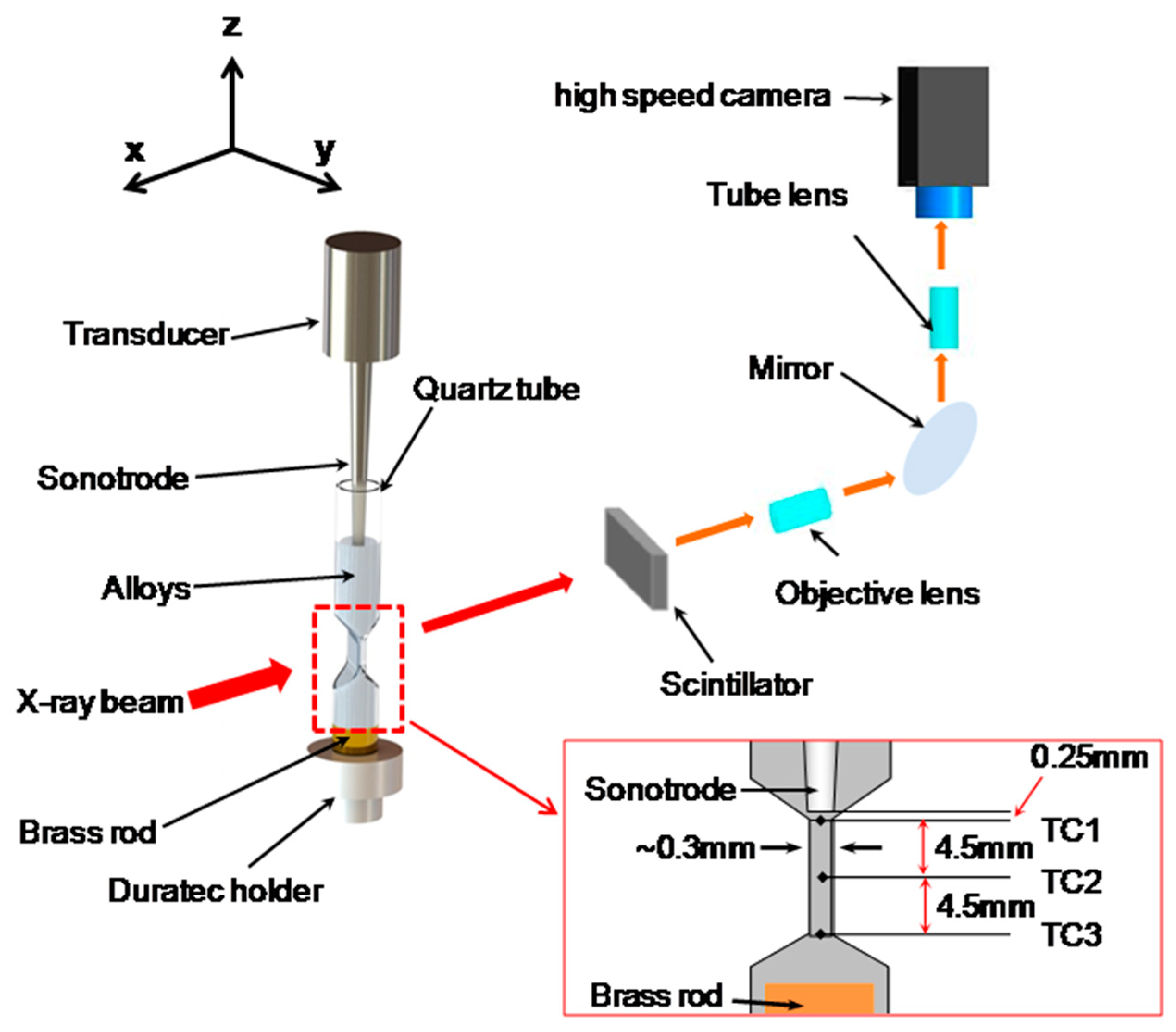
2.2. High-Speed Synchrotron X-ray Imaging
3. Image Processing and Data Analysis
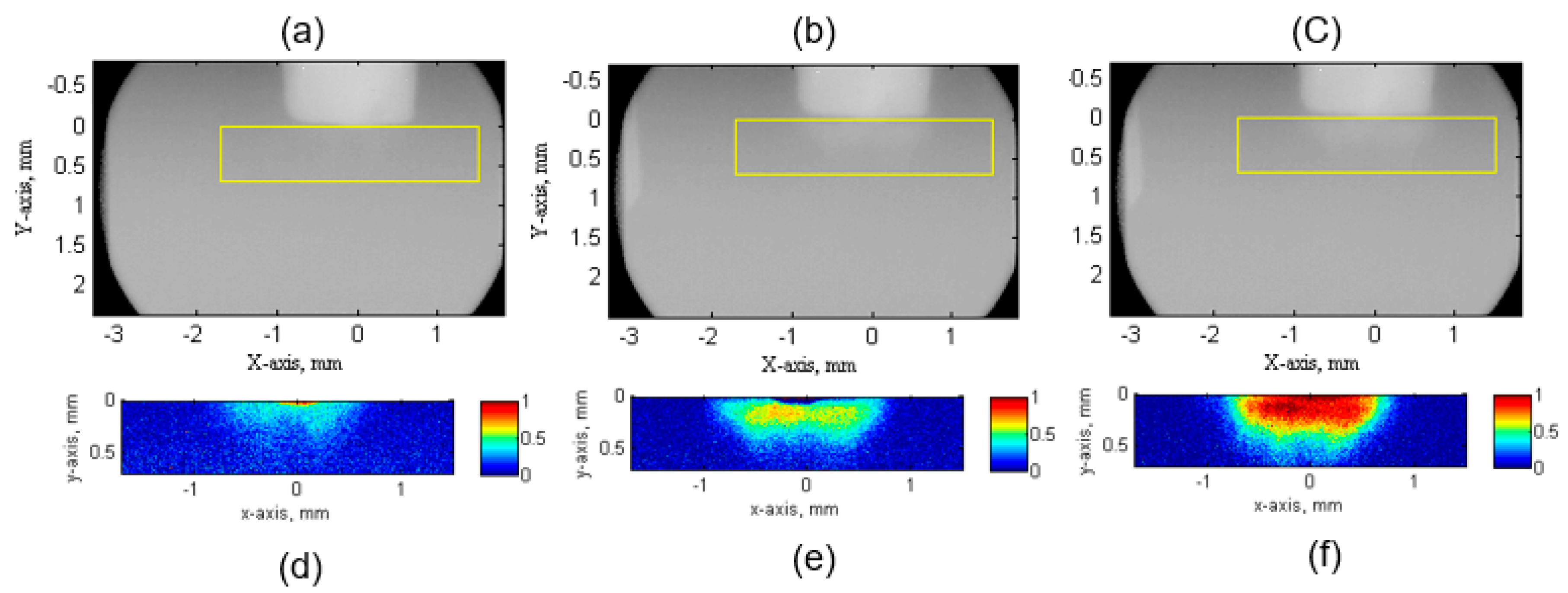
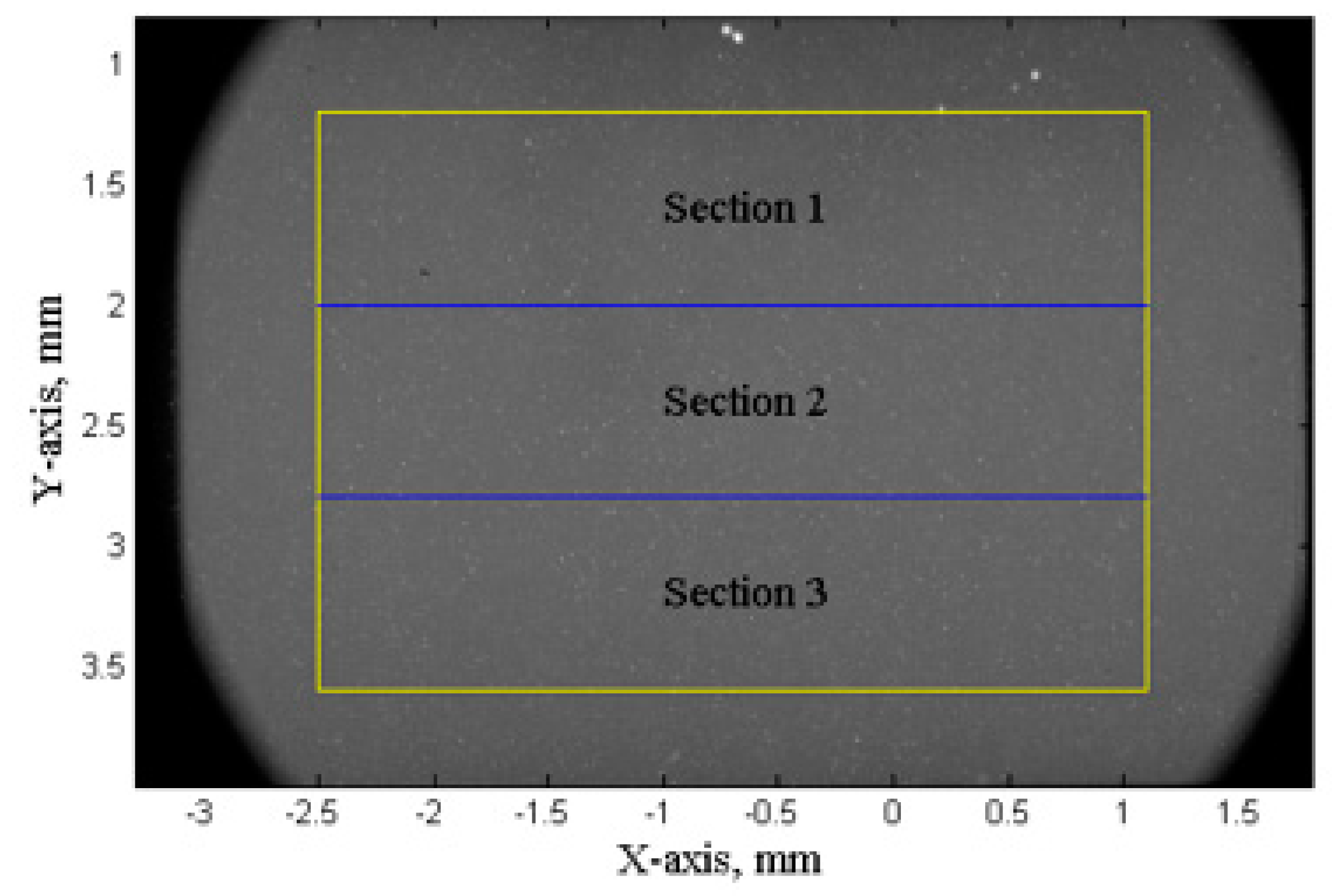
3.1. Bubble Volume Fraction in the Chaotic Cavitation Region
3.2. Bubble Volume Fraction in the Quasi Static Cavitation Region
4. Experimental Results
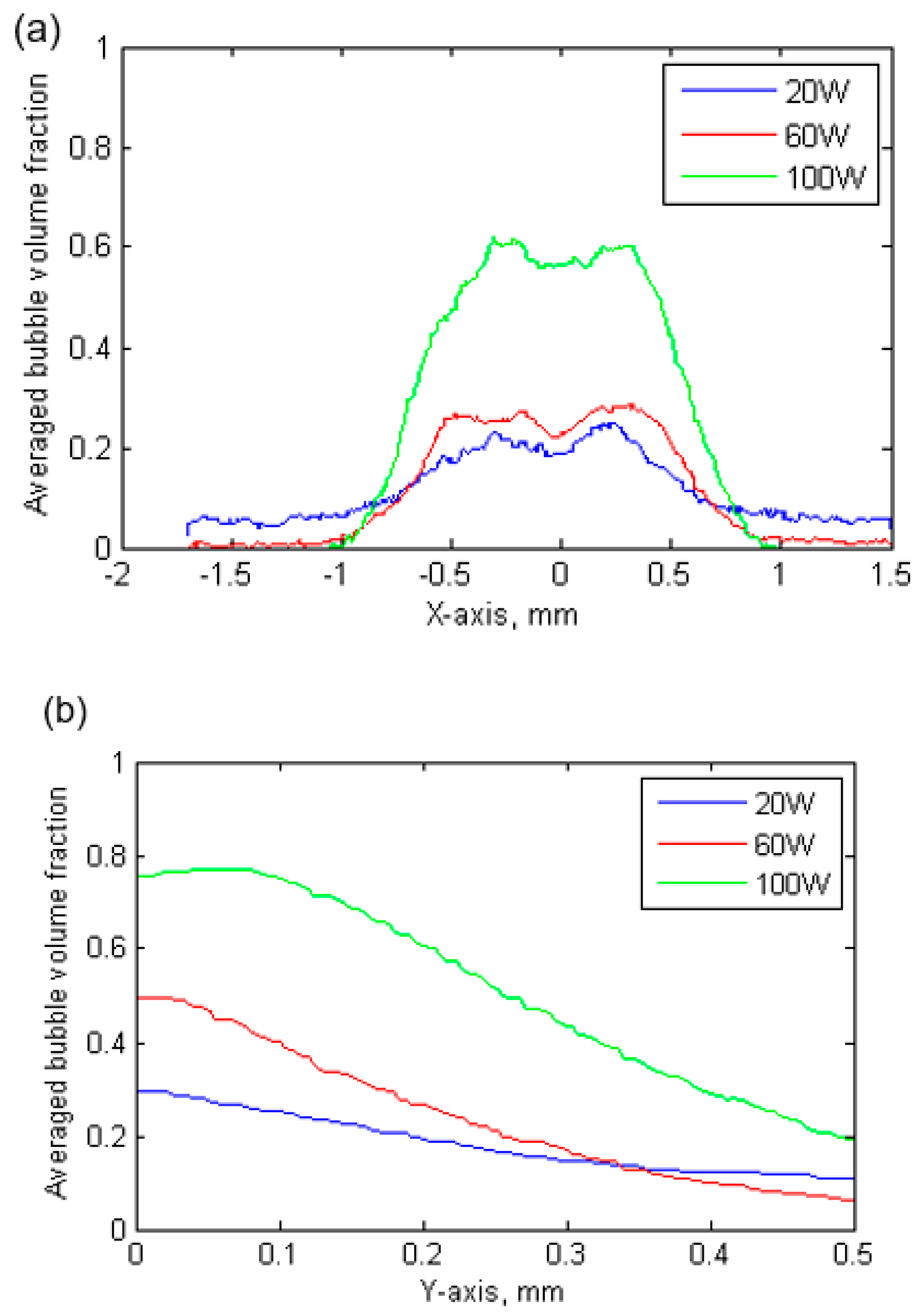
4.1. Bubble Cloud in the Chaotic Cavitation Region
4.2. Bubble Cloud in the Quasi-Static Cavitation Region
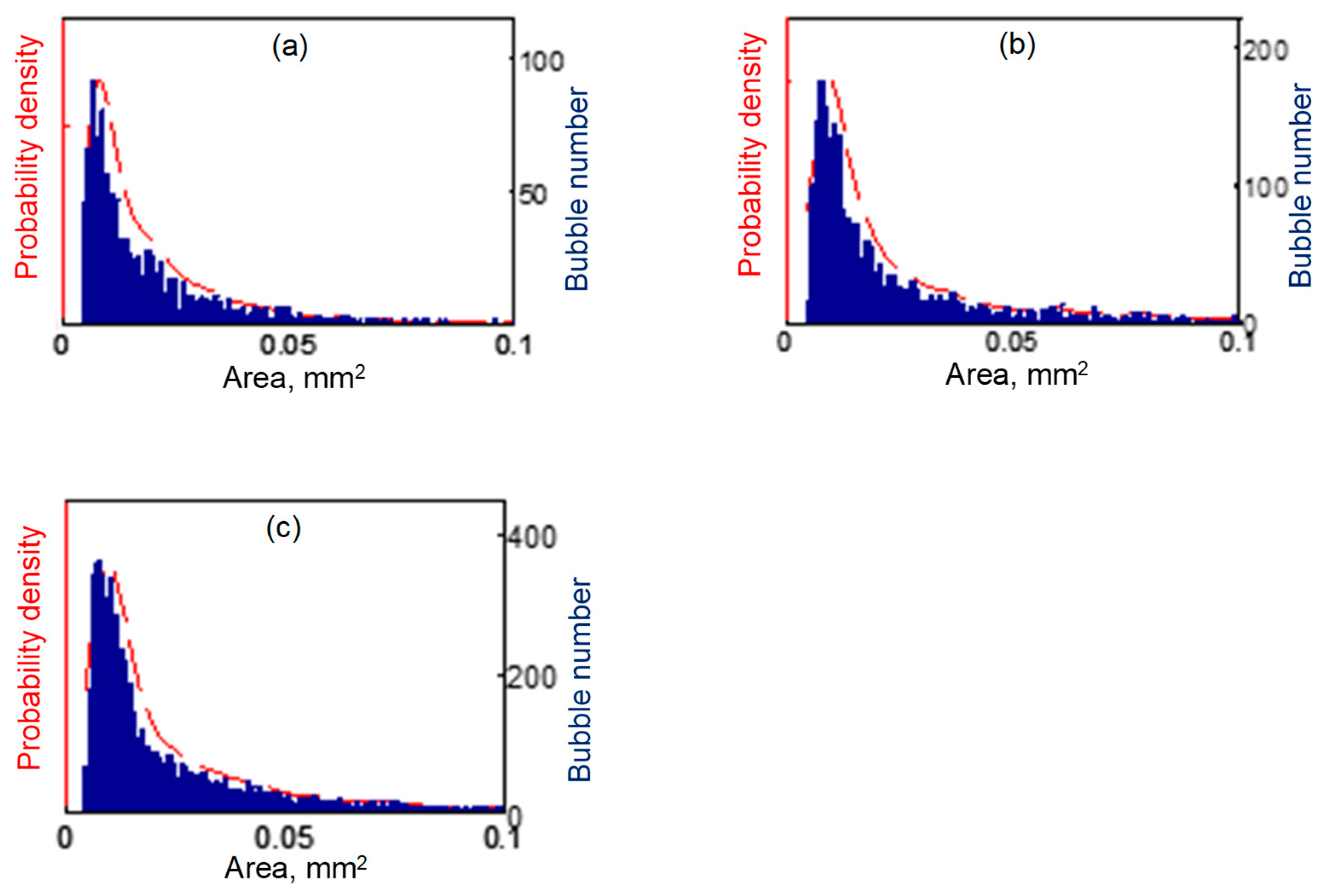
4.2.1. Bubble Size Distribution
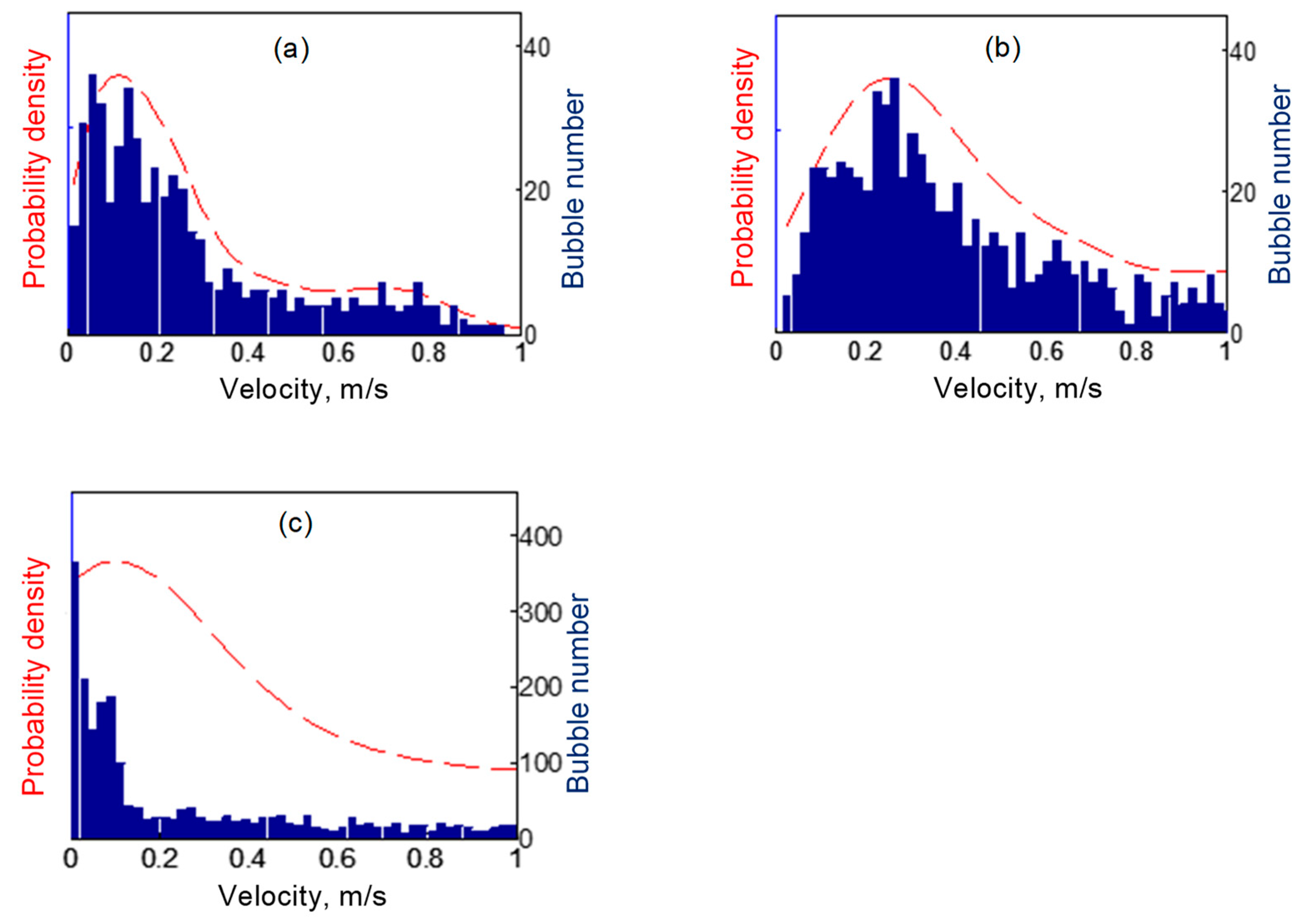
4.2.2. Bubble Velocity Distribution
4.3. Limitation of the Imaging Method
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Harvey, G.; Gachagan, A.; Mutasa, T. Review of High-Power Ultrasound-Industrial Applications and Measurement Methods. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 61, 481–495. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mason, T.J. Sonochemistry; Oxfor University Press Inc.: New York, NY, USA, 1999. [Google Scholar]
- Eskin, G.I.; Eskin, D.G. Ultrasonic Treatment of Light Alloy Melts, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Eskin, D.G.; Mi, J. Solidification Processing of Metal Alloys under External Fields; Springer Nature Switzerland AG: Basel, Switzerland, 2018. [Google Scholar] [CrossRef]
- Rayleigh, L. On the pressure developed in a liquid during the collapse of a spherical cavity. Philos. Mag. Ser. 1917, 6, 94–98. [Google Scholar] [CrossRef]
- Ackerman, E. Pressure Thresholds for biologically active cavitation. J. Appl. Phys. 1953, 24, 1371–1373. [Google Scholar] [CrossRef]
- Flynn, H.G. Physical Acoustics; Mason, W.P., Ed.; Academic Press: New York, NY, USA, 1964; Volume 1, pp. 58–172. [Google Scholar]
- Lauterborn, W.; Kurz, T. Physics of bubble oscillations. Rep. Prog. Phys. 2010, 73, 106501. [Google Scholar] [CrossRef]
- Zeqiri, B.; Gelat, P.N.; Hodnett, M.; Lee, N.D. A novel sensor for monitoring acoustic cavitation. Part I: Concept, theory, and prototype development. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2003, 50, 1342–1350. [Google Scholar] [CrossRef]
- Harris, G.R.; Preston, R.C.; DeReggi, A.S. The impact of piezoelectric PVDF on medical ultrasound exposure measurements, standards, and regulations. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2000, 47, 1321–1335. [Google Scholar] [CrossRef]
- Moussatov, A.; Granger, C.; Dubus, B. Cone-like bubble formation in ultrasonic cavitation field. Ultrason. Sonochem. 2003, 10, 191–195. [Google Scholar] [CrossRef]
- Sijl, J.; Vos, H.J.; Rozendal, T.; de Jong, N.; Lohse, D.; Versluis, M. Combined optical and acoustical detection of single microbubble dynamics. J. Acoust. Soc. Am. 2011, 130, 3271–3281. [Google Scholar] [CrossRef]
- Reibold, R.; Molkenstruck, W. Light-Diffraction Tomography Applied to the Investigation of Ultrasonic Fields. 1. Continous Waves. Acustica 1984, 56, 180–192. [Google Scholar]
- Reibold, R. Light-Diffraction Tomography Applied to the Investigation of Ultrasonic Fields. 2. Standing Waves. Acustica 1987, 63, 283–289. [Google Scholar]
- Price, G.J. Current Trends in Sonochemistry; The Royal Society of Chemistry: Cambridge, UK, 1992. [Google Scholar]
- Price, G.J. ICA 2010—Incorporating Proceedings of the 2010 Annual Conference of the Australian Acoustical Society. In Proceedings of the 20th International Congress on Acoustics 2010, Sydney, Australia, 23–27 August 2010. [Google Scholar]
- Ohl, S.W.; Klaseboer, E.; Khoo, B.C. Bubbles with shock waves and ultrasound: A review. Interface Focus 2015, 5, 15. [Google Scholar] [CrossRef] [PubMed]
- Eskin, G.I. Principles of ultrasonic treatment: Application for light alloys melts. Adv. Perform. Mater. 1997, 4, 223–232. [Google Scholar] [CrossRef]
- Wang, F.; Eskin, D.; Connolley, T.; Mi, J.W. Effect of ultrasonic melt treatment on the refinement of primary Al3Ti intermetallic in an Al-0.4Ti alloy. J. Cryst. Growth 2016, 435, 24–30. [Google Scholar] [CrossRef] [Green Version]
- Mi, J.; Tan, D.; Lee, T. In Situ Synchrotron X-ray Study of Ultrasound Cavitation and Its Effect on Solidification Microstructures. Metall. Mater. Trans. B 2014, 46, 1615–1619. [Google Scholar] [CrossRef] [Green Version]
- Tan, D.; Mi, J. Light Metals Technology 2013; Stone, I., McKay, B., Fan, Z.Y., Eds.; Trans Tech Publications Ltd.: Zürich, Switzerland, 2013; pp. 230–234. [Google Scholar]
- Tan, D.; Lee, T.L.; Khong, J.C.; Connolley, T.; Fezzaa, K.; Mi, J. High Speed Synchrotron X-ray Imaging Studies of the Ultrasound Shockwave and Enhanced Flow during Metal Solidification Processes. Metall. Mater. Trans. A 2015, 46, 2851–2861. [Google Scholar] [CrossRef]
- Wang, F.; Eskin, D.; Mi, J.; Wang, C.; Koe, B.; King, A.; Reinhard, C.; Connolley, T. A synchrotron X-radiography study of the fragmentation and refinement of primary intermetallic particles in an Al-35Cu alloy induced by ultrasonic melt processing. Acta Mater. 2017, 141, 142–153. [Google Scholar] [CrossRef]
- Wang, B.; Tan, D.; Lee, T.L.; Jia, C.K.; Wang, F.; Eskin, D.; Connolley, T.; Fezzaa, K.; Mi, J. Ultrafast synchrotron X-ray imaging studies of microstructure fragmentation in solidification under ultrasound. Acta Mater. 2017, 144, 505–515. [Google Scholar] [CrossRef]
- Furtauer, S.; Li, D.; Cupid, D.; Flandorfer, H. The Cu-Sn phase diagram, Part I: New experimental results. Intermetallics 2013, 34, 142–147. [Google Scholar] [CrossRef] [Green Version]
- Tan, D. In Situ Ultrafast Synchrotron X-ray Imaging Studies of the Dynamics of Ultrasonic Bubbles in Liquids. Ph.D. Thesis, University of Hull, Hull, UK, August 2015. [Google Scholar]
- Drakopoulos, M.; Connolley, T.; Reinhard, C.; Atwood, R.; Magdysyuk, O.; Vo, N.; Hart, M.; Connor, L.; Humphreys, B.; Howell, G.; et al. I12: The Joint Engineering, Environment and Processing (JEEP) beamline at Diamond Light Source. J. Synchrotron Radiat. 2015, 22, 828–838. [Google Scholar] [CrossRef]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Meth. 2012, 9, 671–675. [Google Scholar] [CrossRef]
- Gullikson, E.M. X-ray Data Booklet; Thompson, A.C., Ed.; Centre for X-ray Optics & Advanced Light Source: Berkeley, CA, USA, 2009; pp. 1–43. [Google Scholar]
- Epanechnikov, V.A. Non-Parametric Estimation of a Multivariate Probability Density. Theory Probab. Its Appl. 1969, 14, 153–158. [Google Scholar] [CrossRef]


| Position | Thickness of Liquid Metal (mm) | Grey Level |
|---|---|---|
| g0 | 0 | 145 |
| g1 | 2 | 89 |
| g2 | 0.3 | 97 |
| Ultrasound Power (W) | Ultrasonic Bubble Cloud * FWHM in X-axis (mm) | Ultrasonic Bubble Cloud FWHM in Y-axis (mm) | Maximum Averaged Bubble Volume Fraction in X-axis | Maximum Averaged Bubble Volume Fraction in Y-axis |
|---|---|---|---|---|
| 20 | 1.15 | 0.30 | 0.22 | 0.31 |
| 60 | 1.26 | 0.30 | 0.38 | 0.52 |
| 100 | 1.26 | 0.34 | 0.71 | 0.78 |
| Ultrasound Power (W) | Bubble Size at Maximum Probability Density (mm2) | Bubble Velocity at Maximum Probability Density (m/s) |
|---|---|---|
| 20 | 0.0078 | 0.15 m/s |
| 60 | 0.0098 | 0.28 m/s |
| 100 | 0.0096 | 0.17 m/s |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Connolley, T.; Tzanakis, I.; Eskin, D.; Mi, J. Characterization of Ultrasonic Bubble Clouds in A Liquid Metal by Synchrotron X-ray High Speed Imaging and Statistical Analysis. Materials 2020, 13, 44. https://doi.org/10.3390/ma13010044
Wang C, Connolley T, Tzanakis I, Eskin D, Mi J. Characterization of Ultrasonic Bubble Clouds in A Liquid Metal by Synchrotron X-ray High Speed Imaging and Statistical Analysis. Materials. 2020; 13(1):44. https://doi.org/10.3390/ma13010044
Chicago/Turabian StyleWang, Chuangnan, Thomas Connolley, Iakovos Tzanakis, Dmitry Eskin, and Jiawei Mi. 2020. "Characterization of Ultrasonic Bubble Clouds in A Liquid Metal by Synchrotron X-ray High Speed Imaging and Statistical Analysis" Materials 13, no. 1: 44. https://doi.org/10.3390/ma13010044





