Conductomeric Evaluation of the Release Kinetics of Active Substances from Pharmaceutical Preparations Containing Iron Ions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Dissolution Test
2.3. Electric Conductivity Method Conditions
2.4. Calculations
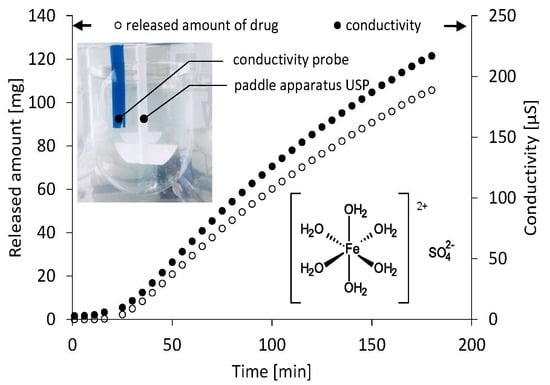
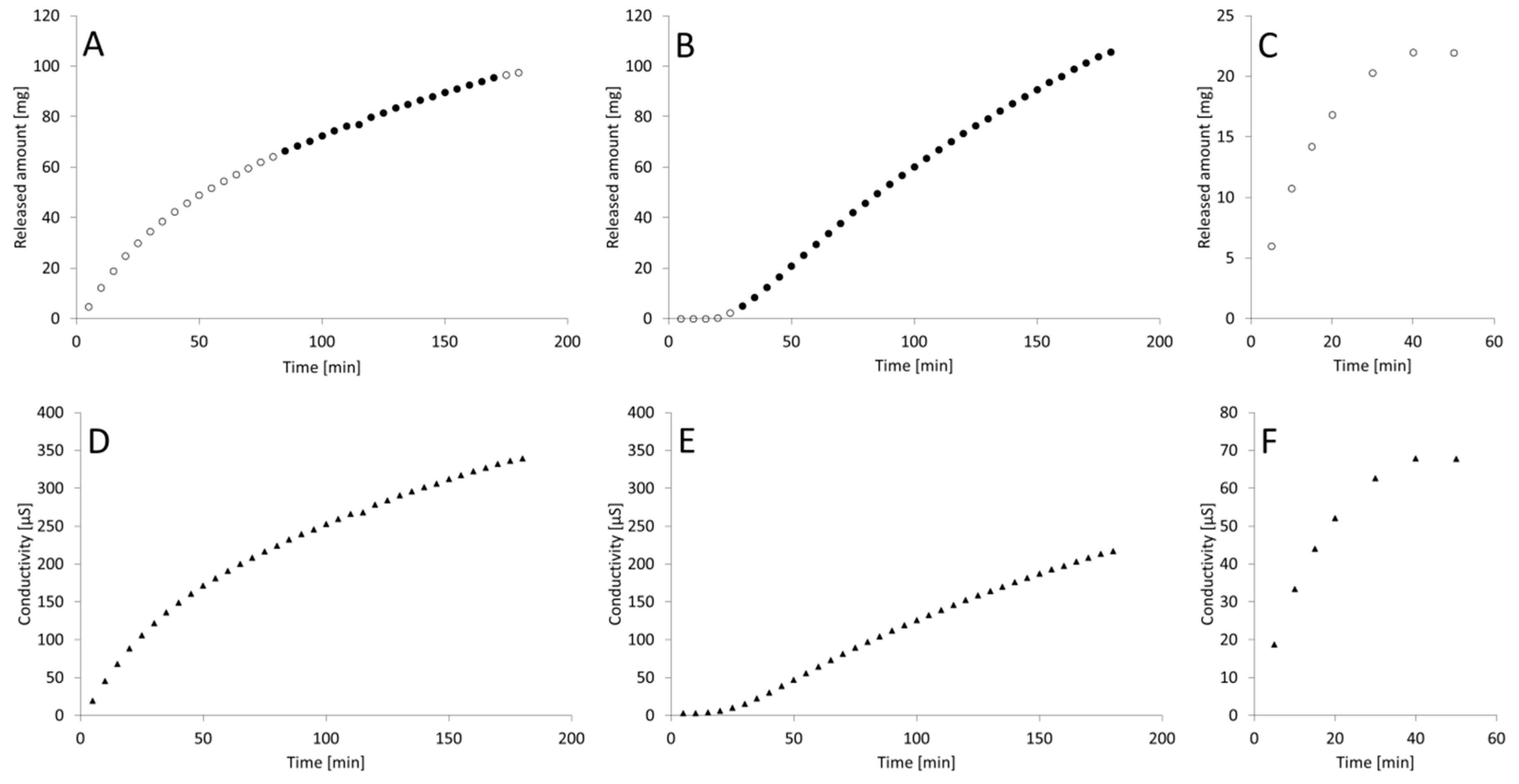
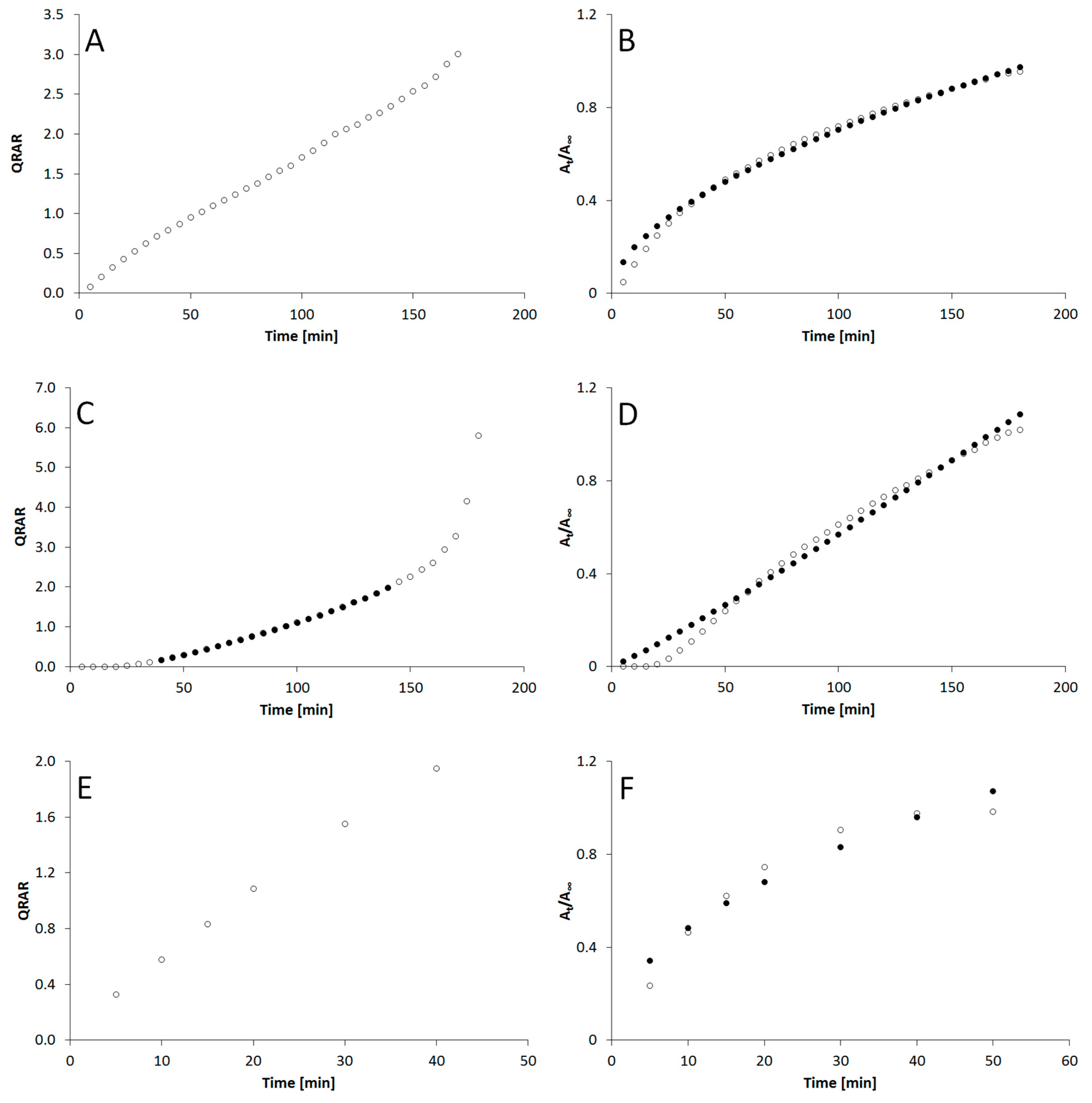
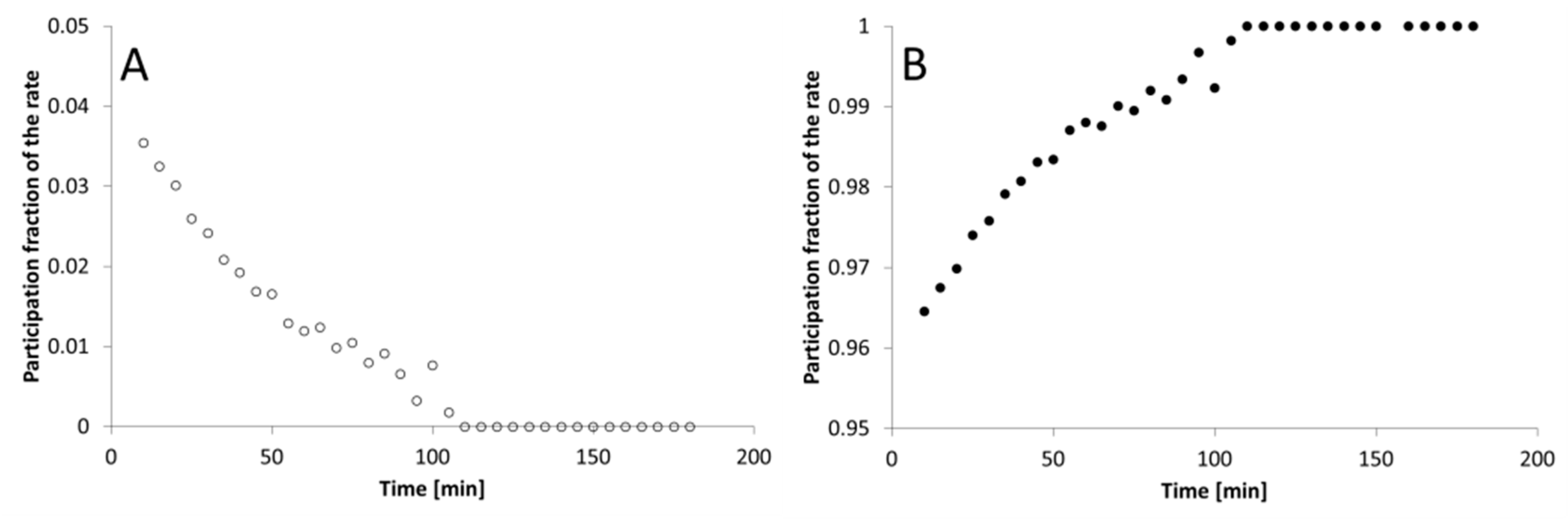
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Vella, J.; Bussuttil, F.; Sammut Bartolo, N.; Sammut, C.; Ferrito, V.; Serracino Inglot, A.; Azzopardi, L.M.; La Ferla, G. A simple HPLC–UV method for the determination of ciprofloxacin in human plasma. J. Chromatogr. B 2015, 989, 80–85. [Google Scholar] [CrossRef] [PubMed]
- Carlucci, G.; Di Federico, L.; Iuliani, P. HPLC-DAD method for the simultaneous determination of zofenopril and hydrochlorothiazide in oral pharmaceutical formulations. J. Sep. Sci. 2010, 33, 1717–1722. [Google Scholar] [CrossRef] [PubMed]
- Bilodeau, L.; Dufresne, G.; Deeks, J.; Clément, G.; Bertrand, J.; Turcotte, S.; Robichaud, A.; Beraldin, F.; Fouquet, A. Determination of vitamin D3 and 25-hydroxyvitamin D3 in foodstuffs by HPLC UV-DAD and LC–MS/MS. J. Food Compos. Anal. 2011, 24, 441–448. [Google Scholar] [CrossRef]
- Karlsson, G.; Winge, S.; Sandberg, H. Separation of monosaccharides by hydrophilic interaction chromatography with evaporative light scattering detection. J. Chromatogr. A 2005, 1092, 246–249. [Google Scholar] [CrossRef] [PubMed]
- Sang-Ho, Y.; Jay-lin, J. Molecular weights and gyration radii of amylopectins determined by high-performance size-exclusion chromatography equipped with multi-angle laser-light scattering and refractive index detectors. Carbohydr. Polym. 2002, 49, 307–314. [Google Scholar] [CrossRef]
- Coufal, P.; Zuska, J.; Van de Goor, T.; Smith, V.; Gaš, B. Separation of twenty underivatized essential amino acids by capillary zone electrophoresis with contactless conductivity detection. Electrphoresis 2003, 24, 671–677. [Google Scholar] [CrossRef] [PubMed]
- Zu, Y.; Li, C.; Fu, Y.; Zhao, C. Simultaneous determination of catechin, rutin, quercetin kaempferol and isorhamnetin in the extract of sea buckthorn (Hippophae rhamnoides L.) leaves by RP-HPLC with DAD. J. Pharmaceut. Biomed. 2006, 41, 714–719. [Google Scholar] [CrossRef] [PubMed]
- Boussèsa, C.; Fereyb, L.; Vedrinesa, E.; Gaudin, K. Using an innovative combination of quality-by-design and green analytical chemistry approaches for the development of a stability indicating UHPLC method in pharmaceutical products. J. Pharmaceut. Biomed. 2015, 115, 114–122. [Google Scholar] [CrossRef] [PubMed]
- Del Barrio, M.A.; Hu, J.; Zhou, P.; Cauchon, N. Simultaneous determination of formic acid and formaldehyde in pharmaceutical excipients using headspace GC/MS. J. Pharmaceut. Biomed. 2006, 41, 738–743. [Google Scholar] [CrossRef] [PubMed]
- Petrović, M.; Hernando, M.D.; Díaz-Cruz, M.S.; Barceló, D. Liquid chromatography–tandem mass spectrometry for the analysis of pharmaceutical residues in environmental samples: A review. J. Chromatogr. A 2005, 1067, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Licht, S.; Naschitz, V.; Halperin, L.; Halperin, N.; Lin, L.; Chen, J.; Ghosh, S.; Liu, B. Analysis of ferrate(VI) compounds and super-iron Fe(VI) battery cathodes: FTIR, ICP, titrimetric, XRD, UV/VIS, and electrochemical characterization. J. Power Sources 2001, 101, 167–176. [Google Scholar] [CrossRef]
- Johansson, J.; Cauchi, M.; Sundgren, M. Multiple fiber-optic dual-beam UV/Vis system with application to dissolution testing. J. Pharmaceut. Biomed. 2002, 29, 469–476. [Google Scholar] [CrossRef]
- Abarcaa, A.; Canfranca, E.; Sierraa, I.; Marina, M.L. A validated flame AAS method for determining magnesium in a multivitamin pharmaceutical preparation. J. Pharmaceut. Biomed. 2001, 25, 941–945. [Google Scholar] [CrossRef]
- Lisik, A.; Prescha, A.; Cavlaz, L.E.; Grajeta, H.; Musiał, W. The evaluation of alternative method of ferrous ions assessment in pharmaceutical preparations. Monatsh. Chem. 2018, 149, 931–937. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dash, S.; Murthy, N.P.; Nath, L.; Chwdhury, P. Kinetic modeling on drug release from kinetic controlled drug delivery systems. Acta Pol. Pharm. 2010, 67, 217–223. [Google Scholar] [PubMed]
- Siepmann, J.; Siepmann, F. Mathematical modeling of drug delivery. Int. J. Pharm. 2008, 364, 328–343. [Google Scholar] [CrossRef] [PubMed]
- Shaikh, H.K.; Kshirsagar, R.V.; Patil, S.G. Mathematical models for drug release characterization: A review. World J. Pharm. Pharm. Sci. 2015, 4, 324–338. [Google Scholar]
- Costa, P.; Sousa Lobo, J.M. Modeling and comparison of dissolution profiles. Eur. J. Pharm. Sci. 2001, 13, 123–133. [Google Scholar] [CrossRef]
- Kalam, M.A.; Humayun, M.; Parvez, N.; Yadav, S.; Garg, A.; Amin, S.; Sultana, Y.; Ali, A. Release kinetics of modified pharmaceutical dosage forms: A rewiev. CJP Sci. 2007, 1, 30–35. [Google Scholar]
- Siepmann, J.; Siepmann, F. Modeling of diffusion controlled drug delivery. J. Control. Release 2012, 160, 351–362. [Google Scholar] [CrossRef] [PubMed]
- Peppas, N.A.; Narasimhand, B. Mathematical models in drug delivery: How modeling has shaped the way we design new drug delivery systems. J. Control. Release 2014, 190, 75–81. [Google Scholar] [CrossRef] [PubMed]
- Council of Europe. European Pharmacopoeia Commission. Dissolution test for solid dosage forms (Chapter 2.9.3). In European Pharmacopoeia, 5th ed.; Council of Europe: Strasburg, Germany, 2005; p. 20903. [Google Scholar]
- International Conference on Harmonisation of Technical Requirements for Registration of Pharmaceuticals for Human Use: Validation of Analytical Procedures: Text and Methodology Q2(R1); Current Step 4 Version Parent Guideline dated 27 October 1994 (Complementary Guideline on Methodology Dated 6 November 1996 Incorporated in November 2005). Available online: https://www.ich.org/fileadmin/Public_Web_Site/ICH_Products/Guidelines/Quality/Q2_R1/Step4/Q2_R1__Guideline.pdf (accessed on 16 October 2017).
- Holowka, E.P.; Bhatia, K.S. Controled Released Systems. In Drug Delivery: Materials Design and Clinical Perspective, 1st ed.; Springer-Verlag: New York, NY, USA, 2014; pp. 7–14. ISBN 978-1-4939-1998-7. [Google Scholar]
| Kinetic Model | Equation | Source |
|---|---|---|
| zero-order | [15,16,17] | |
| first-order | [15,16,17] | |
| Hixson–Crowell | [15,16,17] | |
| Korsmeyer–Peppas | [15,16,17] |
| n | Drug Transport Mechanism | Rate as a Function of Time (t) Transformation |
|---|---|---|
| 0.5 | Fickian diffusion | t−0.5 |
| 0.45 < n = 0.89 | Non-Fickian transport | tn−1 |
| 0.89 | Case II transport | t |
| >0.89 | Super case II transport | tn−1 |
| Composition | k1 (1/min) | k0 (mg/min) | t0.5 (min) | r2 | KS | r2 | Korsmeyer–Peppas KKP n | r2 | |
|---|---|---|---|---|---|---|---|---|---|
| FEP1, 1st stage | 0.174 ± 0.0160 | - | 52.00 (b) ± 2.67 | 0.9995 (a) ± 0.0011 | 0.0160 ± 0.0013 | 0.9933 (b) ± 0.4200 | 0.0512 ± 0.0082 | 0.574 ± 0.029 | 0.9960 ± 0.3633 |
| FEP1, 2nd stage | - | 0.315 ± 0.022 | |||||||
| FEP2 | - | 0.680 ± 0.020 | 89.77 ± 4.09 | 0.9916 ± 0.0027 | 0.0180 ± 0.0009 | 0.9959 (c) ± 0.1360 | 0.0023 ± 0.0008 | 1.192 ± 0.061 | 0.9837 ± 0.0678 |
| FEN3 | 0.0544 ± 0.0031 | - | 11.56 ± 0.54 | 0.9945 ± 0.0034 | 0.0437 ± 0.0045 | 0.9956 (d) ± 0.3719 | 0.1630 ± 0.016 | 0.472 ± 0.025 | 0.9408 ± 0.7519 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lisik, A.; Musiał, W. Conductomeric Evaluation of the Release Kinetics of Active Substances from Pharmaceutical Preparations Containing Iron Ions. Materials 2019, 12, 730. https://doi.org/10.3390/ma12050730
Lisik A, Musiał W. Conductomeric Evaluation of the Release Kinetics of Active Substances from Pharmaceutical Preparations Containing Iron Ions. Materials. 2019; 12(5):730. https://doi.org/10.3390/ma12050730
Chicago/Turabian StyleLisik, Anna, and Witold Musiał. 2019. "Conductomeric Evaluation of the Release Kinetics of Active Substances from Pharmaceutical Preparations Containing Iron Ions" Materials 12, no. 5: 730. https://doi.org/10.3390/ma12050730
APA StyleLisik, A., & Musiał, W. (2019). Conductomeric Evaluation of the Release Kinetics of Active Substances from Pharmaceutical Preparations Containing Iron Ions. Materials, 12(5), 730. https://doi.org/10.3390/ma12050730