Sample Sizes Based on Weibull Distribution and Normal Distribution for FRP Tensile Coupon Test
Abstract
:1. Introduction
2. Sample Size Based on Weibull Distribution
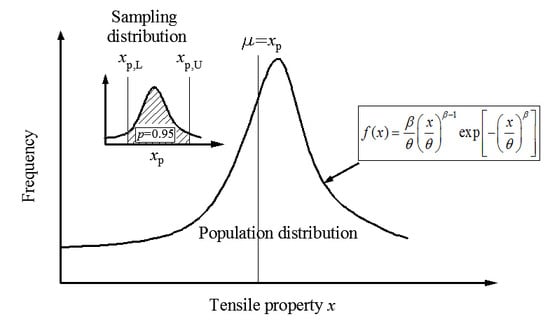
2.1. Introduction to Weibull Distribution
2.2. Percentile of the Mean Value
2.3. Sample Size Analysis
3. Sample Size Based on Normal Distribution
4. Comparison and Recommendation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Explanation for the Determination of Sample Size 5 and 7
References
- Zhao, X.; Zhang, L. State-of-the-art review on FRP strengthened steel structures. Eng. Struct. 2007, 29, 1808–1823. [Google Scholar] [CrossRef]
- Corradi, M.; Borri, A.; Castori, G.; Coventry, K. Experimental Analysis of Dynamic Effects of FRP Reinforced Masonry Vaults. Materials 2015, 8, 8059–8071. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liang, H.; Li, S.; Lu, Y.; Yang, T. Reliability Analysis of Bond Behaviour of CFRP-Concrete Interface under Wet–Dry Cycles. Materials 2018, 11, 741. [Google Scholar] [CrossRef] [PubMed]
- Liang, H.; Li, S.; Lu, Y.; Hu, J. Electrochemical performance of corroded reinforced concrete columns strengthened with fiber reinforced polymer. Compos. Struct. 2019, 207, 576–588. [Google Scholar] [CrossRef]
- Li, S.; Hu, J.; Lu, Y.; Liang, H. Durability of CFRP strengthened steel plates under wet and dry cycles. Int. J. Steel Struct. 2018, 18, 381–390. [Google Scholar] [CrossRef]
- Hollaway, L.C.; Teng, J.G. Strengthening and Rehabilitation of Civil Infrastructures Using Fibre Reinforced Polymer (FRP) Composites; Woodhead Publishing Limited: Cambridge, UK, 2008. [Google Scholar]
- Rousakis, T.C. Reusable and recyclable nonbonded composite tapes and ropes for concrete columns confinement. Compos. Part B Eng. 2016, 103, 15–22. [Google Scholar] [CrossRef]
- Ghafoori, E.; Motavalli, M. Flexural and interfacial behavior of metallic beams strengthened by prestressed bonded plates. Compos. Struct. 2013, 101, 22–34. [Google Scholar] [CrossRef]
- Wang, W.W.; Dai, J.G.; Harries, K.A. Intermediate crack-induced debonding in RC beams externally strengthened with prestressed FRP laminates. J. Reinf. Plast. Comp. 2013, 32, 1842–1857. [Google Scholar] [CrossRef]
- Li, W.; Ghafoori, E.; Lu, Y.; Li, S.; Motavalli, M. Analytical solution for stiffness prediction of bonded CFRP-to-steel double strap joints. Eng. Struct. 2018, 177, 190–197. [Google Scholar] [CrossRef]
- Ghafoori, E.; Motavalli, M.; Botsis, J.; Herwig, A.; Galli, M. Fatigue strengthening of damaged metallic beams using prestressed unbonded and bonded CFRP plates. Int. J. Fatigue 2012, 44, 303–315. [Google Scholar] [CrossRef]
- Huang, H.; Wang, W.W.; Dai, J.G.; Brigham, J.C. Fatigue behavior of reinforced concrete beams strengthened with externally bonded prestressed CFRP sheets. J. Compos. Constr. 2016, 21, 4016108. [Google Scholar] [CrossRef]
- De Souza Sánchez Filho, E.; Silva Filho, J.J.H.; Perlingeiro, M.S.P.L.; de Figueiredo Guerrante, I. Bond strength of carbon fiber composites glued to concrete surface. Struct. Concrete 2018, 19, 536–547. [Google Scholar] [CrossRef]
- Lu, Y.; Hu, J.; Li, S.; Tang, W. Active and passive protection of steel reinforcement in concrete column using carbon fibre reinforced polymer against corrosion. Electrochim. Acta 2018, 278, 124–136. [Google Scholar] [CrossRef]
- Chen, C.; Cheng, L. Predicting Flexural Fatigue Performance of RC Beams Strengthened with Externally Bonded FRP due to FRP Debonding. J. Bridge Eng. 2017, 22, 04017082. [Google Scholar] [CrossRef]
- Rousakis, T.C.; Saridaki, M.E.; Mavrothalassitou, S.A.; Hui, D. Utilization of hybrid approach towards advanced database of concrete beams strengthened in shear with FRPs. Compos. Part B Eng. 2016, 85, 315–335. [Google Scholar] [CrossRef]
- Ghafoori, E.; Schumacher, A.; Motavalli, M. Fatigue behavior of notched steel beams reinforced with bonded CFRP plates: Determination of prestressing level for crack arrest. Eng. Struct. 2012, 45, 270–283. [Google Scholar] [CrossRef]
- Ghafoori, E.; Motavalli, M.; Nussbaumer, A.; Herwig, A.; Prinz, G.S.; Fontana, M. Design criterion for fatigue strengthening of riveted beams in a 120-year-old railway metallic bridge using pre-stressed CFRP plates. Compos. Part B Eng. 2015, 68, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.W.; Dai, J.G.; Harries, K.A.; Zhang, L. Prediction of prestress losses in RC beams externally strengthened with prestressed CFRP sheets/plates. J. Reinf. Plast. Comp. 2014, 33, 699–713. [Google Scholar] [CrossRef]
- JSCE-E 531-1995. Test Method for Tensile Properties of Continuous Fiber Reinforcing Materials; JSCE: Tokyo, Japan, 1995. [Google Scholar]
- BS EN ISO 527-1-2012. Plastics—Determination of Tensile Properties; The British Standards Institution: London, UK, 2012. [Google Scholar]
- ASTM D3039-07. Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials; ASTM: West Conshohocken, PA, USA, 2008. [Google Scholar]
- GB/T 1446-2005. Fibre-Reinforced Plastics Composites-The Generals for Determination of Properties; Chinese Standard Press: Beijing, China, 2005. [Google Scholar]
- Zureick, A.; Bennett, R.M.; Ellingwood, B.R. Statistical characterization of fiber-reinforced polymer composite material properties for structural design. J. Struct. Eng. 2006, 132, 1320–1327. [Google Scholar] [CrossRef]
- Atadero, R.A.; Karbhari, V.M. Calibration of resistance factors for reliability based design of externally-bonded FRP composites. Compos. Part B Eng. 2008, 39, 665–679. [Google Scholar] [CrossRef]
- Shaw, A.; Sriramula, S.; Gosling, P.D.; Chryssanthopoulos, M.K. A critical reliability evaluation of fibre reinforced composite materials based on probabilistic micro and macro-mechanical analysis. Compos. Part B Eng. 2010, 41, 446–453. [Google Scholar] [CrossRef]
- Gomes, S.; Dias-da-Costa, D.; Neves, L.A.C.; Hadigheh, S.A.; Fernandes, P.; Júlio, E. Probabilistic-based characterisation of the mechanical properties of CFRP laminates. Constr. Build. Mater. 2018, 169, 132–141. [Google Scholar] [CrossRef]
- Alqam, M.; Bennett, R.M.; Zureick, A. Three-parameter vs. two-parameter Weibull distribution for pultruded composite material properties. Compos. Struct. 2002, 58, 497–503. [Google Scholar] [CrossRef]
- Sánchez-Heres, L.F.; Ringsberg, J.W.; Johnson, E. Influence of mechanical and probabilistic models on the reliability estimates of fibre-reinforced cross-ply laminates. Struct. Saf. 2014, 51, 35–46. [Google Scholar] [CrossRef]
- Atadero, R.A. Development of Load and Resistance Factor Design for FRP Strengthening of Reinforced Concrete Structures. Ph.D. Thesis, University of California, San Diego, CA, USA, 2006. [Google Scholar]
- Bain, L.J. Statistical Analysis of Reliability and Life-Testing Models: Theory and Methods; Marcel Dekker: New York, NY, USA, 1978; pp. 227–242. [Google Scholar]
- MILHDBK-17-1F. Composite Materials Handbook—Volume 1: Polymer Matrix Composites: Guidelines for Characterization of Structural Materials; Department of Defence: Washington, DC, USA, 2002.
- Atadero, R.A.; Karbhari, V.M. Sources of uncertainty and design values for field-manufactured FRP. Compos. Struct. 2009, 89, 83–93. [Google Scholar] [CrossRef]
- Wang, N.; Ellingwood, B.R. Estimating nominal strength of built-up CFRP laminates from standardized specimen tests. Struct. Saf. 2014, 47, 24–28. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, X.; Iwashita, K.; Sasaki, T.; Hamaguchi, Y. Tensile fatigue behaviour of FRP and hybrid FRP sheets. Compos. Part B Eng. 2010, 41, 396–402. [Google Scholar] [CrossRef]
- Hulatt, J.; Hollaway, L.; Thorne, A. Preliminary investigations on the environmental effects on new heavyweight fabrics for use in civil engineering. Compos. Part B Eng. 2002, 33, 407–414. [Google Scholar] [CrossRef]
- Sriramula, S.; Chryssanthopoulos, M.K. Quantification of uncertainty modelling in stochastic analysis of FRP composites. Compos. Part A Appl. Sci. 2009, 40, 1673–1684. [Google Scholar] [CrossRef]
- Shi, J.W.; Zhu, H.; Wu, G.; Wu, Z.S. Tensile behavior of FRP and hybrid FRP sheets in freeze-thaw cycling environments. Compos. Part B Eng. 2014, 60, 239–247. [Google Scholar] [CrossRef]

| 0.05 | 0.1 | 0.15 | 0.2 | |
|---|---|---|---|---|
| 24.95 | 12.15 | 7.91 | 5.8 | |
| 0.4401 | 0.4507 | 0.4616 | 0.4728 |
| n | ||||||||
|---|---|---|---|---|---|---|---|---|
| 10 | −2.5028 | 2.7384 | −2.5154 | 2.7670 | −2.4851 | 2.8421 | −2.4602 | 2.9134 |
| 11 | −2.4770 | 2.7047 | −2.4885 | 2.7341 | −2.4632 | 2.8040 | −2.4459 | 2.8676 |
| 12 | −2.4529 | 2.6732 | −2.4634 | 2.7032 | −2.4426 | 2.7683 | −2.4322 | 2.8250 |
| 13 | −2.4304 | 2.6436 | −2.4401 | 2.6741 | −2.4235 | 2.7349 | −2.4192 | 2.7855 |
| 14 | −2.4094 | 2.6160 | −2.4184 | 2.6469 | −2.4056 | 2.7038 | −2.4067 | 2.7489 |
| 15 | −2.3899 | 2.5902 | −2.3983 | 2.6215 | −2.3889 | 2.6747 | −2.3949 | 2.7150 |
| 16 | −2.3718 | 2.5661 | −2.3798 | 2.5976 | −2.3735 | 2.6477 | −2.3836 | 2.6838 |
| 18 | −2.3395 | 2.5229 | −2.3469 | 2.5547 | −2.3458 | 2.5993 | −2.3626 | 2.6287 |
| 20 | −2.3120 | 2.4857 | −2.3192 | 2.5174 | −2.3221 | 2.5578 | −2.3437 | 2.5824 |
| 24 | −2.2694 | 2.4268 | −2.2771 | 2.4579 | −2.2853 | 2.4927 | −2.3116 | 2.5128 |
| 28 | −2.2405 | 2.3851 | −2.2495 | 2.4149 | −2.2599 | 2.4474 | −2.2861 | 2.4676 |
| 32 | −2.2218 | 2.3565 | −2.2327 | 2.3848 | −2.2432 | 2.4170 | −2.2664 | 2.4405 |
| 36 | −2.2107 | 2.3375 | −2.2235 | 2.3642 | −2.2329 | 2.3976 | −2.2514 | 2.4257 |
| 40 | −2.2046 | 2.3251 | −2.2192 | 2.3504 | −2.2268 | 2.3856 | −2.2405 | 2.4186 |
| 44 | −2.2016 | 2.3167 | −2.2176 | 2.3409 | −2.2233 | 2.3781 | −2.2328 | 2.4153 |
| 48 | −2.1998 | 2.3103 | −2.2169 | 2.3338 | −2.2211 | 2.3727 | −2.2277 | 2.4128 |
| 52 | −2.1973 | 2.2993 | −2.2139 | 2.3233 | −2.2163 | 2.3641 | −2.2227 | 2.4043 |
| 56 | −2.1907 | 2.2920 | −2.2082 | 2.3154 | −2.2117 | 2.3553 | −2.2201 | 2.3931 |
| 60 | −2.1861 | 2.2835 | −2.2053 | 2.3054 | −2.2103 | 2.3438 | −2.2189 | 2.3814 |
| 64 | −2.1813 | 2.2768 | −2.2001 | 2.2988 | −2.2075 | 2.3351 | −2.2186 | 2.3700 |
| 68 | −2.1776 | 2.2727 | −2.1942 | 2.2968 | −2.2031 | 2.3314 | −2.2194 | 2.3607 |
| n | ||||||||
|---|---|---|---|---|---|---|---|---|
| 10 | 0.966 | 1.032 | 0.931 | 1.068 | 0.893 | 1.104 | 0.853 | 1.144 |
| 11 | 0.968 | 1.030 | 0.934 | 1.064 | 0.899 | 1.098 | 0.862 | 1.136 |
| 12 | 0.970 | 1.029 | 0.938 | 1.060 | 0.904 | 1.093 | 0.869 | 1.129 |
| 13 | 0.971 | 1.027 | 0.941 | 1.057 | 0.909 | 1.089 | 0.875 | 1.123 |
| 14 | 0.972 | 1.026 | 0.943 | 1.055 | 0.913 | 1.085 | 0.881 | 1.117 |
| 15 | 0.974 | 1.025 | 0.946 | 1.052 | 0.916 | 1.081 | 0.886 | 1.113 |
| 16 | 0.975 | 1.024 | 0.948 | 1.050 | 0.920 | 1.078 | 0.891 | 1.108 |
| 18 | 0.976 | 1.022 | 0.952 | 1.047 | 0.925 | 1.072 | 0.899 | 1.101 |
| 20 | 0.978 | 1.021 | 0.955 | 1.044 | 0.930 | 1.068 | 0.905 | 1.095 |
| 24 | 0.980 | 1.019 | 0.960 | 1.039 | 0.938 | 1.061 | 0.915 | 1.085 |
| 28 | 0.982 | 1.017 | 0.963 | 1.036 | 0.943 | 1.055 | 0.923 | 1.077 |
| 32 | 0.983 | 1.016 | 0.966 | 1.033 | 0.947 | 1.051 | 0.928 | 1.072 |
| 36 | 0.985 | 1.015 | 0.968 | 1.031 | 0.951 | 1.048 | 0.933 | 1.067 |
| 40 | 0.985 | 1.014 | 0.970 | 1.029 | 0.953 | 1.046 | 0.936 | 1.063 |
| 44 | 0.986 | 1.013 | 0.971 | 1.028 | 0.956 | 1.043 | 0.939 | 1.060 |
| 48 | 0.987 | 1.013 | 0.973 | 1.027 | 0.958 | 1.041 | 0.942 | 1.057 |
| 52 | 0.987 | 1.012 | 0.974 | 1.026 | 0.959 | 1.040 | 0.944 | 1.055 |
| 56 | 0.988 | 1.012 | 0.975 | 1.025 | 0.961 | 1.038 | 0.946 | 1.052 |
| 60 | 0.988 | 1.011 | 0.976 | 1.024 | 0.962 | 1.037 | 0.948 | 1.051 |
| 64 | 0.989 | 1.011 | 0.977 | 1.023 | 0.964 | 1.035 | 0.950 | 1.049 |
| 68 | 0.989 | 1.011 | 0.977 | 1.022 | 0.965 | 1.034 | 0.952 | 1.047 |
| 0.05 | 0.10 | 0.15 | 0.20 | |
|---|---|---|---|---|
| Sample size | <10 | 17 | 35 | 63 |
| Sample COV | 0.05 | 0.10 | 0.15 | 0.20 |
|---|---|---|---|---|
| Sample size | 7 | 18 | 37 | 64 |
| Sample COV | 0.05 | 0.10 | 0.15 | 0.20 |
|---|---|---|---|---|
| Relative error limit | 6.2% | 12.4% | 18.6% | 24.8% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Li, W.; Tang, W.; Li, B.; Zhang, D. Sample Sizes Based on Weibull Distribution and Normal Distribution for FRP Tensile Coupon Test. Materials 2019, 12, 126. https://doi.org/10.3390/ma12010126
Yang Y, Li W, Tang W, Li B, Zhang D. Sample Sizes Based on Weibull Distribution and Normal Distribution for FRP Tensile Coupon Test. Materials. 2019; 12(1):126. https://doi.org/10.3390/ma12010126
Chicago/Turabian StyleYang, Yongxin, Weijie Li, Wenshui Tang, Biao Li, and Dengfeng Zhang. 2019. "Sample Sizes Based on Weibull Distribution and Normal Distribution for FRP Tensile Coupon Test" Materials 12, no. 1: 126. https://doi.org/10.3390/ma12010126