Study of Flexural Response in Strain Hardening Cementitious Composites Based on Proposed Parametric Model
Abstract
:1. Introduction
2. Research Significance
3. Construction of Methods
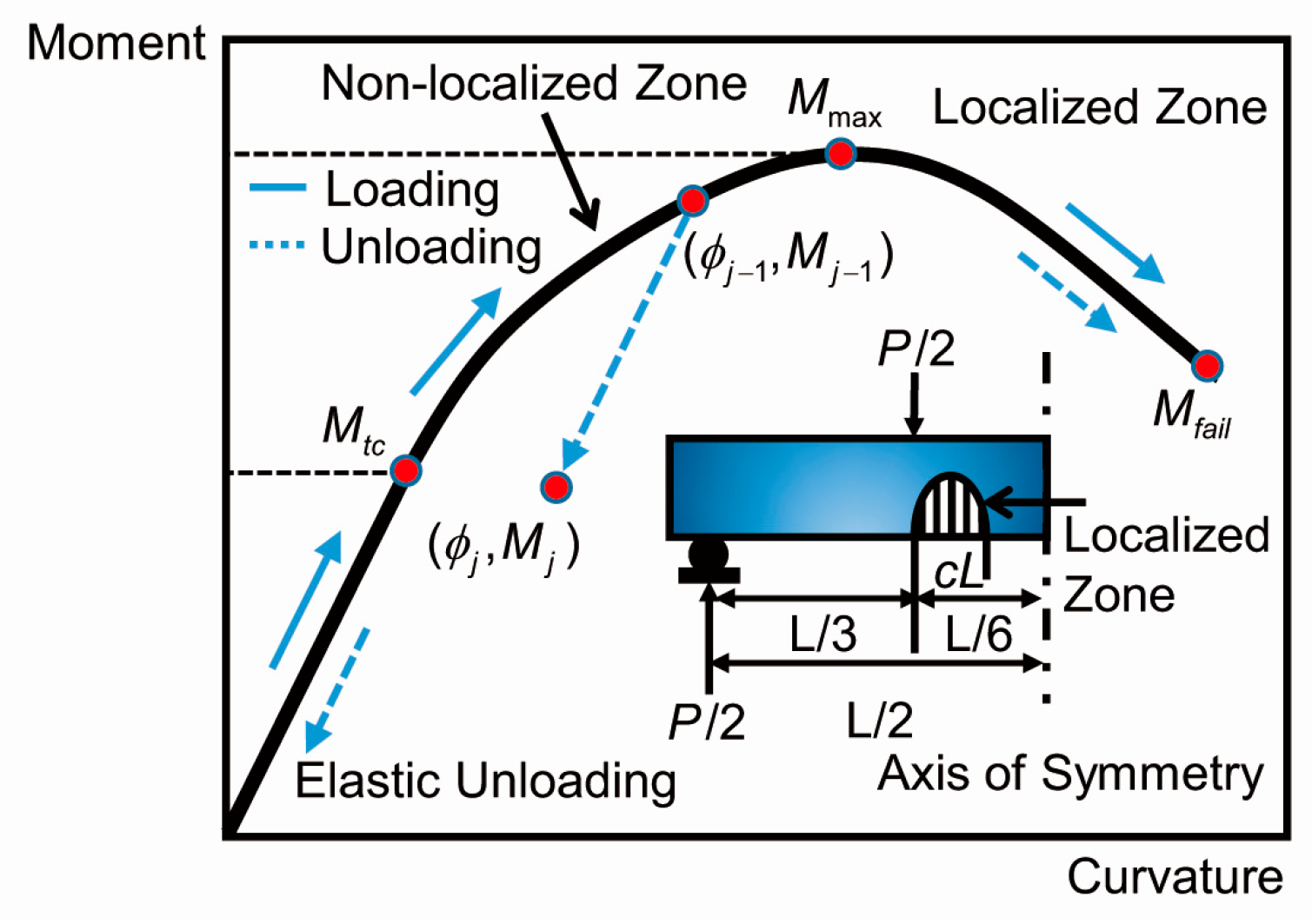
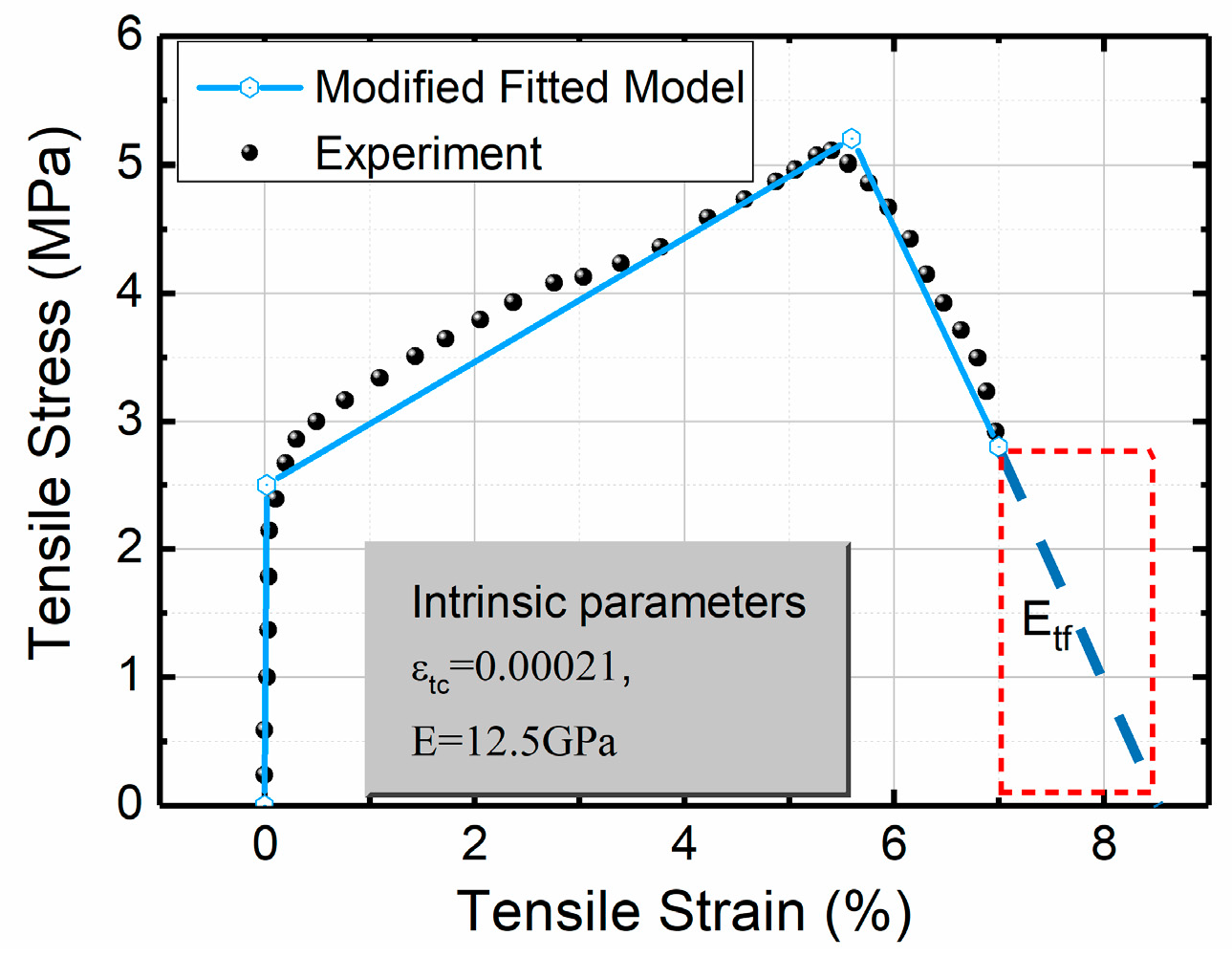
3.1. Proposed Solutions for the Moment-Curvature Diagram of the SHCCs
3.2. Crack-Localization Rules
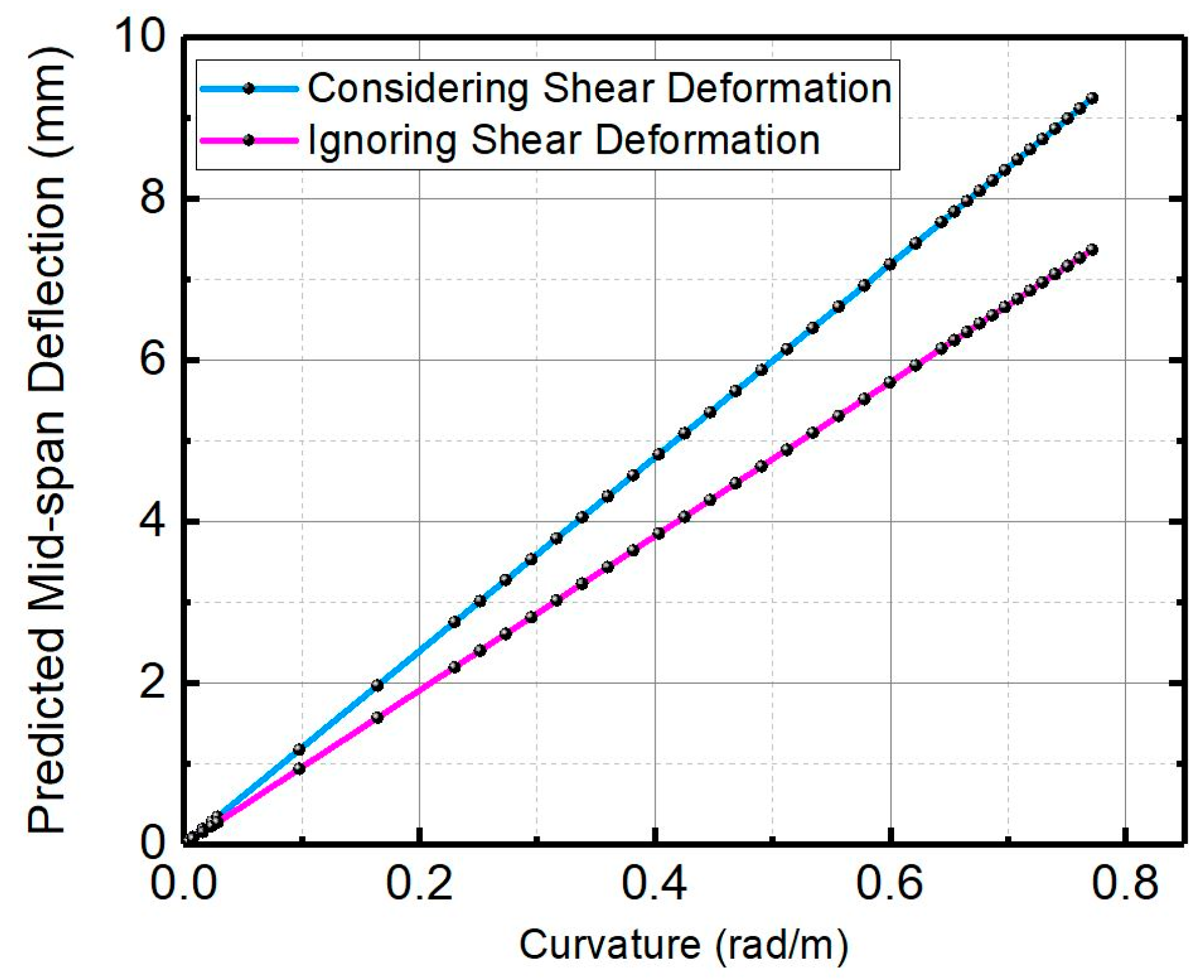
3.3. Procedures to Obtain the Load-Deflection Behavior from a Four-Point Bending Test
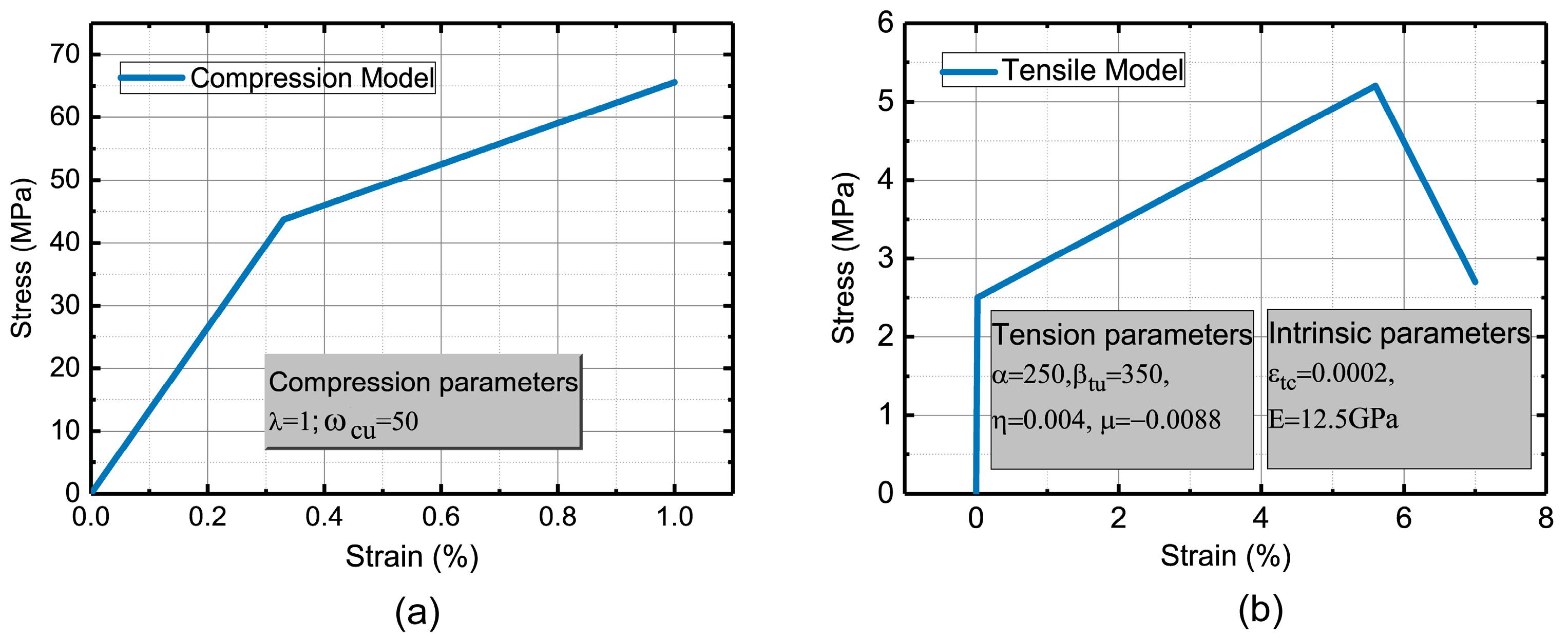
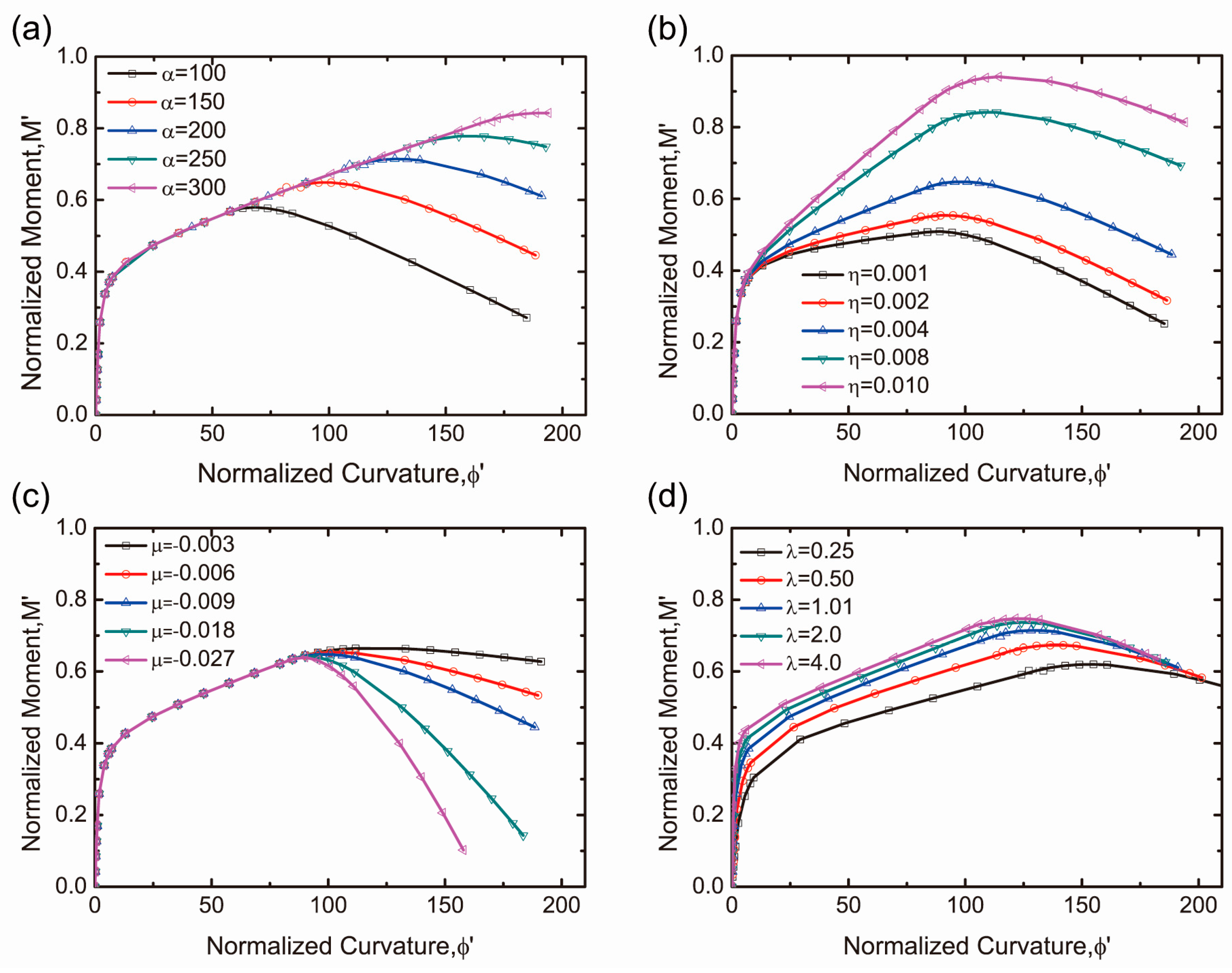
4. Parametric Study of Material Parameters
5. Simulation and Discussion
6. Summary and Future Work
- The parametric study reveals that the tensile parameters mainly dominate the flexural performance in the moment-curvature diagram. Specifically, the transition strain α and post-cracking tensile stiffness η have a direct influence on the peak flexural strength, and the failure stiffness μ has a vital impact on post-peak response. Compared to the tension parameters, the influence of compressive parameters on bending behavior is insignificant.
- The calculation of mid-deflection is affected by the shear effect which depends upon the ratio of specimen’s height to span length. Generally, when the specimen size is 100 × 100 × 400 mm3 or 76.2 × 101.6 × 355.6 mm3 the expression of deflection requires it to take the term into account caused by the shear deflection.
- The predicted load-deflection curve, based upon considering shear effect and post-peak response, presents reasonable consistency when compared with the experiment results under a four point-bending test, especially in the peak and softening portions. The results help to form a reasonable procedure for using the UM method which is utilized to determine the tensile behavior of the SHCCs accurately.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, V.C.; Mishra, D.K.; Wu, H.C. Matrix design for pseudo-strain-hardening fibre reinforced cementitious composites. Mater. Struct. 1995, 28, 586–595. [Google Scholar] [CrossRef]
- Qian, S.; Zhou, J.; De Rooij, M.R.; Schlangen, E.; Ye, G.; Van Breugel, K. Self-healing behavior of strain hardening cementitious composites incorporating local waste materials. Cem. Concr. Compos. 2009, 31, 613–621. [Google Scholar] [CrossRef]
- Yu, K.; Wang, Y.; Yu, J.; Xu, S. A strain-hardening cementitious composites with the tensile capacity up to 8%. Constr. Build. Mater. 2017, 137, 410–419. [Google Scholar] [CrossRef]
- Kang, J.; Bolander, J.E. Multiscale modeling of strain-hardening cementitious composites. Mech. Res. Commun. 2016, 78, 47–54. [Google Scholar] [CrossRef]
- Li, V.C. From micromechanics to structural engineering-the design of cementitous composites for civil engineering applications. JSCE J. Struct. Mech. Earthq. Eng. 1993, 10, 37–48. [Google Scholar]
- Herbert, E.N.; Li, V.C. Self-healing of micro cracks in engineered cementitious composites (ECC) under a natural environment. Materials 2013, 6, 2831–2845. [Google Scholar] [CrossRef]
- Yun, M.L.; Li, V.C. Durable repair of aged infrastructures using trapping mechanism of engineered cementitious composites. Cem. Concr. Compos. 1997, 19, 373–385. [Google Scholar] [CrossRef]
- Kamada, T.; Li, V.C. The effects of surface preparation on the fracture behavior of ECC/concrete repair system. Cem. Concr. Compos. 2000, 22, 423–431. [Google Scholar] [CrossRef] [Green Version]
- Lepech, M.D.; Li, V.C. Application of ECC for bridge deck link slabs. Mater. Struct. 2009, 42, 1185. [Google Scholar] [CrossRef]
- Kim, Y.Y.; Fischer, G.; Li, V.C. Performance of bridge deck link slabs designed with ductile engineered cementitious composite. Struct. J. 2004, 101, 792–801. [Google Scholar] [CrossRef]
- Fukuyama, H.; Suwada, H.J. Experimental response of HPFRCC dampers for structural control. J. Adv. Concr. Technol. 2003, 1, 317–326. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, W. Experimental study on mechanical behaviour of circular reinforced concrete columns strengthened with FRP textile and ECC. J. Southeast Univ. Nat. Sci. Ed. 2016, 5, 031. [Google Scholar]
- Zheng, Y.-Z.; Wang, W.W.; Brigham, J.C. Flexural behaviour of reinforced concrete beams strengthened with a composite reinforcement layer: BFRP grid and ECC. Constr. Build. Mater. 2016, 115, 424–437. [Google Scholar] [CrossRef] [Green Version]
- Ma, H.; Qian, S.; Zhang, Z.; Lin, Z.; Li, V.C. Tailoring engineered cementitious composites with local ingredients. Constr. Build. Mater. 2015, 101, 584–595. [Google Scholar] [CrossRef]
- Pan, Z.; Wu, C.; Liu, J.; Wang, W.; Liu, J. Study on mechanical properties of cost-effective polyvinyl alcohol engineered cementitious composites (PVA-ECC). Constr. Build. Mater. 2015, 78, 397–404. [Google Scholar] [CrossRef]
- Wang, S.; Li, V.C. Engineered cementitious composites with high-volume fly ash. ACI Mater. J. 2007, 104, 233–241. [Google Scholar] [CrossRef]
- Zhou, Y.; Xi, B.; Yu, K.; Sui, L.; Xing, F. Mechanical properties of hybrid ultra-high performance engineered cementitous composites incorporating steel and polyethylene fibers. Materials 2018, 11, 1448. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Li, V.C. Tailoring of pre-existing flaws in ECC matrix for saturated strain hardening. In Proceedings of the FRAMCOS-5, Vail, CO, USA, 12–16 April 2004; pp. 1005–1012. [Google Scholar]
- Li, V.C.; Wu, H.C.; Maalej, M.; Mishra, D.K.; Hashida, T. Tensile behavior of cement-based composites with random discontinuous steel fibers. J. Am. Ceram. Soc. 2010, 79, 74–78. [Google Scholar] [CrossRef]
- Kanakubo, T. Tensile characteristics evaluation method for ductile fiber-reinforced cementitious composites. J. Adv. Concr. Technol. 2006, 4, 3–17. [Google Scholar] [CrossRef]
- Kanda, T.; Kanakubo, T.; Nagai, S.; Maruta, M. Technical consideration in producing ECC pre-cast structural element. In Proceedings of the International RILEM Workshop on High Performance Fiber Reinforced Cementitious Composites in Structural Applications; RILEM Publications SARL: Paris, France, 2006; pp. 229–242. [Google Scholar]
- Soranakom, C.; Mobasher, B. Correlation of tensile and flexural responses of strain softening and strain hardening cement composites. Cem. Concr. Compos. 2008, 30, 465–477. [Google Scholar] [CrossRef]
- Soranakom, C.; Mobasher, B. Closed-form moment-curvature expressions for homogenized fiber-reinforced concrete. ACI Mater. J. 2007, 104, 351–359. [Google Scholar]
- Lopez, J.A.; Serna, P.; Navarro-Gregori, J.; Camacho, E. An inverse analysis method based on deflection to curvature transformation to determine the tensile properties of UHPFRC. Mater. Struct. 2015, 48, 3703–3718. [Google Scholar] [CrossRef]
- Ostergaard, L.; Walter, R.; Olesen, J.F. Method for determination of tensile properties of engineered cementitious composites (ECC). In Proceedings of the 3rd International Conference on Construction Materials, Vancouver, BC, Canada, 22–24 August 2005. [Google Scholar]
- Paegle, I.; Minelli, F.; Fischer, G. Cracking and load-deformation behavior of fiber reinforced concrete: Influence of testing method. Cem. Concr. Compos. 2016, 73, 147–163. [Google Scholar] [CrossRef]
- Qian, S.; Li, V.C. Simplified inverse method for determining the tensile strain capacity of strain hardening cementitious composites. J. Adv. Concr. Technol. 2008, 5, 235–246. [Google Scholar] [CrossRef]
- Qian, S.; Li, V.C. Simplified inverse method for determining the tensile properties of strain hardening cementitious composites (SHCC). J. Adv. Concr. Technol. 2008, 6, 353–363. [Google Scholar] [CrossRef]
- Maalej, M.; Li, V.C. Flexural/tensile strength ratio in engineered cementitious composites. J. Mater. Civ. Eng. 1994, 6, 513–528. [Google Scholar] [CrossRef]
- Method of Test for Bending Moment-Curvature Curve of Fiber-Reinforced Cementitious Composites 2007–Jci-S-003-2007; Japanese Concrete Institute Standard Committee: Tokyo, Japan, 2007.
- ASTM C1609/C1609M-05. Standard Test Method for Flexural Performance of Fiber-Reinforced Concrete (Using Beam with Third-Point Loading); ASTM International: West Conshohocken, PA, USA, 2005. [Google Scholar]
- Fischer, G.D. Deformation Behavior of Reinforced ECC Flexural Members under Reversed Cyclic Loading Conditions. Ph.D. Dissertation, University of Michigan, Ann Arbor, MI, USA, 2002. [Google Scholar]
- Hillerborg, A. Analysis of fracture by means of the fictitious crack model, particularly for fiber reinforced concrete. Int. J. Cem. Compos. 1980, 2, 177–184. [Google Scholar]
- Rossi, P. Ultra-high-performance fiber-reinforced concretes. Concr. Int. 2001, 23, 1216–1221. [Google Scholar]
- Suryanto, B.; Reynaud, R.; Cockburn, B. Sectional analysis of engineered cementitious composite beams. Mag. Concr. Res. 2018, 70, 1135–1148. [Google Scholar] [CrossRef]

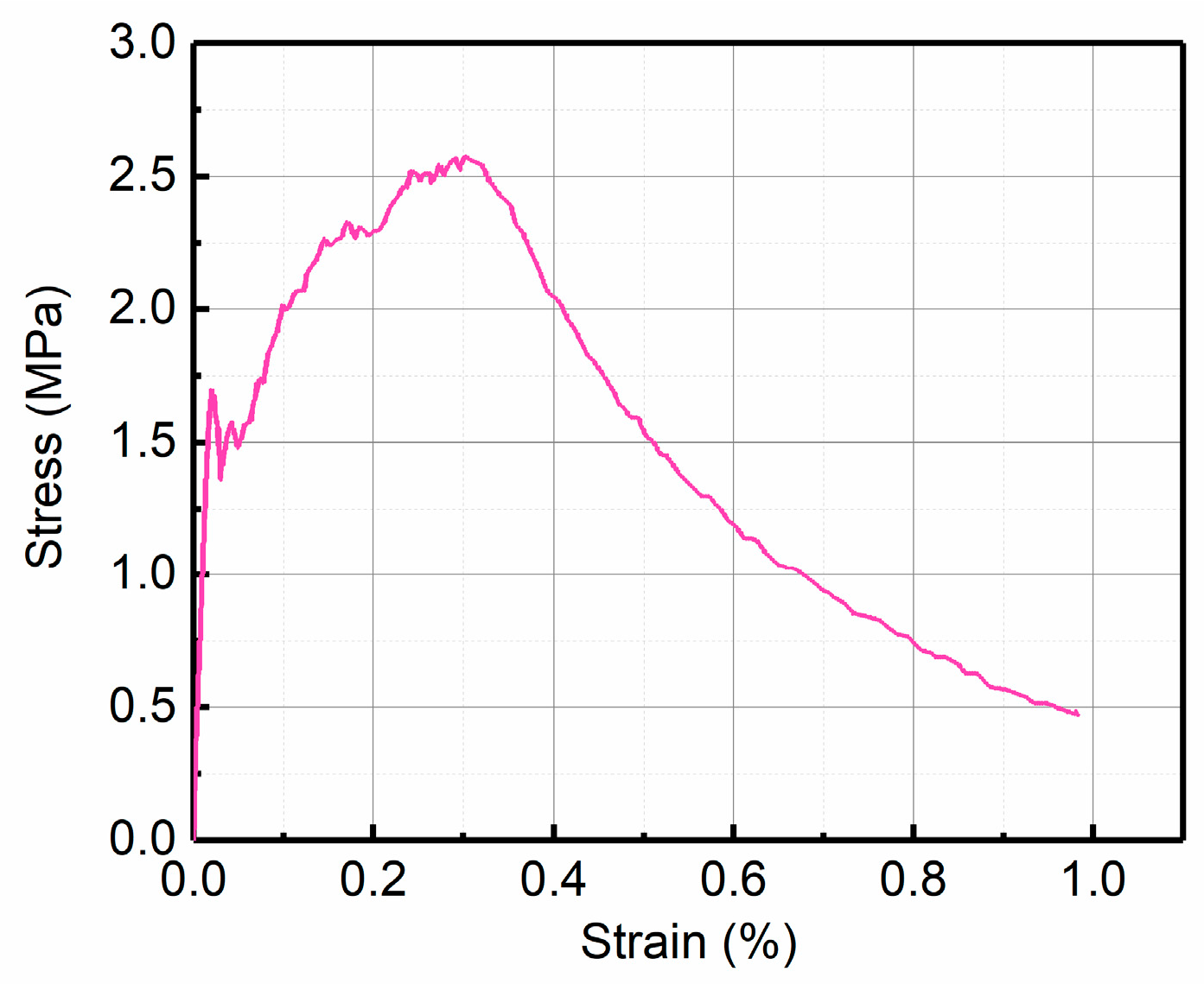
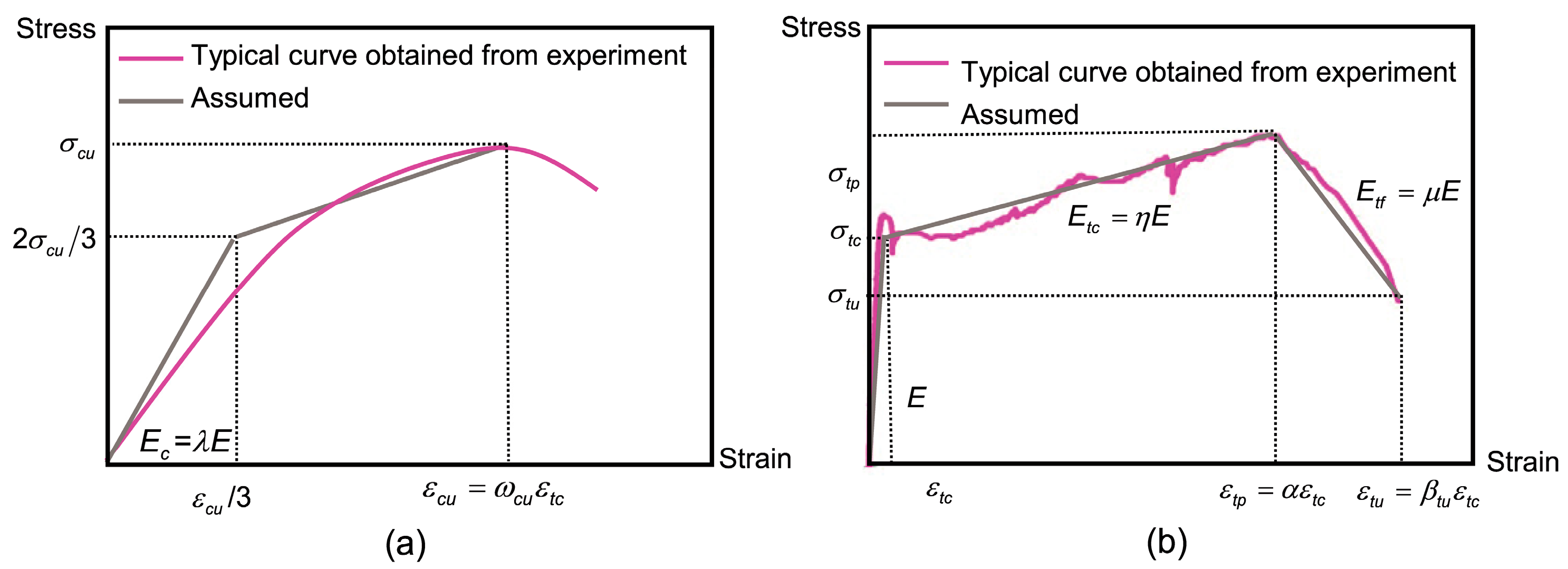
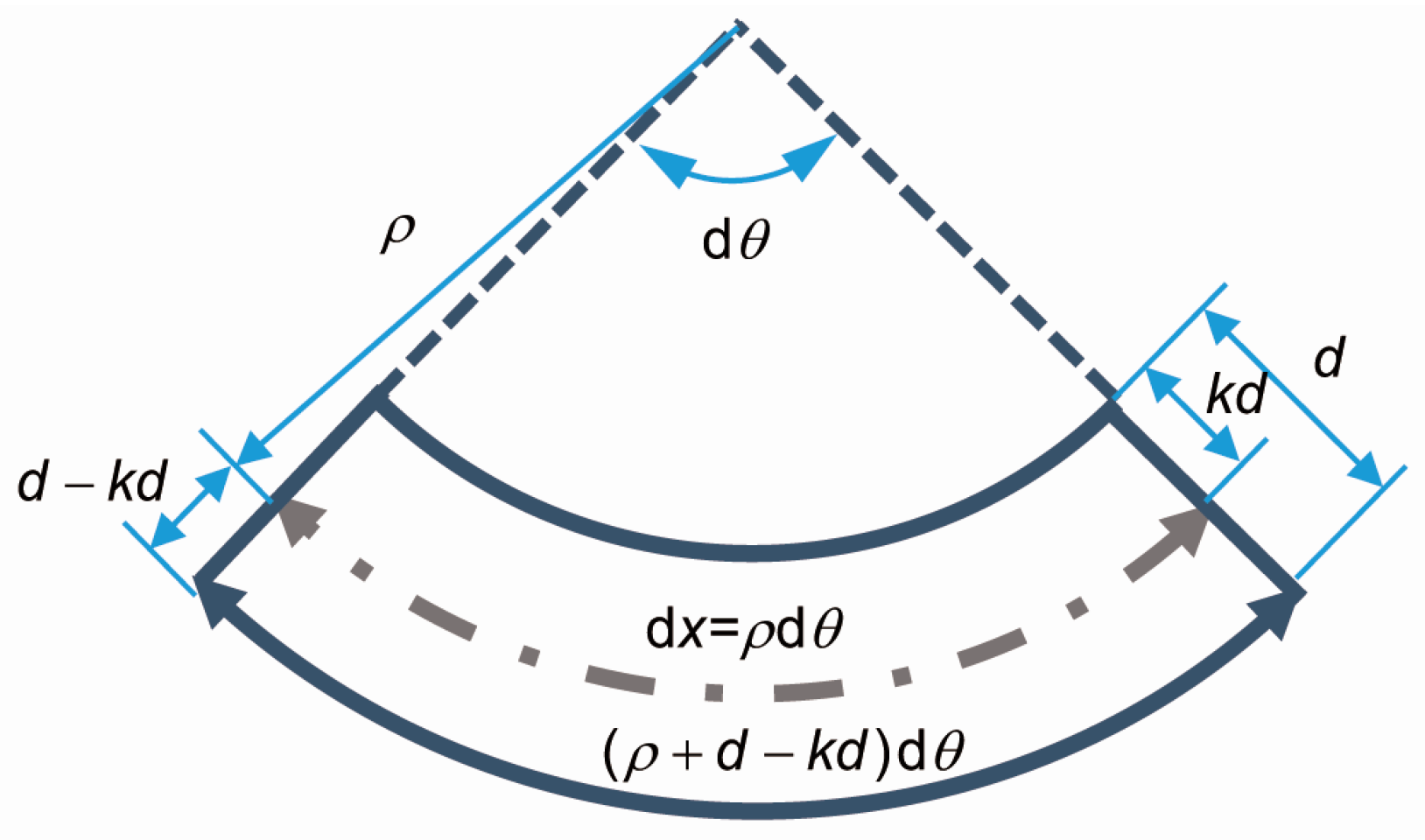
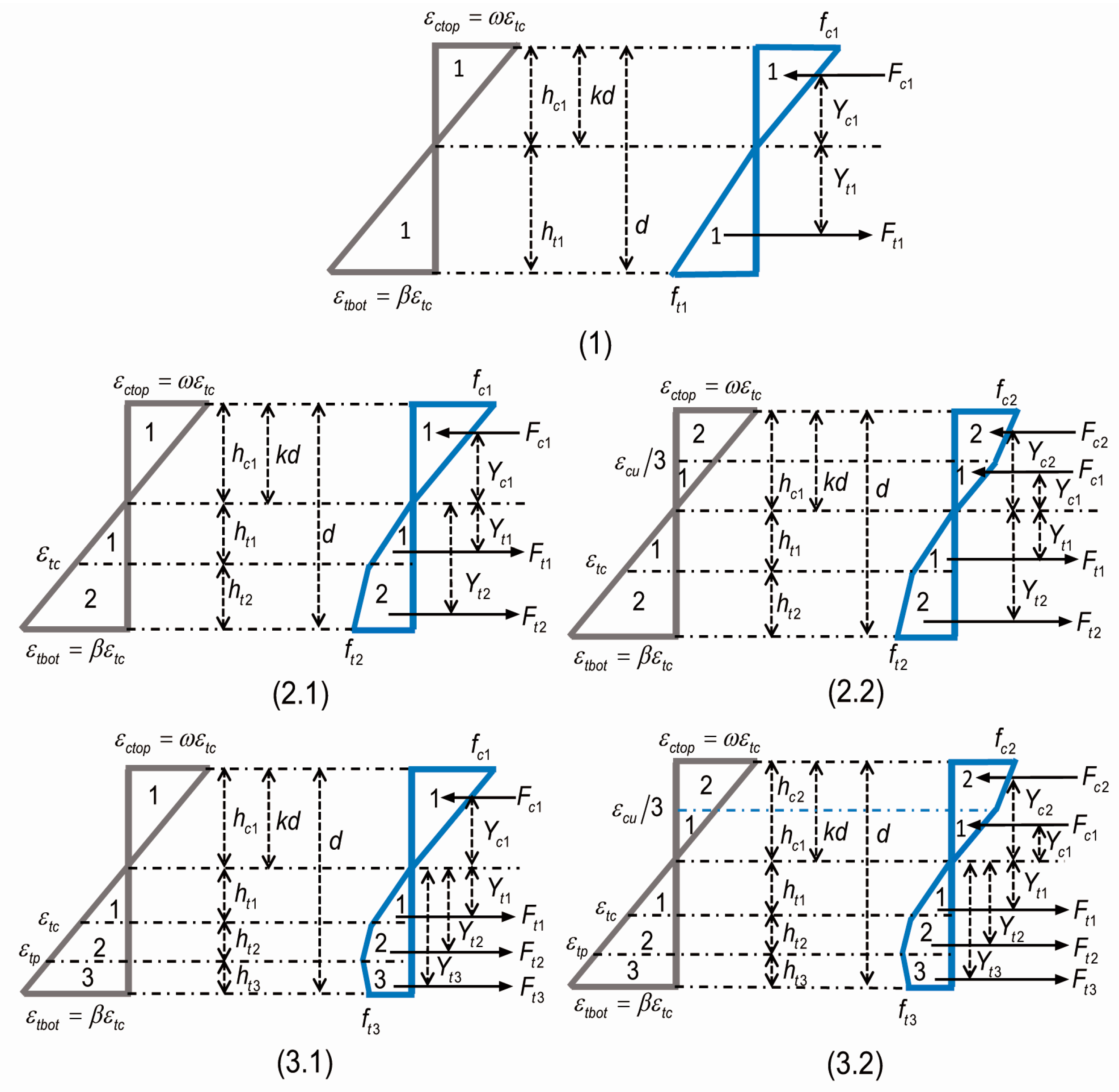



| Stage | Tension | Compression |
|---|---|---|
| 1 | 1 < β ≤ 1 | 0 ≤ ω ≤ ωcu/3 |
| 2.1 | 1 < β ≤ α | 0 ≤ ω ≤ ωcu/3 |
| 2.2 | 1 < β ≤ α | ωcu/3 ≤ ω ≤ ωcu |
| 3.1 | α < β ≤ βtu | 0 ≤ ω ≤ ωcu/3 |
| 3.2 | α < β ≤ βtu | ωcu/3 ≤ ω ≤ ωcu |
| Stage | Force Equilibrium | Internal Moment |
|---|---|---|
| 1 | ∑F1 = −Fc1 + Ft1 | M1 = Fc1Yc1 + Ft1Yt1 |
| 2.1 | ∑F2.1 = −Fc1 + Ft1 + Ft2 | M2.1 = Fc1Yc1 + Ft1Yt1 + Ft2Yt2 |
| 2.2 | ∑F2.2 = −Fc1 − Fc2 + Ft1 + Ft2 | M2.2 = Fc1Yc1 + Fc2Yc2 + Ft1Yt1 + Ft2Yt2 |
| 3.1 | ∑F3.1 = −Fc1 + Ft1 + Ft2 + Ft3 | M3.1 = Fc1Yc1 + Ft1Yt1 + Ft2Yt2 + Ft3Yt3 |
| 3.2 | ∑F3.2 = −Fc1 − Fc2 + Ft1 + Ft2 + Ft3 | M3.1 = Fc1Yc1 + Fc2Yc2 + Ft1Yt1 + Ft2Yt2 + Ft3Yt3 |
| Stage | k | M′ |
|---|---|---|
| 1 | ||
| 2.1 | ||
| 2.2 | ||
| 3.1 | ||
| 3.2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, Z.; Huang, Z.; Li, H.; Chen, W. Study of Flexural Response in Strain Hardening Cementitious Composites Based on Proposed Parametric Model. Materials 2019, 12, 113. https://doi.org/10.3390/ma12010113
Qi Z, Huang Z, Li H, Chen W. Study of Flexural Response in Strain Hardening Cementitious Composites Based on Proposed Parametric Model. Materials. 2019; 12(1):113. https://doi.org/10.3390/ma12010113
Chicago/Turabian StyleQi, Zhanfeng, Zhiyi Huang, Hui Li, and Wenhua Chen. 2019. "Study of Flexural Response in Strain Hardening Cementitious Composites Based on Proposed Parametric Model" Materials 12, no. 1: 113. https://doi.org/10.3390/ma12010113





