Investigation of the Propagation of Stress Wave in Nickel-Titanium Shape Memory Alloys
Abstract
:1. Introduction
1.1. Thermodynamic
1.2. Generalized Plasticity
2. Theoretical Framework
2.1. Thermodynamics
2.2. Governing Equations
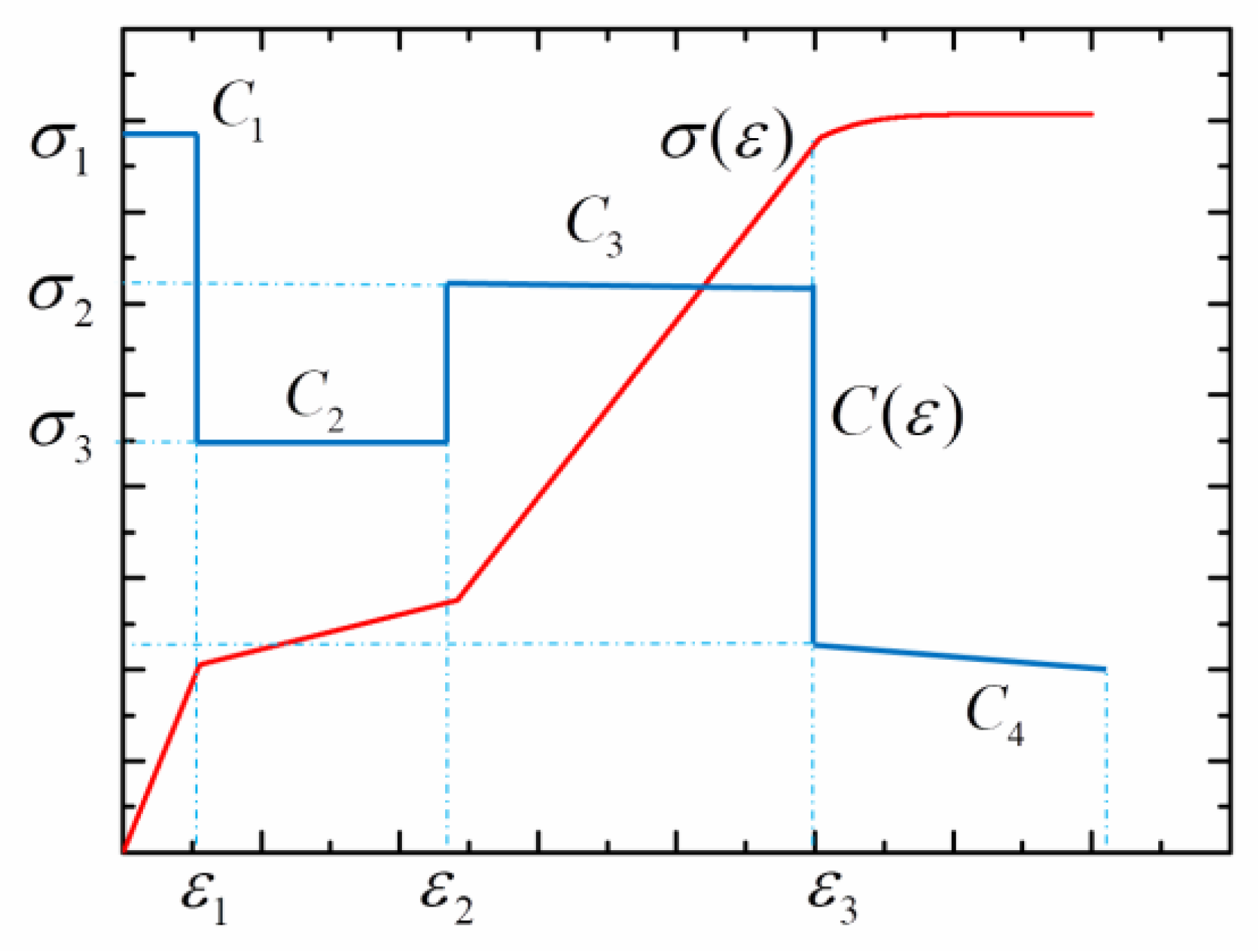
2.3. Phase Transition Evolution
2.4. Evolution of Plasticity
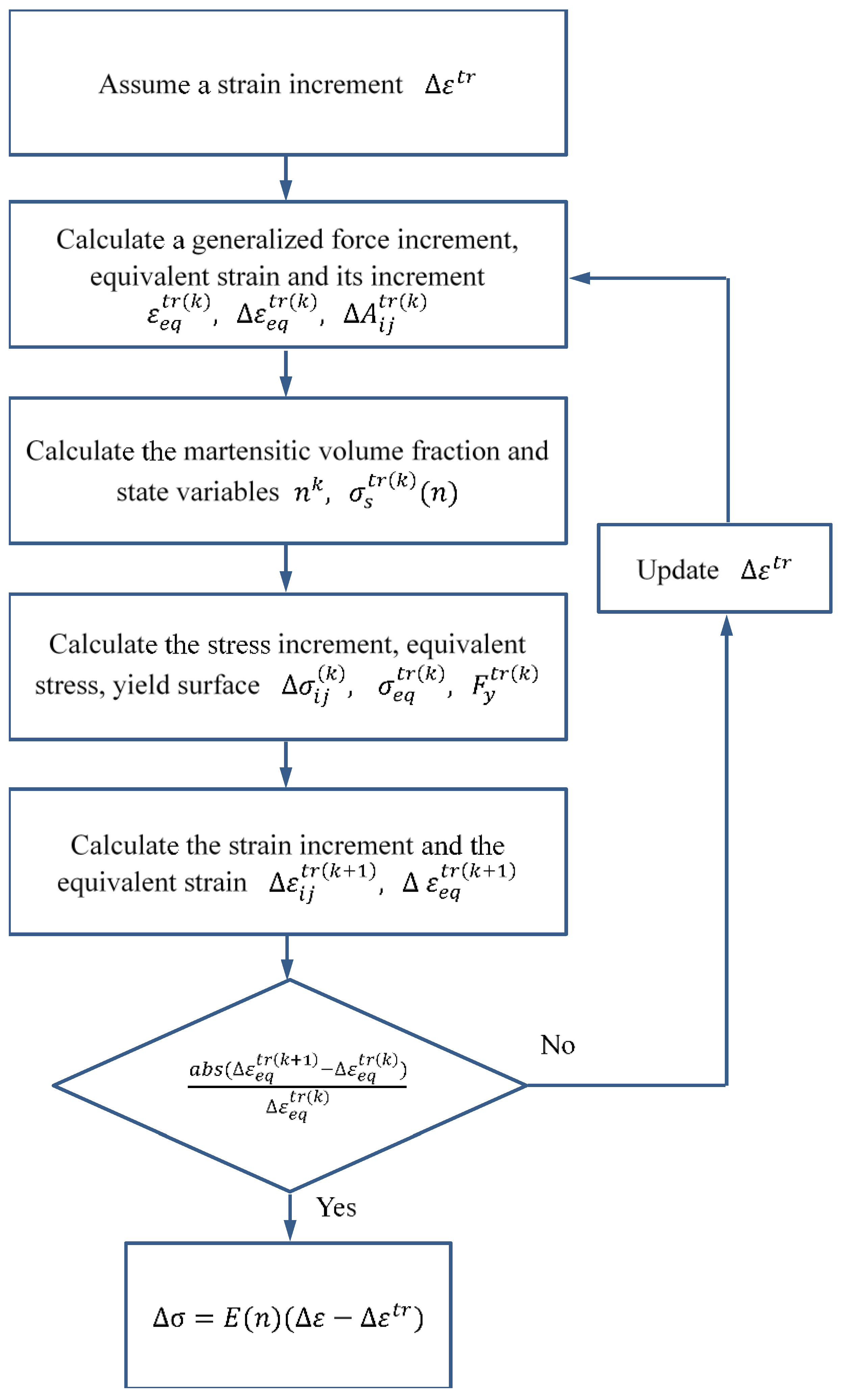
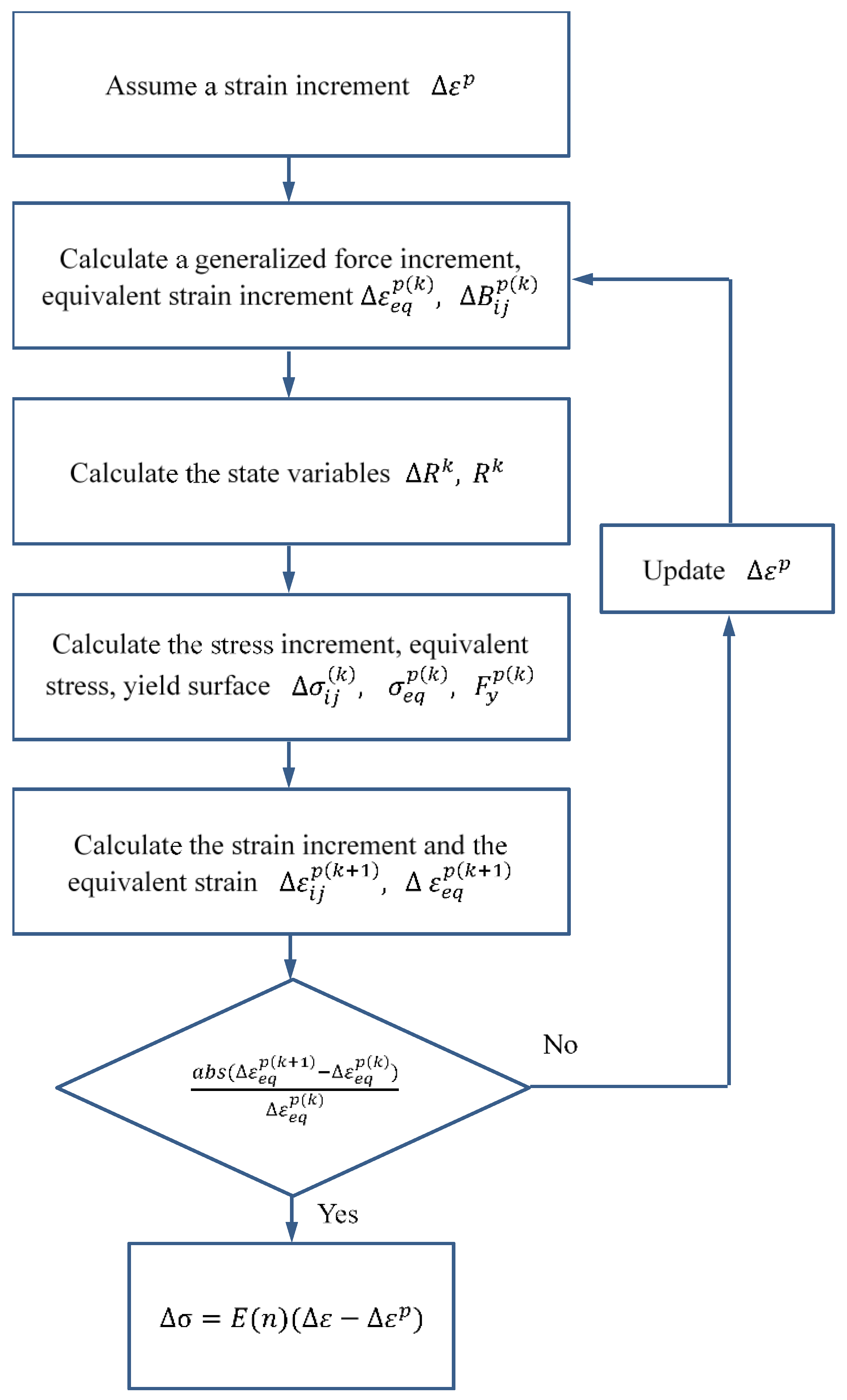
2.5. Iteration Algorithm
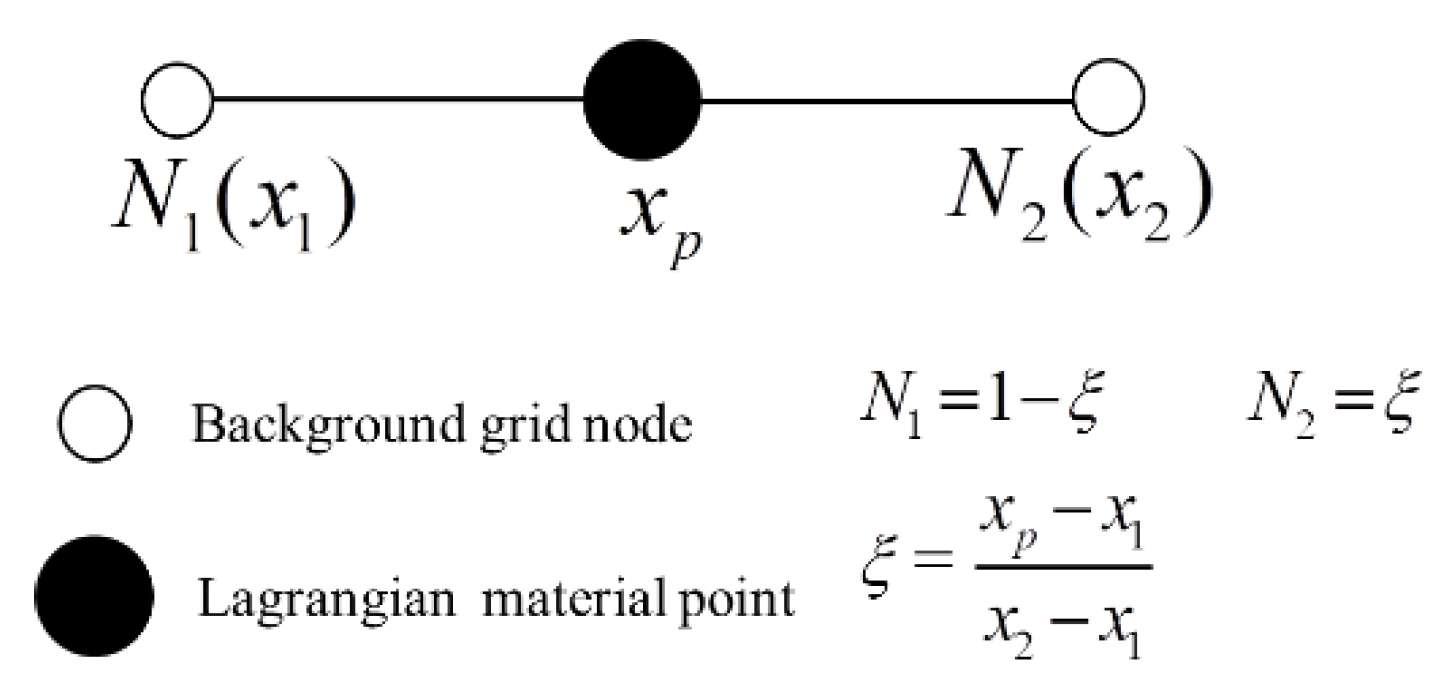
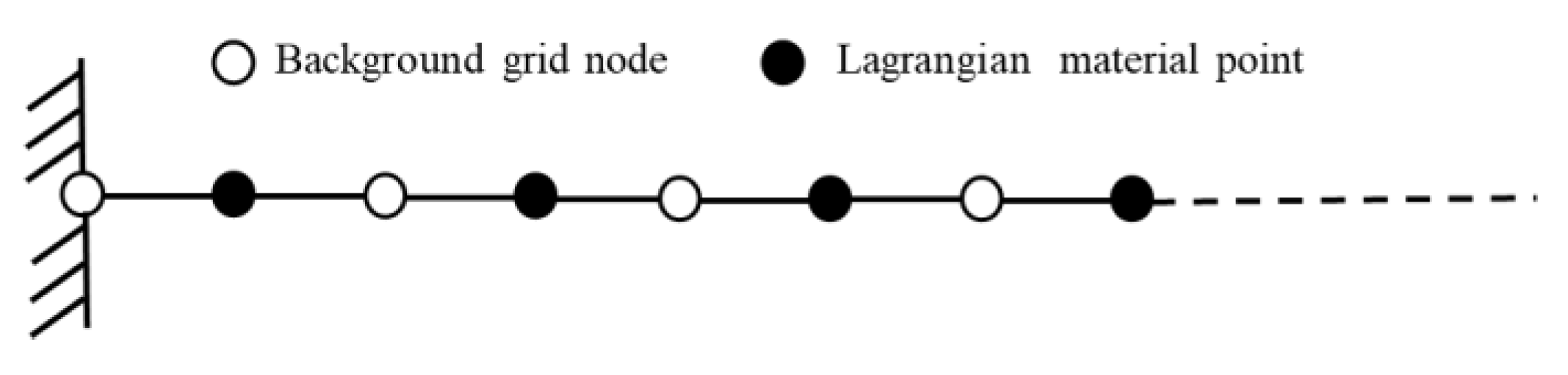
2.6. MPM
3. Results and Discussion
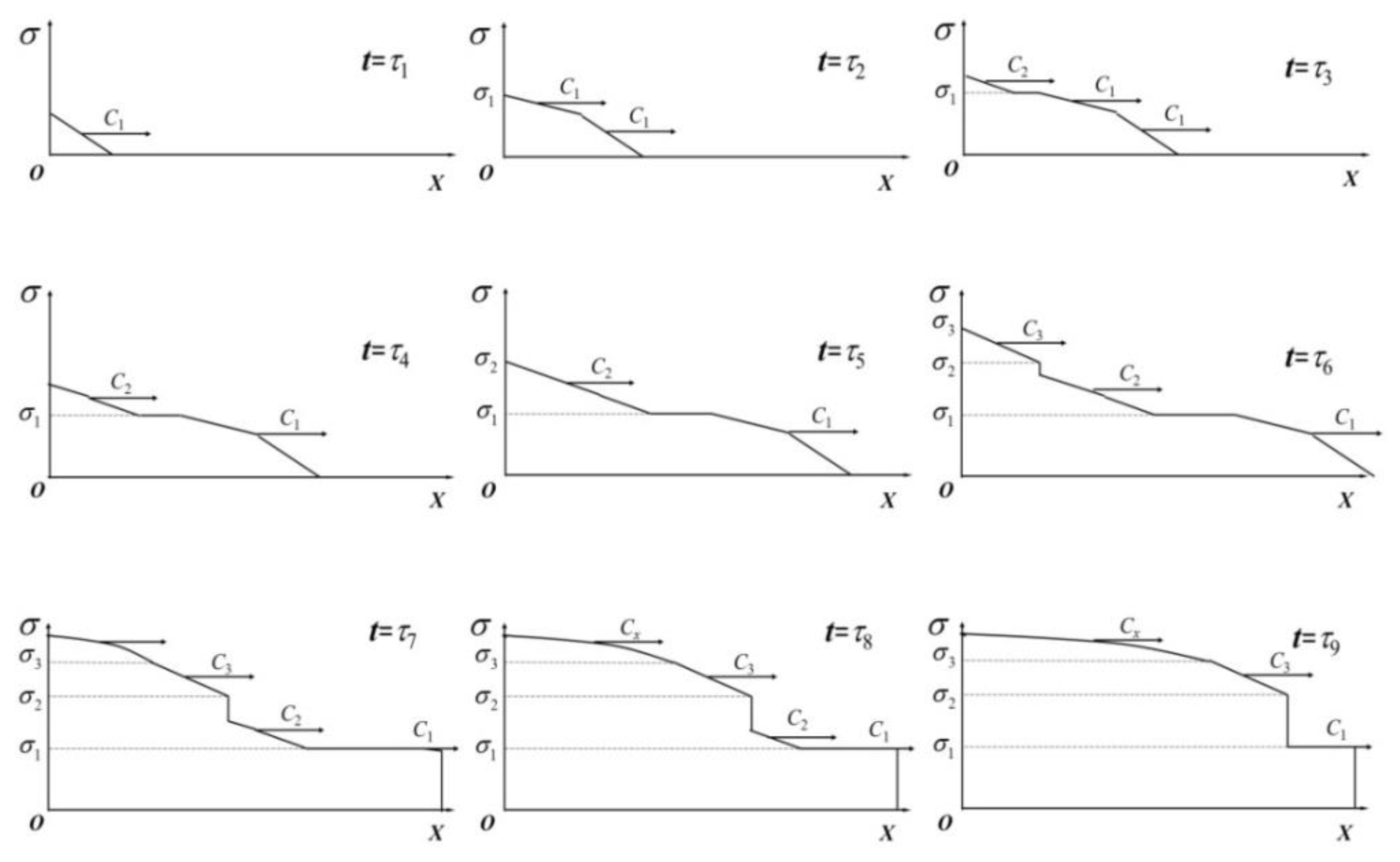
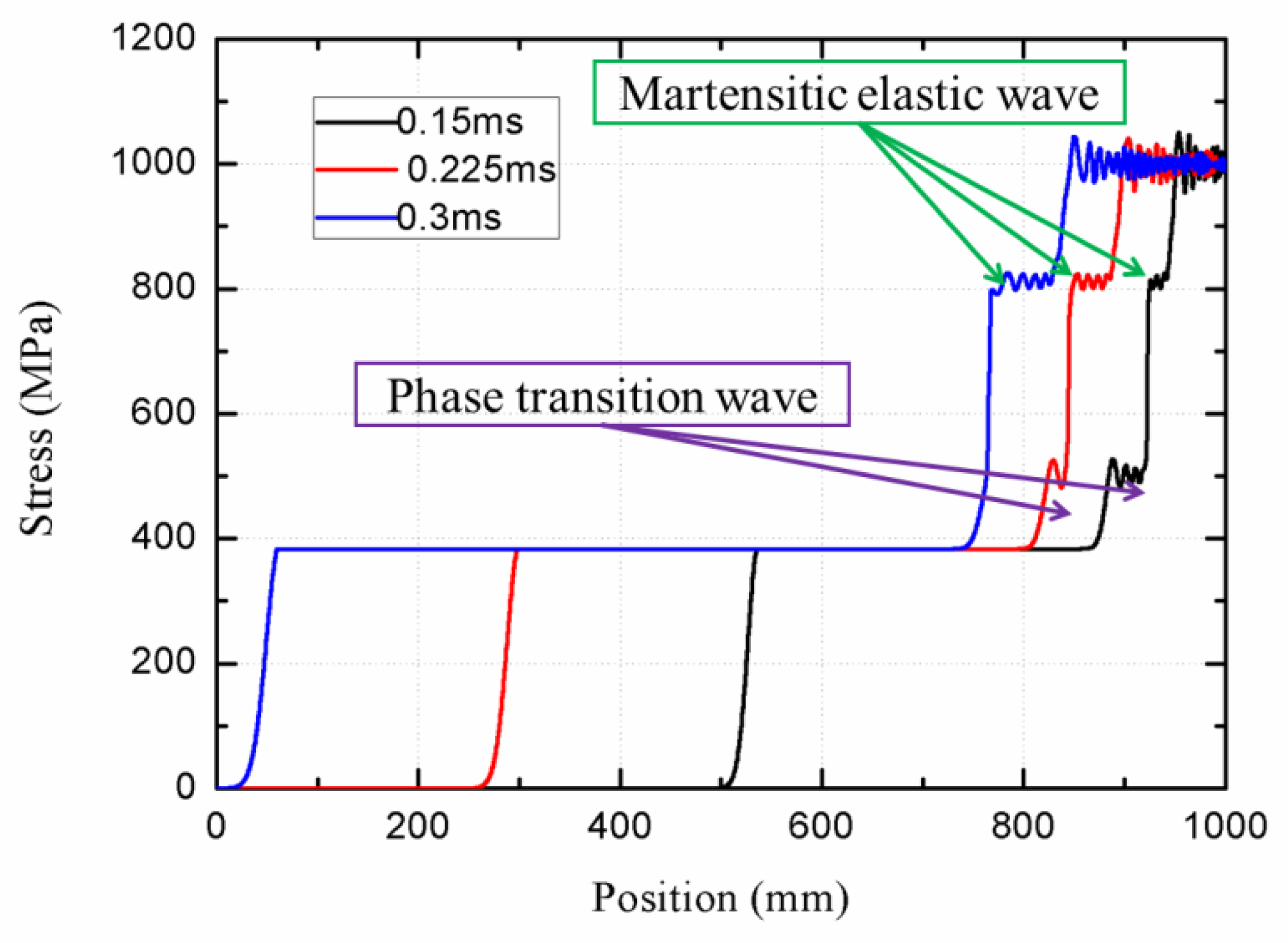
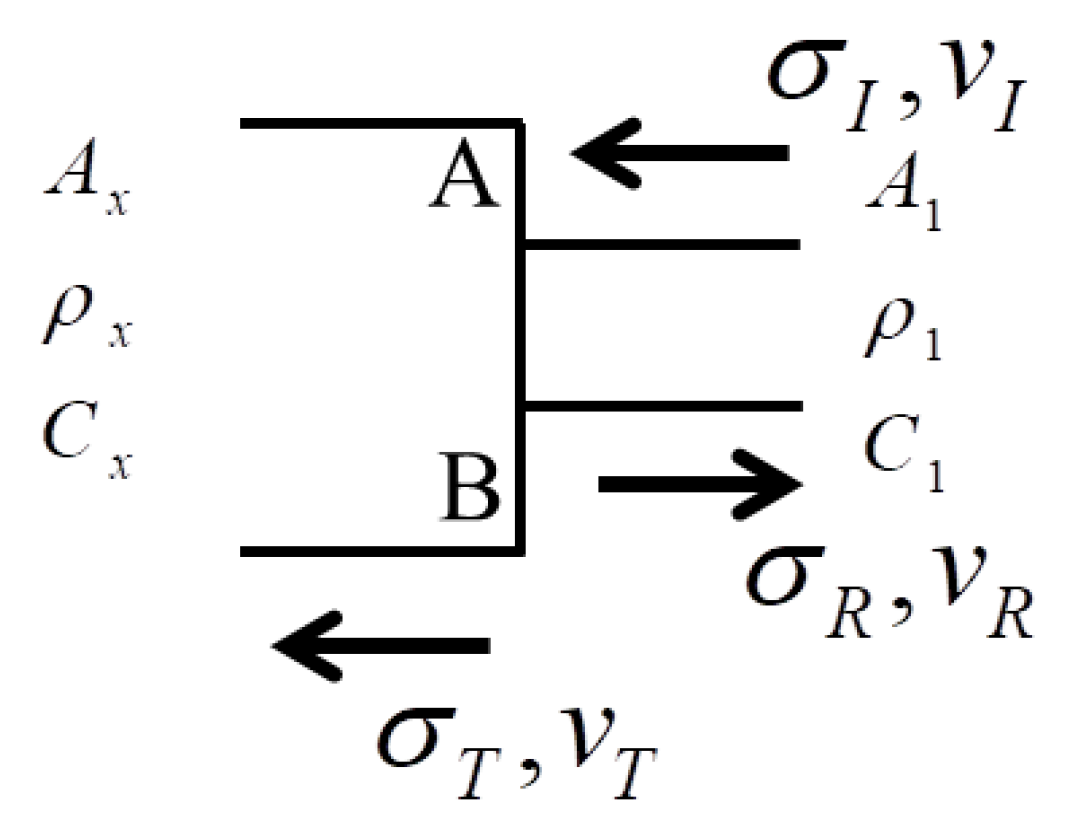
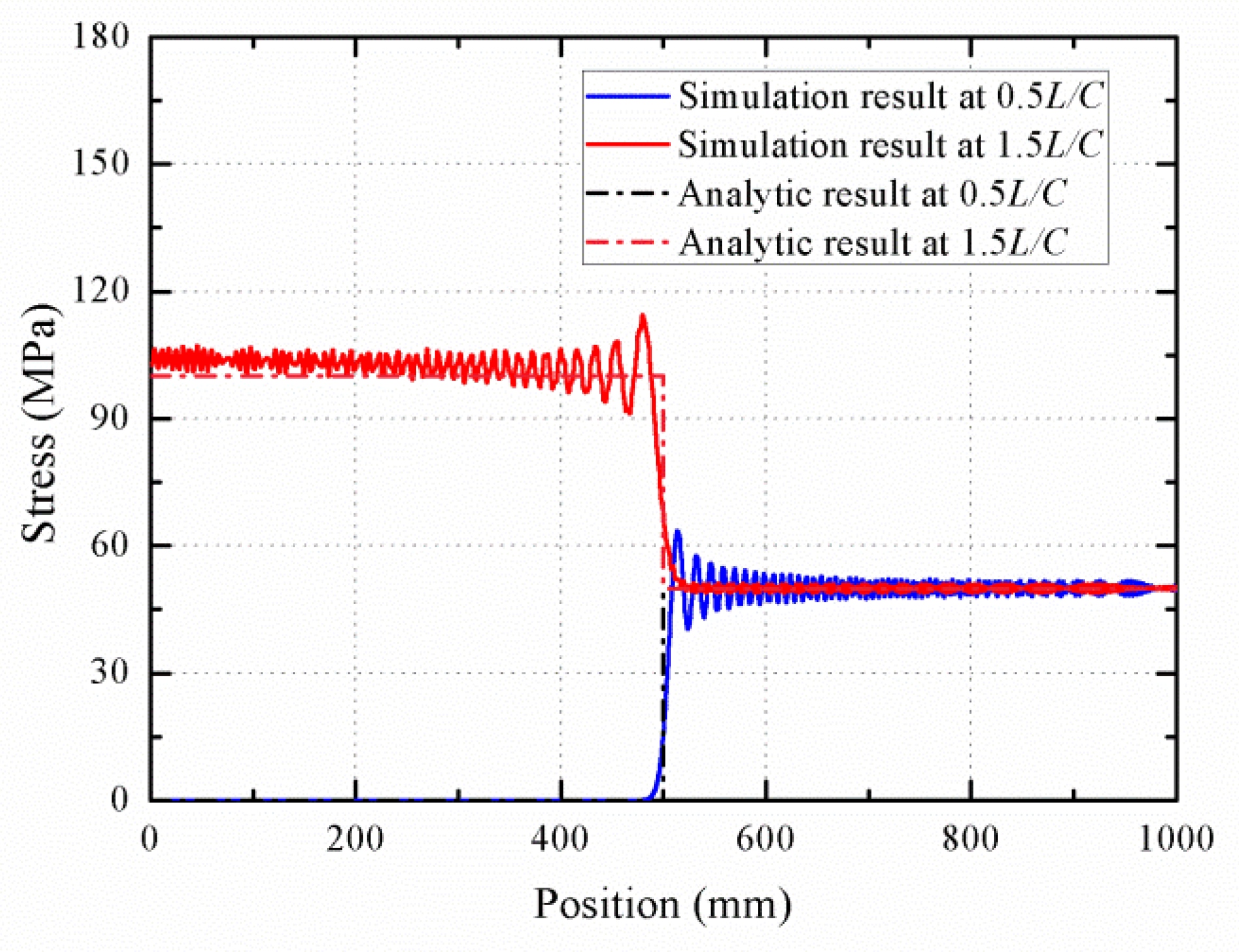
3.1. Stress Wave Analysis
3.2. Reflection Analysis
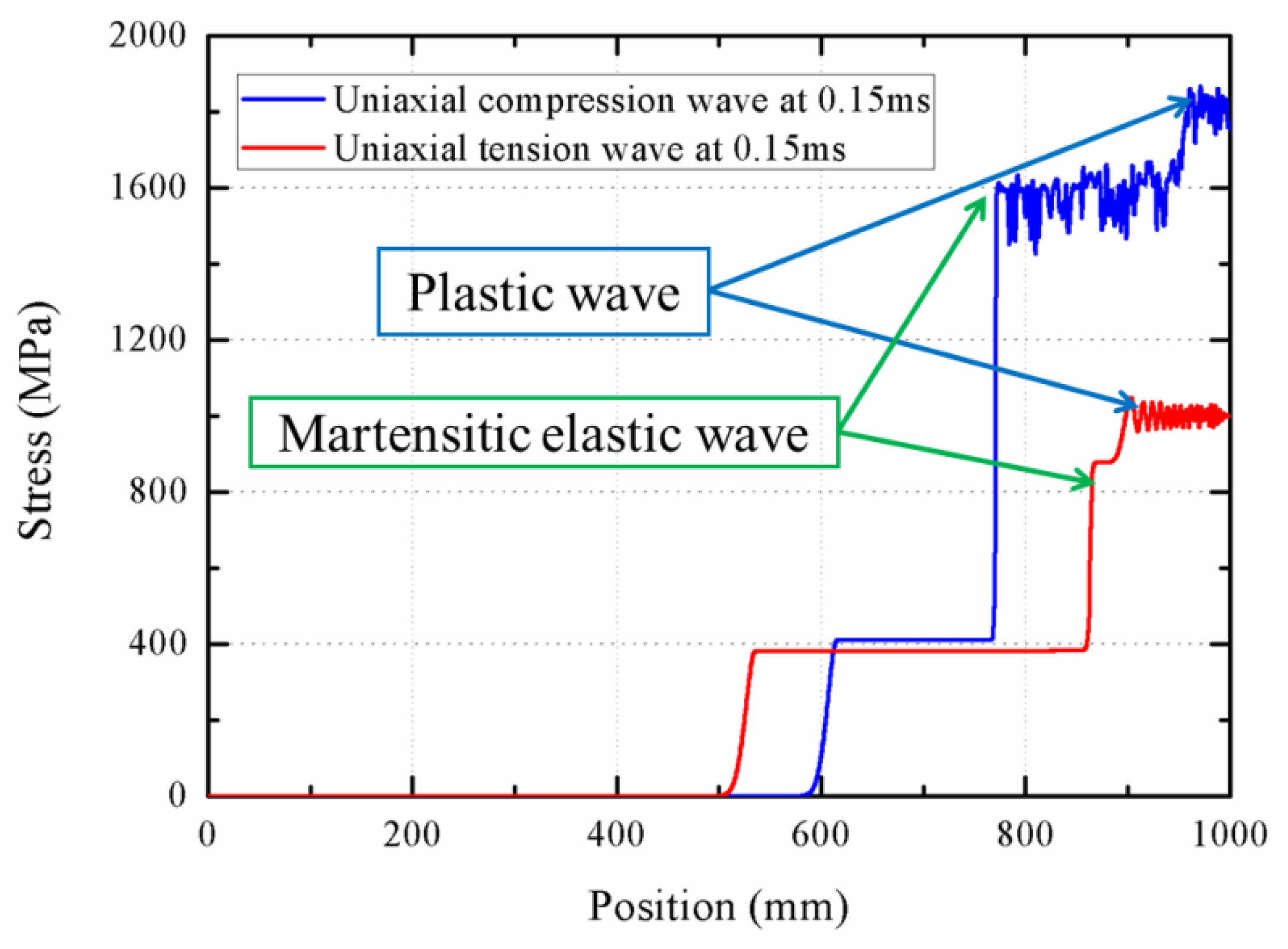
3.3. Effect of the Loading Direction
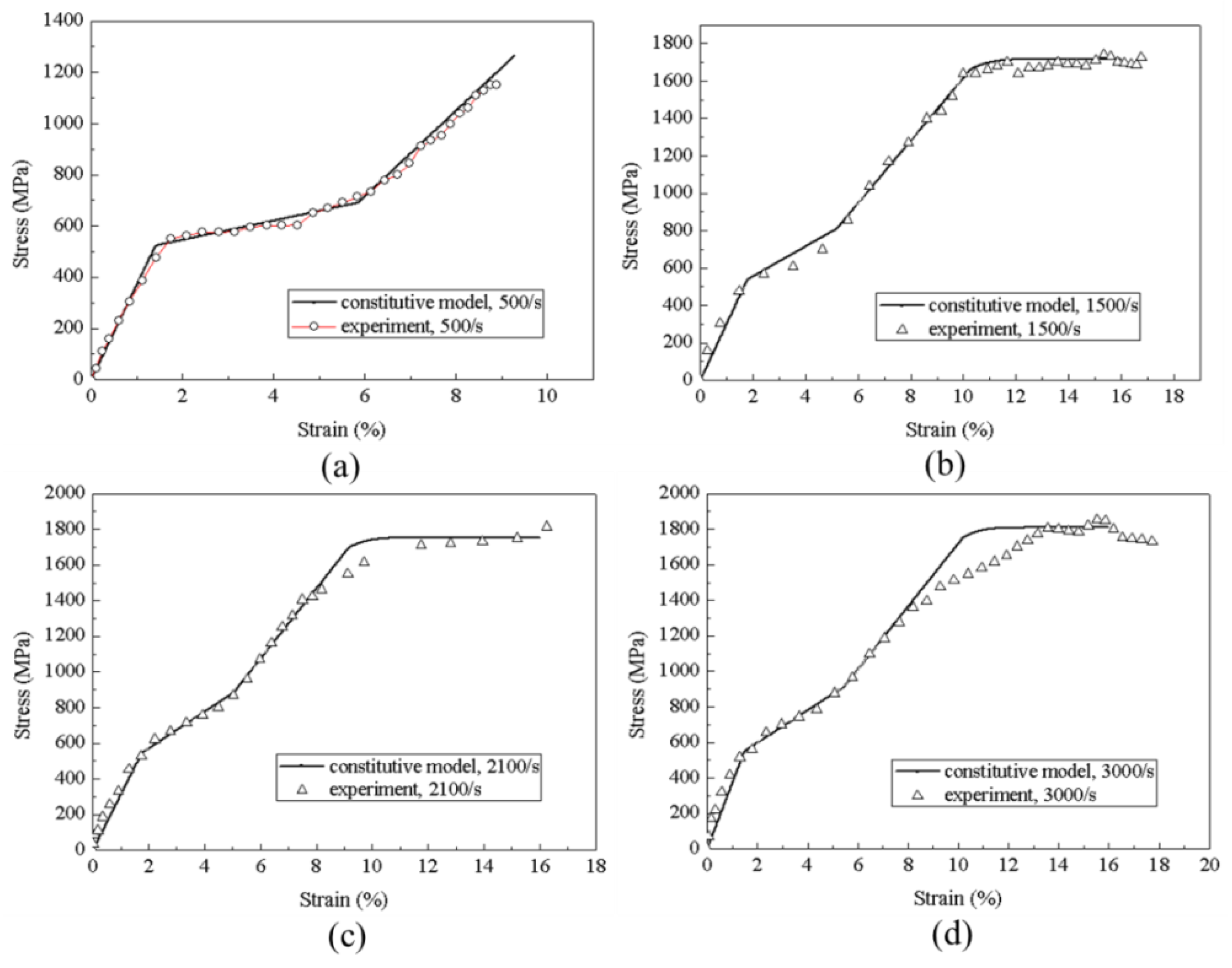
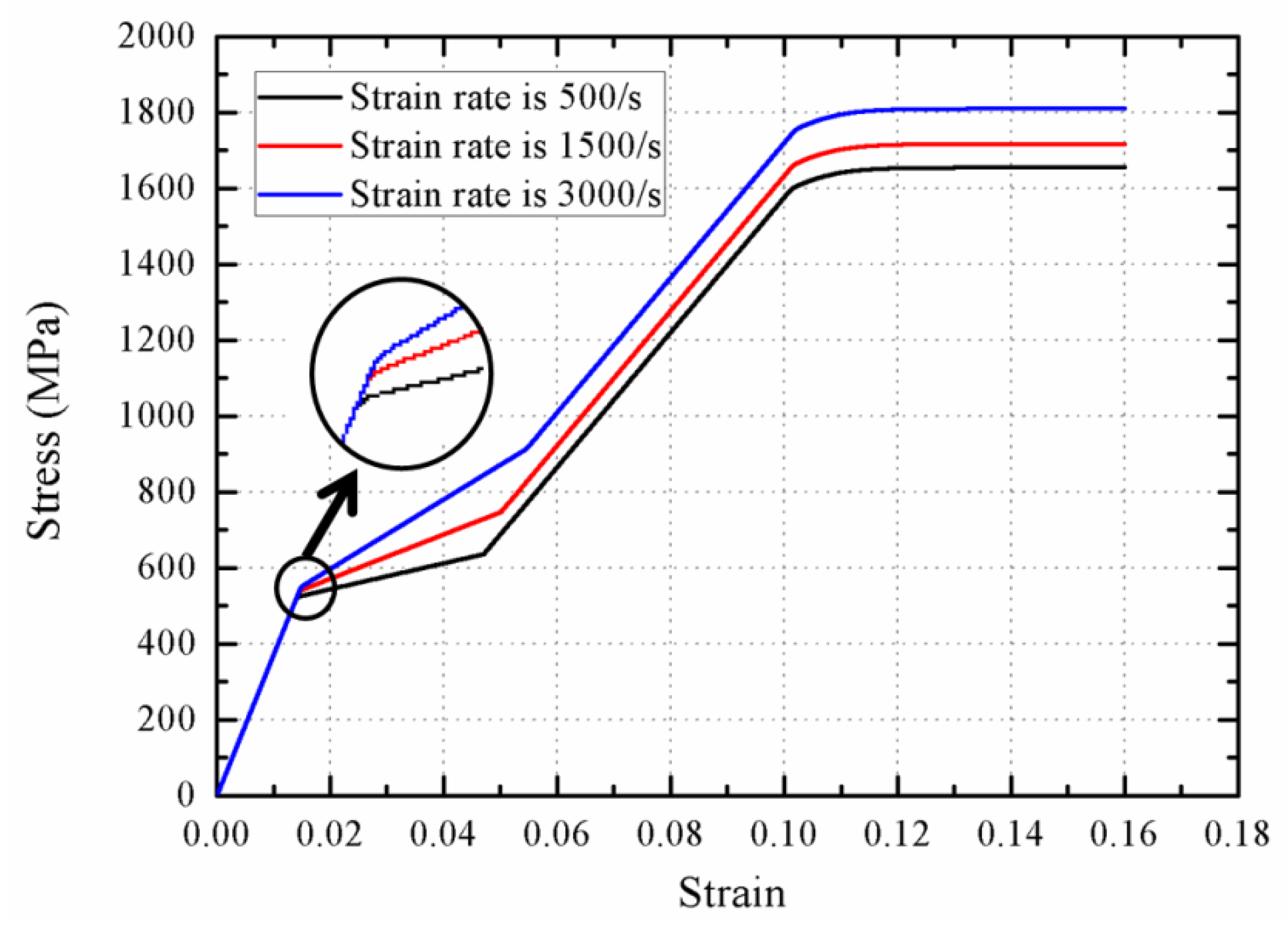
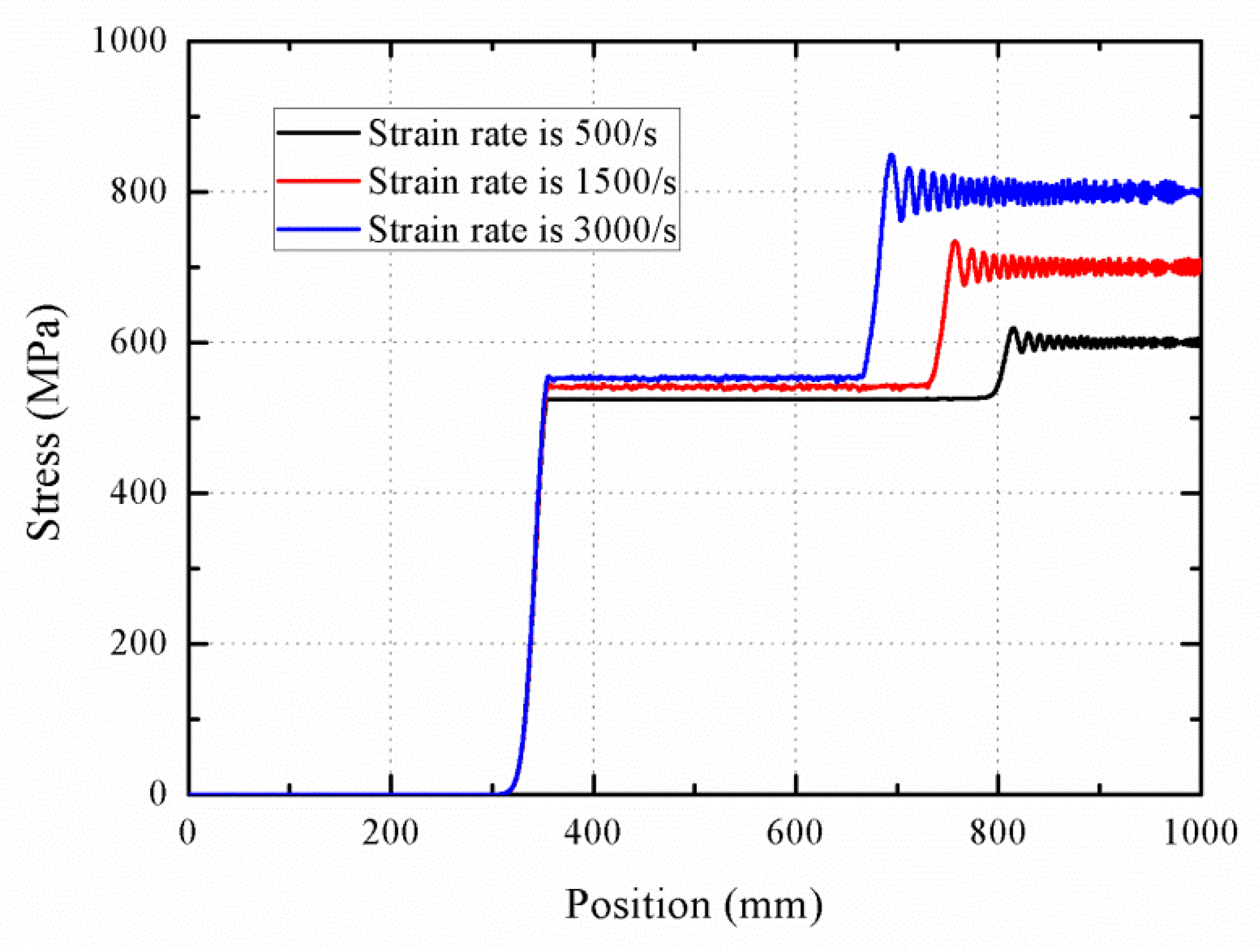
3.4. Effect of the Strain Rate
4. Conclusions
- (1)
- It is found that the stress wave obtained exhibits an obvious three-wave structure. During the process of wave propagation, the wave velocity in the phase transition is less than the one of austenite elastic wave, and the martensitic elastic wave follows the phase transition wave till the phase transition wave disappear. Herein, the three-wave structure degenerates into a double-wave structure.
- (2)
- Due to the occurrence of the phase transition wave during the wave reflection at the fixed boundary, the stress does not increase to two times as much as that of the original one. The stress increment is proportional to C2, which is proved by MPM solution.
- (3)
- The influences of loading direction and stain rate are investigated comprehensively. It is found that the velocity of phase transition wave increases with increasing strain rate. In addition, the loading direction has a distinct effect on the martensitic elastic wave and plastic wave propagation. The martensite elastic wave velocity under tensile condition is less than that with compressive loading, but the plastic wave velocity under compression is less than that by tensile loading.
Author Contributions
Funding
Conflicts of Interest
References
- Jani, J.M.; Leary, M.; Subic, A.; Gibson, M.A. A review of shape memory alloy research, applications and opportunities. Mater. Des. 2014, 56, 1078–1113. [Google Scholar] [CrossRef]
- Otsuka, K.; Ren, X. Physical metallurgy of Ti–Ni-based shape memory alloys. Prog. Mater. Sci. 2005, 50, 511–678. [Google Scholar] [CrossRef] [Green Version]
- Cisse, C.; Zaki, W.; Zineb, T.B. A review of constitutive models and modeling techniques for shape memory alloys. Int. J. Plast. 2016, 76, 244–284. [Google Scholar] [CrossRef]
- Manchiraju, S.; Anderson, P.M. Coupling between martensitic phase transformations and plasticity: A microstructure-based finite element model. Int. J. Plast. 2010, 26, 1508–1526. [Google Scholar] [CrossRef]
- Yu, C.; Kang, G.; Kan, Q.; Song, D. A micromechanical constitutive model based on crystal plasticity for thermo-mechanical cyclic deformation of NiTi shape memory alloys. Int. J. Plast. 2013, 44, 161–191. [Google Scholar] [CrossRef]
- Yu, C.; Kang, G.; Kan, Q. A micromechanical constitutive model for grain size dependent thermo-mechanically coupled inelastic deformation of super-elastic NiTi shape memory alloy. Int. J. Plast. 2018, 105, 99–127. [Google Scholar] [CrossRef]
- Ackland, G.J.; Jones, A.P.; Noble-Eddy, R. Molecular dynamics simulations of the martensitic phase transition process. Mater. Sci. Eng. A 2008, 481, 11–17. [Google Scholar] [CrossRef]
- Kastner, O.; Eggeler, G.; Weiss, W.; Ackland, G.J. Molecular dynamics simulation study of microstructure evolution during cyclic martensitic transformations. J. Mech. Phys. Solids 2011, 59, 1888–1908. [Google Scholar] [CrossRef]
- Tanaka, K.; Kobayashi, S.; Sato, Y. Thermomechanics of transformation pseudoelasticity and shape memory effect in alloys. Int. J. Plast. 1986, 2, 59–72. [Google Scholar] [CrossRef]
- Boyd, J.G.; Lagoudas, D.C. A thermodynamical constitutive model for shape memory materials. Part i. The monolithic shape memory alloy. Int. J. Plast. 1996, 12, 805–842. [Google Scholar] [CrossRef]
- Boyd, J.G.; Lagoudas, D.C. A thermodynamical constitutive model for shape memory materials. Part ii. The SMA composite material. Int. J. Plast. 1996, 12, 843–873. [Google Scholar] [CrossRef]
- Lagoudas, D.C.; Hartl, D.; Chemisky, Y.; Machado, L.; Popov, P. Constitutive model for the numerical analysis of phase transformation in polycrystalline shape memory alloys. Int. J. Plast. 2012, 32–33, 155–183. [Google Scholar] [CrossRef]
- Auricchio, F.; Taylor, R.L. Shape-memory alloys: Modelling and numerical simulations of the finite-strain superelastic behavior. Comput. Method Appl. Mech. Eng. 1997, 143, 175–194. [Google Scholar] [CrossRef]
- Auricchio, F. A robust integration-algorithm for a finite-strain shape-memory-alloy superelastic model. Int. J. Plast. 2001, 17, 971–990. [Google Scholar] [CrossRef]
- Kan, Q.; Kang, G. Constitutive model for uniaxial transformation ratchetting of super-elastic NiTi shape memory alloy at room temperature. Int. J. Plast. 2010, 26, 441–465. [Google Scholar] [CrossRef]
- Shi, X.; Zeng, X.; Chen, H. Constitutive model for the dynamic response of a NiTi shape memory alloy. Mater. Res. Express 2016, 3, 076502. [Google Scholar] [CrossRef]
- Sadeghi, O.; Bakhtiari-Nejad, M.; Yazdandoost, F.; Shahab, S.; Mirzaeifar, R. Dissipation of cavitation-induced shock waves energy through phase transformation in NiTi alloys. Int. J. Mech. Sci. 2018, 137, 304–314. [Google Scholar] [CrossRef]
- Xi, W.; Xia, W.; Wu, X.; Wei, Y.; Huang, C. Microstructure and mechanical properties of an austenite NiTi shape memory alloy treated with laser induced shock. Mater. Sci. Eng. A 2013, 578, 1–5. [Google Scholar] [Green Version]
- Wang, X.; Xia, W.; Wu, X.; Wei, Y.; Huang, C. In-situ investigation of dynamic deformation in niti shape memory alloys under laser induced shock. Mech. Mater. 2017, 114, 69–75. [Google Scholar] [CrossRef]
- Bekker, A.; Jimenez-Victory, J.C.; Popov, P.; Lagoudas, D.C. Impact induced propagation of phase transformation in a shape memory alloy rod. Int. J. Plast. 2002, 18, 1447–1479. [Google Scholar] [CrossRef]
- Fǎciu, C.; Molinari, A. On the longitudinal impact of two phase transforming bars. Elastic versus a rate-type approach. Part i: The elastic case. Int. J. Solids Struct. 2006, 43, 497–522. [Google Scholar] [CrossRef]
- Dong, Y.; Wang, D.; Randolph, M.F. Investigation of impact forces on pipeline by submarine landslide using material point method. Ocean Eng. 2017, 146, 21–28. [Google Scholar] [CrossRef]
- Liu, P.; Liu, Y.; Zhang, X.; Guan, Y. Investigation on high-velocity impact of micron particles using material point method. Int. J. Impact Eng. 2015, 75, 241–254. [Google Scholar] [CrossRef]
- Lian, Y.P.; Zhang, X.; Zhou, X.; Ma, S.; Zhao, Y.L. Numerical simulation of explosively driven metal by material point method. Int. J. Impact Eng. 2011, 38, 238–246. [Google Scholar] [CrossRef]
- Dhakal, T.R.; Zhang, D.Z. Material point methods applied to one-dimensional shock waves and dual domain material point method with sub-points. J. Comput. Phys. 2016, 325, 301–313. [Google Scholar] [CrossRef] [Green Version]
- Chaboche, J.L.; Kanouté, P.; Azzouz, F. Cyclic inelastic constitutive equations and their impact on the fatigue life predictions. Int. J. Plast. 2012, 35, 44–66. [Google Scholar] [CrossRef]




| Ni | Co | Cu | Cr | Fe | Nb | C | H | O | N | Ti |
|---|---|---|---|---|---|---|---|---|---|---|
| 55.72% | 0.005% | 0.005% | 0.005% | 0.012% | 0.005% | 0.045% | 0.001% | 0.03% | 0.001% | 44.17% |
| Parameter | Value | Unit | Parameter | Value | Unit |
|---|---|---|---|---|---|
| 53,453 | MPa | 9280 | MPa | ||
| 0.3 | - | 0.3 | - | ||
| 380 | MPa | 552 | MPa | ||
| 730 | MPa | 0.044 | - | ||
| CA | 3.7 | MPa/K | CM | 5.4 | MPa/K |
| C1 | 0.038 | - | C2 | 0.075 | - |
| C3 | 0.012 | - | |||
| k1 | 400 | - | k2 | 600 | - |
| k3 | 400 | - | k4 | 800 | - |
| z1 | 10 | MPa | z2 | 170 | MPa |
| n1 | 3.0 | - | n2 | 3.0 | - |
| m | 50 | - | R1 | 260 | MPa |
| Parameter | Value | Unit | Parameter | Value | Unit |
|---|---|---|---|---|---|
| 37,130 | MPa | 19,280 | MPa | ||
| 0.3 | - | 0.3 | - | ||
| 409 | MPa | 552 | MPa | ||
| 1550 | MPa | 0.034 | - | ||
| CA | - | MPa/K | CM | 5.4 | MPa/K |
| C1 | 0.0337 | - | C2 | 0.0002 | - |
| C3 | 4 × 10−5 | - | |||
| k1 | 400 | - | k2 | 800 | - |
| k3 | 400 | - | k4 | 800 | - |
| z1 | 10 | MPa | z2 | 170 | MPa |
| n1 | 3.0 | - | n2 | 3.0 | - |
| m | 250 | - | R1 | 50 | MPa |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Y.; Zeng, X.; Chen, H.; Chen, J.; Wang, F. Investigation of the Propagation of Stress Wave in Nickel-Titanium Shape Memory Alloys. Materials 2018, 11, 1215. https://doi.org/10.3390/ma11071215
Cui Y, Zeng X, Chen H, Chen J, Wang F. Investigation of the Propagation of Stress Wave in Nickel-Titanium Shape Memory Alloys. Materials. 2018; 11(7):1215. https://doi.org/10.3390/ma11071215
Chicago/Turabian StyleCui, Yehui, Xiangguo Zeng, Huayan Chen, Jun Chen, and Fang Wang. 2018. "Investigation of the Propagation of Stress Wave in Nickel-Titanium Shape Memory Alloys" Materials 11, no. 7: 1215. https://doi.org/10.3390/ma11071215





