An Electroelastic Solution for Functionally Graded Piezoelectric Circular Plates under the Action of Combined Mechanical Loads
Abstract
:1. Introduction
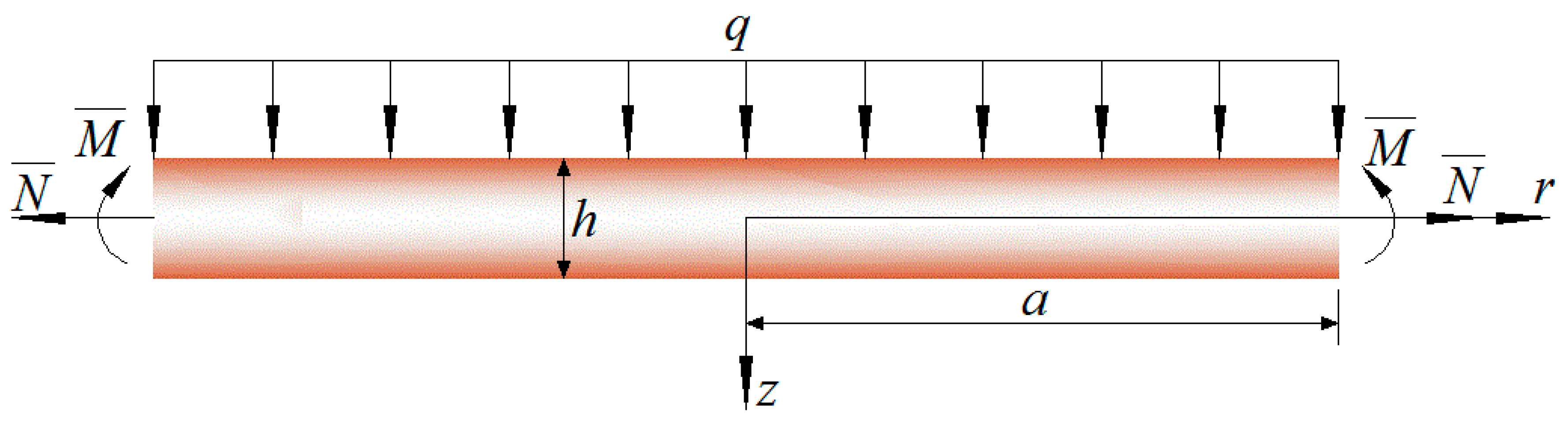
2. Basic Equations and Their Electroelastic Solution
3. Comparisons and Discussions
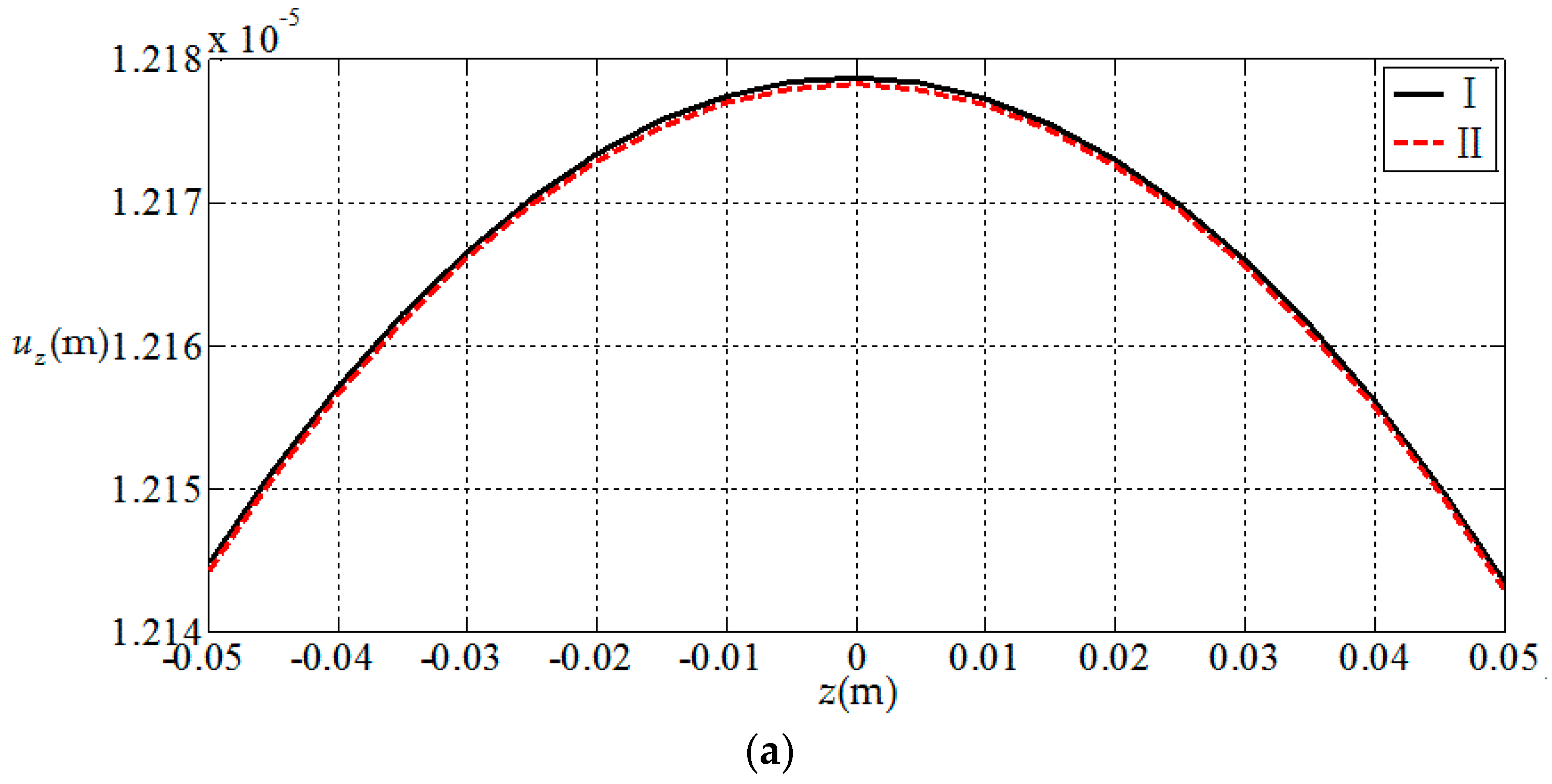
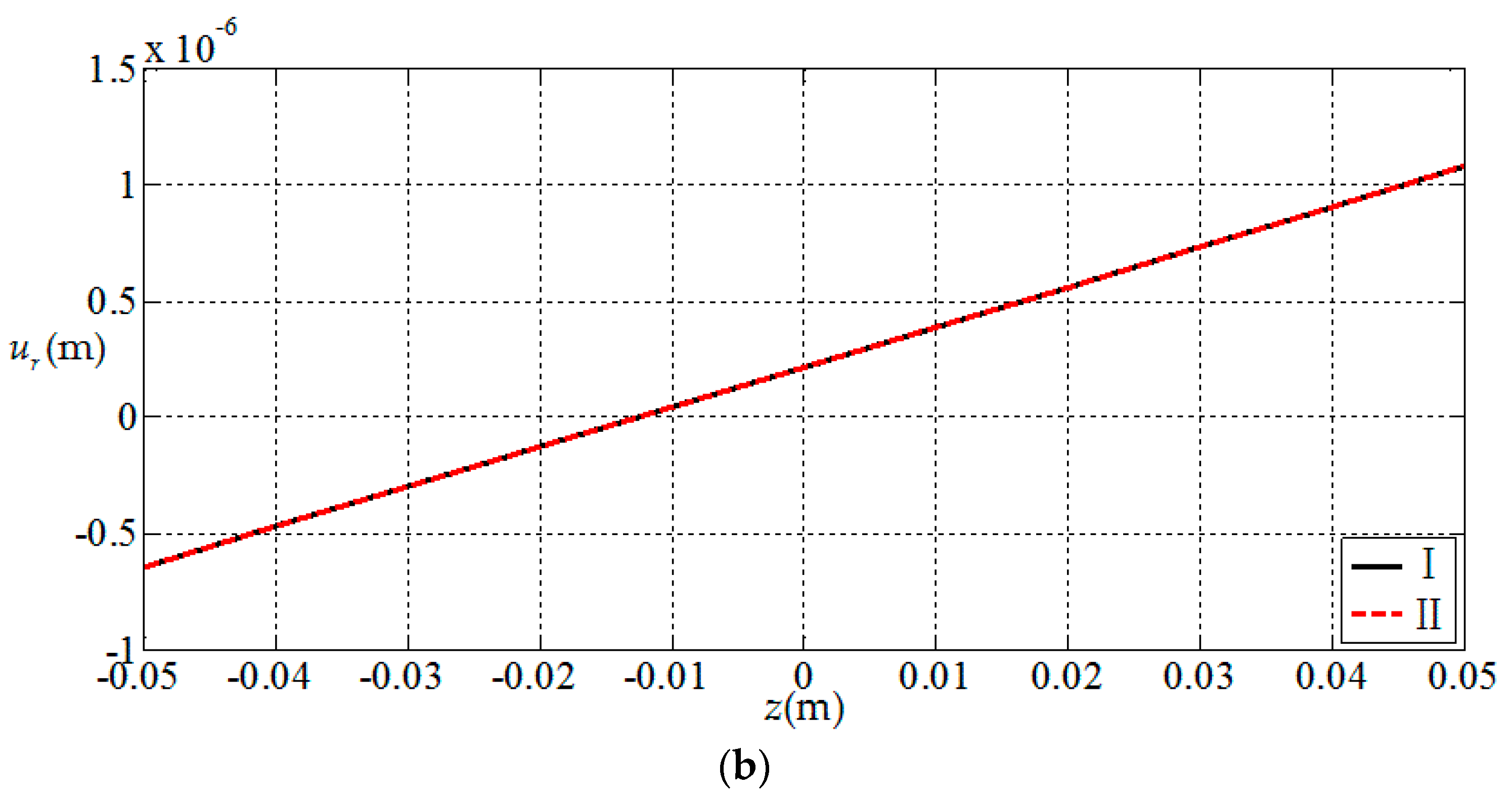
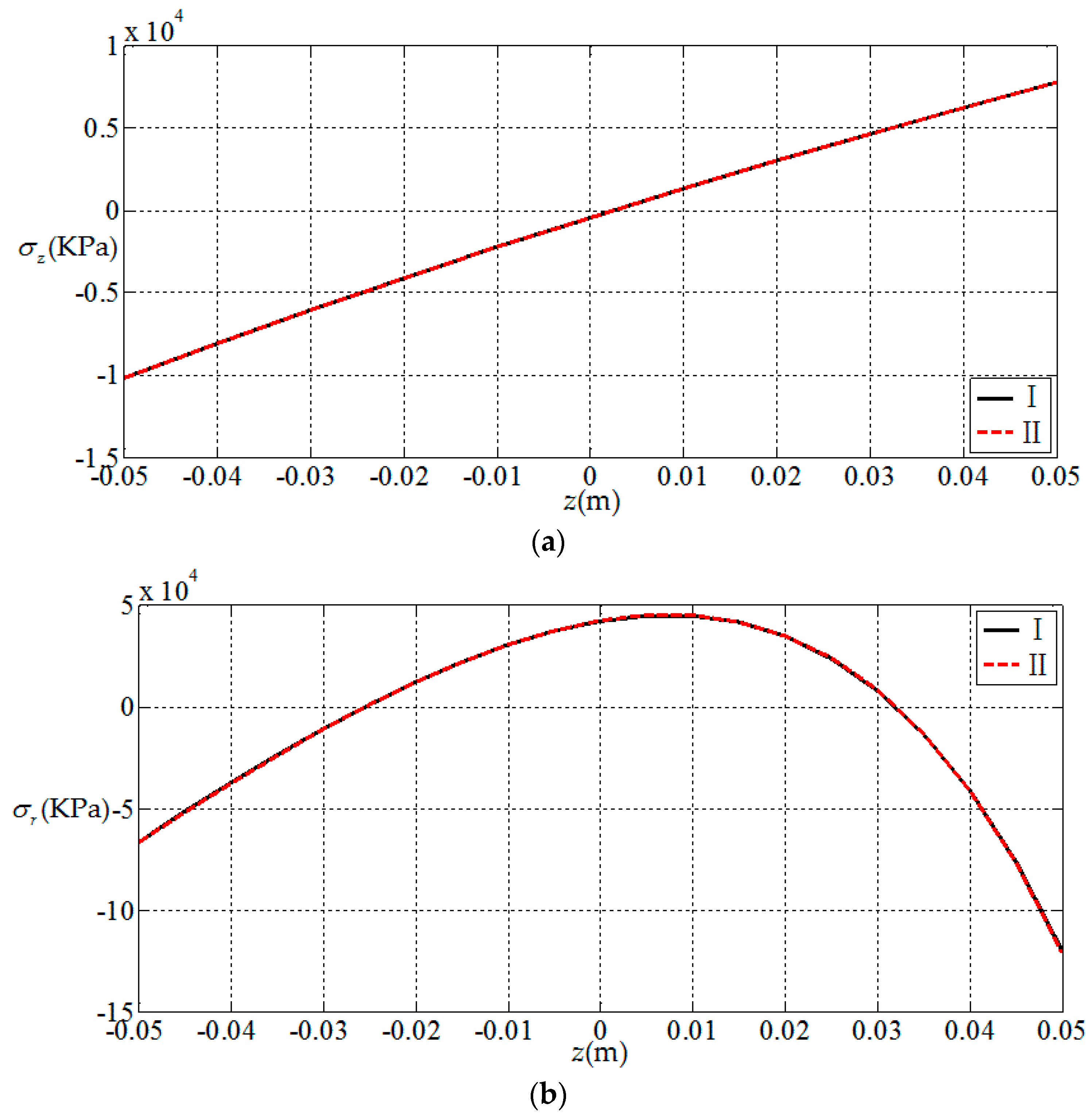
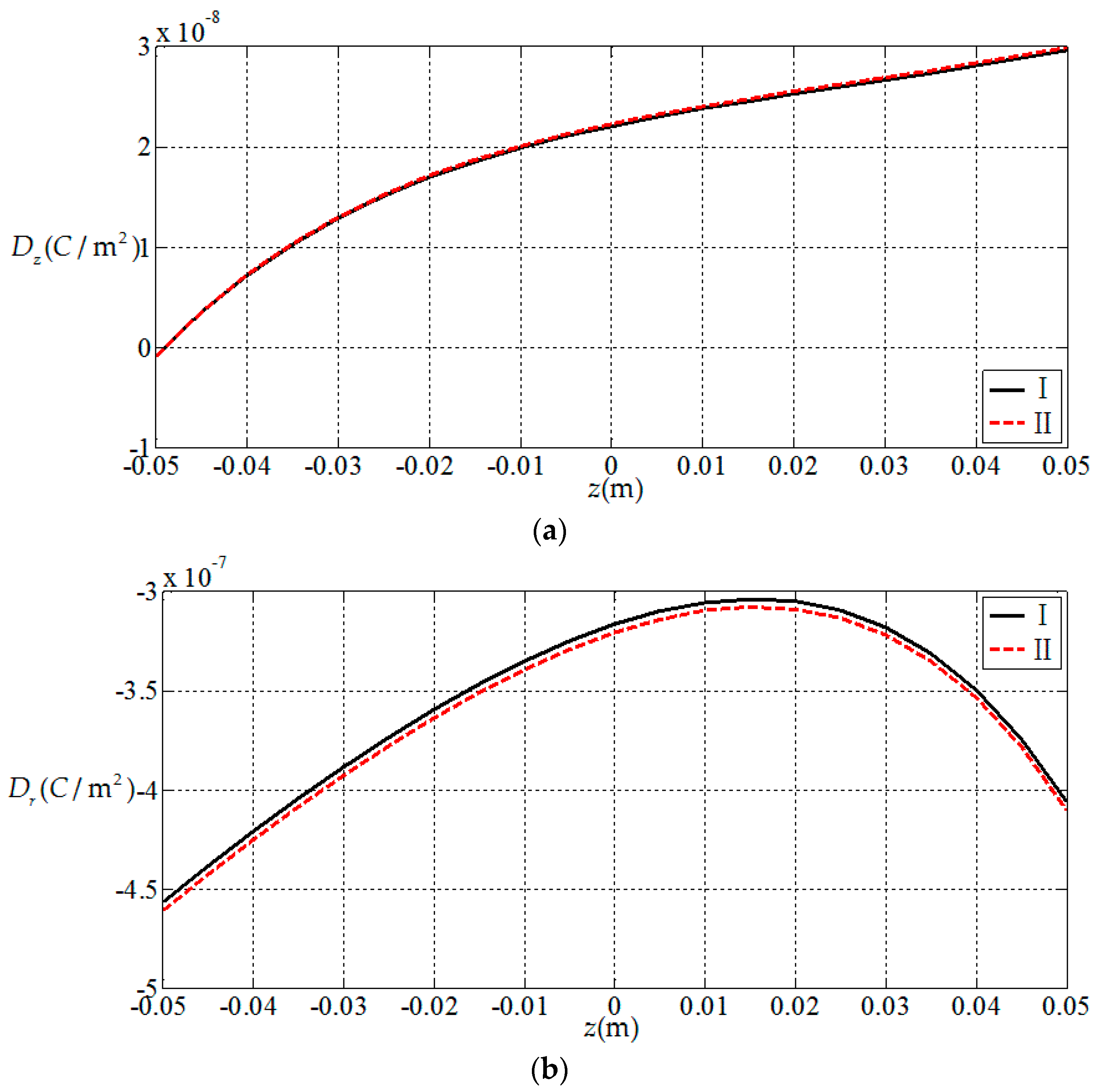
3.1. Comparisions with Existing Result
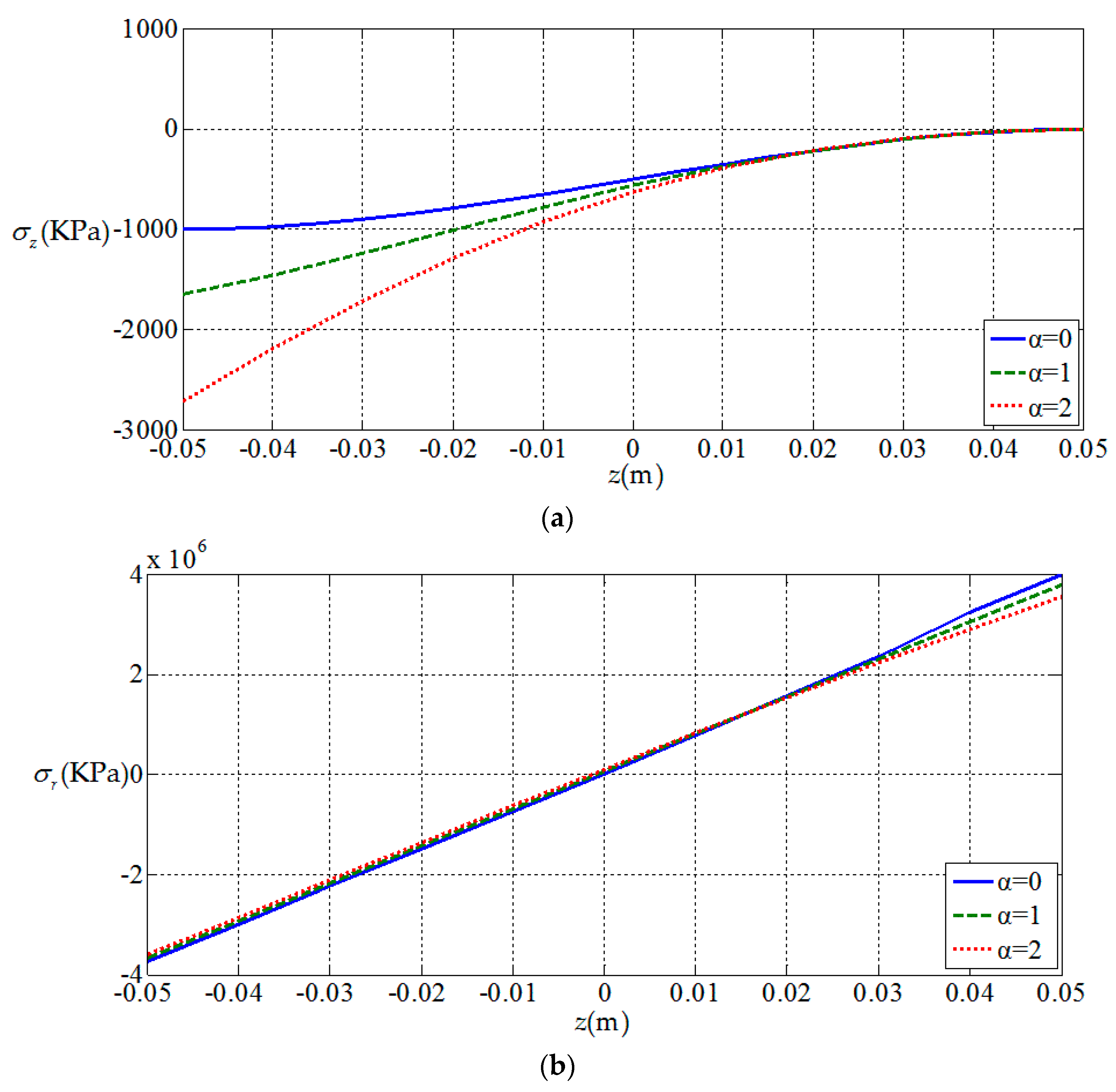
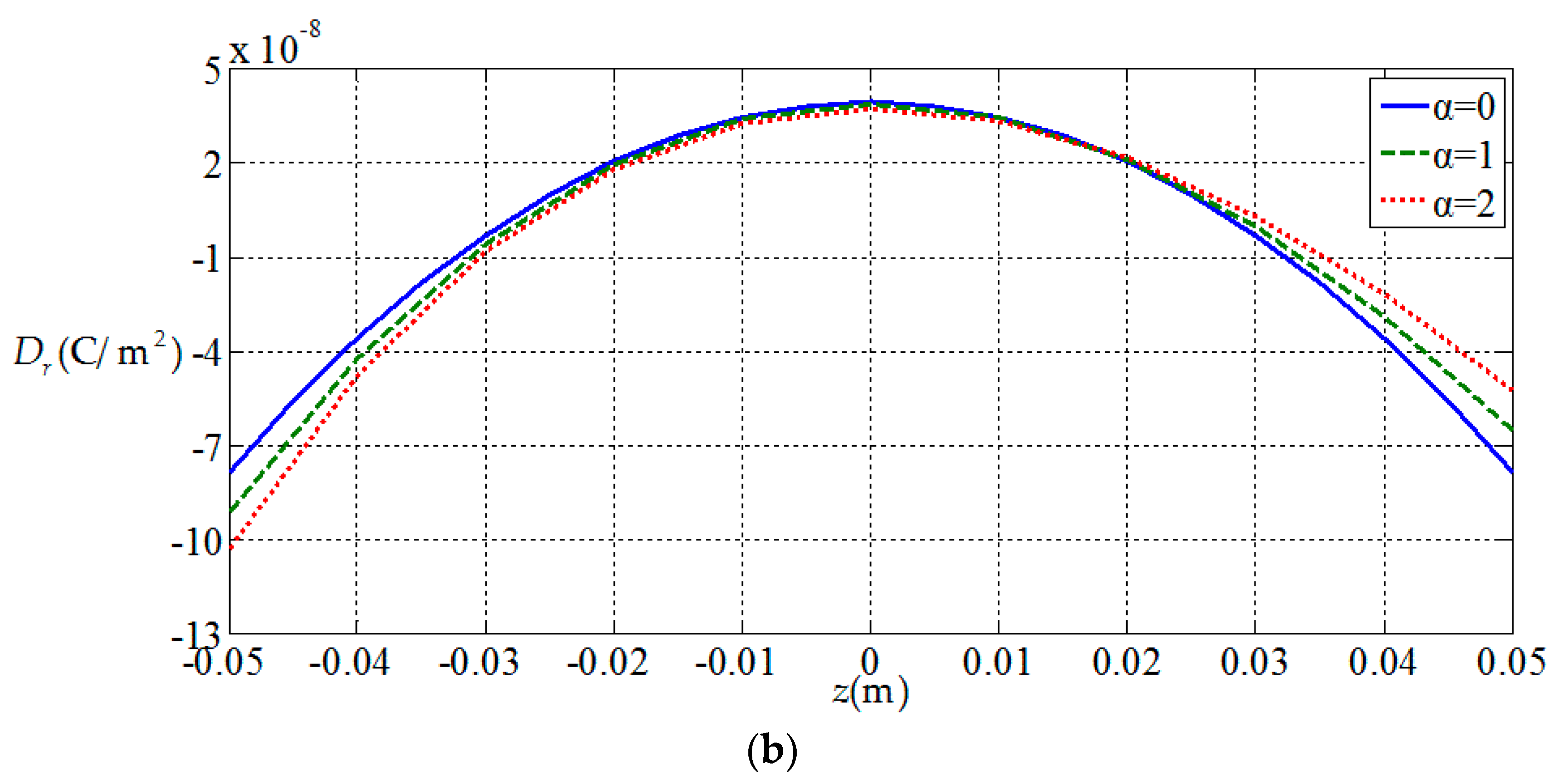
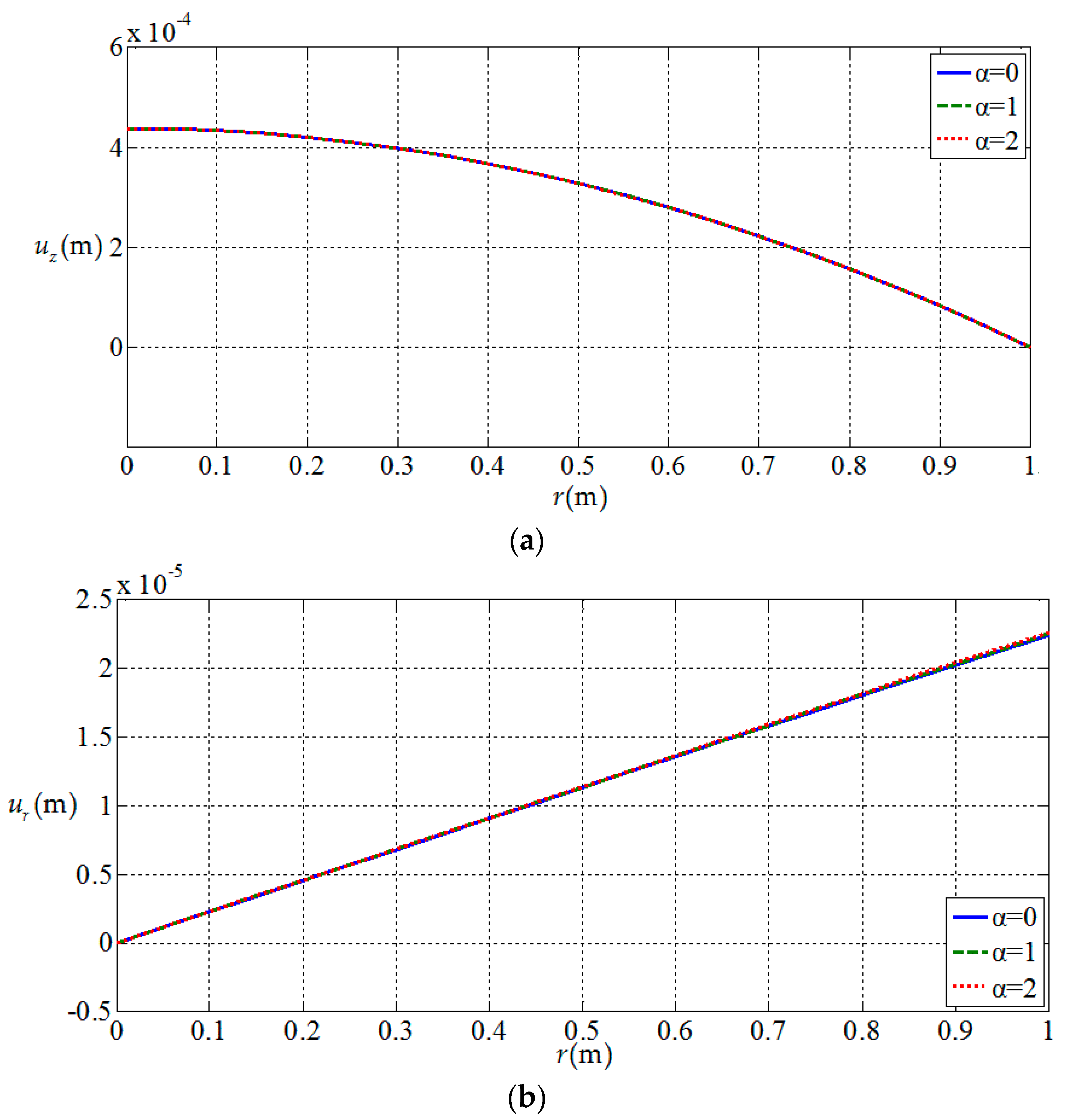
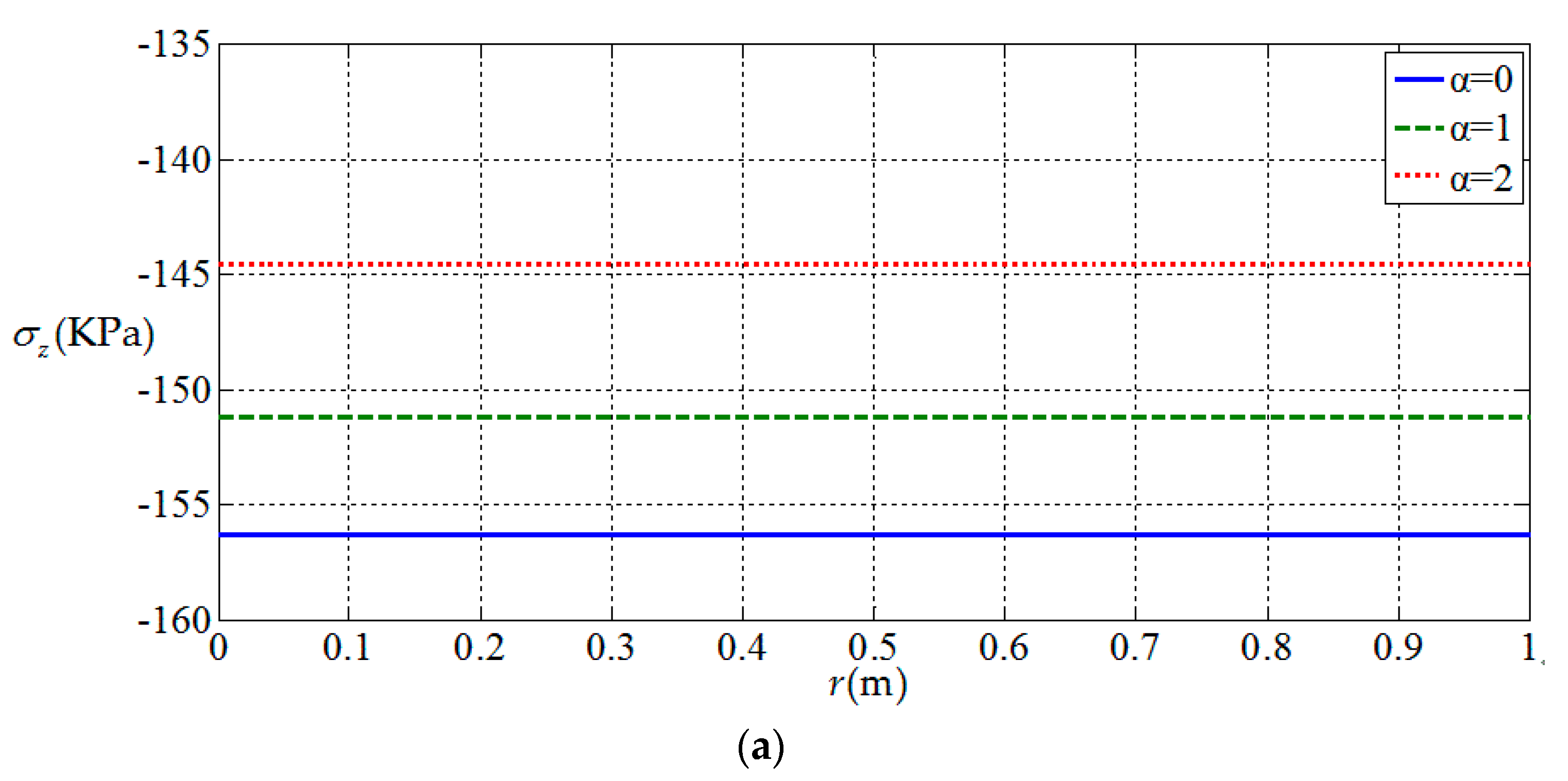
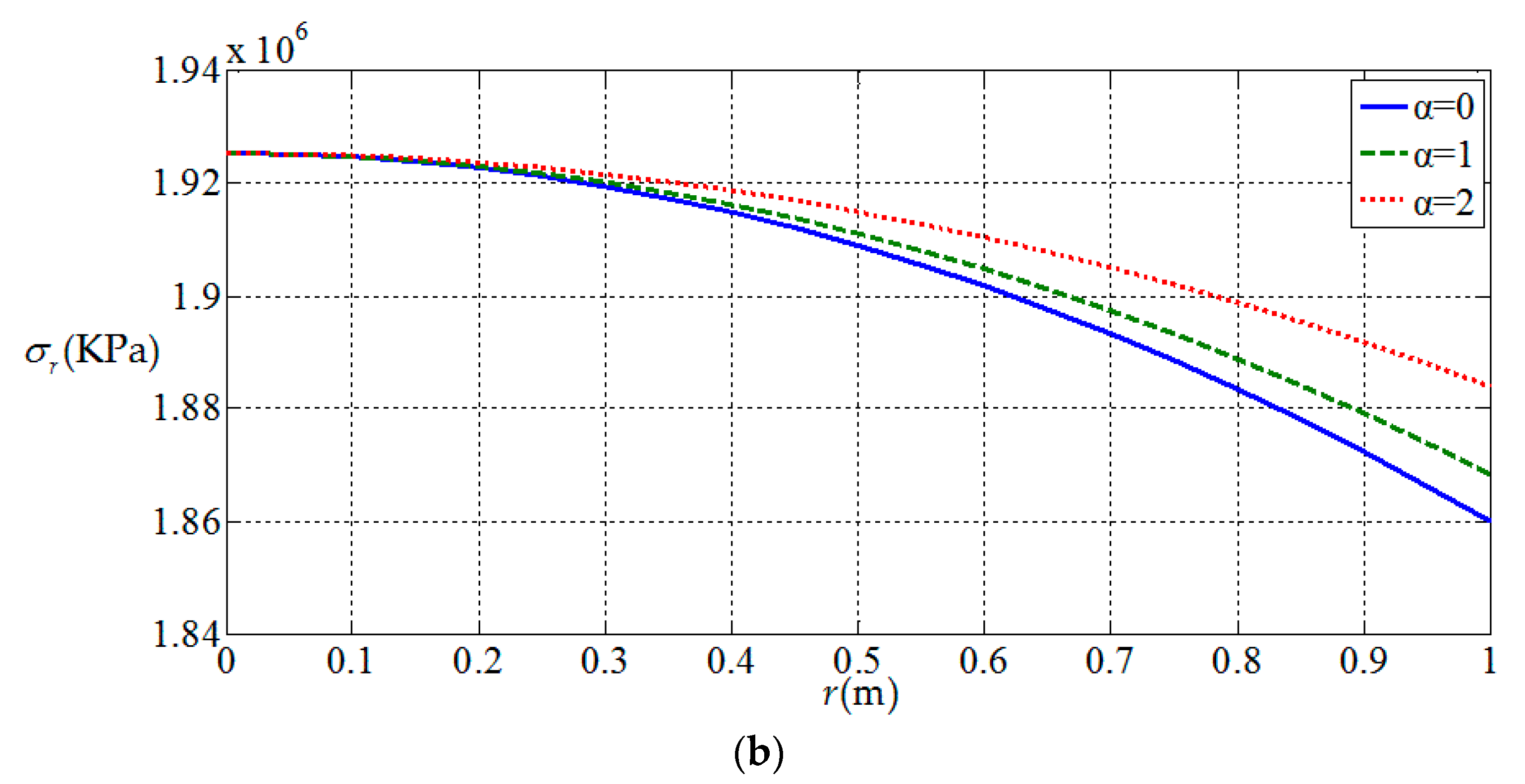
3.2. Influences of Functionally Graded Parameters
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Koizumi, M. The concept of FGM, ceramic transactions. Funct. Grad. Mater. 1993, 34, 3–10. [Google Scholar]
- Reddy, J.N.; Wang, C.M.; Kitipornchai, S. Axisymmetric bending of functionally graded circular and annular plates. Eur. J. Mech. A/Solids 1999, 18, 185–199. [Google Scholar] [CrossRef]
- Ma, L.S.; Wang, T.J. Nonlinear bending and post-buckling of functionally graded circular plates under mechanical and thermal loadings. Int. J. Solids Struct. 2003, 40, 3311–3330. [Google Scholar] [CrossRef]
- Chi, S.H.; Chung, Y.L. Mechanical behavior of functionally graded material plates under transverse load–Part I: Analysis. Int. J. Solids Struct. 2006, 43, 3657–3674. [Google Scholar] [CrossRef]
- Li, X.Y.; Ding, H.J.; Chen, W.Q. Pure bending of simply supported circular plate of transversely isotropic functionally graded material. J. Zhejiang Univ. 2006, 7, 1324–1328. [Google Scholar] [CrossRef]
- Naderi, A.; Saidi, A.R. On pre-buckling configuration of functionally graded Mindlin rectangular plates. Mech. Res. Commun. 2010, 37, 535–538. [Google Scholar] [CrossRef]
- Martínez-Pañeda, E.; Gallego, R. Numerical analysis of quasi-static fracture in functionally graded materials. Int. J. Mech. Mater. Des. 2015, 11, 405–424. [Google Scholar] [CrossRef]
- He, X.T.; Pei, X.X.; Sun, J.Y.; Zheng, Z.L. Simplified theory and analytical solution for functionally graded thin plates with different moduli in tension and compression. Mech. Res. Commun. 2016, 74, 72–80. [Google Scholar] [CrossRef]
- Fu, Y.; Yao, J.; Wan, Z.; Zhao, G. Free vibration analysis of moderately thick orthotropic functionally graded plates with general boundary restraints. Materials 2018, 11, 273. [Google Scholar] [CrossRef] [PubMed]
- Brischetto, S.; Torre, R. Effects of order of expansion for the exponential matrix and number of mathematical layers in the exact 3D static analysis of functionally graded plates and shells. Appl. Sci. 2018, 8, 110. [Google Scholar] [CrossRef]
- Brischetto, S. A 3D layer-wise model for the correct imposition of transverse shear/normal load conditions in FGM shells. Int. J. Mech. Sci. 2018, 136, 50–66. [Google Scholar] [CrossRef]
- Tang, Y.; Yang, T.Z. Post-buckling behavior and nonlinear vibration analysis of a fluid-conveying pipe composed of functionally graded material. Compos. Struct. 2018, 185, 393–400. [Google Scholar] [CrossRef]
- Rao, S.S.; Sunar, M. Piezoelectricity and its use in disturbance sensing and control of flexible structures: A survey. Appl. Mech. Rev. 1994, 47, 113–123. [Google Scholar] [CrossRef]
- Tani, J.; Takagi, T.; Qiu, J. Intelligent material systems: Application of functional materials. Appl. Mech. Rev. 1998, 51, 505–521. [Google Scholar] [CrossRef]
- Pohanka, M. Overview of piezoelectric biosensors, immunosensors and DNA sensors and their applications. Materials 2018, 11, 448. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.H.; Meng, Z.Y. Operational principle, fabrication and displacement characteristic of a functionally gradient piezoelectric ceramic actuator. Sens. Actuators A Phys. 1995, 48, 169–176. [Google Scholar] [CrossRef]
- Wu, C.C.M.; Kahn, M.; Moy, W. Piezoelectric ceramics with functional gradients: A new application in material design. J. Am. Ceram. Soc. 1996, 79, 809–812. [Google Scholar] [CrossRef]
- Shelley, W.F.; Wan, S.; Bowman, K.J. Functionally graded piezoelectric ceramics. Mater. Sci. Forum 1999, 308–311, 515–520. [Google Scholar] [CrossRef]
- Taya, M.; Almajid, A.A.; Dunn, M.; Takahashi, H. Design of bimorph piezo-composite actuators with functionally graded microstructure. Sens. Actuators A Phys. 2003, 107, 248–260. [Google Scholar] [CrossRef]
- Dineva, P.; Gross, D.; Müller, R.; Rangelov, T. Dynamic stress and electric field concentration in a functionally graded piezoelectric solid with a circular hole. Z. Angew. Math. Mech. 2011, 91, 110–124. [Google Scholar] [CrossRef]
- Chen, W.Q.; Ding, H.J. Bending of functionally graded piezoelectric rectangular plates. Acta Mech. Solida Sin. 2000, 13, 312–319. [Google Scholar]
- Zhang, P.W.; Zhou, Z.G.; Li, G.Q. Interaction of four parallel non-symmetric permeable mode-III cracks with different lengths in a functionally graded piezoelectric material plane. Z. Angew. Math. Mech. 2009, 89, 767–788. [Google Scholar] [CrossRef]
- Wu, R.A.; Zhong, Z.; Jin, B. Three dimensional analysis of rectangular functionally graded piezoelectric plates. Acta Mech. Solida Sin. 2002, 23, 43–49. [Google Scholar]
- Zhong, Z.; Shang, E.T. Three dimensional exact analysis of functionally gradient piezothermoelectrc material rectangular plate. Acta Mech. Solida Sin. 2003, 35, 533–552. [Google Scholar]
- Zhong, Z.; Shang, E.T. Three-dimensional exact analysis of a simply supported functionally gradient piezoelectric plate. Int. J. Solids Struct. 2003, 40, 5335–5352. [Google Scholar] [CrossRef]
- Zhu, H.W.; Li, Y.C.; Yang, C.J. Finite element solution of functionally graded piezoelectric plates. Chin. Q. Mech. 2005, 26, 567–571. [Google Scholar]
- Lu, P.; Lee, H.P.; Lu, C. An exact solution for simply supported functionally graded piezoelectric laminates in cylindrical bending. Int. J. Mech. Sci. 2005, 47, 437–458. [Google Scholar] [CrossRef]
- Lu, P.; Lee, H.P.; Lu, C. Exact solutions for simply supported functionally graded piezoelectric laminates by stroh-like formalism. Compos. Struct. 2006, 72, 352–363. [Google Scholar] [CrossRef]
- Zhang, X.R.; Zhong, Z. Three dimensional exact solution for free vibration of functionally gradient piezoelectric circular plate. Chin. Q. Mech. 2005, 26, 81–86. [Google Scholar]
- Liu, P.; Yu, T.T.; Bui, T.Q.; Zhang, C.Z.; Xu, Y.P.; Lim, C.W. Transient thermal shock fracture analysis of functionally graded piezoelectric materials by the extended finite element method. Int. J. Solids Struct. 2014, 51, 2167–2182. [Google Scholar] [CrossRef]
- Yu, T.T.; Bui, T.Q.; Liu, P.; Zhang, C.Z.; Hirose, S. Interfacial dynamic impermeable cracks analysis in dissimilar piezoelectric materials under coupled electromechanical loading with the extended finite element method. Int. J. Solids Struct. 2015, 67–68, 205–218. [Google Scholar] [CrossRef]
- Li, X.Y. Axisymmetric Problems of Functionally Graded Circular and Annular Plates with Transverse Isotropy. Ph.D. Thesis, Zhejiang University, Hangzhou, China, April 2007. [Google Scholar]
- Li, X.Y.; Ding, H.J.; Chen, W.Q. Three-dimensional analytical solution for a transversely isotropic functionally graded piezoelectric circular plate subject to a uniform electric potential difference. Sci. China Ser. G Phys. Mech. Astron. 2008, 51, 1116–1125. [Google Scholar] [CrossRef]
- Yu, T.; Zhong, Z. Bending analysis of a functionally graded piezoelectric cantilever beam. Sci. China Ser. G Phys. Mech. Astron. 2007, 50, 97–108. [Google Scholar] [CrossRef]
- He, X.T.; Wang, Y.Z.; Shi, S.J.; Sun, J.Y. An electroelastic solution for functionally graded piezoelectric material beams with different moduli in tension and compression. J. Intell. Mater. Syst. Struct. 2018, 29, 1649–1669. [Google Scholar] [CrossRef]
- Li, X.; Sun, J.Y.; Dong, J.; He, X.T. One-dimensional and two-dimensional analytical solutions for functionally graded beams with different moduli in tension and compression. Materials 2018, 11, 830. [Google Scholar] [CrossRef] [PubMed]
- He, X.T.; Li, Y.H.; Liu, G.H.; Yang, Z.X.; Sun, J.Y. Non-Linear bending of functionally graded thin plates with different moduli in tension and compression and its general perturbation solution. Appl. Sci. 2018, 8, 731. [Google Scholar]






| Property | Constants |
|---|---|
| Elastic(109N/m2) | , , , , , |
| Piezoelectric(C/m2) | , , , |
| Dielectric(F/m) | , |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.-x.; He, X.-t.; Li, X.; Lian, Y.-s.; Sun, J.-y. An Electroelastic Solution for Functionally Graded Piezoelectric Circular Plates under the Action of Combined Mechanical Loads. Materials 2018, 11, 1168. https://doi.org/10.3390/ma11071168
Yang Z-x, He X-t, Li X, Lian Y-s, Sun J-y. An Electroelastic Solution for Functionally Graded Piezoelectric Circular Plates under the Action of Combined Mechanical Loads. Materials. 2018; 11(7):1168. https://doi.org/10.3390/ma11071168
Chicago/Turabian StyleYang, Zhi-xin, Xiao-ting He, Xue Li, Yong-sheng Lian, and Jun-yi Sun. 2018. "An Electroelastic Solution for Functionally Graded Piezoelectric Circular Plates under the Action of Combined Mechanical Loads" Materials 11, no. 7: 1168. https://doi.org/10.3390/ma11071168





