Crystal Structure and Thermoelectric Properties of Lightly Substituted Higher Manganese Silicides
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. XRD Patterns and Microstructures
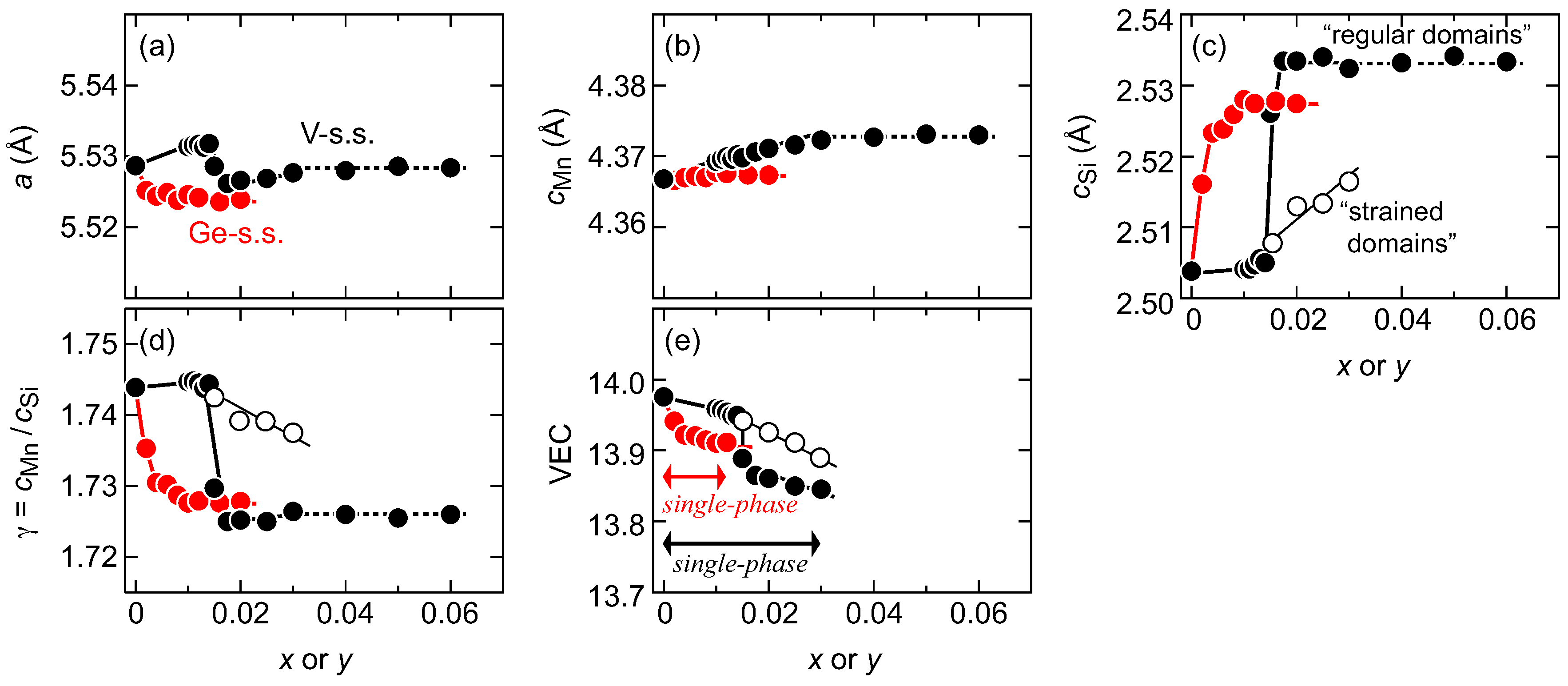
3.2. Lattice Parameters
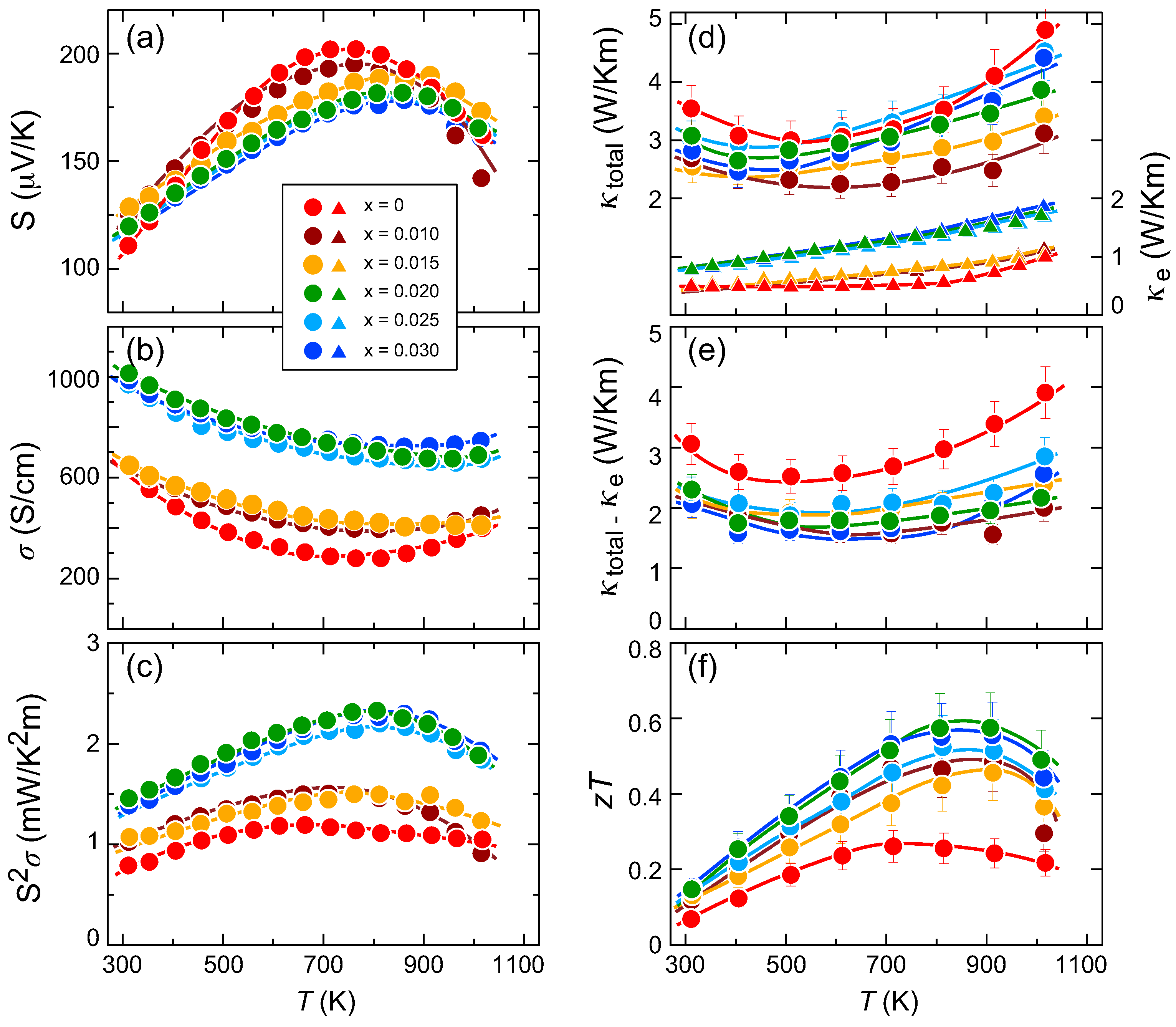
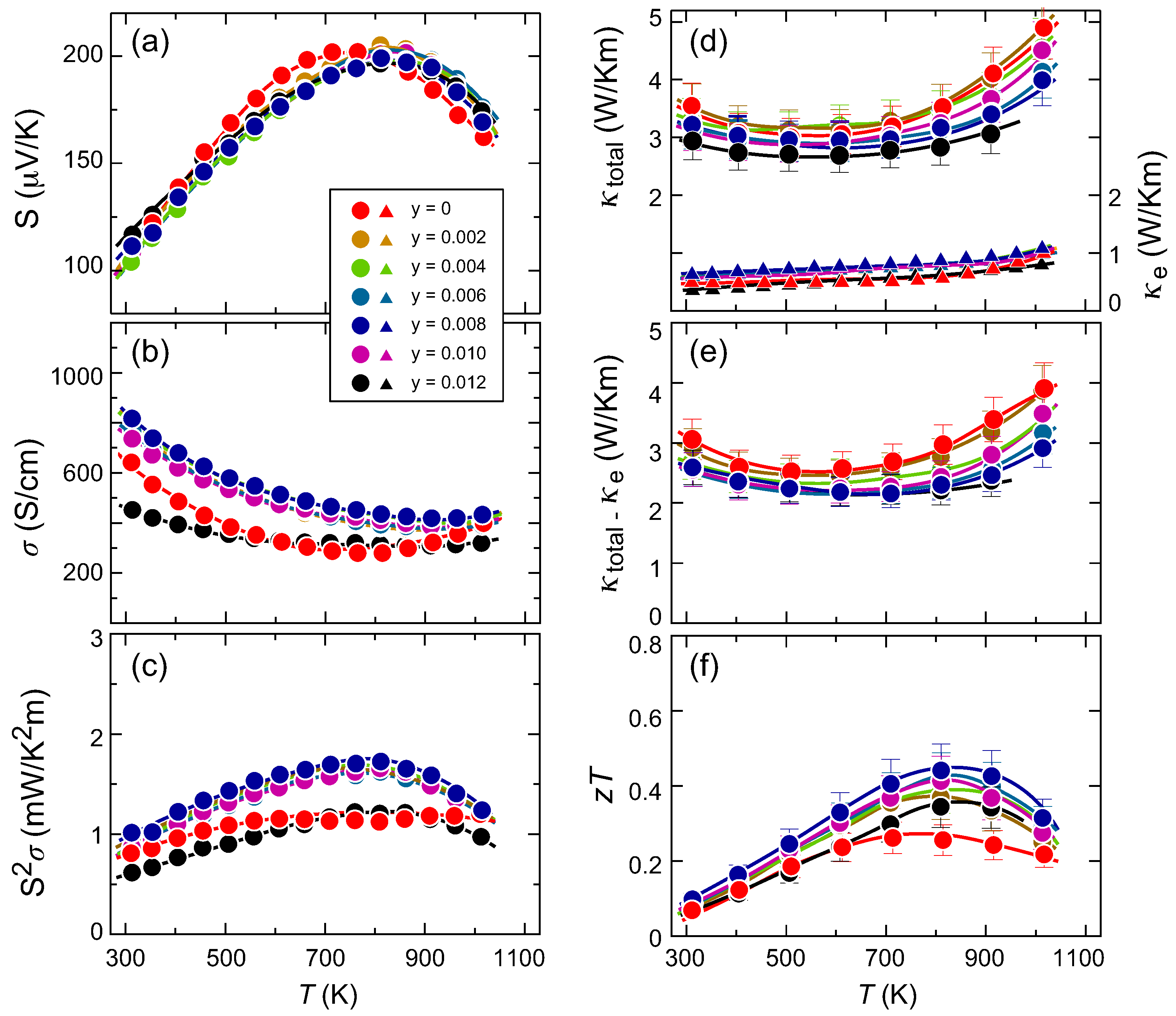
3.3. Thermoelectric Properties
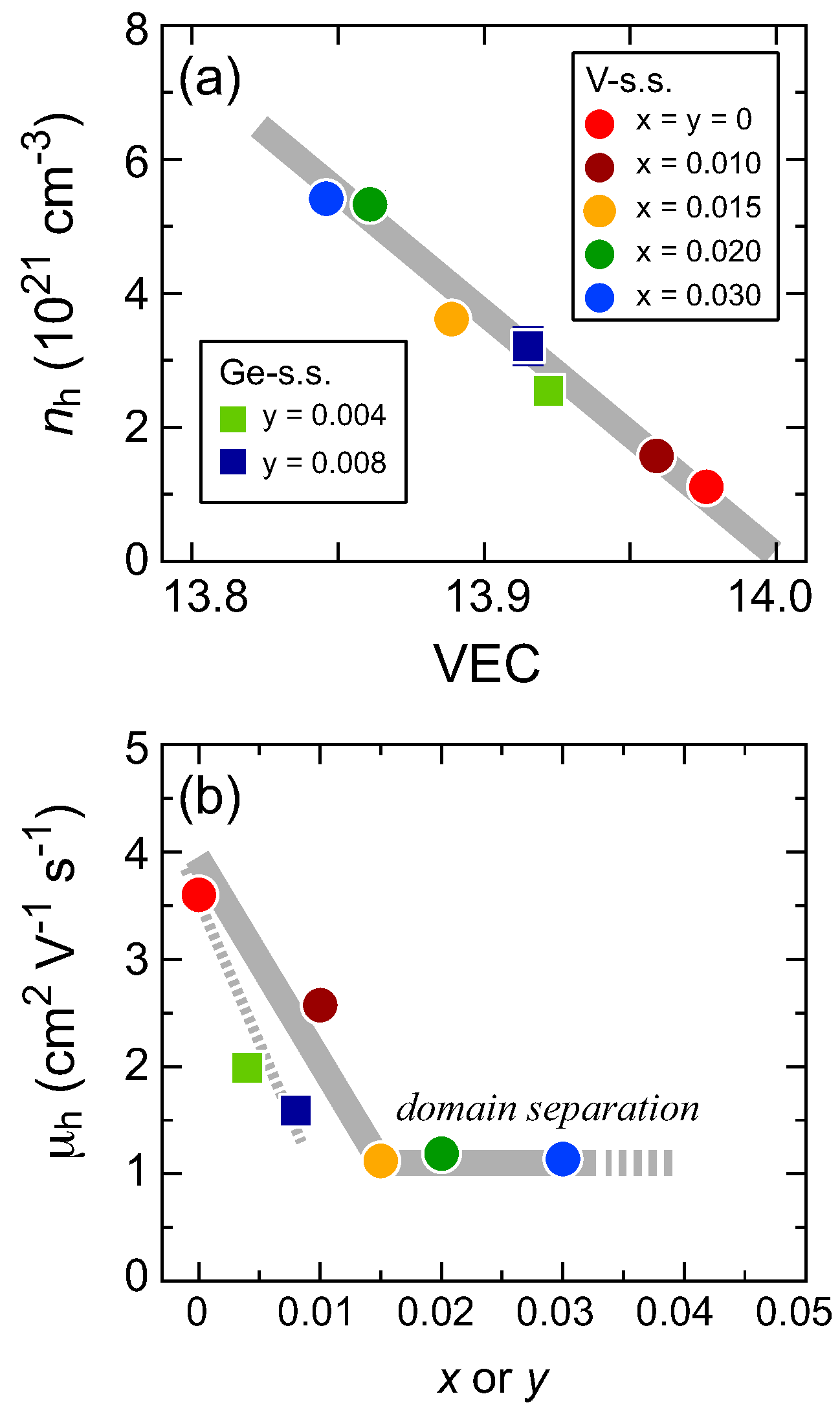
3.4. Effects of Domain Separation on TE Properties
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zaitsev, V.K. Thermoelectric properties of anisotropic MnSi1.75. In CRC Handbook of Thermoelectrics; Rowe, D.M., Ed.; CRC Press: New York, NY, USA, 1995; Section 25; ISBN 9780849301469. [Google Scholar]
- Fedorov, M.I.; Zaitsev, V.K. Thermoelectrics of transition metal silicides. In Thermoelectrics Handbook: Macro to Nano; Rowe, D.M., Ed.; CRC Press: Boca Raton, FL, USA, 2006; Section 31; ISBN 9780849322648. [Google Scholar]
- Miyazaki, Y. Higher Manganese Silicides. In Materials Aspect of Thermoelectricity; Uher, C., Ed.; CRC Press: Boca Raton, FL, USA, 2017; Chapter 13; ISBN 9781498754903. [Google Scholar]
- Aoyama, I.; Fedorov, M.I.; Zaitsev, V.K.; Solomkin, F.Y.; Eremin, I.S.; Samunin, A.Y.; Mukoujima, M.; Sano, S.; Tsuji, T. Effects of Ge Doping on Micromorphology of MnSi in MnSi∼1.7 and on Their Thermoelectric Transport Properties. Jpn. J. Appl. Phys. 2005, 44, 8562. [Google Scholar] [CrossRef]
- Zhou, A.J.; Zhu, T.J.; Zhao, X.B.; Yang, S.H.; Dasgupta, T.; Stiewe, C.; Hassdorf, R.; Mueller, E. Improved Thermoelectric Performance of Higher Manganese Silicides with Ge Additions. J. Electron. Mater. 2010, 39, 2002. [Google Scholar] [CrossRef]
- Lee, H.; Kim, G.; Lee, B.; Kim, J.; Choi, S.M.; Lee, K.H.; Lee, W. Effect of Si content on the thermoelectric transport properties of Ge-doped higher manganese silicides. Scripta Mater. 2017, 135, 72. [Google Scholar] [CrossRef]
- Ponnambalam, V.; Morelli, D. Effect of Cr and Fe Substitution on the Transport Properties of the Nowotny Chimney-Ladder MnSiδ (1.73 < δ < 1.75) Compounds. J. Electron. Mater. 2012, 41, 1389. [Google Scholar] [CrossRef]
- Truong, D.Y.N.; Berthebaud, D.; Gascoin, F.; Kleinke, H. Molybdenum, Tungsten, and Aluminium Substitution for Enhancement of the Thermoelectric Performance of Higher Manganese Silicides. J. Electron. Mater. 2015, 44, 3603. [Google Scholar] [CrossRef]
- Barczak, S.A.; Downie, R.A.; Popuri, S.R.; Decourt, R.; Pollet, M.; Bos, J.W.G. Thermoelectric properties of Fe and Al double substituted MnSiγ (γ∼1.73). J. Solid State Chem. 2015, 227, 55. [Google Scholar] [CrossRef]
- Bernard-Granger, G.; Soulier, M.; Ihou-Mouko, H.; Navone, C.; Boidot, M.; Leforestier, J.; Simon, J. Microstructure investigations and thermoelectrical properties of a P-type polycrystalline higher manganese silicide material sintered from a gas-phase atomized powder. J. Alloy. Compd. 2015, 618, 403. [Google Scholar] [CrossRef]
- Yamamoto, A.; Ghodke, S.; Miyazaki, H.; Inukai, M.; Nishino, Y.; Matsunami, M.; Takeuchi, T. Thermoelectric properties of supersaturated Re solid solution of higher manganese silicides. Jpn. J. Appl. Phys. 2016, 55, 020301. [Google Scholar] [CrossRef]
- Yoshikura, M.; Itoh, T. Thermoelectric Properties of Higher Manganese Silicide Compounds Synthesized by MG-PDS Method. J. Jpn. Powder Powder Met. 2010, 57, 242. (In Japanese) [Google Scholar] [CrossRef]
- Sadia, Y.; Gelbstein, Y. Silicon-Rich Higher Manganese Silicides for Thermoelectric Applications. J. Electron. Mater. 2012, 41, 1504. [Google Scholar] [CrossRef]
- Truong, D.Y.N.; Kleinke, H.; Gascoin, F. Preparation of pure Higher Manganese Silicides through wet ball milling and reactive sintering with enhanced thermoelectric properties. Intermetallics 2015, 66, 127. [Google Scholar] [CrossRef]
- Ivanova, L.D.; Abrikosov, N.K.; Elagina, E.I.; Khvostikova, V.D. Production and investigation of the properties of single crystals of the higher manganese silicide. Izv. Akad. NaukSSSR Neorg. Mater. 1969, 5, 1933. [Google Scholar]
- Kojima, T.; Nishida, I.; Sakata, T. Crystal growth of Mn15Si26. J. Cryst. Growth 1979, 47, 589. [Google Scholar] [CrossRef]
- Miyazaki, Y.; Hamada, H.; Hayashi, K.; Yubuta, K. Crystal Structure and Thermoelectric Properties of Lightly Vanadium-Substituted Higher Manganese Silicides (Mn1−xVx)Siγ. J. Electron. Mater. 2017, 46, 2705. [Google Scholar] [CrossRef]
- Yamamoto, A. Determination of composite crystal structures and superspace groups. Acta Cryst. 1993, A49, 831–846. [Google Scholar] [CrossRef]
- Petricek, V.; Dusek, M.; Palatinus, L. Crystallographic Computing System JANA2006: General features. Z. Kristallogr. 2014, 229, 345–352. [Google Scholar] [CrossRef]
- Inoue, T.; Chikazumi, S.; Nagasaki, S.; Tanuma, S. (Eds.) Agne Periodic Table; AGNE Technology Center: Tokyo, Japan, 2001. [Google Scholar]
- Miyazaki, Y.; Kikuchi, Y. Higher Manganese Silicide, MnSiγ. In Thermoelectric Nanomaterials; Koumoto, K., Mori, T., Eds.; Springer: Berlin, Germany, 2013; Chapter 7; ISBN 978-3-642-37536-1. [Google Scholar]
- Chen, X.; Weathers, A.; Carrete, J.; Mukhopadhyay, S.; Delaire, O.; Stewart, D.A.; Mingo, N.; Girard, S.N.; Ma, J.; Abernathy, D.L.; et al. Twisting phonons in complex crystals with quasi-one-dimensional substructures. Nat. Commun. 2015, 6, 7723. [Google Scholar] [CrossRef] [PubMed]
- Kawasumi, I.; Sakata, M.; Nishida, I.; Masumoto, K. Crystal growth of manganese silicide, MnSi∼1.73 and semiconducting properties of Mn15Si26. J. Mater. Sci. 1981, 16, 355. [Google Scholar] [CrossRef]
- Dudkin, L.D.; Kuznetsova, E.S. Study of Mn-Si system in the Si-rich region. Dokl. Akad. NaukSSSR 1961, 141, 94. (In Russian) [Google Scholar]
- Kikuchi, Y.; Nakajo, T.; Hayashi, K.; Miyazaki, Y. High temperature X-ray diffraction study on incommensurate composite crystal MnSiγ—(3+1)-dimensional superspace approach. J. Alloy. Compd. 2014, 616, 263. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miyazaki, Y.; Hamada, H.; Nagai, H.; Hayashi, K. Crystal Structure and Thermoelectric Properties of Lightly Substituted Higher Manganese Silicides. Materials 2018, 11, 926. https://doi.org/10.3390/ma11060926
Miyazaki Y, Hamada H, Nagai H, Hayashi K. Crystal Structure and Thermoelectric Properties of Lightly Substituted Higher Manganese Silicides. Materials. 2018; 11(6):926. https://doi.org/10.3390/ma11060926
Chicago/Turabian StyleMiyazaki, Yuzuru, Haruki Hamada, Hiroki Nagai, and Kei Hayashi. 2018. "Crystal Structure and Thermoelectric Properties of Lightly Substituted Higher Manganese Silicides" Materials 11, no. 6: 926. https://doi.org/10.3390/ma11060926




