Impact of Interstitial Ni on the Thermoelectric Properties of the Half-Heusler TiNiSn
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. X-ray Powder Diffraction
3.2. Neutron Powder Diffraction
3.3. Synchrotron X-ray Powder Diffraction
3.4. Scanning Electron Microscopy
3.5. Thermoelectric Properties
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rowe, D.M. Thermoelectrics and Its Energy Harvesting; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Tritt, T.M. Thermoelectric Phenomena, Materials, and Applications. In Annual Review of Materials Research; Clarke, D.R., Fratzl, P., Eds.; Annual Reviews: Palo Alto, CA, USA, 2011; Volume 41, pp. 433–448. [Google Scholar]
- Zebarjadi, M.; Esfarjani, K.; Dresselhaus, M.S.; Ren, Z.F.; Chen, G. Perspectives on thermoelectrics: From fundamentals to device applications. Energy Environ. Sci. 2012, 5, 5147–5162. [Google Scholar] [CrossRef]
- Liu, W.S.; Jie, Q.; Kim, H.S.; Ren, Z.F. Current progress and future challenges in thermoelectric power generation: From materials to devices. Acta Mater. 2015, 87, 357–376. [Google Scholar] [CrossRef]
- Snyder, G.J.; Toberer, E.S. Complex thermoelectric materials. Nat. Mater. 2008, 7, 105–114. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Gao, S.; Zeng, X.; Dehkordi, A.M.; Tritt, T.M.; Poon, S.J. Uncovering high thermoelectric figure of merit in (Hf,Zr)NiSn half-Heusler alloys. Appl. Phys. Lett. 2015, 107, 041902. [Google Scholar] [CrossRef]
- Gurth, M.; Rogl, G.; Romaka, V.V.; Grytsiv, A.; Bauer, E.; Rogl, P. Thermoelectric high ZT half-Heusler alloys Ti1−x−y ZrxHfyNiSn (0 ≤ x ≤ 1; 0 ≤ y ≤ 1). Acta Mater. 2016, 104, 210–222. [Google Scholar] [CrossRef]
- Yan, X.A.; Joshi, G.; Liu, W.S.; Lan, Y.C.; Wang, H.; Lee, S.; Simonson, J.W.; Poon, S.J.; Tritt, T.M.; Chen, G.; et al. Enhanced Thermoelectric Figure of Merit of p-Type Half-Heuslers. Nano Lett. 2011, 11, 556–560. [Google Scholar] [CrossRef] [PubMed]
- Rausch, E.; Balke, B.; Deschauer, T.; Ouardi, S.; Felser, C. Charge carrier concentration optimization of thermoelectric p-type half-Heusler compounds. APL Mater. 2015, 3, 105. [Google Scholar] [CrossRef]
- Fu, C.G.; Bai, S.Q.; Liu, Y.T.; Tang, Y.S.; Chen, L.D.; Zhao, X.B.; Zhu, T.J. Realizing high figure of merit in heavy-band p-type half-Heusler thermoelectric materials. Nat. Commun. 2015, 6, 6888. [Google Scholar] [CrossRef] [PubMed]
- He, R.; Huang, L.H.; Wang, Y.M.; Samsonidze, G.; Kozinsky, B.; Zhang, Q.Y.; Ren, Z.F. Enhanced thermoelectric properties of n-type NbCoSn half-Heusler by improving phase purity. APL Mater. 2016, 4, 104804. [Google Scholar] [CrossRef]
- Ferluccio, D.A.; Smith, R.I.; Buckman, J.; Bos, J.W.G. Impact of Nb vacancies and p-type doping of the NbCoSn-NbCoSb half-Heusler thermoelectrics. Phys. Chem. Chem. Phys. 2018, 20, 3979–3987. [Google Scholar] [CrossRef] [PubMed]
- Xia, K.; Liu, Y.; Anand, S.; Snyder, G.J.; Xin, J.; Yu, J.; Zhao, X.; Zhu, T. Enhanced Thermoelectric Performance in 18-Electron Nb0.8CoSb Half-Heusler Compound with Intrinsic Nb Vacancies. Adv. Funct. Mater. 2018, 28, 1705845. [Google Scholar]
- Bos, J.W.G.; Downie, R.A. Half-Heusler thermoelectrics: A complex class of materials. J. Phys. Condens. Matter 2014, 26, 433201. [Google Scholar] [CrossRef] [PubMed]
- Zhu, T.J.; Fu, C.G.; Xie, H.H.; Liu, Y.T.; Zhao, X.B. High Efficiency Half-Heusler Thermoelectric Materials for Energy Harvesting. Adv. Energy Mater. 2015, 5, 1500588. [Google Scholar] [CrossRef]
- Douglas, J.E.; Birkel, C.S.; Miao, M.S.; Torbet, C.J.; Stucky, G.D.; Pollock, T.M.; Seshadri, R. Enhanced thermoelectric properties of bulk TiNiSn via formation of a TiNi2Sn second phase. Appl. Phys. Lett. 2012, 101, 183902. [Google Scholar] [CrossRef]
- Chai, Y.W.; Kimura, Y. Nanosized precipitates in half-Heusler TiNiSn alloy. Appl. Phys. Lett. 2012, 100, 033114. [Google Scholar] [CrossRef]
- Downie, R.A.; MacLaren, D.A.; Smith, R.I.; Bos, J.W.G. Enhanced thermoelectric performance in TiNiSn-based half-Heuslers. Chem. Commun. 2013, 49, 4184–4186. [Google Scholar] [CrossRef] [PubMed]
- Birkel, C.S.; Douglas, J.E.; Lettiere, B.R.; Seward, G.; Verma, N.; Zhang, Y.C.; Pollock, T.M.; Seshadri, R.; Stucky, G.D. Improving the thermoelectric properties of half-Heusler TiNiSn through inclusion of a second full-Heusler phase: Microwave preparation and spark plasma sintering of TiNi1+xSn. Phys. Chem. Chem. Phys. 2013, 15, 6990–6997. [Google Scholar] [CrossRef] [PubMed]
- Kirievsky, K.; Gelbstein, Y.; Fuks, D. Phase separation and antisite defects in the thermoelectric TiNiSn half-Heusler alloys. J. Solid State Chem. 2013, 203, 247–254. [Google Scholar] [CrossRef]
- Page, A.; Uher, C.; Poudeu, P.F.; Van der Ven, A. Phase separation of full-Heusler nanostructures in half-Heusler thermoelectrics and vibrational properties from first-principles calculations. Phys. Rev. B 2015, 92, 174102. [Google Scholar] [CrossRef]
- Hazama, H.; Matsubara, M.; Asahi, R.; Takeuchi, T. Improvement of thermoelectric properties for half-Heusler TiNiSn by interstitial Ni defects. J. Appl. Phys. 2011, 110, 063710. [Google Scholar] [CrossRef]
- Downie, R.A.; Smith, R.I.; MacLaren, D.A.; Bos, J.-W.G. Metal Distributions, Efficient n-Type Doping, and Evidence for in-Gap States in TiNiMySn (M = Co, Ni, Cu) half-Heusler Nanocomposites. Chem. Mater. 2015, 27, 2449–2459. [Google Scholar] [CrossRef] [Green Version]
- Downie, R.A.; Barczak, S.A.; Smith, R.I.; Bos, J.W.G. Compositions and thermoelectric properties of XNiSn (X = Ti, Zr, Hf) half-Heusler alloys. J. Mater. Chem. C 2015, 3, 10534–10542. [Google Scholar] [CrossRef]
- Douglas, J.E.; Birkel, C.S.; Verma, N.; Miller, V.M.; Miao, M.S.; Stucky, G.D.; Pollock, T.M.; Seshadri, R. Phase stability and property evolution of biphasic Ti-Ni-Sn alloys for use in thermoelectric applications. J. Appl. Phys. 2014, 115, 043720. [Google Scholar] [CrossRef]
- Chai, Y.W.; Yoshioka, K.; Kimura, Y. Intrinsic point defects in thermoelectric half-Heusler alloys. Scr. Mater. 2014, 83, 13–16. [Google Scholar] [CrossRef]
- Chai, Y.W.; Kimura, Y. Microstructure evolution of nanoprecipitates in half-Heusler TiNiSn alloys. Acta Mater. 2013, 61, 6684–6697. [Google Scholar] [CrossRef]
- Douglas, J.E.; Echlin, M.P.; Lenthe, W.C.; Seshadri, R.; Pollock, T.M. Three-dimensional multimodal imaging and analysis of biphasic microstructure in a Ti-Ni-Sn thermoelectric material. APL Mater. 2015, 3, 096107. [Google Scholar] [CrossRef]
- Douglas, J.E.; Chater, P.A.; Brown, C.M.; Pollock, T.M.; Seshadri, R. Nanoscale structural heterogeneity in Ni-rich half-Heusler TiNiSn. J. Appl. Phys. 2014, 116, 163514. [Google Scholar] [CrossRef]
- Barczak, S.A.; Halpin, J.E.; Buckman, J.; Decourt, R.; Pollet, M.; Smith, R.I.; MacLaren, D.A.; Bos, J.-W.G. Grain-by-Grain Compositional Variations and Interstitial Metals—A New Route toward Achieving High Performance in Half-Heusler Thermoelectrics. ACS Appl. Mater. Interfaces 2018, 10, 4786–4793. [Google Scholar] [CrossRef] [PubMed]
- Larson, A.C.; Von Dreele, R.B. General Structure Analysis System (GSAS); Los Alamos National Laboratory Report; LAUR: Baltimore, MD, USA, 2000; pp. 86–748. [Google Scholar]
- Toby, B.H. EXPGUI, a graphical user interface for GSAS. J. Appl. Crystallogr. 2001, 34, 210–213. [Google Scholar] [CrossRef]
- Putley, E.H. The Hall Effect and Related Phenomena; Butterworth: London, UK, 1960. [Google Scholar]
- Asaad, M.; Buckman, J.; Smith, R.I.; Bos, J.W.G. Thermoelectric properties and high-temperature stability of the Ti1−xVxCoSb1−xSnx half-Heusler alloys. RSC Adv. 2016, 6, 56511–56517. [Google Scholar] [CrossRef]
- Tang, Y.L.; Li, X.S.; Martin, L.H.J.; Reyes, E.C.; Ivas, T.; Leinenbach, C.; Anand, S.; Peters, M.; Snyder, G.J.; Battaglia, C. Impact of Ni content on the thermoelectric properties of half-Heusler TiNiSn. Energy Environ. Sci. 2018, 11, 311–320. [Google Scholar] [CrossRef]
- Kim, H.S.; Gibbs, Z.M.; Tang, Y.L.; Wang, H.; Snyder, G.J. Characterization of Lorenz number with Seebeck coefficient measurement. APL Mater. 2015, 3, 041506. [Google Scholar] [CrossRef]
- Callaway, J. Model for Lattice Thermal Conductivity at Low Temperatures. Phys. Rev. 1959, 113, 1046–1051. [Google Scholar] [CrossRef]
- Yang, J.; Meisner, G.P.; Chen, L. Strain field fluctuation effects on lattice thermal conductivity of ZrNiSn-based thermoelectric compounds. Appl. Phys. Lett. 2004, 85, 1140–1142. [Google Scholar] [CrossRef]
- Petersen, A.; Bhattacharya, S.; Tritt, T.M.; Poon, S.J. Critical analysis of lattice thermal conductivity of half-Heusler alloys using variations of Callaway model. J. Appl. Phys. 2015, 117, 035706. [Google Scholar] [CrossRef]
- Kirievsky, K.; Shlimovich, M.; Fuks, D.; Gelbstein, Y. An ab initio study of the thermoelectric enhancement potential in nano-grained TiNiSn. Phys. Chem. Chem. Phys. 2014, 16, 20023–20029. [Google Scholar] [CrossRef] [PubMed]
- Downie, R.A.; MacLaren, D.A.; Bos, J.W.G. Thermoelectric performance of multiphase XNiSn (X = Ti, Zr, Hf) half-Heusler alloys. J. Mater. Chem. A 2014, 2, 6107–6114. [Google Scholar] [CrossRef] [Green Version]
- Miyamoto, K.; Kimura, A.; Sakamoto, K.; Ye, M.; Cui, Y.; Shimada, K.; Namatame, H.; Taniguchi, M.; Fujimori, S.I.; Saitoh, Y.; et al. In-gap electronic states responsible for the excellent thermoelectric properties of Ni-based half-Heusler alloys. Appl. Phys. Express 2008, 1, 081901. [Google Scholar] [CrossRef]
- Do, D.T.; Mahanti, S.D.; Pulikkoti, J.J. Electronic structure of Zr-Ni-Sn systems: Role of clustering and nanostructures in half-Heusler and Heusler limits. J. Phys. Condens. Matter 2014, 26, 275501. [Google Scholar] [CrossRef] [PubMed]
- Downie, R.A.; Popuri, S.R.; Ning, H.P.; Reece, M.J.; Bos, J.W.G. Effect of Spark Plasma Sintering on the Structure and Properties of Ti1−xZrxNiSn Half-Heusler Alloys. Materials 2014, 7, 7093–7104. [Google Scholar] [CrossRef] [PubMed]
- Goldsmid, H.J.; Sharp, J.W. Estimation of the thermal band gap of a semiconductor from Seebeck measurements. J. Electron. Mater. 1999, 28, 869–872. [Google Scholar] [CrossRef]
- Xie, H.H.; Wang, H.; Fu, C.G.; Liu, Y.T.; Snyder, G.J.; Zhao, X.B.; Zhu, T.J. The intrinsic disorder related alloy scattering in ZrNiSn half-Heusler thermoelectric materials. Sci. Rep. 2014, 4, 6888. [Google Scholar] [CrossRef] [PubMed]
- Andrea, L.; Hug, G.; Chaput, L. Ab initio phonon properties of half-Heusler NiTiSn, NiZrSn and NiHfSn. J. Phys. Condens. Matter 2015, 27, 425401. [Google Scholar] [CrossRef] [PubMed]
- Eliassen, S.N.H.; Katre, A.; Madsen, G.K.H.; Persson, C.; Lovvik, O.M.; Berland, K. Lattice thermal conductivity of TixZryHf1−x−yNiSn half-Heusler alloys calculated from first principles: Key role of nature of phonon modes. Phys. Rev. B 2017, 95, 045202. [Google Scholar] [CrossRef]
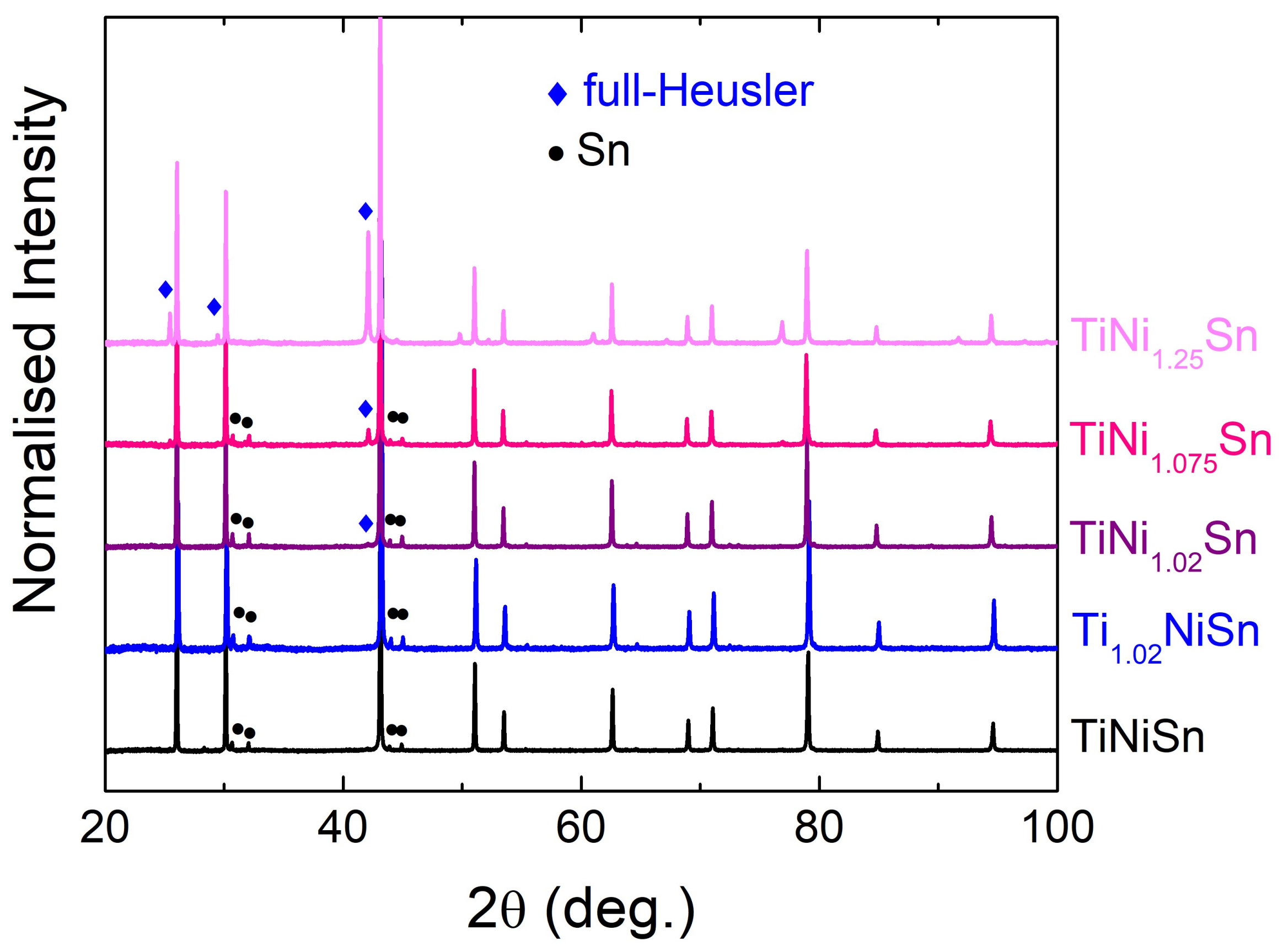
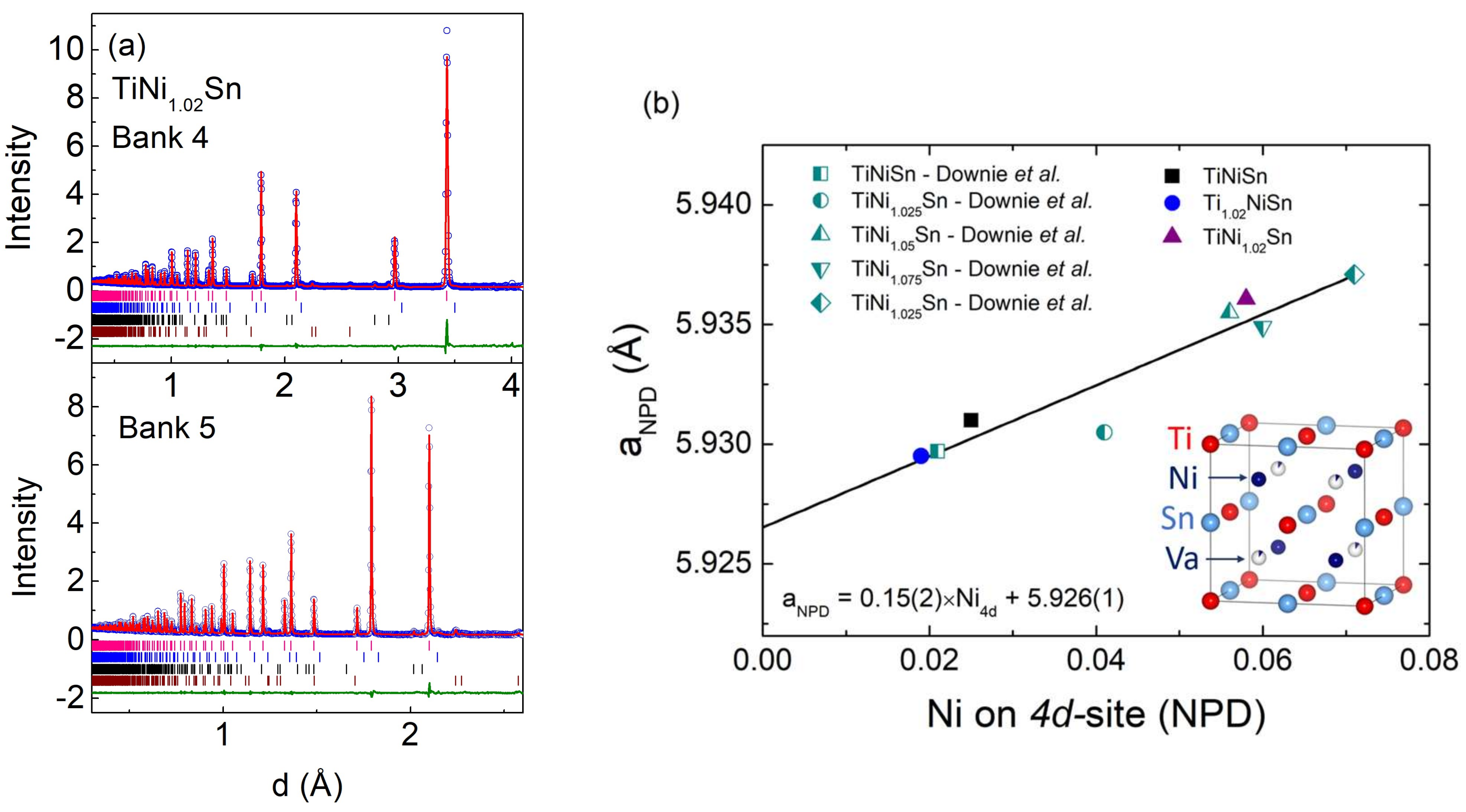
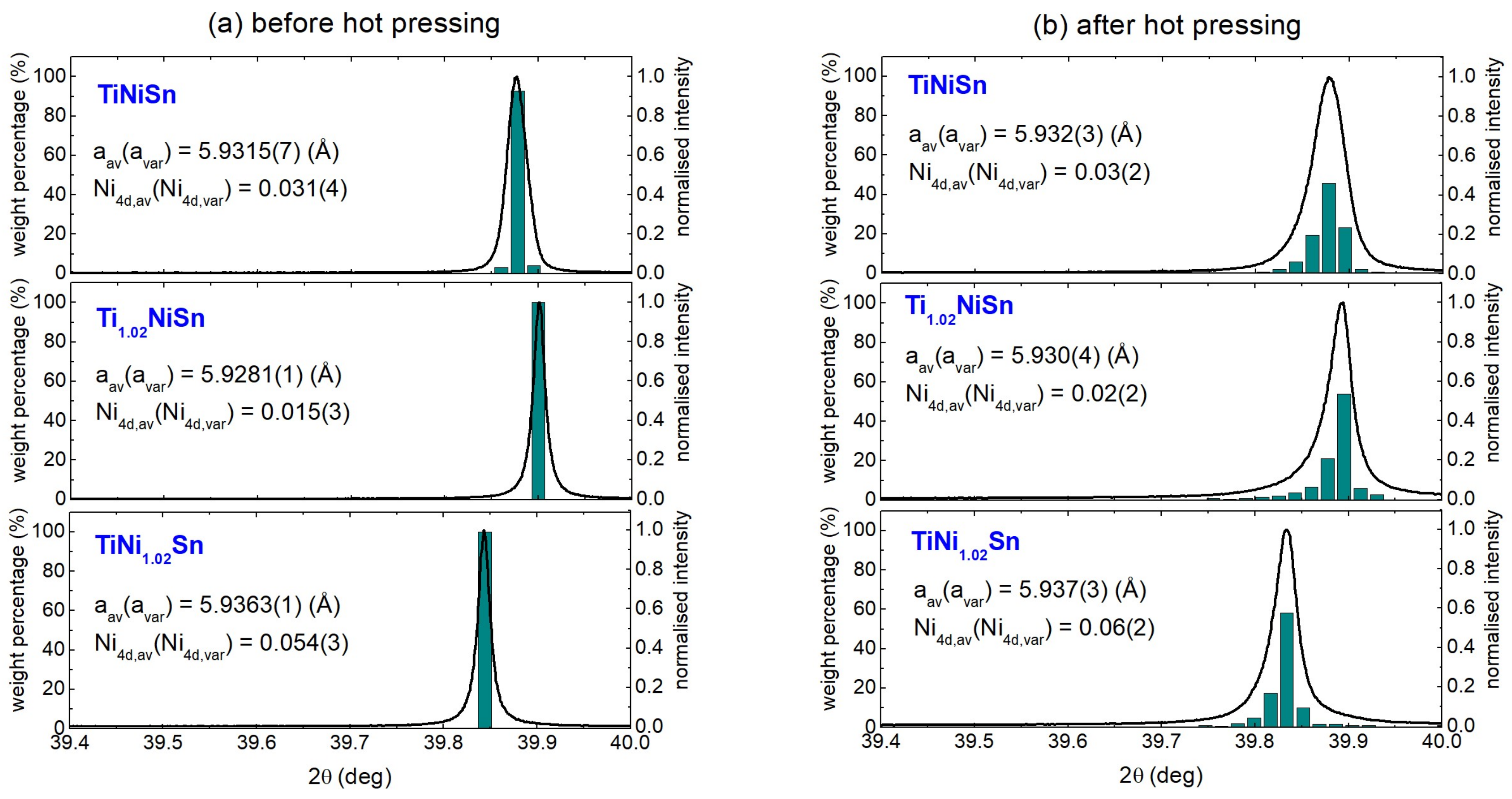


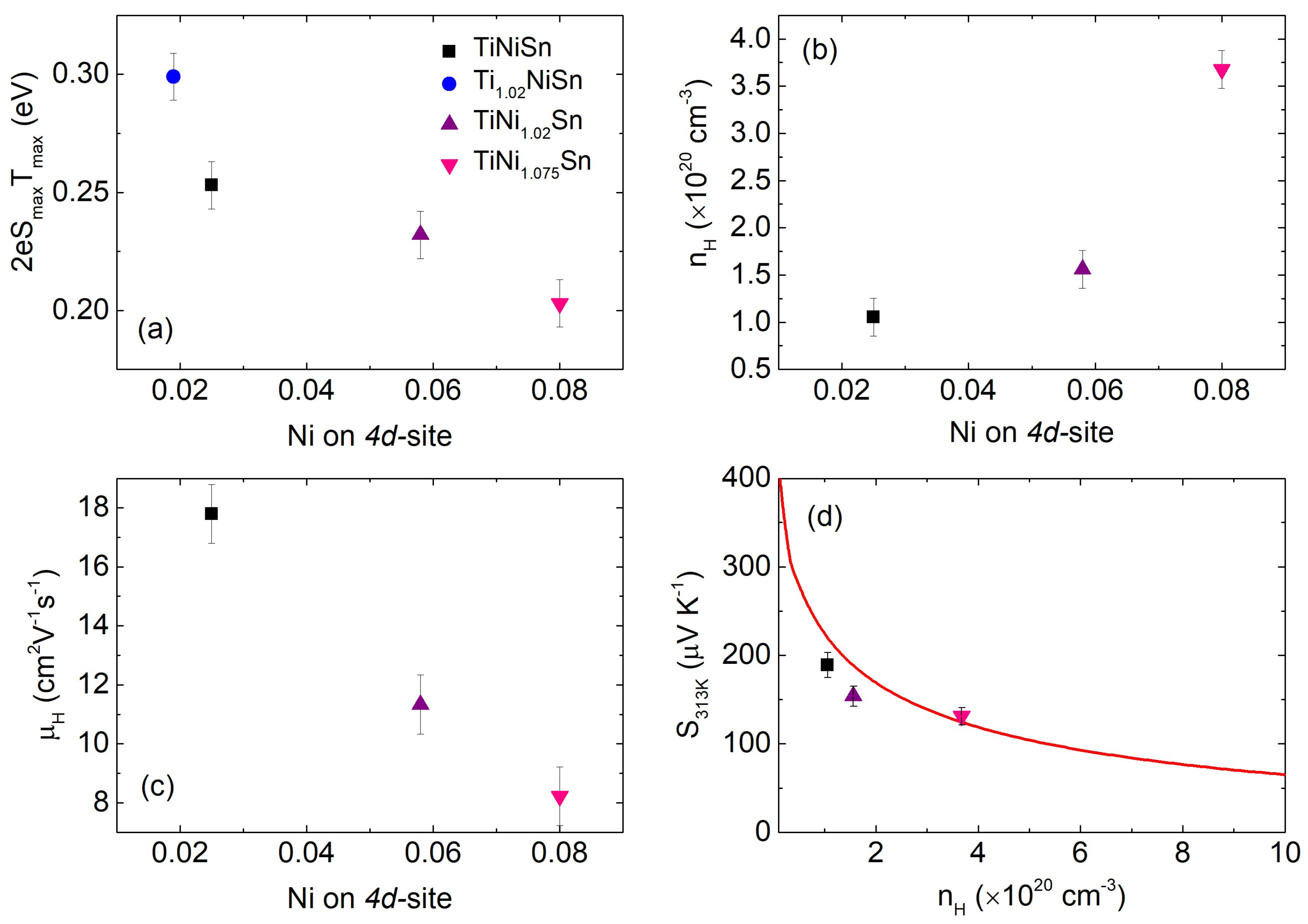
| Composition | Half-Heusler | Full-Heusler | Sn | Percentage Density | ||
|---|---|---|---|---|---|---|
| a (Å) | wt % | a (Å) | wt % | wt % | ||
| TiNiSn | 5.9304(1) | 97.7(1) | - | - | 2.3(1) | 88(2) |
| Ti1.02NiSn | 5.9292(1) | 95.9(1) | - | - | 4.1(1) | 94(2) |
| TiNi1.02Sn | 5.9382(1) | 93.8(1) | 6.072(2) | 2.1(3) | 4.1(1) | 95(2) |
| TiNi1.075Sn | 5.9384(1) | 92.8(1) | 6.0745(3) | 4.7(2) | 2.5(1) | 95(2) |
| TiNi1.25Sn | 5.9391(1) | 73.7(2) | 6.0770(1) | 26.3(2) | - | 90(2) |
| Ti1.02NiSn | TiNi1.02Sn | ||
|---|---|---|---|
| a (Å) | - | 5.92951(4) | 5.93607(3) |
| Ti (4a) | Occ | 0.978(3) | 0.977(2) |
| - | Uiso | 0.00455(8) | 0.00435(7) |
| Ni (4c) | Uiso | 0.413(4) | 0.00470(4) |
| Ni (4d) | Occ | 0.019(1) | 0.058(1) |
| - | Uiso | 0.413(4) | 0.00470(4) |
| Sn (4b) | Uiso | 0.00387(6) | 0.00415(5) |
| Wt% Sn | - | 2.5(2) | 3.4(2) |
| Wt% Ti | - | 3.8(2) | 4.0(2) |
| wRp (%) | Bank 3 | 2.9 | 2.5 |
| - | Bank 4 | 2.2 | 1.9 |
| - | Bank 5 | 2.0 | 1.9 |
| Rp (%) | Bank 3 | 2.6 | 2.4 |
| - | Bank 4 | 4.0 | 4.0 |
| - | Bank 5 | 2.9 | 2.7 |
| Composition | Ni 4d-Site Occupancy | κ323K-LT/ρ (W m−1 K−1) | Γ b | ΓM |
|---|---|---|---|---|
| TiNiSn | 0.025(1) | 6.0 | 0.06 | 0.06 |
| Ti1.02NiSn | 0.019(1) | 7.0 | 0.04 | 0.04 |
| TiNi1.02Sn | 0.058(1) | 5.1 | 0.09 | 0.13 |
| TiNi1.075Sn | 0.08(1) a | 4.2 | 0.13 | 0.16 |
| TiNi1.25Sn | 0.09(1) a | 4.4 | - | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barczak, S.A.; Buckman, J.; Smith, R.I.; Baker, A.R.; Don, E.; Forbes, I.; Bos, J.-W.G. Impact of Interstitial Ni on the Thermoelectric Properties of the Half-Heusler TiNiSn. Materials 2018, 11, 536. https://doi.org/10.3390/ma11040536
Barczak SA, Buckman J, Smith RI, Baker AR, Don E, Forbes I, Bos J-WG. Impact of Interstitial Ni on the Thermoelectric Properties of the Half-Heusler TiNiSn. Materials. 2018; 11(4):536. https://doi.org/10.3390/ma11040536
Chicago/Turabian StyleBarczak, Sonia A., Jim Buckman, Ronald I. Smith, Annabelle R. Baker, Eric Don, Ian Forbes, and Jan-Willem G. Bos. 2018. "Impact of Interstitial Ni on the Thermoelectric Properties of the Half-Heusler TiNiSn" Materials 11, no. 4: 536. https://doi.org/10.3390/ma11040536






