Heat-Assisted Multiferroic Solid-State Memory
Abstract
:1. Introduction
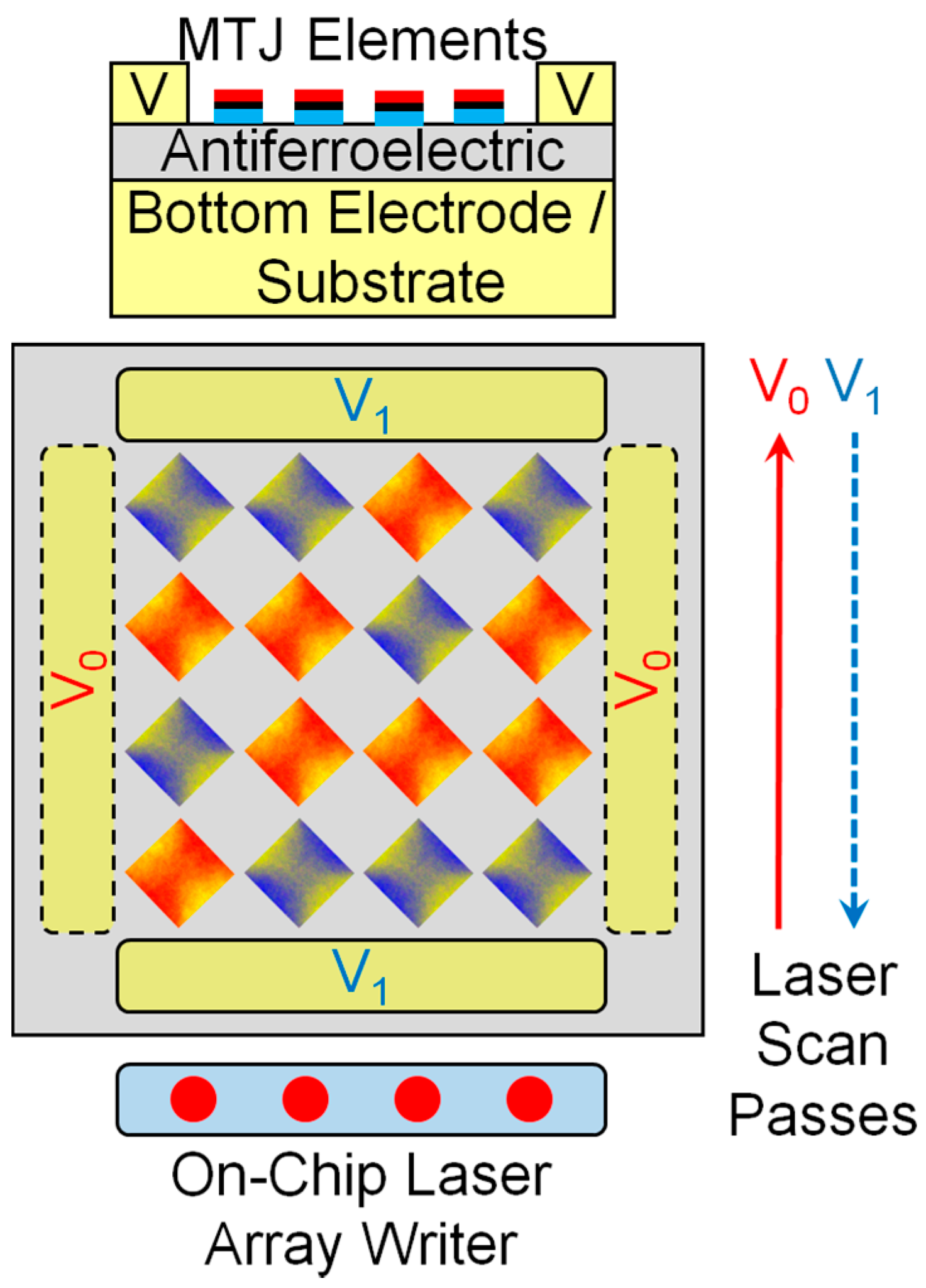
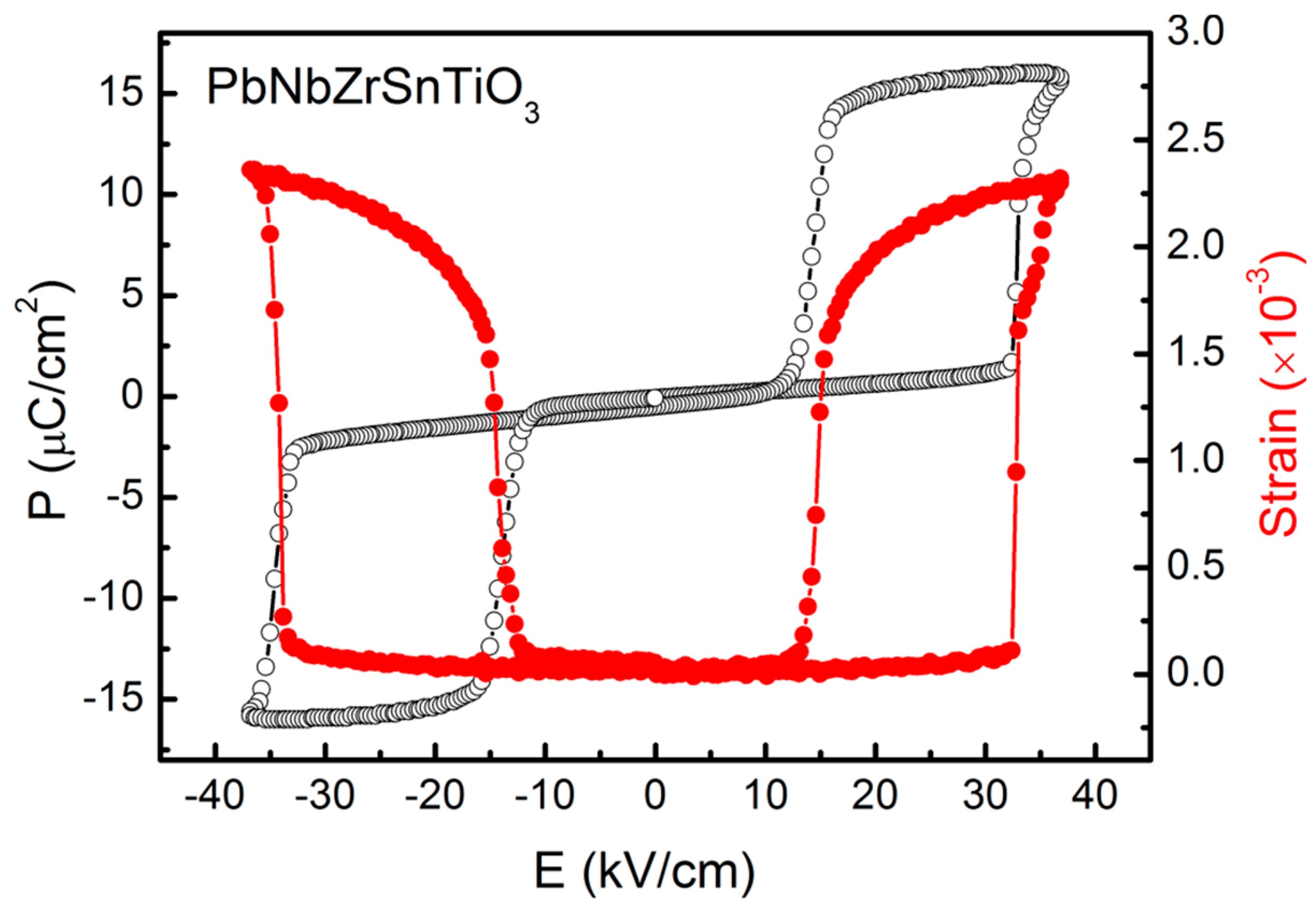
1.1. Heat-Assisted Multiferroic Memory
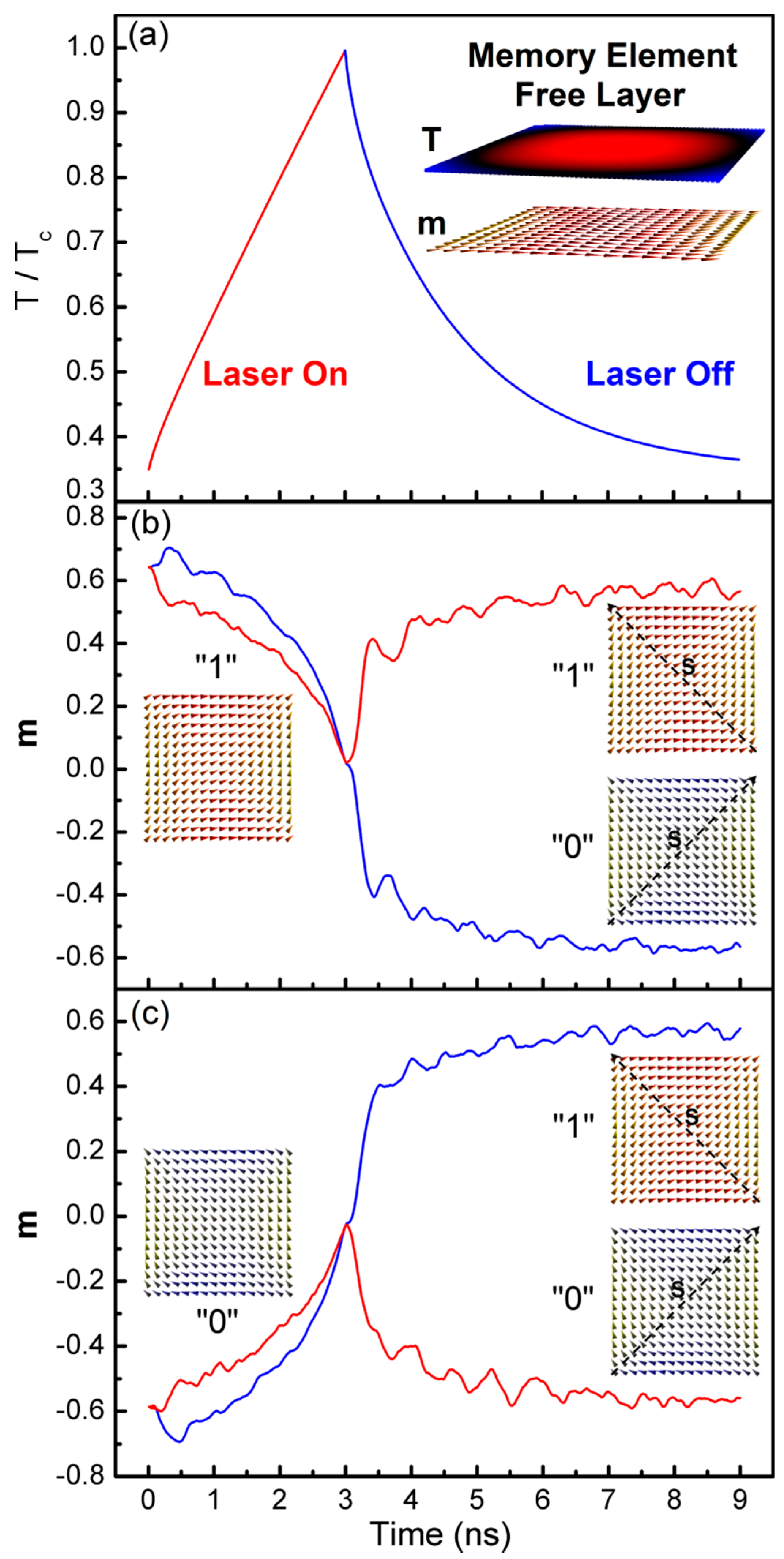
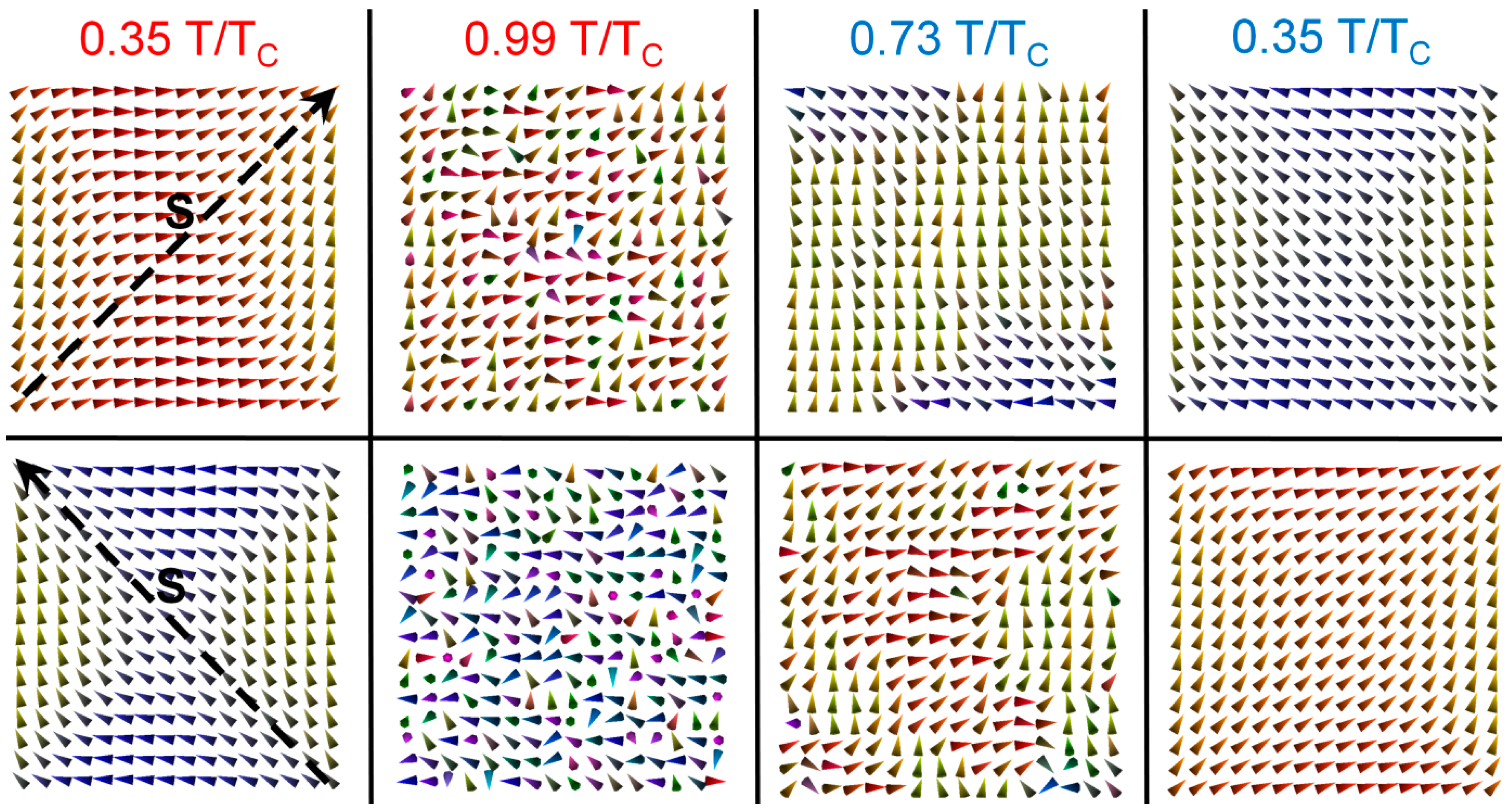
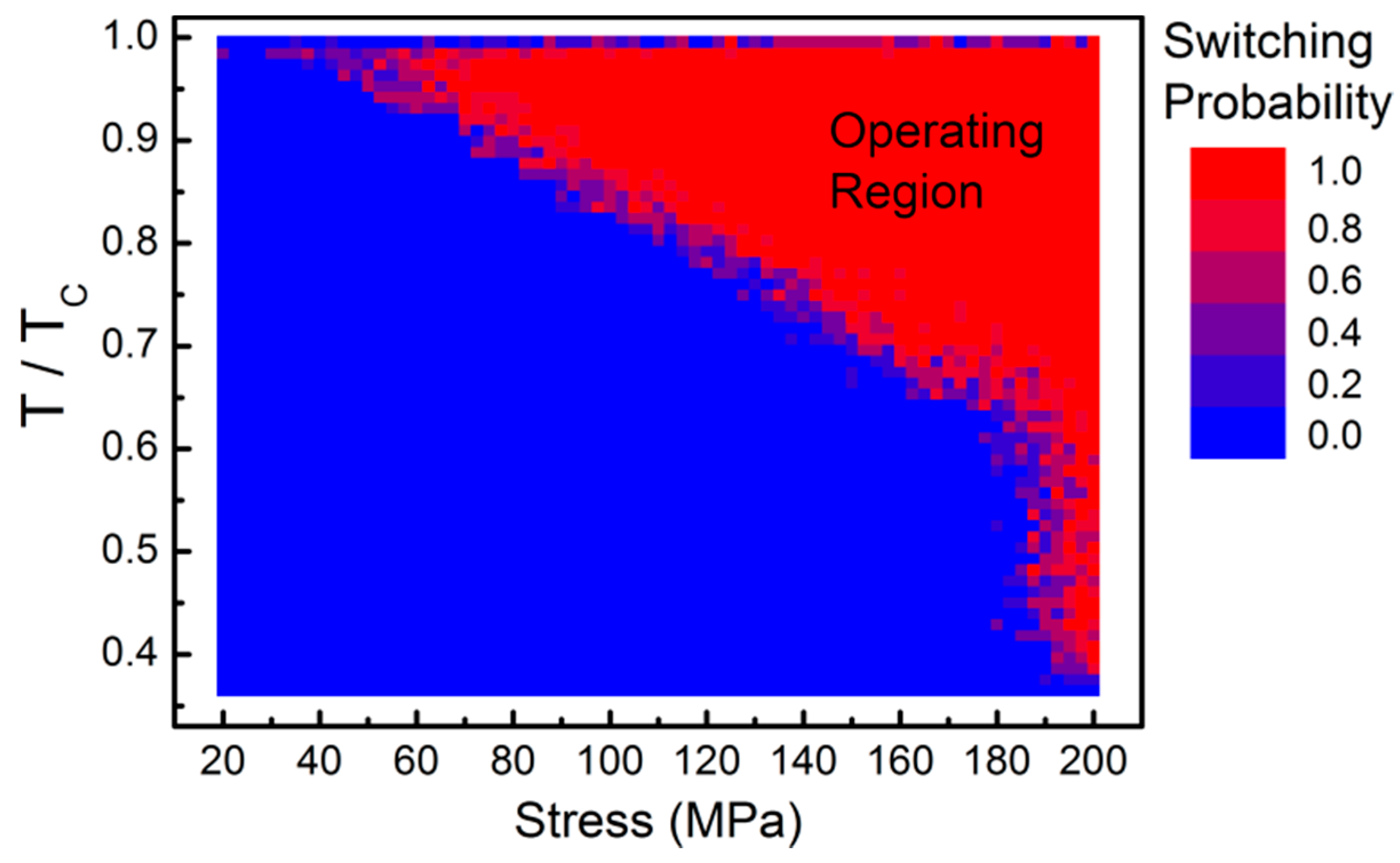
1.2. Temperature-Dependent Magnetisation Switching Modelling
2. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ishiwara, H. Ferroelectric Random Access Memories. J. Nanosci. Nanotechnol. 2012, 12, 7619–7627. [Google Scholar] [CrossRef] [PubMed]
- Diao, Z.; Li, Z.; Wang, S.; Ding, Y.; Panchula, A.; Chen, E.; Wang, L.-C.; Huai, Y. Spin-transfer torque switching in magnetic tunnel junctions and spin-transfer-torque random access memory. J. Phys. Condens. Matter 2007, 19, 165209. [Google Scholar] [CrossRef]
- Kawahara, T.; Ito, K.; Takemura, R.; Ohno, H. Spin-transfer torque RAM technology: Review and prospect. Microelectron. Reliab. 2012, 52, 613–627. [Google Scholar] [CrossRef]
- Khvalkovski, A.V.; Apalkov, D.; Watts, S.; Chepulskii, R.; Beach, R.S.; Ong, A.; Tang, X.; Driskill-Smith, A.; Butler, W.H.; Visscher, P.B. Basic principles of STT-MRAM cell operation in memory arrays. J. Phys. D Appl. Phys. 2013, 46, 074001. [Google Scholar] [CrossRef]
- Dieny, B.; Chshiev, M. Perpendicular magnetic anisotropy at transition metal/oxide interfaces and applications. Rev. Mod. Phys. 2017, 89, 025008. [Google Scholar] [CrossRef]
- Braganca, P.M.; Katine, J.A.; Emley, N.C.; Mauri, D.; Childress, J.R.; Rice, P.M.; Delenia, E.; Ralph, D.C.; Buhrman, R.A. A three-terminal approach to developing spin-torque written magnetic random access memory cells. IEEE Trans. Nanotechnol. 2009, 8, 190–195. [Google Scholar] [CrossRef]
- Parkin, S.S.P.; Hayashi, M.; Thomas, L. Magnetic Domain-Wall Racetrack Memory. Science 2008, 320, 190. [Google Scholar] [CrossRef] [PubMed]
- Parkin, S.; Yang, S.-H. Memory on the racetrack. Nat. Nanotechnol. 2015, 10, 195–198. [Google Scholar] [CrossRef] [PubMed]
- Eerenstein, W.; Wiora, M.; Prieto, J.L.; Scott, J.F.; Mathur, N.D. Giant sharp and persistent converse magnetoelectric effects in multiferroic epitaxial heterostructures. Nat. Mater. 2007, 6, 348. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Bur, A.; Zhao, P.; Mohanchandra, K.P.; Wong, K.; Wang, K.L.; Lynch, C.S.; Carman, G.P. Giant electric-field-induced reversible and permanent magnetization reorientation on magnetoelectric Ni/(011) [Pb(Mg 1/3 Nb 2/3) O3](1−x)–[PbTiO3]x heterostructure. Appl. Phys. Lett. 2011, 98, 012504. [Google Scholar]
- Ma, J.; Hu, J.; Li, Z.; Nan, C.W. Recent Progress in Multiferroic Magnetoelectric Composites: From Bulk to Thin Films. Adv. Mater. 2011, 23, 1062–1087. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Zhao, Y.G.; Li, P.S.; Yang, J.J.; Rizwan, S.; Zhang, J.X.; Seidel, J.; Qu, T.L.; Yang, Y.J.; Luo, Z.L.; et al. Electric-Field Control of Nonvolatile Magnetization in Co40Fe40B20/Pb(Mg1/3Nb2/3)0.7Ti0.3O3 Structure at Room Temperature. Phys. Rev. Lett. 2012, 108, 137203. [Google Scholar] [CrossRef] [PubMed]
- Pertsev, N.A.; Kohlstedt, H. Resistive switching via the converse magnetoelectric effect in ferromagnetic multilayers on ferroelectric substrates. Nanotechnology 2010, 21, 475202. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Chen, A.; Li, D.; Zhao, Y.; Zhang, S.; Yang, L.; Liu, Y.; Zhu, M.; Zhang, H.; Han, X. Electric Field Manipulation of Magnetization Rotation and Tunneling Magnetoresistance of Magnetic Tunnel Junctions at Room Temperature. Adv. Mater. 2014, 26, 4320–4325. [Google Scholar] [CrossRef] [PubMed]
- Pantel, D.; Goetze, S.; Hesse, D.; Alexe, M. Reversible electrical switching of spin polarization in multiferroic tunnel junctions. Nat. Mater. 2012, 11, 289. [Google Scholar] [CrossRef] [PubMed]
- Garcia, V.; Bibes, M.; Bocher, L.; Valencia, S.; Kronast, F.; Crassous, A.; Moya, X.; Enouz-Vedrenne, S.; Gloter, A.; Imhoff, D.; et al. Ferroelectric Control of Spin Polarization. Science 2010, 327, 1106–1110. [Google Scholar] [CrossRef] [PubMed]
- Chu, Y.-H.; Martin, L.W.; Holcomb, M.B.; Gajek, M.; Han, S.J.; He, Q.; Balke, N.; Yang, C.H.; Lee, D.; Hu, W.; et al. Electric-field control of local ferromagnetism using a magnetoelectric multiferroic. Nat. Mater. 2008, 7, 478. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.-G.; Li, M.; Hageman, S.; Chien, C.L. Electric-field-assisted switching in magnetic tunnel junctions. Nat. Mater. 2011, 11, 64. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Wang, C.; Liu, Y.; Zhang, Z.; Jin, Q.Y.; Duan, C.-G. Magnetization switching by combining electric field and spin-transfer torque effects in a perpendicular magnetic tunnel junction. Sci. Rep. 2016, 6, 18719. [Google Scholar] [CrossRef] [PubMed]
- Hao, X.; Zhai, J.; Kong, L.B.; Xu, Z. A comprehensive review on the progress of lead zirconate-based antiferroelectric materials. Prog. Mater. Sci. 2014, 63, 1–57. [Google Scholar] [CrossRef]
- Vopson, M.M.; Tan, X. Nonequilibrium polarization dynamics in antiferroelectrics. Phys. Rev. B 2017, 96, 014104. [Google Scholar] [CrossRef]
- Lepadatu, S.; Stewart, M.; Cain, M.G. Quantification of electromechanical coupling measured with piezoresponse force microscopy. J. Appl. Phys. 2014, 116, 066806. [Google Scholar] [CrossRef]
- Peng, R.-C.; Hu, J.M.; Momeni, K.; Wang, J.J.; Chen, L.Q.; Nan, C.W. Fast 180° magnetization switching in a strain-mediated multiferroic heterostructure driven by a voltage. Sci. Rep. 2016, 6, 27561. [Google Scholar] [CrossRef] [PubMed]
- Vopsaroiu, M.; Matthew, J.A.D.; Thompson, S.M. A new experimental design for noncontact giant magnetoresistance measurements using the magnetorefractive effect. Rev. Sci. Inst. 2004, 75, 3127–3130. [Google Scholar] [CrossRef]
- Parkin, S.S.P.; Kaiser, C.; Panchula, A.; Rice, P.M.; Hughes, B.; Samant, M.; Yang, S.H. Giant tunnel magnetoresistance at room temperature with MgO (100) tunnel barriers. Nat. Mater. 2004, 3, 862. [Google Scholar] [CrossRef] [PubMed]
- Weller, D.; Parker, G.; Mosendz, O.; Lyberatos, A.; Mitin, D.; Safonova, N.Y.; Albrecht, M. FePt heat assisted magnetic recording media. J. Vac. Sci. Technol. B 2016, 34, 060801. [Google Scholar] [CrossRef]
- Chen, J.Y.; He, L.; Wang, J.P.; Li, M. All-Optical Switching of Magnetic Tunnel Junctions with Single Subpicosecond Laser Pulses. Phys. Rev. Appl. 2017, 7, 021001. [Google Scholar] [CrossRef]
- Lepadatu, S. Interaction of magnetization and heat dynamics for pulsed domain wall movement with Joule heating. J. Appl. Phys. 2016, 120, 163908. [Google Scholar] [CrossRef]
- Yu, P.; Jin, X.F.; Kudrnovský, J.; Wang, D.S.; Bruno, P. Curie temperatures of fcc and bcc nickel and permalloy: Supercell and Green’s function methods. Phys. Rev. B 2008, 77, 054431. [Google Scholar] [CrossRef]
- Garanin, D.A. Fokker-Planck and Landau-Lifshitz-Bloch equations for classical ferromagnets. Phys. Rev. B 1997, 55, 3050. [Google Scholar] [CrossRef]
- Atxitia, U.; Chubykalo-Fesenko, O.; Kazantseva, N.; Hinzke, D.; Nowak, U.; Chantrell, R.W. Micromagnetic modeling of laser-induced magnetization dynamics using the Landau-Lifshitz-Bloch equation. Appl. Phys. Lett. 2007, 91, 232507. [Google Scholar] [CrossRef] [Green Version]
- Brown, W.F., Jr. Micromagnetics; Interscience; Springer: New York, NY, USA, 1963; Chapter 8. [Google Scholar]
- Ounadjela, K.; Lefakis, H.; Speriosu, V.S.; Hwang, C.; Alexopoulos, P.S. Thickness dependence of magnetization and magnetostriciton of NiFe and NiFeRh films. J. Phys. 1988, 12, C8-1709. [Google Scholar]
- Stewart, M.; Lepadatu, S.; McCartney, L.N.; Cain, M.G.; Wright, L.; Crain, J.; Newns, D.M.; Martyna, G.J. Electrode size and boundary condition independent measurement of the effective piezoelectric coefficient of thin films. APL Mater. 2015, 3, 026103. [Google Scholar] [CrossRef]
- Evans, R.F.L.; Hinzke, D.; Atxitia, U.; Nowak, U.; Chantrell, R.W.; Chubykalo-Fesenko, O. Stochastic form of the Landau-Lifshitz-Bloch equation. Phys. Rev. B 2012, 85, 014433. [Google Scholar] [CrossRef]
- Mil’shtejn, G.N. Approximate Integration of Stochastic Differential Equations. Theory Probab. Appl. 1975, 19, 557–562. [Google Scholar] [CrossRef]
- Néel, L. Théorie du traînage magnétique des ferromagnétiques en grains fins avec application aux terres cuites. Ann. Geophys. 1949, 5, 99. [Google Scholar]
- Brown, W.F., Jr. Thermal fluctuations of a single domain particle. Phys. Rev. 1963, 130, 1677. [Google Scholar] [CrossRef]
- Yoon, K.S.; Park, J.H.; Choi, J.H.; Yang, J.Y.; Lee, C.H.; Kim, C.O.; Hong, J.P. Performance of Co/Al2O3/NiFeCo/Al2O3/NiFe magnetic tunnel junctions prepared by a two-step rf plasma oxidation method. Appl. Phys. Lett. 2001, 79, 1160. [Google Scholar] [CrossRef]
- Lepadatu, S.; Saarikoski, H.; Beacham, R.; Benitez, M.J.; Moore, T.A.; Burnell, G.; Sugimoto, S.; Yesudas, D.; Wheeler, M.C.; Miguel, J.; et al. Synthetic ferrimagnet nanowires with very low critical current density for coupled domain wall motion. Sci. Rep. 2017, 7, 1640. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lepadatu, S.; Vopson, M.M. Heat-Assisted Multiferroic Solid-State Memory. Materials 2017, 10, 991. https://doi.org/10.3390/ma10090991
Lepadatu S, Vopson MM. Heat-Assisted Multiferroic Solid-State Memory. Materials. 2017; 10(9):991. https://doi.org/10.3390/ma10090991
Chicago/Turabian StyleLepadatu, Serban, and Melvin M. Vopson. 2017. "Heat-Assisted Multiferroic Solid-State Memory" Materials 10, no. 9: 991. https://doi.org/10.3390/ma10090991





