Controlled Shrinkage of Expanded Glass Particles in Metal Syntactic Foams
Abstract
:1. Introduction
2. Results and Discussion
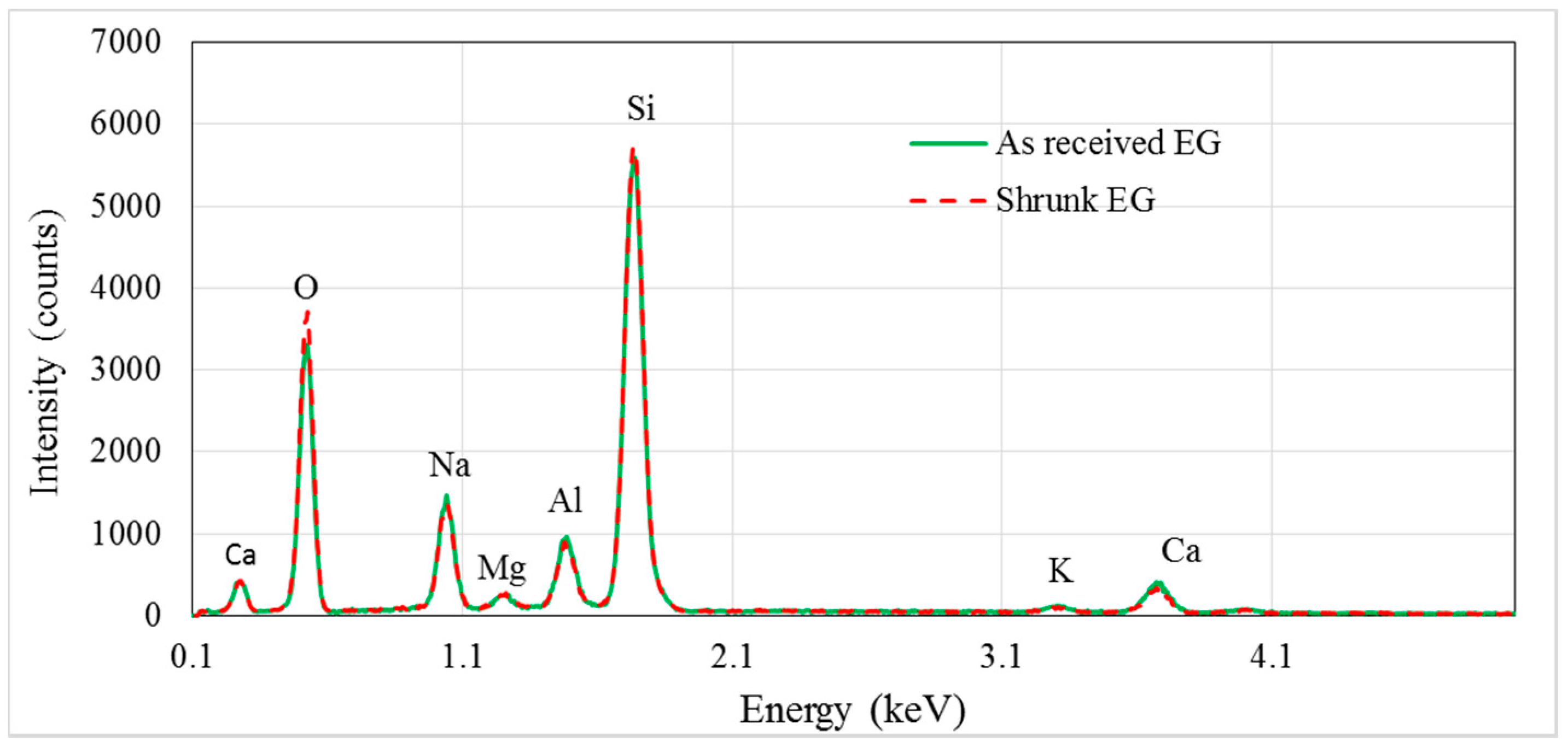
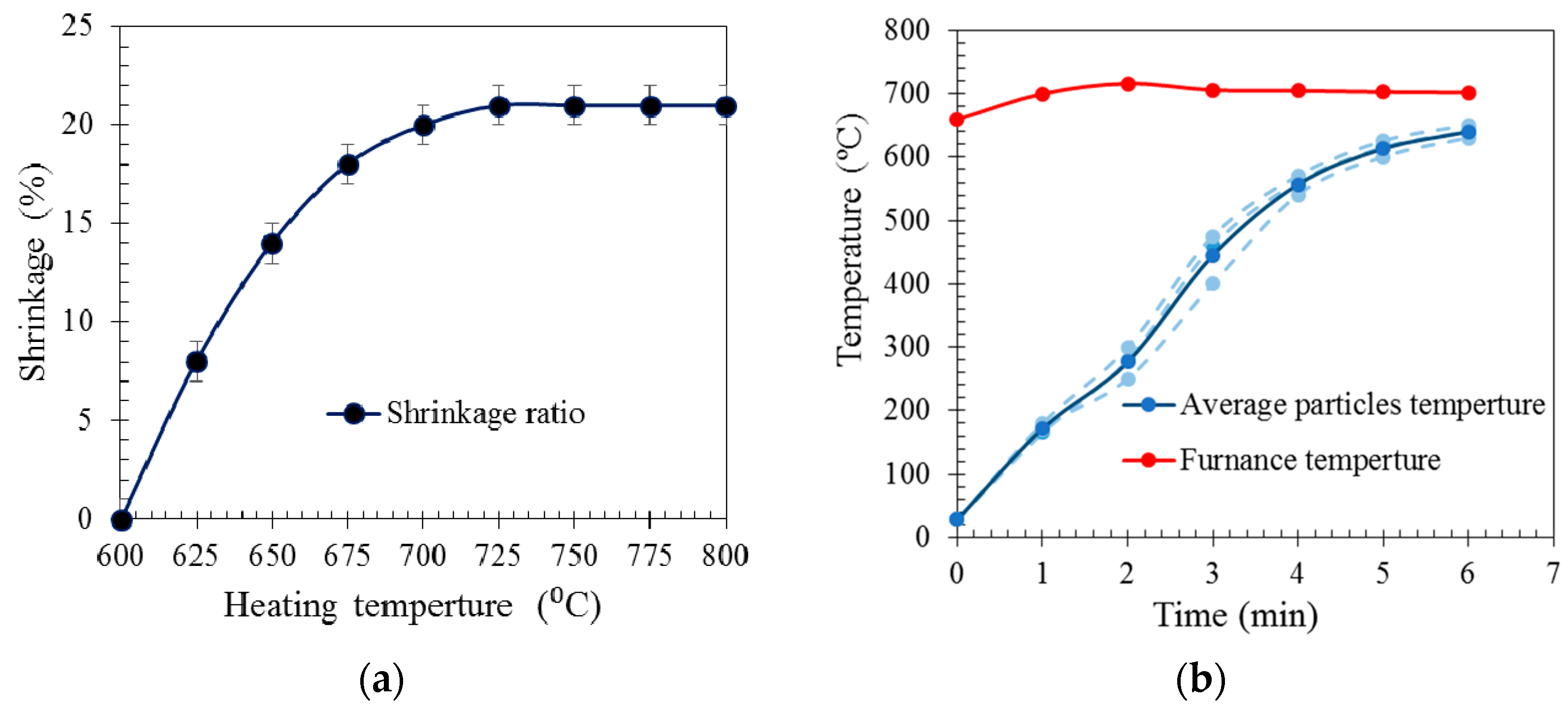
2.1. EG Particle Characteristics
2.2. Structural Characteristics of MSF
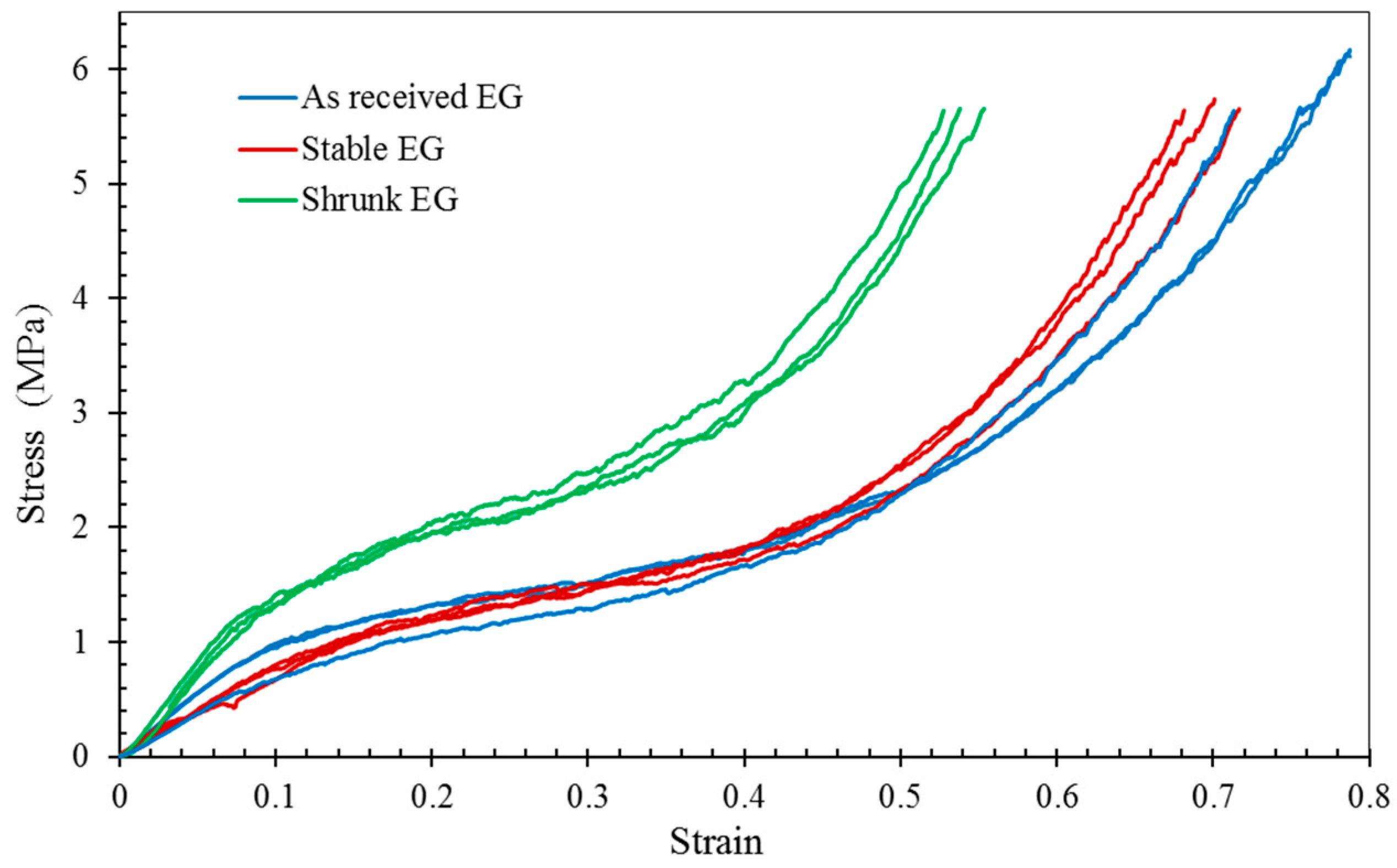
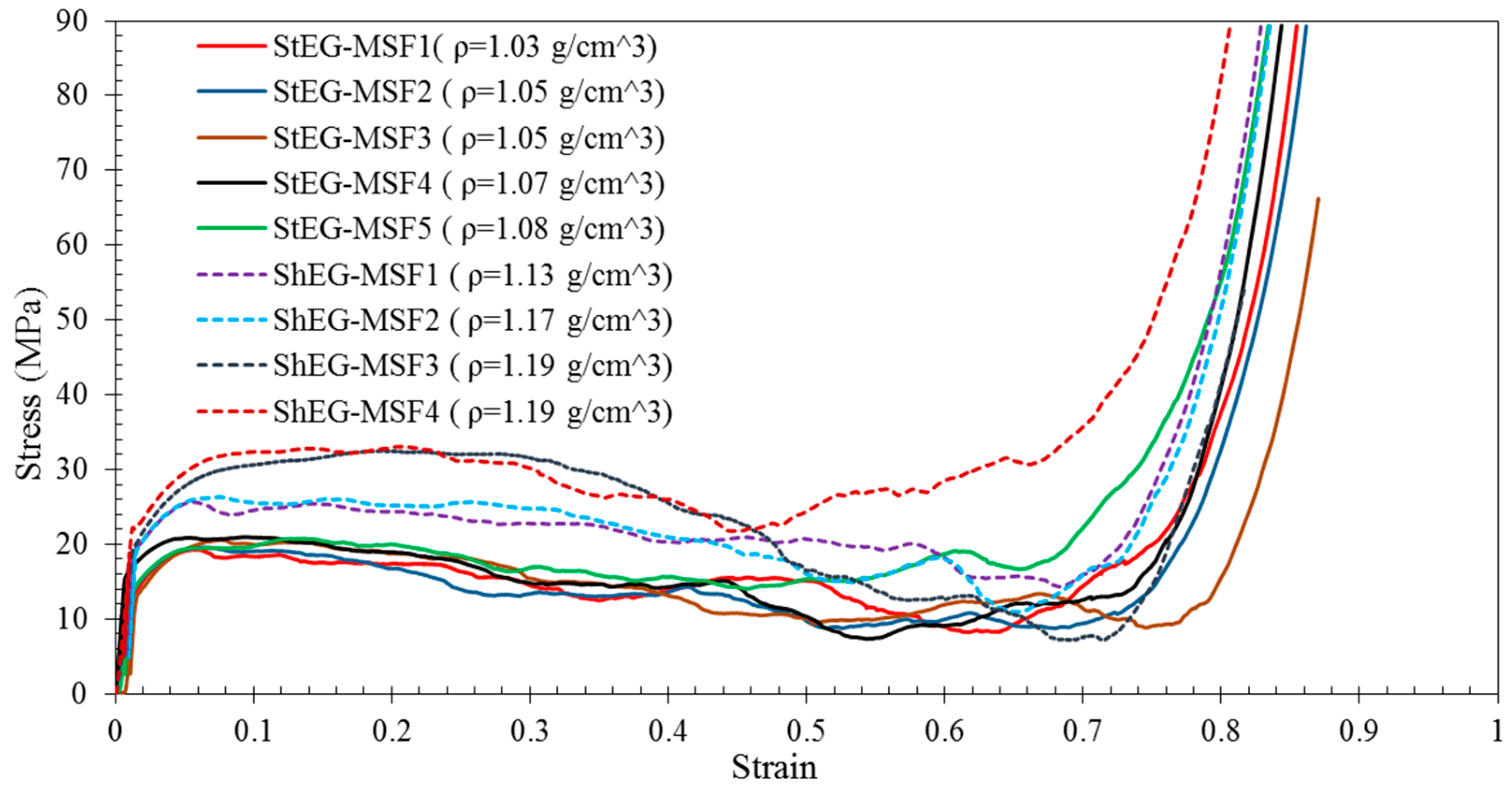
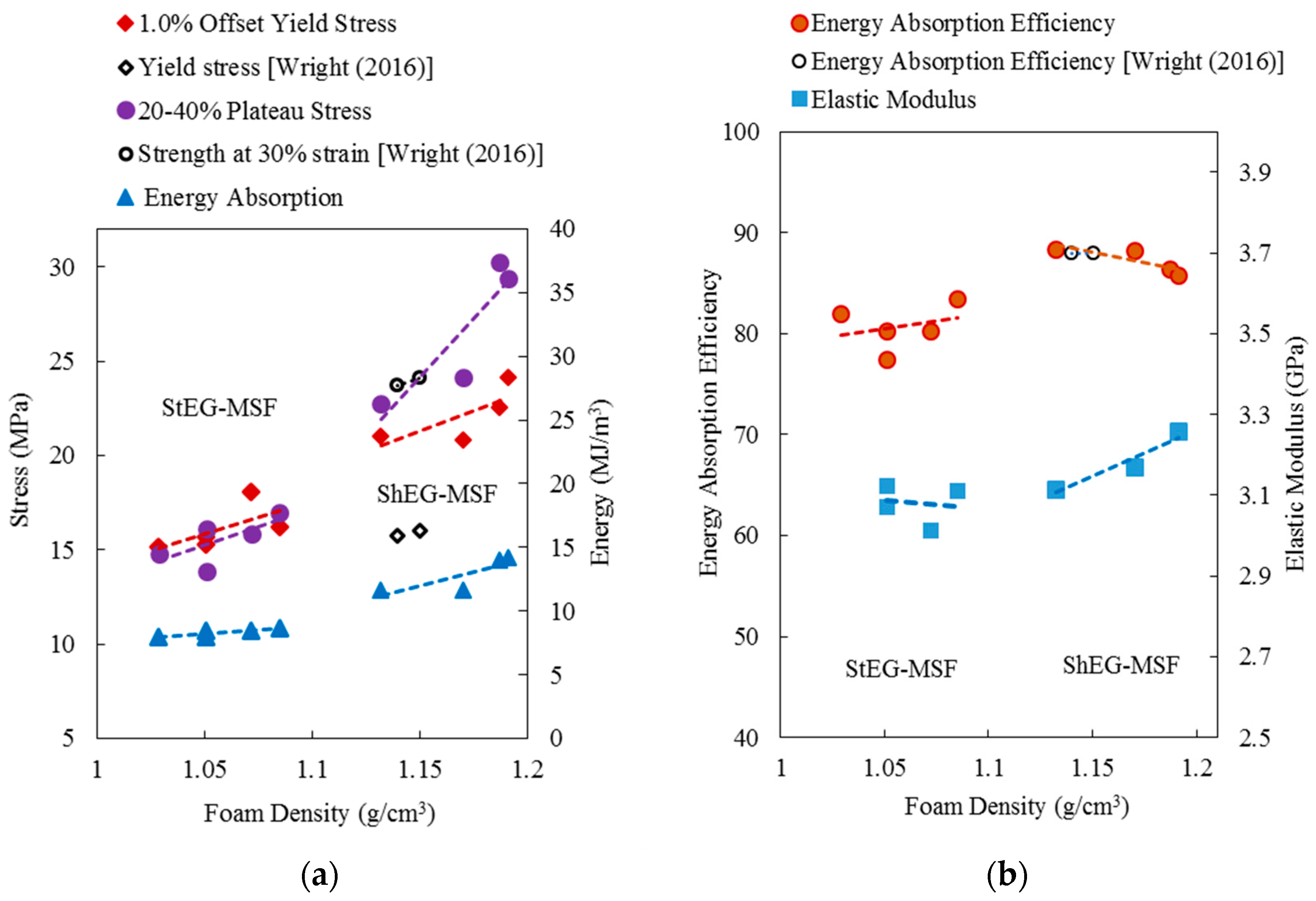
2.3. Compressive Properties of EG-MSF
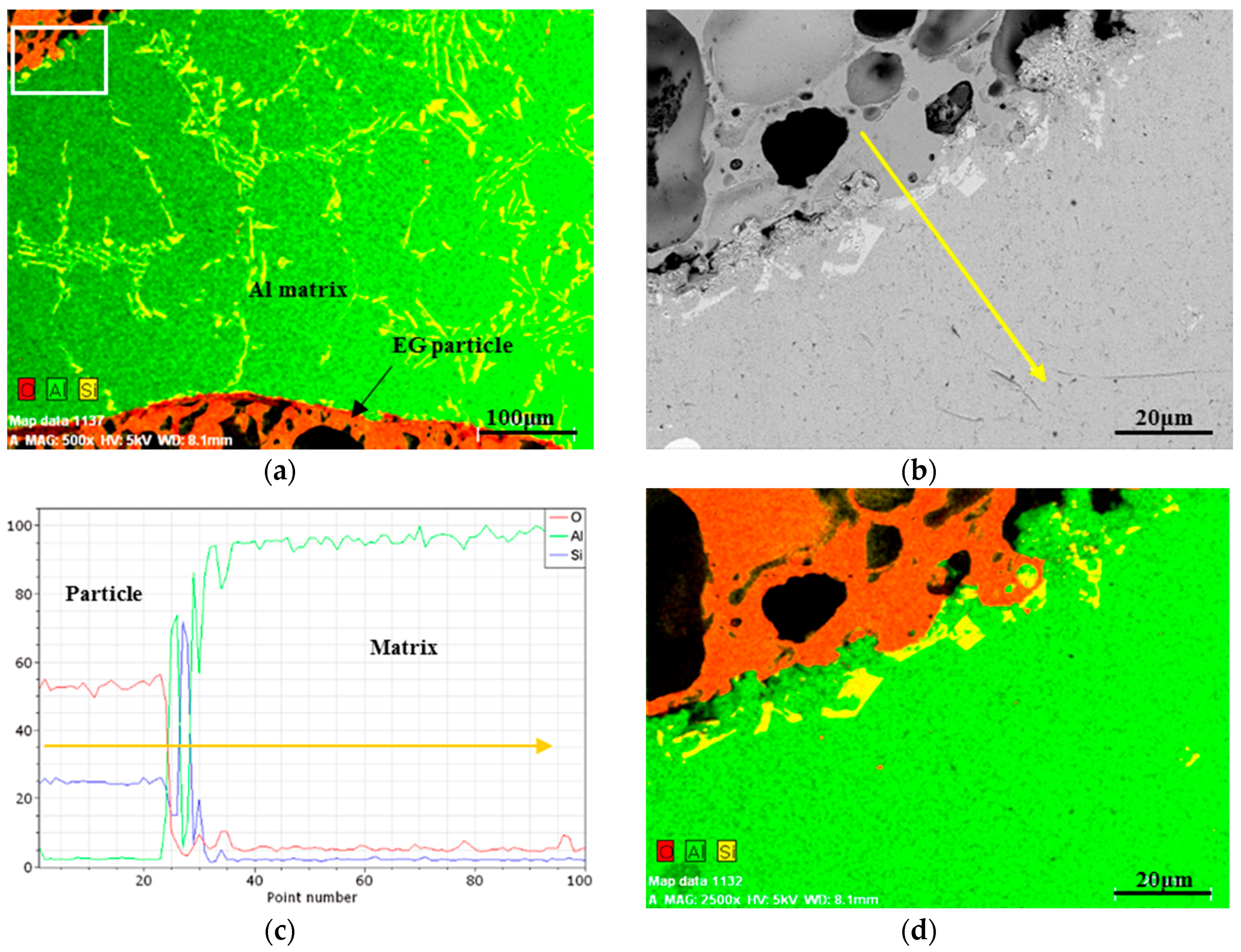
2.4. Deformation Mechanism of EG-MSF
3. Methodology
3.1. Characterisation of EG Particles
3.2. EG-MSF Sample Preparation
3.3. EG-MSF Characterisation
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Banhart, J. Aluminium foams for lighter vehicles. Int. J. Veh. Des. 2005, 37, 114–125. [Google Scholar] [CrossRef]
- Jang, W.-Y.; Hsieh, W.-Y.; Miao, C.-C.; Yen, Y.-C. Microstructure and mechanical properties of ALPORAS closed-cell aluminium foam. Mater. Charact. 2015, 107, 228–238. [Google Scholar] [CrossRef]
- Shunmugasamy, V.C.; Mansoor, B.; Gupta, N. Cellular Magnesium Matrix Foam Composites for Mechanical Damping Applications. JOM 2016, 68, 279–287. [Google Scholar] [CrossRef]
- Cochran, J.K.; Sanders, T.H.; Strbik, O.M., III; Wedding, C.A. Metal Syntactic Foam. U.S. Patent 8,815,408, 26 August 2014. [Google Scholar]
- Zhang, L.P.; Zhao, Y.Y. Mechanical response of Al matrix syntactic foams produced by pressure infiltration casting. J. Compos. Mater. 2007, 41, 2105–2117. [Google Scholar] [CrossRef]
- Gupta, N.; Rohatgi, P.K. Metal Matrix Syntactic Foams: Processing, Microstructure, Properties and Applications; DEStech Publications, Inc.: Lancaster, PA, USA, 2014; ISBN 13 9781932078831. [Google Scholar]
- Mitrović, S.; Babić, M.; Miloradović, N.; Bobić, I.; Stojanović, B.; Džunić, D.; Pantić, M. Wear Characteristics of Hybrid Composites Based on Za27 Alloy Reinforced with Silicon Carbide and Graphite Particles. Tribol. Ind. 2014, 36, 204–210. [Google Scholar]
- Hartmann, M.; Reindel, K.; Singer, R.F. Fabrication and properties of syntactic magnesium foams. In Proceedings of the 1998 MRS Spring Symposium, San Francisco, CA, USA, 13–15 April 1998. [Google Scholar]
- Rajan, T.P.D.; Pillai, R.M.; Pai, B.C.; Satyanarayana, K.G.; Rohatgi, P.K. Fabrication and characterisation of Al-7Si-0.35Mg/fly ash metal matrix composites processed by different stir casting routes. Compos. Sci. Technol. 2007, 67, 3369–3377. [Google Scholar] [CrossRef]
- Orth, A.; Steinbach, S.; Dennstedt, A.; Ratke, L. Aerogel-filled metals: A syntactic cellular material. Mater. Sci. Technol. 2017, 33, 299–306. [Google Scholar] [CrossRef]
- Peroni, L.; Scapin, M.; Avalle, M.; Weise, J.; Lehmhus, D. Dynamic mechanical behavior of syntactic iron foams with glass microspheres. Mater. Sci. Eng. A 2012, 552, 364–375. [Google Scholar] [CrossRef]
- Rohatgi, P.K.; Alaraj, S.; Gupta, N. Pressure infiltration synthesis of lightweight syntactic aluminum matrix composites. In Proceedings of the 20th Technical Conference of the American Society for Composites 2005, Philadelphia, PA, USA, 7–9 September 2005; DEStech Publications: Philadelphia, PA, USA, 2005. [Google Scholar]
- Rohatgi, P.K.; Gupta, N.; Schultz, B.F.; Luong, D.D. The synthesis, compressive properties, and applications of metal matrix syntactic foams. JOM 2011, 63, 36–42. [Google Scholar]
- Daoud, A.; Abou El-khair, M.T.; Abdel-Aziz, M.; Rohatgi, P. Fabrication, microstructure and compressive behavior of ZC63 Mg–microballoon foam composites. Compos. Sci. Technol. 2007, 67, 1842–1853. [Google Scholar] [CrossRef]
- Taherishargh, M.; Belova, I.V.; Murch, G.E.; Fiedler, T. Low-density expanded perlite–aluminium syntactic foam. Mater. Sci. Eng. A 2014, 604, 127–134. [Google Scholar] [CrossRef]
- Broxtermann, S.; Taherishargh, M.; Belova, I.V.; Murch, G.E.; Fiedler, T. On the compressive behaviour of high porosity expanded Perlite-Metal Syntactic Foam (P-MSF). J. Alloys Compd. 2017, 691, 690–697. [Google Scholar] [CrossRef]
- Wang, C.-F.; Zhou, F.; Gu, H.-Z.; Zhu, H.-X.; Li, Y.-W. Preparation and microstructure of Al-intercalated vermiculite. In Proceedings of the 2011 International Conference on Chemical, Material and Metallurgical Engineering, ICCMME 2011, Beihai, China, 23–25 December 2011; Trans Tech Publications: Beihai, China, 2012. [Google Scholar]
- Taherishargh, M.; Belova, I.V.; Murch, G.E.; Fiedler, T. Pumice/aluminium syntactic foam. Mater. Sci. Eng. A (Struct. Mater. Prop. Microstruct. Process.) 2015, 635, 102–108. [Google Scholar] [CrossRef]
- Bazzaz Bonabi, S.; Kahani Khabushan, J.; Kahani, R.; Honarbakhsh Raouf, A. Fabrication of metallic composite foam using ceramic porous spheres “Light Expanded Clay Aggregate” via casting process. Mater. Des. 2014, 64, 310–315. [Google Scholar] [CrossRef]
- Sommariva, L.; Weinberger, K. Energy and natural resources saving in the production of expanded glass granules. Chem. Eng. Trans. 2015, 43, 2437–2442. [Google Scholar]
- Garkida, A.; Hwang, J.-Y.; Huang, X.; Okuofu, C.A.; Ahuwan, A.M.; Li, B. The shrinkage behaviour of recycled glass compacts. In Proceedings of the 2008 EPD Congress. Sessions and Symposia sponsored by the Extraction; Processing Division (EPD) of The Minerals, Metals; Materials Society (TMS), New Orleans, LA, USA, 9–13 March 2008; Minerals, Metals, Materials Society: Warrendale, PA, USA, 2008. [Google Scholar]
- Palmero, P.; Formia, A.; Antonaci, P.; Brini, S.; Tulliani, J.-M. Geopolymer technology for application-oriented dense and lightened materials. Elaboration and characterization. Ceram. Int. 2015, 41, 12967–12979. [Google Scholar] [CrossRef]
- Poraver Expanded Glass. Available online: http://www.poraver.com/us/poraver-expanded-glass (accessed on 1 June 2017).
- Bumanis, G.; Bajare, D.; Locs, J.; Korjakins, A. Alkali-silica reactivity of foam glass granules in structure of lightweight concrete. Constr. Build. Mater. 2013, 47, 274–281. [Google Scholar] [CrossRef]
- Latimer, R.A.; Latimer, M.D. A New Type of Porous Absorber. Sintered expanded glass granulates as a high strength absorber. In Proceedings of the 20th International Congress on Acoustics, ICA 2010, Sydney, Australia, 23–27 August 2010; pp. 1–3. [Google Scholar]
- Huber, O.; Klaus, H. Cellular composites in lightweight sandwich applications. Mater. Lett. 2009, 63, 1117–1120. [Google Scholar] [CrossRef]
- Schmidt, M.; Pöllmann, H.; Egersdorfer, A.; Goske, J.; Winter, S. The use of a recycled glass powder and a expanded glass containing metakaolin in different binder systems. In Proceedings of the 34th International Conference on Cement Microscopy, Halle, Germany, 1–4 April 2012; International Cement Microscopy Association: Halle, Germany, 2012. [Google Scholar]
- Wright, A.; Kennedy, A. The Processing and Properties of Syntactic Al Foams Containing Low Cost Expanded Glass Particles. Adv. Eng. Mater. 2016. [Google Scholar] [CrossRef]
- Prado, M.O.; Zanotto, E.D.; Muller, R. Model for sintering polydispersed glass particles. J. Non-Cryst. Solids 2001, 279, 169–178. [Google Scholar] [CrossRef]
- McCullough, K.Y.G.; Fleck, N.A.; Ashby, M.F. Uniaxial stress-strain behaviour of aluminium alloy foams. Acta Mater. 1999, 47, 2323–2330. [Google Scholar] [CrossRef]
- Orbulov, I.N.; Dobranszky, J.; Nemeth, A. Microstructural characterisation of syntactic foams. J. Mater. Sci. 2009, 44, 4013–4019. [Google Scholar] [CrossRef]
- Yoshikawa, N.; Hattori, A.; Taniguchi, S. Growth Rate of Reaction Layer between SiO2 and Molten Al above 1473 K. Mater. Trans. 2005, 46, 842–845. [Google Scholar] [CrossRef]
- Kadkhodapour, J.; Raeisi, S. Micro-macro investigation of deformation and failure in closed-cell aluminum foams. Comput. Mater. Sci. 2014, 83, 137–148. [Google Scholar] [CrossRef]
- Van Vlack, L.H. Element of Matreials Science and Engineering; Addison-Wesley: Reading, MA, USA, 1975; pp. 273–274. [Google Scholar]
- Rohatgi, P.K.; Kim, J.K.; Gupta, N.; Alaraj, S.; Daoud, A. Compressive characteristics of A356/fly ash cenosphere composites synthesized by pressure infiltration technique. Compos. Part A Appl. Sci. Manuf. 2006, 37, 430–437. [Google Scholar] [CrossRef]
- Wang, Q.G. Microstructural effects on the tensile and fracture behavior of aluminum casting alloys A356/357. Metall. Mater. Trans. A (Phys. Metall. Mater. Sci.) 2003, 34A, 2887–2899. [Google Scholar] [CrossRef]
- Ferguson, J.B.; Santa Maria, J.A.; Schultz, B.F.; Rohatgi, P.K. Al–Al2O3 syntactic foams—Part II: Predicting mechanical properties of metal matrix syntactic foams reinforced with ceramic spheres. Mater. Sci. Eng. A 2013, 582, 423–432. [Google Scholar] [CrossRef]
- International Organization for Standardization. ISO_13314 Mechanical Testing of Metals—Ductility Testing—Compression Test for Porous and Cellular Metals; International Organization for Standardization: Geneva, Switzerland, 2011. [Google Scholar]



| Particles Group | Bulk Density g/cm3 | Particle Density g/cm3 | Packing Density ( | True Density g/cm3 |
|---|---|---|---|---|
| As-received EG | 0.19 | 0.33 | 0.58 | 2.81 |
| Stable EG | 0.20 | 0.34 | 0.59 | 2.81 |
| Shrunk EG | 0.27 | 0.43 | 0.63 | 2.81 |
| Sample | Foam Weight (g) | Foam Volume (cm3) | Foam Density (g/cm3) | Matrix Volume Fraction (%) | EG Volume Fraction (%) | Void Volume Fraction (%) |
|---|---|---|---|---|---|---|
| StEG-MSF1 | 22.30 | 21.65 | 1.03 | 30.97 | 60.61 | 8.42 |
| StEG-MSF2 | 23.86 | 22.69 | 1.05 | 31.77 | 58.82 | 9.41 |
| StEG-MSF3 | 23.98 | 22.79 | 1.05 | 31.80 | 58.82 | 9.38 |
| StEG-MSF4 | 24.33 | 22.68 | 1.07 | 32.57 | 58.82 | 8.61 |
| StEG-MSF5 | 24.65 | 22.68 | 1.08 | 33.09 | 58.82 | 8.09 |
| ShEG-MSF1 | 22.48 | 19.85 | 1.13 | 32.17 | 62.79 | 5.04 |
| ShEG-MSF2 | 24.71 | 22.11 | 1.17 | 33.60 | 62.79 | 3.61 |
| ShEG-MSF3 | 25.06 | 21.11 | 1.19 | 34.22 | 62.79 | 2.99 |
| ShEG-MSF4 | 23.40 | 21.10 | 1.19 | 34.38 | 62.79 | 2.83 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Sahlani, K.; Taherishargh, M.; Kisi, E.; Fiedler, T. Controlled Shrinkage of Expanded Glass Particles in Metal Syntactic Foams. Materials 2017, 10, 1073. https://doi.org/10.3390/ma10091073
Al-Sahlani K, Taherishargh M, Kisi E, Fiedler T. Controlled Shrinkage of Expanded Glass Particles in Metal Syntactic Foams. Materials. 2017; 10(9):1073. https://doi.org/10.3390/ma10091073
Chicago/Turabian StyleAl-Sahlani, Kadhim, Mehdi Taherishargh, Erich Kisi, and Thomas Fiedler. 2017. "Controlled Shrinkage of Expanded Glass Particles in Metal Syntactic Foams" Materials 10, no. 9: 1073. https://doi.org/10.3390/ma10091073
APA StyleAl-Sahlani, K., Taherishargh, M., Kisi, E., & Fiedler, T. (2017). Controlled Shrinkage of Expanded Glass Particles in Metal Syntactic Foams. Materials, 10(9), 1073. https://doi.org/10.3390/ma10091073





