A Novel Approach to Estimate the Plastic Anisotropy of Metallic Materials Using Cross-Sectional Indentation Applied to Extruded Magnesium Alloy AZ31B
Abstract
:1. Introduction
2. Experiment Investigation
2.1. Material
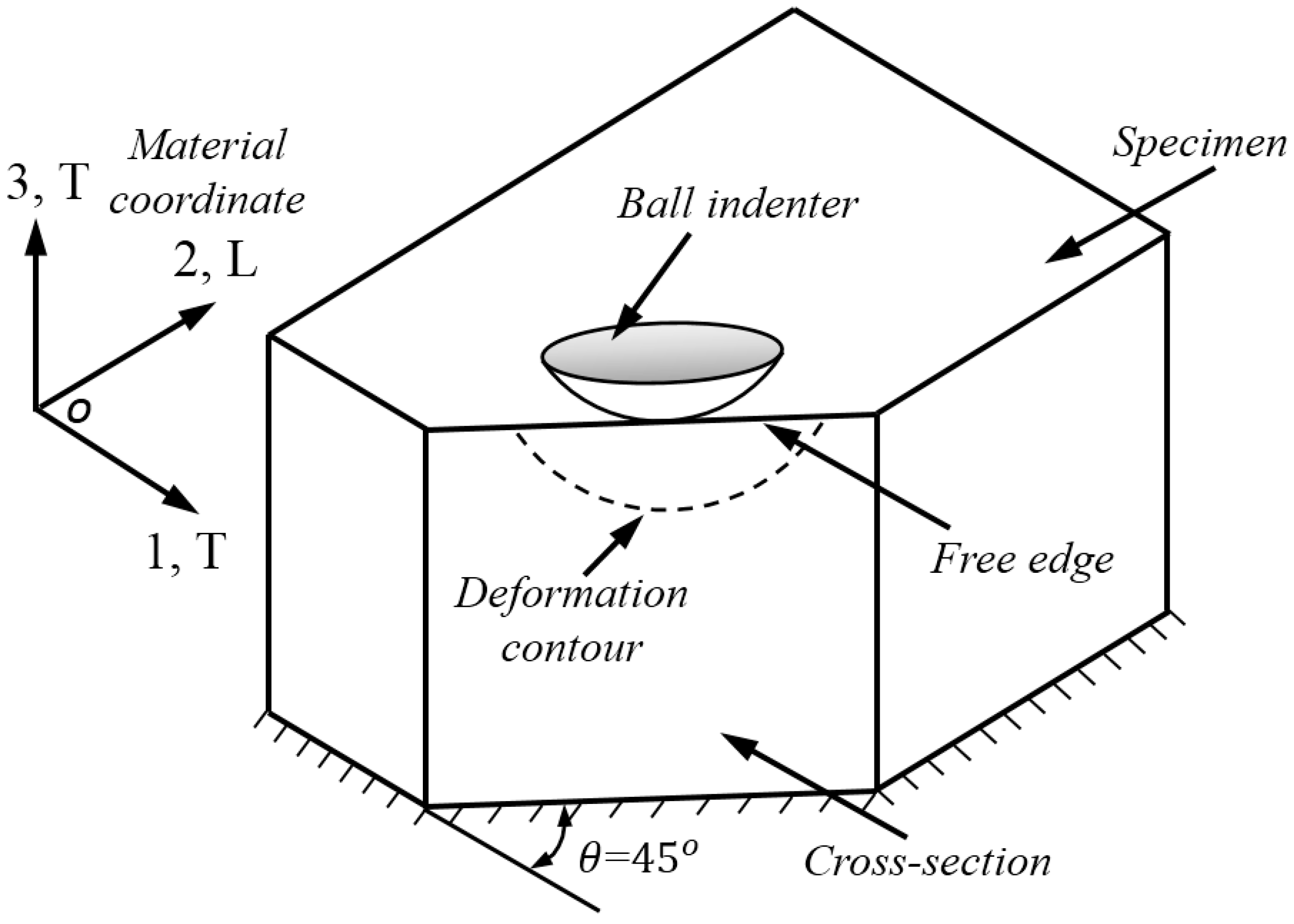
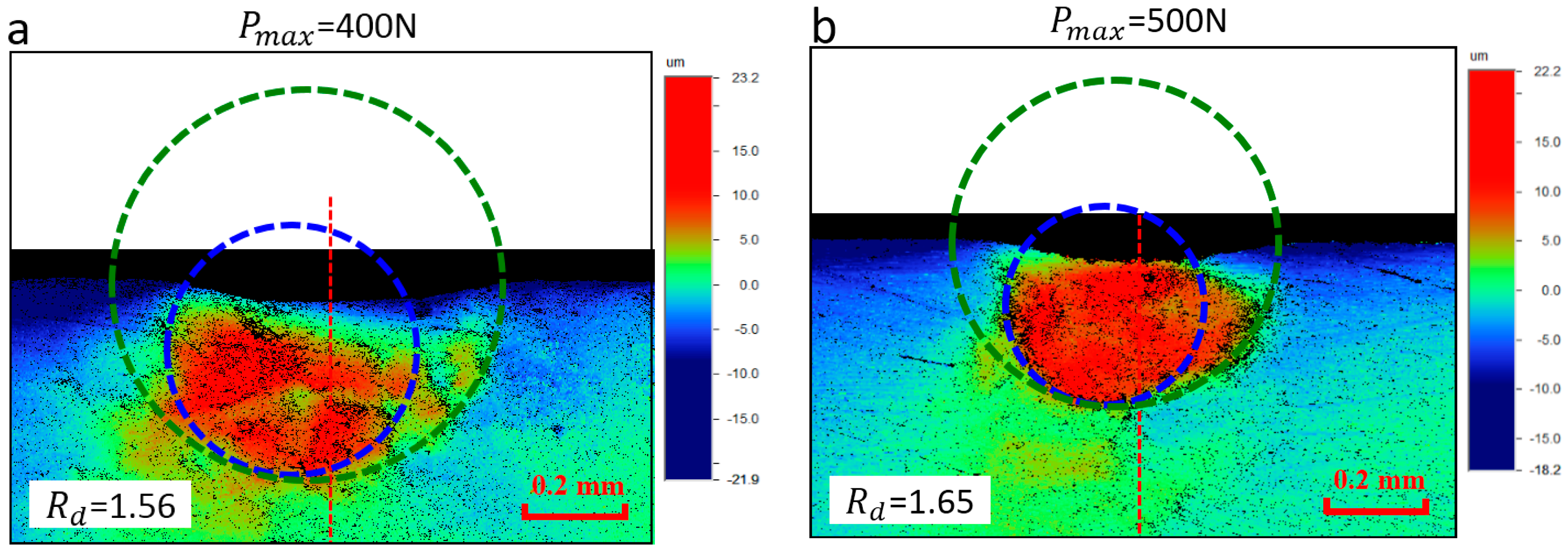
2.2. Cross-Sectional Indentation
3. Methods
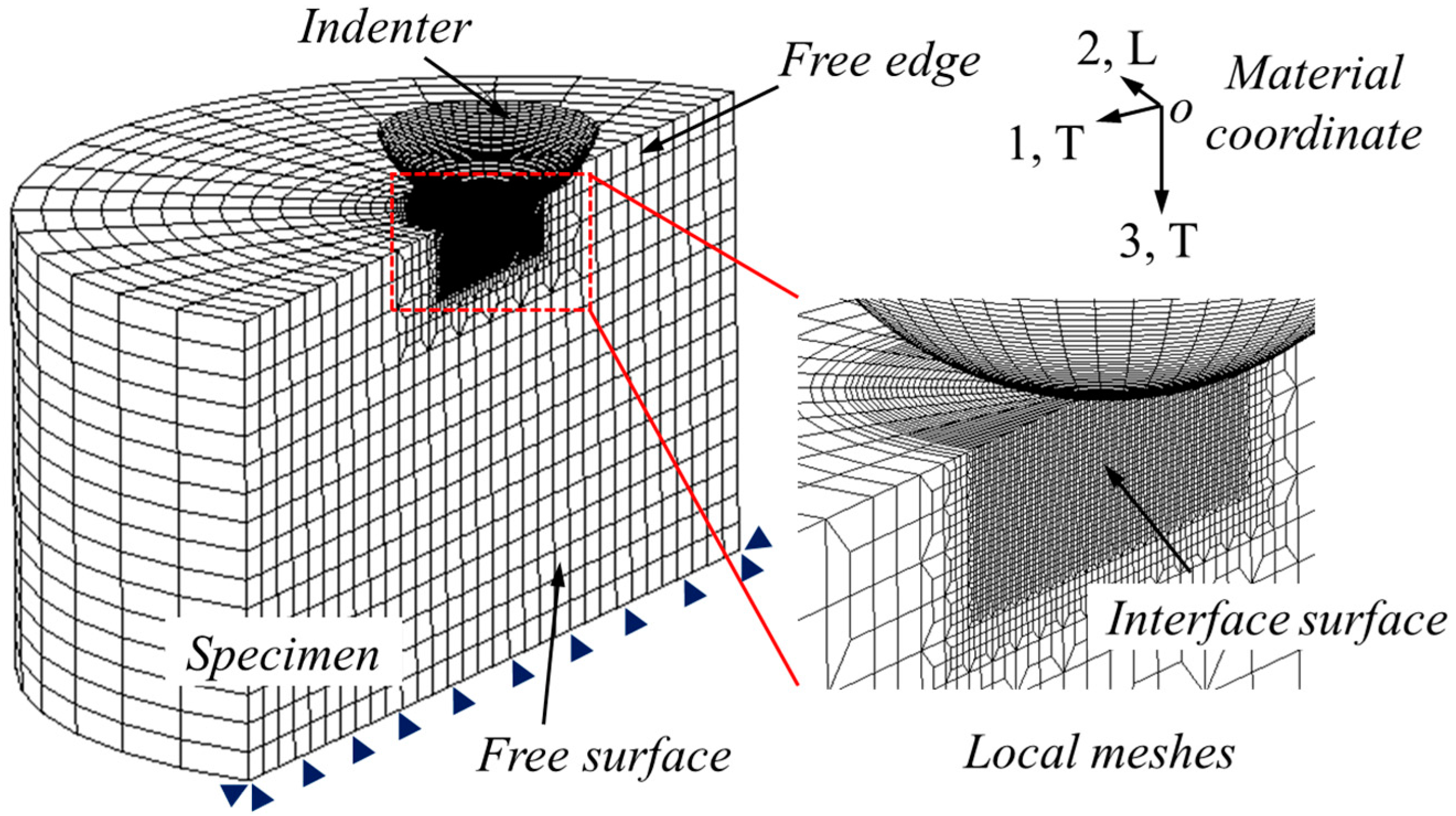
3.1. Simulation Setup
3.2. Finite Element Modelling
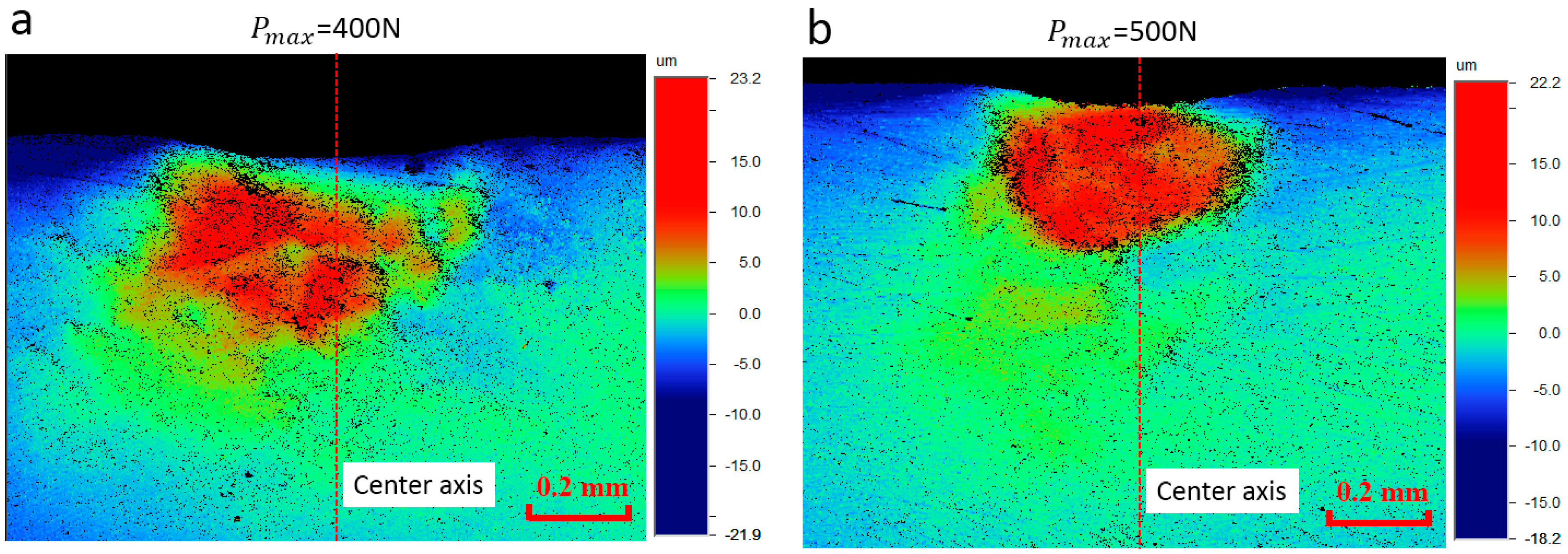
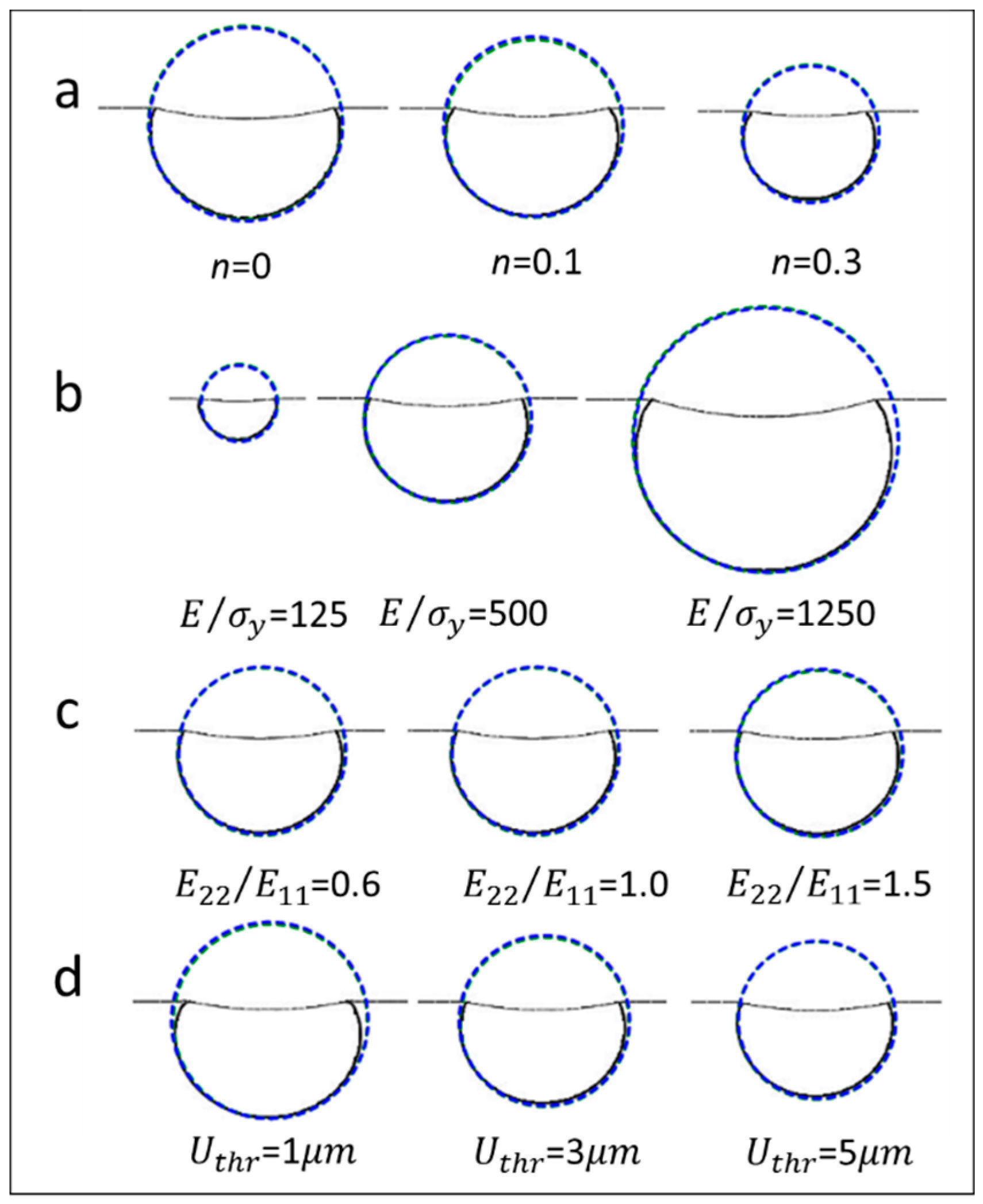
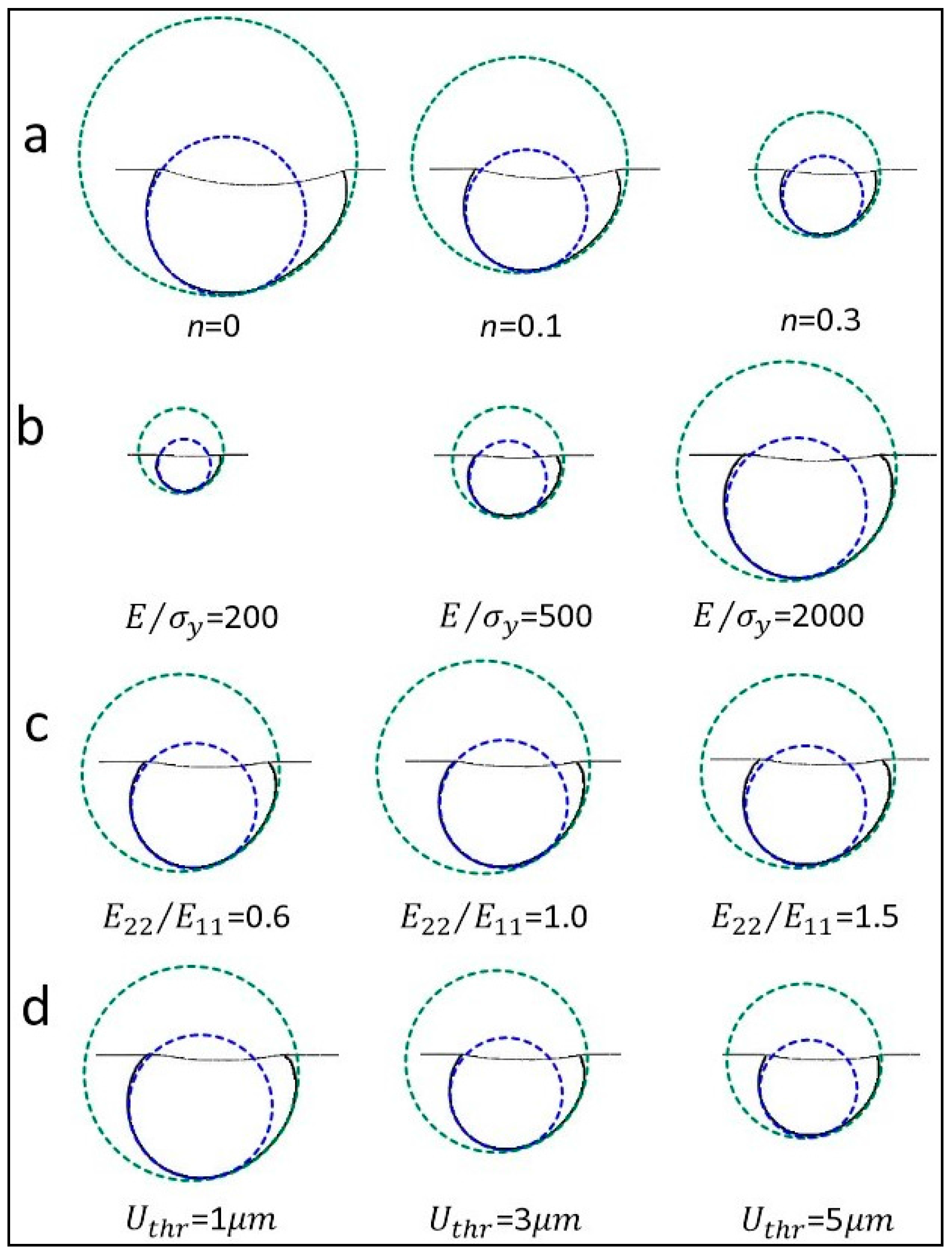
3.3. Characterization of the Out-of-Plane Deformation Contour
4. Fundamental Relationship between and
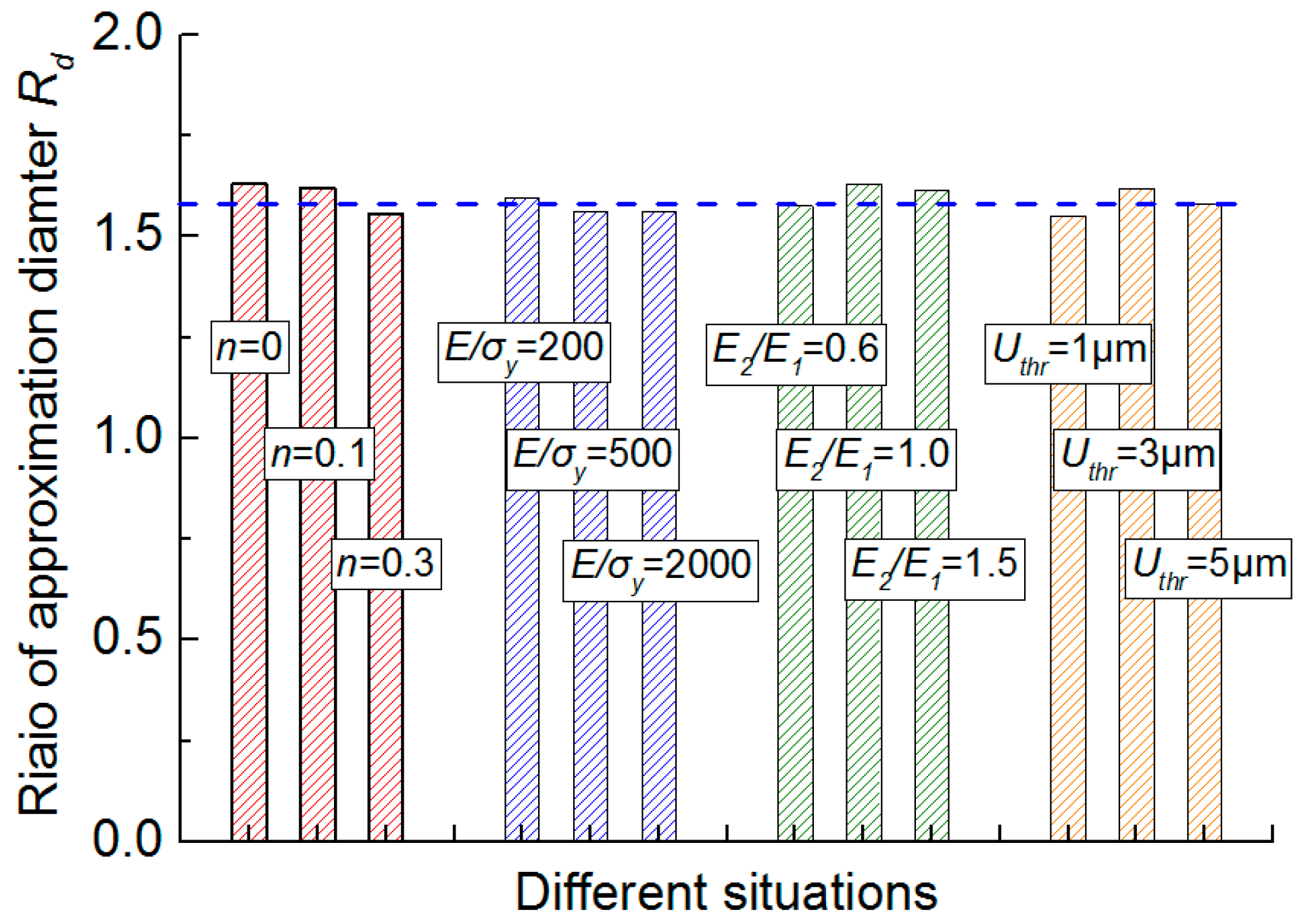
4.1. Results Obtained from Numerical Simulation
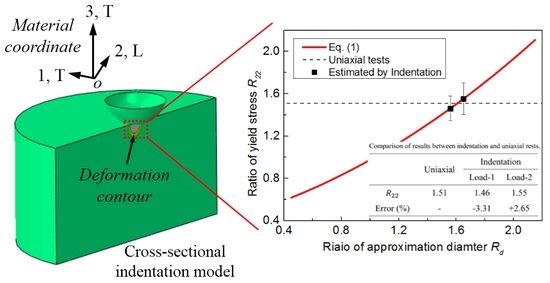
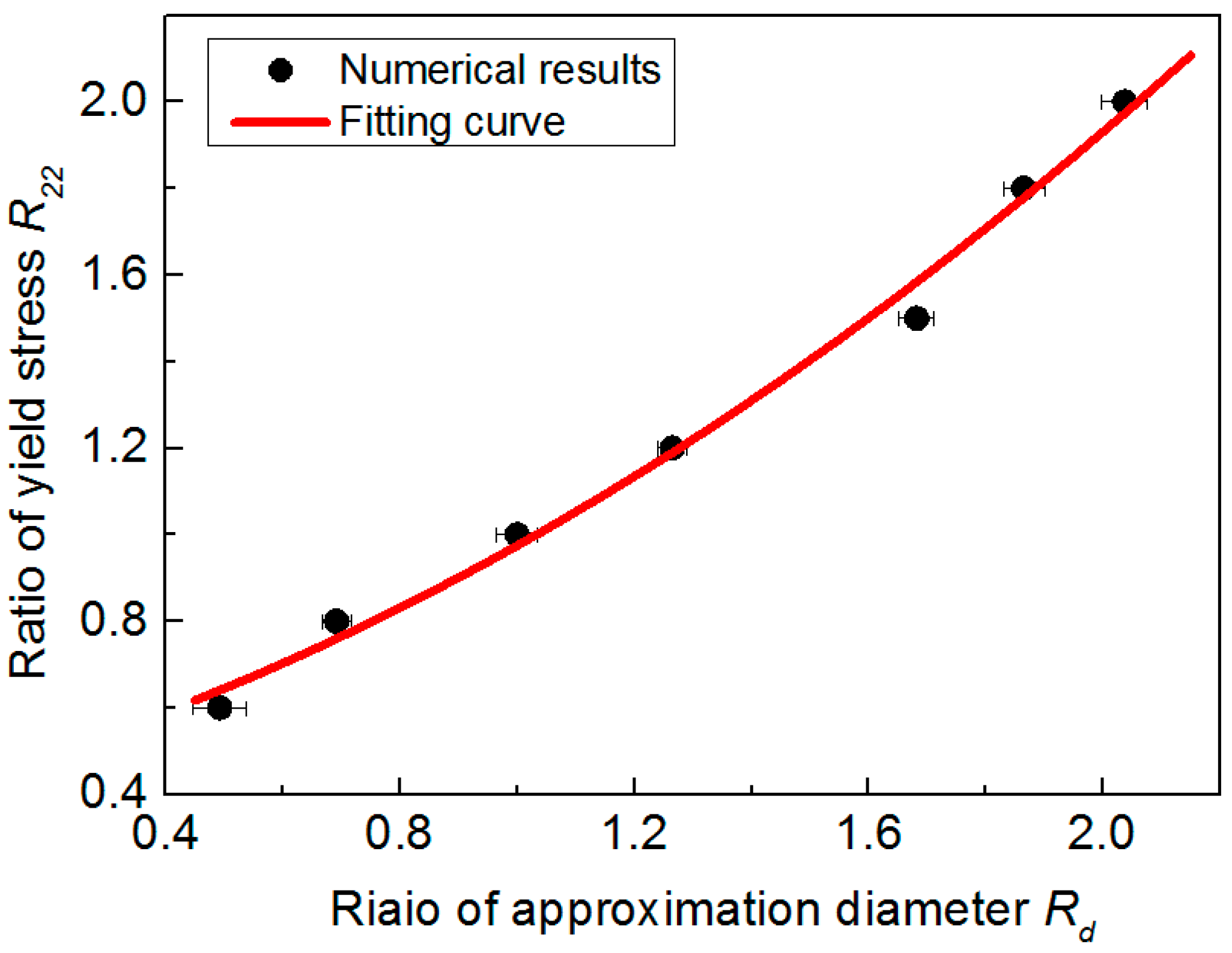
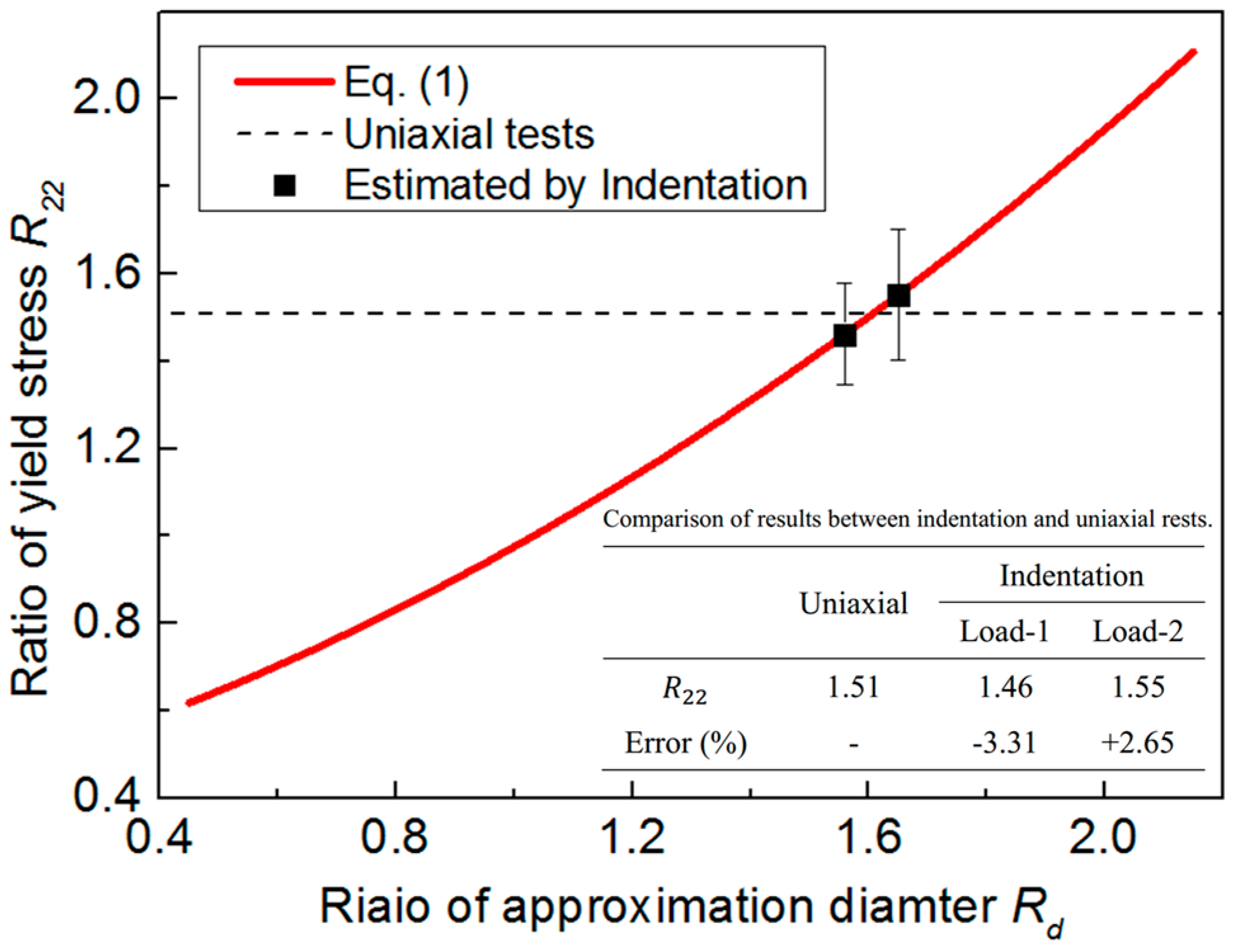
4.2. Comparison with the Experiment
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tabor, D. The Hardness of Metals; Oxford University Press: London, UK, 1951. [Google Scholar]
- Wang, W.; Wu, J.; Hui, Y.; Kun, Z.; Zhan, X.; Guo, R. Identification of elastic-plastic properties of metal materials by using the residual imprint of spherical indentation. Mater. Sci. Eng. A 2016, 679, 143–154. [Google Scholar] [CrossRef]
- Zambaldi, C.; Raabe, D. Plastic anisotropy of γ-TiAl revealed by axisymmetric indentation. Acta Mater. 2010, 58, 3516–3530. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic-modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Patel, D.K.; Kalidindi, S.R. Correlation of spherical nanoindentation stress-strain curves to simple compression stress-strain curves for elastic-plastic isotropic materials. Acta Mater. 2016, 112, 295–302. [Google Scholar] [CrossRef]
- Moussa, C.; Hernot, X.; Bartier, O.; Delattre, G.; Collin, J.M.; Mauvoisin, G. Mechanical characterization of carbonitrided steel with spherical indentation using the average representative strain. Mater. Des. 2016, 89, 1191–1198. [Google Scholar] [CrossRef] [Green Version]
- Roy, T.K. Assessing hardness and fracture toughness in sintered zinc oxide ceramics through indentation technique. Mater. Sci. Eng. A 2015, 640, 267–274. [Google Scholar] [CrossRef]
- Wang, X.; Wang, C.J.; Atkinson, A. Interface fracture toughness in thermal barrier coatings by cross-sectional indentation. Acta Mater. 2010, 60, 6152–6163. [Google Scholar] [CrossRef]
- Attar, H.; Ehtemam-Haghighi, S.; Kent, D.; Okulov, I.V.; Wendrock, H.; Bnisch, M.; Volegov, A.S.; Calin, M.; Eckert, J.; Dargusch, M.S. Nanoindentation and wear properties of Ti and Ti-TiB composite materials produced by selective laser melting. Mater. Sci. Eng. A 2017, 688, 20–26. [Google Scholar] [CrossRef]
- Ehtemam-Haghighi, S.; Cao, G.; Zhang, L.C. Nanoindentation study of mechanical properties of Ti based alloys with Fe and Ta additions. J. Alloys Comp. 2017, 692, 892–897. [Google Scholar] [CrossRef]
- Ehtemam-Haghighi, S.; Prashanth, K.G.; Attar, H.; Chaubey, A.K.; Cao, G.H.; Zhang, L.C. Evaluation of mechanical and wear properties of Ti-xNb-7Fe alloys designed for biomedical applications. Mater. Des. 2016, 111, 592–599. [Google Scholar] [CrossRef]
- Vlassak, J.J.; Nix, W.D. Measuring the elastic properties of anisotropic materials by means of indentation experiments. J. Mech. Phys. Solids 1994, 42, 1223–1245. [Google Scholar] [CrossRef]
- Bocciarelli, M.; Bolzon, G.; Maier, G. Parameter identification in anisotropic elastoplasticity by indentation and imprint mapping. Mech. Mater. 2005, 37, 855–868. [Google Scholar] [CrossRef]
- Nakamura, T.; Gu, Y. Identification of elastic-plastic anisotropic parameters using instrumented indentation and inverse analysis. Mech. Mater. 2007, 39, 340–356. [Google Scholar] [CrossRef]
- Bolzon, G.; Talassi, M. An effective inverse analysis tool for parameter identification of anisotropic materials. Int. J. Mech. Sci. 2013, 77, 130–144. [Google Scholar] [CrossRef]
- Yonezu, A.; Yoneda, K.; Hirakata, H.; Sakihara, M.; Minoshima, K. A simple method to evaluate anisotropic plastic properties based on dimensionless function of single spherical indentation-Application to SiC whisker-reinforced aluminum alloy. Mater. Sci. Eng. A 2010, 527, 7646–7657. [Google Scholar] [CrossRef]
- Kalkhoran, S.M.; Choi, W.B.; Gouldstone, A. Estimation of plastic anisotropy in Ni–5% Al coatings via spherical indentation. Acta Mater. 2012, 60, 803–810. [Google Scholar] [CrossRef]
- Wang, M.; Wu, J.; Zhan, X.; Guo, R.; Hui, Y.; Fan, H. On the determination of the anisotropic plasticity of metal materials by using instrumented indentation. Mater. Des. 2016, 111, 98–107. [Google Scholar] [CrossRef]
- Garmestani, H.; Kalidindi, S.R.; Williams, L.; Bacaltchuk, G.M.; Fountain, C.; Lee, E.W.; Es-Said, O.S. Modeling the evolution of anisotropy in Al-Li alloys: Application to Al-Li 2090-T8E41. Int. J. Plast. 2002, 18, 1373–1393. [Google Scholar] [CrossRef]
- Yoshida, F.; Hamasaki, H.; Uemori, T. A user-friendly 3D yield function to describe anisotropy of steel sheets. Int. J. Plast. 2013, 45, 119–139. [Google Scholar] [CrossRef]
- Zhang, H.; Diehl, M.; Roters, F.; Raabe, D. A virtual laboratory using high resolution crystal plasticity simulations to determine the initial yield surface for sheet metal forming operations. Int. J. Plast. 2015, 80, 111–138. [Google Scholar] [CrossRef]
- Lankford, W.T.; Snyder, S.C.; Bauscher, J.A. New criteria for predicting the press performance of deep drawing sheets. Trans. Am. Soc. Met. 1950, 42, 1197–1231. [Google Scholar]
- Wang, Y.N.; Huang, J.C. The role of twinning and untwining in yielding behavior in hot-extruded Mg-Al-Zn alloy. Acta Mater. 2007, 55, 897–905. [Google Scholar] [CrossRef]
- Yan, H.; Chen, R.S.; Han, E.H. Room-temperature ductility and anisotropy of two rolled Mg–Zn–Gd alloys. Mater. Sci. Eng. A 2010, 527, 3317–3322. [Google Scholar] [CrossRef]
- Yi, S.; Bohlen, J.; Heinemann, F.; Letzig, D. Mechanical anisotropy and deep drawing behavior of AZ31 and ZE10 magnesium alloy sheets. Acta Mater. 2010, 58, 592–605. [Google Scholar] [CrossRef]
- Tang, W.; Huang, S.; Li, D.; Peng, Y. Mechanical anisotropy and deep drawing behaviors of AZ31 magnesium alloy sheets produced by unidirectional and cross rolling. J. Mater. Process. Technol. 2015, 215, 320–326. [Google Scholar] [CrossRef]
- Kim, W.J.; Yoo, S.J.; Chen, Z.H.; Jeong, H.T. Grain size and texture control of Mg–3Al–1Zn alloy sheet using a combination of equal-channel angular rolling and high-speed-ratio differential speed-rolling processes. Scr. Mater. 2009, 60, 897–900. [Google Scholar] [CrossRef]
- Li, X.; Al-Samman, T.; Gottstein, G. Mechanical properties and anisotropy of ME20 magnesium sheet produced by unidirectional and cross rolling. Mater. Des. 2011, 32, 4385–4393. [Google Scholar] [CrossRef]
- Stanford, N.; Barnett, M.R. The origin of “rare earth” texture development in extruded Mg-based alloys and its effect on tensile ductility. Mater. Sci. Eng. A 2008, 496, 399–408. [Google Scholar] [CrossRef]
- Stanford, N.; Atwell, D.; Beer, A.; Davies, C.; Barnett, M.R. Effect of microalloying with rare-earth elements on the texture of extruded magnesium-based alloys. Scr. Mater. 2008, 59, 772–775. [Google Scholar] [CrossRef]
- Crooks, R.; Wang, Z.; Levit, V.I.; Shenoy, R.N. Microtexture, microstructure and plastic anisotropy of AA2195. Mater. Sci. Eng. A 1998, 257, 145–152. [Google Scholar] [CrossRef]
- Alexander, B.-B.; Carl, B.; Franck, A.T.G.; Daniel, L. Modelling of anisotropy for Al–Li 2099 T83 extrusions and effect of precipitate density. Mater. Sci. Eng. A 2016, 673, 581–586. [Google Scholar]
- Alexander, B.-B.; Carl, B.; Franck, A.T.G.; Daniel, L.; Julien, B.; Mathieu, B. Characterization of Al-Li 2099 extrusions and the influence of fiber texture on the anisotropy of static mechanical properties. Mater. Sci. Eng. A 2014, 597, 62–69. [Google Scholar]
- Rioja, R.J. Fabrication method to manufacture isotropic Al-Li alloys and products for space and aerospace applications. Mater. Sci. Eng. A 1998, 257, 100–107. [Google Scholar] [CrossRef]
- Yonezu, A.; Kuwahara, Y.; Yoneda, K.; Hirakata, H.; Minoshima, K. Estimation of the anisotropic plastic property using single spherical indentation-An FEM study. Comp. Mater. Sci. 2009, 47, 611–619. [Google Scholar] [CrossRef]
- Hill, R. A theory of the yielding and plastic flow of anisotropic metals. Proc. R. Soc. A 1948, 193, 281–297. [Google Scholar] [CrossRef]
- Donohue, B.R.; Ambrus, A.; Kalidindi, S.R. Critical evaluation of the indentation data analyses methods for the extraction of isotropic uniaxial mechanical properties using finite element models. Acta Mater. 2012, 60, 3943–3952. [Google Scholar] [CrossRef]
- ABAQUS; Analysis User’s Manual Version 6.9; Software for Finite Element Analysis and Computer-Aided Engineering; ABAQUS Inc.: Providence, RI, USA, 2009.
- Zhao, M.; Ogasawara, N.; Chiba, N.; Chen, X. A new approach to measure the elastic-plastic properties of bulk materials using spherical indentation. Acta Mater. 2006, 54, 23–32. [Google Scholar] [CrossRef]
- Hernot, X.; Moussa, C.; Bartier, O. Study of the concept of representative strain and constraint factor introduced by Vickers indentation. Mech. Mater. 2014, 68, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Bowden, F.P.; Tabor, D. The Friction and Lubrication of Solids; Oxford University Press: Clarendon, VT, USA, 2001. [Google Scholar]
- Bucaille, J.L.; Stauss, S.; Felder, E.; Michler, J. Determination of plastic properties of metals by instrumented indentation using different sharp indenters. Acta Mater. 2003, 51, 1663–1678. [Google Scholar] [CrossRef]
- Barlat, F.; Lege, D.J.; Brem, J.C. A six-component yield function for anisotropic materials. Int. J. Plast. 1991, 7, 693–712. [Google Scholar] [CrossRef]
- Zhang, H.; Jing, X.; Subhash, G.; Kecskes, L.J.; Dowding, R.J. Investigation of shear band evolution in amorphous alloys beneath a Vickers indentation. Acta Mater. 2005, 53, 3849–3859. [Google Scholar] [CrossRef]

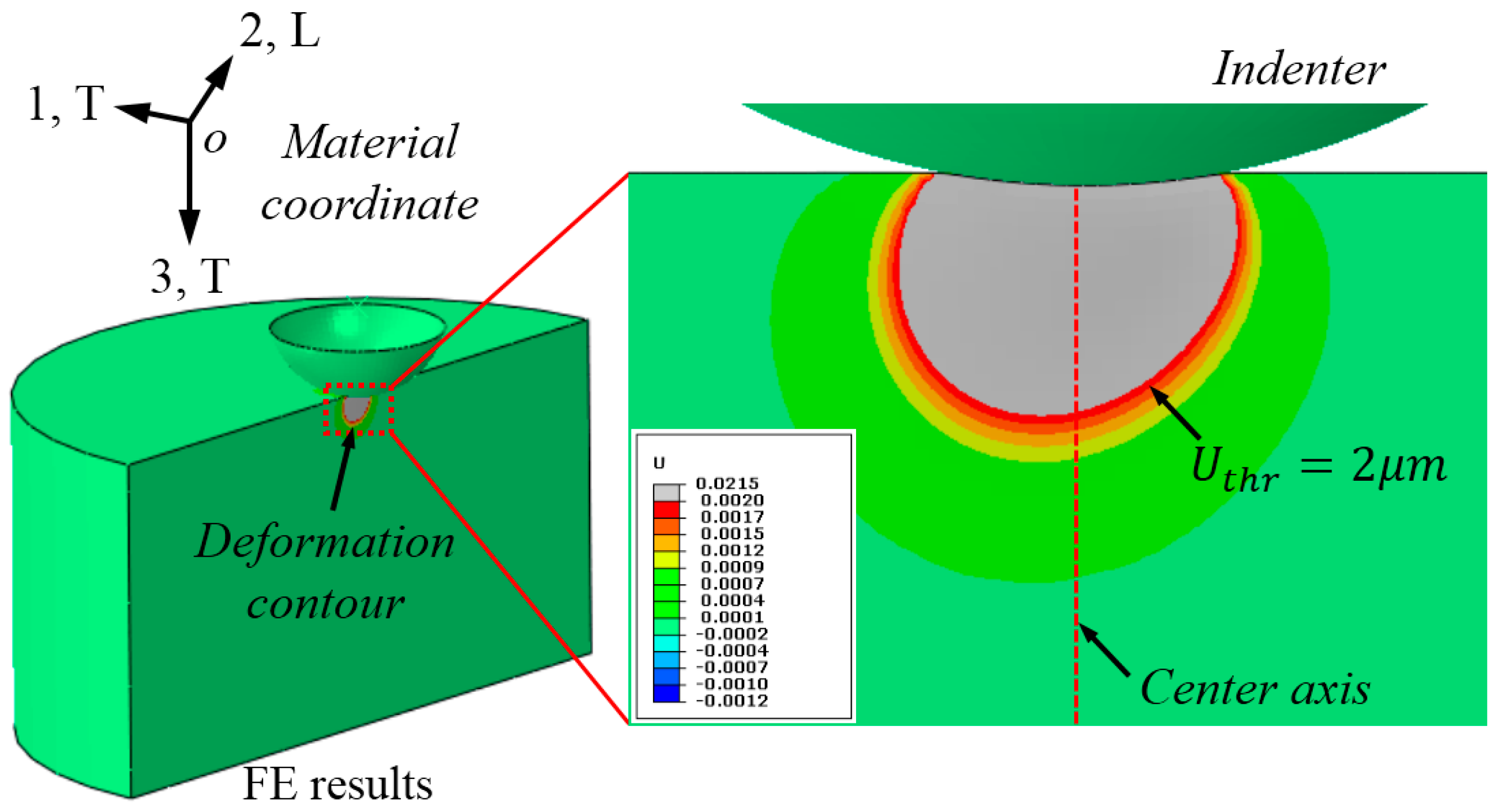
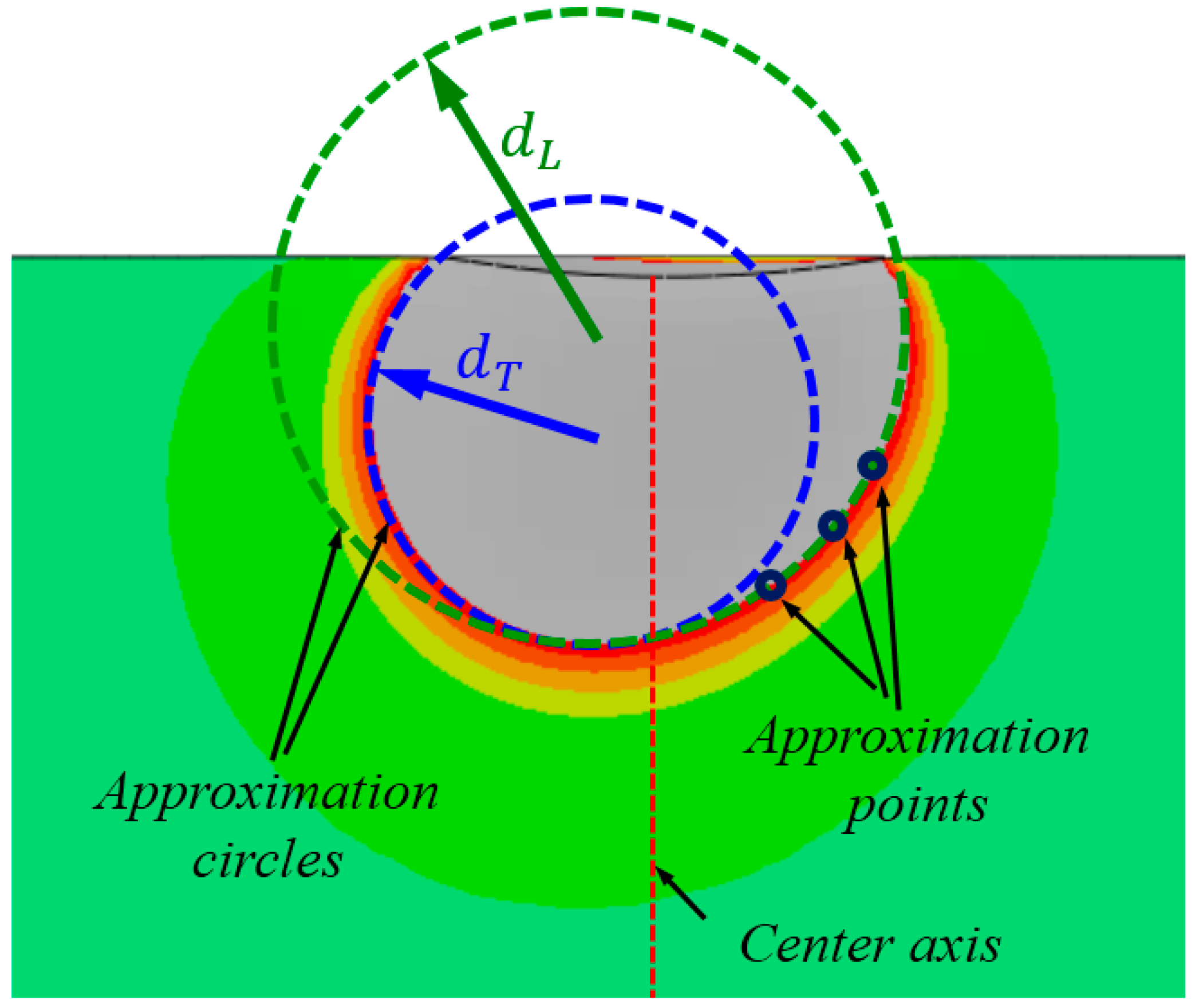
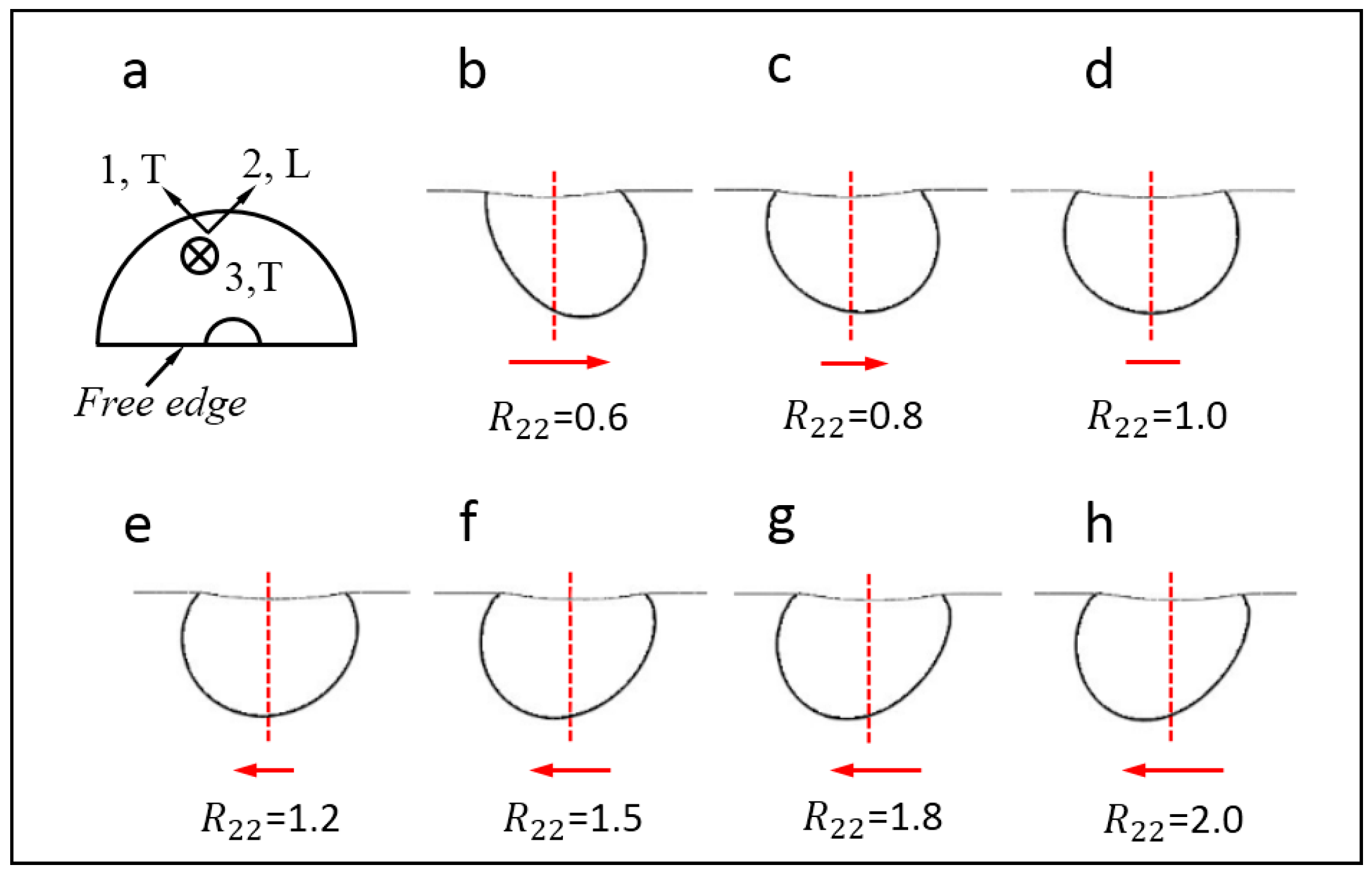
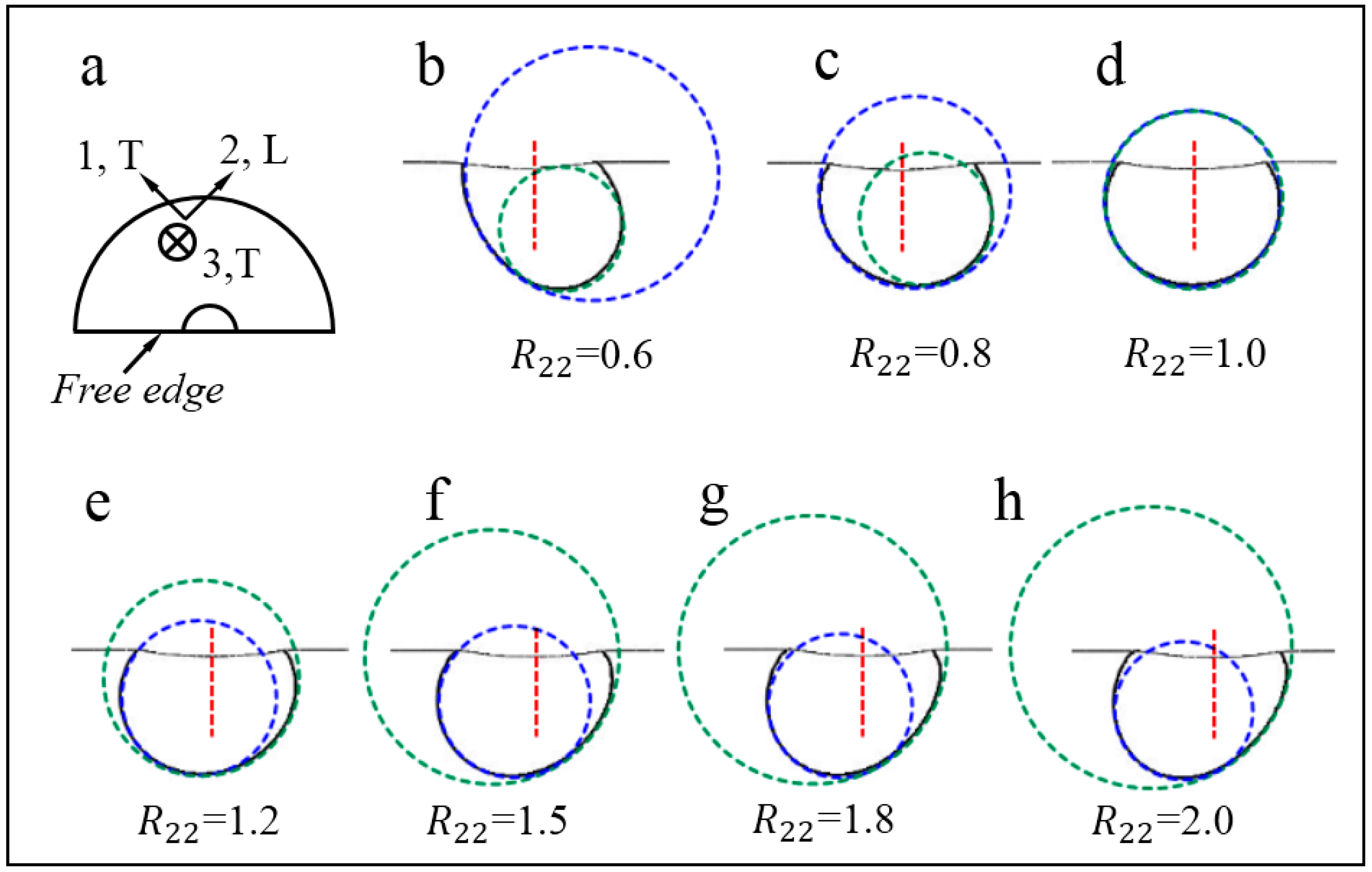
| Chemistry | Al | Zn | Mn | Si | Fe | Cu | Ni | Mg |
|---|---|---|---|---|---|---|---|---|
| wt % | 2.5–3.5 | 0.6–1.4 | 0.2–1.0 | ≤0.80 | ≤0.003 | ≤0.01 | ≤0.001 | Balance |
| AZ31B | E (GPa) | (MPa) | n |
|---|---|---|---|
| 1, T | 33.5 | 64.2 | 0.287 |
| 3, T | 34.5 | 68.5 | 0.260 |
| 2, L | 32.3 | 100.5 | 0.268 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Wu, J.; Wu, H.; Zhang, Z.; Fan, H. A Novel Approach to Estimate the Plastic Anisotropy of Metallic Materials Using Cross-Sectional Indentation Applied to Extruded Magnesium Alloy AZ31B. Materials 2017, 10, 1065. https://doi.org/10.3390/ma10091065
Wang M, Wu J, Wu H, Zhang Z, Fan H. A Novel Approach to Estimate the Plastic Anisotropy of Metallic Materials Using Cross-Sectional Indentation Applied to Extruded Magnesium Alloy AZ31B. Materials. 2017; 10(9):1065. https://doi.org/10.3390/ma10091065
Chicago/Turabian StyleWang, Mingzhi, Jianjun Wu, Hongfei Wu, Zengkun Zhang, and He Fan. 2017. "A Novel Approach to Estimate the Plastic Anisotropy of Metallic Materials Using Cross-Sectional Indentation Applied to Extruded Magnesium Alloy AZ31B" Materials 10, no. 9: 1065. https://doi.org/10.3390/ma10091065