Application of Dynamic Analysis in Semi-Analytical Finite Element Method
Abstract
:1. Introduction
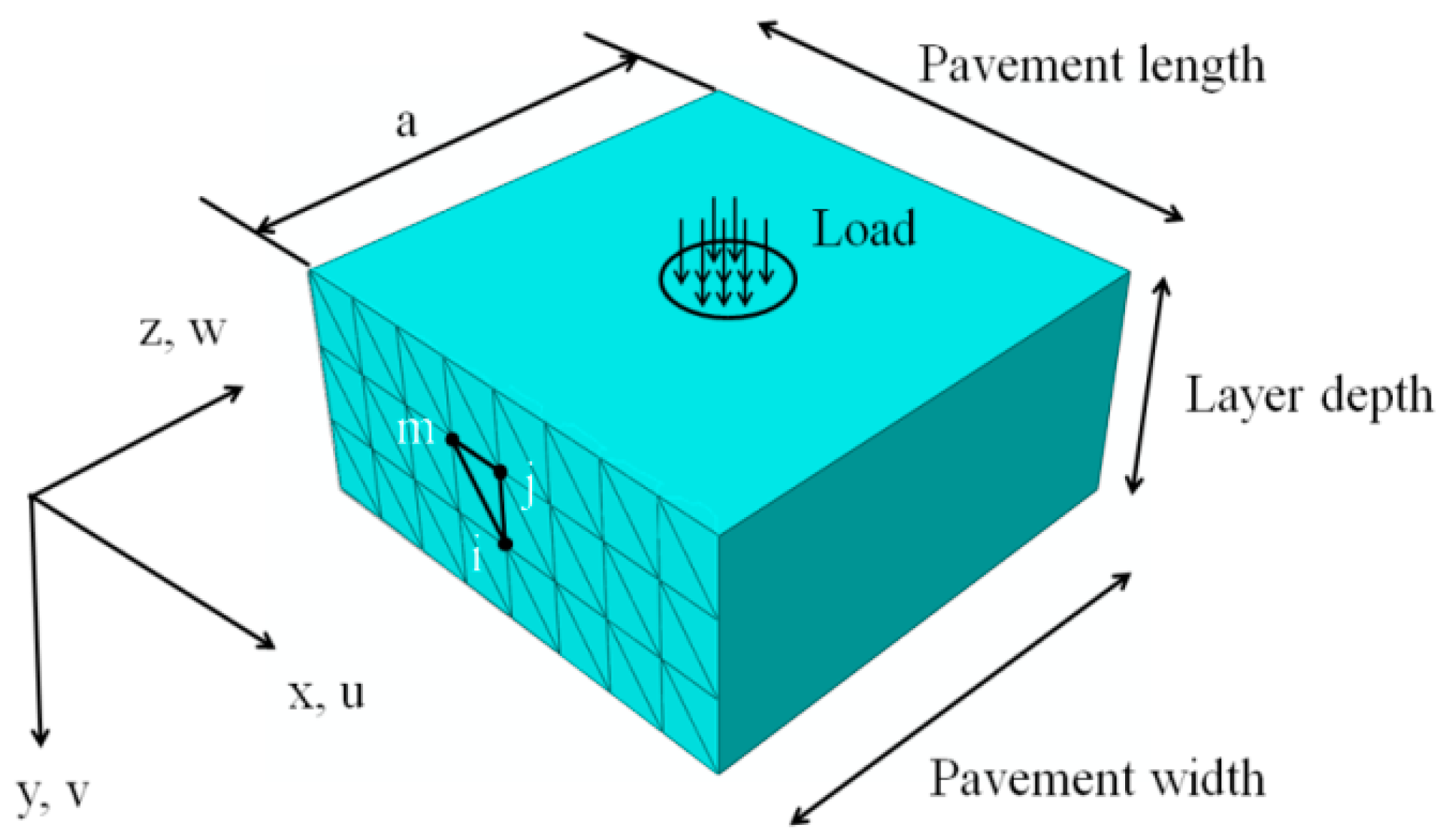
2. Description of Semi-Analytical Finite Element Method
3. Time Discretization for Dynamic Analysis
3.1. Displacement Based Approach
- Step 1: Initial Calculation
- (a)
- Form static stiffness matrix Kll, mass matrix Mll and damping matrix Cll.
- (b)
- Specify time step and integration parameters , .
- (c)
- Calculate integration constants .
- (d)
- Form effective stiffness matrix .
- Step 2: For Each Time Step
- (a)
- Specify initial conditions , and .
- (b)
- Calculate effective load vector .
- (c)
- Solve for node displacement vector at time t according to Equation (27).
- (d)
- Calculate node velocities and accelerations at time t according to Equations (25) and (26).
- (e)
- Go to Step 2 (b) with .
3.2. Acceleration-Based Approach
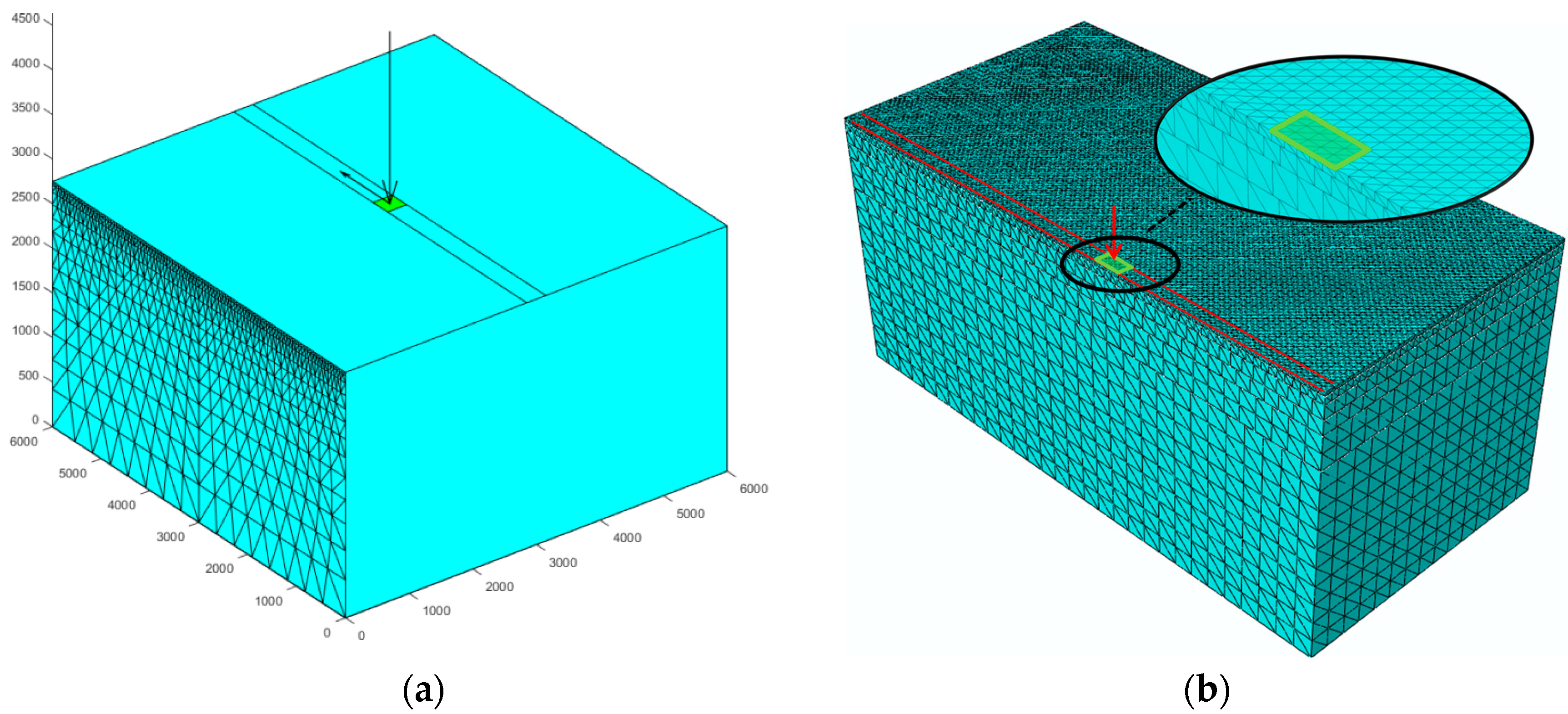
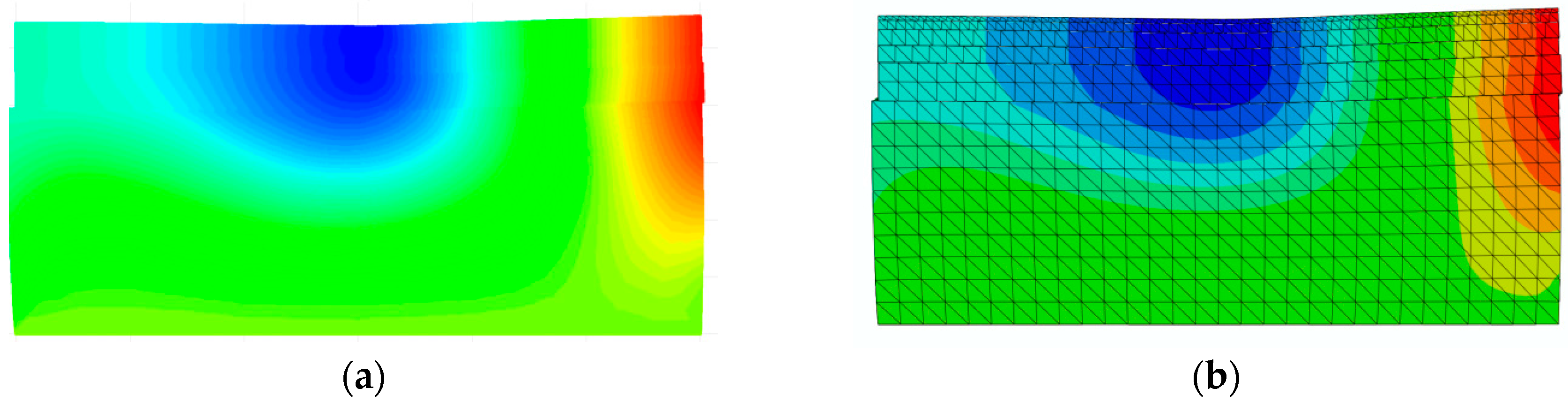
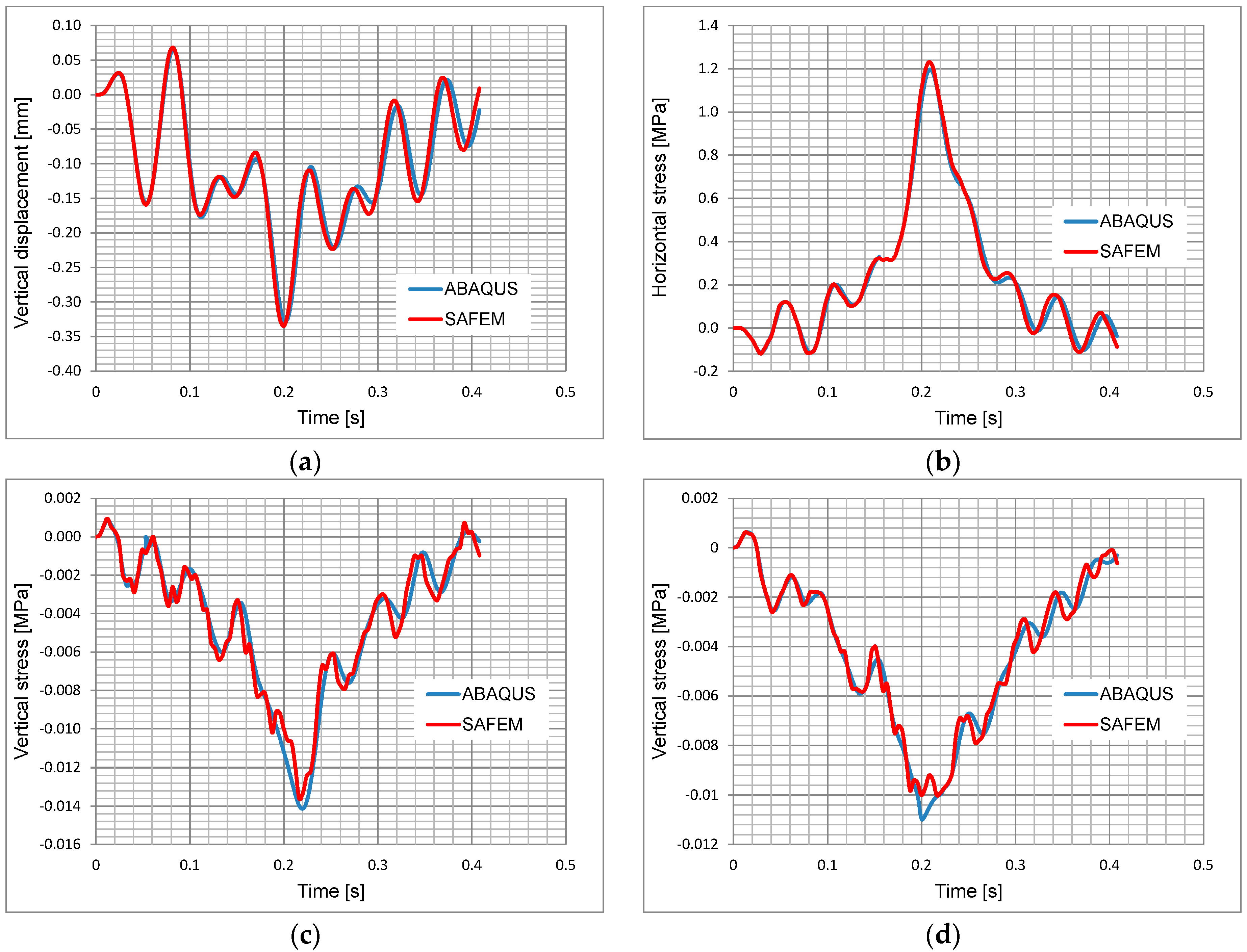
4. Analytical Verification of SAFEM in Dynamic Analyses
5. Experimental Verification of SAFEM in Dynamic Analyses
6. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ghadimi, B. Numerical Modelling for Flexible Pavement Materials Applying Advanced Finite Element Approach to Develop Mechanistic-Empirical Design Procedure. Ph.D. Thesis, Curtin University, Perth, Australia, 2015. [Google Scholar]
- Duncan, J.M.; Monismith, C.L.; Wilson, E.L. Finite element analyses of pavements. Highw. Res. Rec. 1968, 228, 18–33. [Google Scholar]
- Raad, L.; Figueroa, J.L. Load Response of transportation support systems. J. Transp. Eng. 1980, 106, 111–128. [Google Scholar]
- Harichandran, R.; Yeh, M.; Baladi, G. MICH-PAVE: A nonlinear finite element program for analysis of flexible pavements. Transp. Res. Rec. 1990, 1286, 123–131. [Google Scholar]
- Cho, Y.H.; McCullough, B.F.; Weissmann, J. Considerations on Finite element method application in pavement structural analysis. Transp. Res. Rec. 1996, 1539, 96–101. [Google Scholar] [CrossRef]
- Myers, L.A.; Roque, R.; Birgisson, B. Use of two-dimensional finite element analysis to represent bending response of asphalt pavement structures. Int. J. Pavement Eng. 2001, 2, 201–214. [Google Scholar] [CrossRef]
- Holanda, Á.S.; Parente Junior, E.; Araújo, T.D.P.; Melo, L.T.B.; Evangelista Junior, F.; Soares, J.B. Finite element modeling of flexible pavements. In Proceedings of the Iberian Latin American Congress on Computational Methods in Engineering, Belém, Brazil, 3–6 September 2006. [Google Scholar]
- Zaghloul, S.; White, T. Use of a three-dimensional, dynamic finite element program for analysis of flexible pavement. Transp. Res. Rec. 1993, 1388, 60–69. [Google Scholar]
- Desai, C.S.; Whitenack, R. Review of models and the disturbed state concept for thermomechanical analysis in electronic packaging. J. Electron. Packag. 2001, 123, 19–33. [Google Scholar] [CrossRef]
- Desai, C.S. Unified DSC constitutive model for pavement materials with numerical implementation. Int. J. Geomechan. 2007, 7, 83–101. [Google Scholar] [CrossRef]
- Saad, B.; Mitri, H.; Poorooshasb, H. Three-dimensional dynamic analysis of flexible conventional pavement foundation. J. Transp. Eng. 2005, 131, 460–469. [Google Scholar] [CrossRef]
- Beskou, N.D.; Theodorakopoulos, D.D. Dynamic effects of moving loads on road pavements: A review. Soil Dyn. Earthq. Eng. 2011, 31, 547–567. [Google Scholar] [CrossRef]
- Fritz, J.J. Flexible pavement response evaluation using the semi-analytical finite element method. Int. J. Mater. Pavement Des. 2002, 3, 211–225. [Google Scholar]
- Hu, S.; Hu, X.; Zhou, F. Using semi-analytical finite element method to evaluate stress intensity factorsin pavement structure. In Proceedings of the RILEM International Conference on Cracking in Pavements, Chicago, IL, USA, 16–18 June 2008; pp. 637–646. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method for Solid and Structural Mechanics, 6th ed.; Elsevier Butterworth-Heinemann: Oxford, UK, 2005; pp. 498–516. [Google Scholar]
- Liu, P.; Wang, D.; Oeser, M. Leistungsfähige Semi-analytische Methoden zur Berechnung von Asphaltbefestigungen. In Proceedings of the 3rd Dresdner Asphalttage, Dresden, Germany, 12–13 December 2013. (In German). [Google Scholar]
- Liu, P.; Wang, D.; Oeser, M.; Chen, X. Einsatz der Semi-Analytischen Finite-Elemente-Methode zur Beanspruchungszustände von Asphaltbefestigungen. Bauingenieur 2014, 89, 333–339. (In German) [Google Scholar]
- Liu, P.; Wang, D.; Oeser, M. The application of semi-analytical finite element method coupled with infinite element for analysis of asphalt pavement structural response. J. Traffic Transp. Eng. 2015, 2, 48–58. [Google Scholar] [CrossRef]
- Liu, P.; Wang, D.; Otto, F.; Hu, J.; Oeser, M. Application of semi-analytical finite element method to evaluate asphalt pavement bearing capacity. Int. J. Pavement Eng. 2016, 1–10. [Google Scholar] [CrossRef]
- Liu, P.; Wang, D.; Hu, J.; Oeser, M. SAFEM—Software with graphical user interface for fast and accurate finite element analysis of asphalt pavements. J. Test. Evaluat. 2017, 45, 1–15. [Google Scholar] [CrossRef]
- Wilson, E.L. Structural analysis of axisymmetric solids. J. Am. Inst. Aeronaut. Astronaut. 1965, 3, 2269–2274. [Google Scholar] [CrossRef]
- Meissner, H.E. Laterally loaded pipe pile in cohesionless soil. In Proceedings of the 2nd International Conference on Numeric Methods in Geomechanics, Polytechnical Institute and State University, Blacksburg, VA, USA, 20–25 June 1976. [Google Scholar]
- Winnicki, L.A.; Zienkiewicz, O.C. Plastic (or visco-plastic) behaviour of axisymmetric bodies subjected to non-symmetric loading-semi-analytical finite element solution. Int. J. Numer. Methods Eng. 1979, 14, 1399–1412. [Google Scholar] [CrossRef]
- Carter, J.P.; Booker, J.R. Consolidation of axi-symmetric bodies subjected to non axi-symmetric loading. Int. J. Numer. Anal. Methods Geomechan. 1983, 7, 73–281. [Google Scholar] [CrossRef]
- Lai, J.Y.; Booker, J.R. Application of discrete Fourier series to the finite element stress analysis of axi-symmetric solids. Int. J. Numer. Methods Eng. 1991, 31, 619–647. [Google Scholar] [CrossRef]
- Kim, J.R.; Kim, W.D.; Kim, S.J. Parallel computing using semianalytical finite element method. AIAA J. 1994, 32, 1066–1071. [Google Scholar] [CrossRef]
- Newmark, N.M. A method of computation for structural dynamics. ASCE J. Eng. Mech. Div. 1959, 85, 67–94. [Google Scholar]
- Wang, X. Finite Element Method; Tsinghua University Press: Beijing, China, 2003; pp. 479–482. (In Chinese) [Google Scholar]
- Forschungsgesellschaft für Straßen- und Verkehrswesen. Richtlinien für die Standardisierung des Oberbaus von Verkehrsflächen: RStO 12; FGSV-Verlag: Köln, Germany, 2012. (In German) [Google Scholar]
- Research Society for Road and Transportation. Guidelines for the Computational Dimension of the Upper Structure of Road with Asphalt Surface Course: RDO Asphalt 09; FGSV Publisher: Cologne, Germany, 2009. (In German) [Google Scholar]
- Dassault Systemes Simulia Corp. ABAQUS (2011) Analysis User’s Manual; Dassault Systemes Simulia Corp: Providence, RI, USA.
- Liu, P.; Otto, F.; Wang, D.; Balck, H.; Oeser, M. Measurement and evaluation on deterioration of asphalt pavements by geophones. Measurement 2017, 109, 223–232. [Google Scholar] [CrossRef]

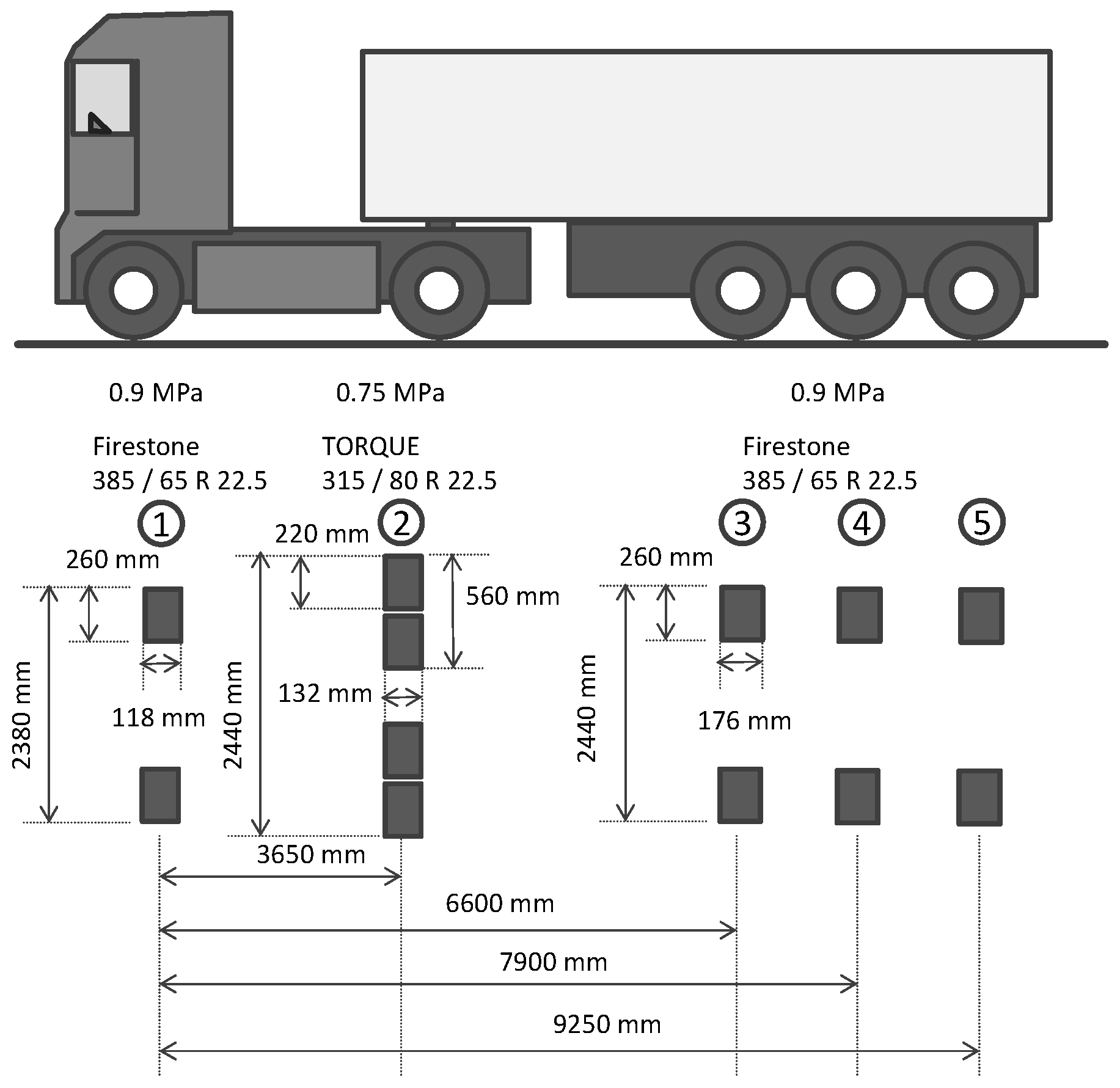
| Layer | Thickness (mm) | E (MPa) | µ | Density (t/mm3) |
|---|---|---|---|---|
| Surface course | 40 | 22,690 | 0.35 | 2.377 × 10−9 |
| Binder course | 80 | 27,283 | 0.35 | 2.448 × 10−9 |
| Asphalt base course | 140 | 17,853 | 0.35 | 2.301 × 10−9 |
| Road base course | 150 | 10,000 | 0.25 | 2.400 × 10−9 |
| Sub-base | 340 | 100 | 0.49 | 2.400 × 10−9 |
| Subgrade | 2000 | 45 | 0.49 | 2.400 × 10−9 |
| Result | SAFEM | ABAQUS | Difference |
|---|---|---|---|
| Vertical displacement (mm) at the top of the surface course | −0.335 | −0.327 | 2.44% |
| Horizontal stress (MPa) at the bottom of the asphalt base course | 0.974 | 0.912 | 6.79% |
| Vertical stress (MPa) at the top of the sub-base course | −0.0104 | −0.0112 | −7.14% |
| Vertical stress (MPa) at the top of the subgrade | −0.0100 | −0.0109 | −8.26% |
| SAFEM | ABAQUS | |
|---|---|---|
| Elements | 1144 | 127,095 |
| Nodes | 2431 | 218,333 |
| Computational time | 10 min | 281 min |
| Measurement | SAFEM | Difference | |
|---|---|---|---|
| Strain along the traffic direction at the bottom of the asphalt base course (10−6) | 81.5 | 86.3 | 5.88% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, P.; Xing, Q.; Wang, D.; Oeser, M. Application of Dynamic Analysis in Semi-Analytical Finite Element Method. Materials 2017, 10, 1010. https://doi.org/10.3390/ma10091010
Liu P, Xing Q, Wang D, Oeser M. Application of Dynamic Analysis in Semi-Analytical Finite Element Method. Materials. 2017; 10(9):1010. https://doi.org/10.3390/ma10091010
Chicago/Turabian StyleLiu, Pengfei, Qinyan Xing, Dawei Wang, and Markus Oeser. 2017. "Application of Dynamic Analysis in Semi-Analytical Finite Element Method" Materials 10, no. 9: 1010. https://doi.org/10.3390/ma10091010





