Numerical Simulation of Droplets Behavior of Cu-Pb Immiscible Alloys Solidifying under Magnetic Field
Abstract
:1. Introduction
2. Mathematical Formulation
3. Droplet Growth Model and Calculations
4. Numerical Results and Discussion
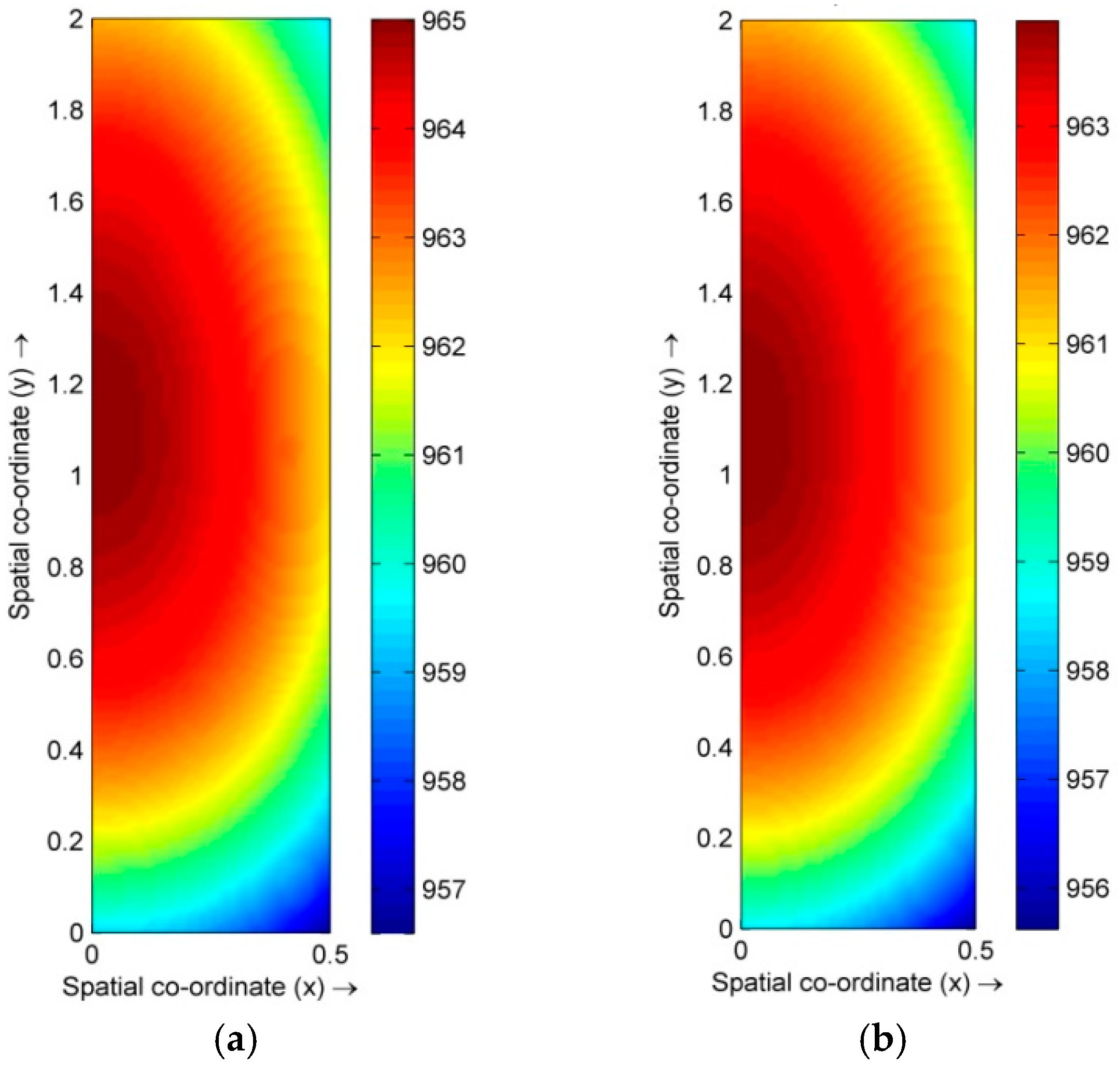
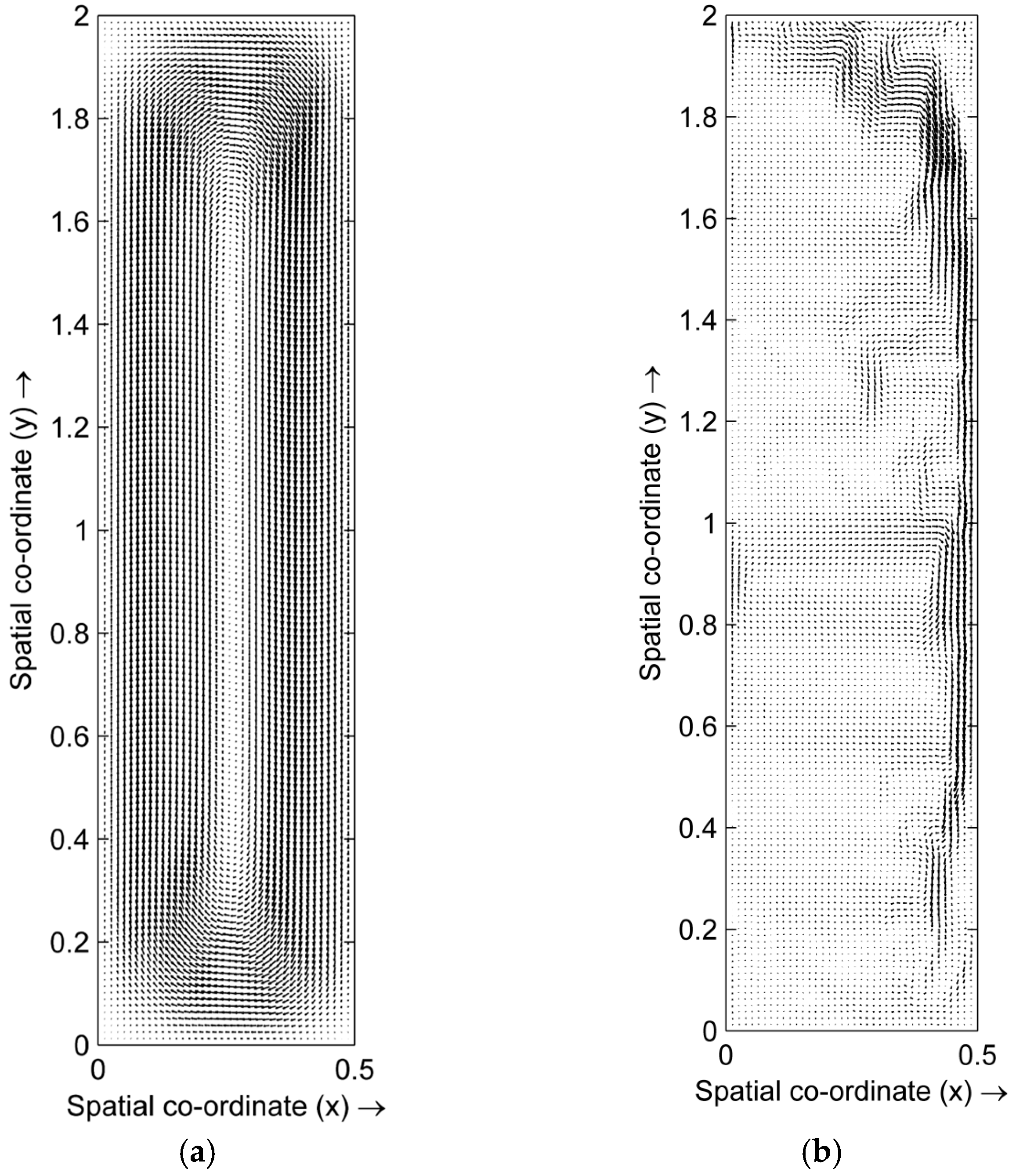
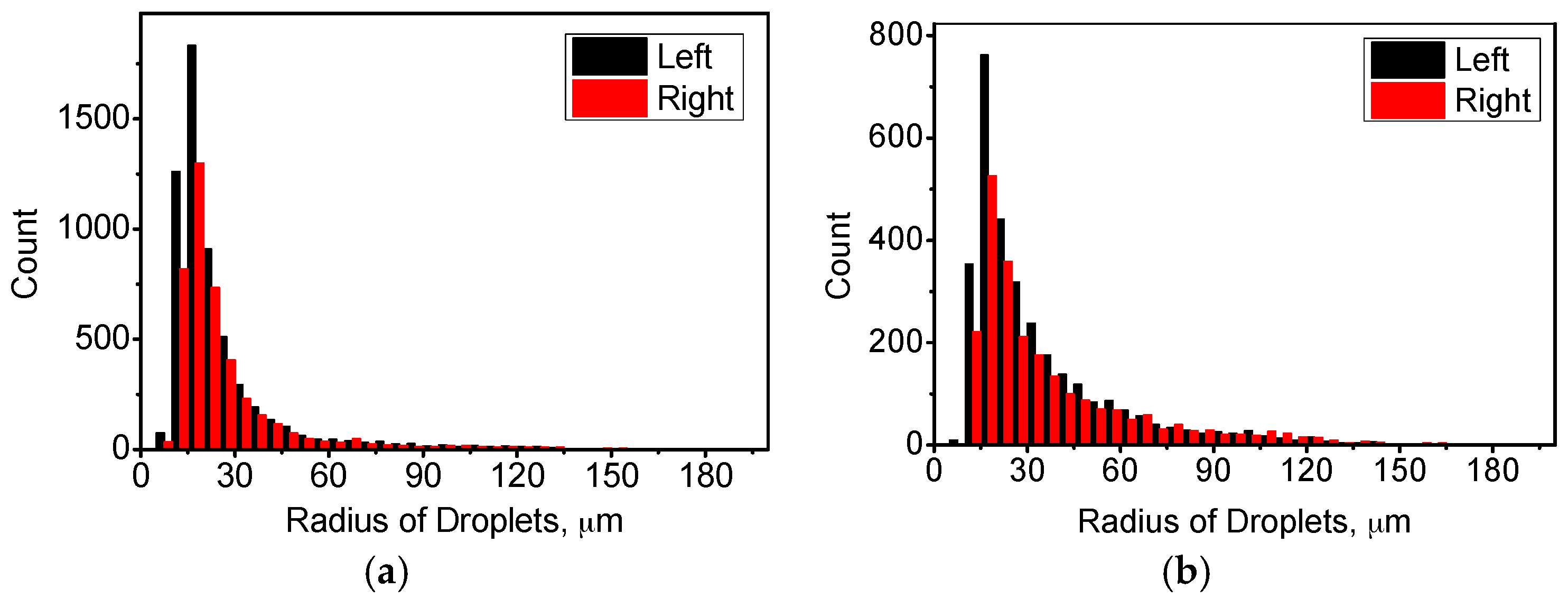
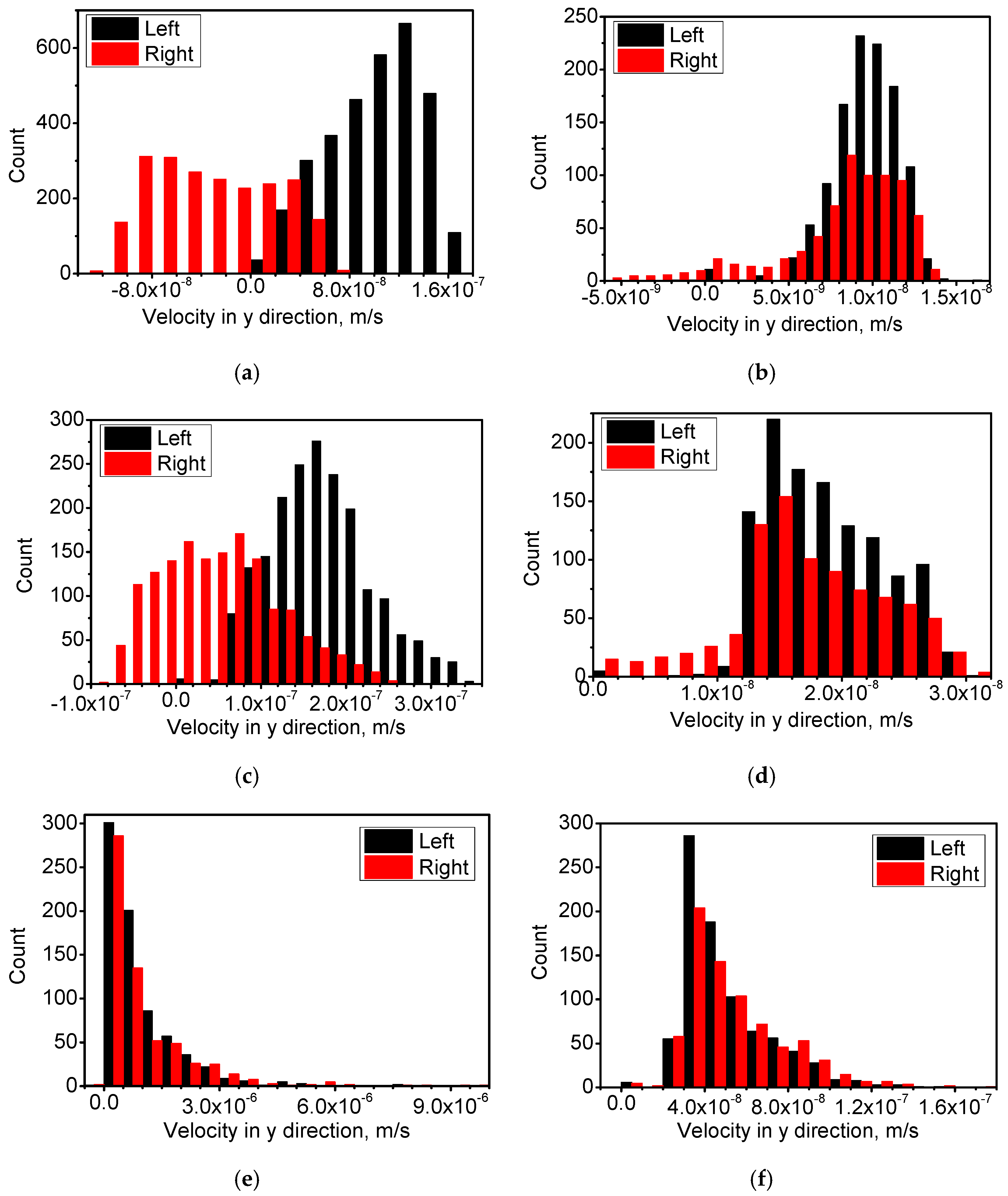
4.1. Distribution of Temperature and Flow Fields
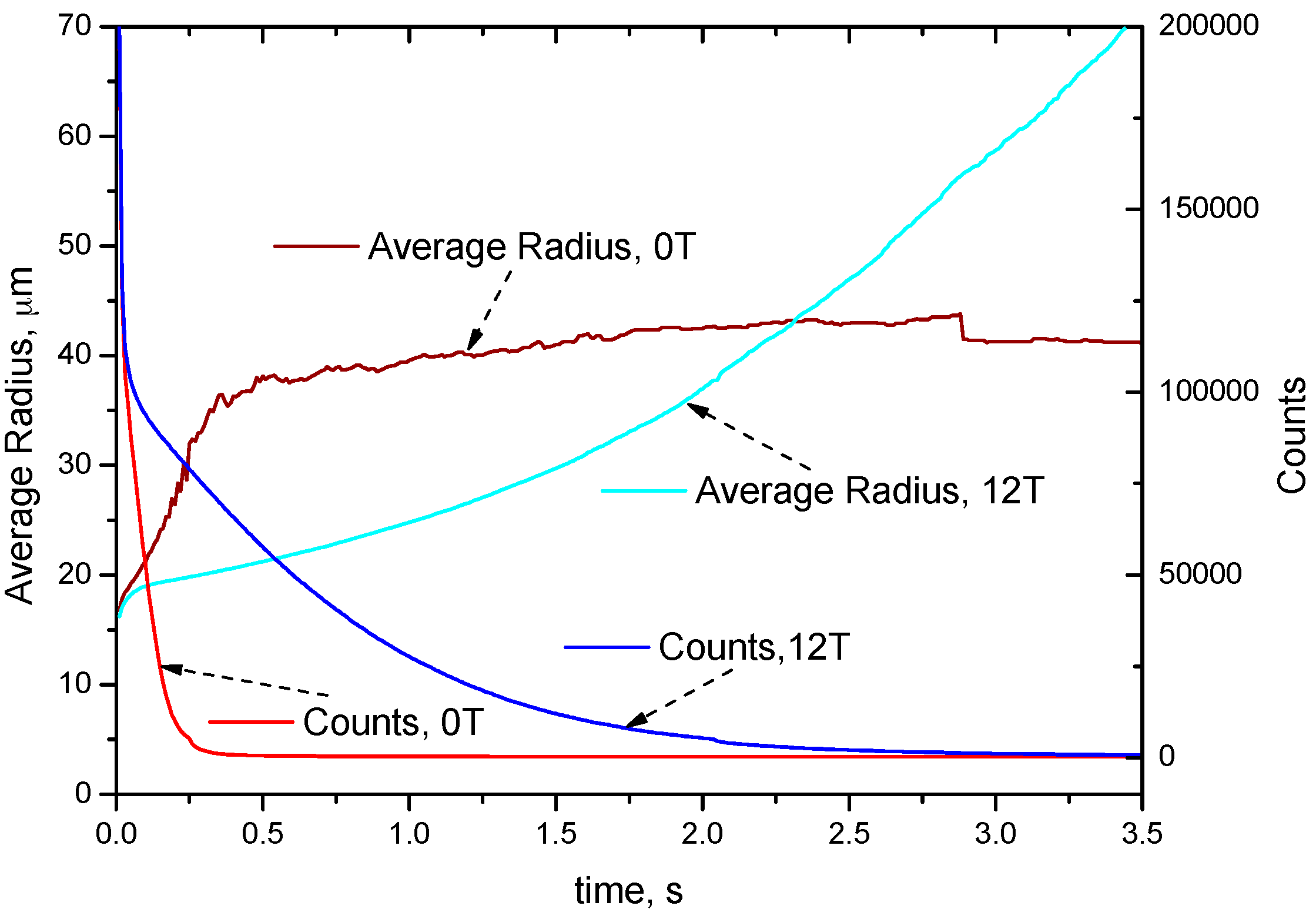
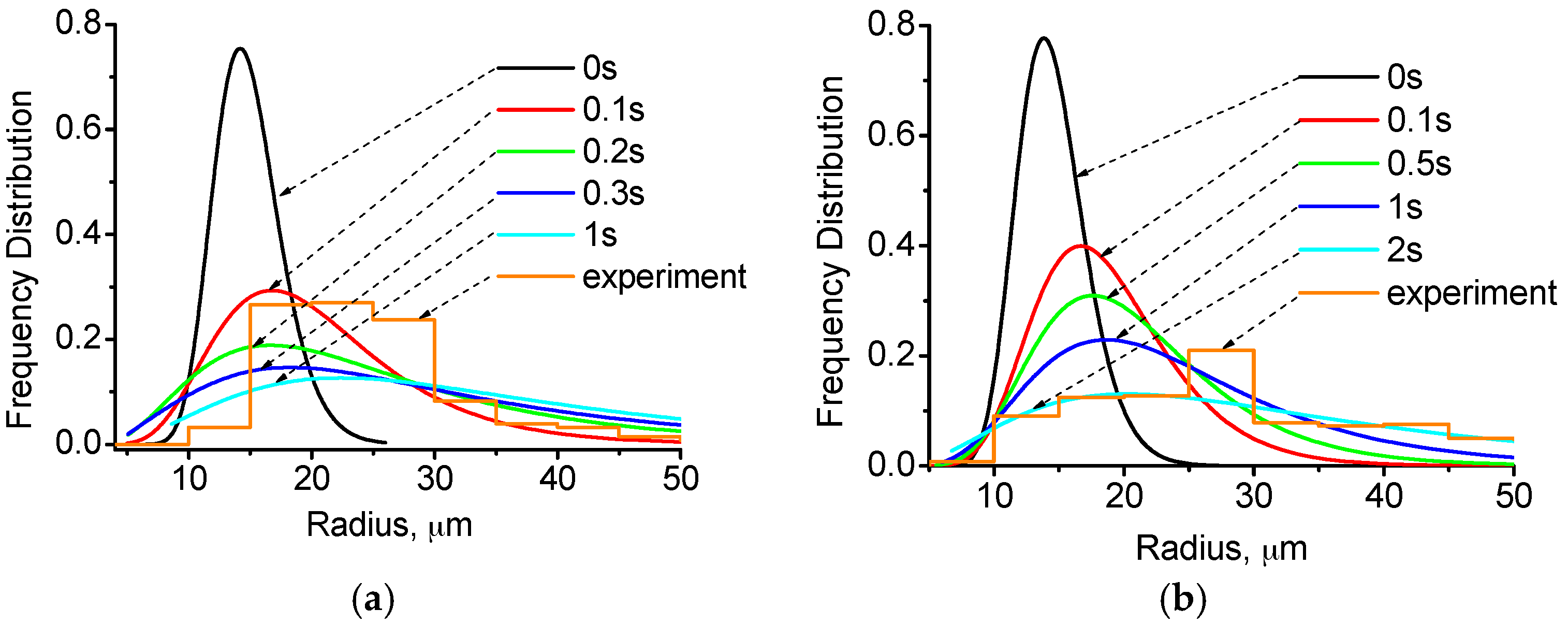
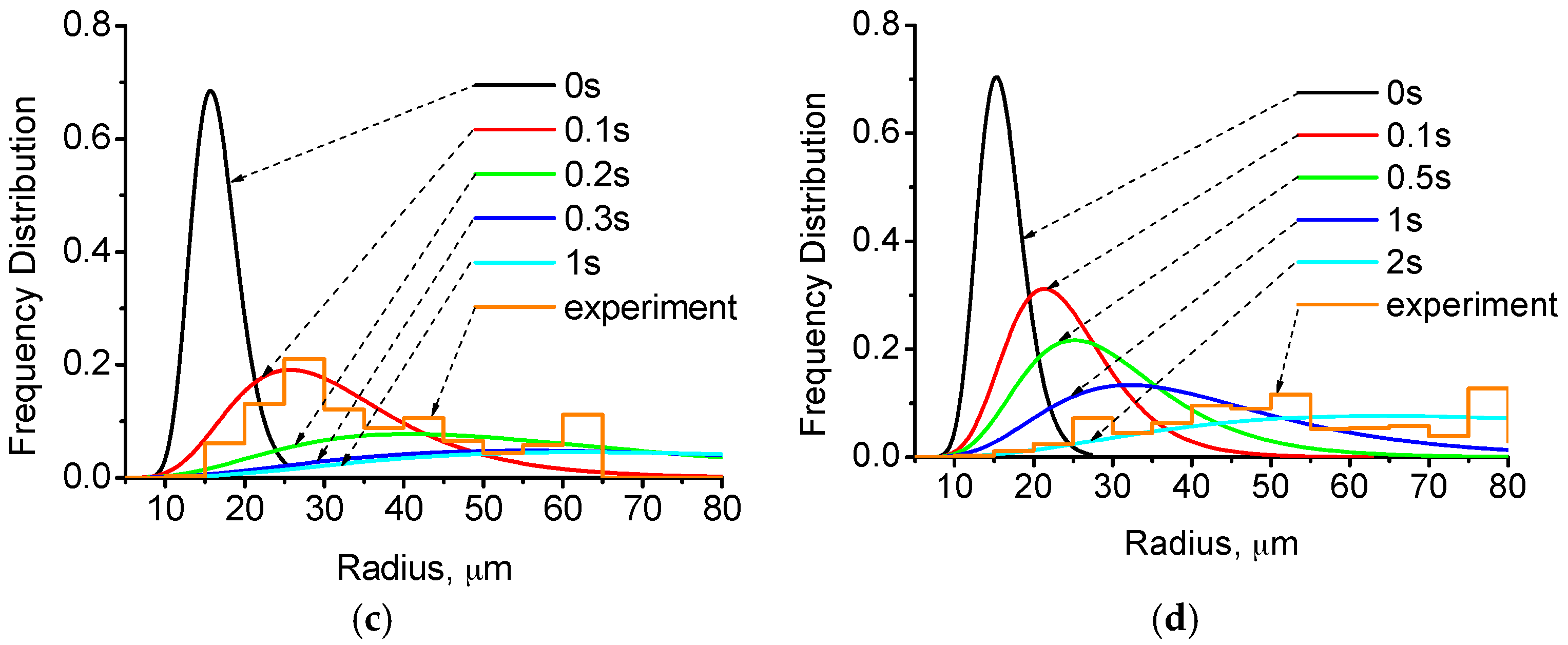
4.2. Distribution of Cu-Rich Droplets
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhao, J.Z.; Ratke, L. A model describing the microstructure evolution during a cooling of immiscible alloys in the miscibility gap. Scr. Mater. 2004, 50, 543–546. [Google Scholar] [CrossRef]
- Ratke, L.; Thieringer, W.K. The influence of particle motion on ostwald ripening in liquids. Acta Metall. 1985, 33, 1793–1802. [Google Scholar] [CrossRef]
- Alkemper, J.; Ratke, L. Concurrent nucleation growth and sedimentation during solidification of Al-Bi alloys. Z. Metallkunde 1994, 85, 365–371. [Google Scholar]
- Rogers, J.R.; Davis, R.H. Modeling of collision and coalescence of droplets during microgravity processing of Zn-Bi immiscible alloys. Metall. Mater.Trans. A 1990, 21, 59–68. [Google Scholar] [CrossRef]
- Ahlborn, H.; Neumann, H.; Schott, H. Segregation behavior of rapidly cooled monotectic Al-In and Al-Pb alloys. Z. Metallkunde 1993, 84, 748–754. [Google Scholar]
- Ratke, L. Coarsening of liquid Al-Pb dispersions under reduced gravity conditions. Mater. Sci. Eng. A 1995, 203, 399–407. [Google Scholar] [CrossRef]
- He, J.; Zhao, J.Z.; Ratke, L. Solidification microstructure and dynamics of metastable phase transformation in undercooled liquid Cu-Fe alloys. Acta Mater. 2006, 54, 1749–1757. [Google Scholar] [CrossRef]
- He, J.; Mattern, N.; Tan, J.; Zhao, J.Z.; Kaban, I.; Wang, Z.; Ratke, L.; Kim, D.H.; Kim, W.T.; Eckert, J. A bridge from monotectic alloys to liquid-phase-separated bulk metallic glasses: Design microstructure and phase evolution. Acta Mater. 2013, 61, 2102–2112. [Google Scholar] [CrossRef]
- Ratke, L.; Diefenbach, S. Liquid immiscible alloys. Mater. Sci. Eng. R-Rep. 1995, 15, 263–347. [Google Scholar] [CrossRef]
- Guo, J.J.; Liu, Y.; Su, Y.Q.; Jia, J.; Ding, H.S.; Zhao, J.Z. Numerical simulation of macrosegregation of indium phase in rapidly solidified Al-In hypermonotectic sheets. Mater. Sci. Technol. 2002, 18, 1286–1292. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, E.G.; Zuo, X.W.; He, J.C. Effect of high magnetic field on solidified structure of Cu-80%Pb hypermonotectic alloy. Acta Metall. Sin. 2008, 44, 165–171. [Google Scholar]
- Yasuda, H.; Ohnaka, I.; Kawakami, O.; Ueno, K.; Kishio, K. Effect of magnetic field on solidification in Cu-Pb monotectic alloys. ISIJ Int. 2003, 43, 942–949. [Google Scholar] [CrossRef]
- Gale, W.F.; Totemeier, T.C. Smithells Metals Reference Book; Elsevier Butterworth-Heinemann: Oxford, UK, 2004. [Google Scholar]
- Mortensen, A.; Felberbaum, L. Capillary shape equilibration of liquid inclusions embedded in a partly soluble solid. Scr. Mater. 2006, 55, 955–958. [Google Scholar]
- Gooneie, A.; Holzer, C. Reinforced local heterogeneities in interfacial tension distribution in polymer blends by incorporating carbon nanotubes. Polymer 2017, 125, 90–101. [Google Scholar] [CrossRef]
- Danov, K.D.; Stanimirova, R.D.; Kralchevsky, P.A.; Marinova, K.G.; Stoyanov, S.D.; Blijdenstein, T.B.; Cox, A.R.; Pelan, E.G. Adhesion of bubbles and drops to solid surfaces, and anisotropic surface tensions studied by capillary meniscus dynamometry. Adv. Colloid Interface Sci. 2016, 233, 223–239. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.-Y.; Xu, J.-Q.; Choi, H.; Konishi, H.; Jin, S.; Li, X.-C. Rapid control of phase growth by nanoparticles. Nat. Commun. 2014, 5, 3879. [Google Scholar] [CrossRef] [PubMed]
- Budai, I.; Kaptay, G. Monotectic Al/Cd alloys with homogeneously dispersed Cd-droplets stabilized by strontium aluminide precipitates. Intermetallics 2011, 19, 423–425. [Google Scholar] [CrossRef]
- Man, T.N.; Zhang, L.; Xu, N.K.; Wang, W.B.; Xiang, Z.L.; Wang, E.G. Effect of Rare-Earth Ce on Macrosegregation in Al-Bi Immiscible Alloys. Metals 2016, 6, 177. [Google Scholar] [CrossRef]
- Reitz, J.R.; Foldy, L.L. The force on a sphere moving through a conducting fluid in the presence of a magnetic field. J. Fluid Mech. 1961, 11, 133–142. [Google Scholar] [CrossRef]
- Ratke, L.; Voorhees, P.W. Growth and Coarsening: Ostwald Ripening in Materials Processing; Springer: Berlin, Germany, 2002. [Google Scholar]
- Kaptay, G. On the temperature gradient induced interfacial gradient force, acting on precipitated liquid droplets in monotectic liquid alloys. Mater. Sci. Forum 2006, 508, 269–274. [Google Scholar] [CrossRef]
- Aboutalebi, R.; Hasan, M.; Guthrie, R.I.L. Coupled turbulent flow, heat, and solute transport in continuous casting processes. Metall. Mater. Trans. B Process. Metall. Mater. Process. Sci. 1995, 26, 731–744. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, X.; Zhuang, L.; Tang, Z.; Hu, W. Numerical simulation of drop Marangoni migration under microgravity. Acta Astronaut. 2004, 54, 325–335. [Google Scholar] [CrossRef]
- Zener, C. Theory of growth of spherical precipitates from solid solutions. J. Appl. Phys. 1949, 20, 950–953. [Google Scholar] [CrossRef]
- Guo, J.J.; Liu, Y.; Jia, J.; Su, Y.Q.; Ding, H.S.; Zhao, J.Z.; Xue, X. Coarsening mode and microstructure evolution of Al-In hypermonotectic alloy during rapidly cooling process. Scr. Mater. 2001, 45, 1197–1204. [Google Scholar]
- Liu, Y.; Guo, J.J.; Jia, J.; Li, Y.X. Simulation of nucleation and coalescence of second phase droplets during earth-based solidification process of immiscible alloys. Trans. Nonferrous Met. Soc. China 2005, 15, 479–484. [Google Scholar]
- Zhang, L.; Wang, E.G.; Zuo, X.W.; He, J.C. Effect of high magnetic field on the transition behavior of Cu-rich particles IN Cu-80%Pb hypermonotectic alloy. Acta Metall. Sin. 2010, 46, 423–428. [Google Scholar] [CrossRef]

| Parameters | Symbol | Pb-Rich Phase | Cu-Rich Phase |
|---|---|---|---|
| Density/g·cm−3 | ρ | 10.678 − 1.3174 × 10−3(Tc − 327) | 8 − 0.801 × 10−3(Tc − 1083) |
| Resistivity/μΩ·m | 1/σ | 1.263 − 4.7 × 10−4(1000 − Tc) | 0.212 − 1.03 × 10−4(1200 − Tc) |
| Viscosity/N·s·m−2 | η | 0.4636 × 10−3exp(1035.55/Tk) | 0.3009 × 10−3exp(366.83/Tk) |
| Thermal conductivity/Wm−1·K−1 | λ | 26 | 165 |
| Interfacial tension/Nm−1 | δ | 407 × 10−3(1 − Tk/1268)1.22 | |
| Diffusion coefficient | DCu | 420 × 10−9exp(−4850/Tk) | |
| (Cu in Pb)/m2·s−1 | |||
| Specific heat capacity/J·K−1·kg−1 | c | 20.2 × (7.75 − 0.74 × 10−3 Tk) | 495 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Man, T.; Huang, M.; Gao, J.; Zuo, X.; Wang, E. Numerical Simulation of Droplets Behavior of Cu-Pb Immiscible Alloys Solidifying under Magnetic Field. Materials 2017, 10, 1005. https://doi.org/10.3390/ma10091005
Zhang L, Man T, Huang M, Gao J, Zuo X, Wang E. Numerical Simulation of Droplets Behavior of Cu-Pb Immiscible Alloys Solidifying under Magnetic Field. Materials. 2017; 10(9):1005. https://doi.org/10.3390/ma10091005
Chicago/Turabian StyleZhang, Lin, Tiannan Man, Minghao Huang, Jianwen Gao, Xiaowei Zuo, and Engang Wang. 2017. "Numerical Simulation of Droplets Behavior of Cu-Pb Immiscible Alloys Solidifying under Magnetic Field" Materials 10, no. 9: 1005. https://doi.org/10.3390/ma10091005





