1. Introduction
Polymer-based syntactic foams are a class of composites that have hollow microspheres in a matrix material. These are usually made of a polymer matrix reinforced by glass hollow microspheres. The glass hollow microspheres consist of a thin-walled stiff outer glass shell and an inner gas, which are responsible for the unique properties of syntactic foam, including extremely low apparent density, good specific strength, and low thermal conductivity [
1,
2,
3,
4].
A key factor for tailoring and improving the properties of a composite material is to try different properties, by varying reinforcement stiffness, size, volume fraction, and degree of dispersion, as well as by improving the matrix and reinforcement interfacial strength [
5,
6,
7]. In the case of syntactic foam, the ratio of inner to outer radius of the hollow microsphere has been identified as an additional important factor which determines its properties [
8]. Since many microstructural parameters as listed above can affect the foam properties, developing analytical and/or numerical models in order to independently distinguish the effect of each parameter for the design and optimization of syntactic foam is important.
Modeling the elastic properties of syntactic foam has been attempted by numerous researchers, since they help determine the structural performance of a material. For instance, Lee and Westmann [
9] analytically derived lower and upper bounds for the shear modulus of syntactic foams. Huang and Gibson [
10] computed the elastic constants by solving the problem of a cube containing a hollow sphere for dilute reinforced syntactic foam. Nielsen and Landel [
11,
12] estimated the elastic modulus of syntactic foam by taking the apparent modulus of the hollow microsphere, in terms of their inner and outer radii, and using the conventional composite mechanics theory. Tagliavia et al. [
13] used a semi-analytical approach to investigate the particle-to-particle interaction behavior in syntactic foams. These analytical models provide reasonable predictions for idealized, relatively simple microstructural configurations of the foam. For complicated microstructural model configurations, including loading conditions and materials properties, numerical methods, such as the finite element method (FEM), have been used. For example, Sanders and Gibson [
14,
15] used FEM models to investigate the effect of hollow sphere arrangement on elastic modulus and yield strength of the syntactic foam. Marur [
16] investigated the effect of random distribution of the microspheres on the elasticity of the foam, by comparing the numerical results from a single-sphere embedded unit cell with one containing multiple spheres having random distribution. Yu et al. [
17] studied the effect of microsphere clustering on elastic and yielding behavior of the syntactic foam. Bardella et al. [
18] recently developed a periodic representative volume element (RVE) model including 50 microspheres to investigate the elastic properties of syntactic foam by FEM. More recently, the model has been extended to be able to capture the compressive failure behavior and dynamic response of the foam, by adopting brittle fracture criteria for the microsphere in their model [
19,
20,
21].
It is well known that the adhesion between microspheres and a matrix affects the mechanical properties of syntactic foams. If a strong adhesive force at the interface between the microsphere and the matrix exists, an applied load on the foam could be completely transferred to the microspheres. In the FEM modeling in this case, the interface can be treated as a perfect bond in which the interfacial region is considered to have infinite stiffness and complete load transfer taking place between the matrix and the microsphere. However, the assumption of perfect bonding at the interface leads to erroneous results if the adhesion force between the microsphere and the matrix is weak. In this case, failure of the interface or debonding may occur during the fabrication or when a small load is applied, causing overestimation of the overall modulus and strength of the syntactic foam by the perfect bonding assumption of the model.
Only a few modeling studies dealing with the role of a weak interface on the properties of syntactic foams exist in the literature. Marur [
22] and Yu et al. [
23] used three-phase FEM models to account for the weak interface effect by introducing a thin soft interfacial phase between the microsphere and the matrix. They performed parametric studies on the elastic responses of their models by varying the thickness and stiffness of the interfacial phases in order to have good fits between the model and the experiments. The main limitation of this approach is that the thickness and the stiffness of the interfacial phase are indeed not related to any measurable microstructural feature. The interfacial phase properties had been set arbitrarily without convincing microstructural evidence, and therefore, their physical meaning is still ambiguous. Tagliavia et al. [
3,
24] investigated the effect of microsphere-matrix debonding on the stress state and flexural strength of the syntactic foam, using a pair of spherical-cap cracks on the top and bottom of the interface along the tensile direction. With the FEM calculations, they could analyze the effect of partial debonding, in terms of debonding angle, in detail. Tagliavia et al. [
25] also systematically investigated the debonding energetics using the same concept. Shams and Porfiri [
26] analytically investigated the effect of interfacial debonding on energy storage, displacement fields, and interfacial opening displacements during the deformation of syntactic foams. The above models are based on the realistic microstructural assumptions and are useful for understanding the deformation and fracture behavior of syntactic foam. However, the models are still limited to simple tensile loading cases with one possible type of interfacial debonding. For instance, the experimentally obtained compressive modulus is often much less than the theoretical value [
17,
18,
19,
20], which has not yet been studied through the numerical models with a debonded interface in the literature.
Both the compressive and tensile moduli of a partially debonded syntactic foam are probably weaker than those of a perfectly bonded syntactic foam. The extent of the reduction in the modulus may depend on the debonding geometry. This study aimed at understanding the general relationships between the debonding geometry and the overall apparent modulus of the partially debonded syntactic foam. Idealized models for three different partial debonding concepts were made and used for a parametric numerical study on the elastic properties of the syntactic foam, in terms of debonding fraction and geometry.
2. Geometric and Physical Model Concepts
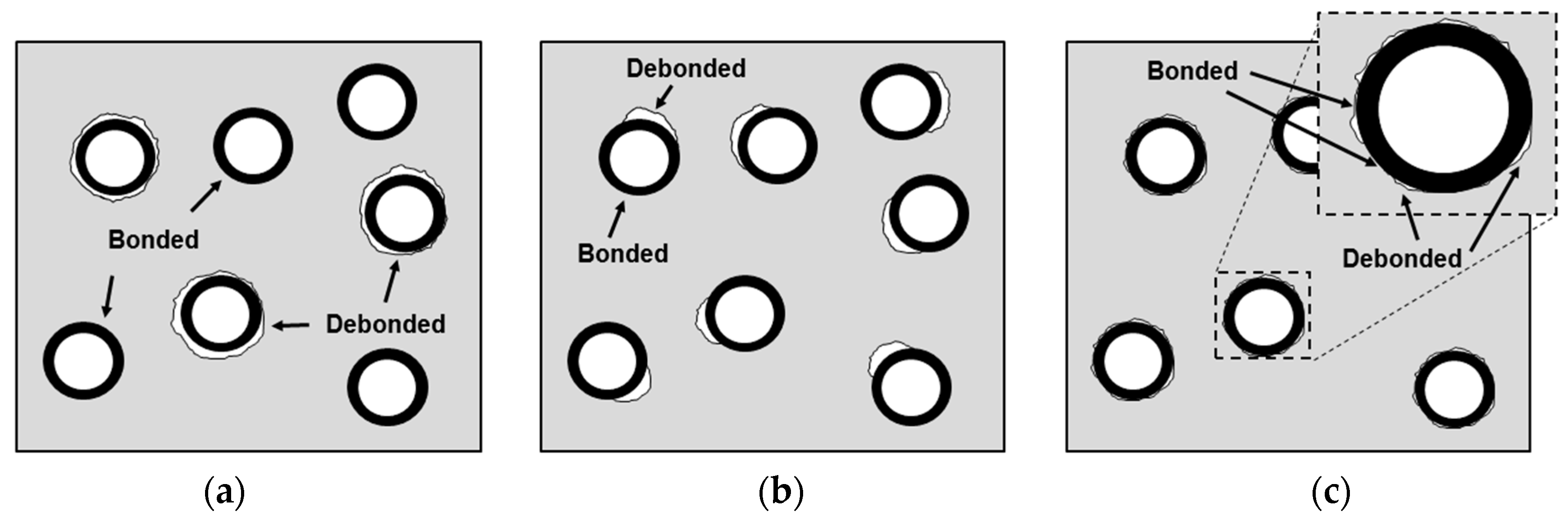
In this study, the effect of the debonding geometry on the interface between the microsphere and the matrix was investigated by defining two interface states, bonded and debonded interfaces, in the numerical models. The bonded interface assumed a perfectly bonded state. Whereas for the debonded interface, an allowance was given for slipping and the formation of a gap between the microsphere and the matrix, thus the load transfer occurred only by contact and there was no load-transfer capacity along the debonding direction. As shown schematically in
Figure 1, three types of debonding geometries were considered:
Mixed model (
Figure 1a): There is a mixture of microspheres having both bonded and debonded interfaces. For each microsphere, the interface is either fully bonded or fully debonded.
Partially debonded model (
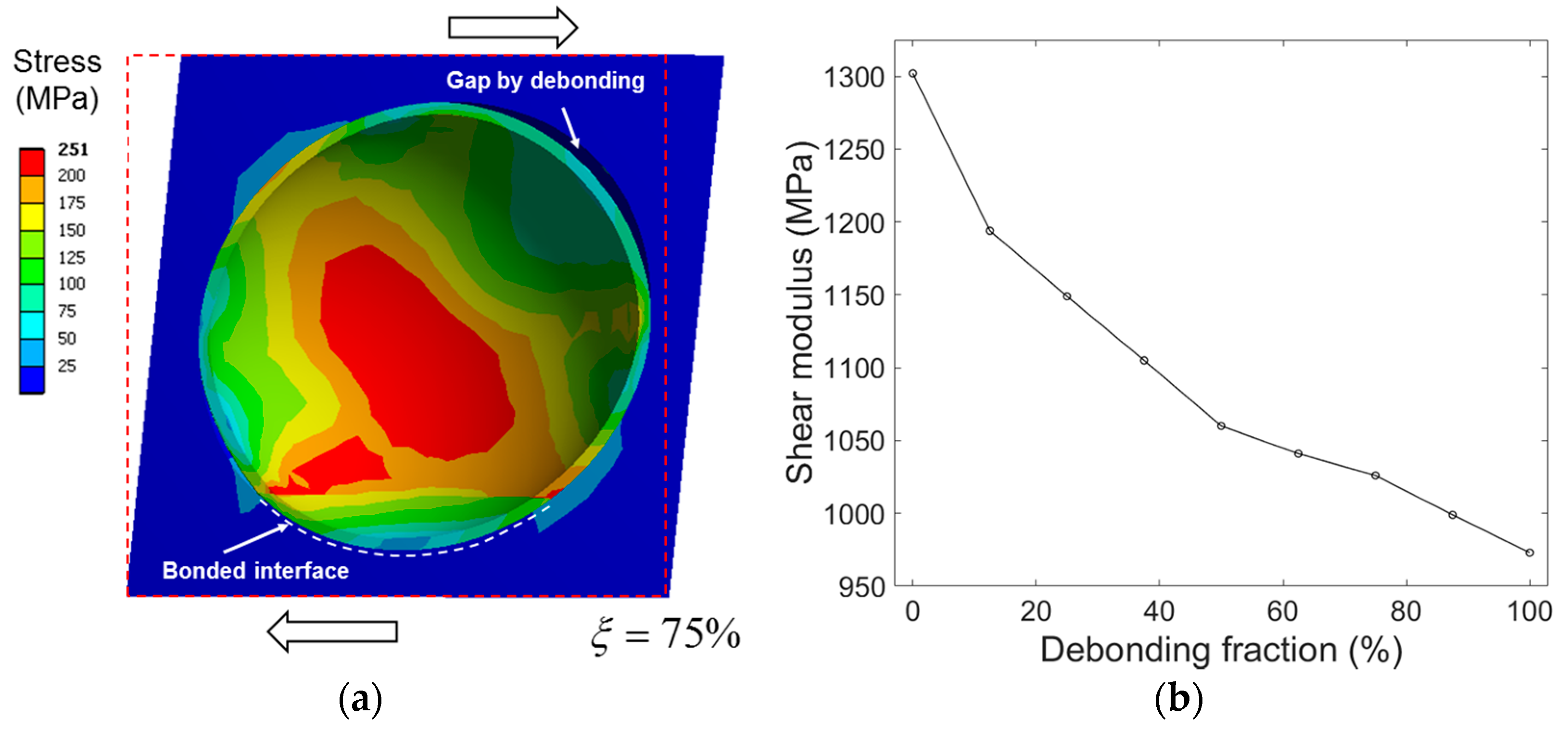
Figure 1b): Each microsphere has an interface which consists of two distinctly divided regions of bonded and debonded states. When the debonded region is smaller than the bonded region, there is a cap-type gap in one side of the interface. The cap-type connection exists in the opposite situation.
Discontinuously bonded model (
Figure 1c): The interface is discontinuously bonded meaning the microsphere and matrix are sparsely interconnected at the interface.
The microstructure of each of the above cases was described by the representative unit cell approach for the FEM modeling. For the mixed model, the previously developed multi-particle unit cell approach was used [
18,
19,
20]. A random sequential adsorption algorithm [
27] was used to generate a random distribution of microspheres. Moreover, it was assumed that the unit cell is representative of the periodically arrayed whole microstructure. Therefore, a microsphere which penetrated the cell boundary was cut by the boundary and reappeared through the opposite side of the boundary.
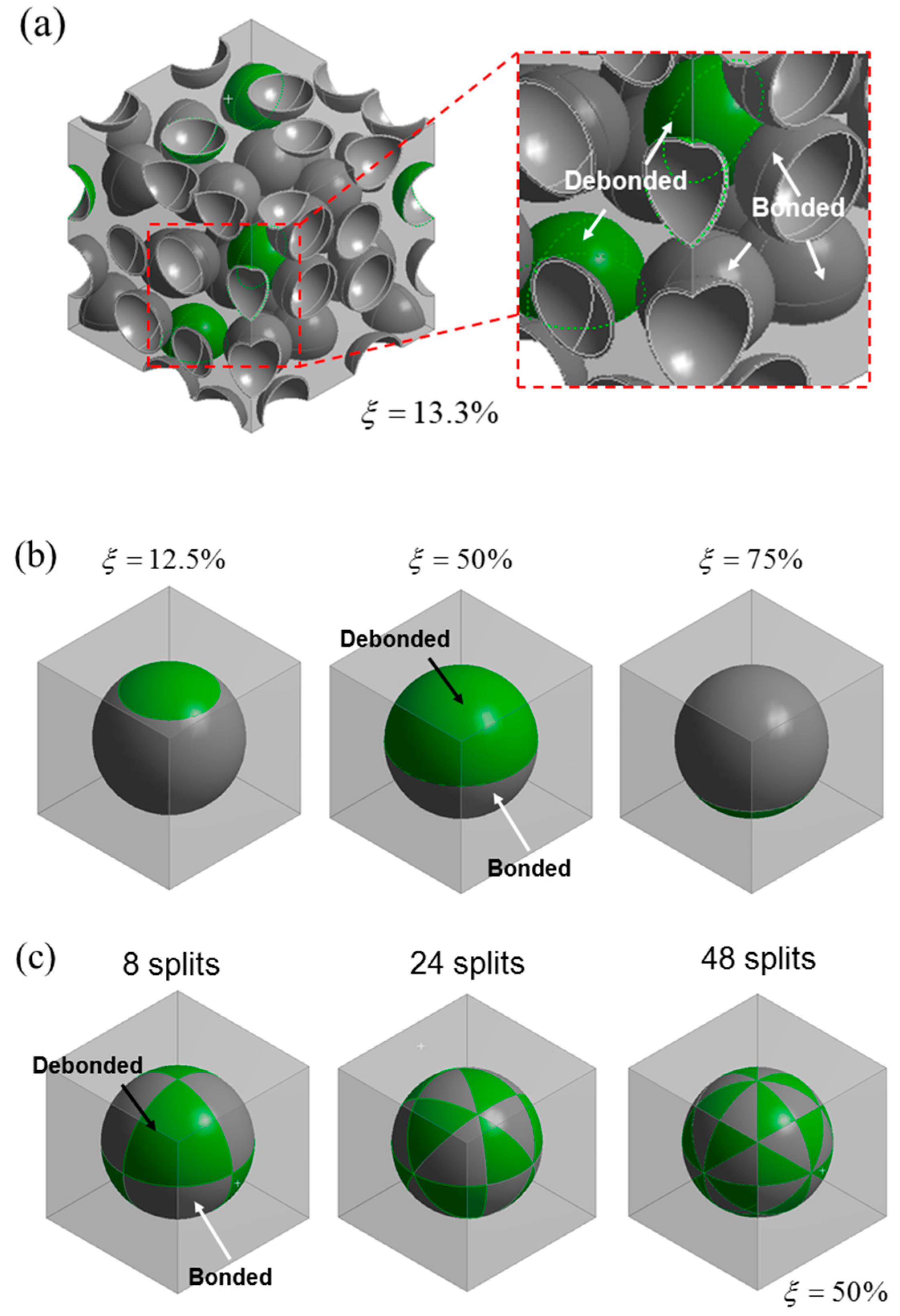
The geometry of the mixed model is shown in
Figure 2a. The model consists of cubic unit cell containing 30 microspheres, with a microsphere volume fraction,
, of 30%. The mesh was made finer close to the interface in order to capture precisely the interaction between the microsphere and the matrix.
In this study, a debonding fraction, , is defined by the area of the debonded interface divided by the total interface area. In the mixed model, the debonded interfaces were set by choosing the microspheres one by one randomly, and applying the debonded condition to their interfaces. Thus, in this case the model with higher means that more microspheres have debonded interfaces.
The microstructures for the partially debonded and discontinuously bonded models were idealized by the single particle unit cell approach. For both of the models,
= 30% was used. The geometries of the models are shown in
Figure 2b,c. A microsphere embedded cubic cell was used for both the models. The
in the partially debonded model was varied by adjusting the distance between the top of the microsphere and the bonded-debonded interface line in the model, as shown in
Figure 2b. In the discontinuously bonded model, a sparsely interconnected interface was idealized by three different geometries where the interfaces were divided into eight, 24, and 48 splits having equal face areas. The divisions of the interfaces were done by 90°, 60°, and 45° inclined planes for the eight, 24, and 48 splits, respectively, as shown in
Figure 2c. The debonded interface was modeled by applying the debonded condition to only half of the total faces of the splits, so that the interconnected areas had chess board-like structures and the
in this model was fixed to 50% for all cases. More details of the finite element mesh used in the study including mesh density and the mesh dependency analysis can be found in the
supplementary document.
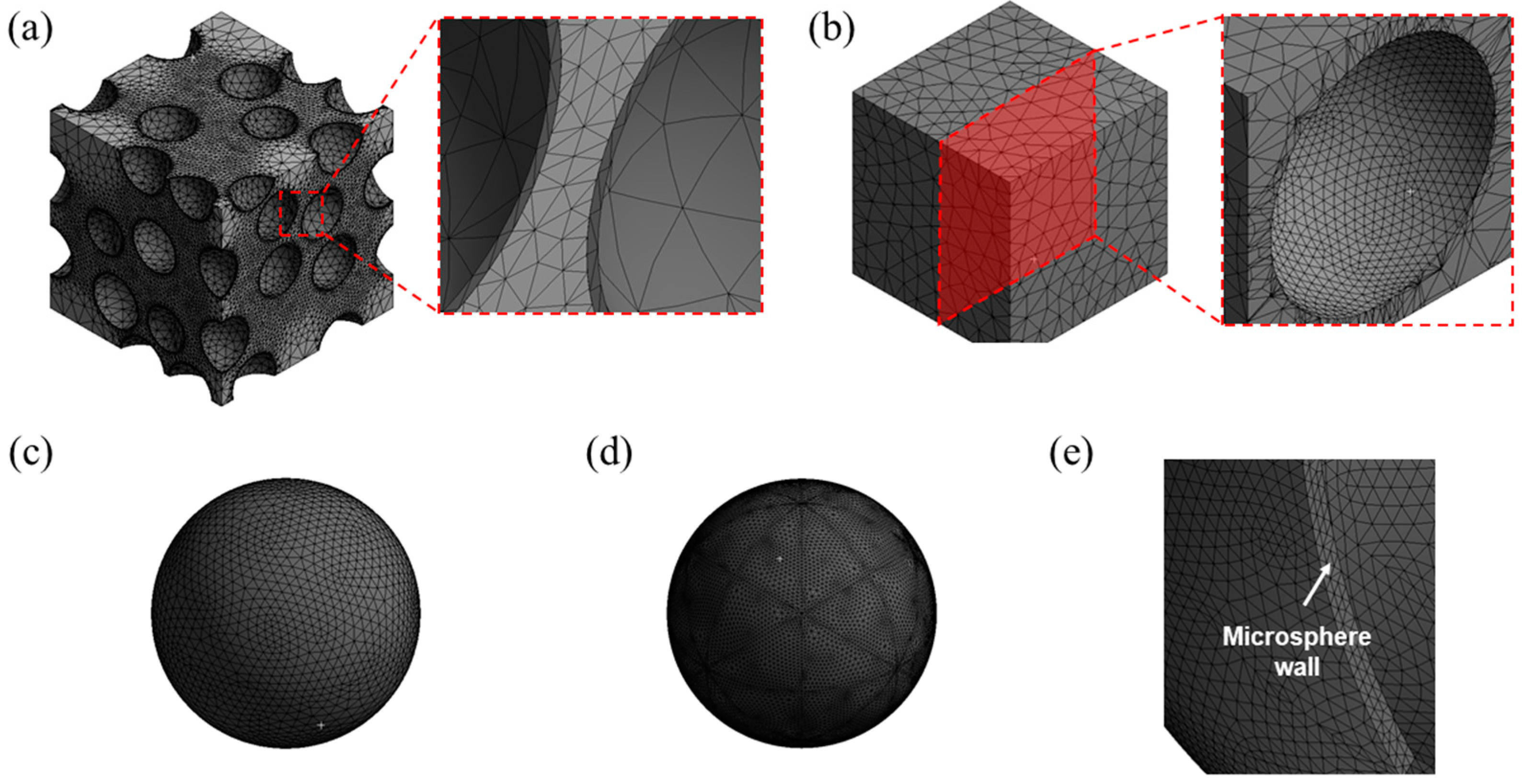
The models used in the study were discretized by finite elements with an automatic meshing algorithm provided by a commercial finite element code Ansys (version 14.5), as shown in
Figure 3. Higher-order, 10-node tetrahedral elements with four integration points (SOLID187, provided by the Ansys) were used to mesh the models. The meshes were made finer in the matrix near the interface to the microsphere in order to accurately capture the contact behavior between the matrix and the microspheres. For the mixed model, the meshes were made by first dividing the interfaces with a mesh density of 1/20 of the diameter of the microsphere. Then, volumetric meshes were made from the surface meshes using the automatic meshing algorithm. The mixed model used in the study had 1,074,541 nodes and 635,343 meshes. As shown in
Figure 3a, each microsphere had only two finite elements in the thickness direction. This was because of the geometrical complexity of the model and the limited mesh density that can be adopted for the calculations. The use of higher-order elements was thus necessary to capture the bending of thin microsphere walls. The validity of the finite element meshes used for the mixed model was checked by comparing with the models in which the microspheres were meshed with brick and shell type elements. The results are described in the
supplementary document.
The geometries of the partially debonded and discontinuously bonded models were simpler than the mixed model. Hence, finer meshes were able to be adopted for the calculations, as shown in
Figure 3b–e. The meshes of the microspheres were made finer than the mixed model, in order to avoid any undesirable stress concentration near the edge of the bond-debond interface. For each model, approximately 45,000 nodes and 22,000 meshes were used.
One important factor for determining elastic properties, using the representative unit cell approach, is choosing the appropriate type of boundary conditions. In the literature, the kinematic uniform, static uniform, orthogonal mixed, and periodic boundary conditions have been frequently used [
28,
29,
30]. As indicated by Huet [
28], the orthogonal mixed boundary condition provides better estimates, along with the periodic boundary condition, than the other two types of boundary conditions. Another advantage of using the orthogonal mixed boundary condition is that it can straightforwardly describe the uniaxial tension and compression behavior with the Poisson effect, using the FEM, without any special treatment. Whereas when using the periodic boundary condition, the Poisson effect, which involves tension or contraction in transverse direction to the loading in uniaxial deformation, is not directly demonstrated and requires special consideration. Therefore, the orthogonal mixed boundary condition was used throughout this study. The elastic properties of each model were estimated using the FEM by applying a 1% tensile and compressive uniaxial strain to the model. Due to the orthogonal mixed boundary condition and the symmetry of the applied load, all of the six outside planes of the cubic unit cells remain on plane after deformation.
The calculations were performed with version 14.5 of the finite element code Ansys, by means of a static structural analysis of the uniaxial deformation. The surface-to-surface interaction between the microsphere and the matrix in the debonded area was modeled by the Coulomb frictional model. In the debonded area, the load was only transferred when contact occurred between the microsphere and the matrix. In the simulations, the contact status was monitored by checking the relative positions of the nodes of the microsphere on the debonded interface to the interface surface of the matrix, and contact occurred when the node penetrated the matrix surface. An augmented Lagrangian contact algorithm was used in both normal and tangential directions. A hard contact condition was defined in the direction normal to the interface plane, meaning the load normal to the interface was perfectly transferred by the contact forces when the two surfaces were in contact. A normal contact stiffness factor of one was used, which is the penalty stiffness relative to the matrix stiffness that acts in the normal direction on the matrix surface, and enforces the displacement compatibility by limiting the penetration of the matrix phase. For the Coulomb friction model, a negligibly small friction coefficient of 0.001 was used for better convergence to restrict the rotational movement of the microsphere without provoking any pronounced effect due to friction.
The glass microsphere-filled polymer foam, with an elastic modulus of 3.2 and 72 GPa for the matrix and the microsphere, respectively, were used for the test cases throughout the study. The Poisson’s ratios for the matrix and the microsphere were 0.33 and 0.22, respectively. The radius ratio, which is the ratio of inner to outer radius of the microsphere, , of 0.95 was used for the calculations.
4. Discussion
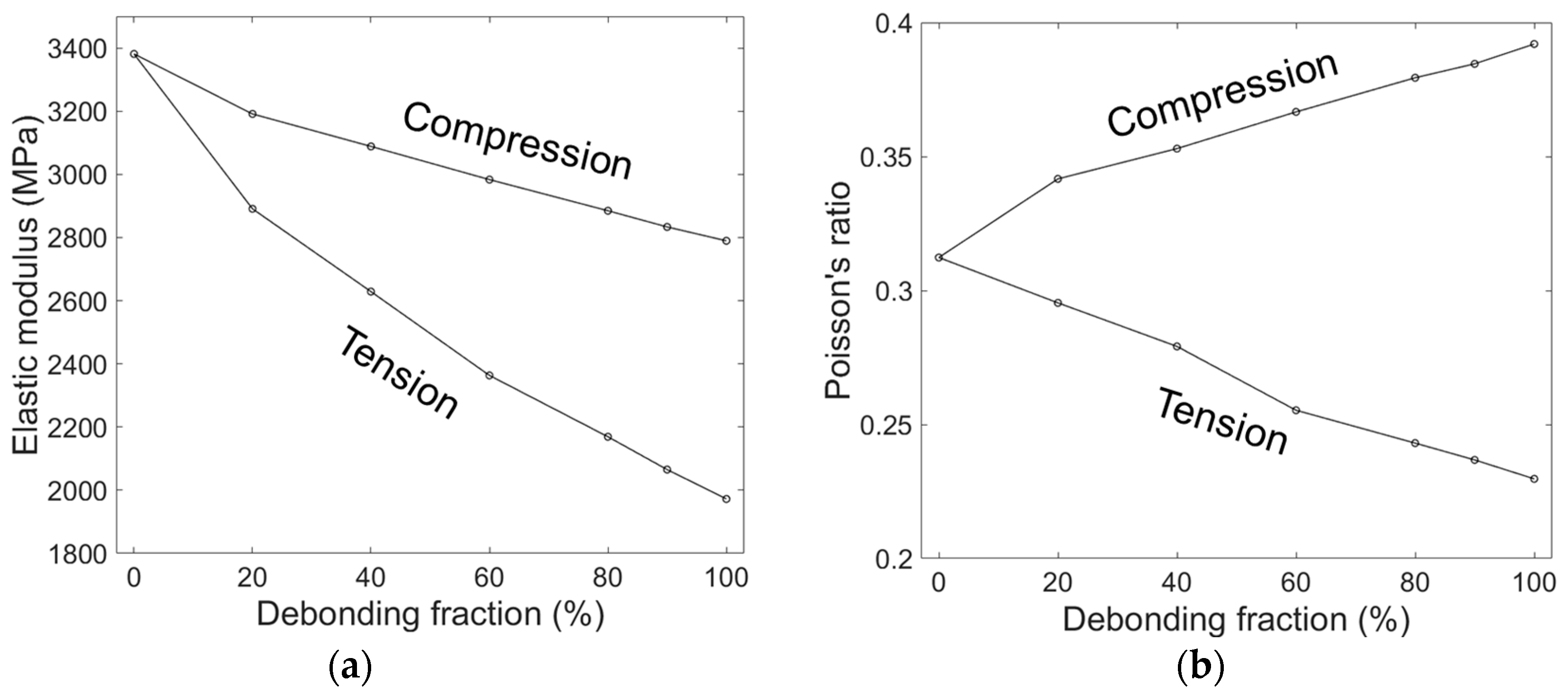
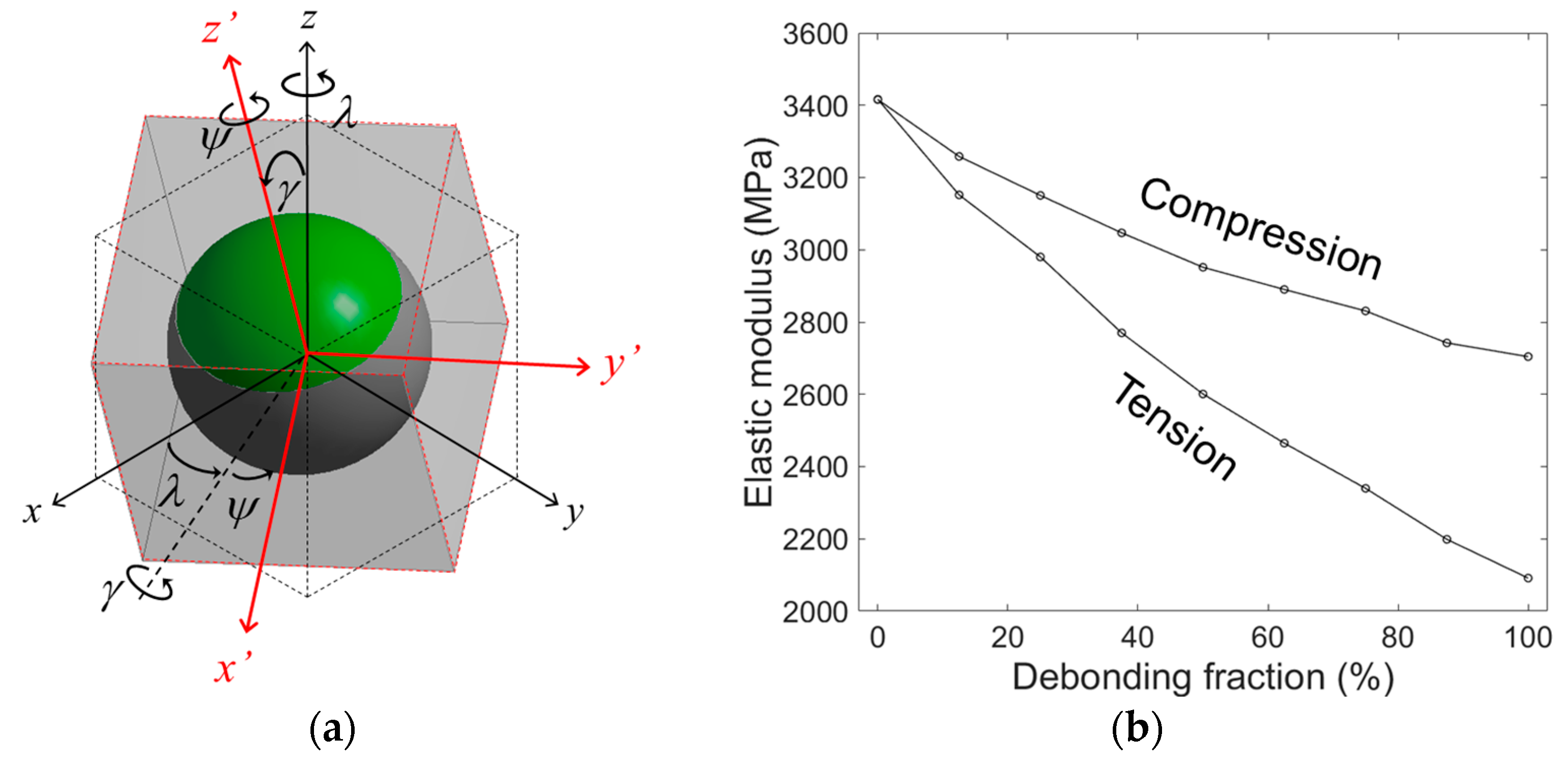
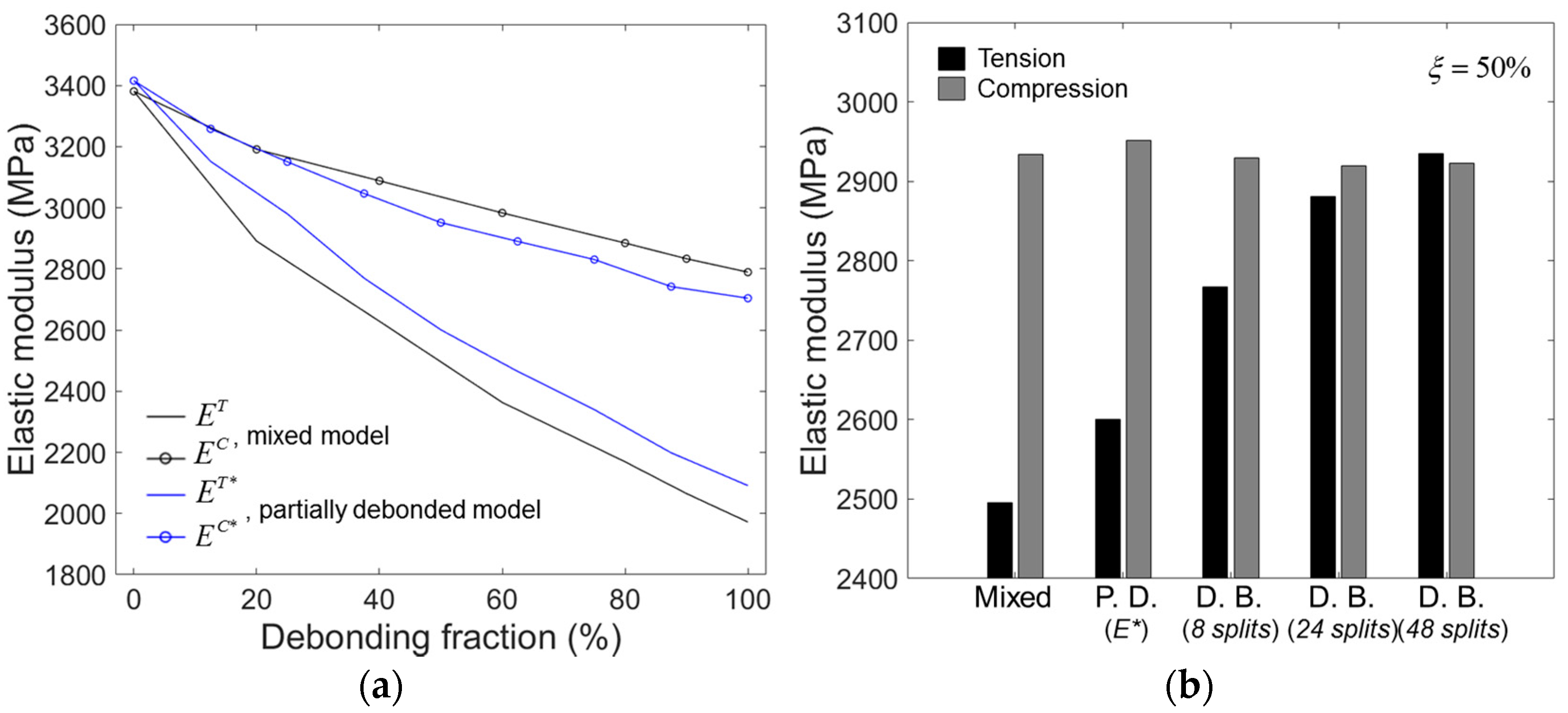
Figure 10 compares the elastic moduli obtained by the models with different debonding geometries. In
Figure 10a, the elastic moduli obtained by the mixed and the partially debonded models are plotted as a function of
. For the partially debonded model, the elastic moduli for the randomly oriented partial debonding (
) were used for comparison. The two models showed almost identical elastic moduli for
= 0% (perfect bonding), slightly deviating from each other for higher
. The compressive moduli obtained by the mixed model was slightly higher than those obtained by the partially debonded model, while the opposite trend was observed for the tensile moduli. However, the deviations in the moduli between the two models were not significant and the two models were fairly well correlated.
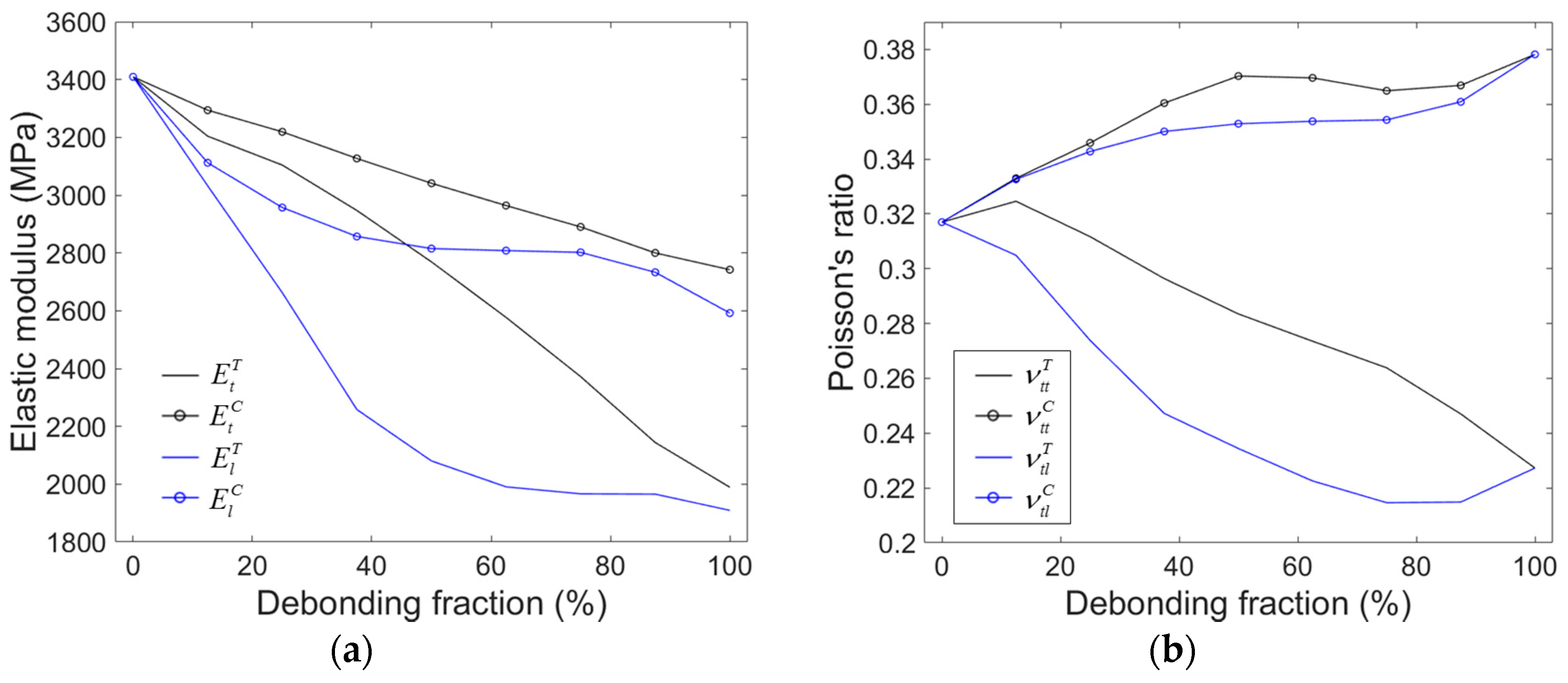
Figure 10b shows the compressive and tensile moduli obtained by all the models tested for
= 50%. It is seen that the compressive modulus is not altered much by changing the debonding geometry, indicating that it almost solely depends on the debonding fraction. In contrast, the tensile modulus strongly depends on the debonding geometry, as shown in the figure. For the fixed
= 50%, the tensile modulus was highest in the mixed model, followed by the partially debonded model, then the discontinuously bonded model with eight, 24, and 48 splits. Given these results, it seems that the tensile modulus relies largely on the relative size of the debonding gap in the model. In the mixed model, each debonding gap’s size corresponded to the full interface area between the microsphere and the matrix. For the other models, the individual debonding gap’s size, in relation to the full interface area, was smaller in the inverse order of their tensile moduli, i.e., 1/2, 1/8, 1/24, and 1/48 for the partially debonded and discontinuously bonded models with eight, 24, and 48 splits, respectively.
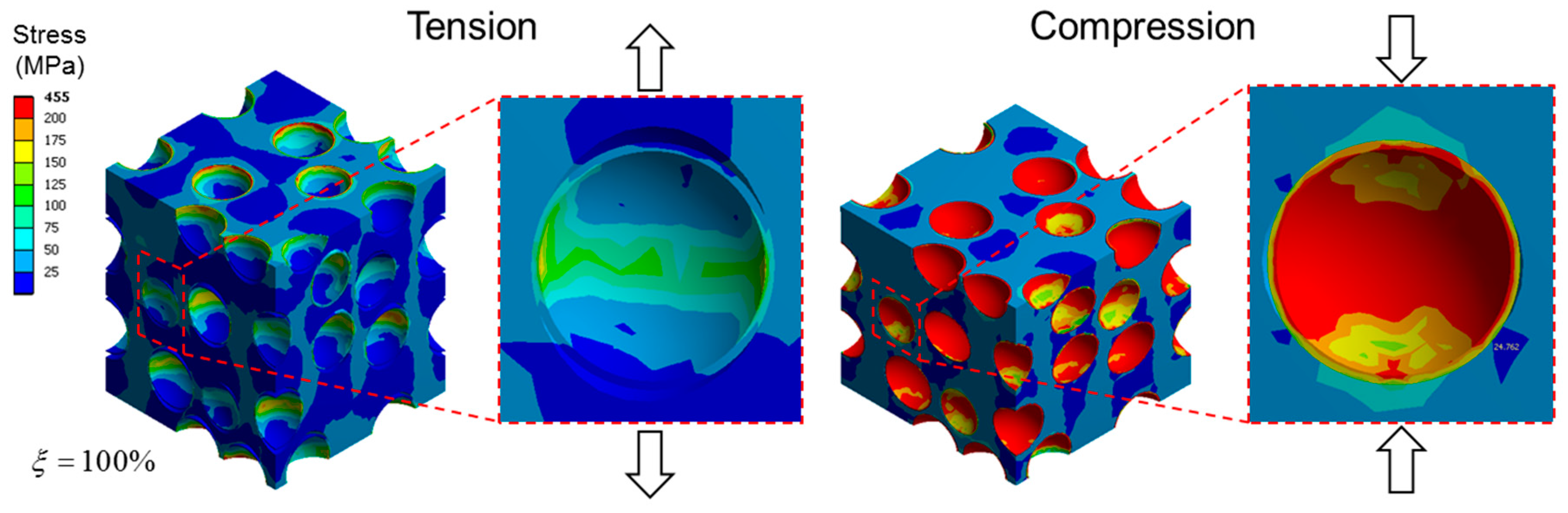
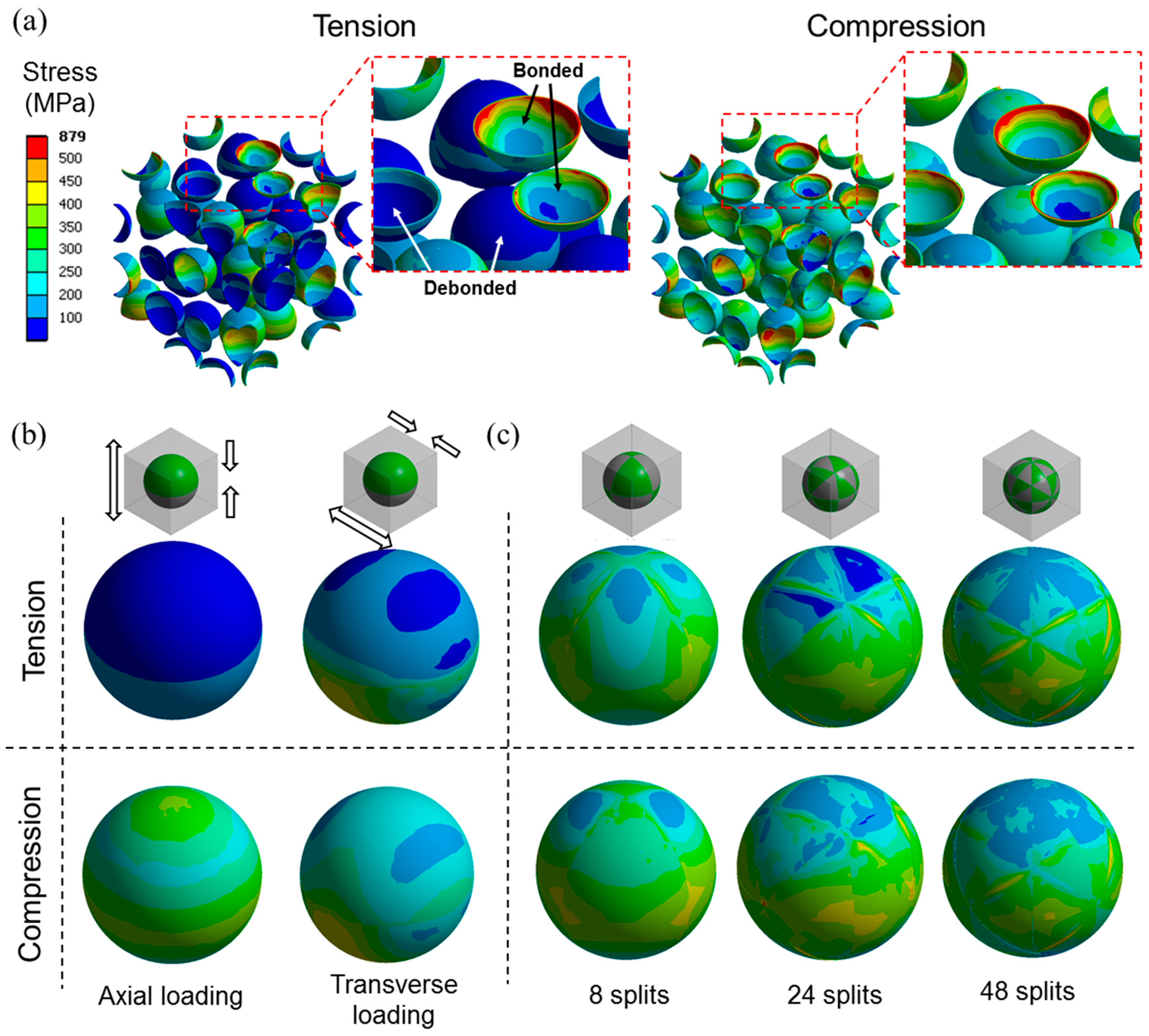
Figure 11 shows the stress distributions in the microspheres for the same models used in
Figure 10b. In the mixed model, the microspheres with the debonded interfaces clearly showed less stress compared to the ones with the bonded interfaces under tensile load (
Figure 11a). This is because the applied load is more efficiently transferred to the microspheres having bonded interfaces than those that were debonded. The stress in the debonded microspheres was much less under tension than compression, indicating that the low tensile modulus of the mixed model under compression can be attributed to the poor load bearing efficiency by the debonded microspheres. This effect is more clearly seen in
Figure 11b, where the stress distribution of the half debonded microspheres in the partially debonded model, in two different loading directions, are presented. With the tensile load in the direction normal to the axisymmetric plane of the model, also known as axial loading, the model exhibited similar behavior to the mixed model, i.e., the stress near the debonded interface was significantly lower under tension than compression due to the poor load bearing efficiency under tension. When the load was applied in the direction perpendicular to the axisymmetric plane, also known as transverse loading, more load was transferred through the debonded interface. The load transfer by the debonded interface becomes more effective when the debonded area is more finely divided, as shown in
Figure 11c in the results of the discontinuously bonded model.
The results presented in
Figure 10 and
Figure 11 indicate that the load transfer with tensile loading through the debonded interface becomes more efficient with finer debonding gaps, for the same
. When the debonding gap is fine enough, the load transfer effect through the debonded interfaces is comparable for tension and compression, as shown by the discontinuously bonded model with the 48 split in
Figure 11c. In this case, the resulting tensile modulus is therefore comparable to that for compression. The finer the debonding gaps, the smaller the gap under tensile load which makes more interfacial area remain in contact during deformation along with more efficient load transfer. This effect may not be dominant under compression since there is no gap formation in the loading direction. This explains why the compressive moduli are not much influenced by the debonding geometry, as shown in
Figure 10b.
When predicting the elastic response of syntactic foam using a simple elastic model with a perfectly bonded interface, it overestimates the experimentally observed elastic moduli of the foam in most cases, as shown in [
3,
17,
18,
19,
20]. Several reasons have indicated as possible factors leading to this overestimation, such as matrix defectiveness [
19] and weak interfacial phase formation between the matrix and microsphere [
22,
23]. In considering the numerical results presented here, the partial interfacial debonding occurring during the processing, or during deformation, at low stress could also be considered as a possible cause for the underestimation. The reduction in elastic modulus by interfacial debonding can be as large as ~20% in the case of compressive loading, and up to 40% in with tension, for the considered syntactic foam as shown in
Figure 10.
It was not possible to perform a direct comparison between the numerical results and the experiments for the purpose of verification, since experimental data for the detailed debonding geometry during loading is not available in the literature. However, the model used here intuitively considers the influence of debonding, which is helpful for gaining a better understanding of the effect of interfacial flaws on the performance of syntactic foam. The models can be easily adopted for syntactic foams having different microstructural parameters, such as for different microsphere wall thicknesses. As an example, a comparison between the mixed model and the analytical model were made and can be found in the
supplementary document.
Notably, some experimental observations can only be explained by considering the partial debonding effect. For instance, Tagliavia et al. [
3] investigated the effect of moisture absorption on the flexural properties of syntactic foams. They observed a 5–25% reduction in the flexural modulus due to a small amount of moisture absorption of less than 3 wt.%, for their syntactic foams with
= 30%. The moisture absorption is known to weaken the adsorption bond between a filler and matrix in a polymeric composite, as it forces itself between the filler and matrix and lowers the interfacial fracture energy, making it easier to debond [
32]. The deterioration of the elastic modulus by this mechanism can be better characterized and quantified by analyzing the tensile and/or compressive modulus before and after the moisture absorption using the model used here. For another example, Rousseau et al. [
33] experimentally determined the compressive moduli of epoxy based syntactic foams with various volume fractions of the glass microsphere up to 30%, using three different types of glass microspheres. In their results, all three types of foams showed linearly varied compressive moduli, in relation to the volume fraction, up to 20%, but this was followed by a pronounced drop in the compressive moduli when increasing the volume fraction from 20 to 30%. Since the materials and processing parameters used to fabricate the samples with 30% were the same as the others, the drop of the compressive moduli is not likely due to the weak interfacial phase formation. The void fraction due to the air entrapment during the fabrication process was at a maximum with only 2.2 % for every specimen. Thus the behavior cannot be solely explained by the matrix defectiveness but can easily interpreted when considering interfacial debonding. Notably, the syntactic foam with
= 0.95 [
33] showed the compressive modulus of ~2800 MPa for
= 30%, which corresponds to the compressive modulus estimated by the partially debonded model with
= 70 %.