The Quantified Characterization Method of the Micro-Macro Contacts of Three-Dimensional Granular Materials on the Basis of Graph Theory
Abstract
:1. Introduction
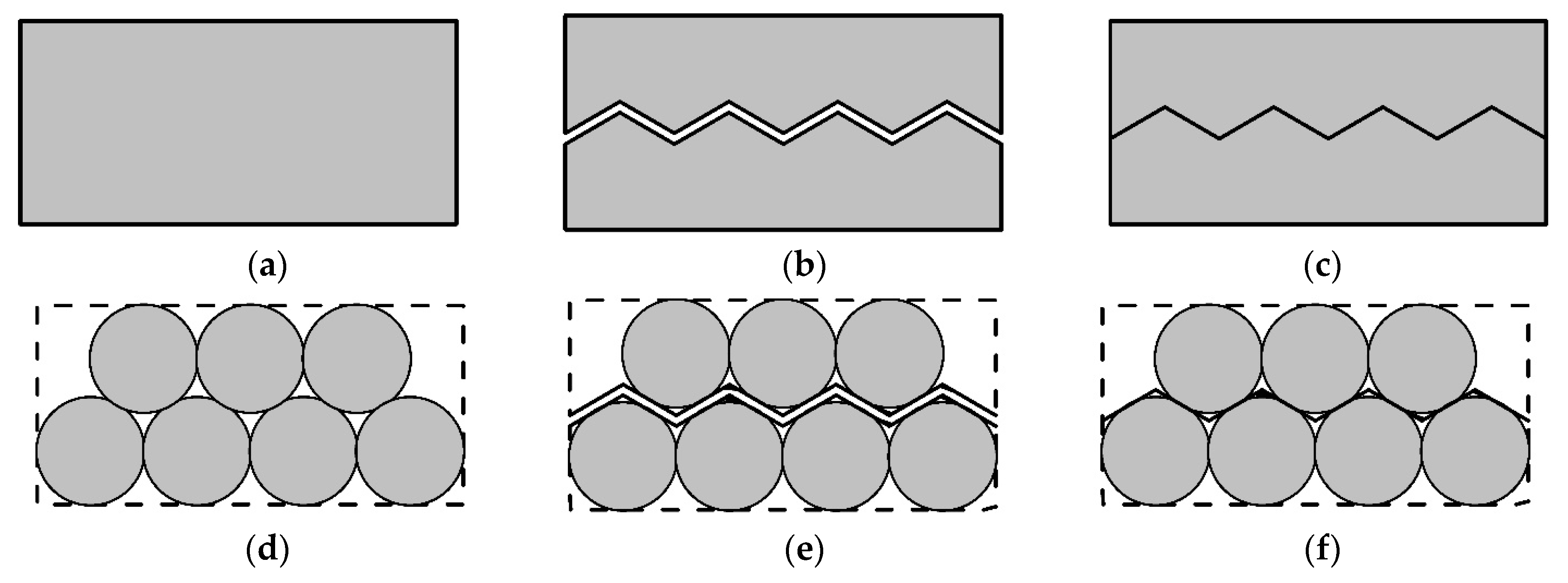
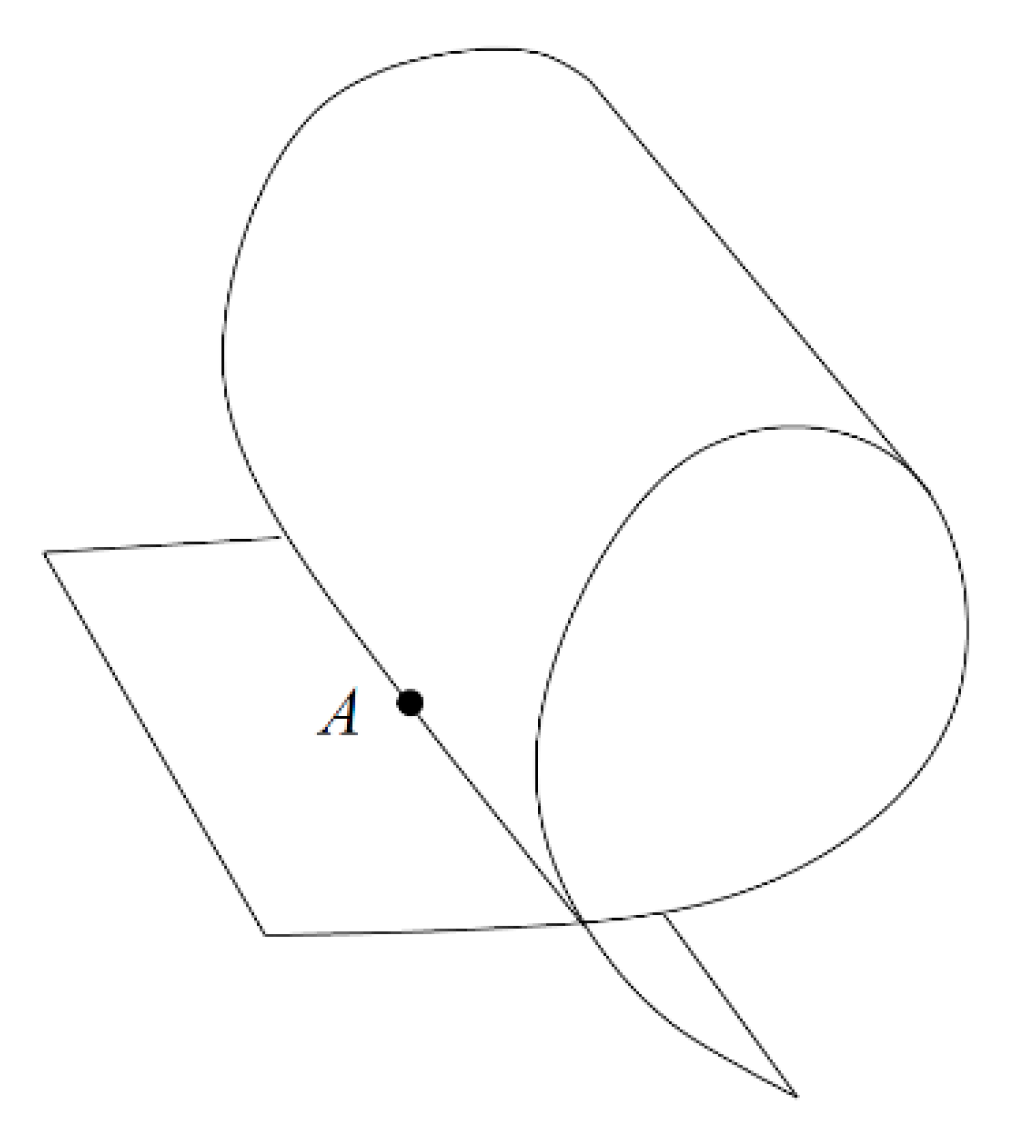
2. The Definition of the Contact
3. Characterization Method of Particle Contact
3.1. The Void Cell System
3.2. The Solid Cell System
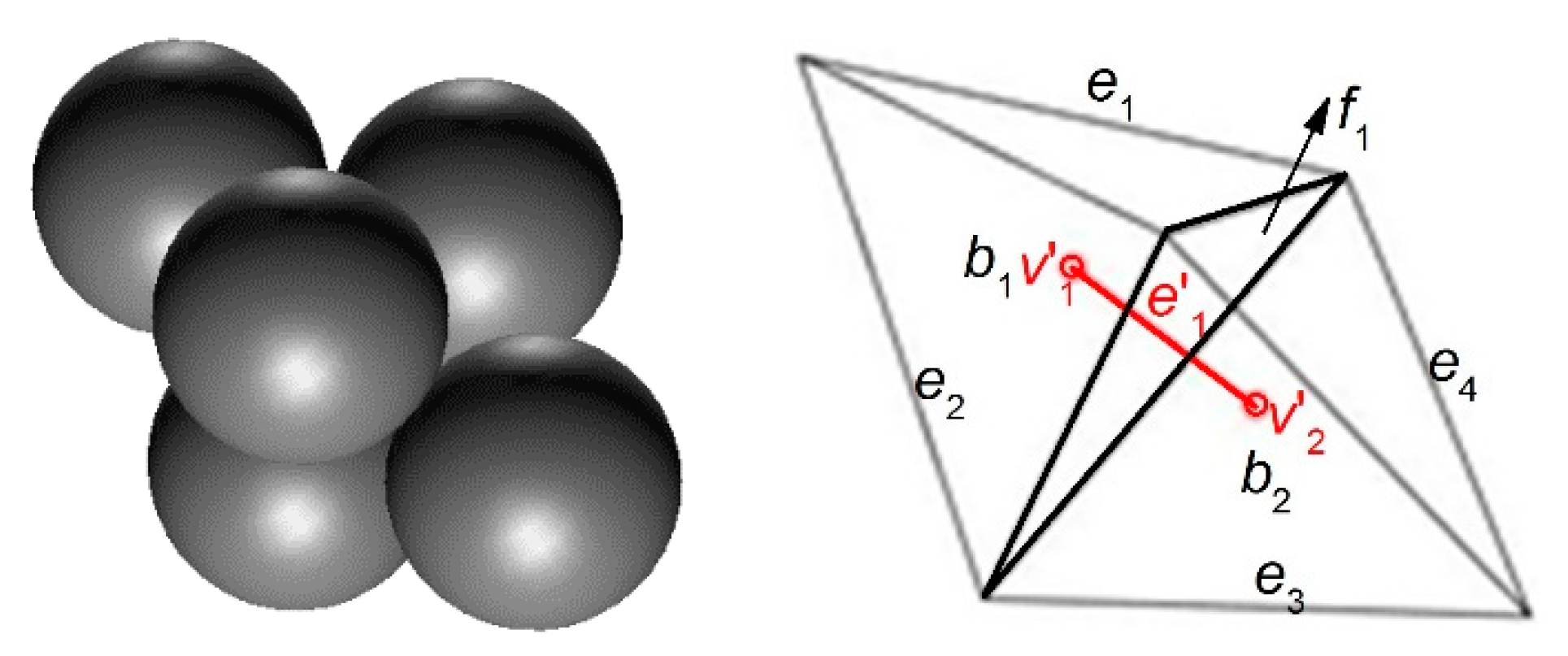
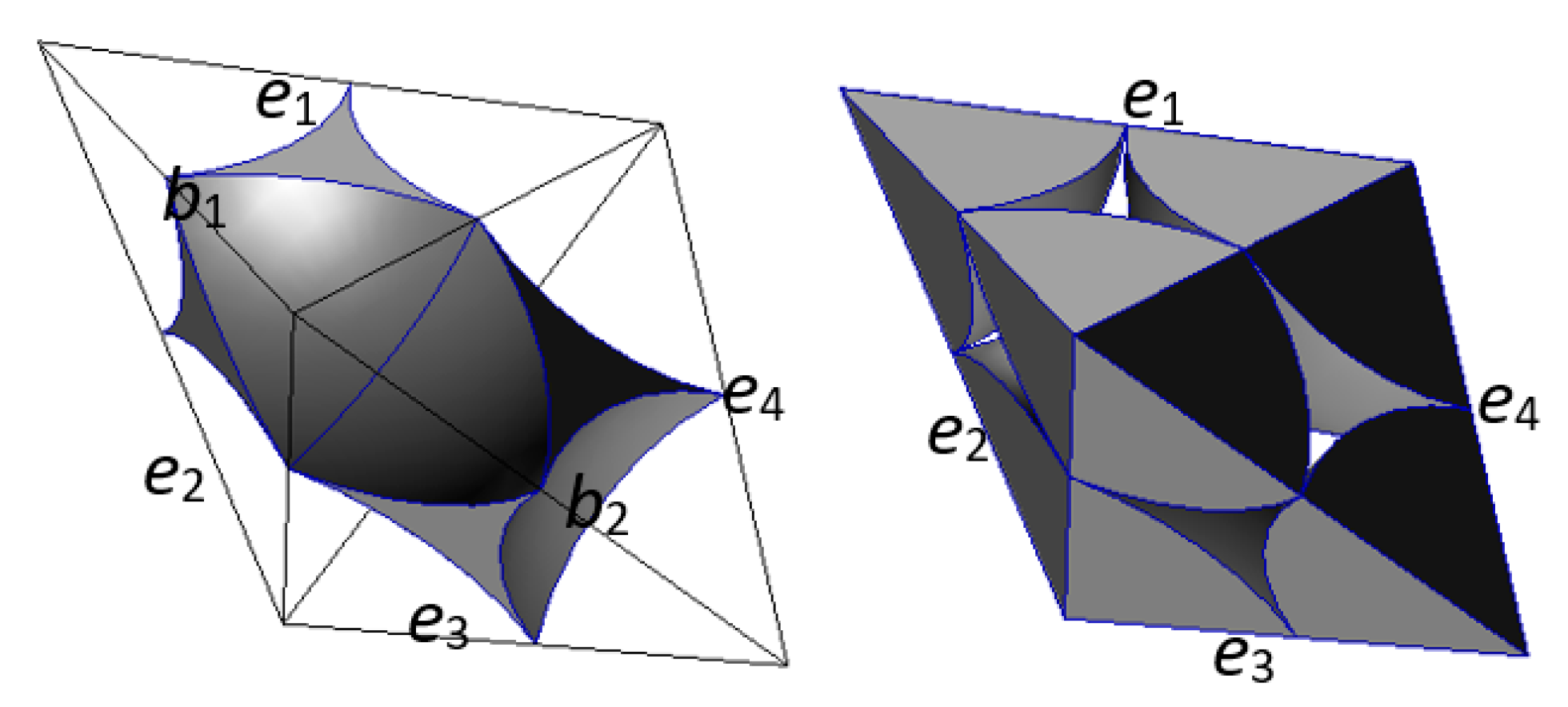
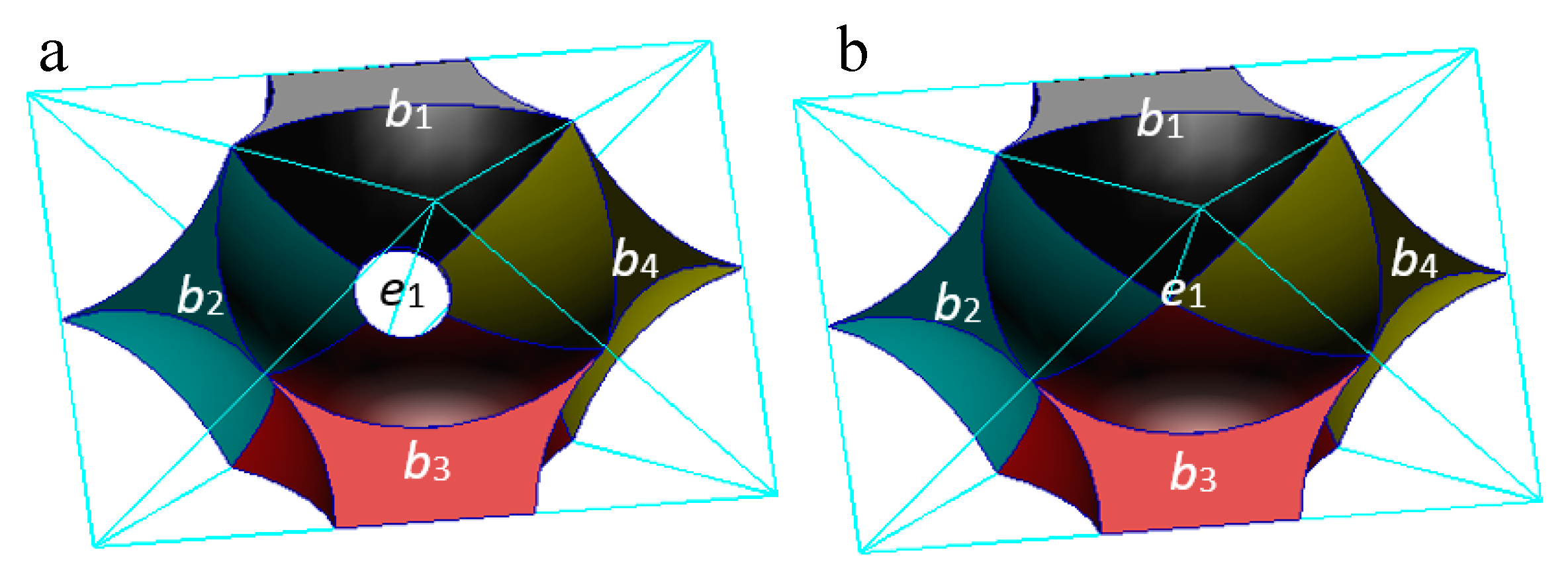
3.3. The Radical Voronoi Tessellation
3.4. The Role of the Particle, the Contact, and the Void
3.5. The Characterization of the Particle Contact
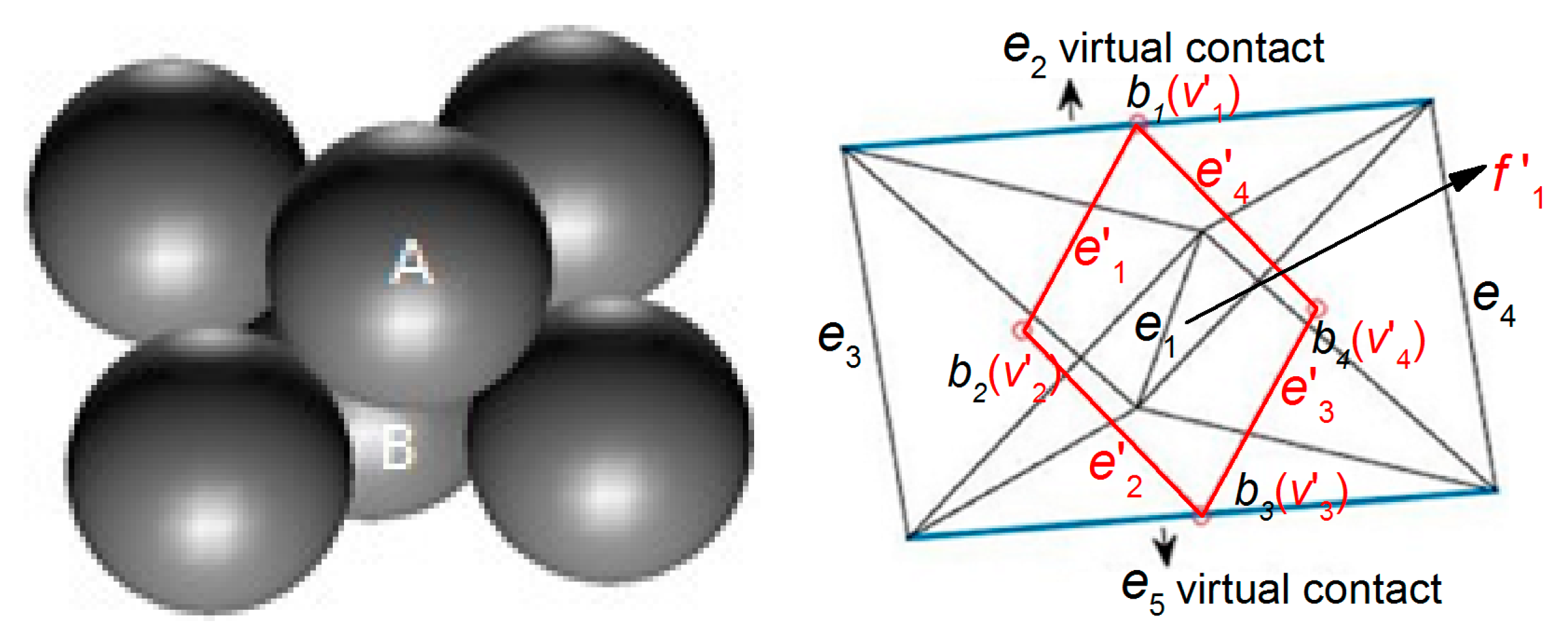
4. Characterization Method of the Macro Contact
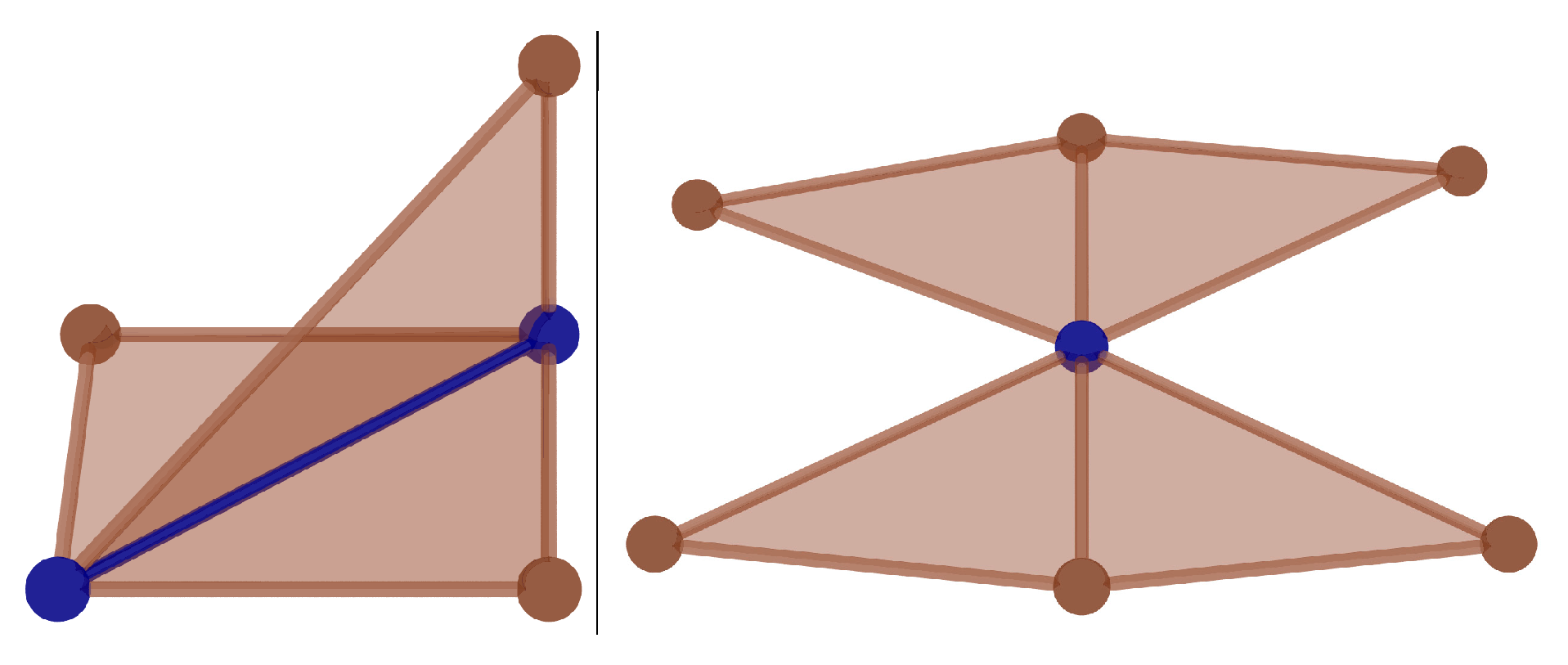
4.1. The Definition of the Macro Contact
4.2. The Characterization of the Macro Contact
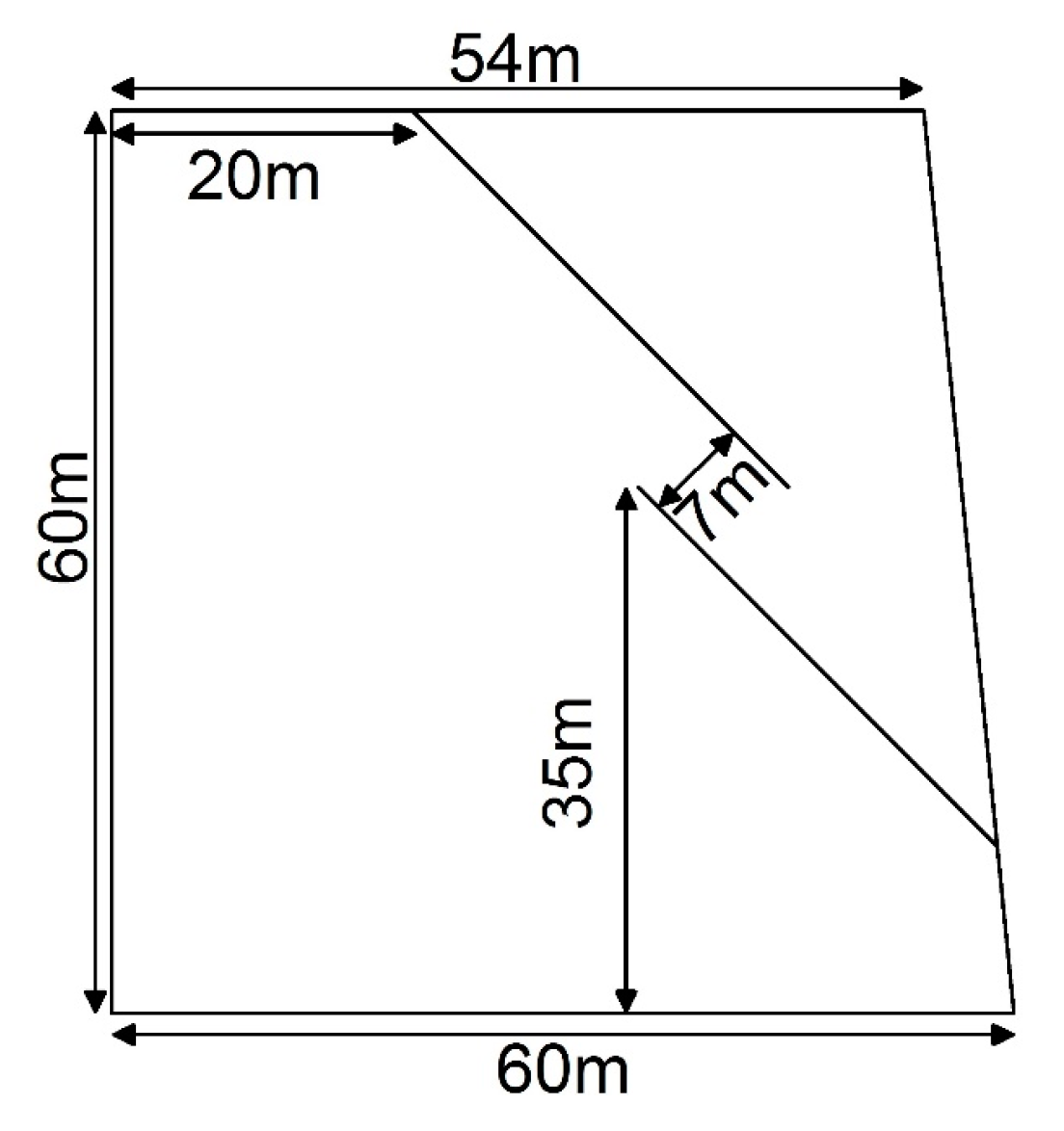
5. The Application with DEM
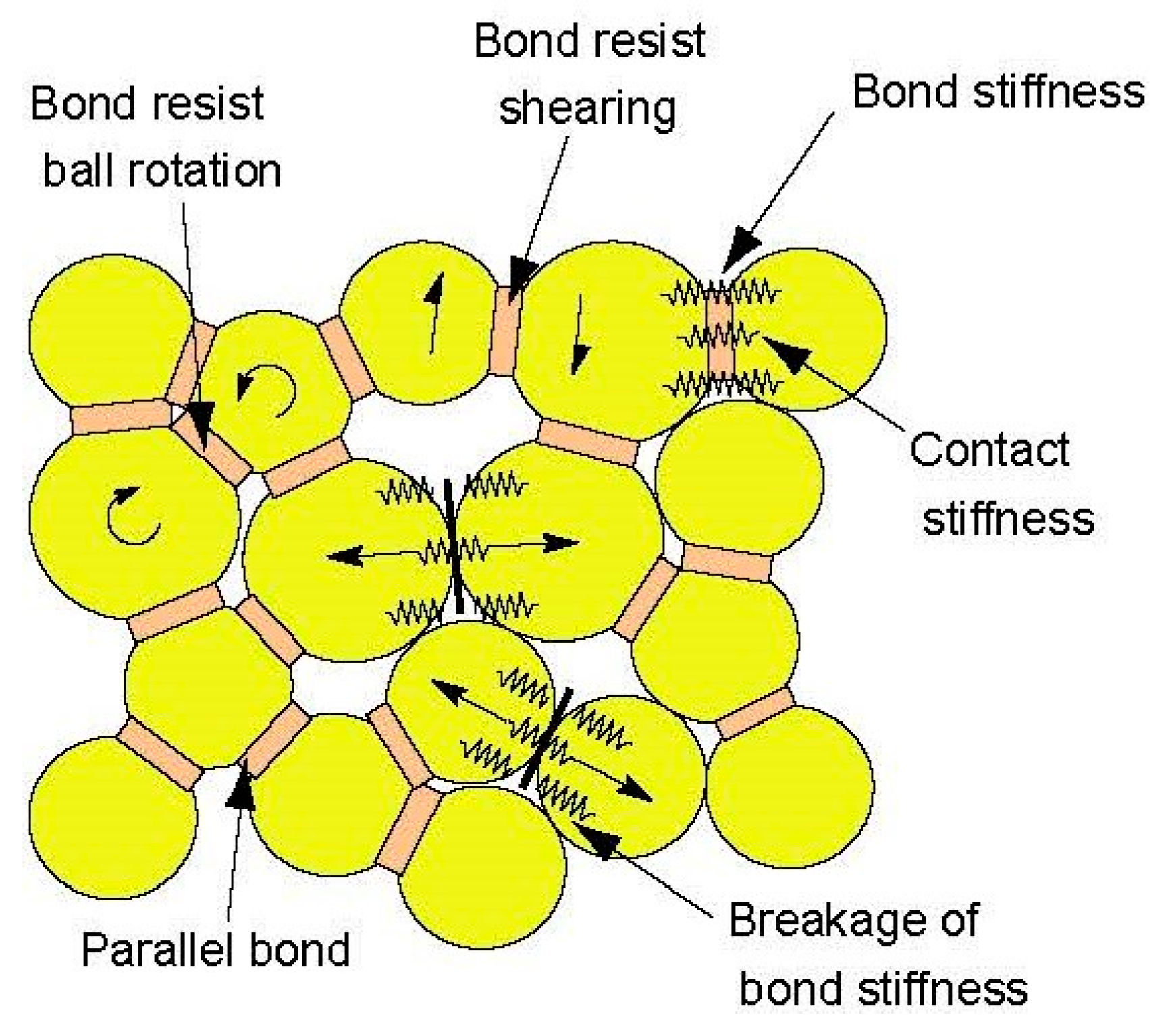
5.1. A Brief Introduction to DEM
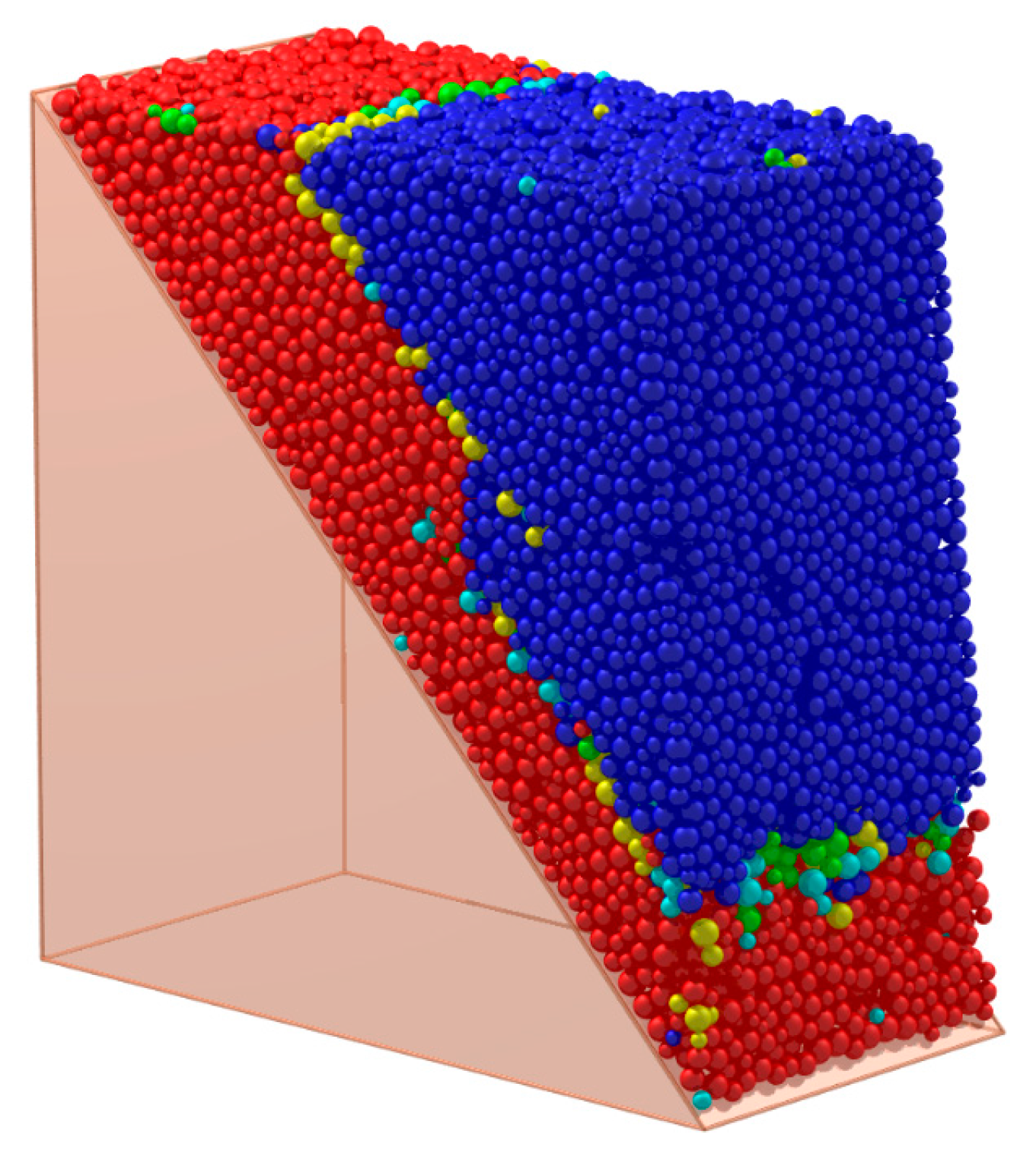
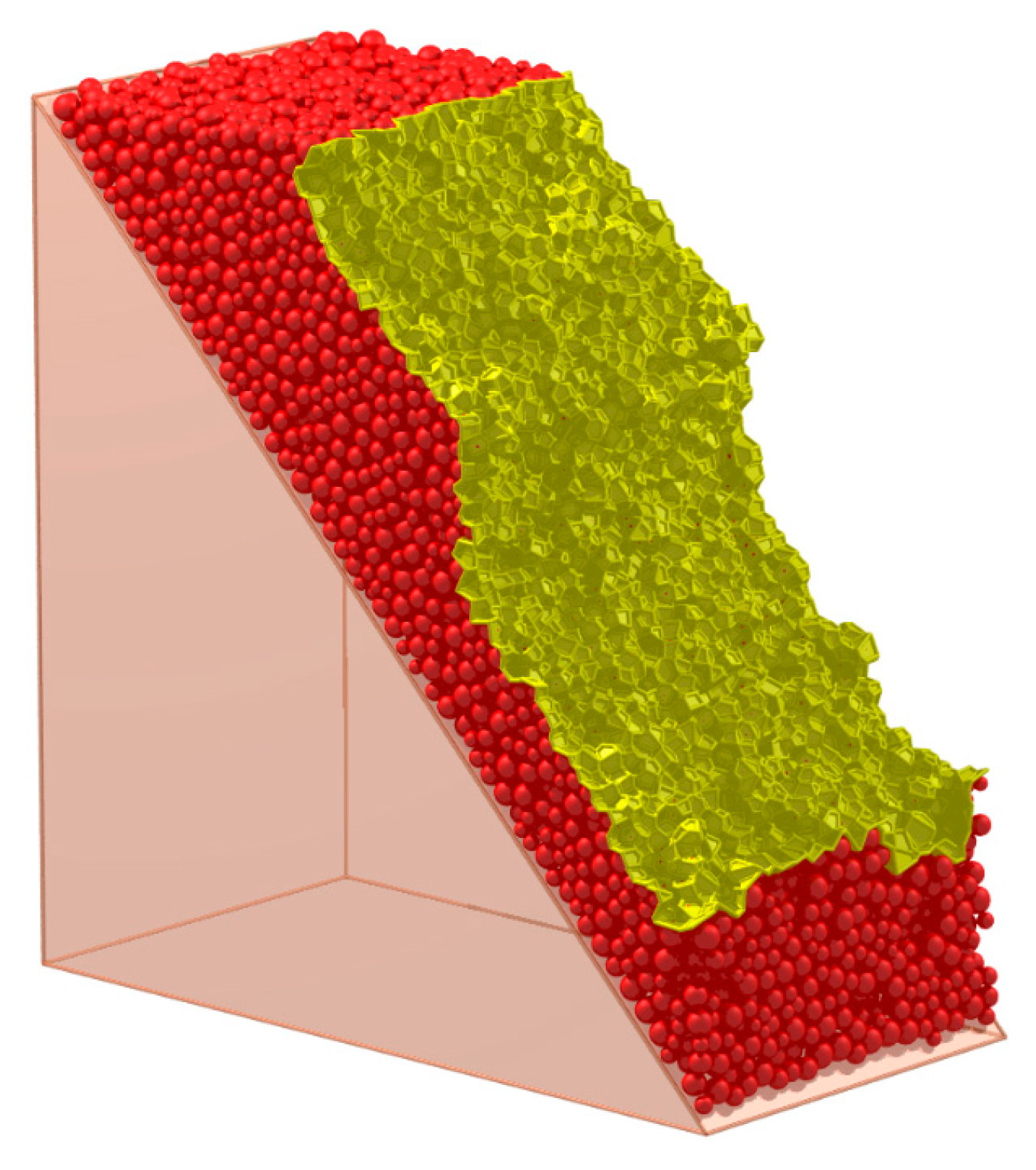
5.2. The Visualization of the Crack
5.3. The Determination of the Failure Route
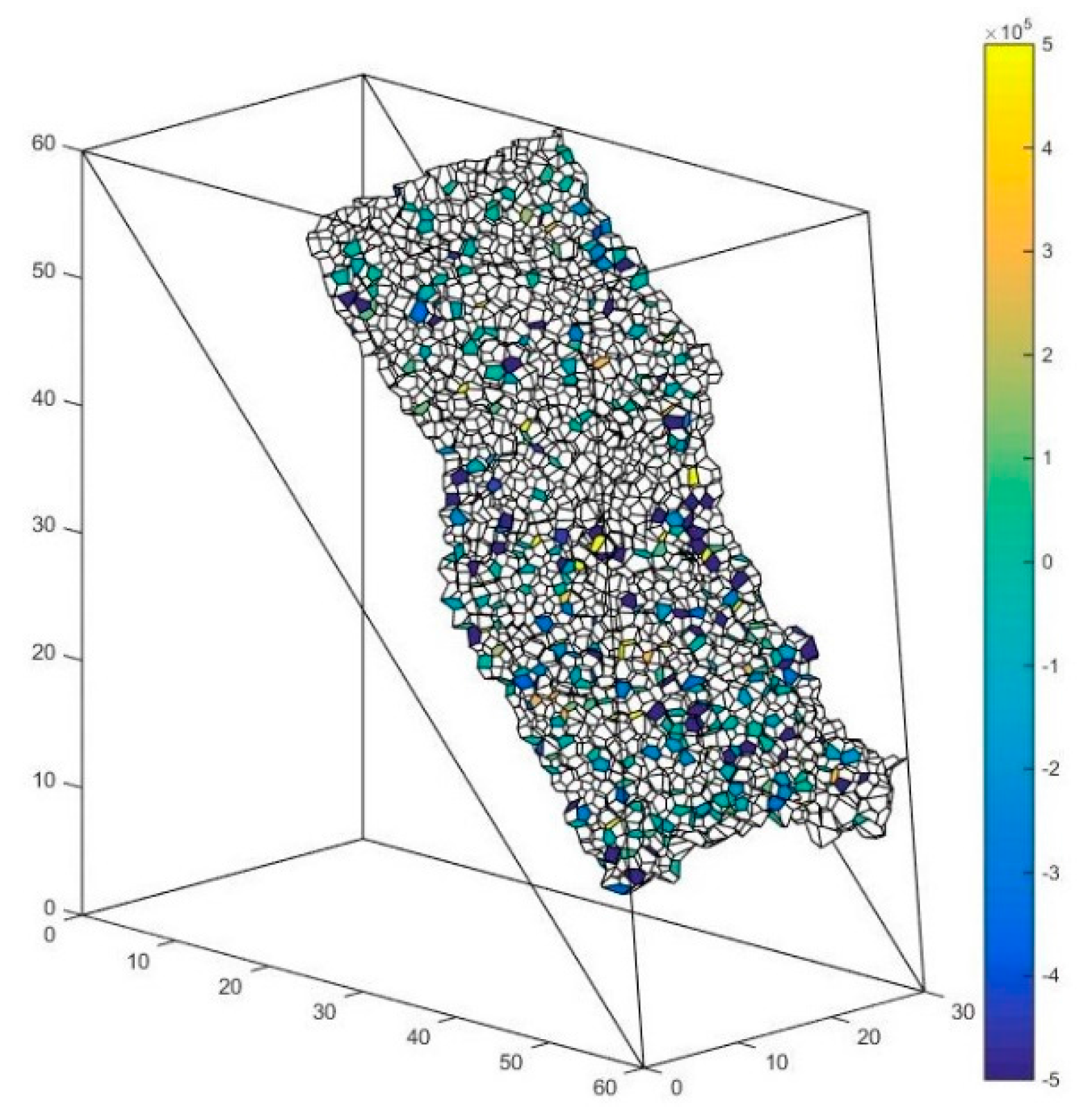
5.4. The Solution of Macro Contact Force
5.5. Summary
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Adler, P.M.; Jacquin, C.G.; Quiblier, J.A. Flow in simulated porous media. Int. J. Multiph. Flow 1990, 16, 691–712. [Google Scholar] [CrossRef]
- Liang, Z.; Ioannidis, M.A.; Chatzis, I. Permeability and electrical conductivity of porous media from 3D stochastic replicas of the microstructure. Chem. Eng. Sci. 2000, 55, 5247–5262. [Google Scholar] [CrossRef]
- Bagi, K. Analysis of microstructural strain tensors for granular assemblies. Int. J. Solids Struct. 2006, 43, 3166–3184. [Google Scholar] [CrossRef]
- Satake, M. A discrete-mechanical approach to granular materials. Int. J. Eng. Sci. 1992, 30, 1525–1533. [Google Scholar] [CrossRef]
- Li, X.; Li, X.-S. Micro-macro quantification of the internal structure of granular materials. J. Eng. Mech. 2009, 135, 641–656. [Google Scholar] [CrossRef]
- Satake, M. Tensorial form definitions of discrete-mechanical quantities for granular assemblies. Int. J. Solids Struct. 2004, 41, 5775–5791. [Google Scholar] [CrossRef]
- Jernot, J.; Prasad, P.B.; Demaleprade, P. Three-dimensional simulation of flow through a porous medium. J. Microsc. 1992, 167, 9–21. [Google Scholar] [CrossRef]
- Lindquist, W.B.; Lee, S.-M.; Coker, D.A.; Jones, K.W.; Spanne, P. Medial axis analysis of void structure in three-dimensional tomographic images of porous media. J. Geophys. Res. 1996, 101, 8297–8310. [Google Scholar] [CrossRef]
- Hilpert, M.; Miller, C.T.; Gray, W.G. Stability of a fluid-fluid interface in a biconical pore segment. J. Colloid Interface Sci. 2003, 267, 397–407. [Google Scholar] [CrossRef]
- Schröder-Turk, G.; Mickel, W.; Kapfer, S.C.; Klatt, M.A.; Schaller, F.M.; Hoffmann, M.J.; Kleppmann, N.; Armstrong, P.; Inayat, A.; Hug, D.; et al. Minkowski tensor shape analysis of cellular, granular and porous structures. Adv. Mater. 2011, 23, 2535–2553. [Google Scholar] [CrossRef] [PubMed]
- Vandamme, J.; Zou, Q. Investigation of slope instability induced by seepage and erosion by a particle method. Comput. Geotech. 2013, 48, 9–20. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Yang, B.; Jiao, Y.; Lei, S. A study on the effects of microparameters on macroproperties for specimens created by bonded particles. Eng. Comput. 2006, 23, 607–631. [Google Scholar] [CrossRef]
- Yoon, J. Application of experimental design and optimization to PFC model calibration in uniaxial compression simulation. Int. J. Rock Mech. Min. Sci. 2013, 44, 871–889. [Google Scholar] [CrossRef]
- Diederichs, M.S. Instability of Hard Rockmasses: The Role of Tensile Damage and Relaxation. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 2000. [Google Scholar]
- Zhang, X.P.; Wong, L.N.Y. Cracking processes in rock-like material containing a single flaw under uniaxial compression: A numerical study based on parallel bonded-particle model approach. Rock Mech. Rock Eng. 2012, 45, 711–737. [Google Scholar] [CrossRef]
- Yang, S.-Q.; Jing, H.-W. Evaluation on strength and deformation behavior of red sandstone under simple and complex loading paths. Eng. Geol. 2013, 164, 1–17. [Google Scholar] [CrossRef]
- Rycroft, C.H.; Grest, G.S.; Landry, J.W.; Bazant, M.Z. Analysis of granular flow in a pebble-bed nuclear reactor. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2006, 74, 021306. [Google Scholar] [CrossRef] [PubMed]
- Rycroft, C.H. Multiscale Modeling in Granular Flow. Ph.D. Thesis, Massachusetts Institute of Technology, Boston, MA, USA, September 2007. [Google Scholar]
- Rycroft, C.H. VORO++: A three-dimensional Voronoi cell library in C++. Chaos 2009, 19, 041111. [Google Scholar] [CrossRef] [PubMed]
- POV-Ray—The Persistence of Vision Raytracer. Available online: http://www.povray.org/ (accessed on 1 March 2017).
- Richard, P.; Oger, L.; Gervois, A.; Troadec, J.P. Tessellation of binary assemblies of spheres. Eur. Phys. J. E 2001, 6, 295–303. [Google Scholar] [CrossRef]
- Annic, C.; Troadec, J.; Gervois, A.; Lemaître, J.; Ammi, M.; Oger, L. Experimental study of radical tesselations of assemblies of discs with size distribution. J. Phys. I 1994, 4, 115–125. [Google Scholar] [CrossRef]
- Foulds, L.R. Graph Theory Applications; Springer: New York, NY, USA, 1992. [Google Scholar]
- Henle, M. A Combinatorial Introduction to Topology; W. H. Freeman & Co.: San Francisco, CA, USA, 1982. [Google Scholar]
- Zorin, D.N. Stationary Subdivision and Multiresolution Surface Representations. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1998. [Google Scholar]
- Liu, X.; Wang, S.; Wang, S.; Wang, E. Fluid-driven fractures in granular materials. Bull. Eng. Geol. Environ. 2015, 74, 621–636. [Google Scholar] [CrossRef]
- Guan, Y.; Liu, X.; Wang, E.; Wang, S. The stability analysis method of the cohesive granular slope on the basis of graph theory. Materials 2017, 10, 240. [Google Scholar] [CrossRef]
- Botsch, M.; Pauly, M.; Rössl, C.; Bischoff, S.; Kobbelt, L. Geometric modeling based on triangle meshes. In Proceedings of the ACM SIGGRAPH, Boston, MA, USA, 30 July–03 August 2006. [Google Scholar]
- Cundall, P.A.; Strack, O.D. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Dondi, G.; Simone, A.; Vignali, V.; Manganelli, G. Numerical and experimental study of granular mixes for asphalts. Powder Technol. 2012, 232, 31–40. [Google Scholar] [CrossRef]
- Itasca, C.G. PFC 3D-User Manual; Itasca Consulting Group: Minneapolis, MN, USA, 1999. [Google Scholar]
- Cho, N.; Martin, C.D.; Sego, D.C. A clumped particle model for rock. Int. J. Rock Mech. Min. Sci. 2007, 44, 997–1010. [Google Scholar] [CrossRef]
- Markauskas, D.; Kačianauskas, R. Compacting of particles for biaxial compression test by the discrete element method. J. Civ. Eng. Manag. 2006, 12, 153–161. [Google Scholar]
- Floyd, R.W. Algorithm 97: Shortest path. Commun. ACM 1962, 5, 345. [Google Scholar] [CrossRef]
- Camones, L.A.M.; do Amaral Vargas, E., Jr.; de Figueiredo, R.P.; Velloso, R.Q. Application of the discrete element method for modeling of rock crack propagation and coalescence in the step-path failure mechanism. Eng. Geol. 2013, 153, 80–94. [Google Scholar] [CrossRef]
- Scholtès, L.; Donzé, F.V. A DEM analysis of step-path failure in jointed rock slopes. Comptes Rendus Méc. 2015, 343, 155–165. [Google Scholar] [CrossRef]







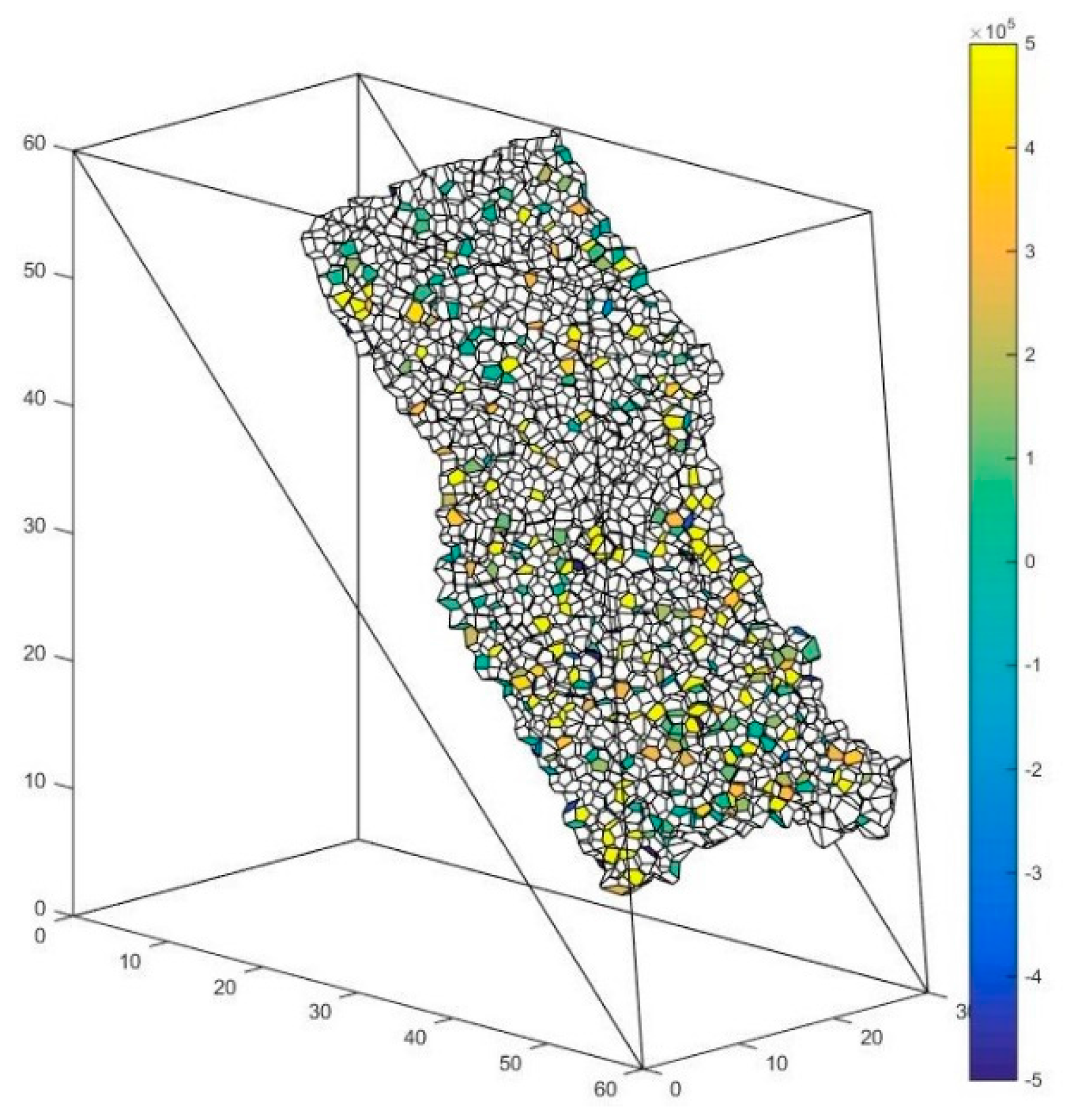
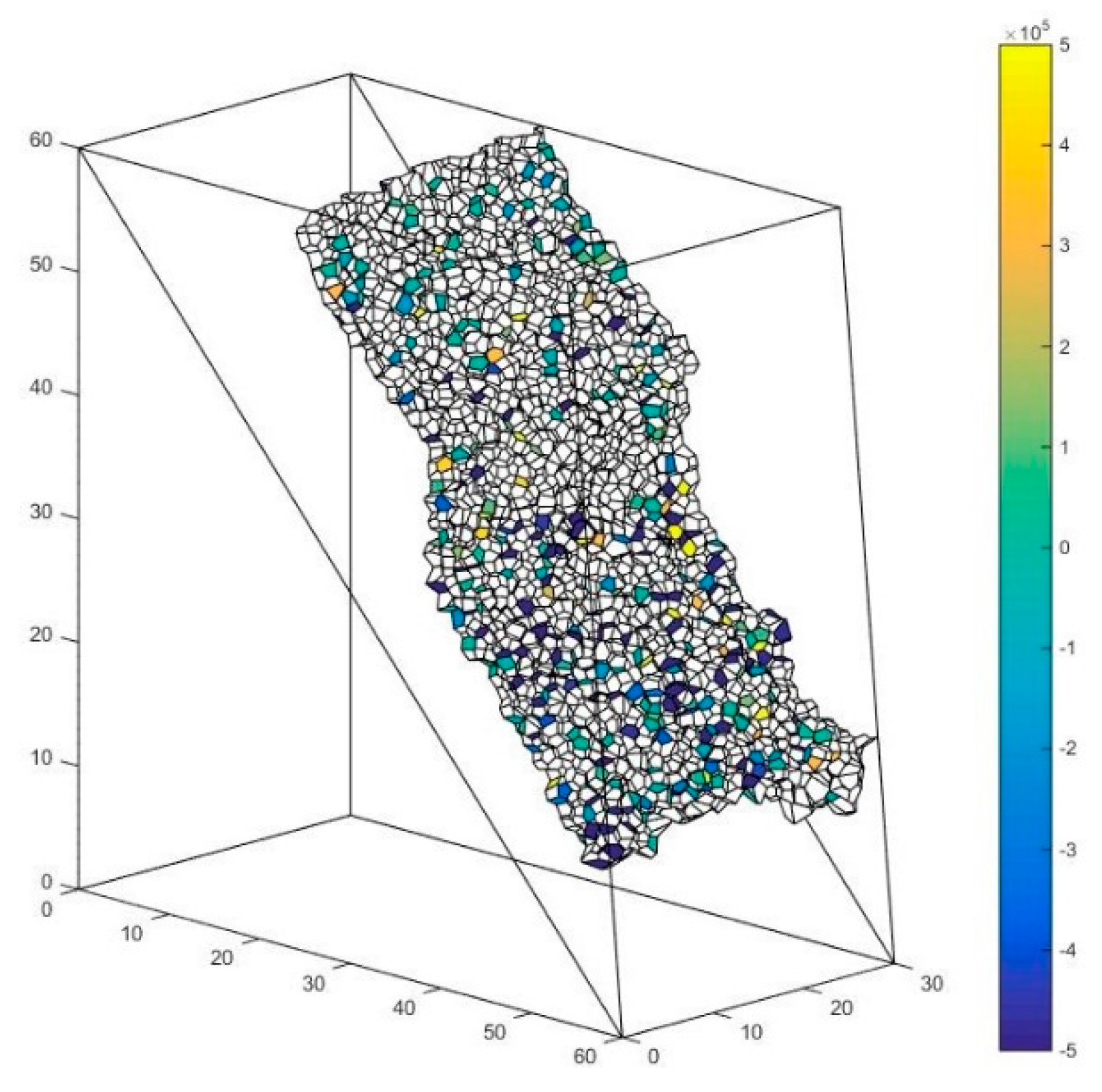
| - | Void Cell System | Solid Cell System |
|---|---|---|
| Particle | Vertex | body |
| (particle center) | (particle cell) | |
| Contact | Edge | Face |
| (particle connection) | (particle contact surface) | |
| Seepage path | Face | Edge |
| (seepage path section) | (seepage pipe) | |
| Void | Body | Vertex |
| (void cell) | (void center) |
| Mesoscopic Parameters | Values |
|---|---|
| Particle density | 2000 kg/m3 |
| Particle radius | 0.5 m–1.0 m |
| Normal contact stiffness | 5 × 108 N/m |
| Shear contact stiffness | 5 × 108 N/m |
| Friction coefficient of the particle surface | 0.1 |
| Normal parallel bond stiffness | 5 × 108 N/m |
| Shear parallel bond stiffness | 5 × 108 N/m |
| Normal parallel bond strength | 4.5 × 106 Pa |
| Shear parallel bond strength | 3.5 × 106 Pa |
| Marco Parameters | Values |
|---|---|
| Soil unit weight | 17 kN/m3 |
| Cohesion | 500 kPa |
| Internal friction angle | 15° |
| Elastic modulus | 300 MPa |
| Poisson’s ratio | 0.2 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, Y.; Wang, E.; Liu, X.; Wang, S.; Luan, H. The Quantified Characterization Method of the Micro-Macro Contacts of Three-Dimensional Granular Materials on the Basis of Graph Theory. Materials 2017, 10, 898. https://doi.org/10.3390/ma10080898
Guan Y, Wang E, Liu X, Wang S, Luan H. The Quantified Characterization Method of the Micro-Macro Contacts of Three-Dimensional Granular Materials on the Basis of Graph Theory. Materials. 2017; 10(8):898. https://doi.org/10.3390/ma10080898
Chicago/Turabian StyleGuan, Yanpeng, Enzhi Wang, Xiaoli Liu, Sijing Wang, and Hebing Luan. 2017. "The Quantified Characterization Method of the Micro-Macro Contacts of Three-Dimensional Granular Materials on the Basis of Graph Theory" Materials 10, no. 8: 898. https://doi.org/10.3390/ma10080898





