Thermoelectric Transport in Nanocomposites
Abstract
:1. Introduction to Thermoelectricity
2. Nanocomposites for Thermoelectricity
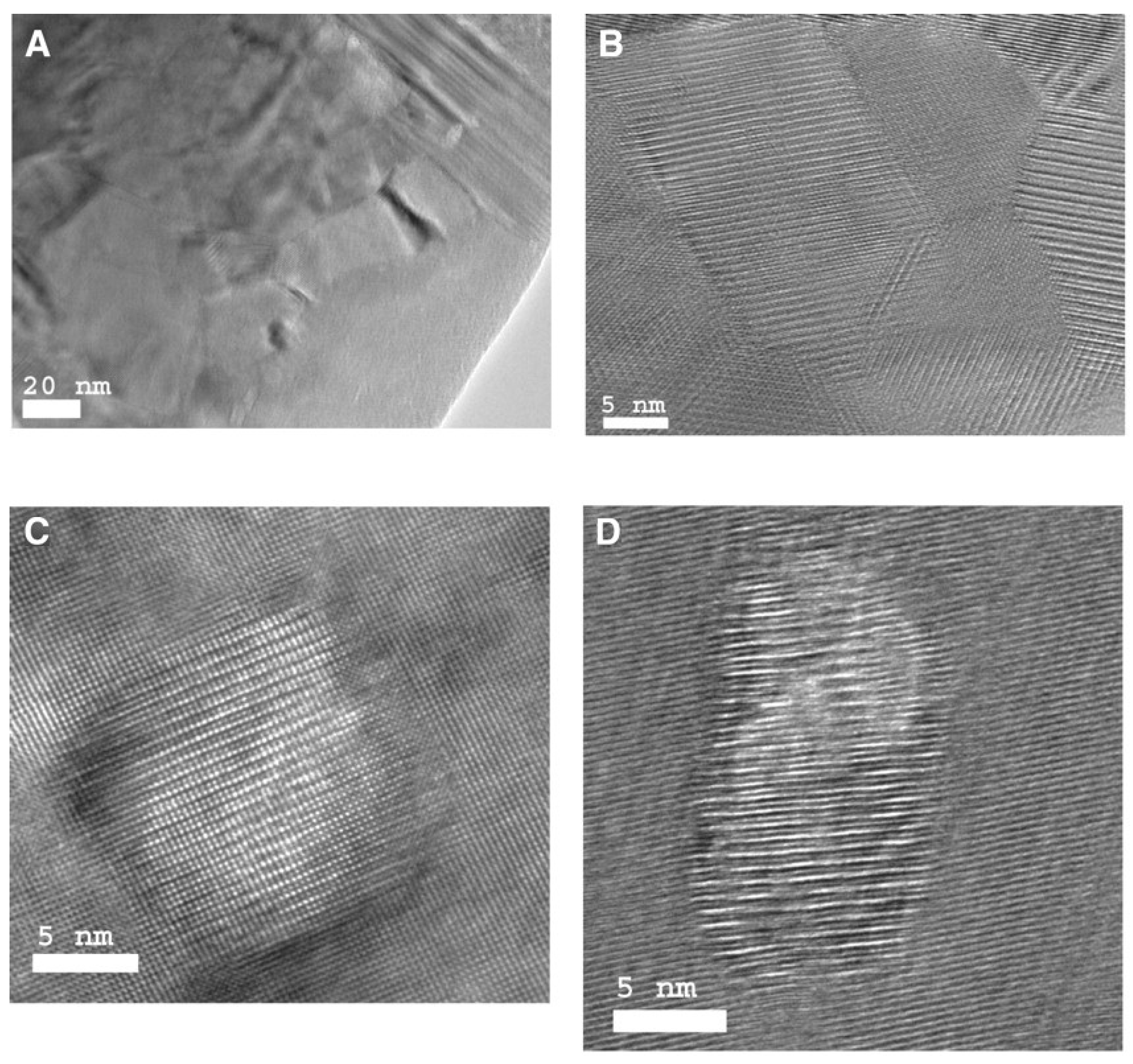
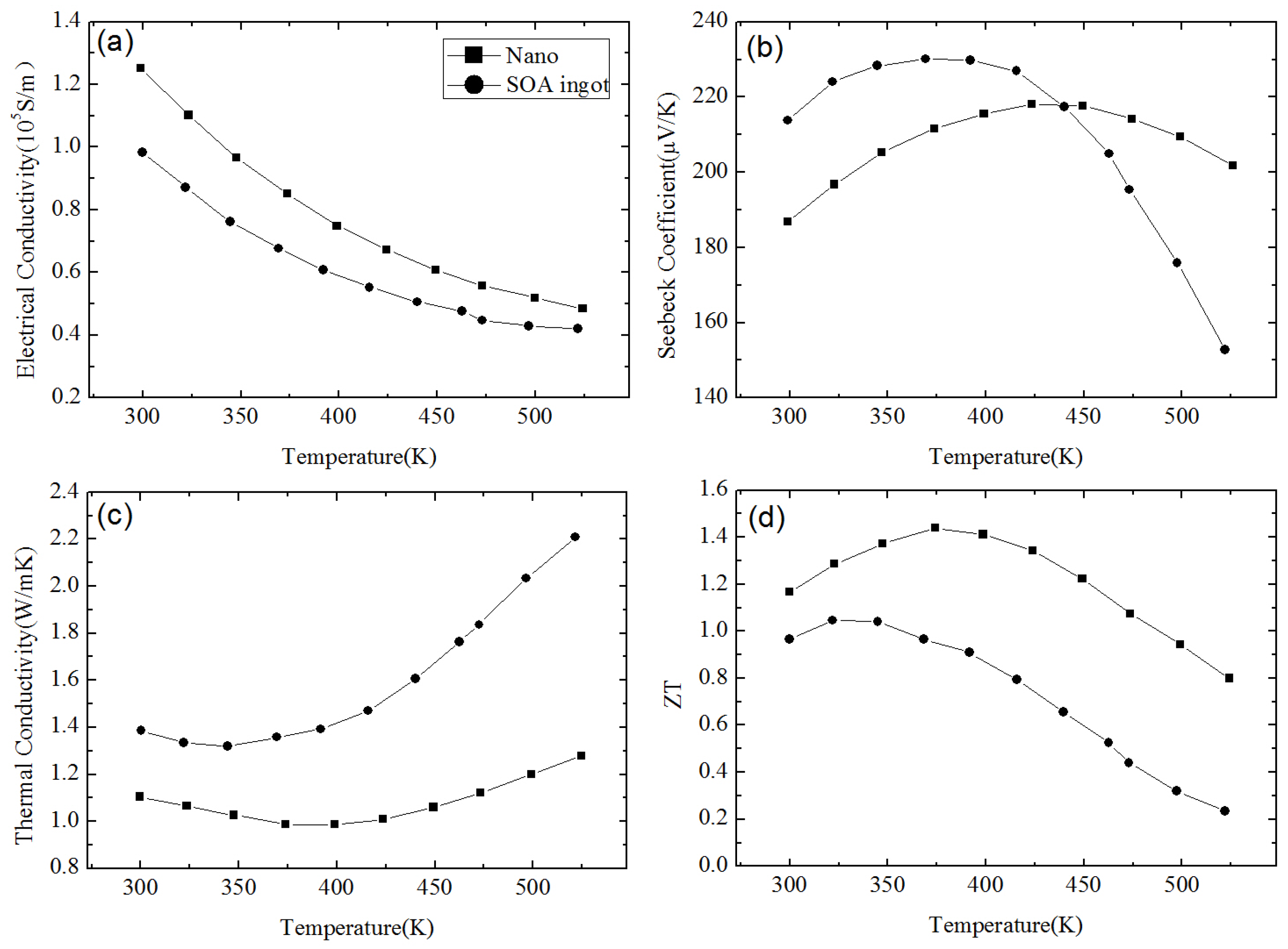
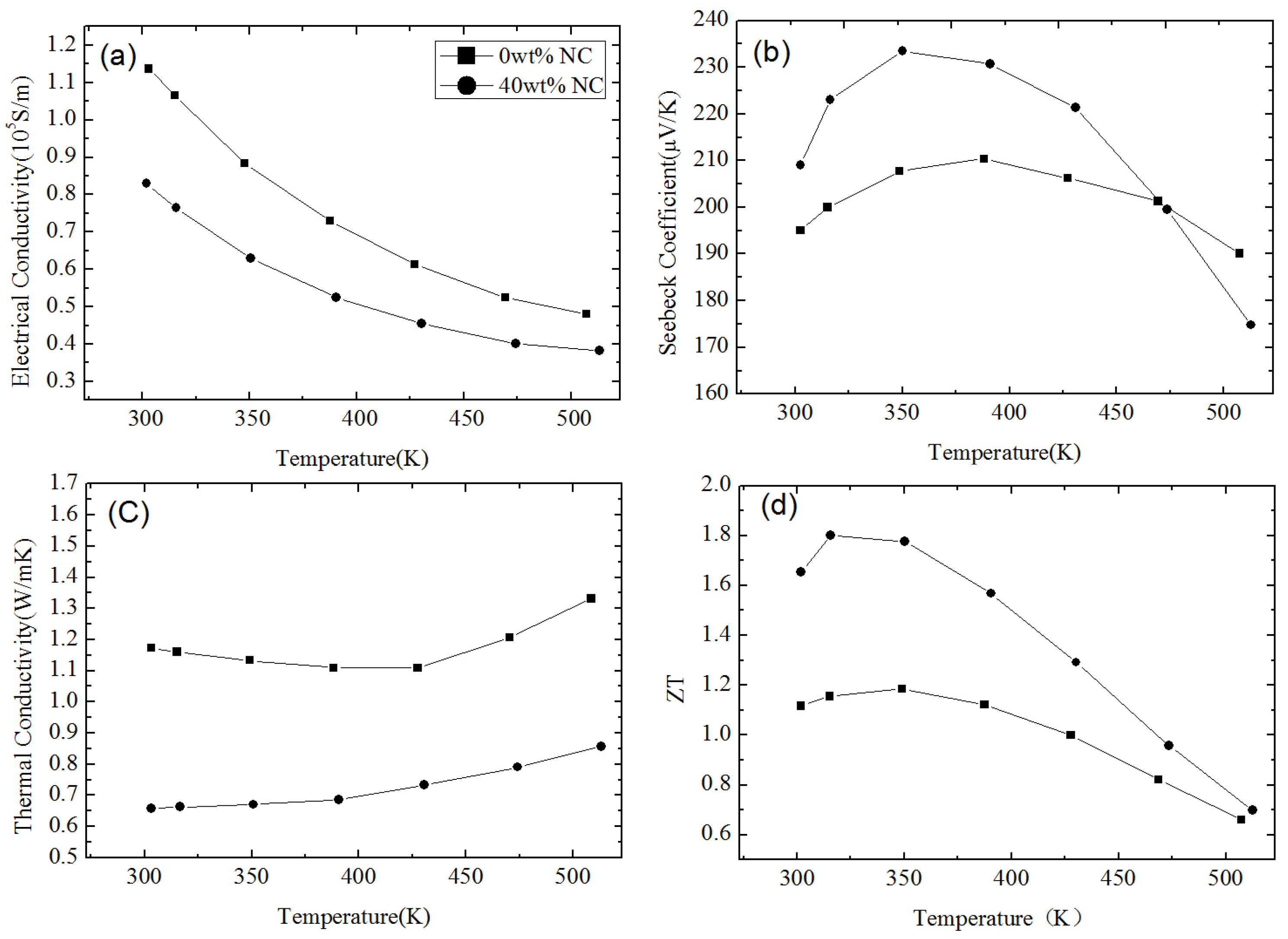
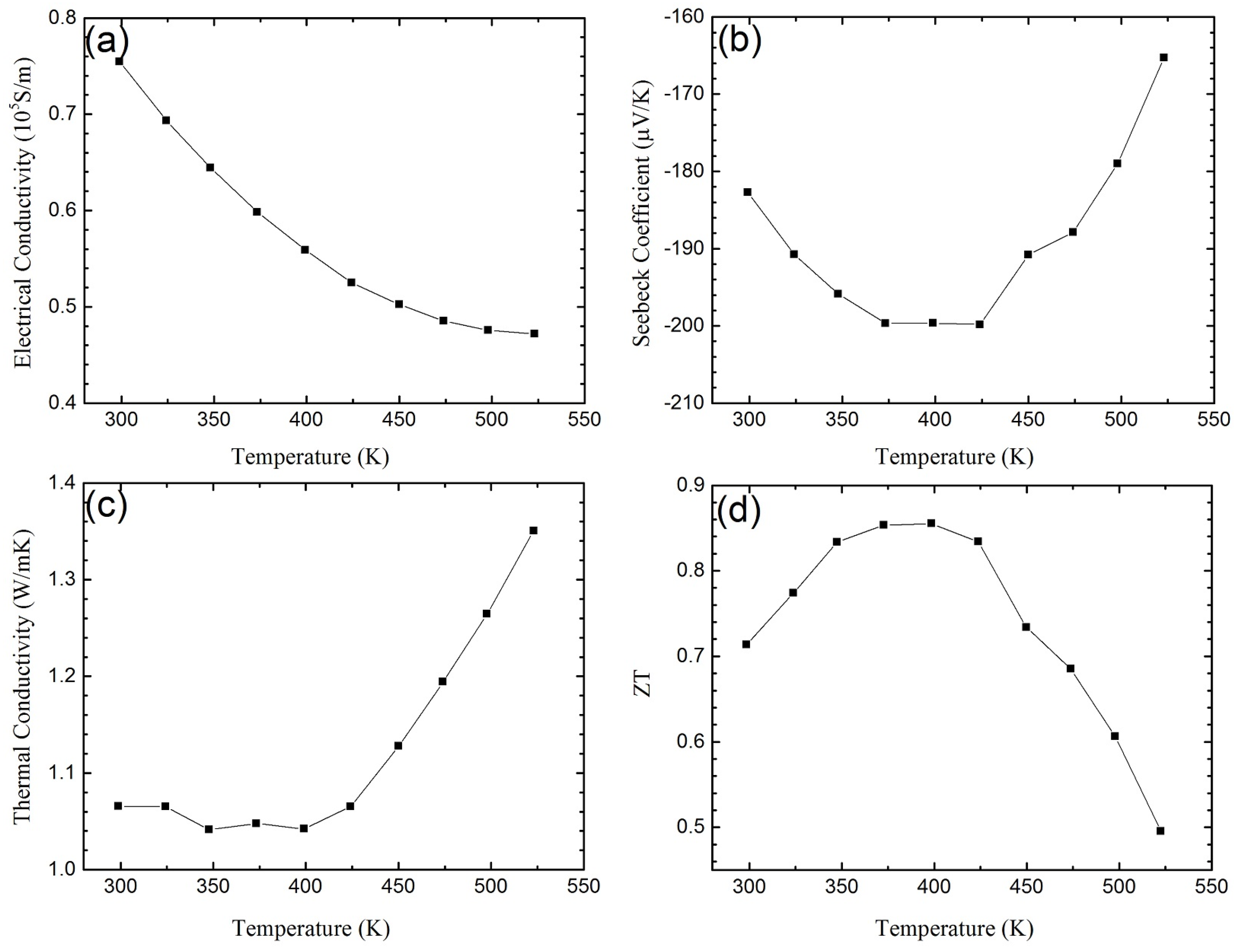
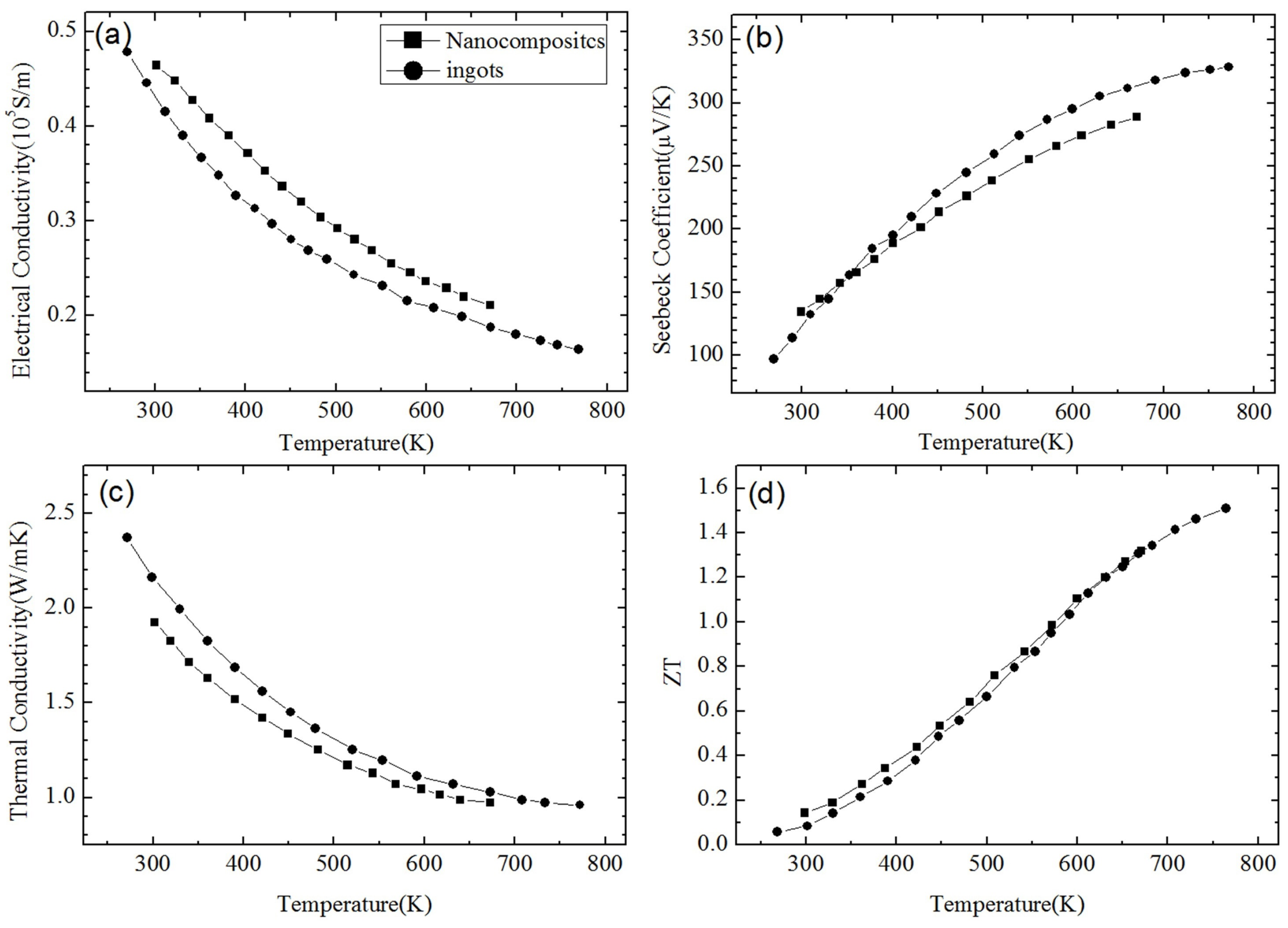
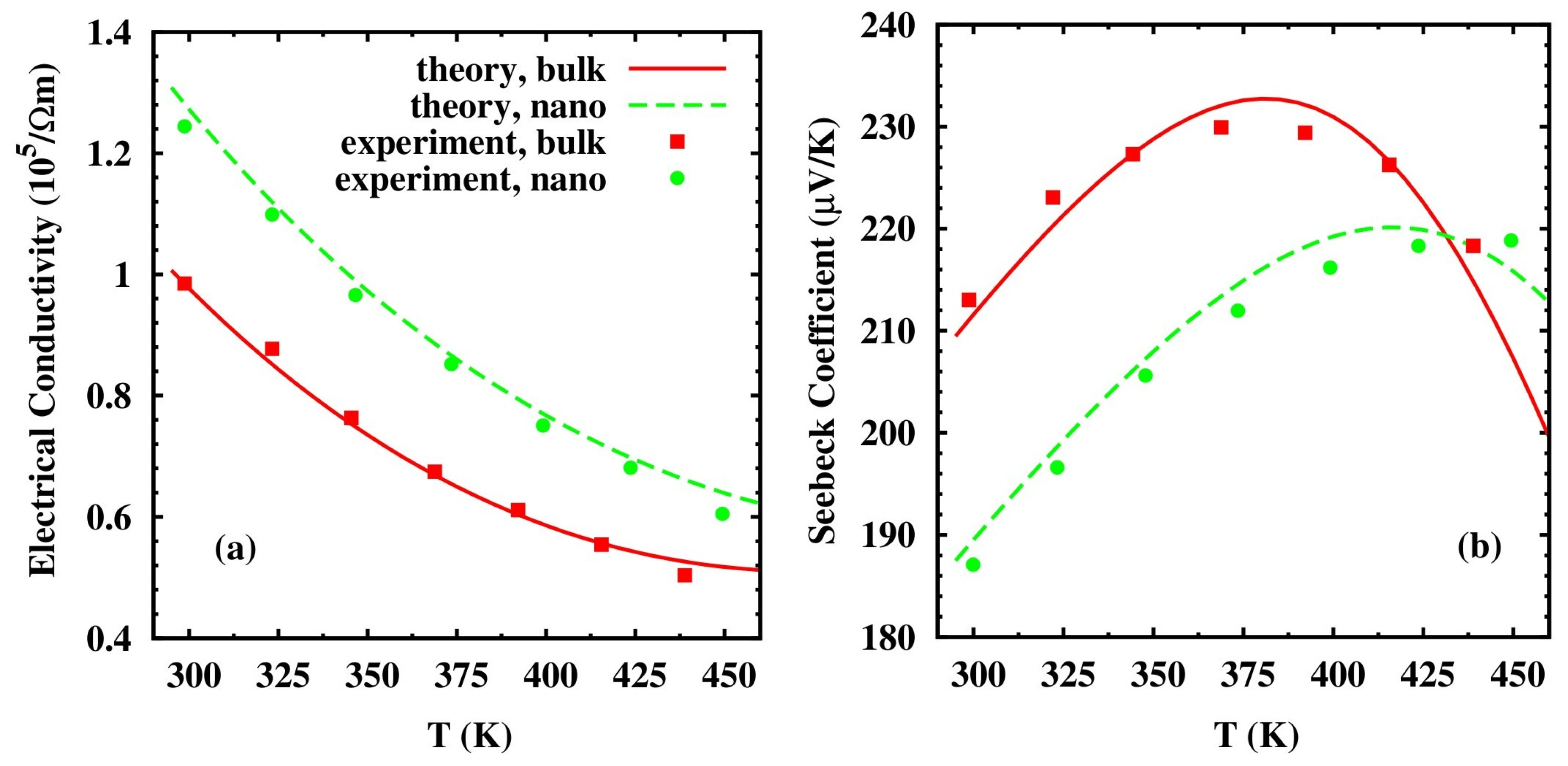
2.1. Bismuth Telluride Based Nanocomposites
2.2. Lead Telluride Based Nanocomposites
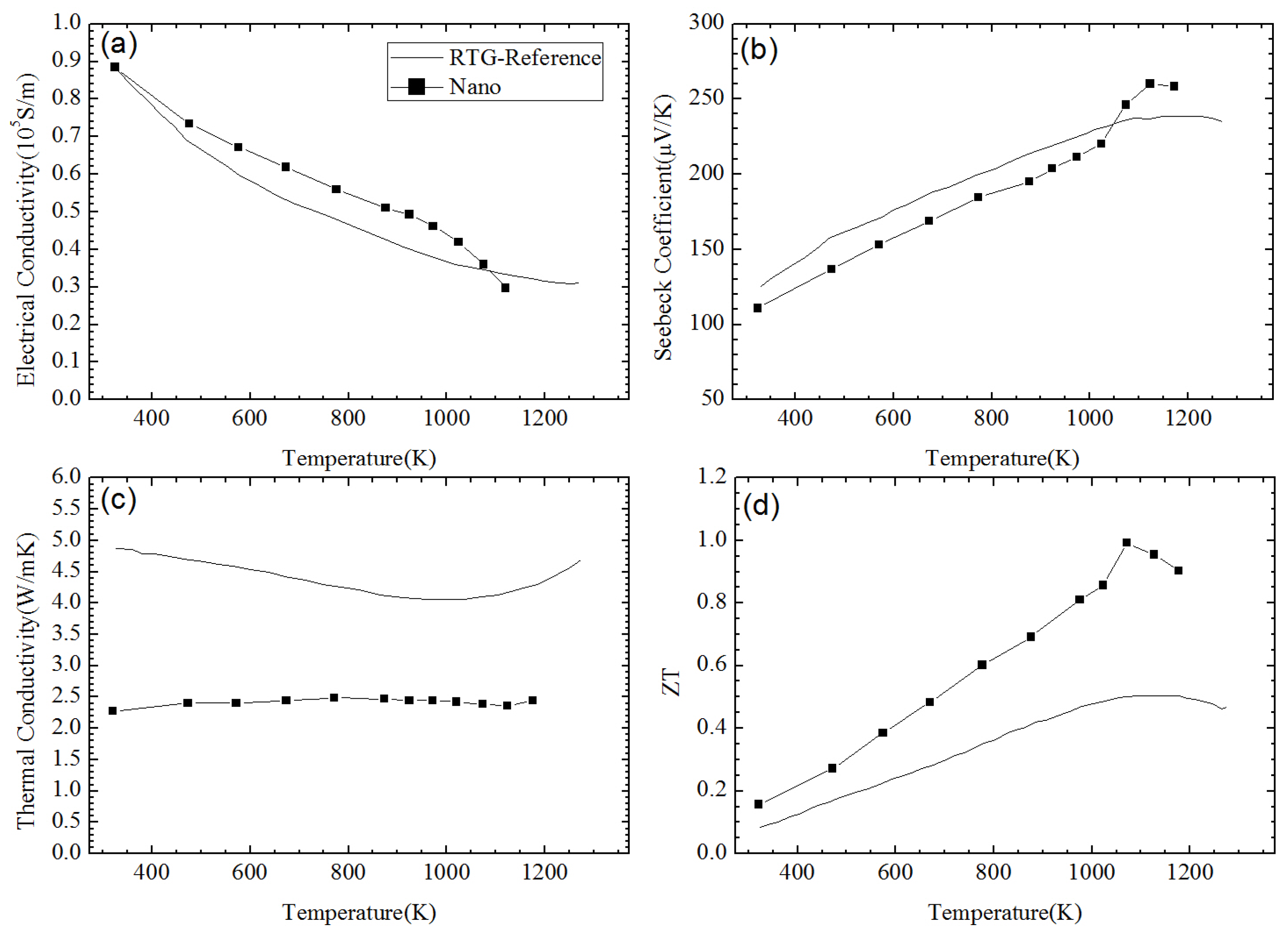
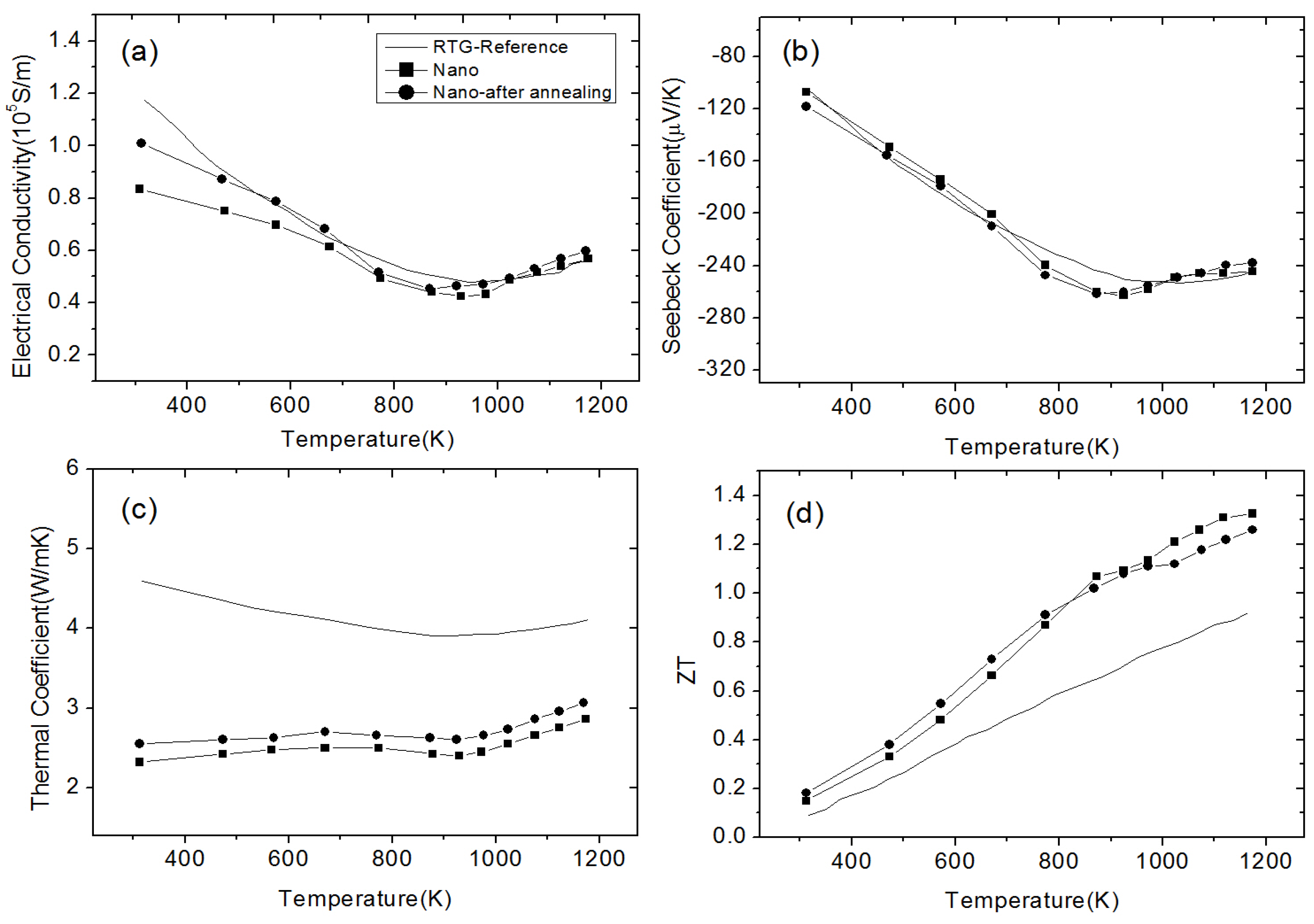
2.3. Silicon Germanium Based Nanocomposites
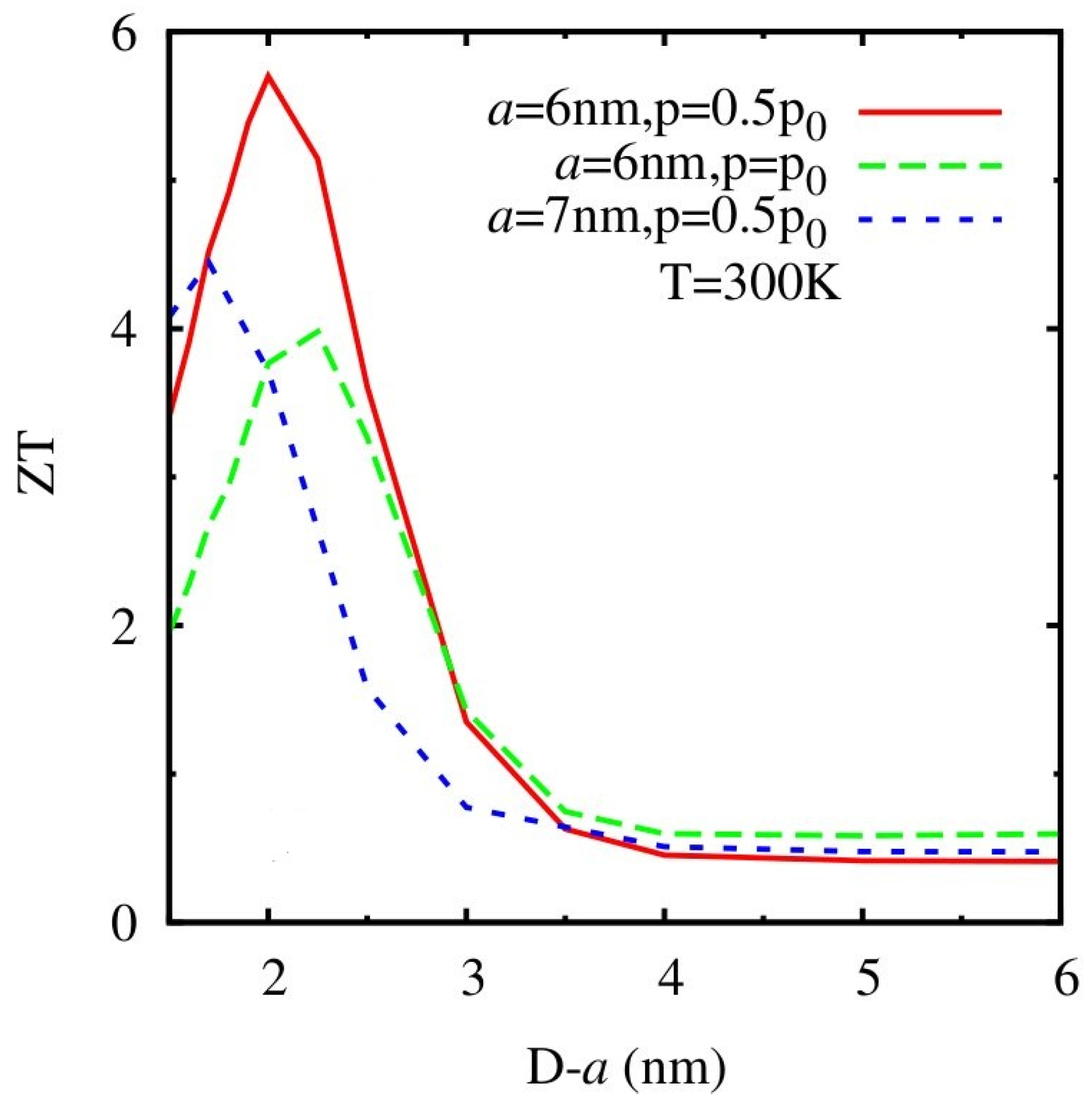
2.4. Other Nanocomposites
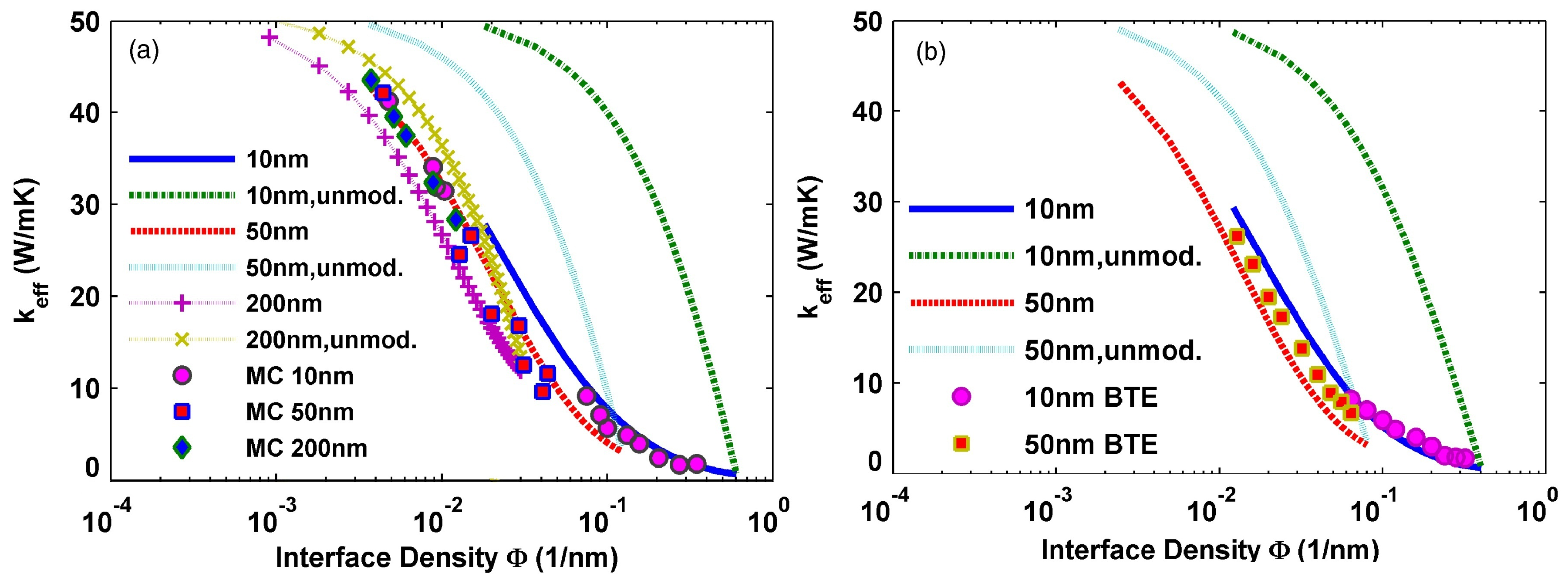
3. Modeling of Phonon Transport
4. Modeling of Electrical Carrier Transport
4.1. Boltzmann Transport Equations for Electrical Transport
4.2. Relaxation Time Model for Carrier-Interface Scattering
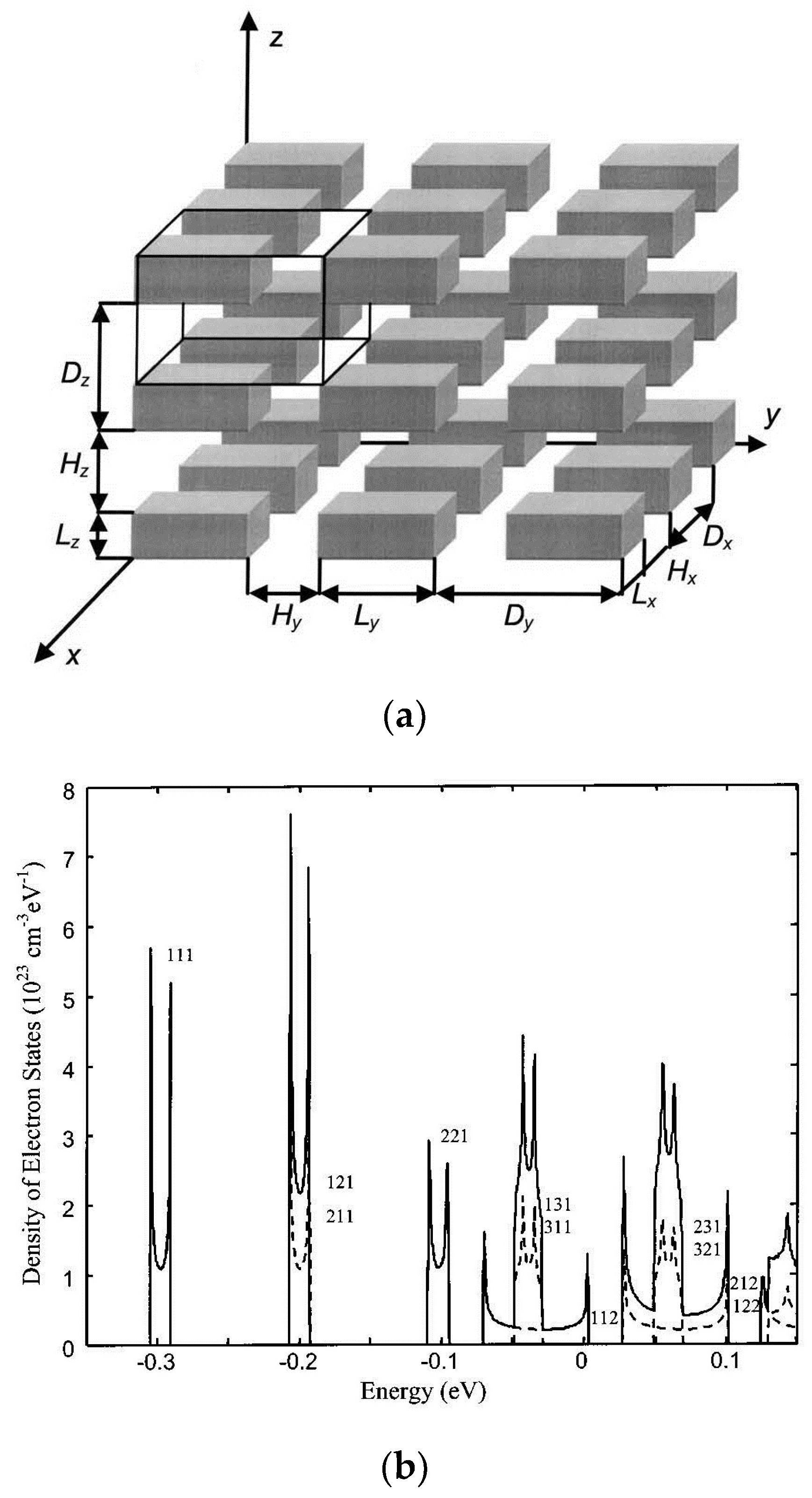
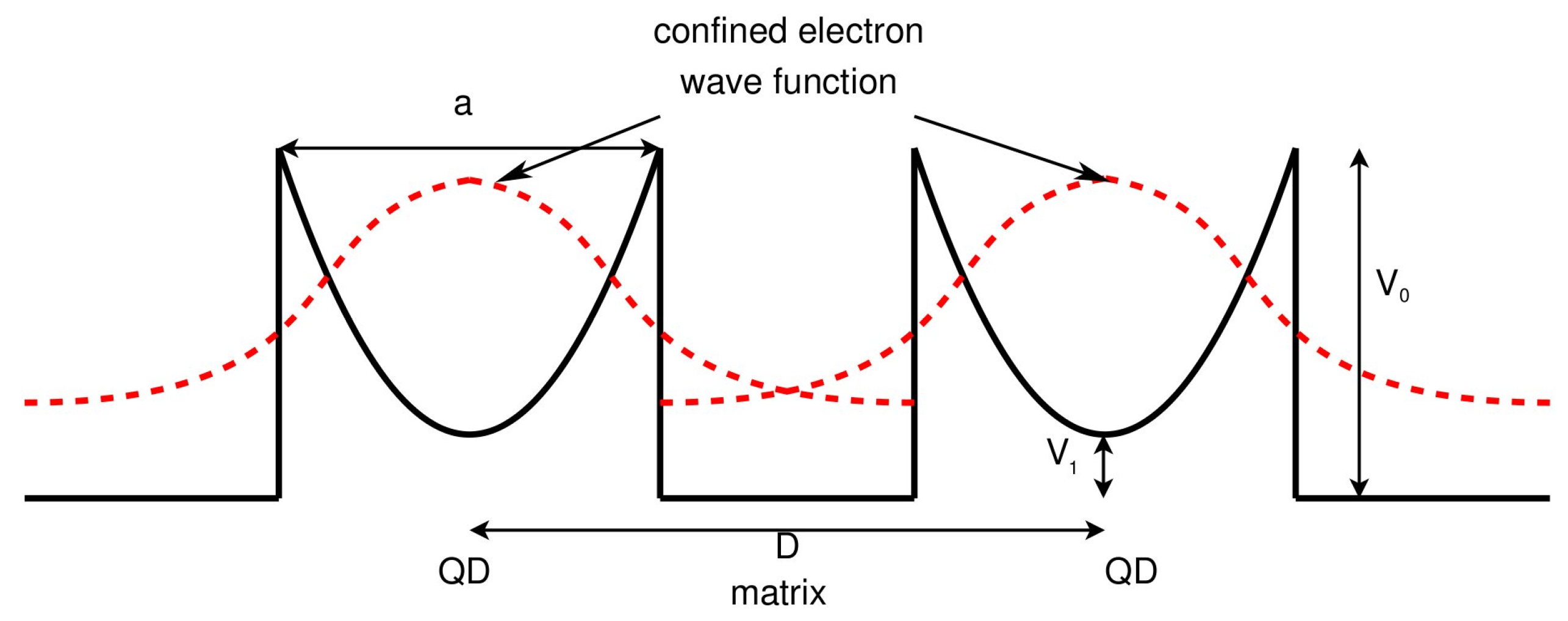
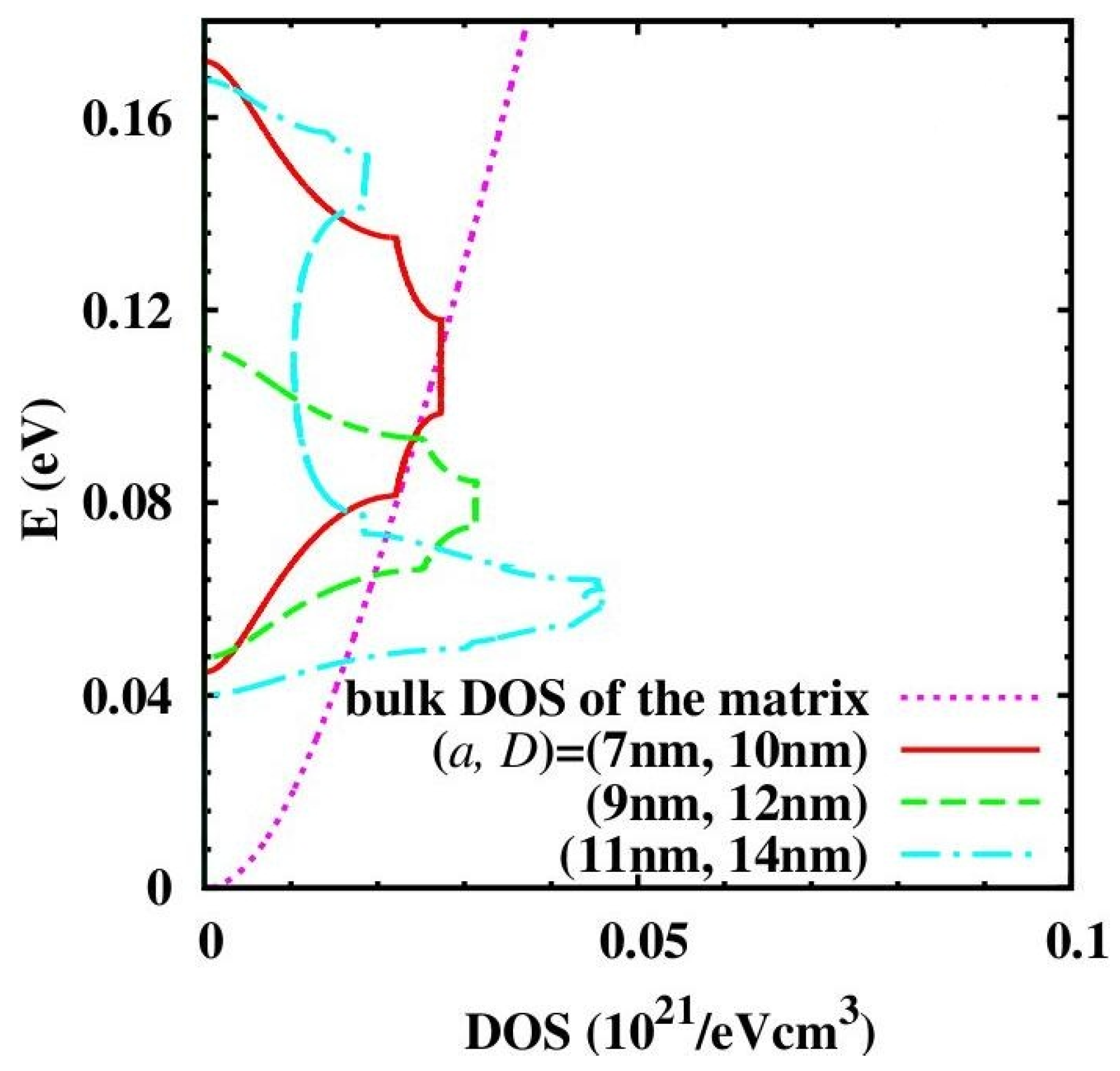
4.3. Band Structure and Relaxation Time Engineering in Nanocomposites
5. Summary
Acknowledgments
Conflicts of Interest
References
- Dresselhaus, M.S.; Chen, G.; Tang, M.Y.; Yang, R.G.; Lee, H.; Wang, D.Z.; Ren, Z.F.; Fleurial, J.P.; Gogna, P. New Directions for Low-Dimensional Thermoelectric Materials. Adv. Mater. 2007, 19, 1043–1053. [Google Scholar] [CrossRef]
- Snyder, G.J.; Toberer, E.S. Complex thermoelectric materials. Nat. Mater. 2008, 7, 105–114. [Google Scholar] [CrossRef] [PubMed]
- DiSalvo, F.J. Thermoelectric cooling and power generation. Science 1999, 285, 703–706. [Google Scholar] [CrossRef] [PubMed]
- Bell, L.E. Cooling, heating, generating power, and recovering waste heat with thermoelectric systems. Science 2008, 321, 1457–1461. [Google Scholar] [CrossRef] [PubMed]
- Tritt, T.M. Semiconductors and Semimetals, 1st ed.; Academic Press: San Diego, CA, USA, 2001. [Google Scholar]
- Ibáñez, M.; Luo, Z.; Genc, A.; Piveteau, L.; Ortega, S.; Cadavid, D.; Dobrozhan, O.; Liu, Y.; Nachtegaal, M.; Zebarjadi, M.; et al. High-performance thermoelectric nanocomposites from nanocrystal building blocks. Nat. Commun. 2016, 7, 10766. [Google Scholar] [CrossRef] [PubMed]
- Shi, X.; Chen, L.; Uher, C. Recent advances in high-performance bulk thermoelectric materials. Int. Mater. Rev. 2016, 61, 379–415. [Google Scholar] [CrossRef]
- Dehkordi, A.M.; Zebarjadi, M.; He, J.; Tritt, T.M. Thermoelectric power factor: Enhancement mechanisms and strategies for higher performance thermoelectric materials. Mater. Sci. Eng. R 2015, 97, 1–22. [Google Scholar] [CrossRef]
- Tan, G.J.; Zhao, L.D.; Kanatzidis, M.G. Rationally Designing High-Performance Bulk Thermoelectric Materials. Chem. Rev. 2016, 116, 12123–12149. [Google Scholar] [CrossRef] [PubMed]
- Zeier, W.G.; Zevalkink, A.; Gibbs, Z.M.; Hautier, G.; Kanatzidis, M.G.; Snyder, G.J. Thinking Like a Chemist: Intuition in Thermoelectric Materials. Angew. Chem. Int. Ed. 2016, 55, 6826–6841. [Google Scholar] [CrossRef] [PubMed]
- Goldsmid, H.J. Thermoelectric Refrigeration, 1st ed.; Plenum Press: New York, NY, USA, 1964. [Google Scholar]
- Rowe, D.M. General Principles and Basic Considerations. In Thermoelectric Handbook: Macro to Nano, 1st ed.; Rowe, D.M., Ed.; CRC Press: New York, NY, USA, 2006; pp. 1–14. [Google Scholar]
- Alam, H.; Ramakrishna, S. A review on the enhancement of figure of merit from bulk to nano-thermoelectric materials. Nano Energy 2013, 2, 190–212. [Google Scholar] [CrossRef]
- Scherrer, H.; Scherrer, S. Thermoelectric Properties of Bismuth Antimony Telluride Solid Solutions. In Thermoelectrics Handbook: Macro to Nano, 1st ed.; Rowe, D.M., Ed.; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Skrabek, E.A.; Trimmer, D.S. Properties of the General TAGS System. In CRC Handbook of Thermoelectrics, 1st ed.; Rowe, D.M., Ed.; CRC Press: Boca Raton, FL, USA, 1995; pp. 267–275. [Google Scholar]
- Pei, Y.Z.; Shi, X.Y.; LaLonde, A.; Wang, H.; Chen, L.D.; Snyder, G.J. Convergence of electronic bands for high performance bulk thermoelectrics. Nature 2011, 473, 66–69. [Google Scholar] [CrossRef] [PubMed]
- Vining, C.B.; Laskow, W.; Hanson, J.O.; van der Beck, R.R.; Gorsuch, P.D. Thermoelectric properties of pressure-sintered Si0. 8Ge0. 2 thermoelectric alloys. J. Appl. Phys. 1991, 69, 4333–4340. [Google Scholar] [CrossRef]
- Zaitsev, V.K.; Fedorov, M.I.; Eremin, I.S.; Gurieva, E.A. Thermoelectrics on the Base of Solid Solutions of Mg2BIV Compounds (BIV = Si, Ge, Sn). In Thermoelectrics Handbook: Macro to Nano, 1st ed.; Rowe, D.M., Ed.; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Luo, W.H.; Li, H.; Fu, F.; Hao, W.; Tang, X.F. Improved Thermoelectric Properties of Al-Doped Higher Manganese Silicide Prepared by a Rapid Solidification Method. J. Electron. Mater. 2011, 40, 1233–1237. [Google Scholar] [CrossRef]
- Zhou, A.J.; Zhu, T.J.; Zhao, X.B.; Yang, S.H.; Dasgupta, T.; Stiewe, C.; Hassdorf, R.; Mueller, E. Improved Thermoelectric Performance of Higher Manganese Silicides with Ge Additions. J. Electron. Mater. 2010, 39, 2002–2007. [Google Scholar] [CrossRef]
- He, J.; Xu, J.T.; Liu, G.Q.; Shao, H.Z.; Tan, X.J.; Liu, Z.; Xu, J.Q.; Jiang, H.C.; Jiang, J. Enhanced thermopower in rock-salt SnTe-CdTe from band convergence. RSC Adv. 2016, 6, 32189–32192. [Google Scholar] [CrossRef]
- Zhao, L.D.; Lo, S.H.; Zhang, Y.S.; Sun, H.; Tan, G.J.; Uher, C.; Wolverton, C.; Dravid, V.P.; Kanatzidis, M.G. Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals. Nature 2014, 508, 373–377. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Morelli, D.T.; Xia, Y.; Zhou, F.; Ozolins, V.; Chi, H.; Zhou, X.Y.; Uher, C. High Performance Thermoelectricity in Earth-Abundant Compounds Based on Natural Mineral Tetrahedrites. Adv. Energy Mater. 2013, 3, 342–348. [Google Scholar] [CrossRef]
- Shen, Q.; Chen, L.; Goto, T.; Hirai, T.; Yang, J.; Meisner, G.P.; Uher, C. Effects of partial substitution of Ni by Pd on the thermoelectric properties of ZrNiSn-based half-Heusler compounds. Appl. Phys. Lett. 2001, 79, 4165–4167. [Google Scholar] [CrossRef]
- Uher, C. Skutterudite-based Thermoelectrics. In Thermoelectrics Handbook: Macro to Nano, 1st ed.; Rowe, D.M., Ed.; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Cohn, J.L.; Nolas, G.S.; Fessatidis, V.; Metcalf, T.H.; Slack, G.A. Glasslike heat conduction in high-mobility crystalline semiconductors. Phys. Rev. Lett. 1999, 82, 779–782. [Google Scholar] [CrossRef]
- Chung, D.Y.; Hogan, T.; Brazis, P.; Rocci-Lane, M.; Kannewurf, C.; Bastea, M.; Uher, C.; Kanatzidis, M.G. CsBi4Te6: A high-performance thermoelectric material for low-temperature applications. Science 2000, 287, 1024–1027. [Google Scholar] [CrossRef] [PubMed]
- Wölfing, B.; Kloc, C.; Teubner, J.; Bucher, E. High performance thermoelectric Tl9BiTe6 with an extremely low thermal conductivity. Phys. Rev. Lett. 2001, 86, 4350–4353. [Google Scholar] [CrossRef] [PubMed]
- Rhyee, J.; Lee, K.H.; Lee, S.M.; Cho, E.; Kim, S.I.; Lee, E.; Kwon, Y.S.; Shim, J.H.; Kotliar, G. Peierls distortion as a route to high thermoelectric performance in In4Se3−δ; crystals. Nature 2009, 459, 965–968. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.L.; Shi, X.; Xu, F.F.; Zhang, L.L.; Zhang, W.Q.; Chen, L.D.; Li, Q.; Uher, C.; Day, T.; Snyder, G.J. Copper ion liquid-like thermoelectrics. Nat. Mater. 2012, 11, 422–425. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Wang, X.; Wang, J.; Cheng, Z.; Dou, S.; Wang, J.; Liu, L. Superior intrinsic thermoelectric performance with zT of 1.8 in single-crystal and melt-quenched highly dense Cu2−xSe bulks. Sci. Rep. 2015, 5, 7671. [Google Scholar] [CrossRef] [PubMed]
- Hochbaum, A.I.; Chen, R.K.; Delgado, R.D.; Liang, W.J.; Garnett, E.C.; Najarian, M.; Majumdar, A.; Yang, P.D. Enhanced thermoelectric performance of rough silicon nanowires. Nature 2008, 451, 163–167. [Google Scholar] [CrossRef] [PubMed]
- Boukai, A.I.; Bunimovich, Y.; Tahir-Kheli, J.; Yu, J.; Goddard, W.A., III; Heath, J.R. Silicon nanowires as efficient thermoelectric materials. Nature 2008, 451, 168–171. [Google Scholar] [CrossRef] [PubMed]
- Hung, N.T.; Hasdeo, E.H.; Nugraha, A.R.T.; Dresselhaus, M.S.; Saito, R. Quantum Effects in the Thermoelectric Power Factor of Low-Dimensional Semiconductors. Phys. Rev. Lett. 2016, 117, 036602. [Google Scholar] [CrossRef] [PubMed]
- Venkatasubramanian, R.; Siivola, E.; Colpitts, T.; O’Quinn, B. Thin-film thermoelectric devices with high room-temperature figures of merit. Nature 2001, 413, 597–602. [Google Scholar] [CrossRef] [PubMed]
- Harman, T.C.; Taylor, P.J.; Walsh, M.P.; LaForge, B.E. Quantum dot superlattice thermoelectric materials and devices. Science 2002, 297, 2229–2232. [Google Scholar] [CrossRef] [PubMed]
- Mahan, G.D. Good thermoelectrics. Solid State Phys. 1997, 51, 81–157. [Google Scholar]
- Gudelli, V.K.; Kanchana, V.; Vaitheeswaran, G.; Singh, D.J.; Svane, A.; Christensen, N.E.; Mahanti, S.D. Electronic structure, transport, and phonons of SrAgChF (Ch = S, Se, Te): Bulk superlattice thermoelectrics. Phys. Rev. B 2015, 92, 045206. [Google Scholar] [CrossRef]
- Lin, Y.M.; Dresselhaus, M.S. Thermoelectric properties of superlattice nanowires. Phys. Rev. B 2003, 68, 075304. [Google Scholar] [CrossRef]
- Heremans, J.; Thrush, C.M.; Lin, Y.M.; Cronin, S.; Zhang, Z.; Dresselhaus, M.S.; Mansfield, J.F. Bismuth nanowire arrays: Synthesis and galvanomagnetic properties. Phys. Rev. B 2000, 61, 2921–2930. [Google Scholar] [CrossRef]
- Hicks, L.D.; Dresselhaus, M.S. Effect of quantum-well structures on the thermoelectric figure of merit. Phys. Rev. B 1993, 47, 12727–12731. [Google Scholar] [CrossRef]
- Mao, J.; Liu, Z.; Ren, Z. Size effect in thermoelectric materials. npj Quantum Mater. 2016, 1, 16028. [Google Scholar] [CrossRef]
- Heremans, J.P.; Jovovic, V.; Toberer, E.S.; Saramat, A.; Kurosaki, K.; Charoenphakdee, A.; Yamanaka, S.; Snyder, G.J. Enhancement of Thermoelectric Efficiency in PbTe by Distortion of the Electronic Density of States. Science 2008, 321, 554–557. [Google Scholar] [CrossRef] [PubMed]
- Moizhes, B.Y.; Nemchinsky, V.A. Proceeding of 11th International Conference on Thermoelectrics; University of Texas Press: Arlington, TX, USA, 1992; pp. 232–235. [Google Scholar]
- Rowe, D.M. CRC Handbook of Thermoelectrics; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Zianni, X.; Narducci, D. Parametric modeling of energy filtering by energy barriers in thermoelectric nanocomposites. J. Appl. Phys. 2015, 117, 035102. [Google Scholar] [CrossRef]
- Thiagarajan, S.J.; Wang, W.; Yang, R.G. Nanocomposites as High Efficiency Thermoelectric Materials. In Annual Review of Nano Research, 1st ed.; Cao, G.Z., Zhang, Q.F., Brinker, C.J., Eds.; World Scientific Publisher Co.: Singapore, 2009; pp. 447–492. [Google Scholar]
- Lan, Y.C.; Minnich, A.J.; Chen, G.; Ren, Z.F. Enhancement of Thermoelectric Figure-of-Merit by a Bulk Nanostructuring Approach. Adv. Funct. Mater. 2010, 20, 357–376. [Google Scholar] [CrossRef]
- Korkosz, R.J.; Chasapis, T.C.; Lo, S.; Doak, J.W.; Kim, Y.H.; Wu, C.-I.; Hatzikraniotis, E.; Hogan, T.P.; Seidman, D.N.; Wolverton, C.; et al. High ZT in p-Type (PbTe)1–2x(PbSe)x(PbS)x Thermoelectric Materials. J. Am. Chem. Soc. 2014, 136, 3225–3237. [Google Scholar] [CrossRef] [PubMed]
- Medlin, D.L.; Snyder, G.J. Interfaces in bulk thermoelectric materials: A review for current opinion in colloid and interface science. Curr. Opin. Colloid Interface Sci. 2009, 14, 226–235. [Google Scholar] [CrossRef]
- Goldsmid, H.J. Bismuth telluride and its alloys as materials for thermoelectric generation. Materials 2014, 7, 2577–2592. [Google Scholar] [CrossRef]
- Zhang, C.; Peng, Z.; Li, Z.; Yu, L.; Khor, K.A.; Xiong, Q. Controlled growth of bismuth antimony telluride BixSb2−xTe3 nanoplatelets and their bulk thermoelectric nanocomposites. Nano Energy 2015, 15, 688–696. [Google Scholar] [CrossRef]
- Min, Y.; Roh, J.W.; Yang, H.; Park, M.; Kim, S., II; Hwang, S.; Lee, S.M.; Lee, K.H.; Jeong, U. Surfactant-Free Scalable Synthesis of Bi2Te3 and Bi2Se3 Nanoflakes and Enhanced Thermoelectric Properties of Their Nanocomposites. Adv. Mater. 2013, 25, 1425–1429. [Google Scholar] [CrossRef] [PubMed]
- Poudel, B.; Hao, Q.; Ma, Y.; Lan, Y.C.; Minnich, A.; Yu, B.; Yan, X.; Wang, D.Z.; Muto, A.; Vashaee, D.; et al. High-thermoelectric performance of nanostructured bismuth antimony telluride bulk alloys. Science 2008, 320, 634–638. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Hao, Q.; Poudel, B.; Lan, Y.C.; Yu, B.; Wang, D.Z.; Chen, G.; Ren, Z.F. Enhanced thermoelectric figure-of-merit in p-type nanostructured bismuth antimony tellurium alloys made from elemental chunks. Nano Lett. 2008, 8, 2580–2584. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.Q.; Zhao, X.B.; Zhu, T.J.; Zhang, X.B.; Tu, J.P. Syntheses and thermoelectric properties of Bi2Te3/Sb2Te3 bulk nanocomposites with laminated nanostructure. Appl. Phys. Lett. 2008, 92, 143106. [Google Scholar] [CrossRef]
- Li, Y.; Dou, Y.; Qin, X.; Zhang, J.; Xin, H.; Li, D.; Song, C.; Zou, T.; Liu, Y.; Li, C. Enhanced thermoelectric figure of merit in p-type β-Zn4Sb3/Bi0.4Sb1.6Te3 nanocomposites. RSC Adv. 2016, 6, 12243–12248. [Google Scholar] [CrossRef]
- Li, Y.Y.; Liu, G.X.; Qin, X.Y.; Shan, F.K. Inhibition of minority transport for elevating the thermoelectric figure of merit of CuO/BiSbTe nanocomposites at high temperatures. RSC Adv. 2016, 6, 112050–112056. [Google Scholar] [CrossRef]
- Xie, W.J.; Tang, X.F.; Yan, Y.G.; Zhang, Q.J.; Tritt, T.M. Unique nanostructures and enhanced thermoelectric performance of melt-spun BiSbTe alloys. Appl. Phys. Lett. 2009, 94, 102111. [Google Scholar] [CrossRef]
- Xie, W.J.; He, J.; Kang, H.J.; Tang, X.F.; Zhu, S.; Laver, M.; Wang, S.Y.; Copley, J.R.D.; Brown, C.M.; Zhang, Q.J.; Tritt, T.M. Identifying the specific nanostructures responsible for the high thermoelectric performance of (Bi, Sb)2Te3 nanocomposites. Nano Lett. 2010, 10, 3283–3289. [Google Scholar] [CrossRef] [PubMed]
- Dou, Y.C.; Qin, X.Y.; Li, D.; Li, L.L.; Zou, T.H.; Wang, Q.Q. Enhanced thermopower and thermoelectric performance through energy filtering of carriers in (Bi2Te3)0.2(Sb2Te3)0.8 bulk alloy embedded with amorphous SiO2 nanoparticles. J. Appl. Phys. 2013, 114, 044906. [Google Scholar] [CrossRef]
- Li, Y.Y.; Qin, X.Y.; Li, D.; Zhang, J.; Li, C.; Liu, Y.F.; Song, C.J.; Xin, H.X.; Guo, H.F. Enhanced thermoelectric performance of Cu2Se/Bi0.4Sb1.6Te3 nanocomposites at elevated temperatures. Appl. Phys. Lett. 2016, 108, 062104. [Google Scholar] [CrossRef]
- Fan, S.F.; Zhao, J.N.; Guo, J.; Yan, Q.Y.; Ma, J.; Hng, H.H. p-type Bi0.4Sb1.6Te3 nanocomposites with enhanced figure of merit. Appl. Phys. Lett. 2010, 96, 182104. [Google Scholar] [CrossRef]
- Ebling, D.G.; Jacquot, A.; Böttner, H.; Kirste, L.; Schmidt, J.; Aguirre, M. Influence of Group IV-Te Alloying on Nanocomposite Structure and Thermoelectric Properties of Bi2Te3 Compounds. J. Electron. Mater. 2009, 38, 1450–1455. [Google Scholar] [CrossRef]
- Yan, X.; Poudel, B.; Ma, Y.; Liu, W.S.; Joshi, G.; Wang, H.; Lan, Y.C.; Wang, D.Z.; Chen, G.; Ren, Z.F. Experimental Studies on Anisotropic Thermoelectric Properties and Structures of n-Type Bi2Te2.7Se0.3. Nano Lett. 2010, 10, 3373–3378. [Google Scholar] [CrossRef] [PubMed]
- Dirmyer, M.R.; Martin, J.; Nolas, G.S.; Sen, A.; Badding, J.V. Thermal and Electrical Conductivity of Size-Tuned Bismuth Telluride Nanoparticles. Small 2009, 5, 933–937. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Chen, R.; Fan, X.; Bao, S.; Zhu, W. Thermoelectric properties of silver-doped n-type Bi2Te3-based material prepared by mechanical alloying and subsequent hot pressing. J. Alloy. Compd. 2006, 407, 330–333. [Google Scholar] [CrossRef]
- Yang, J.Y.; Fan, X.A.; Chen, R.G.; Zhu, W.; Bao, S.Q.; Duan, X.K. Consolidation and thermoelectric properties of n-type bismuth telluride based materials by mechanical alloying and hot pressing. J. Alloy. Compd. 2006, 416, 270–273. [Google Scholar] [CrossRef]
- Jiang, Q.H.; Yang, J.Y.; Liu, Y.; He, H.C. Microstructure tailoring in nanostructured thermoelectric materials. J. Adv. Dielectr. 2016, 6, 1630002. [Google Scholar] [CrossRef]
- Fang, H.; Bahk, J.-H.; Feng, T.; Cheng, Z.; Mohammed, A.M.S.; Wang, X.; Ruan, X.; Shakouri, A.; Wu, Y. Thermoelectric Properties of Solution Synthesized n-Type Bi2Te3 Nanocomposites Modulated by Se: An Experimental and Theoretical Study. Nano Res. 2016, 9, 117–127. [Google Scholar] [CrossRef]
- Soni, A.; Zhao, Y.Y.; Yu, L.G.; Aik, M.K.K.; Dresselhaus, M.S.; Xiong, Q.H. Enhanced Thermoelectric Properties of Solution Grown Bi2Te3–xSex Nanoplatelet Composites. Nano Lett. 2012, 12, 1203–1209. [Google Scholar] [CrossRef] [PubMed]
- Soni, A.; Shen, Y.Q.; Yin, M.; Zhao, Y.Y.; Yu, L.G.; Hu, X.; Dong, Z.L.; Khor, K.A.; Dresselhaus, M.S.; Xiong, Q.H. Interface driven energy filtering of thermoelectric power in spark plasma sintered Bi2Te2.7Se0.3 nanoplatelet composites. Nano Lett. 2012, 12, 4305–4310. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.H.; Mata, M.D.L.; Li, Z.; Belarre, F.J.; Arbiol, J.; Khor, K.A.; Poletti, D.P.; Zhu, B.B.; Yan, Q.Y.; Xiong, Q.H. Enhanced thermoelectric performance of solution-derived bismuth telluride based nanocomposites via liquid-phase Sintering. Nano Energy 2016, 30, 630–638. [Google Scholar] [CrossRef]
- Hsu, K.F.; Loo, S.; Guo, F.; Chen, W.; Dyck, J.S.; Uher, C.; Hogan, T.; Polychroniadis, E.K.; Kanatzidis, M.G. Cubic AgPbmSbTe2+m: Bulk thermoelectric materials with high figure of merit. Science 2004, 303, 818–821. [Google Scholar] [CrossRef] [PubMed]
- Ke, X.Z.; Chen, C.F.; Yang, J.H.; Wu, L.J.; Zhou, J.; Li, Q.; Zhu, Y.M.; Kent, P.R.C. Microstructure and a Nucleation Mechanism for Nanoprecipitates in PbTe-AgSbTe2. Phys. Rev. Lett. 2009, 103, 145502. [Google Scholar] [CrossRef] [PubMed]
- Quarez, E.; Hsu, K.F.; Pcionek, R.; Frangis, N.; Polychroniadis, E.K.; Kanatzidis, M.G. Nanostructuring, Compositional Fluctuations, and Atomic Ordering in the Thermoelectric Materials AgPbmSbTe2+m. The Myth of Solid Solutions. J. Am. Chem. Soc. 2005, 127, 9177–9190. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Li, J.F.; Nan, C.W.; Zhou, M.; Liu, W.S.; Zhang, Z.B.-P.; Kita, T. High-performance Ag0.8Pb18SbTe20 thermoelectric bulk materials fabricated by mechanical alloying and spark plasma sintering. Appl. Phys. Lett. 2006, 88, 092104. [Google Scholar] [CrossRef]
- Paul, B.; Ajay, K.V.; Banerji, P. Embedded Ag-rich nanodots in PbTe: Enhancement of thermoelectric properties through energy filtering of the carriers. J. Appl. Phys. 2010, 108, 064322. [Google Scholar] [CrossRef]
- Yu, B.; Wang, H.; Poudel, B.; McEnaney, K.; Chen, G.; Ren, Z. Thermoelectric Figure-of-Merit in Bulk p-type PbTe. In Proceedings of the APS March Meeting, Pittsburgh, PA, USA, 16–20 March 2009. [Google Scholar]
- Wang, H.C.; Hwang, J.; Snedaker, M.L.; Kim, I.; Kang, C.Y.; Kim, J.; Stucky, G.D.; Bowers, J.; Kim, W. High Thermoelectric Performance of a Heterogeneous PbTe Nanocomposite. Chem. Mater. 2015, 27, 944–949. [Google Scholar] [CrossRef]
- Martin, J.; Nolas, G.S.; Zhang, W.; Chen, L. PbTe nanocomposites synthesized from PbTe nanocrystals. Appl. Phys. Lett. 2007, 90, 222112. [Google Scholar] [CrossRef]
- Heremans, J.P.; Thrush, C.M.; Morelli, D.T. Thermopower enhancement in lead telluride nanostructures. Phys. Rev. B 2004, 70, 115334. [Google Scholar] [CrossRef]
- Heremans, J.P.; Thrush, C.M.; Morelli, D.T. Thermopower enhancement in PbTe with Pb precipitates. J. Appl. Phys. 2005, 98, 063703. [Google Scholar] [CrossRef]
- Vineis, C.J.; Harman, T.C.; Calawa, S.D.; Walsh, M.P.; Reeder, R.E.; Singh, R.; Shakouri, A. Carrier concentration and temperature dependence of the electronic transport properties of epitaxial PbTe and PbTe/PbSe nanodot superlattices. Phys. Rev. B 2008, 77, 235202. [Google Scholar] [CrossRef]
- Vining, C.B. A model for the high-temperature transport properties of heavily doped n-type silicon-germanium alloys. J. Appl. Phys. 1991, 69, 331–341. [Google Scholar] [CrossRef]
- Joshi, G.; Lee, H.; Lan, Y.C.; Wang, X.W.; Zhu, G.H.; Wang, D.Z.; Gould, R.W.; Cuff, D.C.; Tang, M.Y.; Dresselhaus, M.S.; et al. Enhanced thermoelectric figure-of-merit in nanostructured p-type silicon germanium bulk alloys. Nano Lett. 2008, 8, 4670–4674. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.W.; Lee, H.; Lan, Y.C.; Zhu, G.H.; Joshi, G.; Wang, D.Z.; Yang, J.; Muto, A.J.; Tang, M.Y.; Klatsky, J.; et al. Enhanced thermoelectric figure of merit in nanostructured n-type silicon germanium bulk alloy. Appl. Phys. Lett. 2008, 93, 193121. [Google Scholar] [CrossRef]
- Yu, B.; Zebarjadi, M.; Wang, H.; Lukas, K.; Wang, H.Z.; Wang, D.Z.; Opeil, C.; Dresselhaus, M.S.; Chen, G.; Ren, Z.F. Enhancement of thermoelectric properties by modulation-doping in silicon germanium alloy nanocomposites. Nano Lett. 2012, 12, 2077–2082. [Google Scholar] [CrossRef] [PubMed]
- Zhu, G.H.; Lee, H.; Lan, Y.C.; Wang, X.W.; Joshi, G.; Wang, D.Z.; Yang, J.; Vashaee, D.; Guilbert, H.; Pillitteri, A.; et al. Increased phonon scattering by nanograins and point defects in nanostructured silicon with a low concentration of germanium. Phys. Rev. Lett. 2009, 102, 196803. [Google Scholar] [CrossRef] [PubMed]
- Nozariasbmarz, A.; Zamanipour, Z.; Norouzzadeh, P.; Krasinski, J.S.; Vashaee, D. Enhanced thermoelectric performance in a metal/semiconductor nanocomposite of iron silicide/silicon germanium. RSC Adv. 2016, 6, 49643–49650. [Google Scholar] [CrossRef]
- Zamanipour, Z.; Vashaee, D. Comparison of thermoelectric properties of p-type nanostructured bulk Si0.8Ge0.2 alloy with Si0.8Ge0.2 composites embedded with CrSi2 nano-inclusisons. J. Appl. Phys. 2012, 112, 093714. [Google Scholar] [CrossRef]
- Nam, W.H.; Lim, Y.S.; Choi, S.-M.; Seo, W.-S.; Lee, J.Y. High-Temperature Charge Transport and Thermoelectric Properties of A Degenerately Al-Doped ZnO Nanocomposite. J. Mater. Chem. 2012, 22, 14633–14638. [Google Scholar] [CrossRef]
- Jood, P.; Mehta, R.J.; Zhang, Y.L.; Peleckis, G.; Wang, X.L.; Siegel, R.W.; Borca-Tasciuc, T.; Dou, S.X.; Ramanath, G. Al-doped zinc oxide nanocomposites with enhanced thermoelectric properties. Nano Lett. 2011, 11, 4337–4342. [Google Scholar] [CrossRef] [PubMed]
- Jung, K.H.; Lee, K.H.; Seo, W.S.; Choi, S.M. An Enhancement of a Thermoelectric Power Factor in a Ga-Doped ZnO System: A Chemical Compression by Enlarged Ga Solubility. Appl. Phys. Lett. 2012, 100, 253902. [Google Scholar] [CrossRef]
- Qu, X.R.; Wang, W.; Lv, S.C.; Jia, D.C. Thermoelectric Properties and Electronic Structure of Al-Doped ZnO. Solid State Commun. 2011, 151, 332–336. [Google Scholar] [CrossRef]
- Tsubota, T.; Ohtaki, M.; Eguchi, K.; Arai, H. Thermoelectric Properties of Al-Doped ZnO as a Promising Oxide Material for High-Temperature Thermoelectric Conversion. J. Mater. Chem. 1997, 7, 85–90. [Google Scholar] [CrossRef]
- Ruske, F.; Roczen, M.; Lee, K.; Wimmer, M.; Gall, S.; Hüpkes, J.; Hrunski, D.; Rech, B. Improved electrical transport in Al-doped zinc oxide by thermal treatment. J. Appl. Phys. 2010, 107, 013708. [Google Scholar] [CrossRef]
- Ohtaki, M.; Araki, K.; Yamamoto, K. High Thermoelectric Performance of Dually Doped ZnO Ceramics. J. Electr. Mater. 2009, 38, 1234–1238. [Google Scholar] [CrossRef]
- Chen, D.; Zhao, Y.; Chen, Y.; Wang, B.; Chen, H.; Zhou, J.; Liang, Z. One-Step Chemical Synthesis of ZnO/Graphene Oxide Molecular Hybrids for High-Temperature Thermoelectric Applications. ACS Appl. Mater. Interfaces 2015, 7, 3224–3230. [Google Scholar] [CrossRef] [PubMed]
- Saleemi, M.; Famengo, A.; Fiameni, S.; Boldrini, S.; Battiston, S.; Johnsson, M.; Muhammed, M.; Toprak, M.S. Thermoelectric performance of higher manganese silicide nanocomposites. J. Alloy. Compd. 2015, 619, 31–37. [Google Scholar] [CrossRef]
- Farahi, N.; Prabhudev, S.; Bugnet, M.; Botton, G.A.; Zhao, J.B.; Tse, J.S.; Salvador, J.R.; Kleinke, H. Enhanced figure of merit in Mg2Si0.877Ge0.1Bi0.023/multi wall carbon nanotube nanocomposites. RSC Adv. 2015, 5, 65328–65336. [Google Scholar] [CrossRef]
- Farahi, N.; Prabhudev, S.; Botton, G.A.; Salvador, J.R.; Kleinke, H. Nano- and Microstructure Engineering: An Effective Method for Creating High Efficiency Magnesium Silicide Based Thermoelectrics. ACS Appl. Mater. Interfaces 2016, 8, 34431–34437. [Google Scholar] [CrossRef] [PubMed]
- Tazebay, A.S.; Yi, S.I.; Lee, J.K.; Kim, H.; Bahk, J.-H.; Kim, S.L.; Park, S.-D.; Lee, H.S.; Shakouri, A.; Yu, C. Thermal Transport Driven by Extraneous Nanoparticles and Phase Segregation in Nanostructured Mg2(Si,Sn) and Estimation of Optimum Thermoelectric Performance. ACS Appl. Mater. Interfaces 2016, 8, 7003–7012. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Li, J.C.; Qin, X.Y.; Zhang, J.; Xin, H.X.; Song, C.J.; Wang, L. Enhanced thermoelectric performance in SnSe based composites with PbTe nanoinclusions. Energy 2016, 116, 861–866. [Google Scholar] [CrossRef]
- Mi, J.L.; Zhao, X.B.; Zhu, T.J.; Tu, J.P. Erratum: “Improved thermoelectric figure of merit in n-type CoSb3 based nanocomposites”. Appl. Phys. Lett. 2007, 91, 172116. [Google Scholar] [CrossRef]
- Li, H.; Tang, X.F.; Su, X.L.; Zhang, Q.J.; Uher, C. Nanostructured bulk YbxCo4Sb12 with high thermoelectric performance prepared by the rapid solidification method. J. Phys. D Appl. Phys. 2009, 42, 145409. [Google Scholar] [CrossRef]
- Joshi, G.; Yan, X.; Wang, H.Z.; Liu, W.S.; Chen, G.; Ren, Z.F. Enhancement in Thermoelectric Figure-Of-Merit of an N-Type Half-Heusler Compound by the Nanocomposite Approach. Adv. Energy Mater. 2011, 1, 643–647. [Google Scholar] [CrossRef]
- Yan, X.; Joshi, G.; Liu, W.; Lan, Y.; Wang, H.; Lee, S.; Simonson, J.W.; Poon, S.J.; Tritt, T.M.; Chen, G.; et al. Enhanced thermoelectric figure of merit of p-type half-Heuslers. Nano Lett. 2011, 11, 556–560. [Google Scholar] [CrossRef] [PubMed]
- Bhardwaj, A.; Misra, D.K.; Pulikkotil, J.J.; Auluck, S.; Dhar, A.; Budhani, R.C. Implications of nanostructuring on the thermoelectric properties in half-Heusler alloys. Appl. Phys. Lett. 2012, 101, 133103. [Google Scholar] [CrossRef]
- Lan, J.L.; Liu, Y.C.; Zhan, B.; Lin, Y.H.; Zhang, B.P.; Yuan, X.; Zhang, W.Q.; Xu, W.; Nan, C.-W. Enhanced Thermoelectric Properties of Pb-doped BiCuSeO Ceramics. Adv. Mater. 2013, 25, 5086–5090. [Google Scholar] [CrossRef] [PubMed]
- Kim, W.; Zide, J.; Gossard, A.; Klenov, D.; Stemmer, S.; Shakouri, A.; Majumdar, A. Thermal conductivity reduction and thermoelectric figure of merit increase by embedding nanoparticles in crystalline semiconductors. Phys. Rev. Lett. 2006, 96, 045901. [Google Scholar] [CrossRef] [PubMed]
- Zide, J.M.O.; Bahk, J.-H.; Singh, R.; Zebarjadi, M.; Zeng, G.; Lu, H.; Feser, J.P.; Xu, D.; Singer, S.L.; Bian, Z.X.; et al. High efficiency semimetal/semiconductor nanocomposite thermoelectric materials. J. Appl. Phys. 2010, 108, 123702. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.L.; Yeoh, W.K.; Zheng, R.K.; Zhang, C. Electrical and thermoelectric properties of single-wall carbon nanotube doped Bi2Te3. Appl. Phys. Lett. 2012, 101, 031909. [Google Scholar] [CrossRef]
- Blank, V.D.; Buga, S.G.; Kulbachinskii, V.A.; Kytin, V.G.; Medvedev, V.V.; Popov, Y.M.; Stepanov, P.B.; Skok, V.F. Thermoelectric properties of Bi0.5Sb1.5Te3/C60 nanocomposites. Phys. Rev. B 2012, 86, 075426. [Google Scholar] [CrossRef]
- Zhao, D.; Ning, J.; Wu, D.; Zuo, M. Enhanced Thermoelectric Performance of Cu2SnSe3-Based Composites Incorporated with Nano-Fullerene. Materials 2016, 9, 629. [Google Scholar] [CrossRef]
- Xie, D.; Xu, J.; Liu, G.; Liu, Z.; Shao, H.; Tan, X.; Jiang, J.; Jiang, H. Synergistic Optimization of Thermoelectric Performance in P-Type Bi0.48Sb1.52Te3/Graphene Composite. Energies 2016, 9, 236. [Google Scholar] [CrossRef]
- Li, C.; Qin, X.; Li, Y.; Li, D.; Zhang, J.; Guo, H.; Xin, H.; Song, C. Simultaneous increase in conductivity and phonon scattering in a graphene nanosheets/(Bi2Te3)0.2(Sb2Te3)0.8 thermoelectric nanocomposite. J. Alloy. Compd. 2016, 661, 389–395. [Google Scholar] [CrossRef]
- Li, Z.Y.; Li, J.F.; Zhao, W.Y.; Tan, Q.; Wei, T.R.; Wu, C.F.; Xing, Z.B. PbTe-based thermoelectric nanocomposites with reduced thermal conductivity by SiC nanodispersion. Appl. Phys. Lett. 2014, 104, 113905. [Google Scholar] [CrossRef]
- Ko, D.K.; Kang, Y.J.; Murray, C.B. Enhanced thermopower via carrier energy filtering in solution-processable Pt–Sb2Te3 nanocomposites. Nano Lett. 2011, 11, 2841–2844. [Google Scholar] [CrossRef] [PubMed]
- Talin, A.A.; Jones, R.E.; Hopkins, P.E. Metal–organic frameworks for thermoelectric energy-conversion applications. MRS Bull. 2016, 41, 877–882. [Google Scholar] [CrossRef]
- Culebras, M.; Gόmez, C.M.; Cantarero, A. Review on polymers for thermoelectric applications. Materials 2014, 7, 6701–6732. [Google Scholar] [CrossRef]
- Wei, Q.; Mukaida, M.; Kirihara, K.; Naitoh, Y.; Ishida, T. Recent Progress on PEDOT-Based Thermoelectric Materials. Materials 2015, 8, 732–750. [Google Scholar] [CrossRef]
- Xuan, Y.; Liu, X.; Desbief, S.; Leclère, P.; Fahlman, M.; Lazzaroni, R.; Berggren, M.; Cornil, J.; Emin, D.; Crispin, X. Thermoelectric properties of conducting polymers: The case of poly (3-hexylthiophene). Phys. Rev. B 2010, 82, 115454. [Google Scholar] [CrossRef]
- Bubnova, O.; Khan, Z.U.; Malti, A.; Braun, S.; Fahlman, M.; Berggren, M.; Crispin, X. Optimization of the thermoelectric figure of merit in the conducting polymer poly (3,4-ethylenedioxythiophene). Nat. Mater. 2011, 10, 429–433. [Google Scholar] [CrossRef] [PubMed]
- Taggart, D.K.; Yang, Y.G.; Kung, S.; McIntire, T.M.; Penner, R.M. Enhanced thermoelectric metrics in ultra-long electrodeposited PEDOT nanowires. Nano Lett. 2011, 11, 125–131. [Google Scholar] [CrossRef] [PubMed]
- Nogami, Y.; Kaneko, H.; Ishiguro, T.; Takahashi, A.; Tsukamoto, J.; Hosoito, N. On the metallic states in highly conducting iodine-doped polyacetylene. Solid State Commun. 1990, 76, 583–586. [Google Scholar] [CrossRef]
- Zhang, B.; Sun, J.; Katz, H.E.; Fang, F.; Opila, R.L. Promising thermoelectric properties of commercial PEDOT: PSS materials and their Bi2Te3 powder composites. ACS Appl. Mater. Interfaces 2010, 2, 3170–3178. [Google Scholar] [CrossRef] [PubMed]
- Dudis, D.S.; Ferguson, J.B.; Check, M.; Schmidt, J.E.; Kemp, E.R.; Robbins, T.; Shumaker, J.A.; Chen, C.G.; Seibel, H.A., II. Multidimensional Nanoscopic Approaches to New Thermoelectric Materials. Proc. SPIE 2010, 7683, 76830S. [Google Scholar]
- Casian, A. Violation of the Wiedemann-Franz law in quasi-one-dimensional organic crystals. Phys. Rev. B 2010, 81, 155415. [Google Scholar] [CrossRef]
- Wang, D.; Tang, L.; Long, M.Q.; Shuai, Z.G. First-principles investigation of organic semiconductors for thermoelectric applications. J. Chem. Phys. 2009, 131, 224704. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.Y.; Zhou, J.; Yang, R.G. Thermoelectric properties of molecular nanowires. J. Phys. Chem. C 2011, 115, 24418–24428. [Google Scholar] [CrossRef]
- Yu, C.; Choi, K.; Yin, L.; Grunlan, J.C. Light-weight flexible carbon nanotube based organic composites with large thermoelectric power factors. ACS Nano 2011, 5, 7885–7892. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.; Kim, Y.; Choi, K.; Grunlan, J.C.; Yu, C. Improved thermoelectric behavior of nanotube-filled polymer composites with poly (3,4-ethylenedioxythiophene) poly (styrenesulfonate). ACS Nano 2010, 4, 513–523. [Google Scholar] [CrossRef] [PubMed]
- He, M.; Ge, J.; Lin, Z.; Feng, X.; Wang, X.; Lu, H.; Yang, Y.; Qiu, F. Thermopower Enhancement in Conducting Polymer Nanocomposites via Carrier Energy Scattering at the Organic−Inorganic Semiconductor Interface. Energy Environ. Sci. 2012, 5, 8351–8358. [Google Scholar] [CrossRef]
- Ju, H.; Kim, J. Chemically Exfoliated SnSe Nanosheets and Their SnSe/Poly (3,4-ethylenedioxythiophene): Poly (styrenesulfonate) Composite Films for Polymer Based Thermoelectric Applications. ACS Nano 2016, 10, 5730–5739. [Google Scholar] [CrossRef] [PubMed]
- Coates, N.E.; Yee, S.K.; McCulloch, B.; See, K.C.; Majumdar, A.; Segalman, R.A.; Urban, J.J. Effect of interfacial properties on polymer–nanocrystal thermoelectric transport. Adv. Mater. 2013, 25, 1629–1633. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Song, Z.; Zhang, Q.; Zhou, Z.; Tang, Y.; Wang, L.; Zhu, J.; Luo, W.; Jiang, W. Preparation of bulk Ag NWs/PEDOT: PSS composites: A new model towards high-performance bulk organic thermoelectric materials. RSC Adv. 2015, 5, 45106–45112. [Google Scholar] [CrossRef]
- Stejskal, J. Conducting polymer-silver composites. Chem. Pap. 2013, 67, 814–848. [Google Scholar] [CrossRef]
- Coleman, J.N.; Curran, S.; Dalton, A.B.; Davey, A.P.; McCarthy, B.; Blau, W.; Barklie, B.C. Percolation-dominated conductivity in a conjugated-polymer- carbon-nanotube composite. Phys. Rev. B 1998, 58, 7492. [Google Scholar] [CrossRef]
- Ramasubramaniam, R.; Chen, J.; Liu, H. Homogeneous carbon nanotube/polymer composites for electrical applications. Appl. Phys. Lett. 2003, 83, 2928–2930. [Google Scholar] [CrossRef]
- Biercuk, M.J.; Llaguno, M.C.; Radosavljevic, M.; Hyun, J.K.; Johnson, A.T.; Fischer, J.E. Carbon nanotube composites for thermal management. Appl. Phys. Lett. 2002, 80, 2767. [Google Scholar] [CrossRef]
- Balberg, I. Recent developments in continuum percolation. Philos. Mag. B 1987, 56, 991–1003. [Google Scholar] [CrossRef]
- Nakayama, T.; Yakubo, K.; Orbach, R.L. Dynamical properties of fractal networks: Scaling, numerical simulations, and physical realizations. Rev. Mod. Phys. 1994, 66, 381–443. [Google Scholar] [CrossRef]
- Kirkpatrick, S. Percolation and conduction. Rev. Mod. Phys. 1973, 45, 574–588. [Google Scholar] [CrossRef]
- Shenogina, N.; Shenogin, S.; Xue, L.; Keblinski, P. On the lack of thermal percolation in carbon nanotube composites. Appl. Phys. Lett. 2005, 87, 133106. [Google Scholar] [CrossRef]
- Chen, Y.; He, M.; Liu, B.; Bazan, G.C.; Zhou, J.; Liang, Z. Bendable n-Type Metallic Nanocomposites with Large Thermoelectric Power Factor. Adv. Mater. 2017. [Google Scholar] [CrossRef] [PubMed]
- Jeng, M.S.; Yang, R.G.; Song, D.; Chen, G. Modeling the thermal conductivity and phonon transport in nanoparticle composites using Monte Carlo simulation. J. Heat Transf. 2008, 130, 042410. [Google Scholar] [CrossRef]
- Yang, R.G.; Chen, G. Thermal conductivity modeling of periodic two-dimensional nanocomposites. Phys. Rev. B 2004, 69, 195316. [Google Scholar] [CrossRef]
- Yang, R.G.; Chen, G.; Dresselhaus, M.S. Thermal conductivity of simple and tubular nanowire composites in the longitudinal direction. Phys. Rev. B 2005, 72, 125418. [Google Scholar] [CrossRef]
- Yang, R.G.; Chen, G.; Dresselhaus, M.S. Thermal conductivity modeling of core-shell and tubular nanowires. Nano Lett. 2005, 5, 1111–1115. [Google Scholar] [CrossRef] [PubMed]
- Tian, W.X.; Yang, R.G. Effect of interface scattering on phonon thermal conductivity percolation in random nanowire composites. Appl. Phys. Lett. 2007, 90, 263105. [Google Scholar] [CrossRef]
- Tian, W.X.; Yang, R.G. Thermal conductivity modeling of compacted nanowire composites. J. Appl. Phys. 2007, 101, 054320. [Google Scholar] [CrossRef]
- Prasher, R. Thermal conductivity of composites of aligned nanoscale and microscale wires and pores. J. Appl. Phys. 2006, 100, 034307. [Google Scholar] [CrossRef]
- Prasher, R. Transverse thermal conductivity of porous materials made from aligned nano-and microcylindrical pores. J. Appl. Phys. 2006, 100, 064302. [Google Scholar] [CrossRef]
- Satyala, N.; Vashaee, D. Detrimental influence of nanostructuring on the thermoelectric properties of magnesium silicide. J. Appl. Phys. 2012, 112, 093716. [Google Scholar] [CrossRef]
- Satyala, N.; Vashaee, D. The effect of crystallite size on thermoelectric properties of bulk nanostructured magnesium silicide (Mg2Si) compounds. Appl. Phys. Lett. 2012, 100, 073107. [Google Scholar] [CrossRef]
- Callaway, J. Model for lattice thermal conductivity at low temperatures. Phys. Rev. 1959, 113, 1046–1051. [Google Scholar] [CrossRef]
- Mingo, N.; Hauser, D.; Kobayashi, N.P.; Plissonnier, M.; Shakouri, A. “Nanoparticle-in-Alloy” approach to efficient thermoelectrics: Silicides in SiGe. Nano Lett. 2009, 9, 711–715. [Google Scholar] [CrossRef] [PubMed]
- Minnich, A.; Chen, G. Modified effective medium formulation for the thermal conductivity of nanocomposites. Appl. Phys. Lett. 2007, 91, 073105. [Google Scholar] [CrossRef]
- Nan, C.-W.; Birringer, R.; Clarke, D.R.; Gleiter, H. Effective thermal conductivity of particulate composites with interfacial thermal resistance. J. Appl. Phys. 1997, 81, 6692–6699. [Google Scholar] [CrossRef]
- Ordonez-Miranda, J.; Yang, R.G.; Alvarado-Gil, J.J. On the thermal conductivity of particulate nanocomposites. Appl. Phys. Lett. 2011, 98, 233111. [Google Scholar] [CrossRef]
- Poon, S.J.; Limtragool, K. Nanostructure model of thermal conductivity for high thermoelectric performance. J. Appl. Phys. 2011, 110, 114306. [Google Scholar] [CrossRef]
- Zhou, J.; Li, X.B.; Chen, G.; Yang, R.G. Semiclassical model for thermoelectric transport in nanocomposites. Phys. Rev. B 2010, 82, 115308. [Google Scholar] [CrossRef]
- Bergman, D.J.; Levy, O. Thermoelectric properties of a composite medium. J. Appl. Phys. 1991, 70, 6821–6833. [Google Scholar] [CrossRef]
- Bergman, D.J.; Fel, L.G. Enhancement of thermoelectric power factor in composite thermoelectrics. J. Appl. Phys. 1999, 85, 8205–8216. [Google Scholar] [CrossRef]
- Nag, B.R. Electron Transport in Compound Semiconductors; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Huang, B.L.; Kaviany, M. Ab initio and molecular dynamics predictions for electron and phonon transport in bismuth telluride. Phys. Rev. B 2008, 77, 125209. [Google Scholar] [CrossRef]
- Humphrey, T.E.; O’Dwyer, M.F.; Linke, H. Power optimization in thermionic devices. J. Phys. D Appl. Phys. 2005, 38, 2051–2054. [Google Scholar] [CrossRef]
- Zhu, T.J.; Liu, Y.T.; Fu, C.G.; Heremans, J.P.; Snyder, J.G.; Zhao, X.B. Compromise and Synergy in High-Efficiency Thermoelectric Materials. Adv. Mater. 2017. [Google Scholar] [CrossRef] [PubMed]
- Martin, J.; Wang, L.; Chen, L.D.; Nolas, G.S. Enhanced Seebeck coefficient through energy-barrier scattering in PbTe nanocomposites. Phys. Rev. B 2009, 79, 115311. [Google Scholar] [CrossRef]
- Popescu, A.; Woods, L.M.; Martin, J.; Nolas, G.S. Model of transport properties of thermoelectric nanocomposite materials. Phys. Rev. B 2009, 79, 205302. [Google Scholar] [CrossRef]
- Kishimoto, K.; Tsukamoto, M.; Koyanagi, T. Temperature dependence of the Seebeck coefficient and the potential barrier scattering of n-type PbTe films prepared on heated glass substrates by rf sputtering. J. Appl. Phys. 2002, 92, 5331–5339. [Google Scholar] [CrossRef]
- Yang, R.G.; Chen, G. Thermoelectric Transport in Nanocomposites; Article Number 2006-01-0289; SAE World Congress (Society of Automotive Engineering): Detroit, MI, USA, 2006. [Google Scholar]
- Minnich, A.J.; Lee, H.; Wang, X.W.; Joshi, G.; Dresselhaus, M.S.; Ren, Z.F.; Chen, G.; Vashaee, D. Modeling study of thermoelectric SiGe nanocomposites. Phys. Rev. B 2009, 80, 155327. [Google Scholar] [CrossRef]
- Bachmann, M.; Czerner, M.; Heiliger, C. Ineffectiveness of energy filtering at grain boundaries for thermoelectric materials. Phys. Rev. B 2012, 86, 115320. [Google Scholar] [CrossRef]
- Faleev, S.V.; Léonard, F. Theory of enhancement of thermoelectric properties of materials with nanoinclusions. Phys. Rev. B 2008, 77, 214304. [Google Scholar] [CrossRef]
- Zebarjadi, M.; Esfarjani, K.; Shakouri, A.; Bahk, J.; Bian, Z.X.; Zeng, G.H.; Bowers, J.; Lu, H.; Zide, J.; Gossard, A. Effect of nanoparticle scattering on thermoelectric power factor. Appl. Phys. Lett. 2009, 94, 202105. [Google Scholar] [CrossRef]
- Zebarjadi, M.; Esfarjani, K.; Shakouri, A.; Bian, Z.X.; Bahk, J.H.; Zeng, G.H.; Bowers, J.; Lu, H.; Zide, J.; Gossard, A. Effect of nanoparticles on electron and thermoelectric transport. J. Electron. Mater. 2009, 38, 954–959. [Google Scholar] [CrossRef]
- Zebarjadi, M.; Esfarjani, K.; Bian, Z.X.; Shakouri, A. Low-temperature thermoelectric power factor enhancement by controlling nanoparticle size distribution. Nano Lett. 2011, 11, 225–230. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.H.; Qin, X.Y. Enhanced energy filtering and thermopower from synergetic scatterings of electrons at interface potential barriers (or wells) in semiconductor-based nanocomposites dispersed with metallic particles. J. Appl. Phys. 2011, 110, 124308. [Google Scholar] [CrossRef]
- Atakulov, S.B.A.; Shamsiddnov, A.N. The problem of transport phenomena in polycrystalline semiconductor thin films with potential barriers in the case where the carriers gas degenerated. Solid State Commun. 1985, 56, 215–219. [Google Scholar] [CrossRef]
- Mahan, G.D.; Sofo, J.O. The best thermoelectric. Proc. Natl. Acad. Sci. USA 1996, 93, 7436–7439. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Yang, R.G.; Chen, G.; Dresselhaus, M.S. Optimal bandwidth for high efficiency thermoelectrics. Phys. Rev. Lett. 2011, 107, 226601. [Google Scholar] [CrossRef] [PubMed]
- Jeong, C.; Kim, R.; Lundstrom, M.S. On the best bandstructure for thermoelectric performance: A Landauer perspective. J. Appl. Phys. 2012, 111, 113707. [Google Scholar] [CrossRef]
- Zebarjadi, M.; Joshi, G.; Zhu, G.H.; Yu, B.; Minnich, A.; Lan, Y.C.; Wang, X.W.; Dresselhaus, M.S.; Ren, Z.F.; Chen, G. Power factor enhancement by modulation doping in bulk nanocomposites. Nano Lett. 2011, 11, 2225–2230. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.Y.; Feser, J.P.; Lee, J.; Talapin, D.V.; Segalman, R.; Majumdar, A. Enhanced thermopower in PbSe nanocrystal quantum dot superlattices. Nano Lett. 2008, 8, 2283–2288. [Google Scholar] [CrossRef] [PubMed]
- Fomin, V.M.; Kratzer, P. Thermoelectric transport in periodic one-dimensional stacks of InAs/GaAs quantum dots. Phys. Rev. B 2010, 82, 045318. [Google Scholar] [CrossRef]
- Balandin, A.A.; Lazarenkova, O.L. Mechanism for thermoelectric figure-of-merit enhancement in regimented quantum dot superlattices. Appl. Phys. Lett. 2003, 82, 415–417. [Google Scholar] [CrossRef]
- Lazarenkova, O.L.; Balandin, A.A. Miniband formation in a quantum dot crystal. J. Appl. Phys. 2001, 89, 5509–5515. [Google Scholar] [CrossRef]
- Lazarenkova, O.L.; Balandin, A.A. Electron and phonon energy spectra in a three-dimensional regimented quantum dot superlattice. Phys. Rev. B 2002, 66, 245319. [Google Scholar] [CrossRef]
- Yadav, A.; Pipe, K.P.; Ye, W.; Goldman, R.S. Thermoelectric properties of quantum dot chains. J. Appl. Phys. 2009, 105, 093711. [Google Scholar] [CrossRef]
- Khitun, A.; Wang, K.L.; Chen, G. Thermoelectric figure of merit enhancement in a quantum dot superlattice. Nanotechnology 2000, 11, 327–331. [Google Scholar] [CrossRef]
- Xu, Y.; Li, G. Strain effect analysis on the thermoelectric figure of merit in n-type Si/Ge nanocomposites. J. Appl. Phys. 2012, 111, 054318. [Google Scholar] [CrossRef]
- Popescu, A.; Woods, L.M. Enhanced thermoelectricity in composites by electronic structure modifications and nanostructuring. Appl. Phys. Lett. 2010, 97, 052102. [Google Scholar] [CrossRef]
- Zhou, J.; Yang, R.G. Quantum and classical thermoelectric transport in quantum dot nanocomposites. J. Appl. Phys. 2011, 110, 084317. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, Y.Y.; Sharp, J.; Yang, R.G. Optimal thermoelectric figure of merit in Bi2Te3/Sb2Te3 quantum dot nanocomposites. Phys. Rev. B 2012, 85, 115320. [Google Scholar] [CrossRef]
- Zhou, J.; Yang, R.G. Thermoelectric Transport in Sb2Te3/Bi2Te3 Quantum Dot Nanocomposites. In Proceedings of the ASME IMECE 2011, Denver, CO, USA, 11–17 November 2011; pp. 387–394. [Google Scholar]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics, 1st ed.; Thomson Learning Inc.: Stamford, CT, USA, 1976. [Google Scholar]
- Grenzebach, C.; Anders, F.B.; Czycholl, G.; Pruschke, T. Transport properties of heavy-fermion systems. Phys. Rev. B 2006, 74, 195119. [Google Scholar] [CrossRef]
- Zhou, J.; Yang, R.G. Thermoelectric transport in strongly correlated quantum dot nanocomposites. Phys. Rev. B 2010, 82, 075324. [Google Scholar] [CrossRef]
- Mahan, G.D. Many-Particle Physics; Kluwer Academic/Plenum Publishers: New York, NY, USA, 2000. [Google Scholar]
- Bockelmann, U.; Bastard, G. Phonon scattering and energy relaxation in two-, one-, and zero-dimensional electron gases. Phys. Rev. B 1990, 42, 8947–8951. [Google Scholar] [CrossRef]






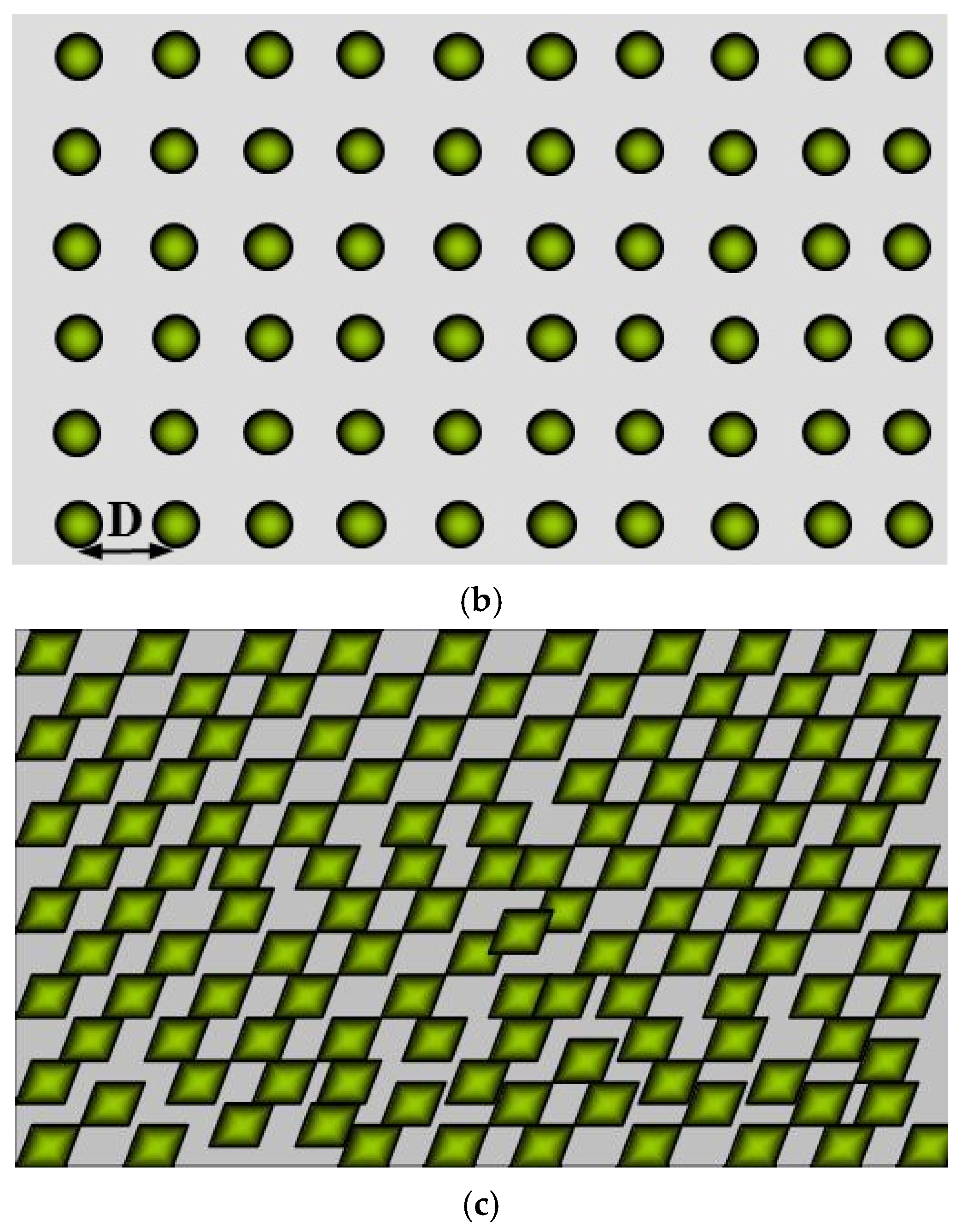
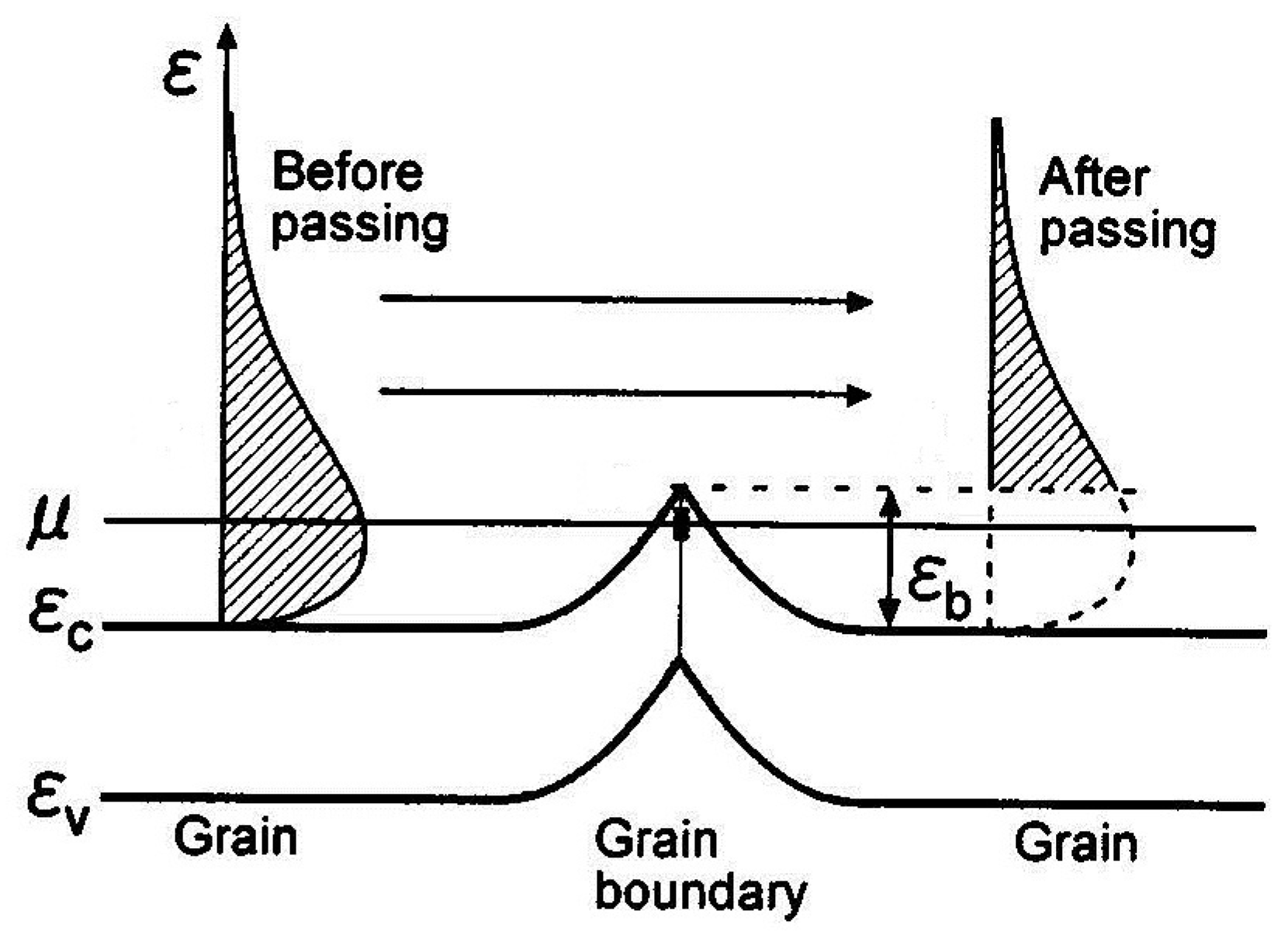
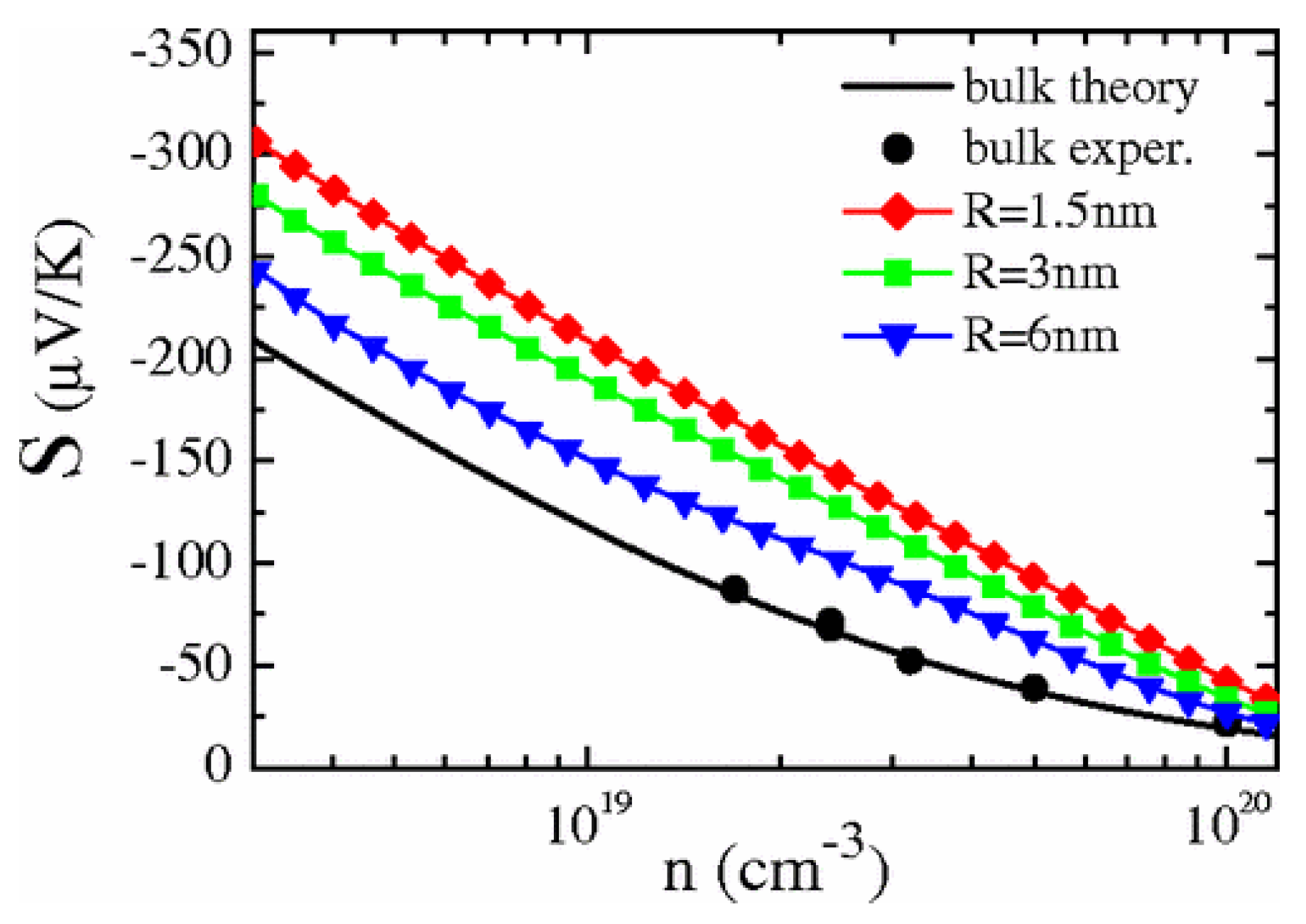
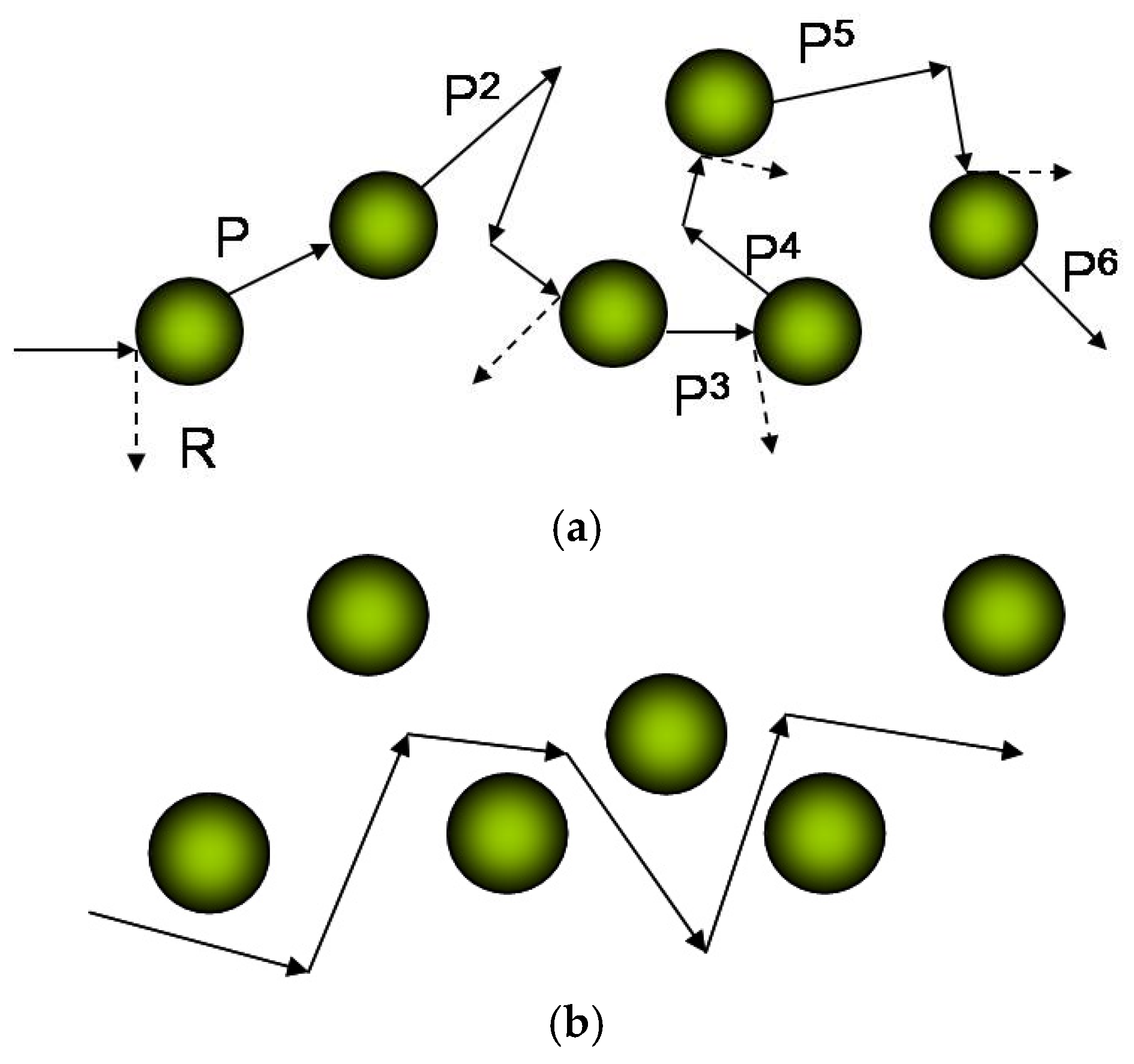
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Hu, J.; Zhou, J.; Yang, R. Thermoelectric Transport in Nanocomposites. Materials 2017, 10, 418. https://doi.org/10.3390/ma10040418
Liu B, Hu J, Zhou J, Yang R. Thermoelectric Transport in Nanocomposites. Materials. 2017; 10(4):418. https://doi.org/10.3390/ma10040418
Chicago/Turabian StyleLiu, Bin, Jizhu Hu, Jun Zhou, and Ronggui Yang. 2017. "Thermoelectric Transport in Nanocomposites" Materials 10, no. 4: 418. https://doi.org/10.3390/ma10040418




