Interfacial Bonding Energy on the Interface between ZChSnSb/Sn Alloy Layer and Steel Body at Microscale
Abstract
:1. Introduction
2. Fundamentals of Molecular Dynamics
3. Interface Simulations with and without Sn Layer
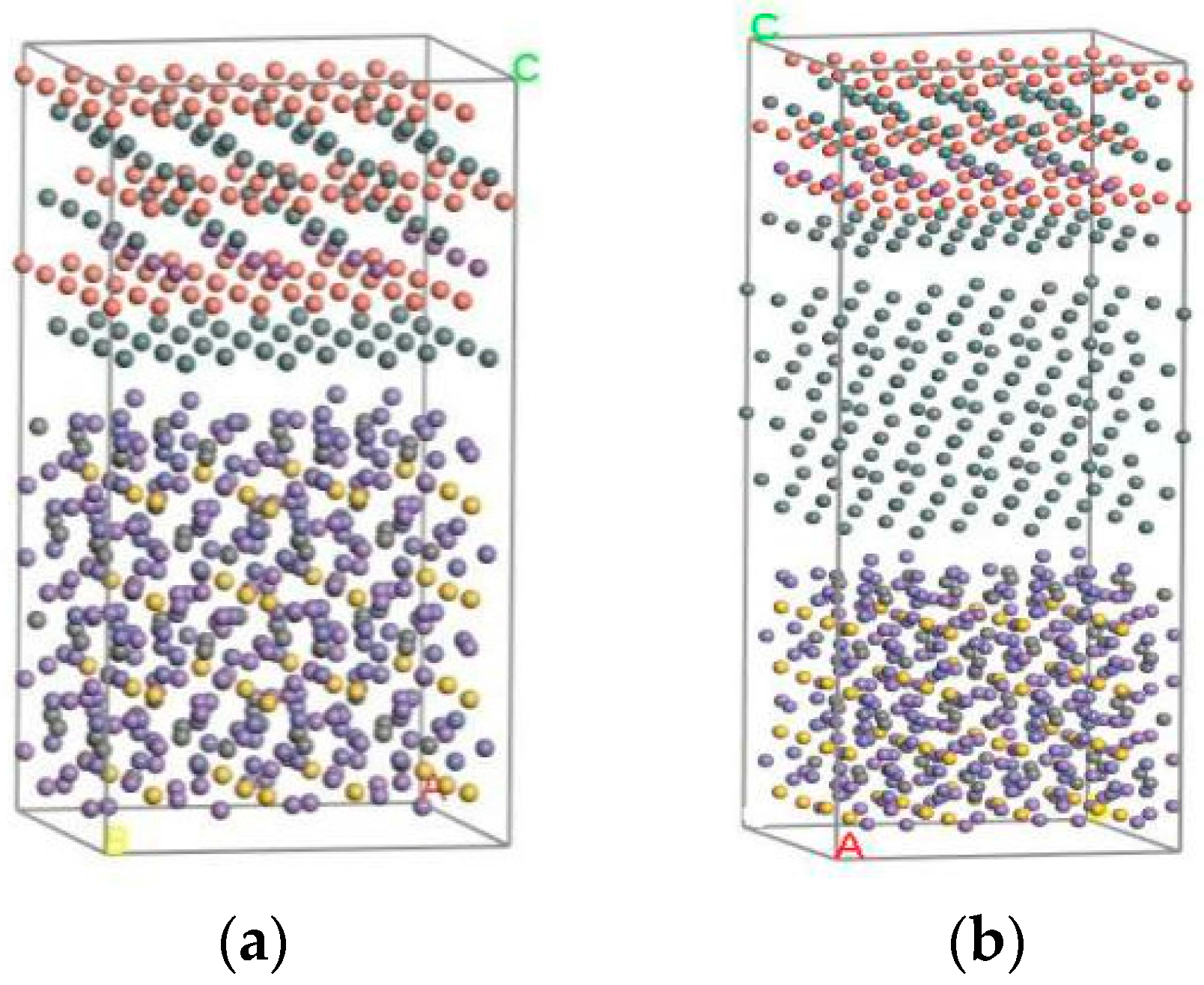
3.1. Establishment of Model
3.2. Analogy Method
3.3. Calculation of Interfacial Bonding Energy
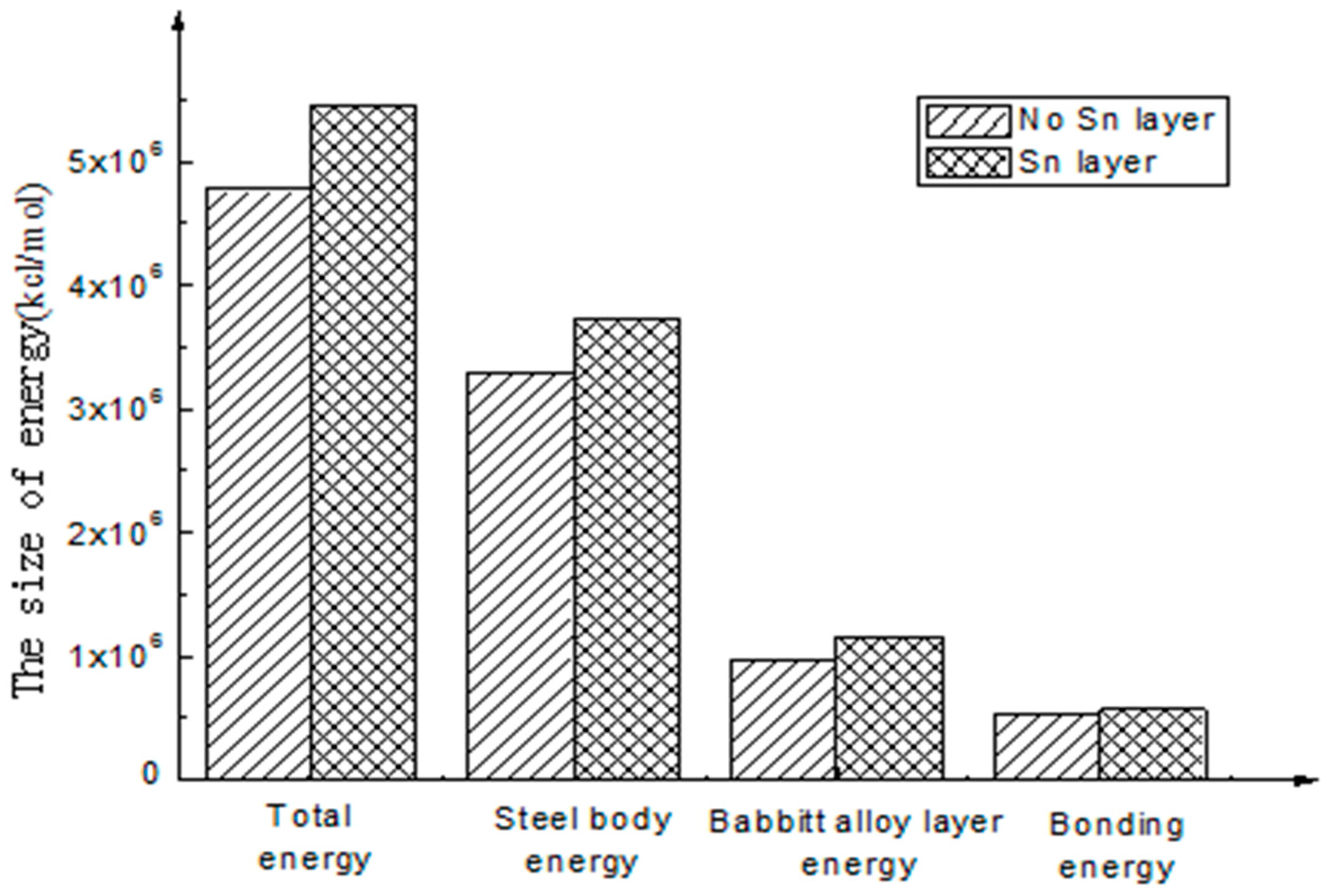
3.4. Simulation Results
- (1)
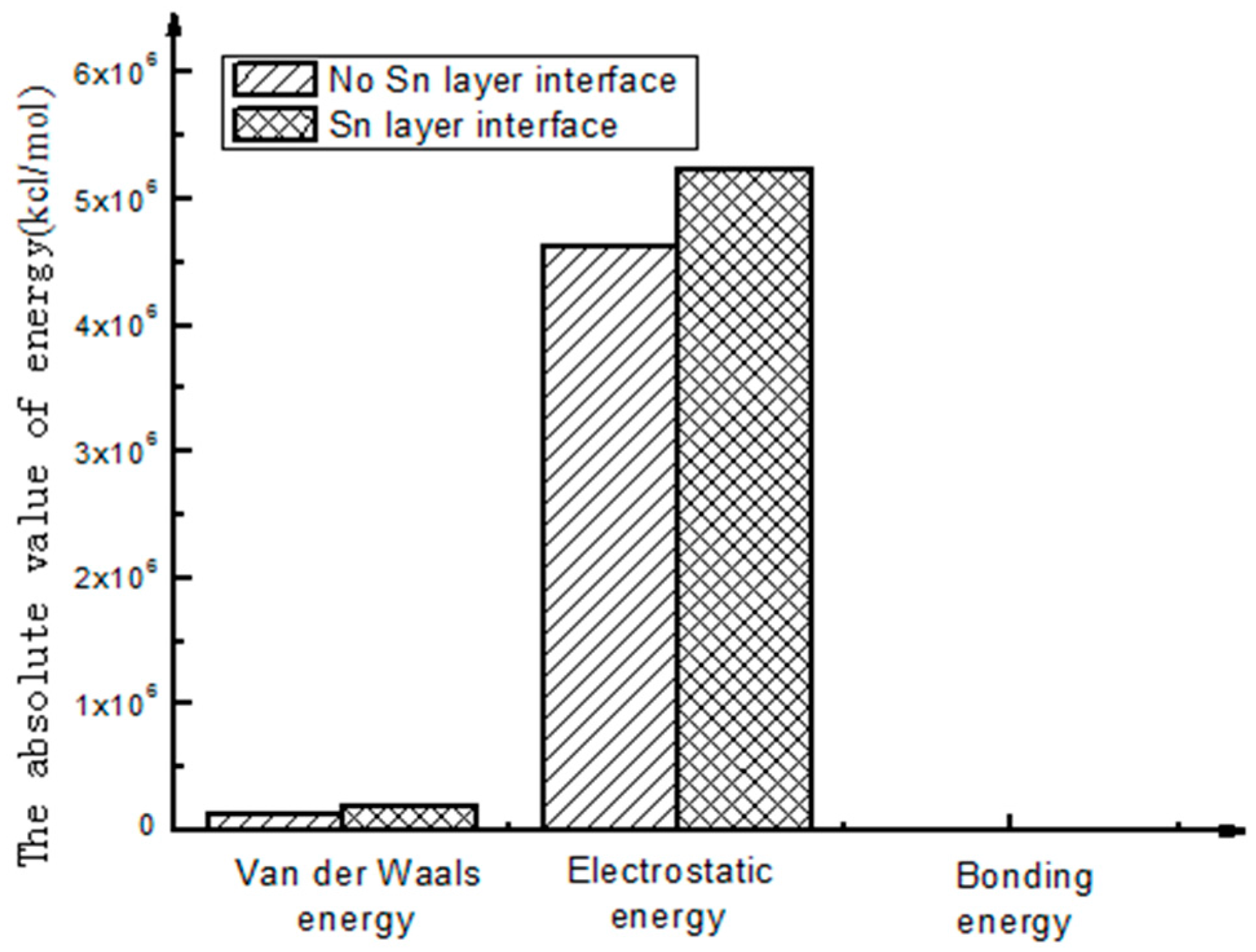
- The calculation results show that the interfacial energy of the interface with Sn layer is slightly larger than that without a Sn layer. As shown in Figure 5, the bonding energy of the interface layer with the Sn layer is larger than that without a Sn layer by 10%. When there is a Sn layer, the bonding performance between steel and Babbitt alloy with a Sn layer is better than that without a Sn layer and is less easily destroyed. The results from the molecular dynamics simulation are consistent with those from the macroscopic law. A Sn layer can buffer the stress concentration due to the mutation of the compositions between the steel body and the lining layer, thus reducing interface mutation and producing better bonding performance between the Babbitt layer and the steel layer.
- (2)
- As seen from the compositions of different interfacial energies, the main forces on an interface structure are Van Der Waals’ force and electrostatic force. The interaction energies among the interfaces are mainly Van Der Waals’ energy and electrostatic energy. Bonding energy can be ignored due to its small fraction. The main factor influencing the interfacial bonding energy is non-bonding energy.
4. Simulation on Interface with Different Babbitt Thickness
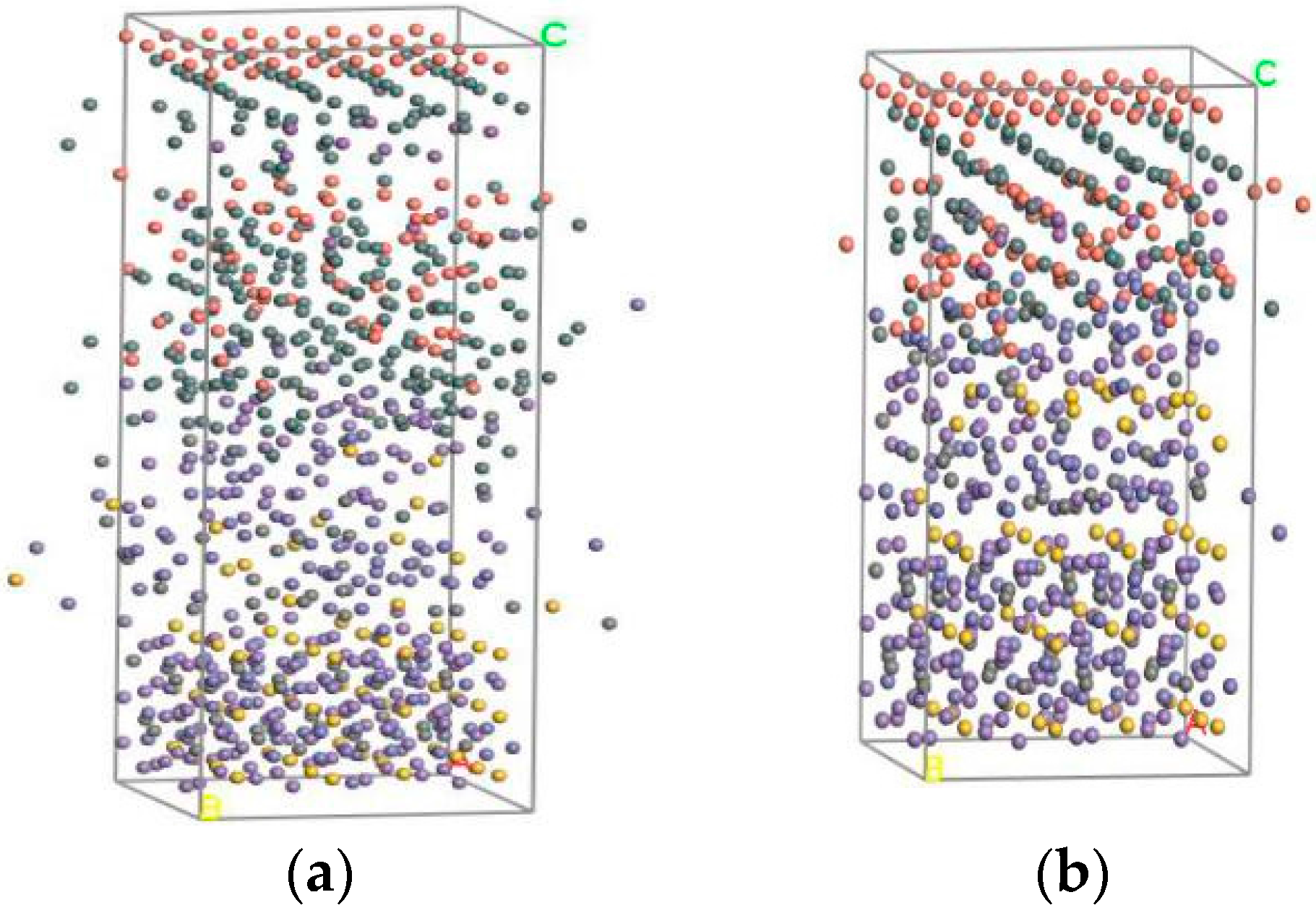
4.1. Simulation Process
4.2. Simulation Results
5. Conclusions
- (1)
- The bonding interface between Babbitt alloy and steel body with or without a Sn layer was simulated using molecular dynamics, and the bonding energies of the bonding interface with or without a Sn layer were obtained respectively. Through comparison, it is concluded that the bonding interface of Babbitt and steel with a Sn layer is better than that without a Sn layer, and the interface bonding energy with a Sn layer is larger than that without a Sn layer by 10%.
- (2)
- From the energy compositions of different interfaces, the main forces acting on the interface structure of the bushing are Van Der Waals’ force and electrostatic force, which play a major role in the interactions between interfaces, and the constraining energy can be neglected. The main factor affecting the interfacial bonding energy is non-bonding energy.
- (3)
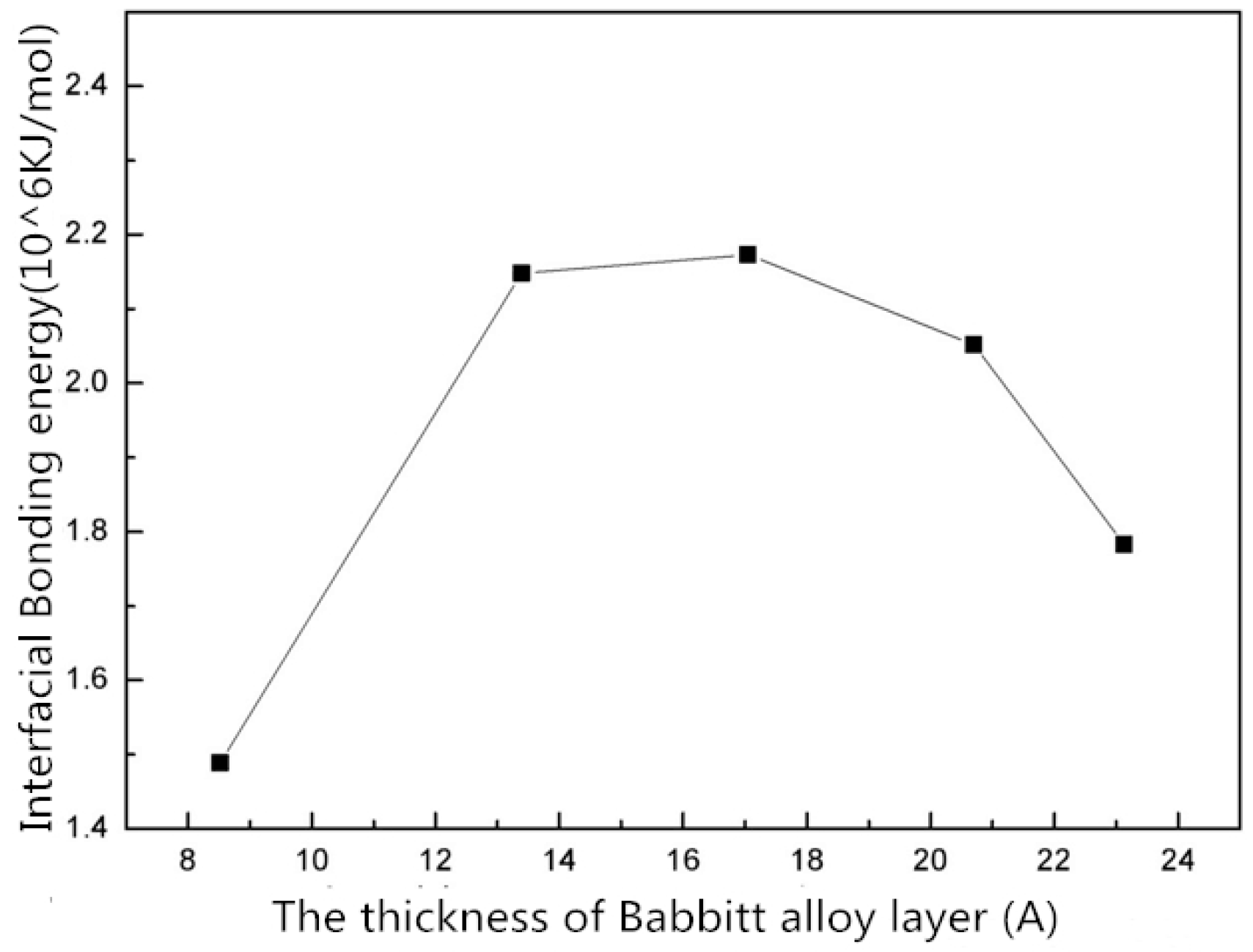
- The interface structures of the Babbitt layer with different thicknesses were quantitatively analyzed using a molecular dynamics simulation. The bonding energy of the interface changes with the thickness of Babbitt in the interface structure. When the thickness of the Babbitt alloy layer is 17.043 Å, the bonding performance of the interface is optimum.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, J.; Huang, Q.; Ding, G. Progress in rolling mill oil-film bearing lubrication theory research. Lubr. Eng. 2012, 37, 112–116. [Google Scholar]
- Wang, J.; Kang, J.; Zhang, Y.; Huang, X. Viscosity monitoring and control on oil-film bearing lubrication with ferrofluids. Tribol. Int. 2014, 75, 61–68. [Google Scholar]
- Wang, J.; Kang, J.; Tang, L. Theoretical and experimental studies for wind turbine’s shrink disk. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2014, 229, 325–334. [Google Scholar]
- Guo, S.; Li, L.; Zhang, G.; Zhao, X. Adhesion analysis of electroless ni coating on SiCp/Al composite mirror substrate. Rare Met. Mater. Eng. 2008, 37, 960–963. [Google Scholar]
- Luo, X.; Qian, G.; Wang, E.G.; Chen, C. Molecular-dynamics simulation of Al/SiC interface structures. Phys. Rev. B 1999, 59, 10125–10131. [Google Scholar] [CrossRef]
- Mo, Z.; Qiao, L.; Sun, Y.; Li, H. Atomistic and mesoscale interface simulation of graphite nanosheet/AgCl/polypyrrole composite. Comput. Mater. Sci. 2009, 45, 981–985. [Google Scholar] [CrossRef]
- Du, L.; Guo, Z.; Zhang, X. SU-8 photoresist and Ni substrate with molecular simulation. Polym. Mater. Sci. Eng. 2010, 26, 168–171. [Google Scholar]
- Yuan, L.; Jing, P.; Liu, Y.; Xu, Z.; Shan, D.; Guo, B. Polycrystalline silver nano molecular dynamics simulations of tensile deformation of nanowires. Acta Phys. Sin. 2014, 63, 268–273. [Google Scholar]
- Melenev, P. Magnetic nanoparticles in fluid environment: Combining molecular dynamics and Lattice-Boltzmann. J. Magn. Magn. Mater. 2016, 431, 145–148. [Google Scholar] [CrossRef]
- Chen, L.; Shi, H.; Wu, H.; Xiang, J. Synthesis and combined properties of novel fluorinated anionic surfactant. Colloids Surf. A Physicochem. Eng. Asp. 2011, 384, 331–336. [Google Scholar] [CrossRef]
- Zhang, D.; Zhao, F.; Li, Y.; Li, P.; Zeng, Q.; Dong, G. Study on tribological properties of multi-layer surface texture on Babbitt alloys surface. Appl. Surf. Sci. 2016, 390, 540–549. [Google Scholar] [CrossRef]
- Kamal, M.; El-Bediwi, A.; Lashin, A.R.; El-Zarka, A.H. Copper effects in mechanical properties of rapidly solidified Sn–Pb–Sb Babbitt bearing alloys. Mater. Sci. Eng. A 2011, 530, 327–332. [Google Scholar] [CrossRef]
- Chen, S.-H.; Lv, Q.; Guo, J.-C.; Hu, S.-Q. Molecular dynamics simulation of polyethylene composites and the tensile properties of graphene. Acta Polym. Sin. 2017, 716–726. [Google Scholar] [CrossRef]
- Becton, M.; Zhang, L.; Wang, X. On the crumpling of polycrystalline graphene by molecular dynamics simulation. Phys. Chem. Chem. Phys. 2015, 17, 6297–6304. [Google Scholar] [CrossRef] [PubMed]
- Liao, R.; Zhu, M.; Zhou, X.; Yang, L.-J.; Yan, J.-M.; Sun, C.-X. Molecular dynamics simulation of oil paper composite medium the diffusion behavior of water molecules. Acta Phys. Chim. Sin. 2011, 27, 815–824. [Google Scholar]
- Sun, C.; Bai, B. Molecular sieving through a graphene nanopore: Non-equilibrium molecular dynamics simulation. Sci. Bull. 2017, 62, 554–562. [Google Scholar] [CrossRef]
- Seifoori, S.; Hajabdollahi, H. Impact behavior of single-layered graphene sheets based on analytical model and molecular dynamics simulation. Appl. Surf. Sci. 2015, 351, 565–572. [Google Scholar] [CrossRef]
- Li, J.; Yang, Y.; Luo, X.; Jing, N.; Li, M.; Huang, B.; Han, M. Advances in molecular dynamics simulation of composite interface. Rare Met. Mater. Eng. 2013, 42, 644–648. [Google Scholar]
- Du, L.; Guo, Z.; Zhang, X. Molecular dynamics simulation of Bonding between crosslinked SU-8 photoresist and Ni substrate. Acta Polym. Sin. 2010, 1, 629–634. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.; Huang, Y.; Xiang, D. Layer thickness test and simulation study of Sn interface. Chin. J. Mech. Eng. 2015, 51, 106–113. [Google Scholar] [CrossRef]
- Li, S.; Urata, S. An atomistic-to-continuum molecular dynamics: Theory, algorithm, and applications. Comput. Methods Appl. Mech. Eng. 2016, 306, 452–478. [Google Scholar] [CrossRef]
- Zhang, H.; Luo, X.; Lin, X.; Lu, X.; Tang, Y. The molecular understanding of interfacial interactions of functionalized graphene and chitosan. Appl. Surf. Sci. 2016, 360, 715–721. [Google Scholar] [CrossRef]
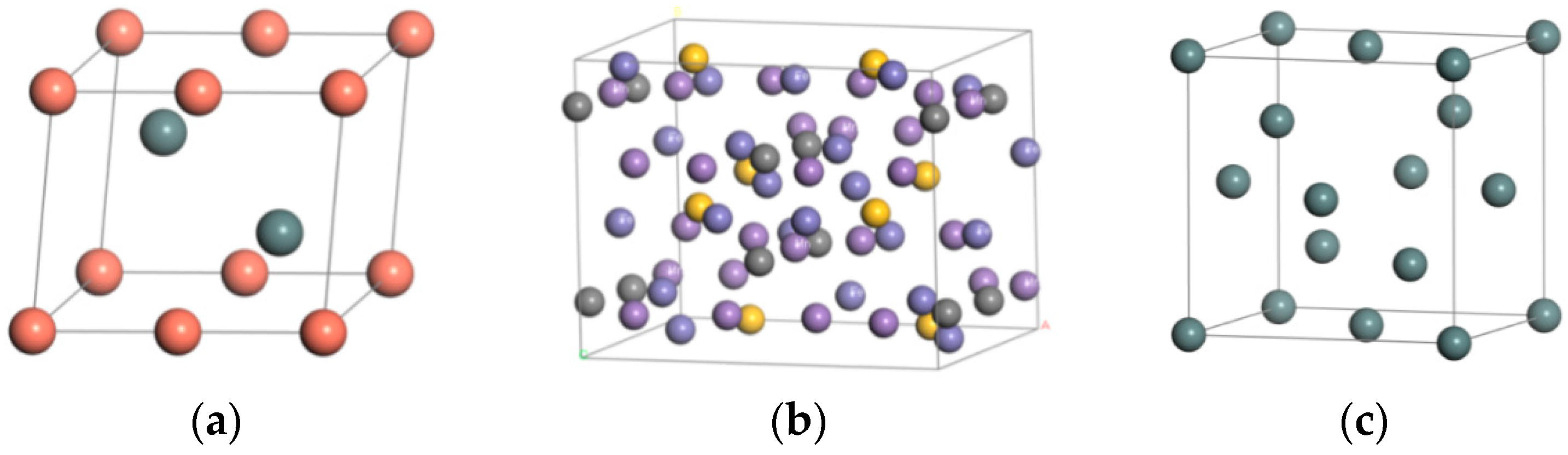
| Material | Steel Body | Sn | Babbitt Metal | |
|---|---|---|---|---|
| Space Group | CMC21 | FD-3M | P63/MMC | |
| Syngony | Orthorhombic system | Orthorhombic system | Hexagonal crystal system | |
| Cell length | a (Å) | 10.108 | 6.491 | 4.217 |
| b (Å) | 7.998 | 6.491 | 4.217 | |
| c (Å) | 7.546 | 6.491 | 5.120 | |
| Cell angle | 90 | 90 | 90 | |
| 90 | 90 | 90 | ||
| 90 | 90 | 120 | ||
| Interface Type | (kcal/mol) | (kcal/mol) | (kcal/mol) | (kcal/mol) |
|---|---|---|---|---|
| Without Sn interface | 4,776,554.60 | 3,291,967.51 | 964,648.17 | 519,938.92 |
| With Sn interface | 5,445,204.16 | 3,720,407.89 | 1,154,367.45 | 570,428.82 |
| Interface Type | Non-Bonding Energy (kcal/mol) | Bonding Energy (kcal/mol) | |
|---|---|---|---|
| Van Der Waals Energy | Electrostatic Energy | ||
| Without Sn interface | 141,536.66 | 4,635,308.39 | −290.45 |
| With Sn interface | 206,368.67 | 5,239,210.25 | −374.76 |
| Babbitt Layer Thickness (Å) | 8.521 | 13.391 | 17.043 | 20.695 | 23.13 |
|---|---|---|---|---|---|
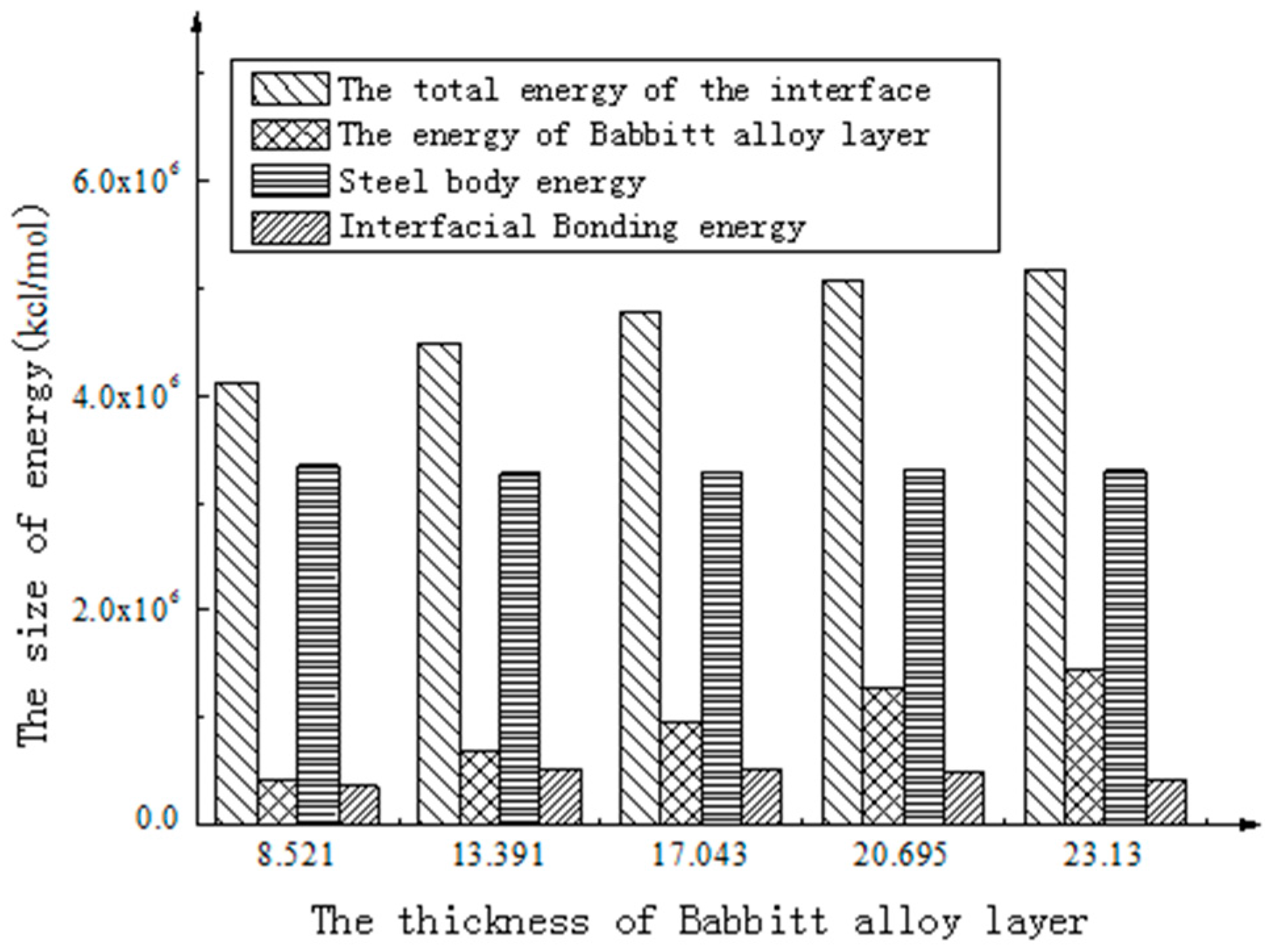
| Total interfacial energy (kcal/mol) | 4,114,386.435 | 4,482,626.633 | 4,776,554.600 | 5,079,386.406 | 5,165,204.487 |
| Babbitt layer energy (kcal/mol) | 411,785.390 | 697,262.041 | 964,648.171 | 1,279,625.574 | 1,441,594.477 |
| Steel body layer energy (kcal/mol) | 3,344,574.554 | 3,271,396.980 | 3,291,967.512 | 3,308,934.658 | 3,297,101.787 |
| Interface Bonding energy (kcal/mol) | 358,026.491 | 513,967.613 | 519,938.918 | 490,826.174 | 426,508.225 |
| Babbitt Layer Thickness (Å) | 8.521 | 13.391 | 17.043 | 20.695 | 23.13 |
|---|---|---|---|---|---|
| Interface Bonding energy (KJ/mol) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Xia, Q.; Ma, Y.; Meng, F.; Liang, Y.; Li, Z. Interfacial Bonding Energy on the Interface between ZChSnSb/Sn Alloy Layer and Steel Body at Microscale. Materials 2017, 10, 1128. https://doi.org/10.3390/ma10101128
Wang J, Xia Q, Ma Y, Meng F, Liang Y, Li Z. Interfacial Bonding Energy on the Interface between ZChSnSb/Sn Alloy Layer and Steel Body at Microscale. Materials. 2017; 10(10):1128. https://doi.org/10.3390/ma10101128
Chicago/Turabian StyleWang, Jianmei, Quanzhi Xia, Yang Ma, Fanning Meng, Yinan Liang, and Zhixiong Li. 2017. "Interfacial Bonding Energy on the Interface between ZChSnSb/Sn Alloy Layer and Steel Body at Microscale" Materials 10, no. 10: 1128. https://doi.org/10.3390/ma10101128




