Improving the Process of Adjusting the Parameters of Finite Element Models of Healthy Human Intervertebral Discs by the Multi-Response Surface Method
Abstract
:1. Introduction
2. Use of FEM for Modeling the Lumbar Intervertebral Disc
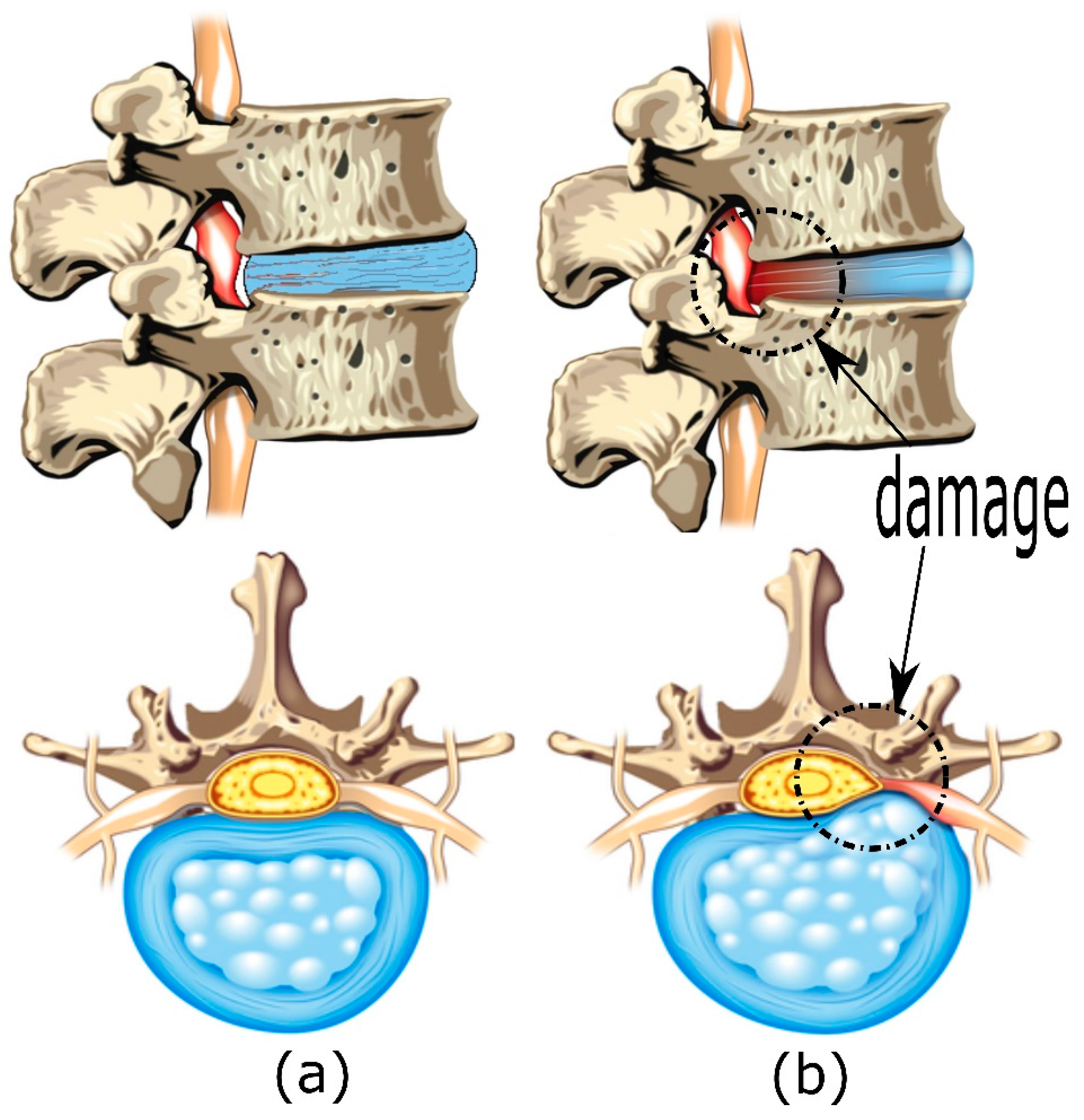
2.1. Biomechanics of the Intervertebral Disc
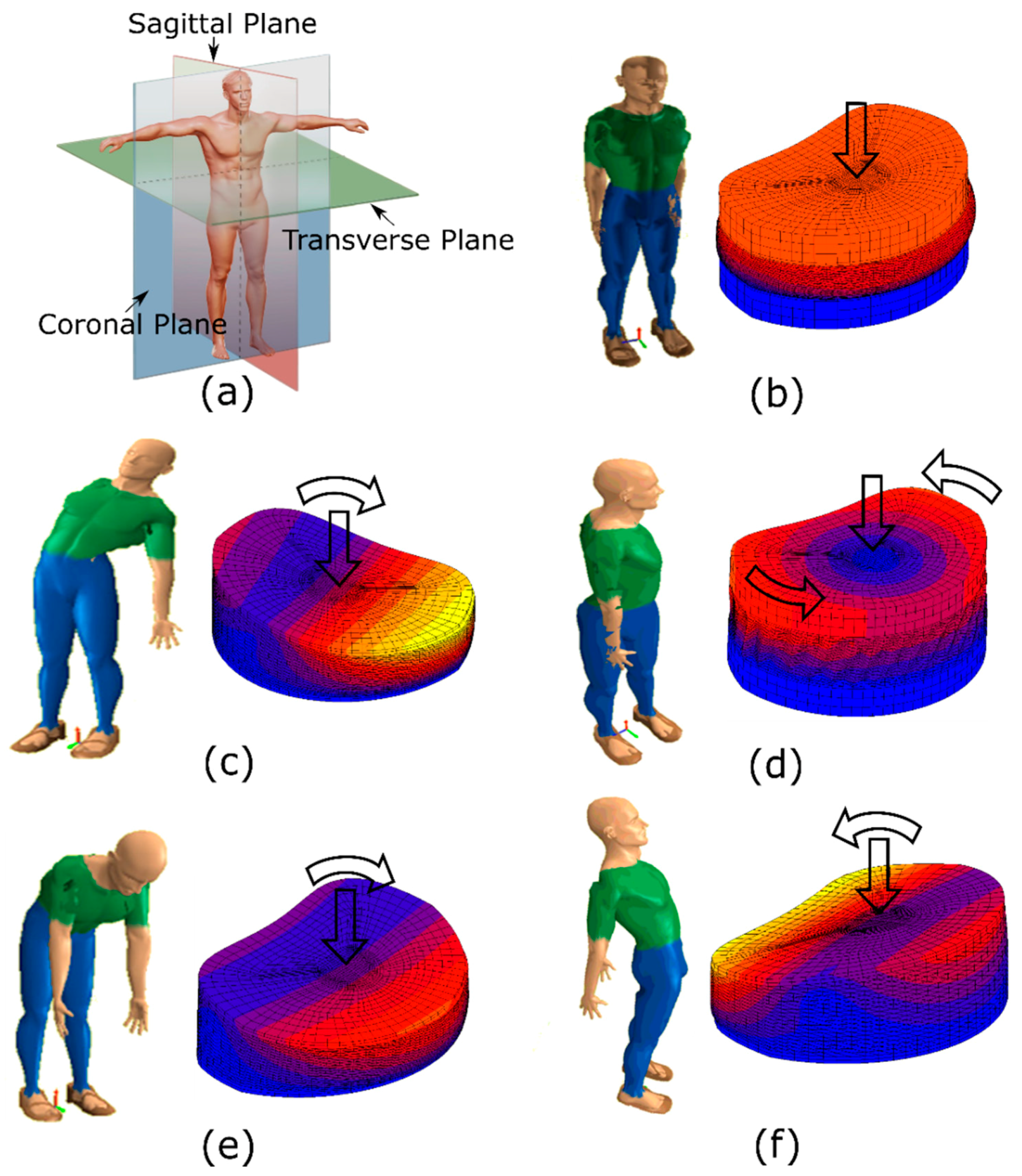
2.2. Spine Movement
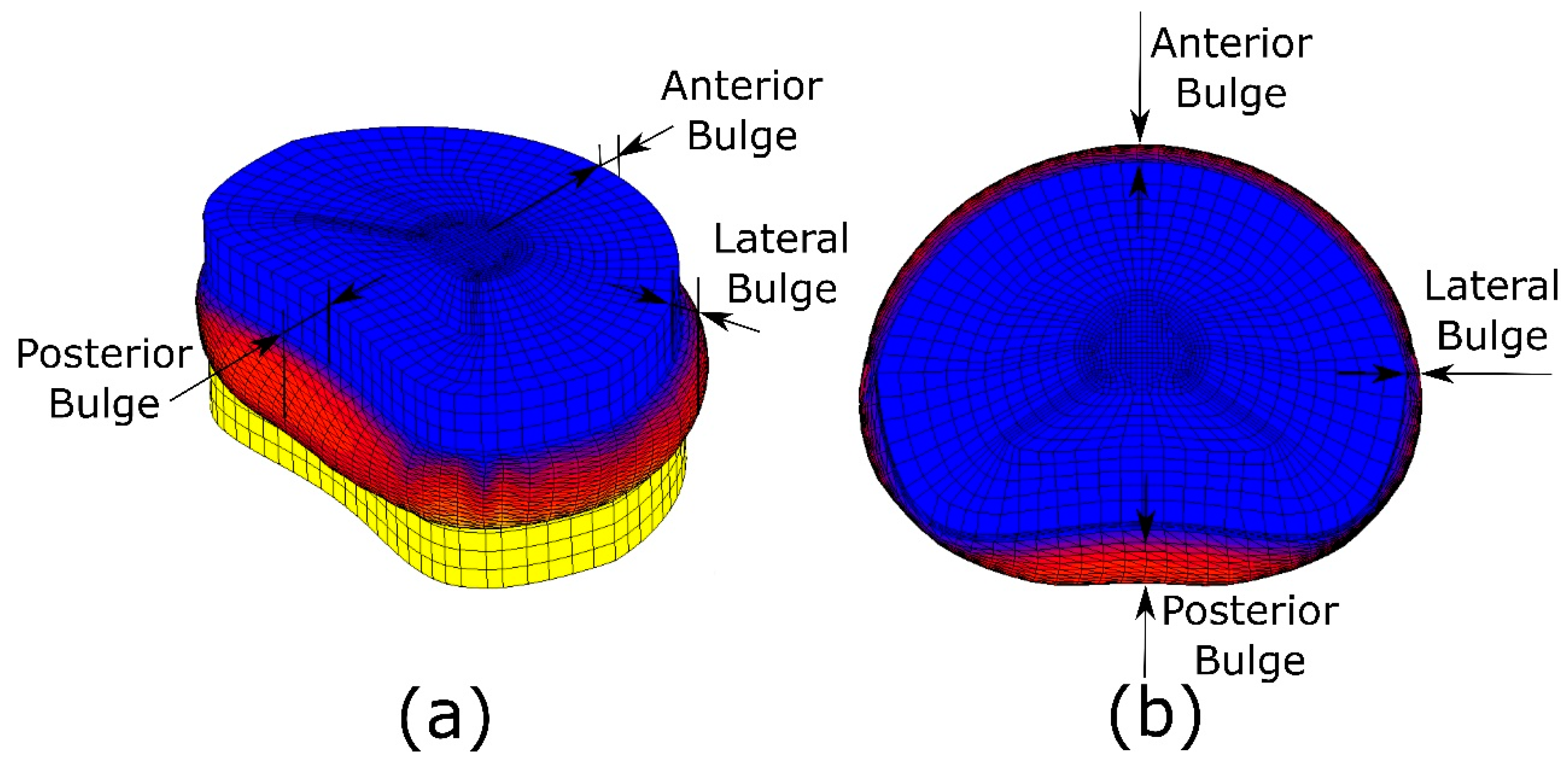
2.3. Bulge
2.4. Experimental Behavior of the Intervertebral Disc
2.4.1. Compression
2.4.2. Flexion and Extension
2.4.3. Lateral Bending
2.4.4. Shear and Torsion
3. FE Model for Modeling the Intervertebral Disc Proposed
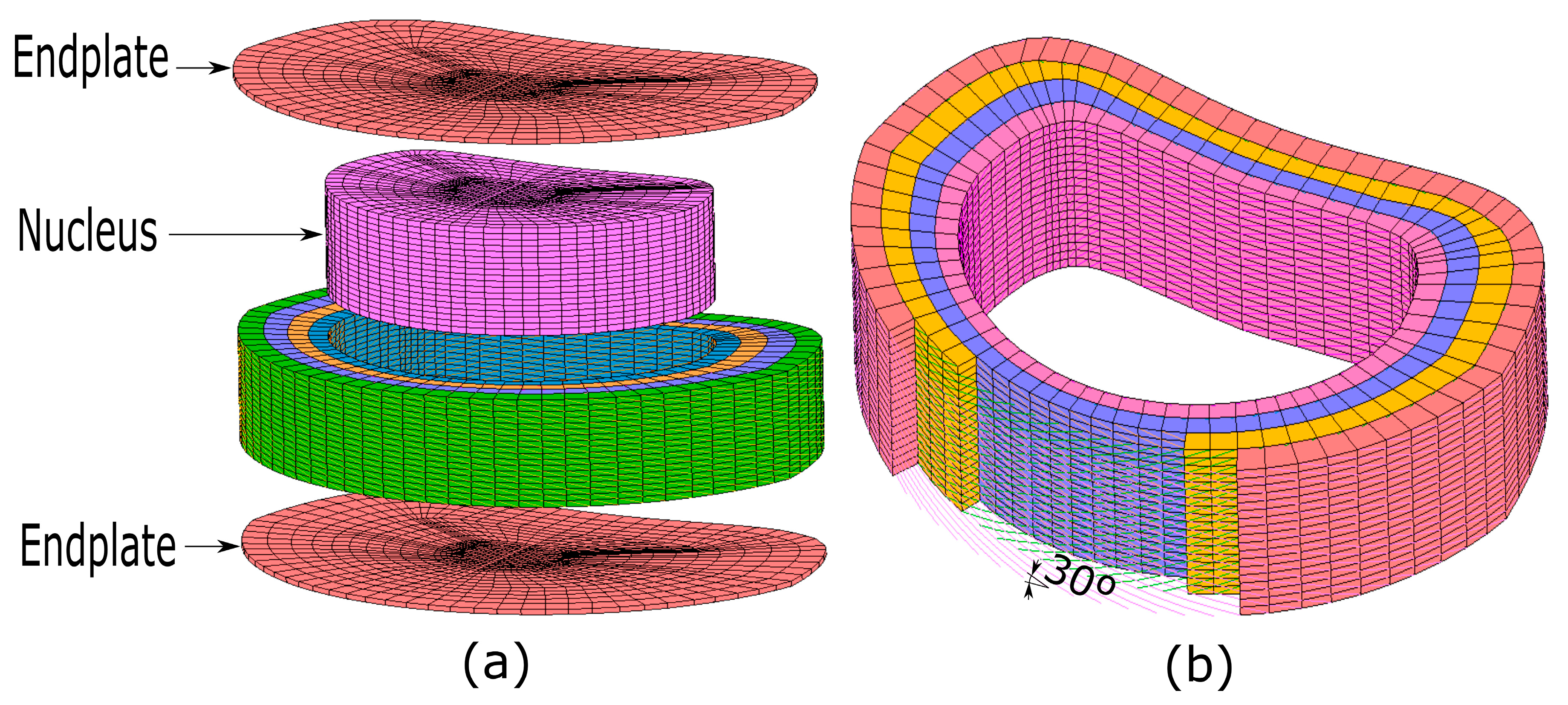
3.1. Configuration of the Finite Element Analysis and Mesh Size
3.2. Intervertebral Disc Dimensions
3.3. Boundary Conditions
4. Design of the Experiments and Design Matrix
4.1. Response Surface Method for Modeling and Optimizing Problems
4.2. Combining FEM and MRS to Optimize Mechanical Problems
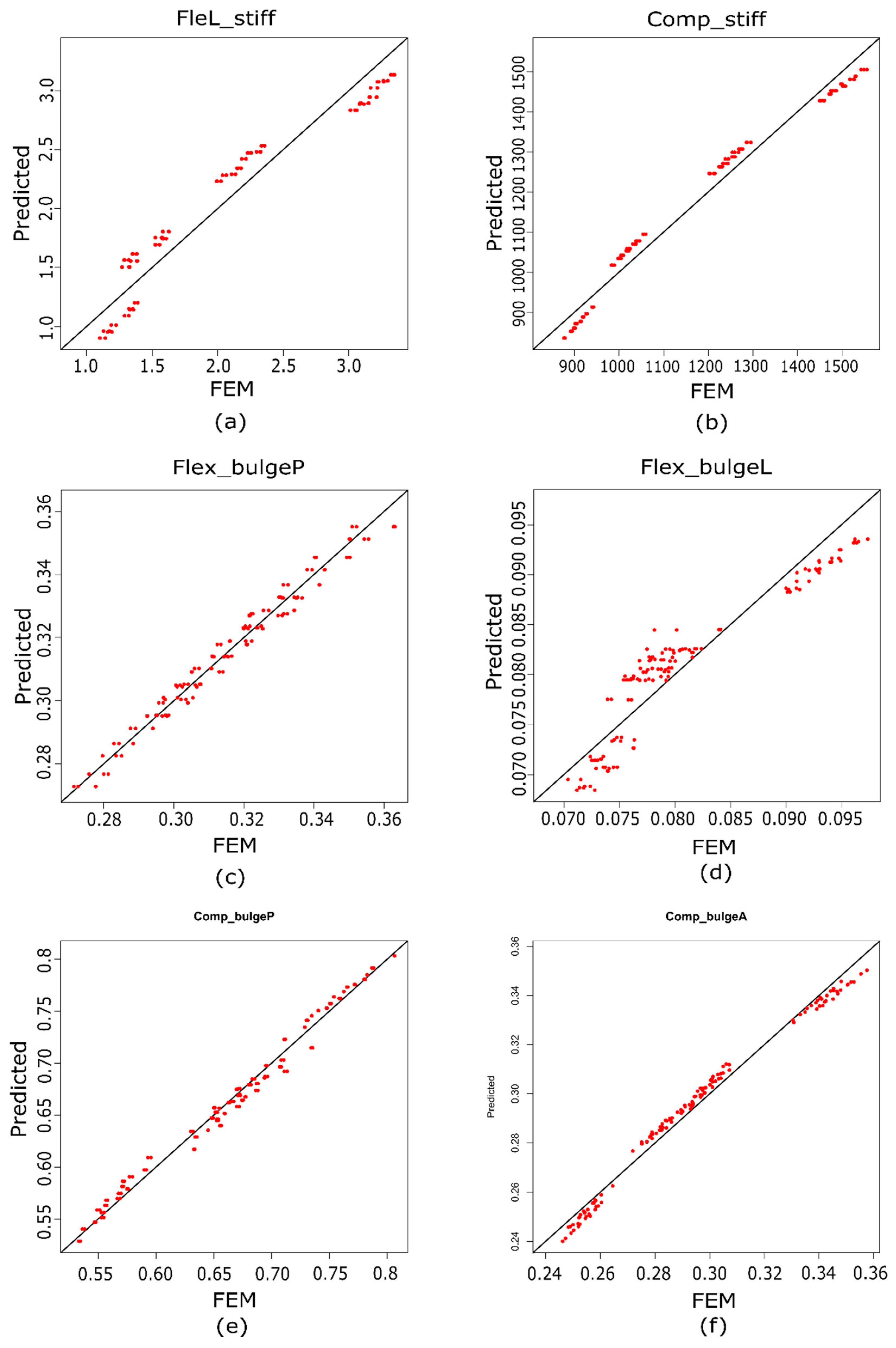
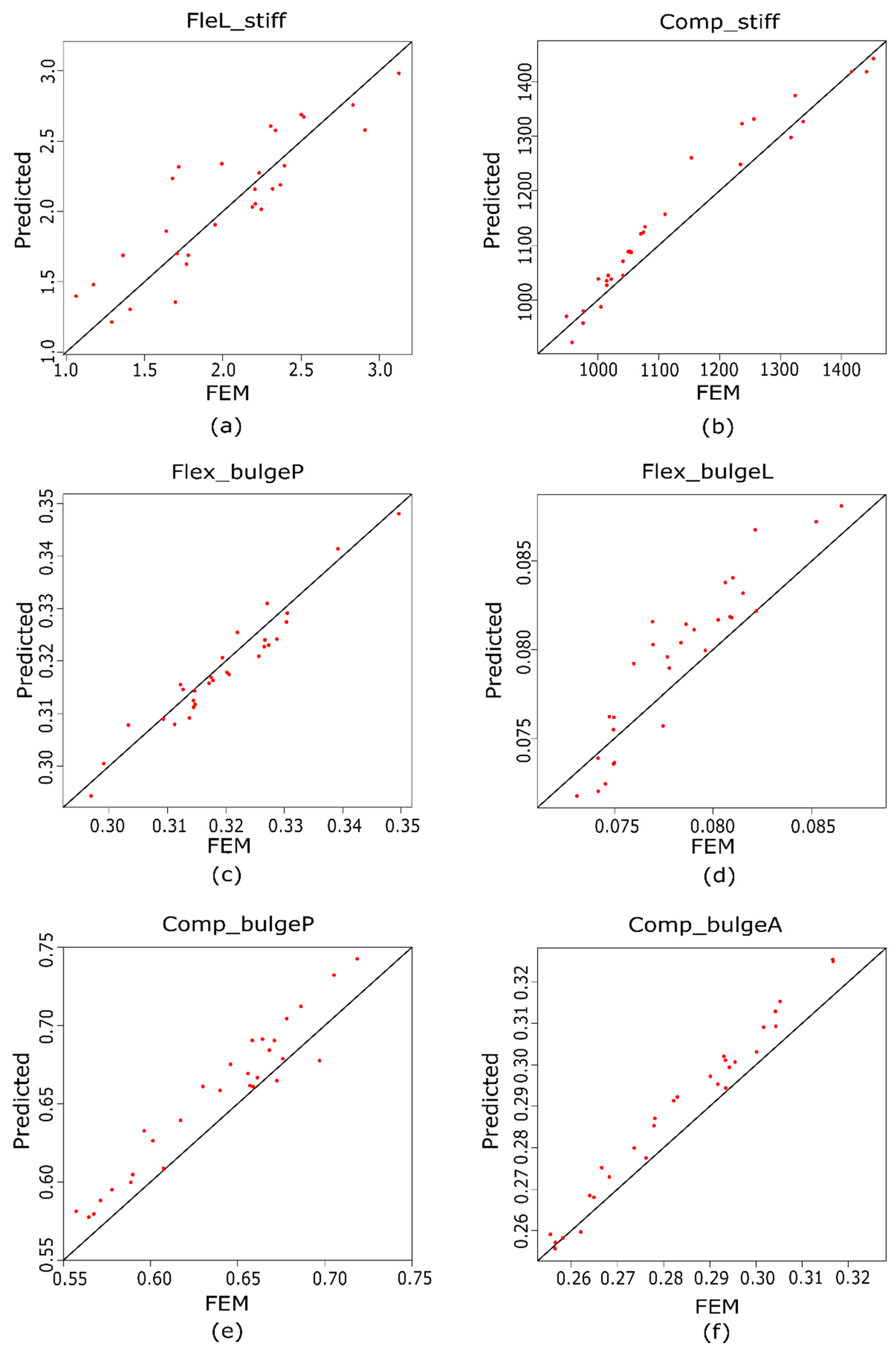
5. Results and Discussion
5.1. FE Models’ Results
5.2. Analysis of Variance
5.3. Multiple Response Optimization
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
List of Symbols/Nomenclature
| MAE | Mean Absolute Error | |
| C10 | Mooney-Rivlin parameter for annulus ground substance | |
| C0 | Mooney-Rivlin parameter for annulus ground substance | |
| Annulus_E | Young’s modulus for the annulus ground substance | (MPa) |
| Annulus_μ | Poisson’s modulus for the annulus ground substance | |
| Fiber12 | Collagen fibers layer 1 | (mm2) |
| Fiber34 | Collagen fibers layer 2 | (mm2) |
| Fiber56 | Collagen fibers layer 3 | (mm2) |
| Fiber78 | Collagen fibers layer 4 | (mm2) |
| Fiber910 | Collagen fibers layer 5 | (mm2) |
| Cartil_E | Young’s modulus for the endplate cartilage | (MPa) |
| Cartil_μ | Poisson’s modulus for the endplate cartilage | - |
| Comp_bulgeA | Bulge Anterior for the Compression Test | (mm) |
| Comp_bulgeL | Bulge Lateral for the Compression Test | (mm) |
| Comp_bulgeP | Bulge Posterior for the Compression Test | (mm) |
| Comp_stiff | Stiffness for the Compression Test | (N/mm) |
| Shear_stiff | Stiffness for the Shear Test | (N/mm) |
| Exte_bulgeL | Bulge Lateral for the Extension Test | (mm) |
| Exte_bulgeP | Bulge Posterior for the Extension Test | (mm) |
| Exte_stiff | Stiffness for the Extension Test | (Nm/°) |
| LBend_bulgeL | Bulge Lateral for the Lateral Bending Test | (mm) |
| LBend_bulgeP | Bulge Posterior for the Lateral Bending Test | (mm) |
| LBend_stiff | Stiffness for the Lateral Bending Test | (Nm/°) |
| Flex_bulgeL | Bulge Lateral for the Flexion Test | (mm) |
| Flex_bulgeP | Bulge Posterior for the Flexion Test | (mm) |
| Flex_stiff | Stiffness for the Flexion Test | (Nm/°) |
| Tors_stiff | Stiffness for the Torsion Test | (Nm/°) |
References
- DiZerega, G.S.; Traylor, M.M.; Alphonso, L.S.; Falcone, S.J. Use of Temporary Implantable Biomaterials to Reduce Leg Pain and Back Pain in Patients with Sciatica and Lumbar Disc Herniation. Materials 2010, 3, 3331–3368. [Google Scholar] [CrossRef]
- Denozière, G. Numerical Modeling of a Ligamentous Lumbar Motion Segment. 2004. Available online: http://www.epnet.com/academic/bussourceprem.asp (accessed on 20 September 2017).
- González Gutiérrez, R.A. Biomechanical Study of Intervertebral Disc Degeneration. Doctoral Thesis, Universitat Politècnica de Catalunya, Catalonia, Spain, 2012. [Google Scholar]
- Iatridis, J.C.; Setton, L.A.; Foster, R.J.; Rawlins, B.A.; Weidenbaum, M.; Mow, V.C. Degeneration affects the anisotropic and nonlinear behaviors of human anulus fibrosus in compression. J. Biomech. 1998, 31, 535–544. [Google Scholar] [CrossRef]
- Rostedt, M.; Ekström, L.; Broman, H.; Hansson, T. Axial stiffness of human lumbar motion segments, force dependence. J. Biomech. 1998, 31, 503–509. [Google Scholar] [CrossRef]
- Liu, Y.K.; Ray, G.; Hirsch, C. The resistance of the lumbar spine to direct shear. Orthop. Clin. N. Am. 1975, 6, 33–49. [Google Scholar]
- Gardner-Morse, M.G.; Stokes, I.A.F. Structural behavior of human lumbar spinal motion segments. J. Biomech. 2004, 37, 205–212. [Google Scholar] [CrossRef] [PubMed]
- Berkson, M.H.; Nachemson, A.L.; Schultz, A.B. Mechanical Properties of Human Lumbar Spine Motion Segments. Part II: Responses in Compression and Shear; Influence of Gross Morphology. J. Biomech. Eng. 1979, 101, 53–57. [Google Scholar] [CrossRef]
- Schultz, A.B.; Warwick, D.N.; Berkson, M.H.; Nachemson, A.L. Mechanical Properties of Human Lumbar Spine Motion Segments—Part I: Responses in Flexion, Extension, Lateral Bending, and Torsion. J. Biomech. Eng. 1979, 101, 46–52. [Google Scholar] [CrossRef]
- Guan, Y.; Yoganandan, N.; Zhang, J.; Pintar, F.A.; Cusick, J.F.; Wolfla, C.E.; Maiman, D.J. Validation of a clinical finite element model of the human lumbosacral spine. Med. Biol. Eng. Comput. 2006, 44, 633–641. [Google Scholar] [CrossRef] [PubMed]
- Shirazi-Adl, S.A.; Shrivastava, S.C.; Ahmed, A.M. Stress analysis of the lumbar disc-body unit in compression. A three-dimensional nonlinear finite element study. Spine 1984, 9, 120–134. [Google Scholar] [CrossRef] [PubMed]
- Fuerte Hernández, A. Caracterización de Vértebras Porcinas para su uso en Aplicaciones Biomecánicas. Master’s Thesis, Instituto Politécnico Nacional, Mexico City, Mexico, 2010. [Google Scholar]
- Cheung, J.T.; Zhang, M.; Leung, A.K.; Fan, Y.B. Three-dimensional finite element analysis of the foot during standing—A material sensitivity study. J. Biomech. 2005, 38, 1045–1054. [Google Scholar] [CrossRef] [PubMed]
- Halloran, J.P.; Petrella, A.J.; Rullkoetter, P.J. Explicit finite element modeling of total knee replacement mechanics. J. Biomech. 2005, 38, 323–331. [Google Scholar] [CrossRef] [PubMed]
- Biddiss, E.A.; Bogoch, E.R.; Meguid, S.A. Three-dimensional finite element analysis of prosthetic finger joint implants. Int. J. Mech. Mater. Des. 2005. [Google Scholar] [CrossRef]
- Elliott, B.; Goswami, T. Implant material properties and their role in micromotion and failure in total hip arthroplasty. Int. J. Mech. Mater. Des. 2012. [Google Scholar] [CrossRef]
- Lostado, R.; Martinez-De-Pison, F.J.; Pernia, A.; Alba, F.; Blanco, J. Combining regression trees and the finite element method to define stress models of highly non-linear mechanical systems. J. Strain Anal. Eng. Des. 2009, 44, 491–502. [Google Scholar] [CrossRef]
- Lostado, R.; Villanueva Roldán, P.; Fernandez Martinez, R.; Mac Donald, B.J. Design and optimization of an electromagnetic servo braking system combining finite element analysis and weight-based multi-objective genetic algorithms. J. Mech. Sci. Technol. 2016, 30, 3591–3605. [Google Scholar] [CrossRef]
- Lostado, R.; Fernandez Martinez, R.; Mac Donald, B.J.; Villanueva, P.M. Combining soft computing techniques and the finite element method to design and optimize complex welded products. Integr. Comput. Aided Eng. 2015, 22, 153–170. [Google Scholar] [CrossRef]
- Casaroli, G.; Villa, T.; Bassani, T.; Berger-Roscher, N.; Wilke, H.-J.; Galbusera, F. Numerical Prediction of the Mechanical Failure of the Intervertebral Disc under Complex Loading Conditions. Materials 2017, 10, 31. [Google Scholar] [CrossRef] [PubMed]
- Belytschko, T.; Kulak, R.; Schultz, A.; Galante, J. Finite element stress analysis of an intervertebral disc. J. Biomech. 1974, 7, 277–285. [Google Scholar] [CrossRef]
- Kulak, R.F.; Belytschko, T.B.; Schultz, A.B.; Galante, J.O. Nonlinear behavior of the human intervertebral disc under axial load. J. Biomech. 1976, 9, 377–386. [Google Scholar] [CrossRef]
- Yang, K.; King, A. Mechanism of facet load transmission as a hypothesis for low-back pain. Spine 1984, 9, 557–565. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, H.; Heuer, F.; Simon, U.; Kettler, A. Application of a new calibration method for a three-dimensional finite element model of a human lumbar annulus fibrosus. Clin. Biomech. 2006, 21, 337–344. [Google Scholar] [CrossRef] [PubMed]
- Ezquerro, F.; Vacas, F.G.; Postigo, S.; Prado, M.; Simón, A. Calibration of the finite element model of a lumbar functional spinal unit using an optimization technique based on differential evolution. Med. Eng. Phys. 2011. [Google Scholar] [CrossRef] [PubMed]
- Somovilla Gómez, F.; Lostado Lorza, R.; Fernandez Martinez, R.; Corral Bobadilla, M.; Escribano Garcia, R. A Proposed Methodology for Setting the Finite Element Models Based on Healthy Human Intervertebral Lumbar Discs. In HAIS 2016: Hybrid Artificial Intelligent Systems, Proceedings of the International Conference on Hybrid Artificial Intelligence Systems, Seville, Spain, 18–20 April 2016; Springer International Publishing: Cham, Switzerland, 2016; pp. 621–633. [Google Scholar]
- Lostado, R.; Escribano García, R.; Fernández Martínez, R. Optimization of operating conditions for a double-row tapered roller bearing. Int. J. Mech. Mater. Des. 2015. [Google Scholar] [CrossRef]
- Del Coz Diaz, J.J.; Garcia-Nieto, P.J.; Alvarez-Rabanal, F.P.; Alonso-Martínez, M.; Dominguez-Hernandez, J.; Perez-Bella, J.M. The use of response surface methodology to improve the thermal transmittance of lightweight concrete hollow bricks by FEM. Constr. Build. Mater. 2014, 52, 331–344. [Google Scholar] [CrossRef]
- Azaouzi, M.; Lebaal, N.; Rauchs, G.; Belouettar, S. Optimal design of multi-step stamping tools based on response surface method. Simul. Model. Pract. Theory 2012, 24, 1–14. [Google Scholar] [CrossRef]
- Baroud, G.; Nemes, J.; Heini, P.; Steffen, T. Load shift of the intervertebral disc after a vertebroplasty: A finite-element study. Eur. Spine J. 2003. [Google Scholar] [CrossRef] [PubMed]
- Shirazi-Adl, A. Nonlinear stress analysis of the whole lumbar spine in torsion—Mechanics of facet articulation. J. Biomech. 1994, 27, 289–299. [Google Scholar] [CrossRef]
- Shirazi-Adl, A.; Ahmed, A.M.; Shrivastava, S.C. Mechanical Response of a Lumbar Motion Segment in Axial Torque Alone and Combined with Compression. Spine 1986, 11, 914–927. [Google Scholar] [CrossRef] [PubMed]
- Pitzen, T.; Geisler, F.H.; Matthis, D.; Müller-Storz, H.; Pedersen, K.; Steudel, W.I. The influence of cancellous bone density on load sharing in human lumbar spine: A comparison between an intact and a surgically altered motion segment. Eur. Spine J. 2001, 10, 23–29. [Google Scholar] [CrossRef] [PubMed]
- Sharma, M.; Langrana, N.; Rodriguez, J. Role of ligaments and facets in lumbar spinal stability. Spine 1995, 20, 887–900. [Google Scholar] [CrossRef] [PubMed]
- Tsouknidas, A.; Michailidis, N.; Savvakis, S.; Anagnostidis, K.; Bouzakis, K.; Kapetanos, G. A Finite Element Model Template to Determine the Mechanical Response of a Lumbar Spine Segment Under Complex Loads. J. Appl. Biomech. 2012, 28, 448–456. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.-J.J.; Chun, H.-J.J.; Kang, K.-T.T. Finite Element Analysis for Comparison of Spinous Process Osteotomies Technique with Conventional Laminectomy as Lumbar Decompression Procedure. Yonsei Med. J. 2015, 56, 146–153. [Google Scholar] [CrossRef] [PubMed]
- Dicko, A.H.; Tong-Yette, N.; Gilles, B.; Faure, F.; Palombi, O. Construction and Validation of a Hybrid Lumbar Spine Model for the Fast Evaluation of Intradiscal Pressure and Mobility. Int. Sci. Index, Med. Health Sci. 2015, 9, 134–145. [Google Scholar]
- Ayturk, U.M. Alterations in Lumbar Spine Mechanics due to Degenerative Disc Disease. Doctoral Thesis, Colorado State University, Fort Collins, CO, USA, 2010. [Google Scholar]
- Grauer, J.N.; Biyani, A.; Faizan, A.; Kiapour, A.; Sairyo, K.; Ivanov, A.; Ebraheim, N.A.; Patel, T.C.; Goel, V.K. Biomechanics of two-level Charité artificial disc placement in comparison to fusion plus single-level disc placement combination. Spine J. 2006, 6, 659–666. [Google Scholar] [CrossRef] [PubMed]
- Dooris, A.; Goel, V.; Grosland, N.; Gilbertson, L. Load-sharing between anterior and posterior elements in a lumbar motion segment implanted with an artificial disc. Spine 2001, 26, E122–E129. [Google Scholar] [CrossRef] [PubMed]
- Smit, T.H.; Odgaard, A.; Schneider, E. Structure and function of vertebral trabecular bone. Spine 1997, 22, 2823–2833. [Google Scholar] [CrossRef] [PubMed]
- González Gutiérrez, R.A.; Rangel Alonso, V.; Gustavo Zambrano Rosas, J. Biomechanics of the Intervertebral Disc in Compression: Experimental and Numerical Study. J. Mech. Eng. Autom. 2015, 5, 39–44. [Google Scholar] [CrossRef]
- Lavaste, F.; Skalli, W.; Robin, S.; Roy-Camille, R.; Mazel, C. Three-dimensional geometrical and mechanical modelling of the lumbar spine. J. Biomech. 1992, 25, 1153–1164. [Google Scholar] [CrossRef]
- Schmidt, H.; Kettler, A.; Heuer, F.; Simon, U.; Claes, L.; Wilke, H.-J. Intradiscal Pressure, Shear Strain, and Fiber Strain in the Intervertebral Disc Under Combined Loading. Spine 2007, 32, 748–755. [Google Scholar] [CrossRef] [PubMed]
- Rohlmann, A.; Zander, T.; Bergmann, G. Effects of fusion-bone stiffness on the mechanical behavior of the lumbar spine after vertebral body replacement. Clin. Biomech. 2006, 21, 221–227. [Google Scholar] [CrossRef] [PubMed]
- Rohlmann, A.; Zander, T.; Schmidt, H.; Wilke, H.-J.; Bergmann, G. Analysis of the influence of disc degeneration on the mechanical behaviour of a lumbar motion segment using the finite element method. J. Biomech. 2006, 39, 2484–2490. [Google Scholar] [CrossRef] [PubMed]
- Ibarz, E.; Herrera, A.; Más, Y.; Rodríguez-Vela, J.; Cegoñino, J.; Puértolas, S.; Gracia, L. Development and kinematic verification of a finite element model for the lumbar spine: Application to disc degeneration. Biomed Res. Int. 2013. Available online: https://www.hindawi.com/journals/bmri/2013/705185/ (accessed on 20 May 2017). [CrossRef] [PubMed]
- Lu, Y.M.M.; Hutton, W.C.C.; Gharpuray, V.M.M. Do bending, twisting, and diurnal fluid changes in the disc affect the propensity to prolapse? A viscoelastic finite element model. Spine 1996, 21, 2570–2579. [Google Scholar] [CrossRef] [PubMed]
- Martinez, J.B.; Oloyede, V.O.A.; Broom, N.D. Biomechanics of load-bearing of the intervertebral disc: An experimental and finite element model. Med. Eng. Phys. 1997, 19, 145–156. [Google Scholar] [CrossRef]
- Denozière, G.; Ku, D.N. Biomechanical comparison between fusion of two vertebrae and implantation of an artificial intervertebral disc. J. Biomech. 2006, 39, 766–775. [Google Scholar] [CrossRef] [PubMed]
- Dietrich, M.; Kedzior, K.; Zagrajek, T. A biomechanical model of the human spinal system. Proc. Inst. Mech. Eng. H 1991, 205, 19–26. [Google Scholar] [CrossRef] [PubMed]
- Eberlain, R.; Holzapfel, G.A.; Shulze-Bauer, C.A.J. An Anisotropic Model for Annulus Tissue and Enhanced Finite Element Analyses of Intact Lumbar Disc Bodies. Comput. Methods Biomech. Biomed. Eng. 2001. [Google Scholar] [CrossRef]
- White, A.A.; Panjabi, M.M. Clinical Biomechanics of the Spine, 2nd ed.; Lippincott: New York, NY, USA, 1990. [Google Scholar]
- Hirsch, C.; Nachemson, A. New observations on the mechanical behavior of lumbar discs. Acta Orthop. Scand. 1954, 23, 254–283. [Google Scholar] [CrossRef] [PubMed]
- Brinckmann, P. Injury of the annulus fibrosus and disc protrusions. An in vitro investigation on human lumbar discs. Spine 1986, 11, 149–153. [Google Scholar] [CrossRef] [PubMed]
- Brinckmann, P.; Horst, M. The influence of vertebral body fracture, intradiscal injection, and partial discectomy on the radial bulge and height of human lumbar discs. Spine 1985, 10, 138–145. [Google Scholar] [CrossRef] [PubMed]
- Klein, J.A.; Hickey, D.S.; Hukins, D.W.L. Radial bulging of the annulus fibrosus during compression of the intervertebral disc. J. Biomech. 1983, 16, 211–217. [Google Scholar] [CrossRef]
- Reuber, M.; Schultz, A.; Denis, F.; Spencer, D. Bulging of Lumbar intervertebral disks. J. Biomech. Eng. 1982, 104, 187–192. [Google Scholar] [CrossRef] [PubMed]
- Brinckmann, P.; Grootenboer, H. Change of Disc Height, Radial Disc Bulge, and Intradiscal Pressure From Discectomy an in Vitro Investigation on Human Lumbar Discs. Spine 1991, 16, 641–646. [Google Scholar] [CrossRef] [PubMed]
- Virgin, W. Experimental investigations into the physical properties of the intervertebral disc. J. Bone Jt. Surg. Br. Vol. 1951, 33B, 607–611. [Google Scholar]
- Schultz, A.B.; Belytschko, T.B.; Andriacchi, T.P.; Galante, J.O. Analog studies of forces in the human spine: Mechanical properties and motion segment behavior. J. Biomech. 1973, 6, 373–383. [Google Scholar] [CrossRef]
- Markolf, K.L. Stiffness and damping characteristics of the thoracic-lumbar spine. In Proceedings of the Workshop on Bioengineering Approaches to the Problems of the Spine; National Institutes of Health: Washington, DC, USA, 1970. [Google Scholar]
- Rolander, S.D.; Blair, W.E. Deformation and fracture of the lumbar vertebral end plate. Orthop. Clin. N. Am. 1975, 6, 75–81. [Google Scholar]
- Brown, T.; Hanse, R.J.; Yorra, A.J. Some mechanical tests on the lumbosacral spine with particular reference to the intervertebral discs; a preliminary report. J. Bone Jt. Surg. Am. 1957, 39–A, 1135–1164. [Google Scholar] [CrossRef]
- Stokes, I.A.; Gardner-Morse, M.; Churchill, D.; Laible, J.P. Measurement of a spinal motion segment stiffness matrix. J. Biomech. 2002, 35, 517–521. [Google Scholar] [CrossRef]
- Panjabi, M.M.; Krag, M.H.; Chung, T.Q. Effects of Disc Injury on Mechanical Behavior of the Human Spine. Spine 1984, 9, 707–713. [Google Scholar] [CrossRef] [PubMed]
- Nachemson, A.L.; Schultz, A.B.; Berkson, M.H.; Warwick, D.N.; Berkson, M.H.; Nachemson, A.L. Mechanical Properties of Human Lumbar Spine Motion Segments. Influences of Age, Sex, Disc Level and Degeneration. J. Biomech. Eng. 1979, 4, 1–8. [Google Scholar]
- Moroney, S.P.; Schultz, A.B.; Miller, J.A.A.; Andersson, G.B.J. Load-displacement properties of lower cervical spine motion segments. J. Biomech. 1988, 21, 769–779. [Google Scholar] [CrossRef]
- Brown, M.D.; Holmes, D.C.; Heiner, A.D.; Wehman, K.F. Intraoperative measurement of lumbar spine motion segment stiffness. Spine 2002, 27, 954–958. [Google Scholar] [CrossRef] [PubMed]
- Keller, T.S.; Spengler, D.M.; Hansson, T.H. Mechanical behavior of the human lumbar spine. I. Creep analysis during static compressive loading. J. Orthop. Res. 1987, 5, 467–478. [Google Scholar] [CrossRef] [PubMed]
- Nachemson, A. Lumbar Intradiscal Pressure: Experimental Studies on Post-Mortem Material. Acta Orthop. 1960, 31, 1–104. [Google Scholar] [CrossRef]
- Miller, J.A.A.; Schultz, A.B.; Warwick, D.N.; Spencer, D.L. Mechanical properties of lumbar spine motion segments under large loads. J. Biomech. 1986, 19, 79–84. [Google Scholar] [CrossRef]
- Adams, M.A.; McNally, D.S.; Dolan, P. ‘Stress’ distributions inside intervertebral discs. The effects of age and degeneration. J. Bone Jt. Surg. Br. 1996, 78, 965–972. [Google Scholar] [CrossRef]
- Adams, M.A.; Hutton, W.; Stott, J.R. The Resistance to flexion of the Lumbar intervertebral joint. Spine 1980, 5, 245–253. [Google Scholar] [CrossRef] [PubMed]
- Guan, Y.; Yoganandan, N.; Moore, J.; Pintar, F.A.; Zhang, J.; Maiman, D.J.; Laud, P. Moment-rotation responses of the human lumbosacral spinal column. J. Biomech. 2007, 40, 1975–1980. [Google Scholar] [CrossRef] [PubMed]
- Busscher, I.; van Dieën, J.H.; Kingma, I.; van der Veen, A.J.; Verkerke, G.J.; Veldhuizen, A.G. Biomechanical characteristics of different regions of the human spine: An in vitro study on multilevel spinal segments. Spine (Phila. Pa. 1976) 2009, 34, 2858–2864. [Google Scholar] [CrossRef] [PubMed]
- Busscher, I.; van Der Veen, A.J.; van Dieën, J.H.; Kingma, I.; Verkerke, G.J.; Veldhuizen, A.G. In vitro biomechanical characteristics of the spine: A comparison between human and porcine spinal segments. Spine (Phila. Pa. 1976) 2010, 35, E35–E42. [Google Scholar] [CrossRef] [PubMed]
- Patwardhan, A.G.; Havey, R.M.; Carandang, G.; Simonds, J.; Voronov, L.I.; Ghanayem, A.J.; Meade, K.P.; Gavin, T.M.; Paxinos, O. Effect of compressive follower preload on the flexion—Extension response of the human lumbar spine. J. Orthop. Res. 2003. [Google Scholar] [CrossRef]
- White, A.A.; Panjabi, M.M. The basic kinematics of the human spine. A review of past and current knowledge. Spine (Phila. Pa. 1976) 1978, 3, 12–20. [Google Scholar] [CrossRef]
- Weisse, B.; Aiyangar, A.K.; Affolter, C.; Gander, R.; Terrasi, G.P.; Ploeg, H. Determination of the translational and rotational stiffnesses of an L4–L5 functional spinal unit using a specimen-specific finite element model. J. Mech. Behav. Biomed. Mater. 2012, 13, 45–61. [Google Scholar] [CrossRef] [PubMed]
- Farfan, H.F.; Cossette, J.W.; Robertson, G.H.; Wells, R.V.; Kraus, H. The Effects of Torsion on the Lumbar Intervertebral Joints. The Role of Torsion in the Production of Disc Degeneration. J. Bone Jt. Surg. 1970, 52, 468–497. [Google Scholar] [CrossRef]
- Adams, M.A.; Hutton, W.C. The Relevance of Torsion to the Mechanical derangement of the Lumbar Spine. Spine 1981, 6, 241–248. [Google Scholar] [CrossRef] [PubMed]
- Haughton, V.M.; Hong Lim, T.; An, H. Intervertebral Disk Appearance Correlated with Stiffness of Lumbar Spinal Motion Segments. AJNR Am. J. Neuroradiol. 1999, 20, 1161–1165. [Google Scholar] [PubMed]
- Vossen, B. Volumetric Locking in Finite Elements. Bachelor Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2008. [Google Scholar]
- Van der Veen, A.J.; Mullender, M.G.; Kingma, I.; van, J.H.; Smit, T.H. Contribution of verftebral bodies, endplates, and intervertebral discs to the compression creep of spinal motion segments. J. Biomech. 2008, 41, 1260–1268. [Google Scholar] [CrossRef] [PubMed]
- Natarajan, R.N.; Andersson, G.B. The influence of lumbar disc height and cross-sectional area on the mechanical response of the disc to physiologic loading. Spine (Phila. Pa. 1976) 1999, 24, 1873–1881. [Google Scholar] [CrossRef]
- Shirazi-Adl, S.A.; Shrivastrava, S.C.; Ahmed, A.M. A 3-D Nonlinear Finite Element Analysis of a Lumbar Disc with annulus modelled as a composite. In 1983 Biomechanics Symposium, Presented at the Applied Mechanics, Bioengineering, and Fluids Engineering Conference, Houston, TX, USA, 19–22 June 1983; The American Society of Mechanical Engineers: New York, NY, USA, 1983; p. 141. [Google Scholar]
- Zhou, S.H.; McCarthy, I.D.; McGregor, A.H.; Coombs, R.R.H.; Hughes, S.P.F. Geometrical dimensions of the lower lumbar vertebrae-analysis of data from digitised CT images. Eur. Spine J. 2000, 9, 242–248. [Google Scholar] [CrossRef] [PubMed]
- Friberg, S.; Hirsch, C. Anatomical and Clinical Studies on Lumbar Disc Degeneration. Acta Orthop. Scand. 1949, 19, 222–242. [Google Scholar] [CrossRef] [PubMed]
- Panjabi, M.M. The Stabilizing System of the Spine. Part I. Function, Dysfunction, Adaptation, and Enhancement. J. Spinal Disord. 1992, 5, 383–389. [Google Scholar] [CrossRef] [PubMed]
- Eijkelkamp, M.F. On the Development of An Artificial Intervertebral Disc. Ph.D. Thesis, University of Groningen, Groningen, The Netherlands, 2002. [Google Scholar]
- Nissan, M.; Gilad, I. Dimensions of human lumbar vertebrae in the sagittal plane. J. Biomech. 1986, 19, 753–758. [Google Scholar] [CrossRef]
- Tibrewal, S.B.; Pearcy, M.J. Lumbar intervertebral disc heights in normal subjects and patients with disc herniation. Spine (Phila. Pa. 1976) 1985, 10, 452–454. [Google Scholar] [CrossRef]
- Wolf, A.; Shoham, M.; Michael, S.; Moshe, R. Morphometric Study of the Human Lumbar Spine for Operation—Workspace Specifications. Spine (Phila. Pa. 1976) 2001, 26, 2472–2477. [Google Scholar] [CrossRef]
- Amonoo-Kuofi, H.S. Morphometric changes in the heights and anteroposterior diameters of the lumbar intervertebral discs with age. J. Anat. 1991, 175, 159–168. [Google Scholar] [PubMed]
- Heuer, F.; Schmidt, H.; Claes, L.; Wilke, H.-J.; Klezl, Z.; Claes, L.; Wilke, H.-J. Stepwise reduction of functional spinal structures increase range of motion and change lordosis angle. J. Biomech. 2007, 40, 271–280. [Google Scholar] [CrossRef] [PubMed]
- Tencer, A.F. Some Static Mechanical Properties of the Lumbar Intervertebral Joint, Intact and Injured. J. Biomech. Eng. 2009, 104, 193. [Google Scholar] [CrossRef]
- Yamamoto, I.; Panjabi, M.M.; Crisco, T.; Oxland, T. Three-dimensional movements of the whole lumbar spine and lumbosacral joint. Spine (Phila. Pa. 1976) 1989, 14, 1256–1260. [Google Scholar] [CrossRef]
- Hayes, M.A.; Howard, T.C.; Gruel, C.R.; Kopta, J.A. Roentgenographic evaluation of lumbar spine flexion-extension in asymptomatic individuals. Spine (Phila. Pa. 1976) 1989, 14, 327–331. [Google Scholar] [CrossRef]
- Dvorák, J.; Panjabi, M.M.; Chang, D.G.; Theiler, R.; Grob, D. Functional radiographic diagnosis of the lumbar spine. Flexion-extension and lateral bending. Spine (Phila. Pa. 1976) 1991, 16, 562–571. [Google Scholar] [CrossRef]
- Pearcy, M.; Portek, I.; Shepherd, J. Three-dimensional X-ray analysis of normal movement in the lumbar spine. Spine (Phila. Pa. 1976) 1984, 9, 294–297. [Google Scholar] [CrossRef]
- Fisher, R.A. The Design of Experiments, 2nd ed.; Hafner Publishing Company: New York, NY, USA, 1937. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Box, G.; Wilson, K. On the Experimental Attainment of Optimum Conditions. J. R. Stat. Soc. Ser. B 1951, 13, 1–45. [Google Scholar]
- Corral Bobadilla, M.; Lostado Lorza, R.; Escribano García, R.; Somovilla Gómez, F.; Vergara González, E. An Improvement in Biodiesel Production from Waste Cooking Oil by Applying Thought Multi-Response Surface Methodology Using Desirability Functions. Energies 2017, 10, 130. [Google Scholar] [CrossRef]
- Lostado, R.; Escribano García, R.; Martínez Calvo, M.; Múgica Vidal, R. Improvement in the Design of Welded Joints of EN 235JR Low Carbon Steel by Multiple Response Surface Methodology. Metals 2016, 6, 205. [Google Scholar] [CrossRef]
- Gelman, A. Analysis of variance? why it is more important than ever. Ann. Stat. 2005, 33, 1–53. [Google Scholar] [CrossRef]
- Derringer, G.; Suich, R. Simultaneous optimization of several response variables. J. Qual. Technol. 1980, 12, 214–219. [Google Scholar]
- Harrington, E. The desirability function. Ind. Qual. Control 1965, 21, 494–498. [Google Scholar]
- Kuhn, M. Desirability: Desirabiliy Function Optimization and Ranking. R Package v.1.6. Available online: https://cran.r-project.org/web/packages/desirability/index.html (accessed on 11 April 2017).
- Marwala, T. Finite-Element-Model Updating Using Computional Intelligence Techniques; Springer: London, UK, 2010. [Google Scholar]
- Lin, D.; Li, Q.; Li, W.; Zhou, S.; Swain, M.V. Design optimization of functionally graded dental implant for bone remodeling. Compos. Part B 2009, 40, 668–675. [Google Scholar] [CrossRef]
- Sadollah, A.; Bahreininejad, A. Optimum gradient material for a functionally graded dental implant using metaheuristic algorithms. J. Mech. Behav. Biomed. Mater. 2011, 4, 1384–1395. [Google Scholar] [CrossRef] [PubMed]
- Rungsiyakull, C.; Li, Q.; Sun, G.; Li, W.; Swain, M.V. Surface morphology optimization for osseointegration of coated implants. Biomaterials 2010, 31, 7196–7204. [Google Scholar] [CrossRef] [PubMed]
- Bahraminasab, M.; Sahari, B.B.; Edwards, K.L.; Farahmand, F.; Hong, T.S.; Arumugam, M.; Jahan, A. Multi-objective design optimization of functionally graded material for the femoral component of a total knee replacement. Mater. Des. 2014, 53, 159–173. [Google Scholar] [CrossRef]
- Lenth, R.V. Response-surface methods in R, using rsm. J. Stat. Softw. 2009, 32, 1–17. [Google Scholar] [CrossRef]
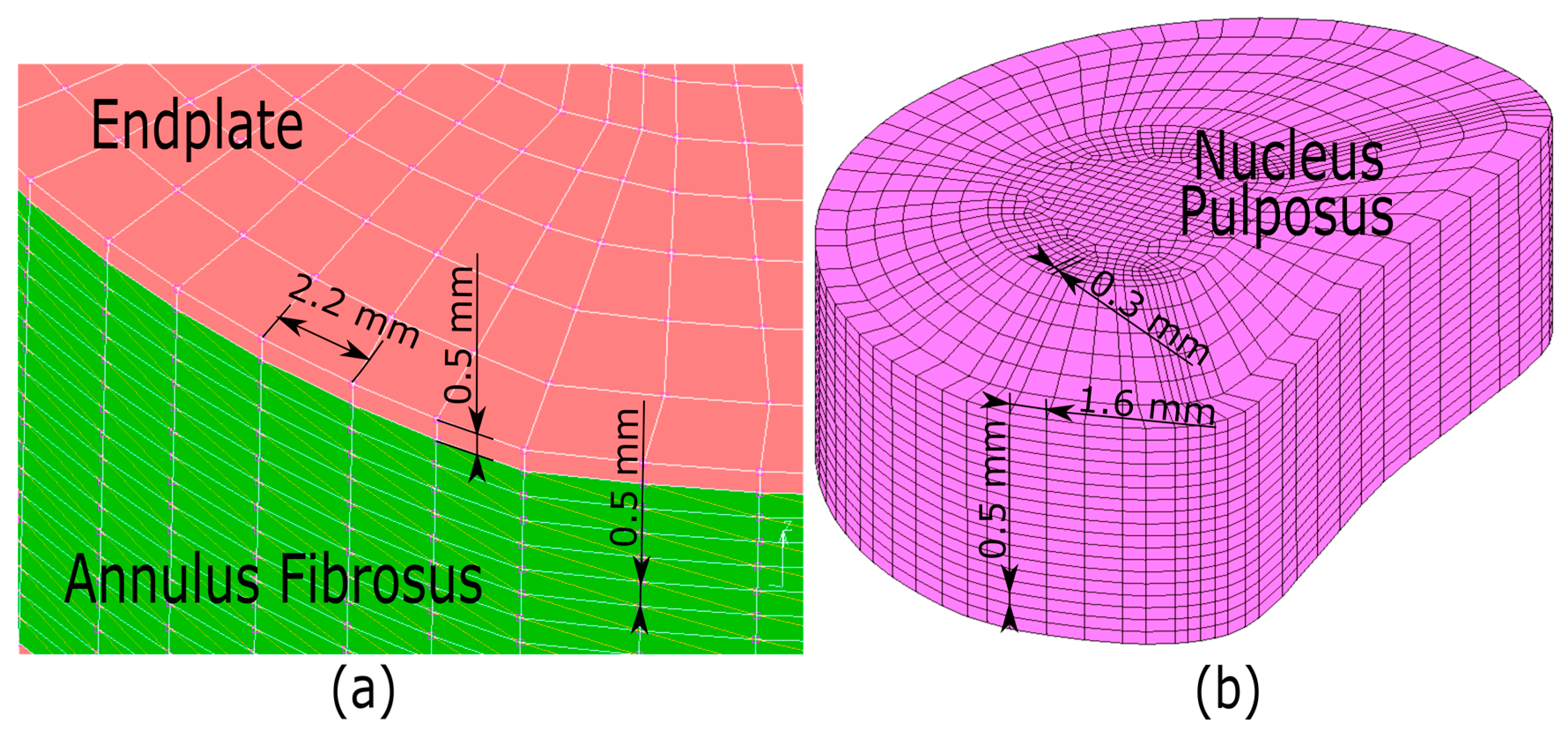
| Nucleus Pulposus | Cartilage Endplate | Annulus Ground | Annulus Fibers | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Authors | FE Parameters | FE Parameters | FE Parameters | FE Parameters | FE Parameters | |||||||||||
| Mooney-Rivlin Max. | Isotropic | Isotropic | Mooney-Rivlin | Isotropic | F1 | F2 | F3 | F4 | F5 | |||||||
| C10 | C0 | E | Μ | E | μ | C10 | C0 | E | μ | E | μ | |||||
| Kim and Chun (2015) [36] | - | - | 1 | 0.4999 | 24 | 0.40 | - | - | 4.2 | 0.45 | 550–358 | 0.3 | ||||
| Dicko et al. (2015) [37] | - | - | 1 | 0.4999 | 24 | 0.40 | 0.18 | 0.045 | - | 0.45 | Non-linear stress-strain curve | |||||
| González et al. (2015) [42] | 0.12 | 0.03 | 0.5 < E < 1 | 0.4 < μ < 0.5 | 20 | 0.3 | - | - | 0.75–5 | 0.35–0.5 | - | - | ||||
| Ibarz, Elena et al. (2014) [47] | 0.0343 | 0.1369 | - | - | - | - | - | - | 4.2 | 0.45 | 550 | 503 | 455 | 408 | 360 | 0.3 |
| Tsouknidas et al (2012) [35] | - | - | 0.2 | 0.4999 | - | - | - | - | 4.2 | 0.45 | 550 | 485 | 440 | 420 | 360 | 0.45 |
| Ayturk, U.M. (2010) [38] | - | - | 1 | 0.4999 | 23.8 | 0.8 | C10 = 0.0146; C20 = −0.0189; C30 = 0.041 | a3 = 0.03; b3 = 120 | ||||||||
| Schmidt, Kettler (2007) [44] | 0.12 | 0.03 | - | 0.4999 | 23.8 | 0.8 | 0.10 | 0.05 | 0.45 | * Stress-strain curve by Shirazi: σ = 23,000 × ε1.9 | ||||||
| Rohlmann et al. (2006) [46] | 0.10 | 0.09 | - | 0.4999 | 23.8 | 0.8 | 0.348 | 0.3 | 0.42 | 0.45 | * Stress-strain curve by Shirazi: σ = 23,000 × ε1.9 | |||||
| Rohlmann, Zander (2006) [45] | 0.10 | 0.09 | - | 0.4999 | - | - | 0.348 | 0.3 | 0.42 | 0.45 | * Stress-strain curve by Shirazi: σ = 23,000 × ε1.9 | |||||
| Grauer et al. (2006) [39] | - | - | 1 | 0.4999 | - | - | - | - | 4.2 | 0.45 | 175 | 175 | 175 | 175 | 175 | - |
| Dietrich, M. et al. (2005) [51] | - | - | 0.012 | 0.4999 | - | - | - | - | 10 | 0.35 | - | - | - | - | - | - |
| Denoziére, G. et al (2004) [2] | - | - | 0.1 | 0.4999 | 12 | 0.3 | - | - | 4.2 | 0.45 | 550 | 485 | 440 | 420 | 360 | 0.3 |
| Baroud et al. (2003) [30] | 0.12 | 0.03 | - | - | - | - | - | - | 8 | 0.45 | 500 | 485 | 420 | 360 | - | - |
| Pitzen et al. (2002) [33] | - | - | 0.1 | 0.4999 | - | - | - | - | 4.2 | 0.45 | 500 | 485 | 420 | 360 | - | - |
| Dooris et al. (2001) [40] | - | - | 1 | 0.49 | - | - | - | - | - | - | - | - | - | - | - | - |
| Eberlain et al. (2001) [52] | Incompress. Fluid | - | - | 23.8 | 0.4 | 0.348 | 0.3 | 4 | 0.4 | * Stress-strain curve by Shirazi:σ = 23,000 × ε1.9 | ||||||
| Martínez et al. (1997) [49] | - | - | - | - | 20 | 0.3 | - | 0.3 | - | - | - | - | - | - | - | - |
| Lu et al. (1996) [48] | - | - | - | - | 20 | 0.3 | - | - | 4.2 | 0.45 | - | - | - | - | - | - |
| Smit et al. (1997) [41] | 0.12 | 0.09 | 0.5 < E < 1 | 0.4999 | - | - | - | - | - | - | - | - | - | - | - | - |
| Sharma et al. (1995) [34] | 0.1 | 0.4999 | - | - | - | - | 4.2 | 0.5 | ||||||||
| Lavaste et al. (1992) [43] | - | - | 1 < E < 4 | 0.5 | - | - | - | - | - | - | - | - | - | - | - | - |
| Shirazi-Adl et al. (1984) [11] | Incompress. Fluid | - | - | - | - | - | - | 4.2 | 0.45 | σ = 23,000 × ε1.9 | ||||||
| Compression Test | |||
| Authors | Stiffness (N/mm) | Load (N) | Range of Load (N) |
| Moroney et al. (1988) [68] | 500 | 74 | |
| Brown et al. (2002) [69] | 400 | 200 | <400 |
| Keller et al. (1987) [70] | 247 | 253 | |
| Berkson et al. (1979) [8] | 800 | 400 | |
| Nachemson et al. (1979) [67] | 571 | 500 | |
| Rostedt et al. (1998) [5] | 810 | 500 | |
| Stokes et al. (2002) [65] | 510 | 500 | 850–500 |
| Panjabi et al. (1984) [66] | 750 | 600 | |
| Gardner-Morse et al. (2004) [7] | 2420 | 850 | |
| Hirsh and Nachemson (1954) [54] | 700 | 1000 | |
| Schultz et al. (1973) [61] | 1500 | 1000 | |
| González Gutierrez (2012) [3] | 833 | 1000 | |
| González Gutierrez (2012) [3] | 933 | 1000 | |
| González Gutierrez (2012) [3] | 1089 | 1000 | 5500–1000 |
| Markolf (1970) [62] | 1800 | 1800 | |
| Virgin (1951) [60] | 2500 | 4500 | |
| Rolander and Blair (1975) [63] | 3000 | 5000 | |
| Brown et al. (1957) [64] | 2300 | 5300 | |
| Bulges Values | |||
| Authors | Anterior/Post/Lateral (mm) | Load (N) | |
| Reuber et al. (1982) [58] | -/0.24/0.66 | 400 | |
| Schmidt, Kettler (2007) [44] | 0.7 to 0.9 | 500 | |
| Shirazi-Adl et al. (1984) [11] | 0.5/0.75/0.35 | 500 | |
| Shirazi-Adl et al. (1984) [11] | 0.7/1/0.4 | 720 | |
| Reuber et al. (1982) [58] | -/0.34/0.8 | 800 | |
| Brinckmann et al. (1991) [59] | 0.15 | 1000 | |
| González Gutierrez (2012) [3] | 0.69 | 1000 | |
| Shirazi-Adl et al. (1984) [11] | 0.8/1.5/0.6 | 1000 | |
| Nachemson, A. (1960) [71] | - | 2000 | |
| Denozière (2004) [2] | 0.5/0.7/0.4 | 2500 | |
| Klein et al. (1983) [57] | 0.6 | - | |
| Flexion/Extension Test | ||
| Authors | Stiffness Values (Nm/°) | Load (Nm) |
| Guan et al. (2007) [75] | 0.82/1.53 | 4 |
| Busscher et al. (2009) [76] | 0.8 | 4 |
| Busscher et al. (2010) [77] | 0.8 | 5 |
| González Gutierrez (2012) [3] | 1.18/1.38 | 5 |
| Patwardhan et al. (2003) [78] | 1.33 | 8 |
| White and Panjabi (1978) [79] | 0.8/2 | 10 |
| Nachemson et al. (1979) [67] | 2.03/3.53 | 10 |
| Gardner-Morse et al. (2004) [7] | 2.04 | 10 |
| Schultz et al. (1979) [9] | 1.92/3.55 | 10.6 |
| Adams et al. (1980) [74] | 1.34 | 10.7 |
| Schultz et al. (1973) [61] | 4.5 | 20 |
| Brown et al. (2002) [69] | 2 | 20 |
| Miller et al. (1986) [72] | 5.51/7.60 | 70 |
| Adams et al. (1996) [73] | 7.3 | 80 |
| Bulges Values | ||
| Authors | Anterior/Post/Lateral (mm) | Load (Nm) |
| Denoziére, G. et al. (2004) [2] | 1.3/1.9/2.6 | 10 |
| Reuber et al. (1982) [58] | -/0.73/0.07 | 3.9 |
| Reuber et al. (1982) [58] | -/1.11/0.21 | 7.9 |
| Lateral Bending Test | ||
| Authors | Stiffness Values (Nm/°) | Load (Nm) |
| Guan et al. (2007) [75] | 0.76 | 4 |
| Busscher et al. (2009) [76] | 0.5 | 4 |
| Busscher et al. (2010) [77] | 0.6 | 5 |
| González Gutierrez (2012) [3] | 1.58 | 5 |
| White and Panjabi (1978) [79] | 0.9 | 10 |
| Nachemson et al. (1979) [67] | 1.1 | 10 |
| Gardner-Morse et al. (2004) [7] | 1.29 | 10 |
| Schultz et al. (1979) [9] | 2 | 10.6 |
| Schultz et al. (1973) [61] | 2.8 | 20 |
| Miller et al. (1986) [72] | 4.35 | 60 |
| Bulges Values | ||
| Authors | Anterior/Post/Lateral (mm) | Load (Nm) |
| Reuber et al. (1982) [58] | -/0.49/0.83 | 3.9 |
| Reuber et al. (1982) [58] | -/1.13/2.11 | 9.8 |
| Shear Test | ||
| Authors | Stiffness (N/mm) | Load (N) |
| Moroney et al. (1988) [68] | 60 | 20 |
| Markolf (1970) [62] | 260 | 150 |
| Miller et al. (1986) [72] | 115 | 150 |
| Liu et al. (1975) [6] | 300 | 450 |
| Weisse et al. (2012) [80] | 830 | 950 |
| Schultz et al. (1979) [9] | 1000 | 980 |
| Schultz et al. (1973) [61] | 685 | 1000 |
| Torsion Test | ||
| Authors | Stiffness (Nm/°) | Load(Nm) |
| Busscher et al. (2009) [76] | 2.5 | 4 |
| Busscher et al. (2010) [77] | 1.6 | 5 |
| González Gutierrez (2012) [3] | 4.4 | 5 |
| Haughton et al. (1999) [83] | 7 | 6.6 |
| Adams et al. (1981) [82] | 1.44 | 7.4 |
| White and Panjabi (1978) [79] | 2.22 | 10 |
| Nachemson et al. (1979) [67] | 8.48 | 10 |
| Gardner-Morse et al. (2004) [7] | 2.1 | 10 |
| Schultz et al. (1979) [9] | 7.07 | 10.6 |
| Schultz et al. (1973) [61] | 4.5 | 30 |
| Farfan et al. (1970) [81] | 2 | 31 |
| Miller et al. (1986) [72] | 10.9 | 70 |
| Test | Author | Load Used | Stiffness | ||
| Compression | Rostedt et al. (1998) [5] | 500 N | 810 N/mm | ||
| Flexion | González Gutierrez (2012) [3] | 5 Nm | 1.18 Nm/° | ||
| Extension | Guan et al. (2007) [75] | 4 Nm | 1.53 Nm/° | ||
| Lateral Bending Bending | Schultz et al. (1979) [9] | 10.6 Nm | 2.0 Nm/° | ||
| Shear | Liu et al. (1975) [6] | 450 N | 300 N/mm | ||
| Torsion | Gardner-Morse et al. (2004) [7] | 10 Nm | 2.1 Nm/° | ||
| Test | Authors | Load Used | Bulge | Bulg | Bulge |
| Anterior (mm) | Posterior (mm) | Lateral (mm) | |||
| Compression | Shirazi-Adl et al. (1984) [11] | 500 N | 0.5 | 0.75 | 0.35 |
| Flexion | Reuber et al. (1982) [58] | 3.9 Nm | - | 0.73 | 0.07 |
| Extension | Reuber et al. (1982) [58] | 3.9 Nm | - | 0.24 | 0.1 |
| Lateral Bending | Reuber et al. (1982) [58] | 9.8 Nm | - | 1.13 | 2.11 |
| Tissue | FE Parameters | Tissue | FE Parameters | ||
|---|---|---|---|---|---|
| Min. | Max. | Min. | Max. | ||
| Nucleus Pulposus | Annulus Fibrosus | ||||
| C10 | 0.11 | 0.14 | Fiber12 | 515.0 | 550.0 |
| C0 | 0.02 | 0.04 | Fiber34 | 503.0 | 515.0 |
| Endplate | Fiber56 | 455.0 | 503.0 | ||
| E | 23.0 | 55.0 | Fiber78 | 408.0 | 455.0 |
| μ | 0.3 | 0.4 | Fiber910 | 360.0 | 408.0 |
| - | - | - | E Annulus Fibrosus | 4.0 | 4.2 |
| - | - | - | μ Annulus Fibrosus | 0.25 | 0.45 |
| Summary of Anatomical Dimensions of L1–L5 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Authors | Group Size (n) | Lumbar Level | Sex | Mean Age (From…to…) | Width (mm) | Depth (mm) | Height (mm) | Area (cm2) |
| Rostedt et al. (1998) [5] | 4 | L3–L4 | - | 45 | - | - | 12 | - |
| Schultz et al. (1979) [9] | 1 | L1–L5 | male | 35 | - | - | - | 1590 |
| Schultz et al. (1979) [9] | 1 | L1–L5 | male | 40 | - | - | - | 1680 |
| Schultz et al. (1979) [9] | 1 | L1–L5 | male | 53 | - | - | - | 1500 |
| Zhou et al. (2000) [88] | 55 | L3–L5 | male | 50 (22–80) | 53 | 37.5 | 12.2 | 1492 ± 173.8 |
| Zhou et al. (2000) [88] | 71 | L3–L5 | female | 49 (22–80) | 50.5 | 35.4 | 11.3 | 1492 ± 173.8 |
| Panjabi (1992) [90] | 60 | L1–L5 | - | 46.3 (19–59) | 48.1 | 34.7 | - | - |
| Eijkelkamp (2002) [91] | 60 | L1–L5 | - | (18–65) | - | - | 13.5 | - |
| Nissan and Gilad (1986) [92] | 157 | L1–L5 | - | 26.8 (20–38) | - | 34.6 | 10.8 | - |
| Tibrewal and Pearcy (1985) [93] | 11 | L1–L5 | - | 29.5 (25–36) | - | 33 | 9.8 | - |
| Wolf et al. (2001) [94] | 55 | L1–L5 | - | (20–90) | 44.1 | 31.7 | - | - |
| Amonoo-Kuofi (1991) [95] | 305 | L1–L5 | male | (10–64) | - | 42.8 | 13.5 | - |
| Amonoo-Kuofi (1991) [95] | 310 | L1–L5 | female | (10–61) | - | 39.9 | 13 | - |
| Schmidt et al. (2006) [24] | - | L4–L5 | - | - | 58.7 | 37.4 | - | - |
| Kim and Chun (2015) [36] | 1 | L4–L5 | male | 46 | - | - | - | 1119 |
| González et al. (2015) [42] | 5 | L2–L3 | male/female | (65–75) | - | - | 9.9 | 1739 |
| González et al. (2015) [42] | 5 | L4–L5 | male/female | (65–75) | - | - | 10 | 1951 |
| Shirazi-Adl et al. (1984) [11] | 1 | L2–L3 | female | 29 | 49.2 | 34 | 11 | 1371 |
| Smit et al. (1997) [41] | - | L4 | - | - | 42 | 35 | - | - |
| Ibarz, Elena et al. (2014) [47] | 25 | L5–S1 | 27.4 | |||||
| Ayturk, U.M. (2010) [38] | - | L1–L5 | female | 49 | - | |||
| Weisse et al. (2012) [80] | - | L4–L5 | male | 43 | 50.3 | 33.7 | 12.8 | - |
| Denozière (2004) [2] | - | L3–L4 | - | - | 50 | 35 | 10 | 1440 |
| Run | C10 | C0 | Fiber 12 | Fiber 34 | Fiber 56 | Fiber 78 | Fiber 910 | Annulus E | Annulus μ | Cartil E | Cartil μ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.11 | 0.02 | 515 | 503 | 455 | 408 | 360 | 4 | 0.25 | 55 | 0.4 |
| 2 | 0.14 | 0.02 | 515 | 503 | 455 | 408 | 360 | 4.2 | 0.45 | 23 | 0.3 |
| 3 | 0.11 | 0.04 | 515 | 503 | 455 | 408 | 360 | 4.2 | 0.45 | 23 | 0.4 |
| 4 | 0.14 | 0.04 | 515 | 503 | 455 | 408 | 360 | 4 | 0.25 | 55 | 0.3 |
| 5 | 0.11 | 0.02 | 550 | 503 | 455 | 408 | 360 | 4.2 | 0.45 | 55 | 0.3 |
| 6 | 0.14 | 0.02 | 550 | 503 | 455 | 408 | 360 | 4 | 0.25 | 23 | 0.4 |
| 7 | 0.11 | 0.04 | 550 | 503 | 455 | 408 | 360 | 4 | 0.25 | 23 | 0.3 |
| 8 | 0.14 | 0.04 | 550 | 503 | 455 | 408 | 360 | 4.2 | 0.45 | 55 | 0.4 |
| 9 | 0.11 | 0.02 | 515 | 515 | 455 | 408 | 360 | 4.2 | 0.25 | 23 | 0.4 |
| 10 | 0.14 | 0.02 | 515 | 515 | 455 | 408 | 360 | 4 | 0.45 | 55 | 0.3 |
| … | … | … | … | … | … | … | … | … | … | … | … |
| 120 | 0.14 | 0.04 | 550 | 503 | 503 | 455 | 408 | 4 | 0.45 | 23 | 0.4 |
| 121 | 0.11 | 0.02 | 515 | 515 | 503 | 455 | 408 | 4 | 0.25 | 55 | 0.4 |
| 122 | 0.14 | 0.02 | 515 | 515 | 503 | 455 | 408 | 4.2 | 0.45 | 23 | 0.3 |
| 123 | 0.11 | 0.04 | 515 | 515 | 503 | 455 | 408 | 4.2 | 0.45 | 23 | 0.4 |
| 124 | 0.14 | 0.04 | 515 | 515 | 503 | 455 | 408 | 4 | 0.25 | 55 | 0.3 |
| 125 | 0.11 | 0.02 | 550 | 515 | 503 | 455 | 408 | 4.2 | 0.45 | 55 | 0.3 |
| 126 | 0.14 | 0.02 | 550 | 515 | 503 | 455 | 408 | 4 | 0.25 | 23 | 0.4 |
| 127 | 0.11 | 0.04 | 550 | 515 | 503 | 455 | 408 | 4 | 0.25 | 23 | 0.3 |
| 128 | 0.14 | 0.04 | 550 | 515 | 503 | 455 | 408 | 4.2 | 0.45 | 55 | 0.4 |
| Run | Comp BulgeA | Comp BulgeL | Comp BulgeP | Comp Stiff | Shear Stiff | Exte BulgeL | Exte BulgeP | Exte Stiff | LBend BulgeL | LBend BulgeP | LBend Stiff | Flex BulgeL | Flex BulgeP | Flex Stiff | Tors Stiff |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.265 | 0.089 | 0.593 | 984.510 | 305.752 | 0.095 | 0.574 | 1.744 | 0.773 | 1.085 | 1.998 | 0.076 | 0.351 | 1.635 | 3.593 |
| 2 | 0.337 | 0.133 | 0.730 | 1271.883 | 281.371 | 0.137 | 0.830 | 2.121 | 0.970 | 1.929 | 1.581 | 0.095 | 0.288 | 1.762 | 3.264 |
| 3 | 0.347 | 0.140 | 0.758 | 1253.827 | 275.927 | 0.139 | 0.861 | 2.094 | 1.386 | 2.136 | 1.320 | 0.093 | 0.301 | 1.646 | 3.150 |
| 4 | 0.256 | 0.085 | 0.553 | 1017.076 | 315.425 | 0.096 | 0.566 | 1.779 | 0.798 | 1.051 | 2.257 | 0.073 | 0.303 | 1.686 | 3.640 |
| 5 | 0.298 | 0.094 | 0.665 | 1500.886 | 306.597 | 0.096 | 0.696 | 2.406 | 0.617 | 1.254 | 3.268 | 0.080 | 0.321 | 2.227 | 3.618 |
| 6 | 0.290 | 0.111 | 0.694 | 897.694 | 284.611 | 0.135 | 0.667 | 1.627 | 1.520 | 1.805 | 1.160 | 0.076 | 0.331 | 1.348 | 3.191 |
| 7 | 0.286 | 0.108 | 0.683 | 891.309 | 285.801 | 0.135 | 0.644 | 1.619 | 1.349 | 1.653 | 1.322 | 0.082 | 0.334 | 1.394 | 3.271 |
| 8 | 0.295 | 0.092 | 0.634 | 1548.473 | 316.704 | 0.095 | 0.685 | 2.461 | 0.672 | 1.188 | 3.215 | 0.076 | 0.280 | 2.309 | 3.682 |
| 9 | 0.290 | 0.113 | 0.711 | 901.414 | 289.552 | 0.132 | 0.661 | 1.661 | 1.531 | 1.892 | 1.130 | 0.078 | 0.349 | 1.338 | 3.320 |
| 10 | 0.304 | 0.095 | 0.670 | 1474.443 | 300.617 | 0.099 | 0.728 | 2.351 | 0.625 | 1.237 | 3.229 | 0.081 | 0.301 | 2.192 | 3.447 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 120 | 0.345 | 0.136 | 0.752 | 1256.486 | 278.278 | 0.139 | 0.875 | 2.063 | 1.322 | 2.070 | 1.382 | 0.090 | 0.284 | 1.673 | 3.016 |
| 121 | 0.260 | 0.088 | 0.596 | 989.416 | 313.213 | 0.094 | 0.574 | 1.749 | 0.778 | 1.086 | 1.990 | 0.076 | 0.352 | 1.635 | 3.665 |
| 122 | 0.333 | 0.131 | 0.731 | 1276.741 | 287.840 | 0.135 | 0.829 | 2.127 | 0.961 | 1.928 | 1.583 | 0.094 | 0.289 | 1.766 | 3.318 |
| 123 | 0.342 | 0.139 | 0.760 | 1258.926 | 282.358 | 0.137 | 0.860 | 2.100 | 1.374 | 2.137 | 1.325 | 0.092 | 0.302 | 1.652 | 3.201 |
| 124 | 0.252 | 0.085 | 0.555 | 1022.062 | 322.997 | 0.095 | 0.565 | 1.783 | 0.801 | 1.052 | 2.250 | 0.073 | 0.304 | 1.686 | 3.723 |
| 125 | 0.294 | 0.092 | 0.667 | 1507.286 | 314.067 | 0.094 | 0.693 | 2.414 | 0.614 | 1.251 | 3.262 | 0.079 | 0.322 | 2.230 | 3.670 |
| 126 | 0.286 | 0.110 | 0.697 | 901.330 | 291.307 | 0.133 | 0.667 | 1.630 | 1.524 | 1.809 | 1.160 | 0.076 | 0.332 | 1.350 | 3.255 |
| 127 | 0.282 | 0.107 | 0.685 | 894.800 | 292.534 | 0.134 | 0.644 | 1.621 | 1.351 | 1.654 | 1.321 | 0.082 | 0.335 | 1.395 | 3.333 |
| 128 | 0.291 | 0.091 | 0.635 | 1555.367 | 324.328 | 0.093 | 0.684 | 2.469 | 0.670 | 1.186 | 3.210 | 0.076 | 0.281 | 2.310 | 3.740 |
| Compression Bulge Anterior BulgeL | ||||||
|---|---|---|---|---|---|---|
| Var. | Df | Sum of Sq. | Mean Square | F Value | p-Value | Significance Code |
| C10 | 1 | 0.00066 | 0.00066 | 35.8 | 2.41 × 10−8 | *** |
| C0 | 1 | 0.00031 | 0.00031 | 16.7 | 8.01 × 10−5 | *** |
| Fiber12 | 1 | 0.00008 | 0.00008 | 4.1 | 4.47 × 10−2 | * |
| Fiber56 | 1 | 0.00006 | 0.00006 | 3.1 | 7.96 × 10−2 | . |
| Fiber78 | 1 | 0.00004 | 0.00004 | 2.0 | 1.58 × 10−1 | |
| Fiber910 | 1 | 0.00005 | 0.00005 | 2.6 | 1.09 × 10−1 | |
| Annulus_E | 1 | 0.00149 | 0.00149 | 81.5 | 4.25 × 10−15 | *** |
| Annulus_μ | 1 | 0.08796 | 0.08796 | 4805.3 | <2.2 × 10−16 | *** |
| Cartil_E | 1 | 0.04237 | 0.04237 | 2314.5 | <2.2 × 10−16 | *** |
| Cartil_μ | 1 | 0.00054 | 0.00054 | 29.4 | 3.24 × 10−7 | *** |
| Residuals | 117 | 0.00214 | 0.00002 | |||
| Compression Bulge Lateral | ||||||
|---|---|---|---|---|---|---|
| Var. | Df | Sum of Sq. | Mean Square | F Value | p-Value | Significance Code |
| C10 | 1 | 0.00021 | 0.00021 | 8.3 | 4.73 × 10−3 | ** |
| C0 | 1 | 0.00010 | 0.00010 | 3.9 | 5.12 × 10−2 | . |
| Fiber12 | 1 | 0.00010 | 0.00010 | 4.0 | 4.89 × 10−2 | * |
| Annulus_E | 1 | 0.00005 | 0.00005 | 2.0 | 1.60 × 10−1 | |
| Annulus_μ | 1 | 0.00999 | 0.00999 | 398.4 | <2.2 × 10−16 | *** |
| Cartil_E | 1 | 0.03378 | 0.03378 | 1347.0 | <2.2 × 10−16 | *** |
| Cartil_μ | 1 | 0.00031 | 0.00031 | 12.3 | 6.31 × 10−4 | *** |
| Residuals | 1200 | 0.00301 | 0.00003 | |||
| Compression Bulge Posterior | ||||||
|---|---|---|---|---|---|---|
| Var. | Df | Sum of Sq. | Mean Square | F Value | p-Value | Significance Code |
| C10 | 1 | 0.02444 | 0.02444 | 323.4 | <2.2 × 10−16 | *** |
| C0 | 1 | 0.01072 | 0.01072 | 141.9 | <2.2 × 10−16 | *** |
| Annulus_E | 1 | 0.01647 | 0.01647 | 217.9 | <2.2 × 10−16 | *** |
| Annulus_μ | 1 | 0.25063 | 0.25063 | 3316.3 | <2.2 × 10−16 | *** |
| Cartil_E | 1 | 0.35753 | 0.35753 | 4730.9 | <2.2 × 10−16 | *** |
| Cartil_μ | 1 | 0.00439 | 0.00439 | 58.2 | 6.11 × 10−12 | *** |
| Residuals | 121 | 0.00914 | 0.00008 | |||
| Compression Stiffness | ||||||
|---|---|---|---|---|---|---|
| Var. | Df | Sum of Sq. | Mean Square | F Value | p-Value | Significance Code |
| C10 | 1 | 19,462 | 19,462 | 14.7 | 2.00 × 10−4 | *** |
| C0 | 1 | 8911 | 8911 | 6.7 | 1.06 × 10−2 | * |
| Annulus_E | 1 | 41,500 | 41,500 | 31.4 | 1.34 × 10−7 | *** |
| Annulus_μ | 1 | 5,389,427 | 5,389,427 | 4074.1 | <2.2 × 10−16 | *** |
| Cartil_E | 1 | 1,054,628 | 1,054,628 | 797.2 | <2.2 × 10−16 | *** |
| Residuals | 122 | 161,387 | 1323 | |||
| Shear Stiffness | ||||||
|---|---|---|---|---|---|---|
| Var. | Df | Sum of Sq. | Mean Square | F Value | p-Value | Significance Code |
| C10 | 1 | 1148.2 | 1148.2 | 438.8 | <2.2 × 10−16 | *** |
| C0 | 1 | 510.6 | 510.6 | 195.1 | <2.2 × 10−16 | *** |
| Fiber12 | 1 | 18.4 | 18.4 | 7.0 | 9.15 × 10−3 | ** |
| Fiber34 | 1 | 14.0 | 14.0 | 5.4 | 2.24 × 10−2 | * |
| Fiber56 | 1 | 73.8 | 73.8 | 28.2 | 5.34 × 10−7 | *** |
| Fiber78 | 1 | 233.3 | 233.3 | 89.2 | 4.82 × 10−16 | *** |
| Fiber910 | 1 | 144.4 | 144.4 | 55.2 | 2.02 × 10−11 | *** |
| Annulus_E | 1 | 4328.4 | 4328.4 | 1654.0 | <2.2 × 10−16 | *** |
| Annulus_μ | 1 | 6817.7 | 6817.7 | 2605.3 | <2.2 × 10−16 | *** |
| Cartil_E | 1 | 28,143.4 | 28,143.4 | 10,754.5 | <2.2 × 10−16 | *** |
| Cartil_μ | 1 | 89.4 | 89.4 | 34.2 | 4.73 × 10−8 | *** |
| Residuals | 116 | 303.6 | 2.6 | |||
| Extension Bulge Lateral Stiffness | ||||||
|---|---|---|---|---|---|---|
| Var. | Df | Sum of Sq. | Mean Square | F Value | p-Value | Significance Code |
| Fiber910 | 1 | 0.00189 | 0.00189 | 12.9 | 4.62 × 10−4 | *** |
| Annulus_μ | 1 | 0.00101 | 0.00101 | 6.9 | 9.74 × 10−3 | ** |
| Cartil_E | 1 | 0.04221 | 0.04221 | 288.7 | <2.2 × 10−16 | *** |
| Residuals | 1244 | 0.01813 | 0.00015 | |||
| Extension Bulge Posterior | ||||||
|---|---|---|---|---|---|---|
| Var. | Df | Sum of Sq. | Mean Square | F Value | p-Value | Significance Code |
| Fiber910 | 1 | 0.29 | 0.29 | 17.9 | 4.54 × 10−5 | *** |
| Annulus_μ | 1 | 0.74 | 0.74 | 45.6 | 4.90 × 10−10 | *** |
| Cartil_E | 1 | 0.41 | 0.41 | 25.0 | 1.94 × 10−6 | *** |
| Residuals | 124 | 2.02 | 0.02 | |||
| Extension Stiffness | ||||||
|---|---|---|---|---|---|---|
| Var. | Df | Sum of Sq. | Mean Square | F Value | p-Value | Significance Code |
| Fiber910 | 1 | 13.2 | 13.2 | 20.4 | 1.45 × 10−5 | *** |
| Annulus_μ | 1 | 8.6 | 8.6 | 13.3 | 3.88 × 10−4 | *** |
| Cartil_E | 1 | 2.3 | 2.3 | 3.5 | 6.42 × 10−2 | . |
| Residuals | 124 | 80.4 | 0.6 | |||
| Lateral Bending Bulge Lateral | ||||||
|---|---|---|---|---|---|---|
| Var. | Df | Sum of Sq. | Mean Square | F Value | p-Value | Significance Code |
| C10 | 1 | 0.03 | 0.03 | 3.2 | 7.57 × 10−2 | . |
| Annulus_μ | 1 | 1.11 | 1.11 | 119.9 | <2.0 × 10−16 | *** |
| Cartil_E | 1 | 10.27 | 10.27 | 1112.5 | <2.0 × 10−16 | *** |
| Cartil_μ | 1 | 0.84 | 0.84 | 91.0 | <2.0 × 10−16 | *** |
| Residuals | 123 | 1.14 | 0.01 | |||
| Lateral Bending Bulge Posterior | ||||||
|---|---|---|---|---|---|---|
| Var. | Df | Sum of Sq. | Mean Square | F Value | p-Value | Significance Code |
| C10 | 1 | 0.26 | 0.26 | 53.7 | 2.84 × 10−11 | *** |
| C0 | 1 | 0.12 | 0.12 | 25.5 | 1.59 × 10−6 | *** |
| Annulus_E | 1 | 0.06 | 0.06 | 11.8 | 8.21 × 10−4 | *** |
| Annulus_μ | 1 | 2.34 | 2.34 | 478.3 | <2.2 × 10−16 | *** |
| Cartil_E | 1 | 17.71 | 17.71 | 3624.2 | <2.2 × 10−16 | *** |
| Cartil_μ | 1 | 0.23 | 0.23 | 47.1 | 3.06 × 10−10 | *** |
| Residuals | 121 | 0.59 | 0.00 | |||
| Lateral Bending Stiffness | ||||||
|---|---|---|---|---|---|---|
| Var. | Df | Sum of Sq. | Mean Square | F Value | p-Value | Significance Code |
| C10 | 1 | 0.08 | 0.08 | 1.9 | 1.68 × 10−1 | |
| Annulus_E | 1 | 0.11 | 0.11 | 2.6 | 1.10 × 10−1 | |
| Annulus_μ | 1 | 11.63 | 11.63 | 265.9 | <2.2 × 10−16 | *** |
| Cartil_E | 1 | 56.69 | 56.69 | 1295.7 | <2.2 × 10−16 | *** |
| Cartil_μ | 1 | 1.15 | 1.15 | 26.3 | 1.11 × 10−6 | *** |
| Residuals | 122 | 5.34 | 0.04 | |||
| Flexion Bulge Lateral | ||||||
|---|---|---|---|---|---|---|
| Var. | Df | Sum of Sq. | Mean Square | F Value | p-Value | Significance Code |
| C10 | 1 | 0.00012 | 0.00012 | 15.7 | 1.25 × 10−4 | *** |
| C0 | 1 | 0.00005 | 0.00005 | 6.2 | 1.38 × 10−2 | * |
| Fiber12 | 1 | 0.00004 | 0.00004 | 5.0 | 2.74 × 10−2 | * |
| Annulus_E | 1 | 0.00002 | 0.00002 | 3.0 | 8.73 × 10−2 | . |
| Annulus_μ | 1 | 0.00313 | 0.00313 | 416.0 | <2.2 × 10−16 | *** |
| Cartil_E | 1 | 0.00316 | 0.00316 | 420.0 | <2.2 × 10−16 | *** |
| Cartil_μ | 1 | 0.00012 | 0.00012 | 15.5 | 1.42 × 10−4 | *** |
| Residuals | 120 | 0.00090 | 0.00001 | |||
| Flexion Bulge Posterior | ||||||
|---|---|---|---|---|---|---|
| Var. | Df | Sum of Sq. | Mean Square | F Value | p-Value | Significance Code |
| C10 | 1 | 0.024 | 0.024 | 2130.8 | <2.2 × 10−16 | *** |
| C0 | 1 | 0.011 | 0.011 | 949.1 | <2.2 × 10−16 | *** |
| Annulus_E | 1 | 0.003 | 0.003 | 264.3 | <2.2 × 10−16 | *** |
| Annulus_μ | 1 | 0.016 | 0.016 | 1429.9 | <2.2 × 10−16 | *** |
| Cartil_μ | 1 | 0.000 | 0.000 | 43.1 | 1.36 × 10−9 | *** |
| Residuals | 122 | 0.001 | 0.000 | |||
| Flexion Stiffness | ||||||
|---|---|---|---|---|---|---|
| Var. | Df | Sum of Sq. | Mean Square | F Value | p-Value | Significance Code |
| C10 | 1 | 0.059 | 0.059 | 13.0 | 4.45 × 10−4 | *** |
| C0 | 1 | 0.027 | 0.027 | 5.9 | 1.68 × 10−2 | * |
| Annulus_E | 1 | 0.093 | 0.093 | 20.5 | 1.39 × 10−5 | *** |
| Annulus_μ | 1 | 5.643 | 5.643 | 1243.7 | <2.2 × 10−16 | *** |
| Cartil_E | 1 | 5.706 | 5.706 | 1257.6 | <2.2 × 10−16 | *** |
| Cartil_μ | 1 | 0.044 | 0.044 | 9.6 | 2.42 × 10−3 | ** |
| Residuals | 121 | 0.549 | 0.005 | |||
| Torsion Stiffness | ||||||
|---|---|---|---|---|---|---|
| Var. | Df | Sum of Sq. | Mean Square | F Value | p-Value | Significance Code |
| C10 | 1 | 0.032 | 0.032 | 21.0 | 1.13 × 10−5 | *** |
| C0 | 1 | 0.010 | 0.010 | 6.8 | 1.03 × 10−2 | * |
| Fibra34 | 1 | 0.032 | 0.032 | 20.9 | 1.22 × 10−5 | *** |
| Fiber56 | 1 | 0.016 | 0.016 | 10.6 | 1.47 × 10−3 | ** |
| Fiber78 | 1 | 0.102 | 0.102 | 66.8 | 3.84 × 10−13 | *** |
| Annulus_E | 1 | 1.056 | 1.056 | 691.1 | <2.2 × 10−16 | *** |
| Annulus_μ | 1 | 1.049 | 1.049 | 685.9 | <2.2×10−16 | *** |
| Cartil_E | 1 | 5.539 | 5.539 | 3623.7 | <2.2 × 10−16 | *** |
| Cartil_μ | 1 | 0.087 | 0.087 | 56.9 | 1.04 × 10−11 | *** |
| Residuals | 118 | 0.180 | 0.002 | |||
| Errors and Correlations | Comp_BulgeA | Comp_BulgeL | Comp_BulgeP | Comp_Stiff | Shear_Stiff |
| Correlation | 99.189 | 96.861 | 99.180 | 98.784 | 99.636 |
| MAE | 3.384 | 7.353 | 2.839 | 5.166 | 1.740 |
| RMSE | 3.710 | 7.786 | 3.433 | 5.228 | 2.190 |
| Exte_BulgeL | Exte_BulgeP | Exte_Stiff | LBend_BulgeL | LBen_BulgeP | |
| Correlation | 84.457 | 64.532 | 48.035 | 95.663 | 98.603 |
| MAE | 11.141 | 13.241 | 13.973 | 8.023 | 4.176 |
| RMSE | 17.393 | 19.936 | 21.812 | 9.483 | 5.135 |
| LBend_Stiff | Flex_BulgeL | Flex_BulgeP | Flex_Stiff | Tors_Stiff | |
| Correlation | 96.376 | 93.817 | 98.757 | 97.709 | 98.881 |
| MAE | 8.956 | 8.864 | 3.203 | 6.036 | 3.257 |
| RMSE | 9.072 | 9.840 | 3.607 | 6.441 | 3.997 |
| Errors and Correlations | Comp_BulgeA | Comp_BulgeL | Comp_BulgeP | Comp_Stiff | Shear_Stiff |
| Correlation | 98.801 | 95.648 | 95.429 | 97.603 | 94.763 |
| MAE | 5.998 | 12.781 | 8.063 | 4.835 | 6.320 |
| RMSE | 6.792 | 14.106 | 9.167 | 6.031 | 7.802 |
| Exte_BulgeL | Exte_BulgeP | Exte_Stiff | LBend_BulgeL | LBend_BulgeP | |
| Correlation | 92.228 | 82.880 | 69.068 | 88.825 | 91.281 |
| MAE | 6.595 | 5.537 | 9.807 | 8.575 | 8.315 |
| RMSE | 7.574 | 6.884 | 11.204 | 11.663 | 10.359 |
| LBend_Stiff | Flex_BulgeL | Flex_BulgeP | Flex_Stiff | Tors_Stiff | |
| Correlation | 87.637 | 92.933 | 96.930 | 94.031 | 64.698 |
| MAE | 9.122 | 6.981 | 2.8642 | 5.594 | 10.067 |
| RMSE | 11.125 | 8.152 | 3.193 | 6.883 | 19.505 |
| Var. | Goal | Value | Desirability |
|---|---|---|---|
| C10 | inRange → 0.125 | 0.102 | 1.000 |
| C0 | inRange → 0.03 | 0.015 | 1.000 |
| Fiber12 | inRange → 532.5 | 518.133 | 1.000 |
| Fiber34 | inRange → 509 | 500.083 | 1.000 |
| Fiber56 | inRange → 479 | 517.692 | 1.000 |
| Fiber78 | inRange → 431.5 | 463.054 | 1.000 |
| Fiber910 | inRange → 384 | 366.794 | 1.000 |
| Annulus_E | inRange → 4.1 | 3.951 | 1.000 |
| Annulus_μ | inRange → 0.35 | 0.201 | 1.000 |
| Cartil_E | inRange → 39 | 42.121 | 1.000 |
| Cartil_μ | inRange → 0.35 | 0.430 | 1.000 |
| Comp_bulgeA | target → 0.5 | 0.265 | 0.262 |
| Comp_bulgeL | target → 0.35 | 0.097 | 0.244 |
| Comp_bulgeP | target → 0.75 | 0.650 | 0.651 |
| Comp_stiff | target → 810 | 826.143 | 0.983 |
| Shear_stiff | target → 300 | 298.124 | 0.964 |
| Exte_bulgeL | target → 0.1 | 0.100 | 1.000 |
| Exte_bulgeP | target → 0.24 | 0.490 | 0.711 |
| Exte_stiff | target → 1.53 | 2.167 | 0.867 |
| LBend_bulgeL | target → 2.11 | 1.235 | 0.534 |
| LBend_bulgeP | target → 1.13 | 1.459 | 0.792 |
| LBend_stiff | target → 2 | 1.465 | 0.634 |
| Flex_bulgeL | target → 0.07 | 0.074 | 0.873 |
| Flex_bulgeP | target → 0.73 | 0.375 | 0.381 |
| Flex_stiff | target → 1.18 | 1.357 | 0.880 |
| Tors_stiff | target → 2.1 | 3.401 | 0.451 |
| Overall Desirability | 0.625 |
| Var. | Goal | Value | Desirability |
|---|---|---|---|
| C10 | inRange → 0.125 | 0.105 | 1.000 |
| C0 | inRange → 0.03 | 0.015 | 1.000 |
| Fiber12 | inRange → 532.5 | 541.867 | 1.000 |
| Fiber34 | inRange → 509 | 500.123 | 1.000 |
| Fiber56 | inRange → 479 | 458.643 | 1.000 |
| Fiber78 | inRange → 431.5 | 396.291 | 1.000 |
| Fiber91 | inRange → 384 | 421.320 | 1.000 |
| Annulus_E | inRange → 4.1 | 3.952205 | 1.000 |
| Annulus_μ | inRange → 0.35 | 0.2269 | 1.000 |
| Cartil_E | inRange → 39 | 45.575 | 1.000 |
| Cartil_μ | inRange → 0.35 | 0.2756 | 1.000 |
| Comp_bulgeA | inRange → 0.5 | 0.262 | 1.000 |
| Comp_bulgeL | inRange → 0.35 | 0.089 | 1.000 |
| Comp_bulgeP | inRange → 0.75 | 0.628 | 1.000 |
| Comp_stiff | target → 810 | 900.147 | 0.907 |
| Shear_stiff | target → 300 | 300.000 | 1.000 |
| Exte_bulgeL | inRange → 0.1 | 0.105 | 1.000 |
| Exte_bulgeP | inRange → 0.24 | 0.605 | 1.000 |
| Exte_stiff | target → 1.53 | 1.530 | 0.999 |
| LBend_bulgeL | inRange → 2.11 | 0.895 | 1.000 |
| LBend_bulgeP | inRange → 1.13 | 1.270 | 1.000 |
| LBend_stiff | target → 2 | 1.984 | 0.989 |
| Flex_bulgeL | inRange → 0.07 | 0.076 | 1.000 |
| Flex_bulgeP | inRange → 0.73 | 0.363 | 1.000 |
| Flex_stiff | target → 1.18 | 1.518 | 0.772 |
| Tors_stiff | target → 2.1 | 3.456 | 0.428 |
| Overall Desirability | 0.817 |
| Var. | Goal | Value | Desirability |
|---|---|---|---|
| C10 | inRange → 0.125 | 0.102 | 1.000 |
| C0 | inRange → 0.03 | 0.015 | 1.000 |
| Fiber12 | inRange → 532.5 | 559.341 | 1.000 |
| Fiber34 | inRange → 509 | 512.790 | 1.000 |
| Fiber56 | inRange → 479 | 443.243 | 1.000 |
| Fiber78 | inRange → 431.5 | 396.348 | 1.000 |
| Fiber91 | inRange → 384 | 348.282 | 1.000 |
| Annulus_E | inRange → 4.1 | 3.951 | 1.000 |
| Annulus_μ | inRange → 0.35 | 0.214 | 1.000 |
| Cartil_E | inRange → 39 | 36.933 | 1.000 |
| Cartil_μ | inRange → 0.35 | 0.429 | 1.000 |
| Comp_bulgeA | target → 0.5 | 0.277 | 0.298 |
| Comp_bulgeL | target → 0.35 | 0.101 | 0.257 |
| Comp_bulgeP | target → 0.75 | 0.673 | 0.730 |
| Comp_stiff | inRange → 810 | 821.981 | 1.000 |
| Shear_stiff | inRange → 300 | 287.011 | 1.000 |
| Exte_bulgeL | target → 0.1 | 0.103 | 0.947 |
| Exte_bulgeP | target → 0.24 | 0.481 | 0.722 |
| Exte_stiff | inRange → 1.53 | 2.403 | 1.000 |
| LBend_bulgeL | Target → 2.11 | 1.314 | 0.576 |
| LBend_bulgeP | target → 1.13 | 1.595 | 0.706 |
| LBend_stiff | inRange → 2 | 1.288 | 1.000 |
| Flex_bulgeL | target → 0.07 | 0.075 | 0.846 |
| Flex_bulgeP | target → 0.73 | 0.373 | 0.378 |
| Flex_stiff | inRange → 1.18 | 1.315 | 1.000 |
| Tors_stiff | inRange → 2.1 | 3.311 | 1.000 |
| Overall Desirability | 0.554 |
| Parameters | Criteria 1 | Criteria 2 | Criteria 3 | Experiments | Error |
|---|---|---|---|---|---|
| FEM | FEM | FEM | Standard Test | Normalized MAE | |
| Comp_bulgeA | 0.266 | 0.262 | 0.269 | 0.50 | 0.469 |
| Comp_bulgeL | 0.096 | 0.090 | 0.095 | 0.35 | 0.732 |
| Comp_bulgeP | 0.624 | 0.602 | 0.625 | 0.75 | 0.177 |
| Comp_stiff | 915.640 | 944.360 | 922.740 | 810 | 0.125 |
| Shear_stiff | 302.925 | 304.920 | 299.090 | 300 | 0.010 |
| Exte_bulgeL | 0.106 | 0.099 | 0.106 | 0.10 | 0.041 |
| Exte_bulgeP | 0.527 | 0.559 | 0.538 | 0.24 | 0.539 |
| Exte_stiff | 1.634 | 1.678 | 1.645 | 1.53 | 0.073 |
| LBend_bulgeL | 0.997 | 0.871 | 0.977 | 2.11 | 0.551 |
| LBend_bulgeP | 1.282 | 1.173 | 1.263 | 1.13 | 0.085 |
| LBend_stiff | 1.489 | 2.175 | 1.493 | 2.00 | 0.183 |
| Flex_bulgeL | 0.077 | 0.080 | 0.076 | 0.07 | 0.096 |
| Flex_bulgeP | 0.380 | 0.373 | 0.373 | 0.73 | 0.486 |
| Flex_stiff | 1.488 | 1.524 | 1.500 | 1.18 | 0.213 |
| Tors_stiff | 3.550 | 3.549 | 3.506 | 2.10 | 0.404 |
| Normalized MAE | 0.2782 | 0.2795 | 0.2788 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gómez, F.S.; Lorza, R.L.; Bobadilla, M.C.; García, R.E. Improving the Process of Adjusting the Parameters of Finite Element Models of Healthy Human Intervertebral Discs by the Multi-Response Surface Method. Materials 2017, 10, 1116. https://doi.org/10.3390/ma10101116
Gómez FS, Lorza RL, Bobadilla MC, García RE. Improving the Process of Adjusting the Parameters of Finite Element Models of Healthy Human Intervertebral Discs by the Multi-Response Surface Method. Materials. 2017; 10(10):1116. https://doi.org/10.3390/ma10101116
Chicago/Turabian StyleGómez, Fátima Somovilla, Rubén Lostado Lorza, Marina Corral Bobadilla, and Rubén Escribano García. 2017. "Improving the Process of Adjusting the Parameters of Finite Element Models of Healthy Human Intervertebral Discs by the Multi-Response Surface Method" Materials 10, no. 10: 1116. https://doi.org/10.3390/ma10101116








