A Time-Frequency Analysis Method for Low Frequency Oscillation Signals Using Resonance-Based Sparse Signal Decomposition and a Frequency Slice Wavelet Transform
Abstract
:1. Introduction
2. Resonance-Based Sparse Signal Decomposition
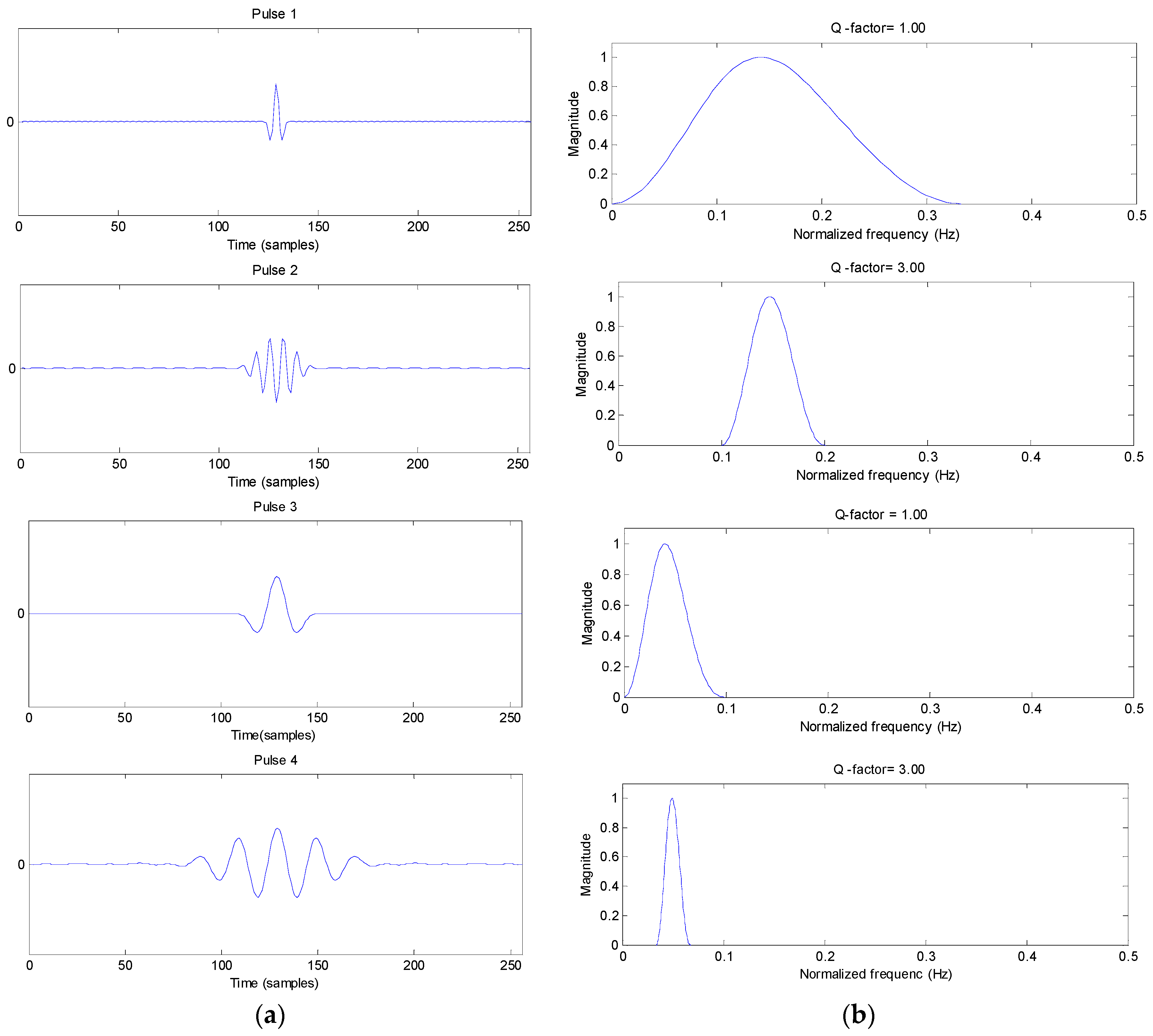
2.1. Q factor, Damping and LFO’s Resonance
2.1.1. Signal Resonance and Q-Factor
2.1.2. LFO’s Resonance
2.2. Tunable Q-Factor Wavelet Transform
2.3. Morphological Component Analysis
3. Frequency Slice Wavelet Transform
3.1. The Definition of Frequency Slice Wavelet Transform
3.2. Frequency Slice Wavelet Inverse Transform
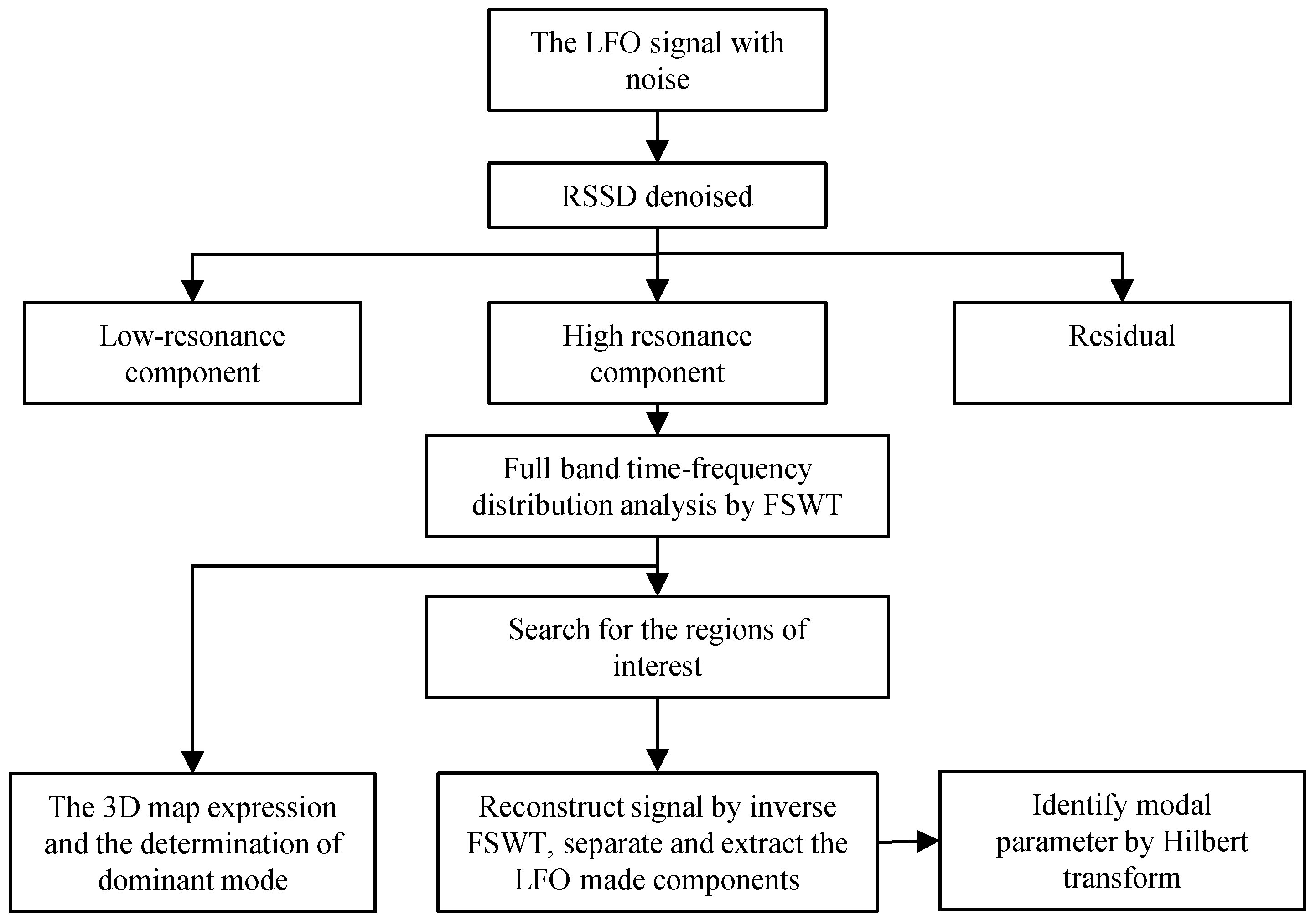
4. Procedure of the LFO Time-Frequency Analysis Method Using RSSD and FSWT
- (1)
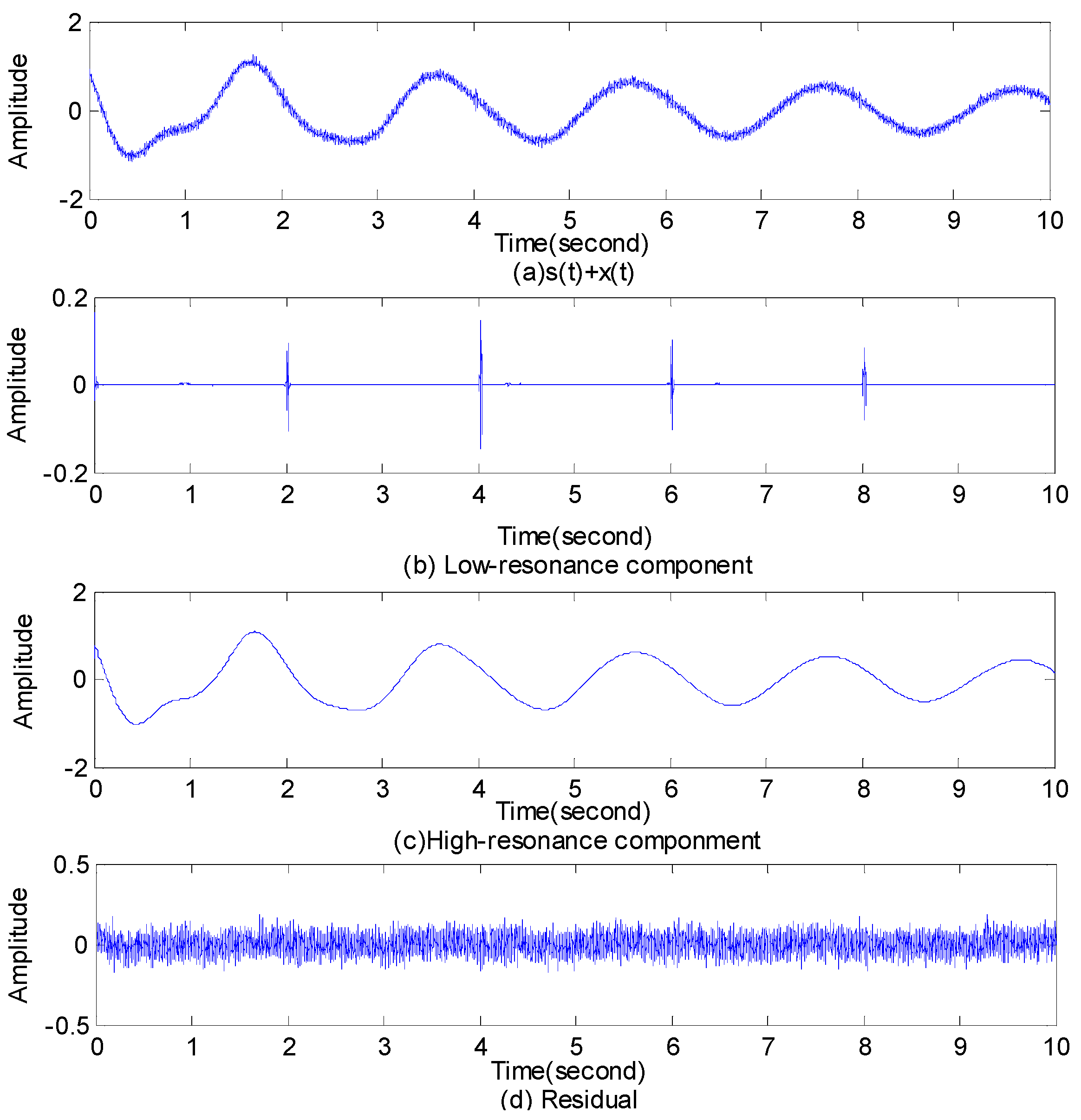
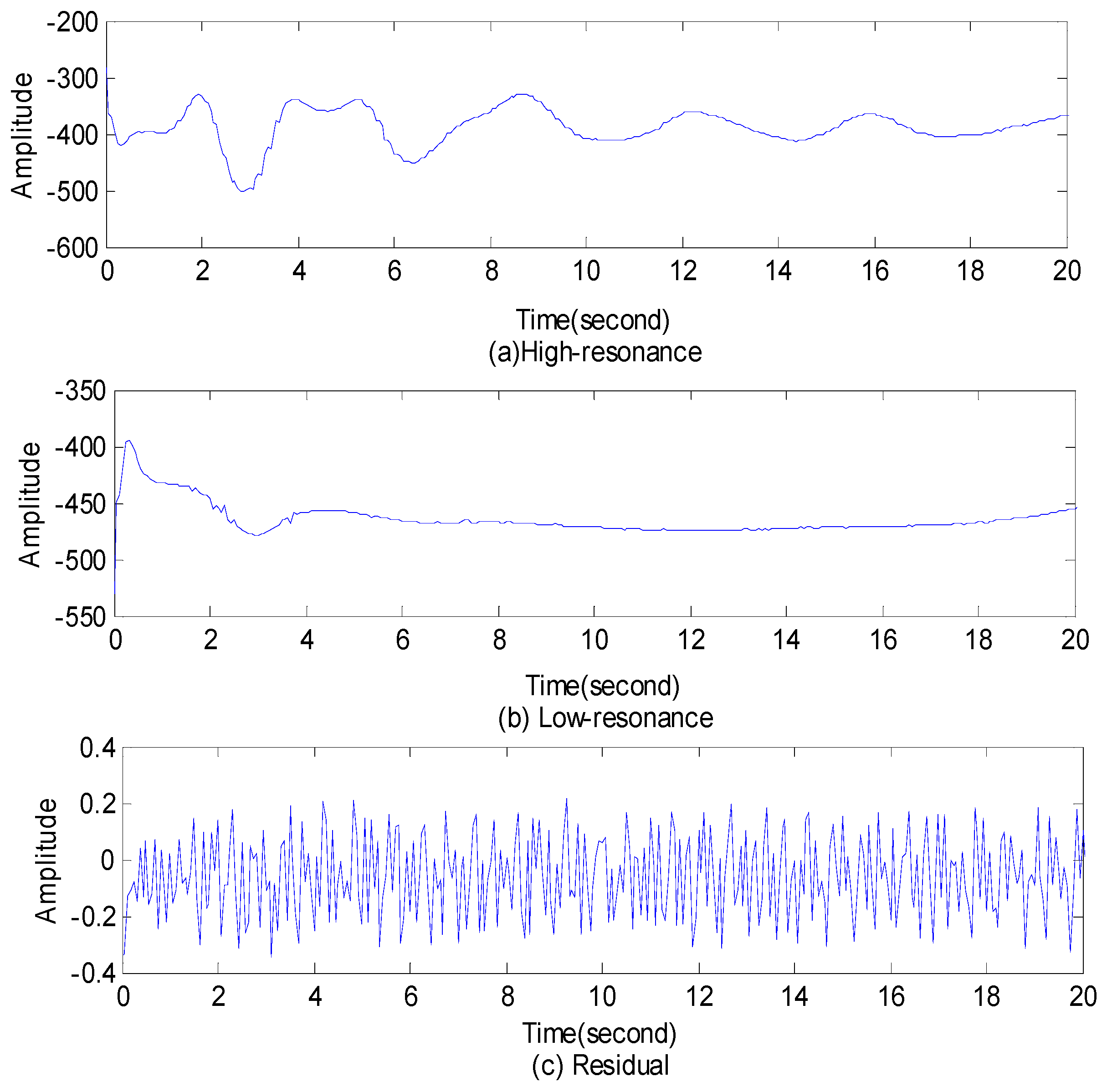
- Decompose the LFO signal with noise by RSSD and get a high-resonance component, a low-resonance component and a residual. The high-resonance component is de-noised LFO signal.
- (2)
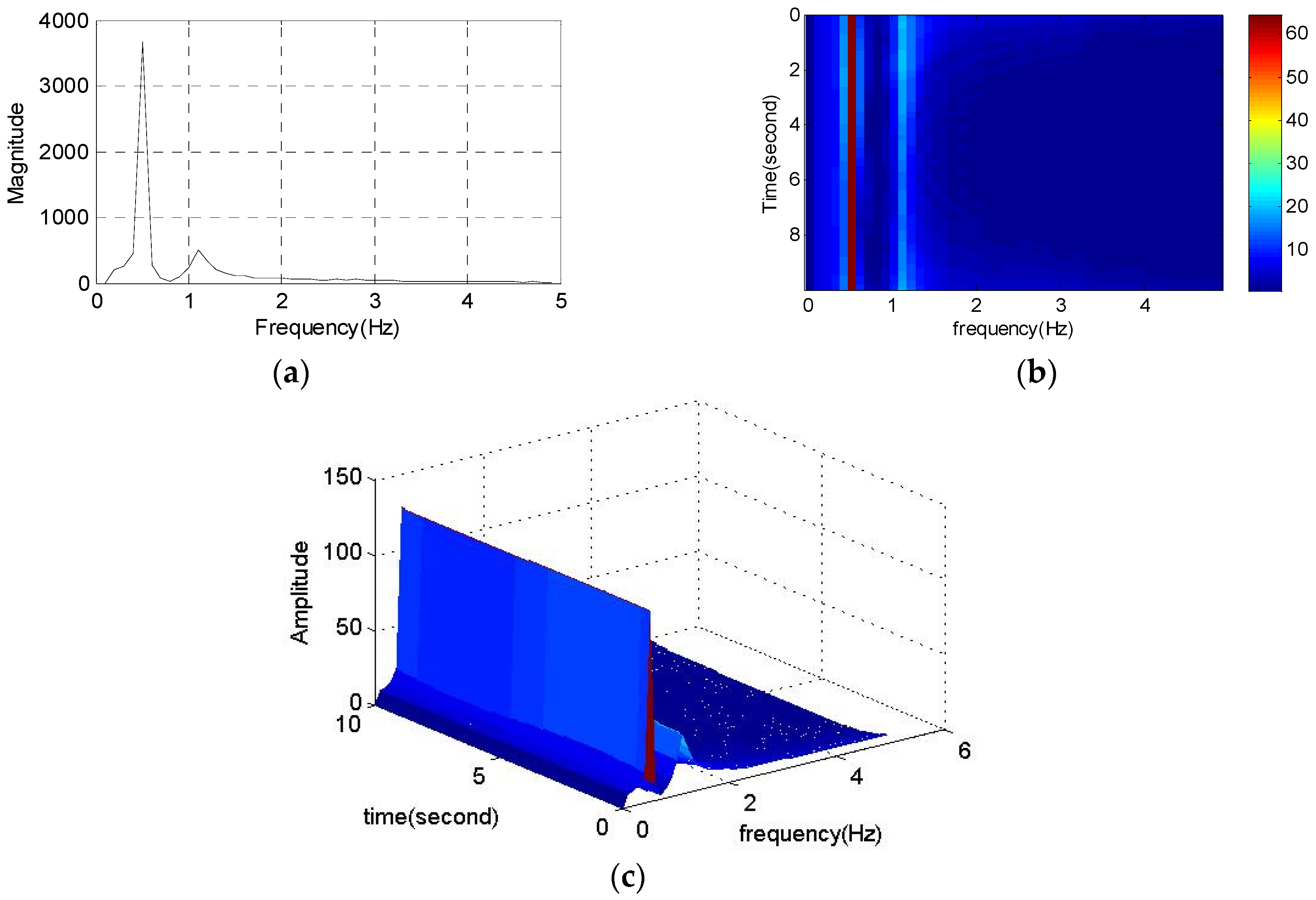
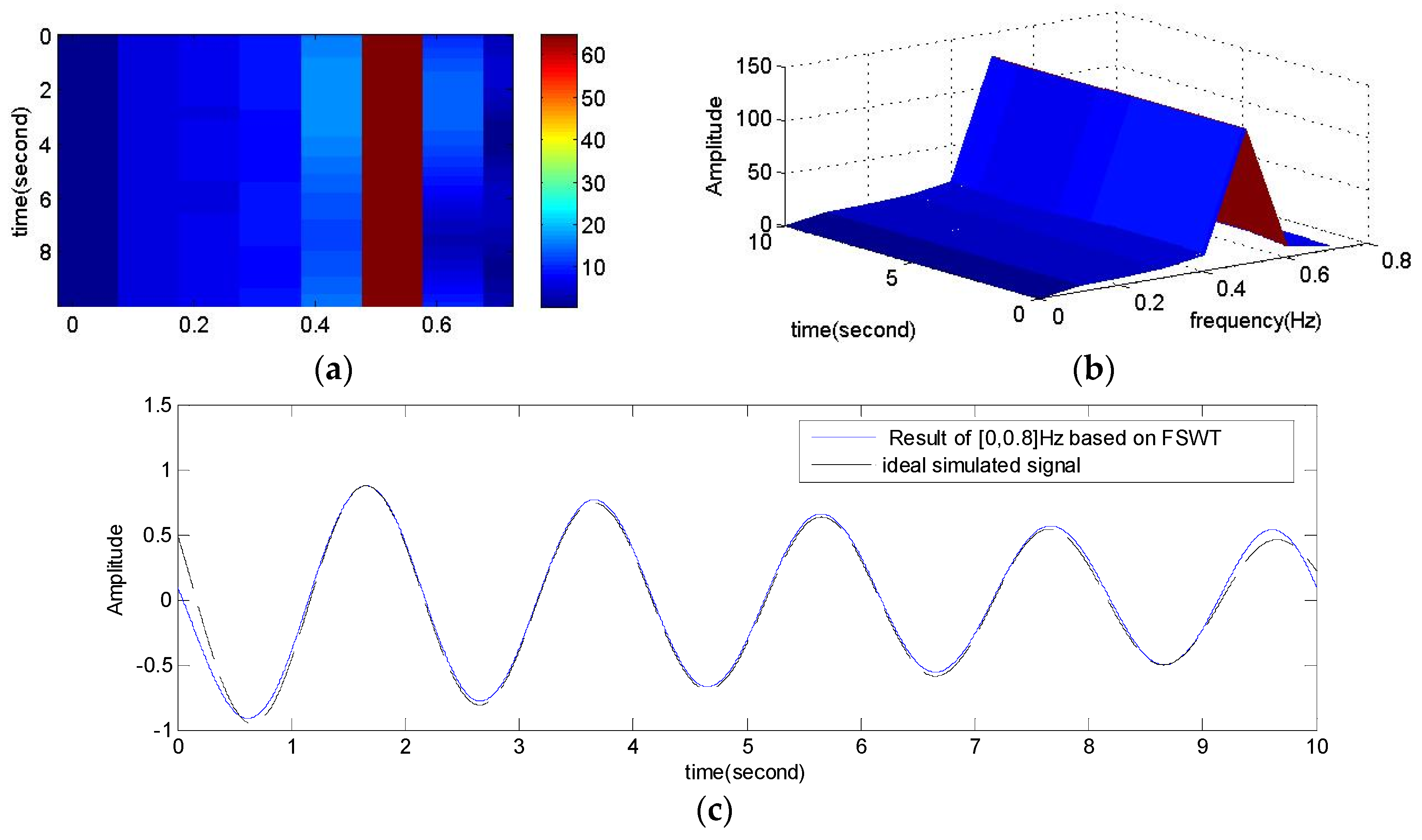
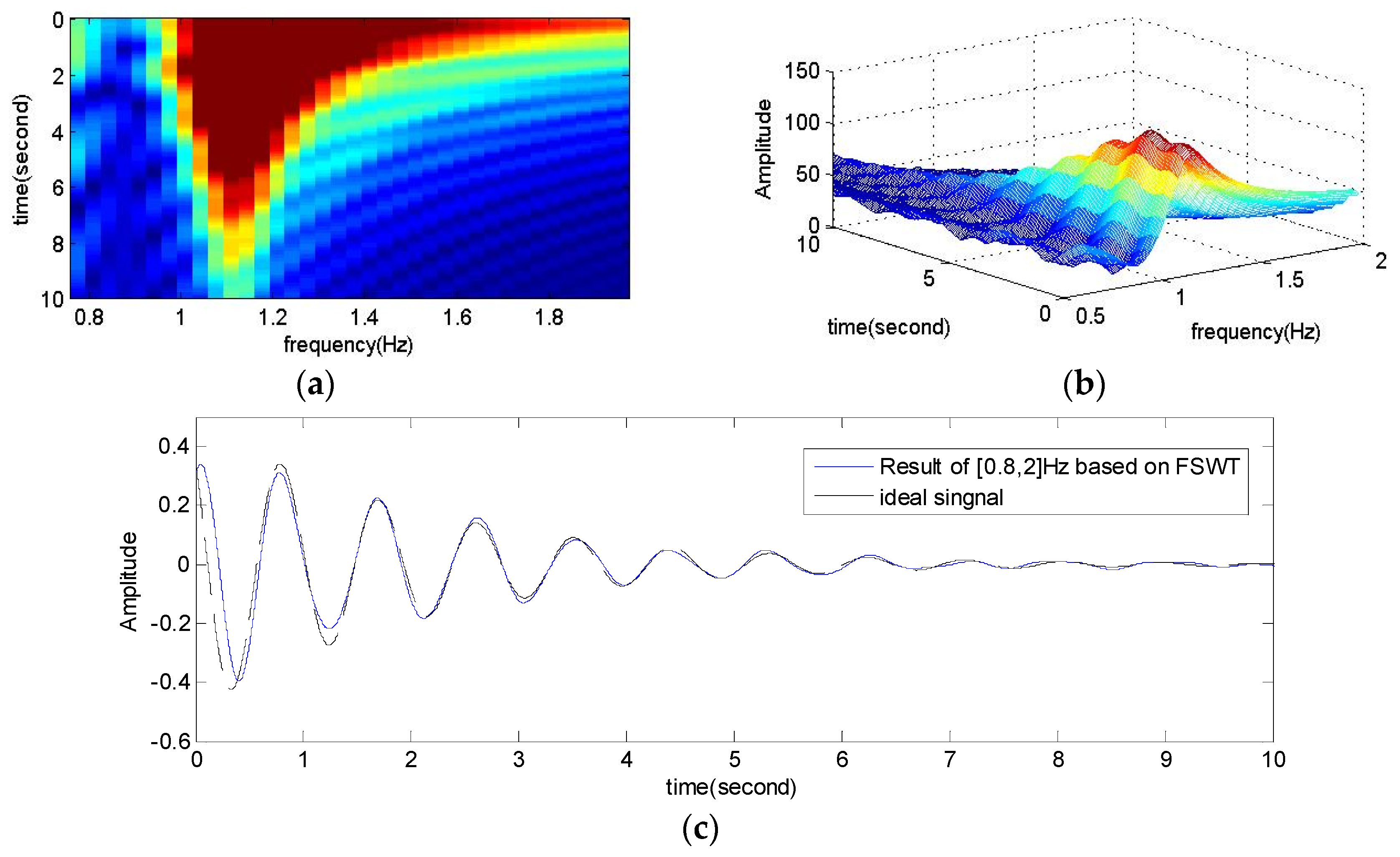
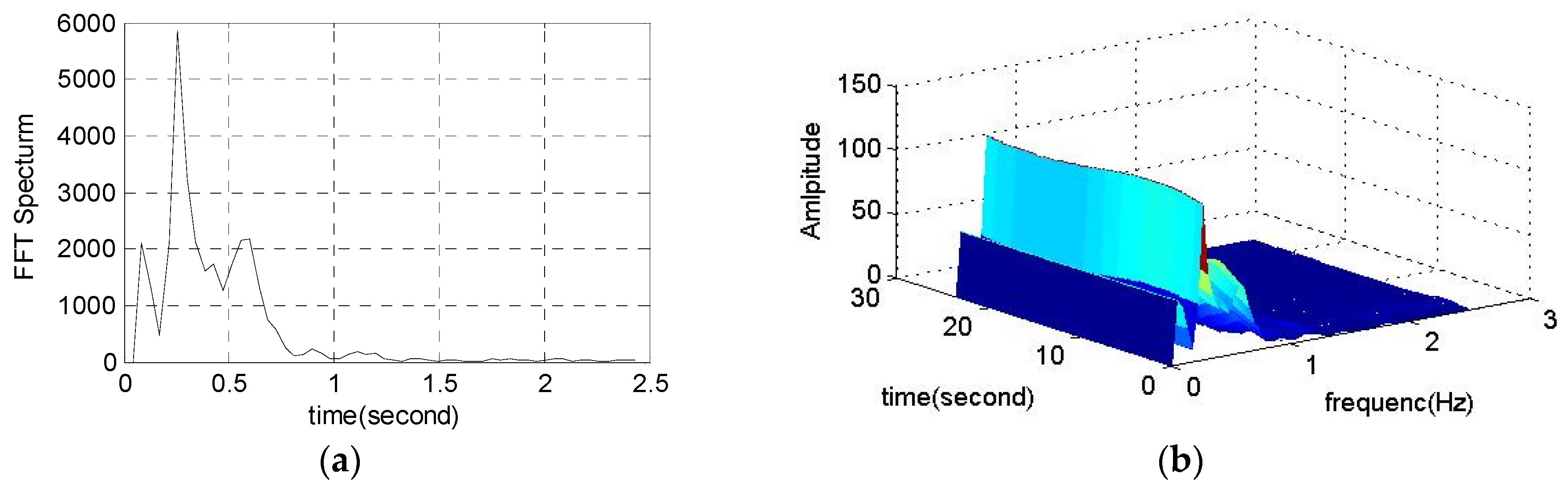
- Transform the high-resonance component by FSWT, and compute the FSWT coefficients using Equation (9), and obtain the full band of its time-frequency distribution. The 3D map expression and dominant mode of the LFO signal can be obtained. After that, search for the regions of interest, called modal domains, in which the main energy is concentrated. Chose a frequency slice [ωi, ωi+1] to get an accurate analysis of the time-frequency feature. Separate and extract the LFO mode components through reconstructing signals by inverse FSWT.
- (3)
5. Simulation
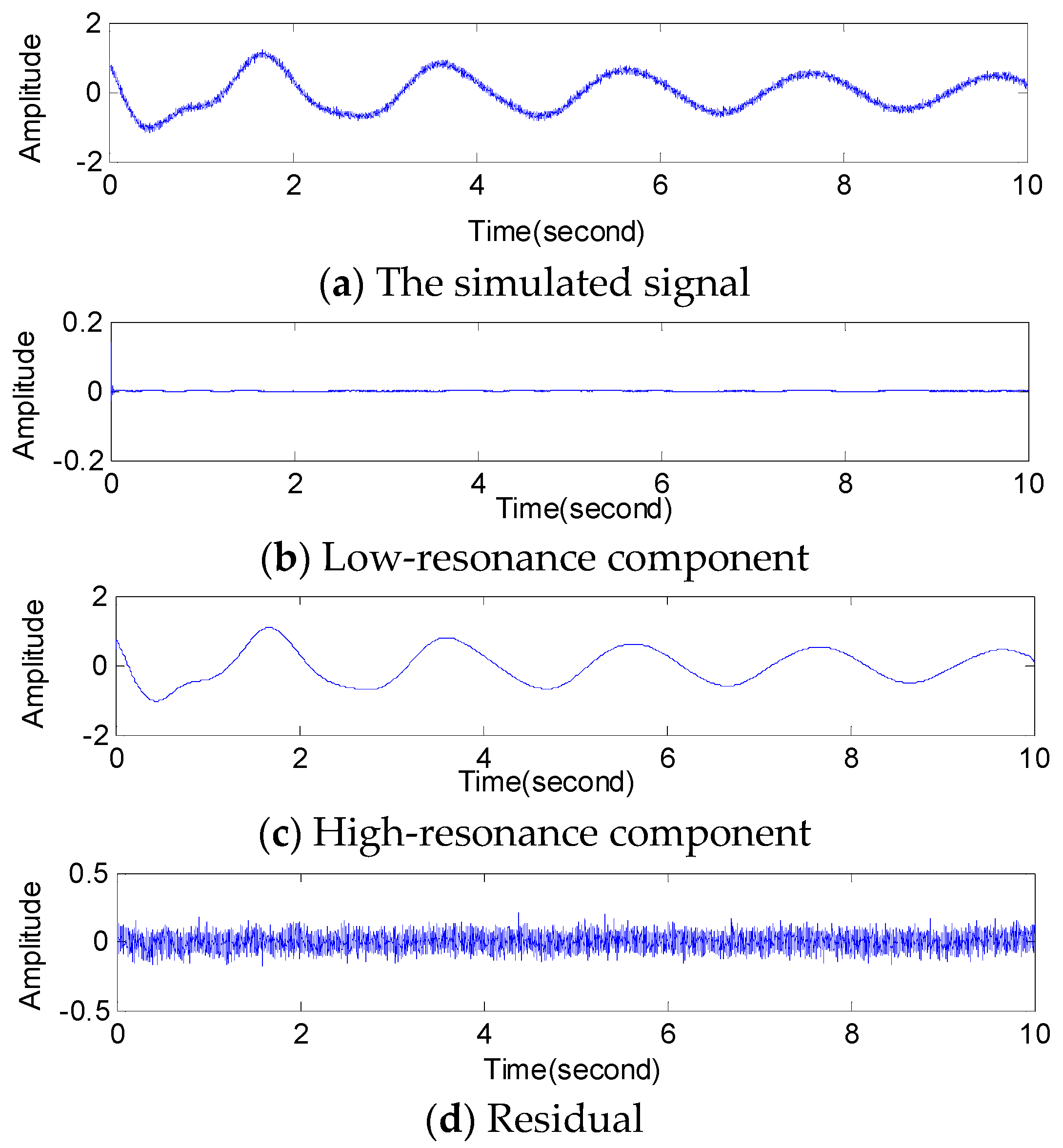
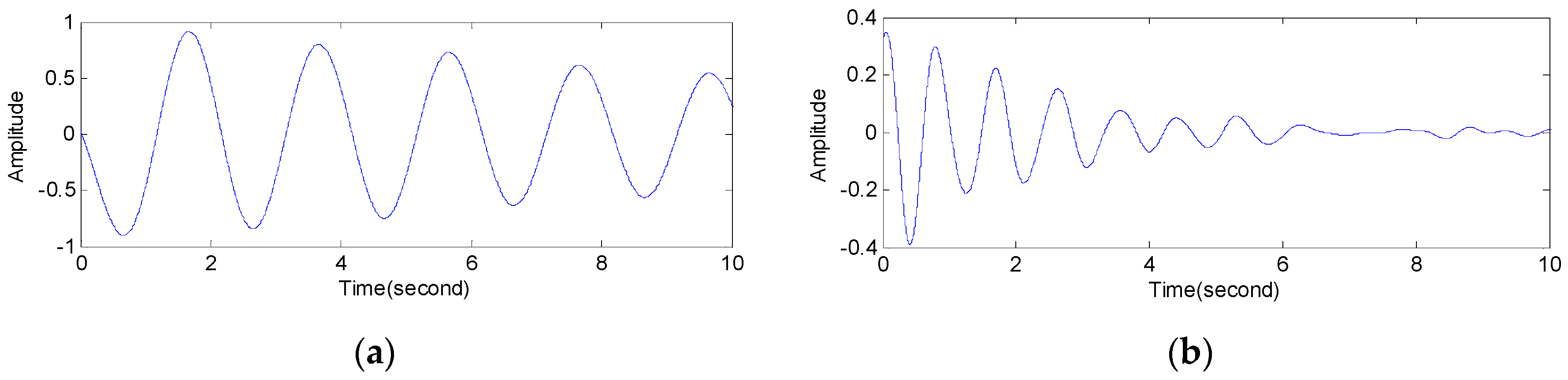
5.1. Denoised RSSD
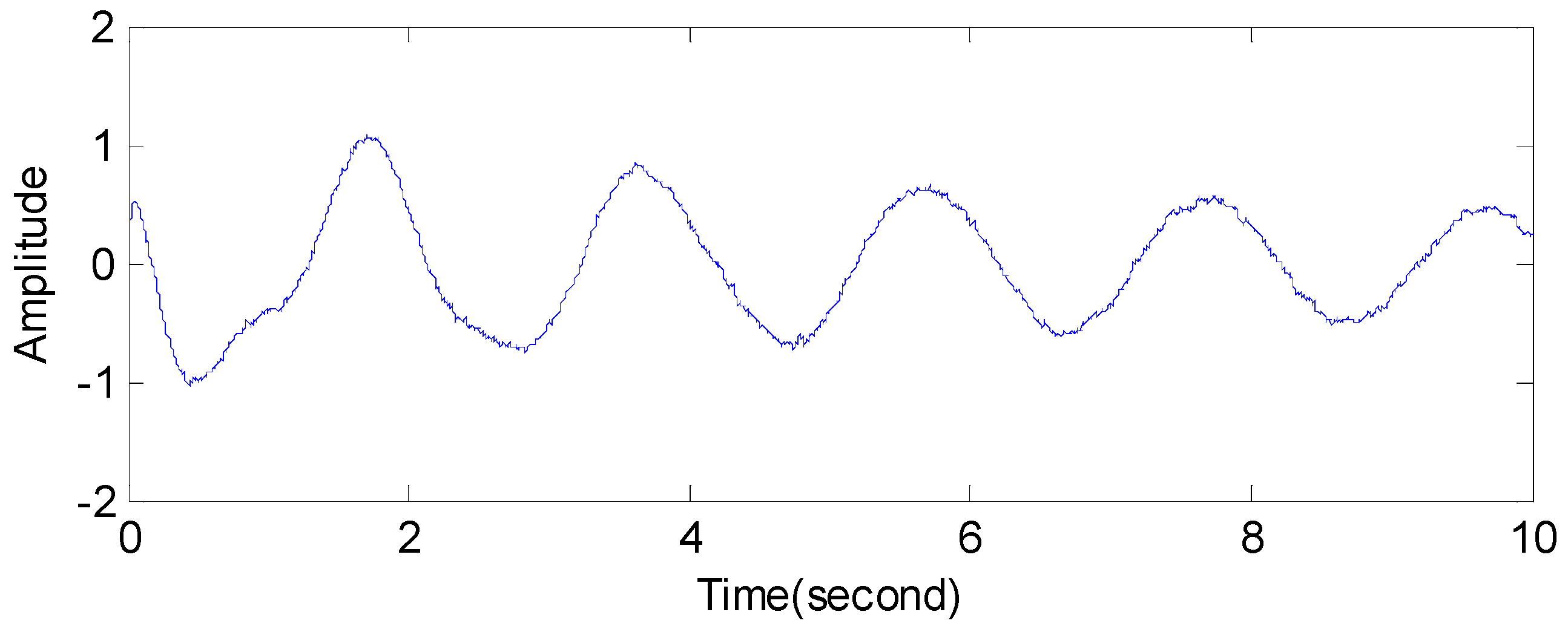
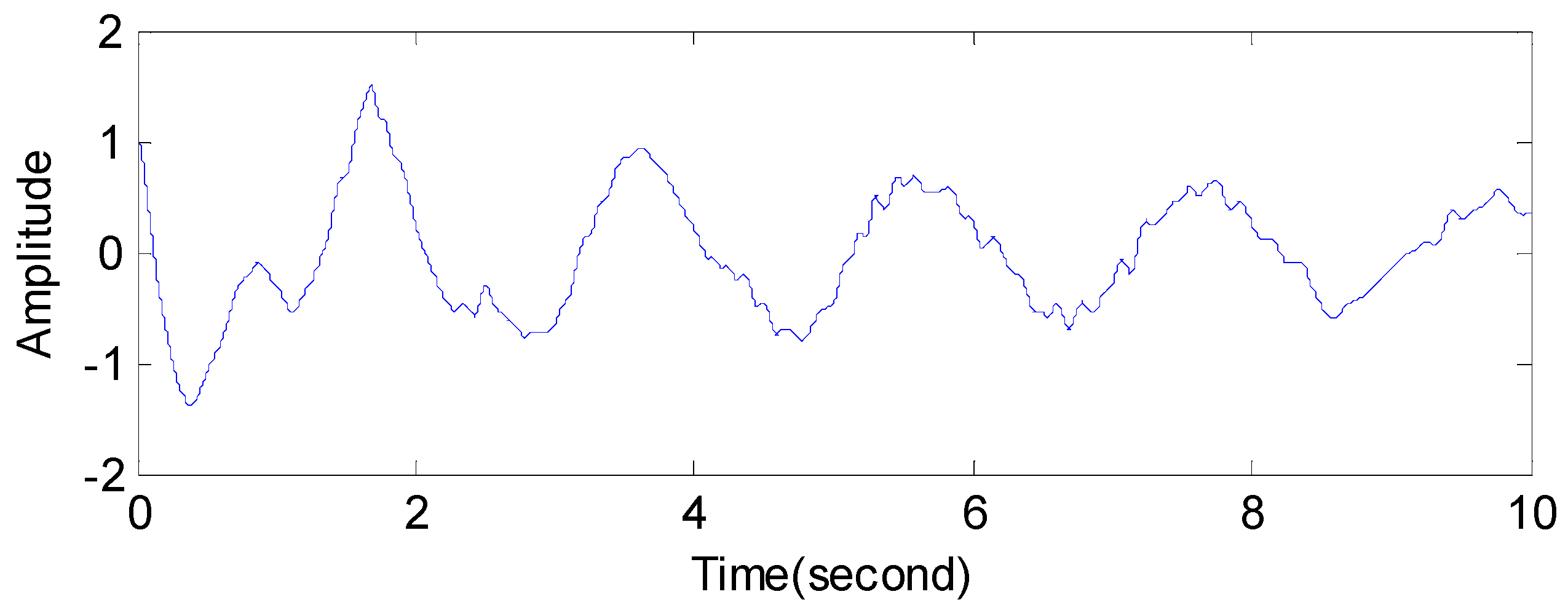
5.1.1. Example 1
5.1.2. Example 2
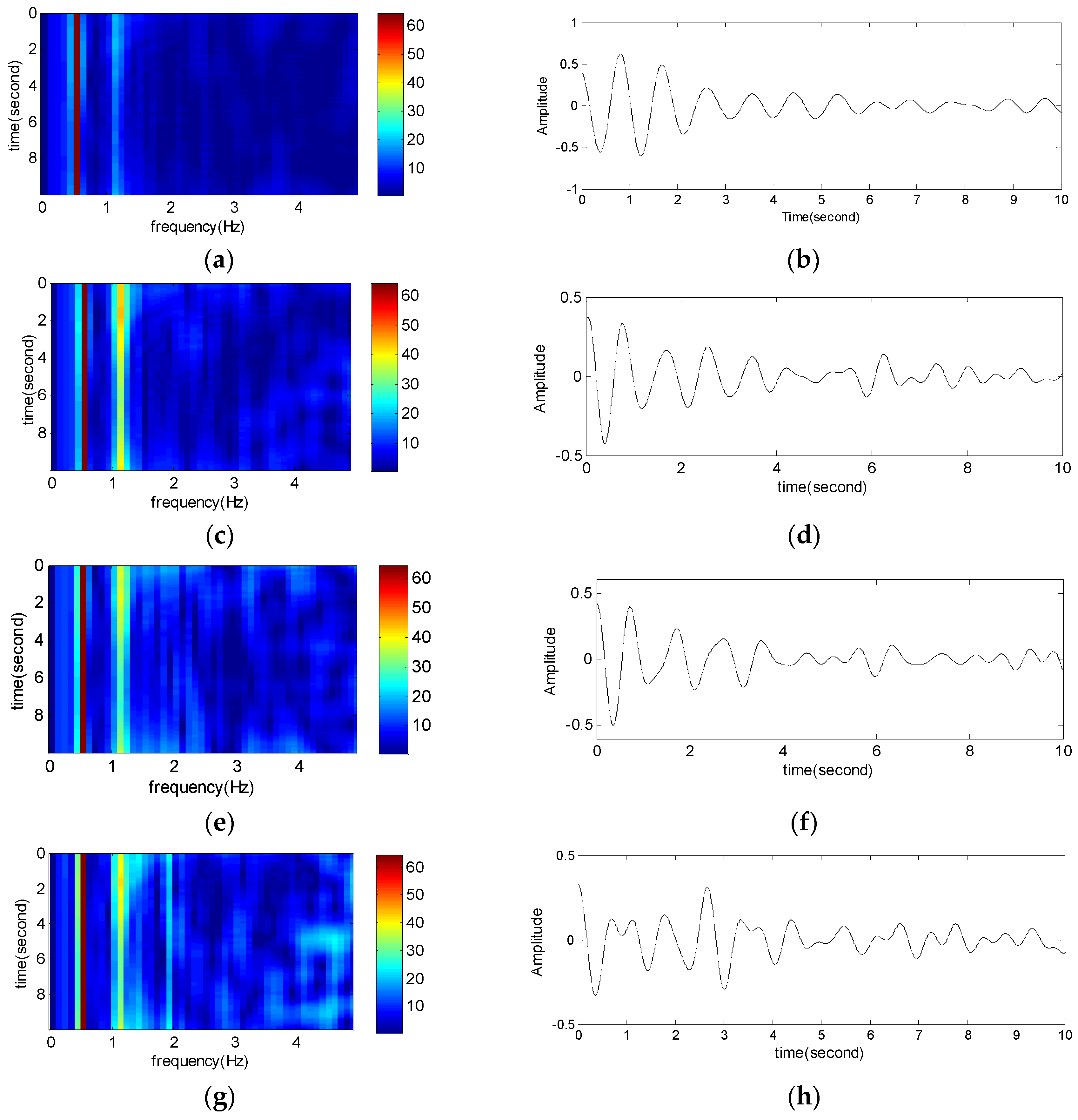
5.2. FSWT Analysis
5.2.1. Full Band Time-Frequency Distribution Analysis by FSWT
5.2.2. Fine Analysis of Frequency Slices Based on FSWT
5.3. Identification of the Parameters of LFO Mode Components by HT
5.4. Impact of Noise on the Accuracy of FSWT-HT
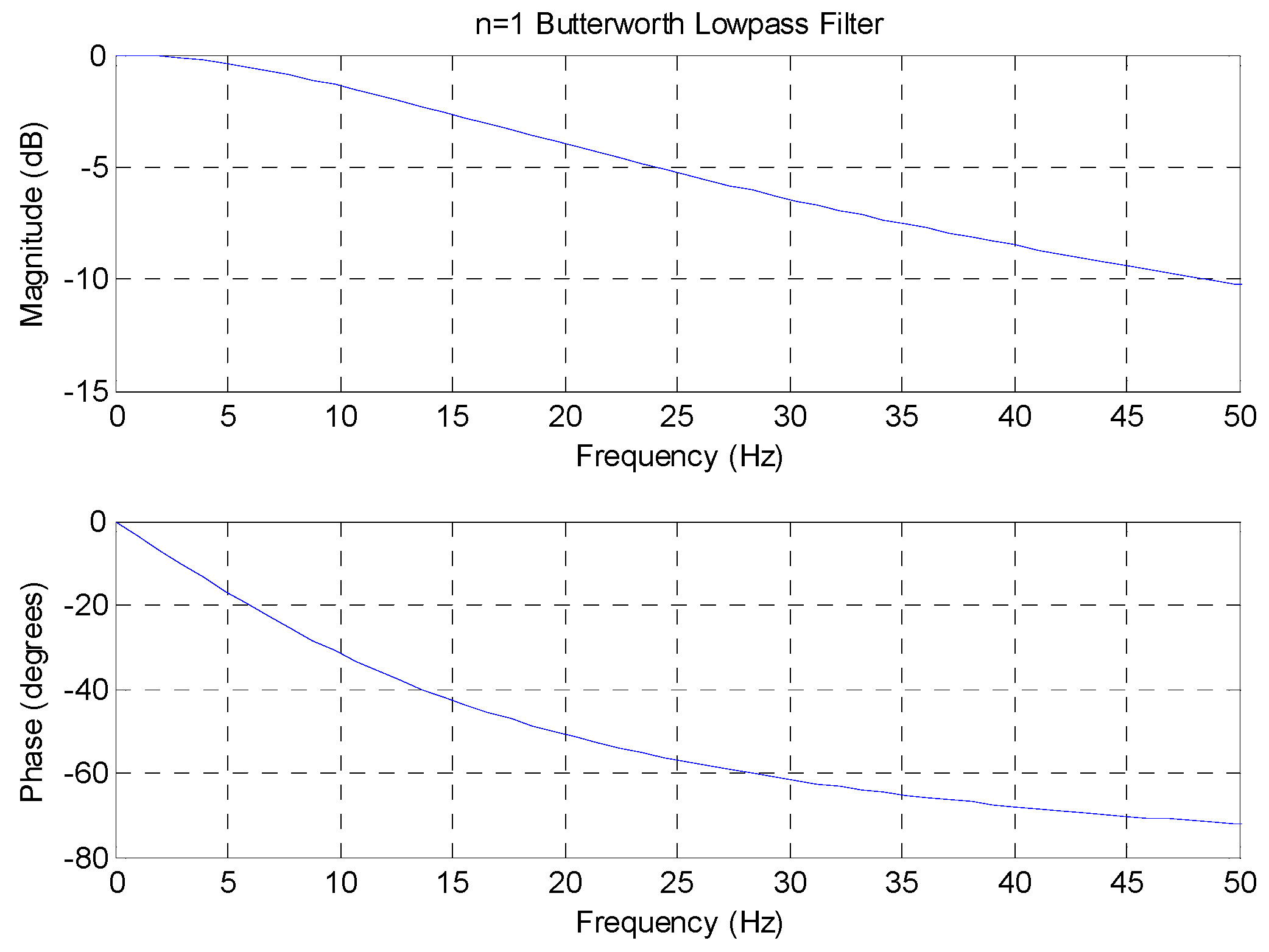
5.5. Comparison with Low Pass Filtering
5.6. Comparison with Other Parameter Identification Methods
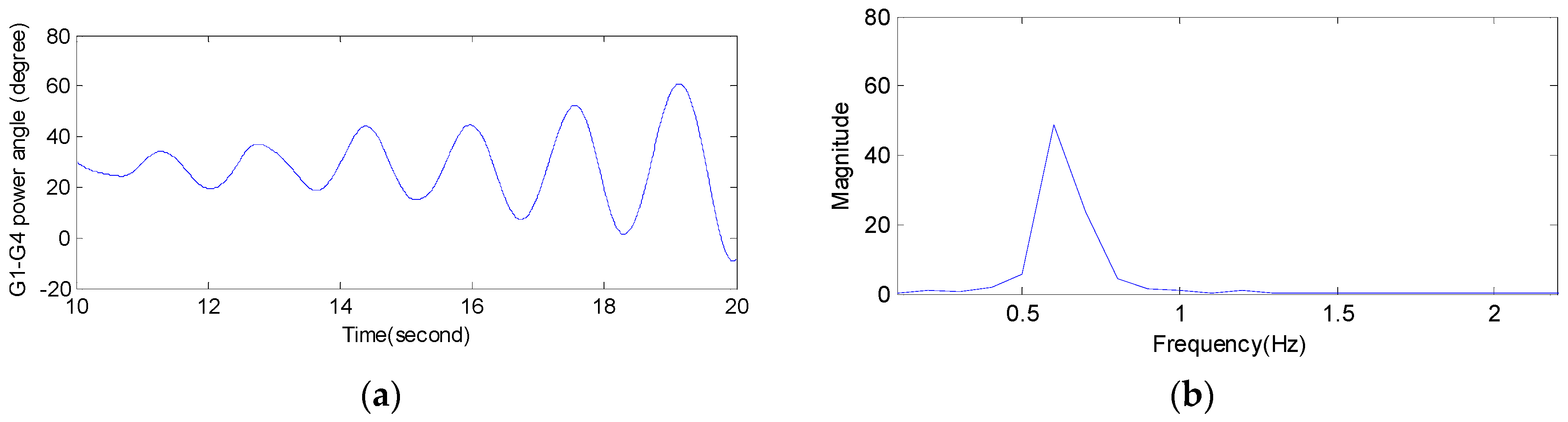
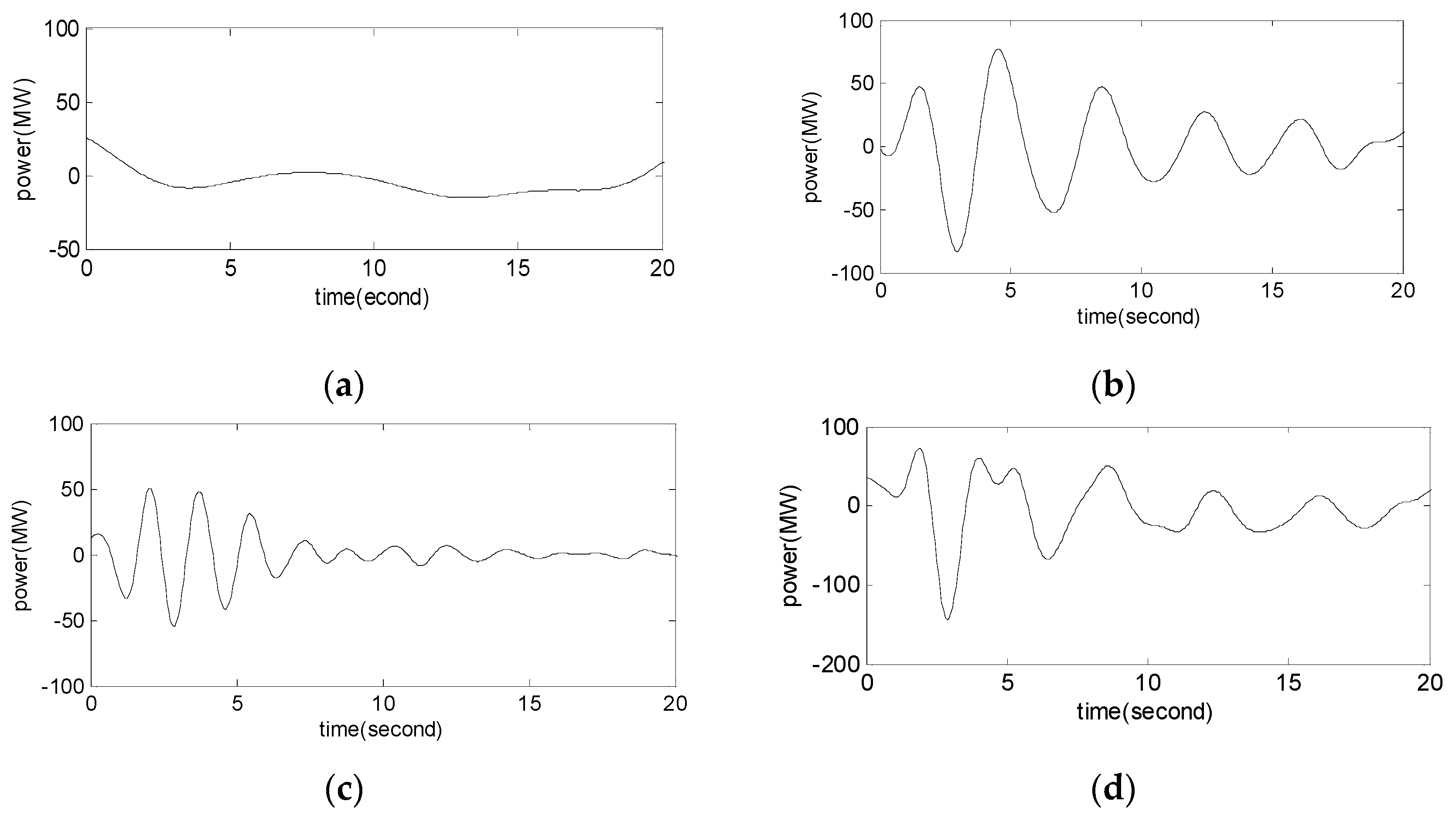
6. Engineering Application
7. Concluding Remarks
- (1)
- RSSD can remove most noise of LFO signals which improved accuracy of LFO modal parameter identification.
- (2)
- FSWT enables the shape of characteristics of LFO modal signal in time-frequency domain to be clearly visible.
- (3)
- RSSD-FSWT can analyze the LFO signal from multiple aspects. Due to full band time-frequency distribution analysis by FSWT, the dominant mode of LFO can be determined, and a 3D map expression of the LFO signal can be obtained. According to fine analysis of frequency slices based on FSWT, we can separate and extract LFO’s modal components. Combining with the Hilbert transform, the parameters of the LFO mode components could be identified accurately.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kishor, N.; Haarla, L.; Seppänen, J.; Mohanty, S.R. Fixed-order controller for reduced-order model for damping of power oscillation in wide area network. Int. J. Electr. Power Energy Syst. 2013, 1, 719–732. [Google Scholar] [CrossRef]
- Pal, A.; Thorp, J.S.; Veda, S.S.; Centeno, V.A. Applying a robust control technique to damp low frequency oscillations in the WECC. Int. J. Electr. Power Energy Syst. 2013, 1, 638–645. [Google Scholar] [CrossRef]
- Wang, T.; Pal, A.; Thorp, J.S.; Wang, Z. Multi-Polytope-Based Adaptive Robust Damping Control in Power Systems Using CART. IEEE Trans. Power Syst. 2015, 30, 1–10. [Google Scholar] [CrossRef]
- Dosiek, L.; Zhou, N.; Pierre, J.W.; Huang, Z.; Trudnowski, D.J. Mode shape estimation algorithms under ambient conditions: A Comparative Review. IEEE Trans. Power Syst. 2013, 2, 779–787. [Google Scholar] [CrossRef]
- Zhou, N.; Pierre, J.; Trudnowski, D. A stepwise regression method for estimating dominant electromechanical modes. IEEE Trans. Power Syst. 2012, 27, 1051–1059. [Google Scholar] [CrossRef]
- Mandadi, K.; Kalyan, K.B. Identification of Inter-Area Oscillations Using Zolotarev Polynomial Based Filter Bank with Eigen Realization Algorithm. IEEE Trans. Power Syst. 2016, 99, 1–10. [Google Scholar] [CrossRef]
- Yan, Z.; Miyamoto, A.; Jiang, Z. An overall theoretical description of frequency slice wavelet transform. Mech. Syst. Signal Proc. 2010, 2, 491–507. [Google Scholar] [CrossRef]
- Yan, Z.; Miyamoto, A.; Jiang, Z. Frequency slice algorithm for modal signal separation and damping identifycation. Comput. Struct. 2011, 1, 14–26. [Google Scholar] [CrossRef]
- Yan, Z.; Miyamoto, A.; Jiang, Z. Frequency slice wavelet transform for transient vibration response analysis. Mech. Syst. Signal Proc. 2009, 5, 1474–1489. [Google Scholar] [CrossRef]
- Selesnick, I.W. Resonance-based signal decomposition: A New Sparsity-Enabled Signal Analysis Method. Signal Proc. 2011, 12, 2793–2809. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control; McGraw-Hill Professional: New York, NY, USA, 2005. [Google Scholar]
- Selesnick, I.W. Wavelet Transform with Tunable Q-Factor. IEEE Trans. Signal Proc. 2011, 8, 3560–3575. [Google Scholar] [CrossRef]
- Afonso, M.V.; Bioucas-Dias, J.M.; Figueiredo, M.A.T. Fast image recovery using variable splitting and constrained optimization. IEEE Trans. Image Proc. A Publ. IEEE Signal Proc. Soc. 2010, 9, 2345–2356. [Google Scholar] [CrossRef] [PubMed]
- Duan, C.D.; Gao, Q. Noval fault diagnosis approach using time-frequency slice analysis and its application. J. Vib. Shock 2011, 9, 1–774. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R. A new view of nonlinear water waves: The Hilbert Spectrum. Annu. Rev. Fluid Mech. 1999, 6, 417–457. [Google Scholar] [CrossRef]
- Li, T.Y.; Gao, L.; Zhao, Y. The analysis for low frequency oscillation based on HHT. Proc. CSEE 2006, 14, 24–30. (In Chinese) [Google Scholar]
- Xiao, J.; Xie, X.; Zhixiang, H.U.; Han, Y. Improved prony method for online identification of low-frequency oscillations in power systems. J. Tsinghua Univ. 2004, 7, 883–887. (In Chinese) [Google Scholar]
- Ni, J.M.; Shen, C.; Liu, F. Estimation of the electromechanical characteristics of power systems based on a revised stochastic subspace method and the stabilization diagram. Sci. China Technol. Sci. 2012, 6, 1677–1687. (In Chinese) [Google Scholar] [CrossRef]
- Tian, L.I.; Yuan, M.Z.; Jun, L.; Li, J.Q.; Yuan, J.T.; Cai, G.W.; Qian, K. Method of modal parameter identification of power system low frequency oscillation based on EMD and SSI. Power Syst. Prot. Control. 2011, 8, 6–10. (In Chinese) [Google Scholar]
- Kumaresan, R.; Tufts, D.W.; Scharf, L.L. A prony method for noisy data: Choosing the Signal Components and Selecting the Order in Exponential Signal Models. Proc. IEEE 1984, 2, 230–233. [Google Scholar] [CrossRef]
- Li, D.H.; Cao, Y.J. An online identification method for power system low-frequency oscillation based on fuzzy filtering and prony algorithm. Autom. Electr. Power Syst. 2007, 1, 14–19. [Google Scholar]
- Ghasemi, H.; Canizares, C.; Moshref, A. Oscillatory stability limit prediction using stochastic subspace identification. IEEE Trans. Power Syst. 2006, 2, 736–745. [Google Scholar] [CrossRef]
- Li, T.; Yuan, M.; Xu, G.; Cai, G.; Liu, Z.; Bai, B. An inter-harmonics high-accuracy detection method based on stochastic subspace and stabilization diagram. Autom. Electr. Power Syst. 2011, 20, 50–54. (In Chinese) [Google Scholar]
- Boudraa, A.O.; Cexus, J.C. Emd-based signal filtering. IEEE Trans. Instrum. Meas. 2007, 6, 2196–2202. [Google Scholar] [CrossRef]


| LFO Mode | Amplitude (Ai) | Oscillation Frequency (fi) | Damping Ratio (ξi) | Damping Factor (σi) | Phase Shift (Φi) |
|---|---|---|---|---|---|
| 1 | 1 | 0.5 | 0.02 | 0.0628 | 60° |
| 2 | 0.5 | 1.1 | 0.07 | 0.4837 | 45° |
| Mode | True Value | FSWT-HT | ||
|---|---|---|---|---|
| Identification Result | Error (%) | |||
| 1 | Oscillation frequency (Hz) | 0.5000 | 0.4980 | 0.40 |
| Damping ratio | 0.0200 | 0.0196 | 2.00 | |
| 2 | Oscillation frequency (Hz) | 1.1000 | 1.1101 | 0.92 |
| Damping ratio | 0.0700 | 0.0666 | 4.86 | |
| Mode | Standard Deviation (σ) | Oscillation Frequency (Hz) | Error (%) | Damping Ratio | Error (%) |
|---|---|---|---|---|---|
| 1 | 0.1 | 0.4980 | 0.400 | 0.0188 | 6.000 |
| 2 | 1.1101 | 0.92 | 0.0657 | 6.143 | |
| 1 | 0.5 | 0.4978 | 0.440 | 0.0190 | 5.000 |
| 2 | 1.1031 | 0.282 | 0.0637 | 9.000 | |
| 1 | 1 | 0.4968 | 0.640 | 0.0181 | 9.500 |
| 2 | 1.1131 | 1.20 | 0.0613 | 12.429 | |
| 1 | 1.5 | 0.4975 | 0.500 | 0.0171 | 14.500 |
| 2 | 1.1156 | 1.418 | 0.0571 | 18.428 | |
| 1 | 2 | 0.4977 | 0.460 | 0.0170 | 15.000 |
| 2 | 1.1221 | 2.009 | 0.0470 | 32.857 |
| Method | Mode | Oscillation Frequency (Hz) | Error (%) | Damping Ratio | Error (%) |
|---|---|---|---|---|---|
| Prony | 1 | 0.4502 | 9.960 | 0.0240 | 20.00 |
| 2 | 1.1616 | 5.609 | 0.0580 | 17.14 | |
| SSI | 1 | 0.4766 | 4.680 | 0.0222 | 11.00 |
| 2 | 1.1573 | 5.209 | 0.0753 | 7.571 | |
| EMD-SSI | 1 | 0.4860 | 2.800 | 0.0214 | 7.000 |
| 2 | 1.1502 | 4.727 | 0.0743 | 6.142 | |
| RSSD-SSI | 1 | 0.5060 | 1.200 | 0.0206 | 3.000 |
| 2 | 1.1302 | 2.745 | 0.0730 | 2.857 | |
| RSSD-FSWT | 1 | 0.4978 | 0.440 | 0.0192 | 4.000 |
| 2 | 1.1030 | 0.272 | 0.0667 | 4.714 |
| Mode | Oscillation Frequency (Hz) | Damping Ratio | |
|---|---|---|---|
| 1 | RSSD-SSI | 0.5356 | 0.0556 |
| RSSD-FSWT | 0.5244 | 0.0542 | |
| EMD-SSI | 05354 | 0.0571 | |
| 2 | RSSD-SSI | 0.2510 | 0.0541 |
| RSSD-FSWT | 0.2508 | 0.0538 | |
| EMD-SSI | 0.2658 | 0.0562 | |
| 3 | RSSD-SSI | 0.1220 | 0.0149 |
| RSSD-FSWT | 0.1215 | 0.0145 | |
| EMD-SSI | 0.1199 | 0.0123 | |
| 4 | RSSD-SSI | - | - |
| RSSD-FSWT | - | - | |
| EMD-SSI | 0.0411 | 0.0993 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Li, Z.; Nie, Y. A Time-Frequency Analysis Method for Low Frequency Oscillation Signals Using Resonance-Based Sparse Signal Decomposition and a Frequency Slice Wavelet Transform. Energies 2016, 9, 151. https://doi.org/10.3390/en9030151
Zhao Y, Li Z, Nie Y. A Time-Frequency Analysis Method for Low Frequency Oscillation Signals Using Resonance-Based Sparse Signal Decomposition and a Frequency Slice Wavelet Transform. Energies. 2016; 9(3):151. https://doi.org/10.3390/en9030151
Chicago/Turabian StyleZhao, Yan, Zhimin Li, and Yonghui Nie. 2016. "A Time-Frequency Analysis Method for Low Frequency Oscillation Signals Using Resonance-Based Sparse Signal Decomposition and a Frequency Slice Wavelet Transform" Energies 9, no. 3: 151. https://doi.org/10.3390/en9030151





