Effects of Freestream Turbulence in a Model Wind Turbine Wake
Abstract
:1. Introduction
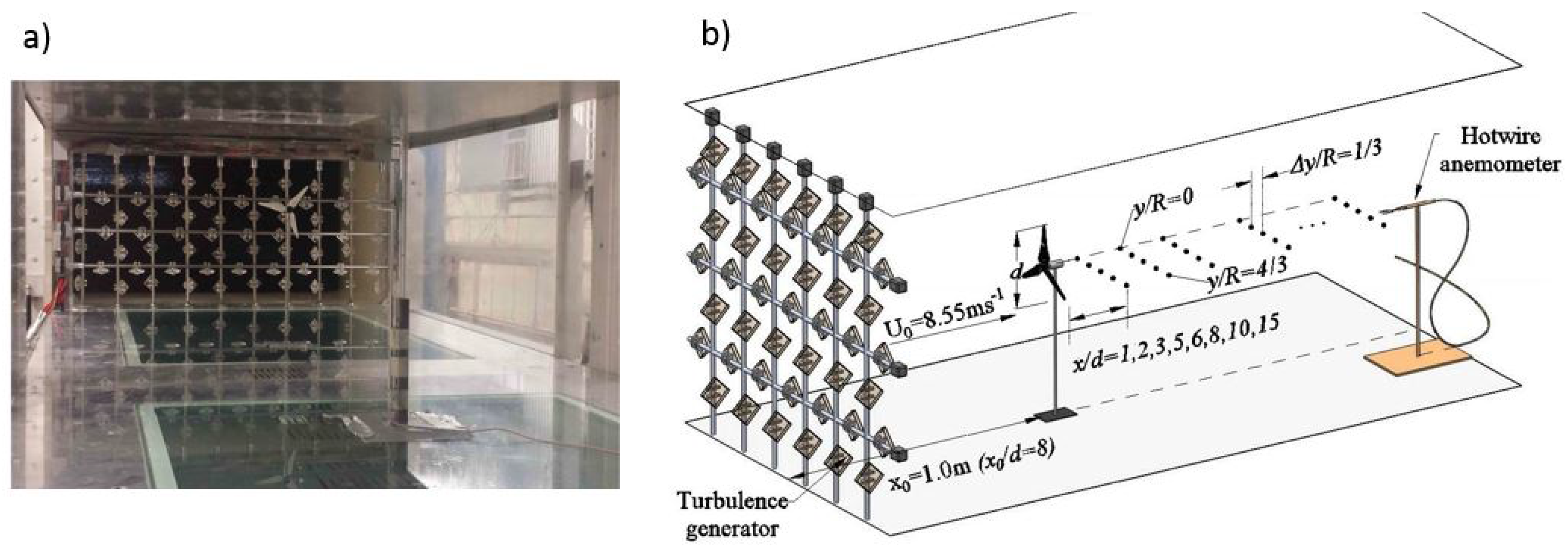
2. Experimental Setup
3. Results and Discussion
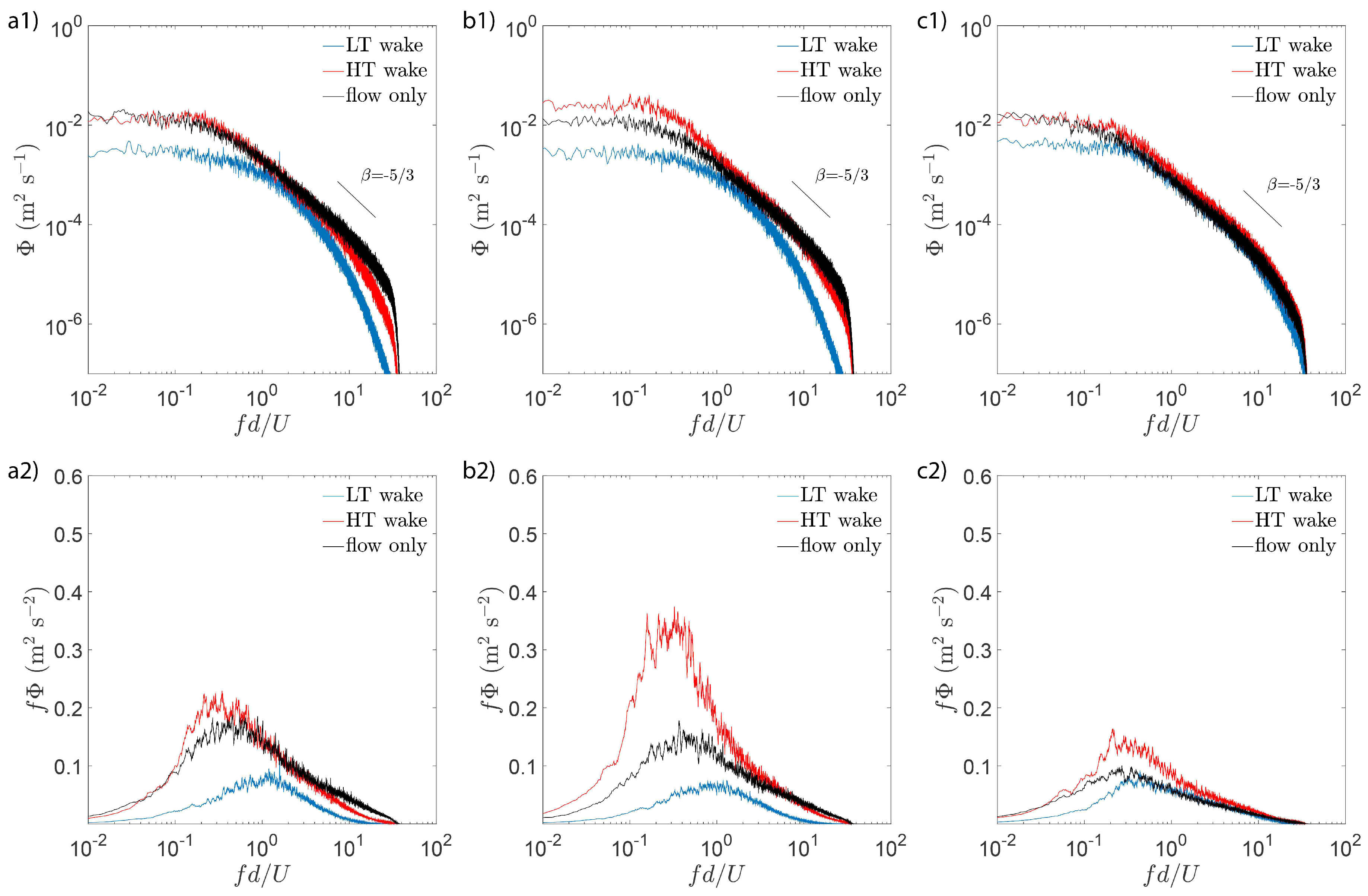
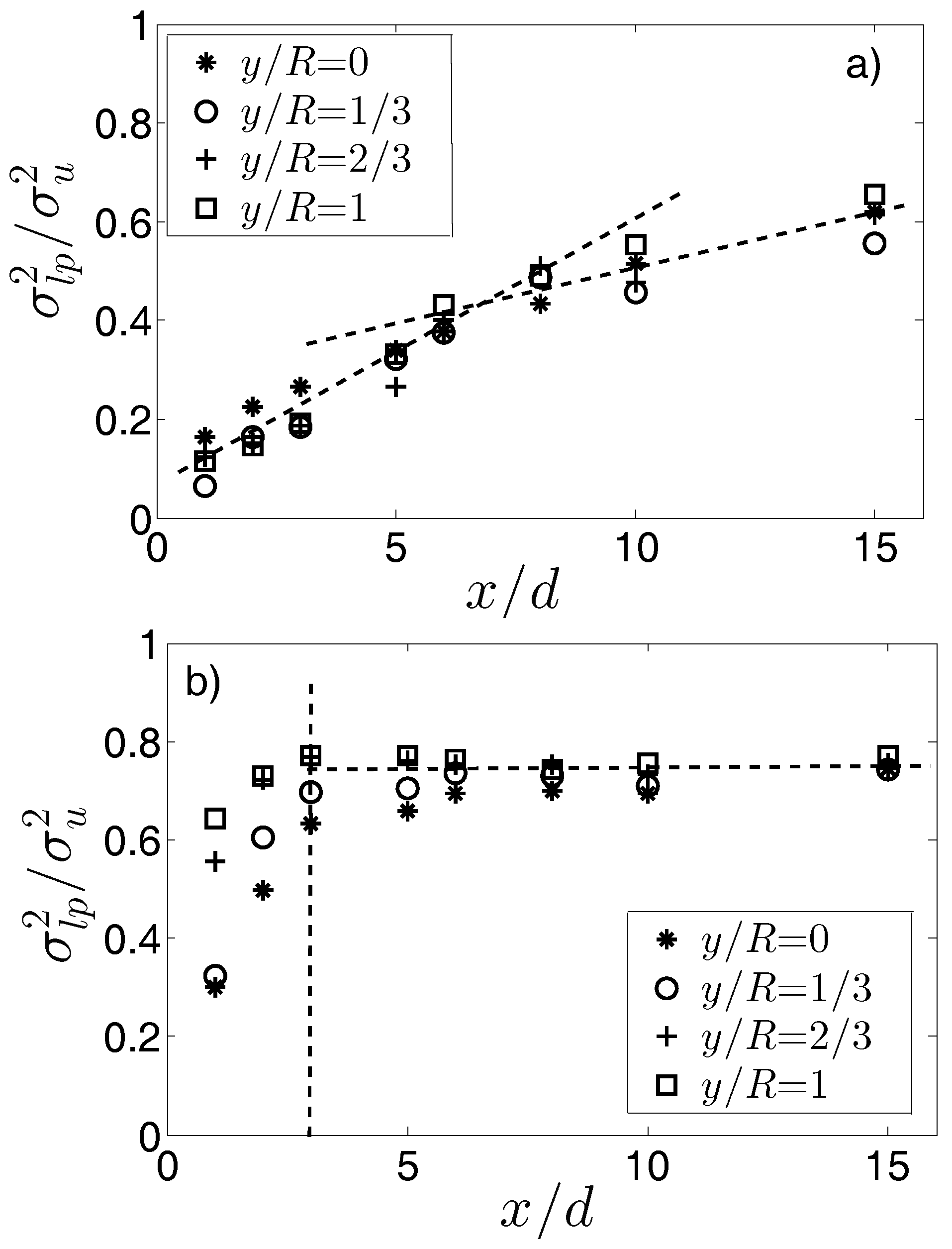
3.1. Background Turbulence Modulation on the Wake Velocity Spectra
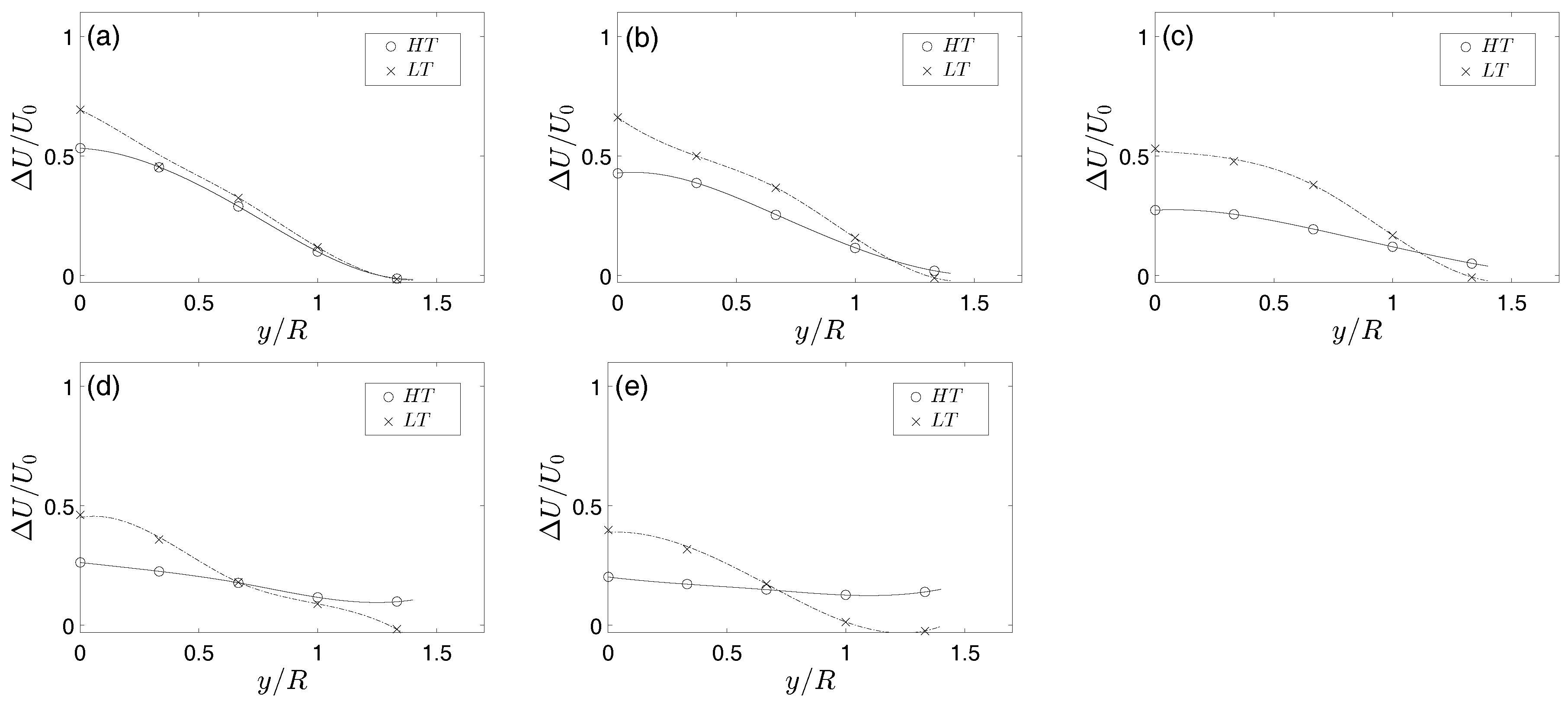
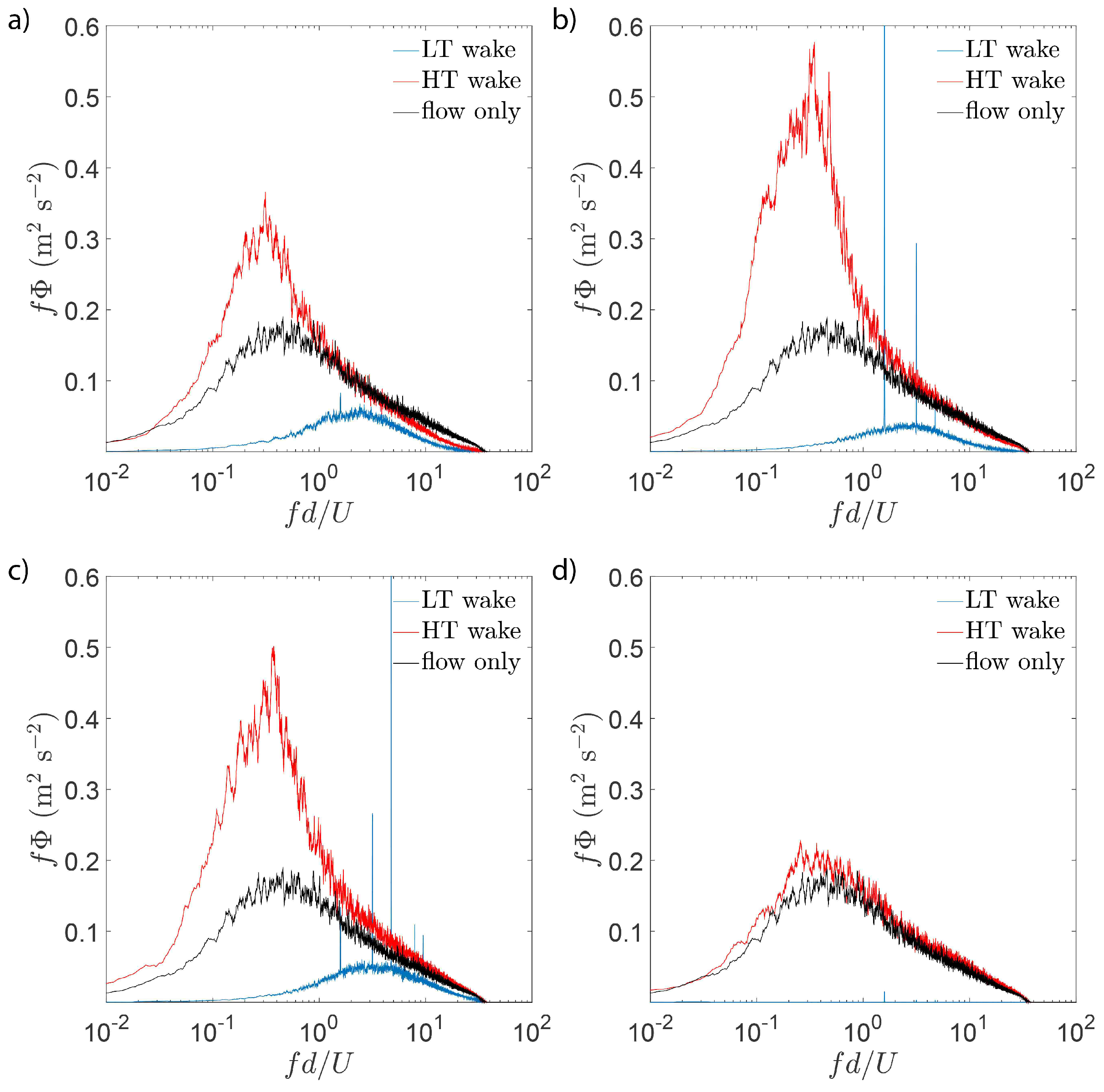
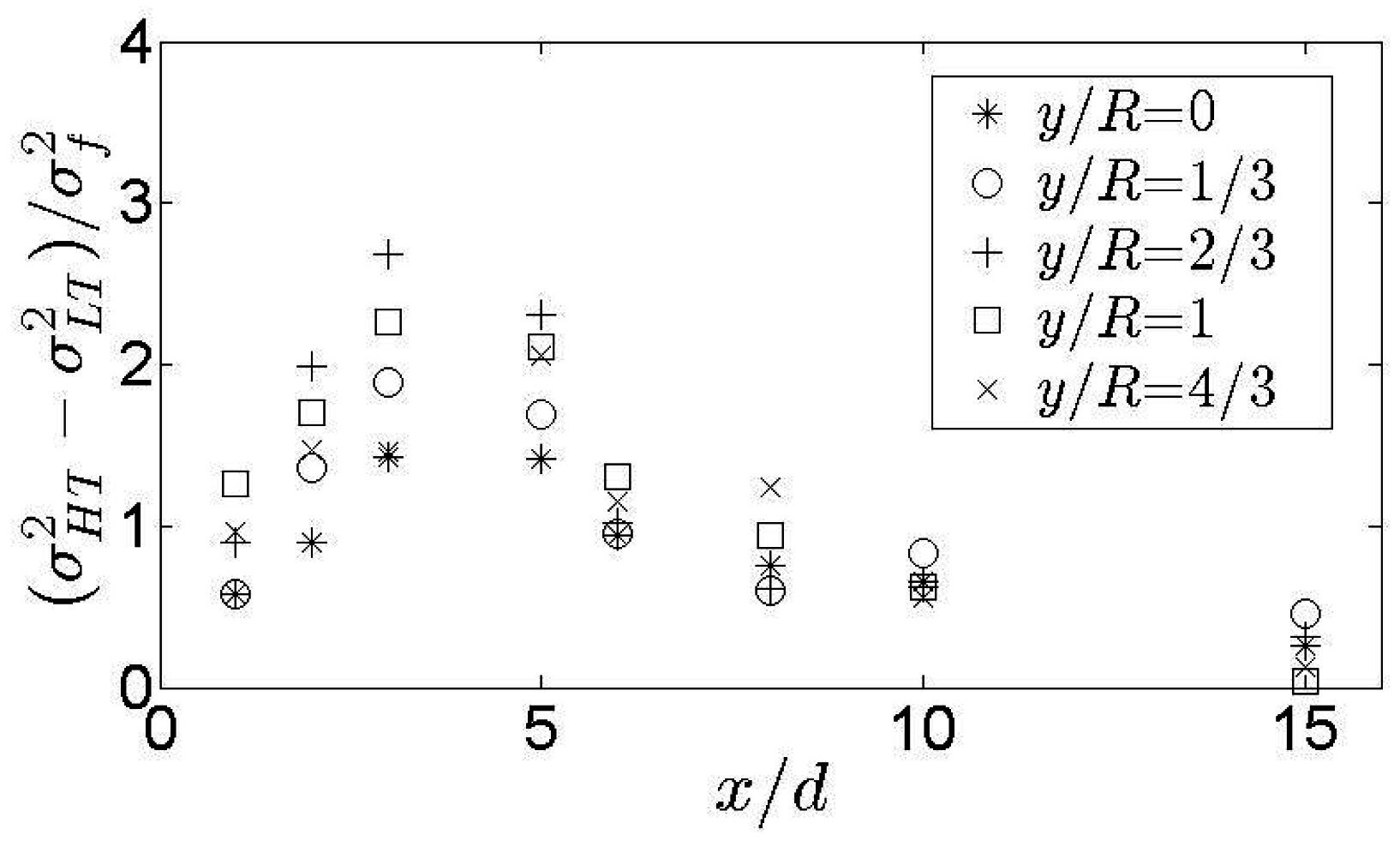
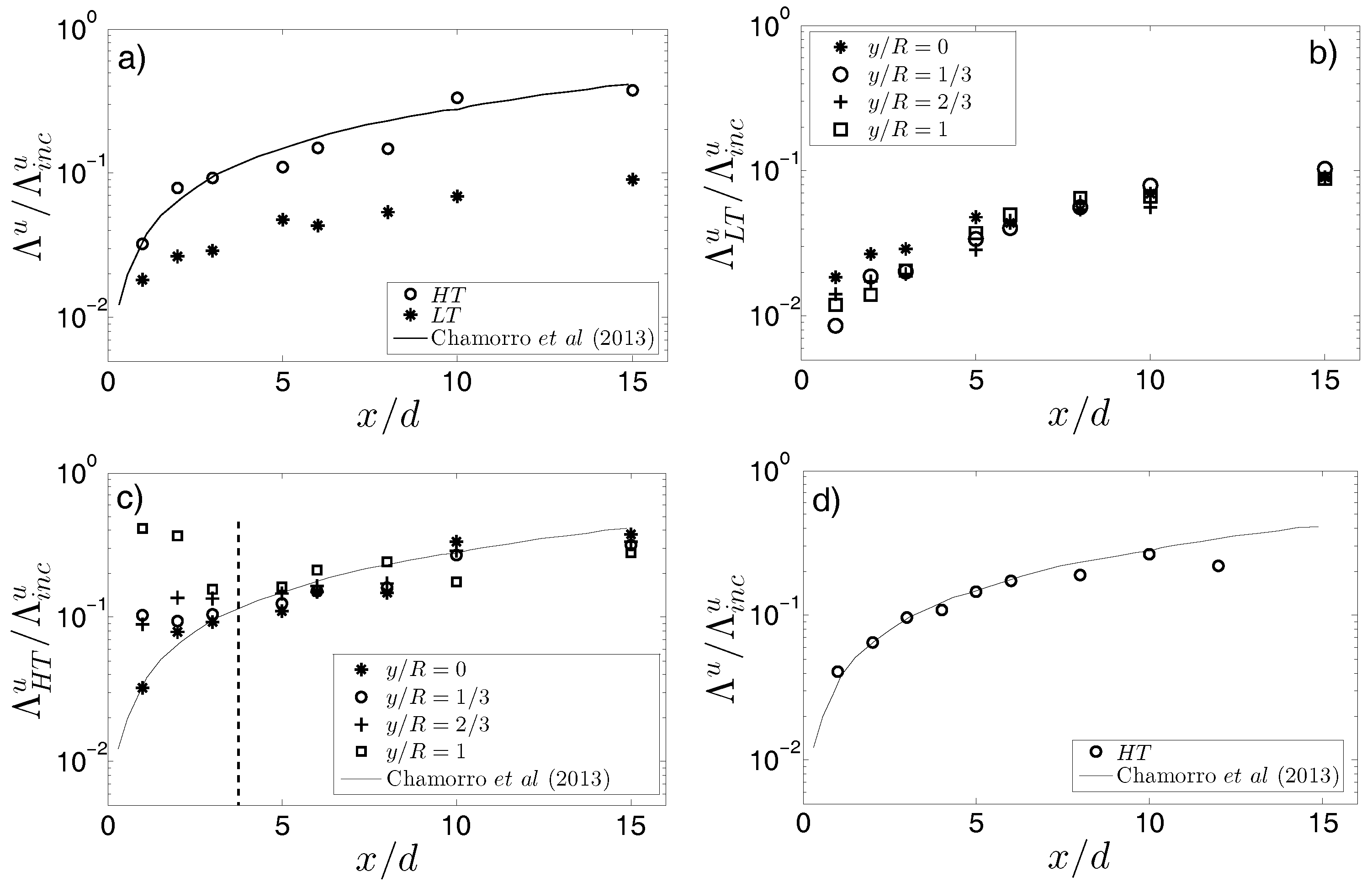
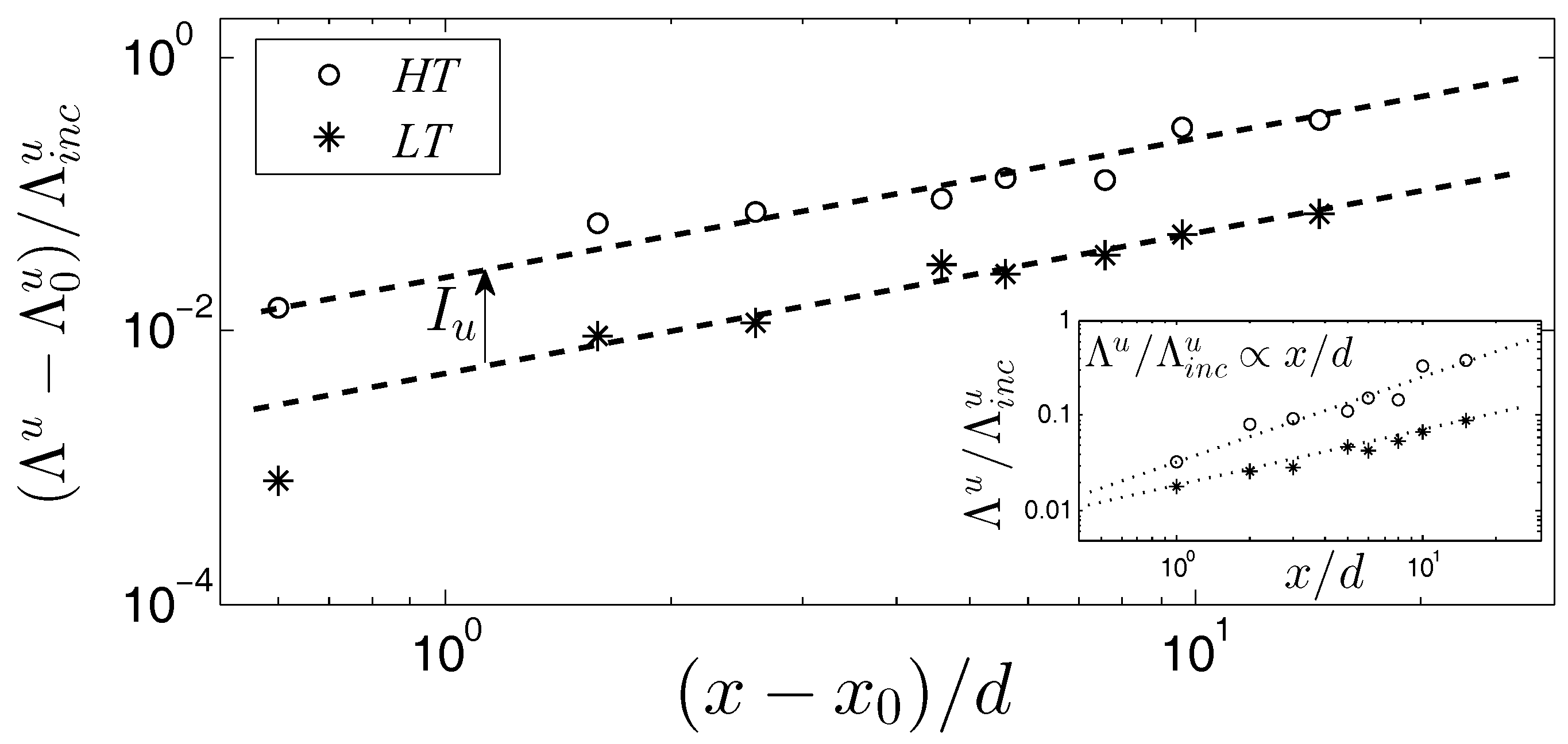
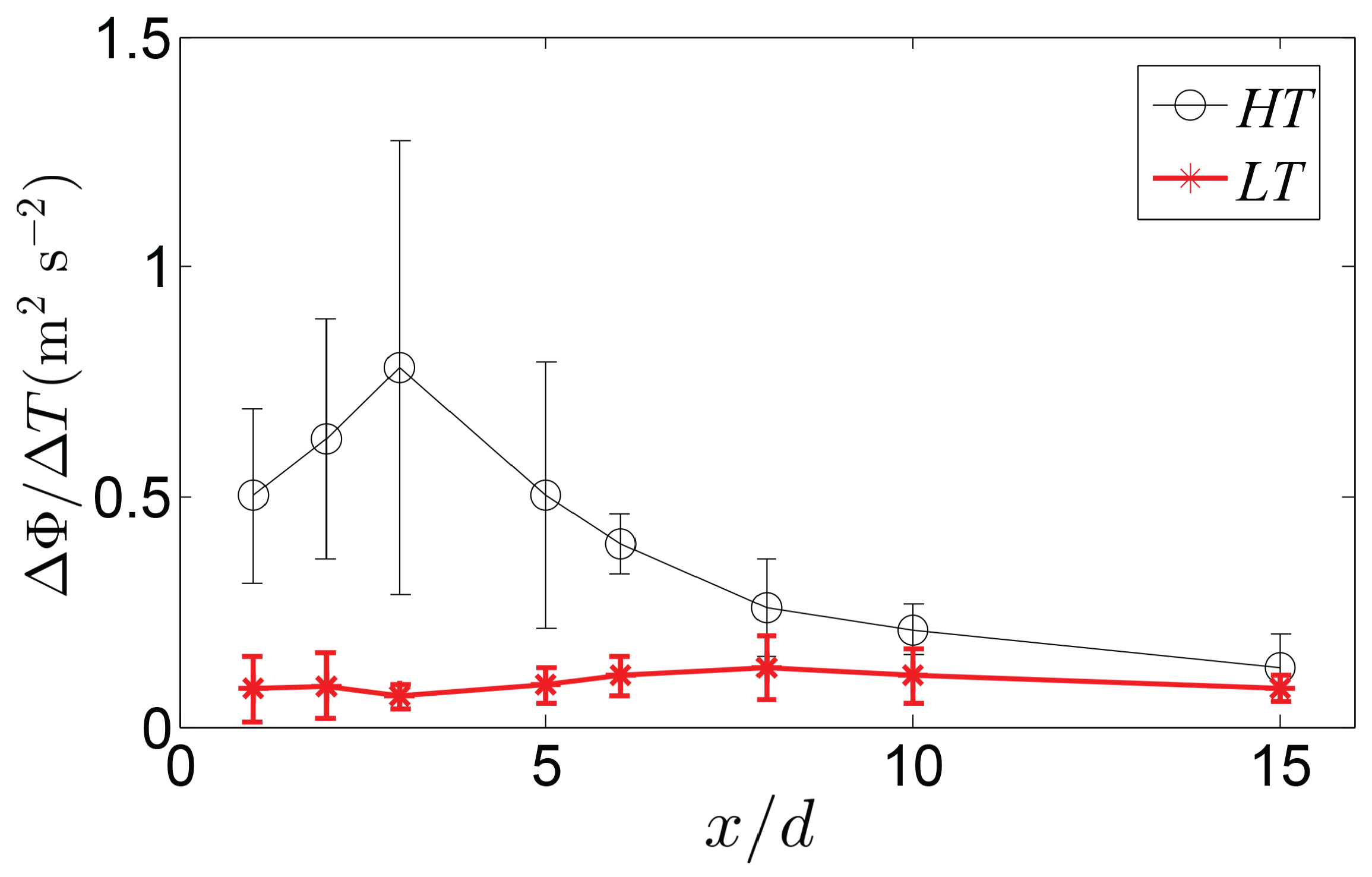
3.2. Evolution of the Large-Scale Motions
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chamorro, L.P.; Sotiropoulos, F. Turbulent flow inside and above a wind farm: A wind-tunnel study. Energies 2011, 4, 1916–1936. [Google Scholar] [CrossRef]
- Vermeer, L.J.; Sørenson, J.N.; Crespo, A. Wind turbine wake aerodynamics. Prog. Aerosp. Sci. 2003, 39, 467–510. [Google Scholar] [CrossRef]
- Jensen, N.O. A Bote on Wind Generator Interaction; Riso National Laboratory: Roskilde, Denmark, 1983. [Google Scholar]
- Peña, A.; Rathmann, O. Atmospheric Stability-dependent infinite wind-farm models and wake-decay coefficient. Wind Energy 2014, 17, 1269–1285. [Google Scholar] [CrossRef] [Green Version]
- Chu, C.R.; Chiang, P.H. Turbulence effects on the wake flow and power production of a horizontal-axis wind turbine. J. Wind Eng. Ind. Aerodyn. 2014, 124, 82–89. [Google Scholar] [CrossRef]
- Göçmen, T.; van der Laan, P.; Réthoré, P.E.; Diaz, A.P.; Larsen, G.C.; Ott, S. Wind turbine wake models developed at the technical university of Denmark: A Review. Renew. Sustain. Energy Rev. 2016, 60, 752–769. [Google Scholar] [CrossRef] [Green Version]
- Quarton, D.; Ainslie, J. Turbulence in wind turbine wakes. J. Wind Eng. Ind. Aerodyn. 1989, 14, 15–23. [Google Scholar]
- Crespo, A.; Herna, J. Turbulence characteristics in wind turbine wakes. J. Wind Eng. Ind. Aerodyn. 1996, 61, 71–85. [Google Scholar] [CrossRef]
- Frandsen, S.T.; Thøgersen, M.L. Integrated fatigue loading for wind turbines in wind farms by combining ambient turbulence and wakes. Wind Eng. 1999, 23, 327–339. [Google Scholar]
- Ozbay, A.; Tian, W.; Yang, Z.; Hu, H. An experimental investigation on the wake interference of multiple wind turbines in atmospheric boundary layer winds. In Proceedings of the 30th AIAA Applied Aerodynamics Conference, New Orleans, LA, USA, 25–28 June 2012.
- Trujillo, J.J.; Bingöl, F.; Larsen, G.C.; Mann, J.; Kühn, M. Light detection and ranging measurements of wake dynamics. Part II: Two-dimensional scanning. Wind Energy 2011, 14, 61–75. [Google Scholar] [CrossRef]
- Barthelmie, R.J.; Larsen, G.C.; Frandsen, S.T.; Folkerts, L.; Rados, K.; Pryor, S.C.; Schepers, G. Comparison of wake model simulations with offshore wind turbine wake profiles measured by sodar. J. Atmos. Ocean. Technol. 2006, 23, 888–901. [Google Scholar] [CrossRef]
- Medici, D.; Alfredsson, P.H. Measurements on a wind turbine wake: 3D effects and bluff body vortex shedding. Wind Energy 2006, 9, 219–236. [Google Scholar] [CrossRef]
- Howard, K.B.; Singh, A.; Sotiropoulos, F.; Guala, M. On the statistics of wind turbine wake meandering: An experimental investigation. Phys. Fluids 2015, 27, 075103. [Google Scholar] [CrossRef]
- Chamorro, L.P.; Guala, M.; Arndt, R.E.A.; Sotiropoulos, F. On the evolution of turbulent scales in the wake of a wind turbine model. J. Turbul. 2012, 13, 1–13. [Google Scholar] [CrossRef]
- Singh, A.; Howard, K.B.; Guala, M. On the homogenization of turbulent flow structures in the wake of a model wind turbine. Phys. Fluids 2014, 26, 025103. [Google Scholar] [CrossRef]
- Chamorro, L.; Hill, C.; Morton, S.; Ellis, C.; Arndt, R.; Sotiropoulos, F. On the interaction between a turbulent open channel flow and an axial-flow turbine. J. Fluid Mech. 2013, 716, 658–670. [Google Scholar] [CrossRef]
- Chamorro, L.P.; Hill, C.; Neary, V.S.; Gunawan, B.; Arndt, R.E.A.; Sotiropoulos, F. Effects of energetic coherent motions on the power and wake of an axial-flow turbine. Phys. Fluids 2015, 27, 055104. [Google Scholar] [CrossRef]
- Apt, J. The spectrum of power from wind turbines. J. Power Sources 2007, 169, 369–374. [Google Scholar] [CrossRef]
- Milan, P.; Wächter, M.; Peinke, J. Turbulent character of wind energy. Phys. Rev. Lett. 2013, 110, 138701. [Google Scholar] [CrossRef] [PubMed]
- Chamorro, L.P.; Lee, S.J.; Olsen, D.; Milliren, C.; Marr, J.; Arndt, R.E.A.; Sotiropoulos, F. Turbulence effects on a full—Scale 2.5 MW horizontal—Axis wind turbine under neutrally stratified conditions. Wind Energy 2015, 18, 339–349. [Google Scholar] [CrossRef]
- Tobin, N.; Zhu, H.; Chamorro, L.P. Spectral behaviour of the turbulence-driven power fluctuations of wind turbines. J. Turbul. 2015, 16, 832–846. [Google Scholar] [CrossRef]
- Adrian, R.; Meinhart, C.; Tomkins, C. Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 2000, 422, 1–54. [Google Scholar] [CrossRef]
- Shiu, H.; van Dam, C.; Johnson, E.; Barone, M.; Phillips, R.; Straka, W.; Fontaine, A.; Jonson, M. A design of a hydrofoil family for current-driven marine-hydrokinetic turbines. In Proceedings of the 20th International Conference on Nuclear Engineering and the American Society of Mechanical Engineers 2012 Power Conference, Anaheim, CA, USA, 30 July–3 August 2012; pp. 839–847.
- Abkar, M.; Sharifi, A.; Porté-Agel, F. Wake flow in a wind farm during a diurnal cycle. J. Turbul. 2016, 17, 420–441. [Google Scholar] [CrossRef]
- España, G.; Aubrun, S.; Loyer, S.; Devinant, P. Wind tunnel study of the wake meandering downstream of a modelled wind turbine as an effect of large scale turbulent eddies. J. Wind Eng. Ind. Aerodyn. 2012, 101, 24–33. [Google Scholar] [CrossRef]
- Williamson, C.H. Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 1996, 28, 477–539. [Google Scholar] [CrossRef]
- Durao, D.; Heitor, M.; Pereira, J. Measurements of turbulent and periodic flows around a square cross-section cylinder. Exp. Fluids 1988, 6, 298–304. [Google Scholar] [CrossRef]
- Jang, Y.I.; Lee, S.J. Visualization of turbulent flow around a sphere at subcritical Reynolds numbers. J. Vis.-Jpn. 2007, 10, 359–366. [Google Scholar] [CrossRef]
- Counihan, J. Adiabatic atmospheric boundary layers: A review and analysis of data from the period 1880–1972. Atmos. Environ. 1975, 9, 871–905. [Google Scholar] [CrossRef]
- Mikkelsen, K. Effect of Free Stream Turbulence on Wind Turbine Performance. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2013. [Google Scholar]
- Von Karman, T. Progress in the statistical theory of turbulence. Proc. Natl. Acad. Sci. USA 1948, 34, 530–539. [Google Scholar] [CrossRef] [PubMed]

© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, Y.; Liu, H.; Aggarwal, R.; Singh, A.; Chamorro, L.P. Effects of Freestream Turbulence in a Model Wind Turbine Wake. Energies 2016, 9, 830. https://doi.org/10.3390/en9100830
Jin Y, Liu H, Aggarwal R, Singh A, Chamorro LP. Effects of Freestream Turbulence in a Model Wind Turbine Wake. Energies. 2016; 9(10):830. https://doi.org/10.3390/en9100830
Chicago/Turabian StyleJin, Yaqing, Huiwen Liu, Rajan Aggarwal, Arvind Singh, and Leonardo P. Chamorro. 2016. "Effects of Freestream Turbulence in a Model Wind Turbine Wake" Energies 9, no. 10: 830. https://doi.org/10.3390/en9100830






