An Intelligent Fuzzy Logic Controller for Maximum Power Capture of Point Absorbers
Abstract
:1. Introduction
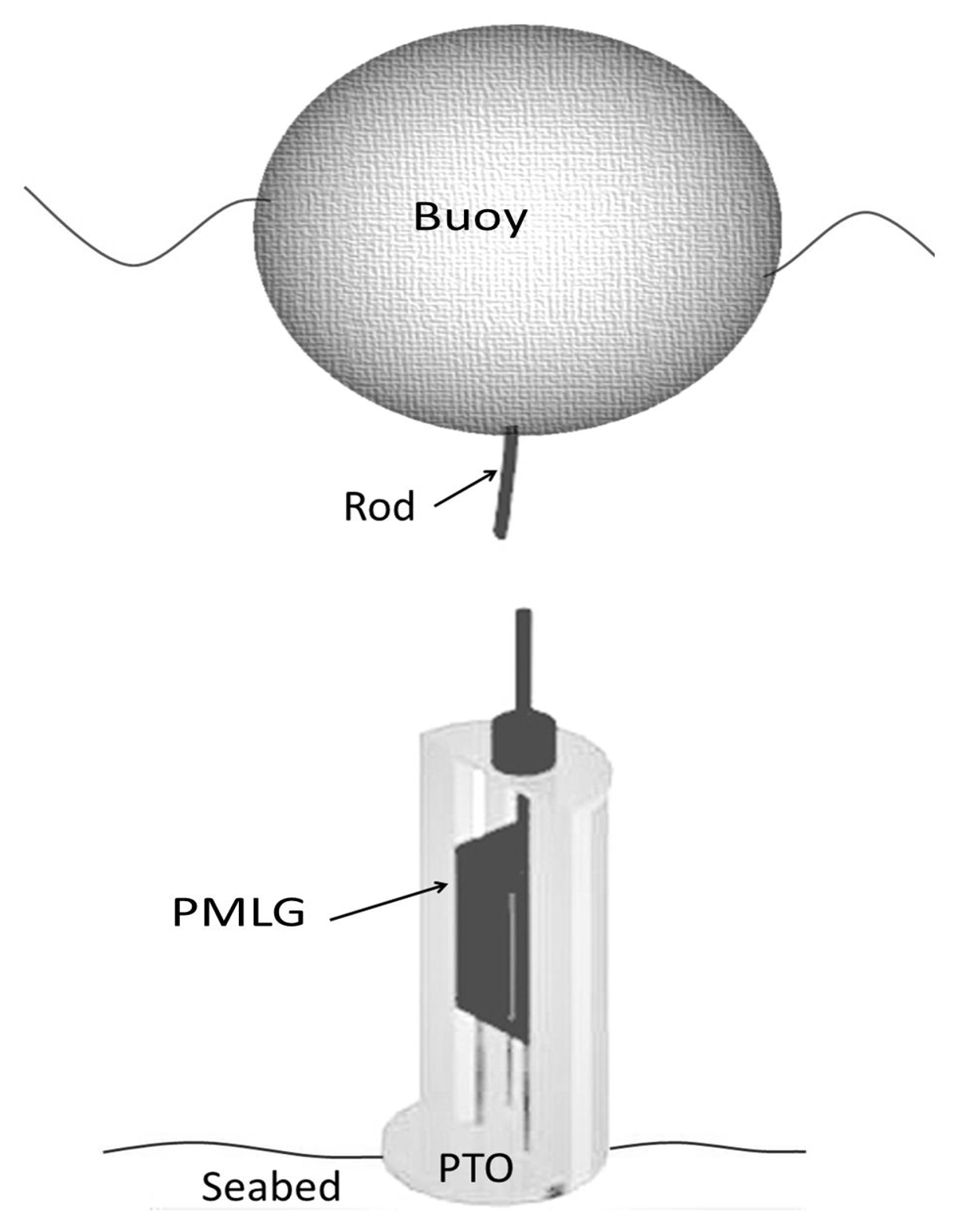
2. Heaving WEC Dynamics
- The wave excitation force, fe(t), is simply the force exerted by the incident waves on the WEC floater assuming that it is held motionless;
- The hydrodynamic radiation force, fr(t), is the force that both the oscillating body and the surrounding fluid apply on each, due to the alteration of the pressure field over the submerged portion of the buoy as the waves are created;
- The buoyancy stiffness force, fb(t), which results from the imbalance between the floater weight and the weight of the displaced fluid during oscillation. The buoyancy force is a function of the buoy displacement z(t), water density ρ, the gravitational acceleration g, and the water plane area Aw, such that fb(t) = ρgAwz(t). Note that the water plane area Aw is assumed to be fixed for the sake of simplicity. Therefore, the buoyancy stiffness coefficient is defined as Sb = ρgAw;
- The drag force, fd(t), which is a nonlinear resistive force exerted by the water on the reciprocating buoy, where fd(t) = 0.5ρAwCD|ż(t)|ż(t), where CD is the drag coefficient;
- The mooring system force, fm(t), is a force applied on the buoy by a tight mooring lines. In this study, in order to keep the buoy in place, it is moored to two neighboring floating mooring points (e.g., small buoys). The mooring force is modeled to have a nonlinear spring effect, , where Sm and Lm are the mooring cable stiffness and the cable horizontal length, respectively [17,18];
- The restoring force, frs(t), which represents the force applied by the auxiliary spring units installed between the translator of the PMLG and the system's point of interaction at the seabed. frs(t) is modelled as a spring force, such as, frs(t) = Srsz(t), where Srs represents the spring stiffness coefficient;
- The losses force, fl(t), which includes the losses due to friction, viscosity, and non-ideal PTO mechanisms. In practice, this force is nonlinear and time variant, however, for convenience, it is modeled as a linear time-invariant resistive force, that is fl(t) = Rlż(t), where Rl represents the losses damping coefficient;
- The input force, fu(t), which is the force applied by the PTO system on the WEC. This force is usually governed by a controller to maximize the captured energy.
2.1. State Space Representation of the WEC Model
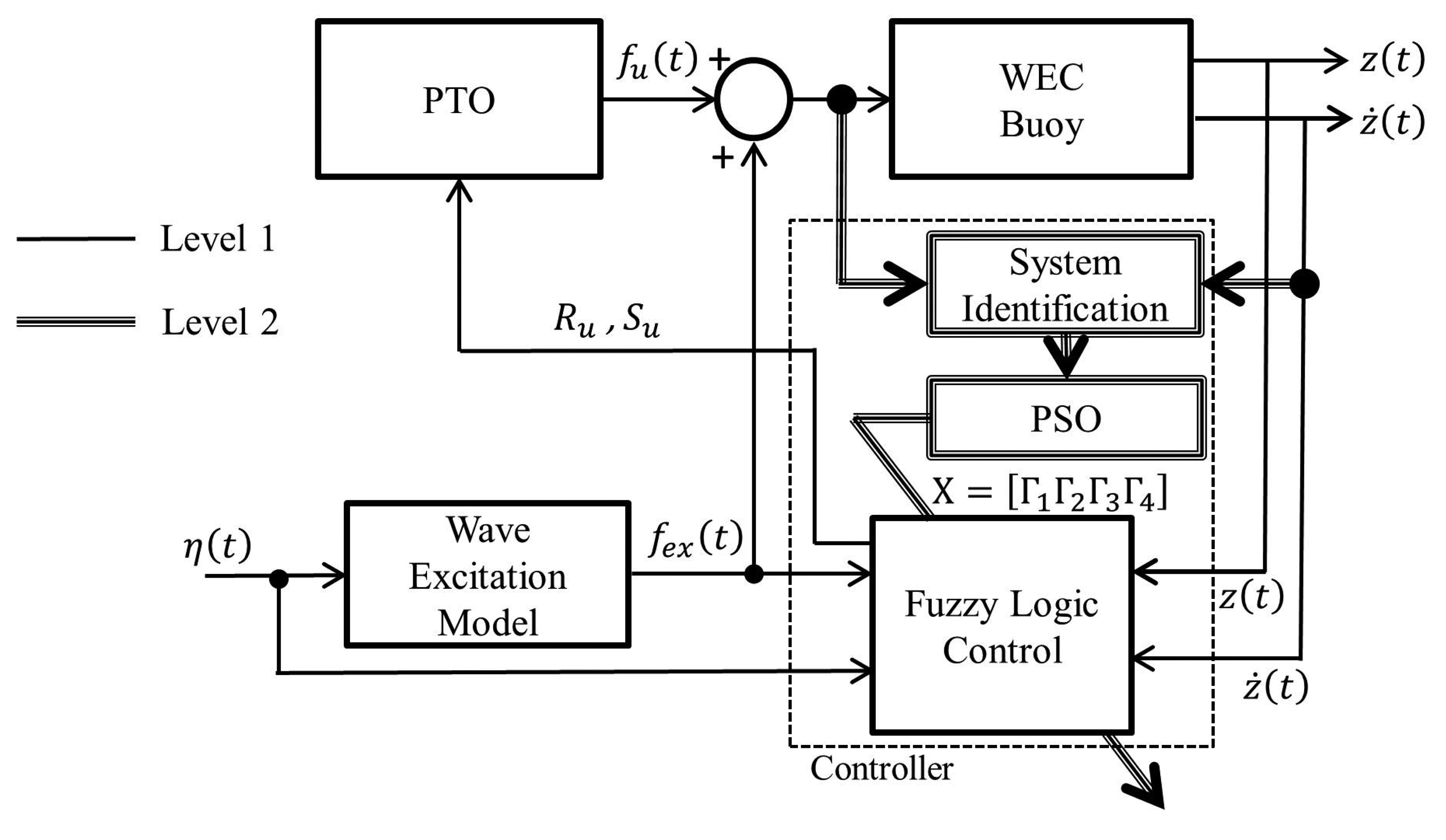
3. Controller Design
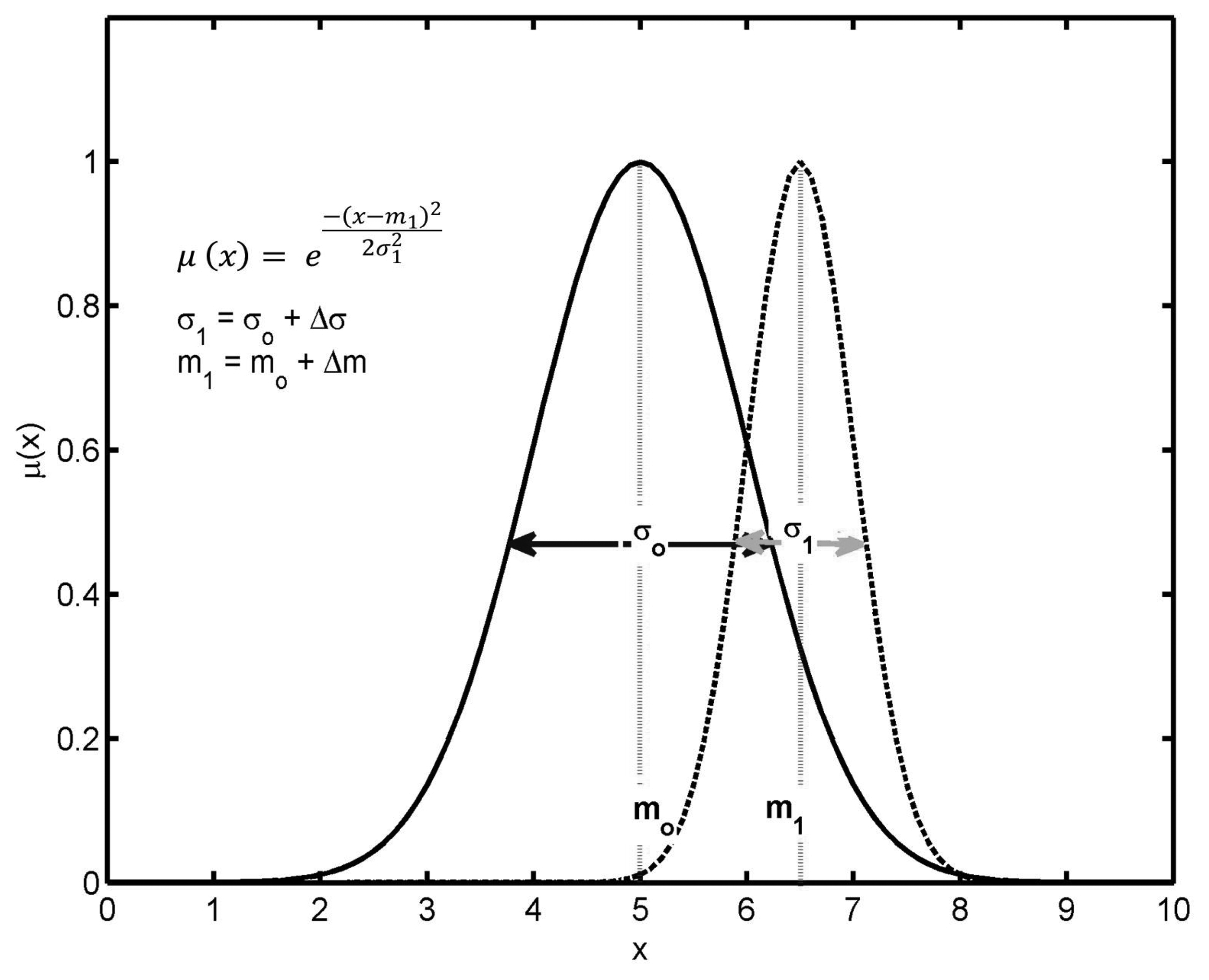
3.1. Fixed Structure Fuzzy Logic Controller (FS-FLC)
3.2. PSO-Fuzzy Logic Controller (PSO-FLC)
4. Results and Discussion
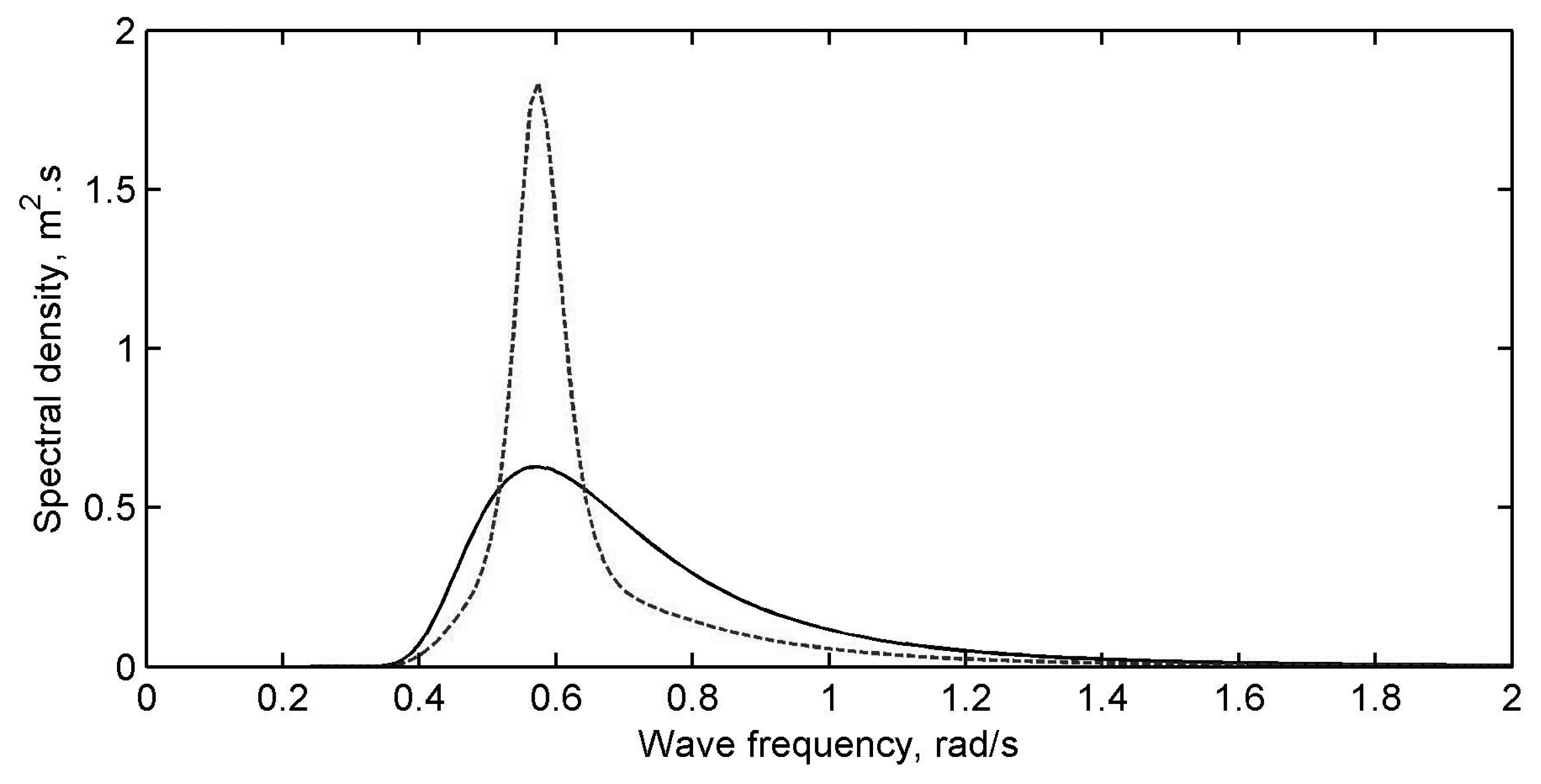
4.1. Simulation Setup
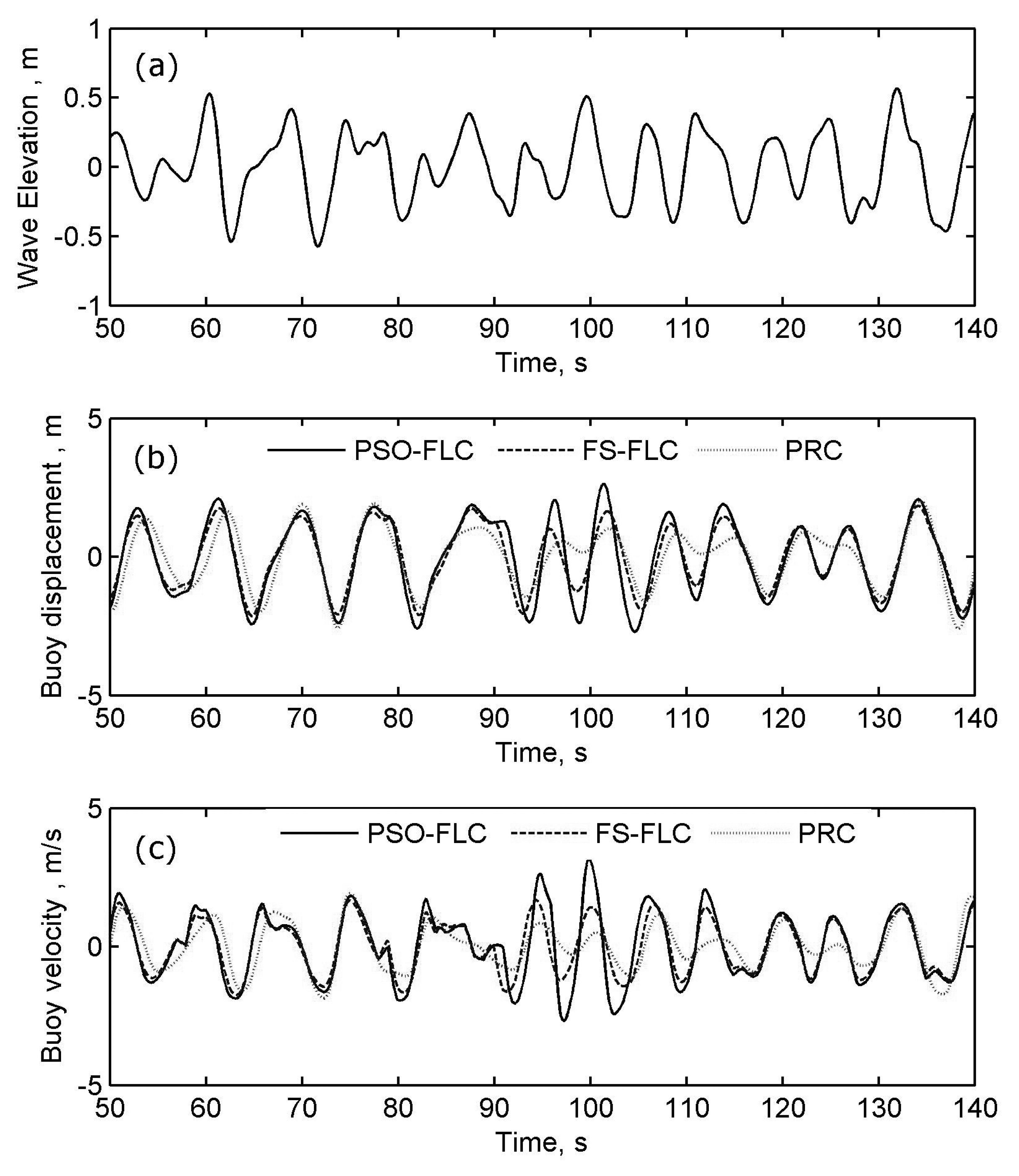
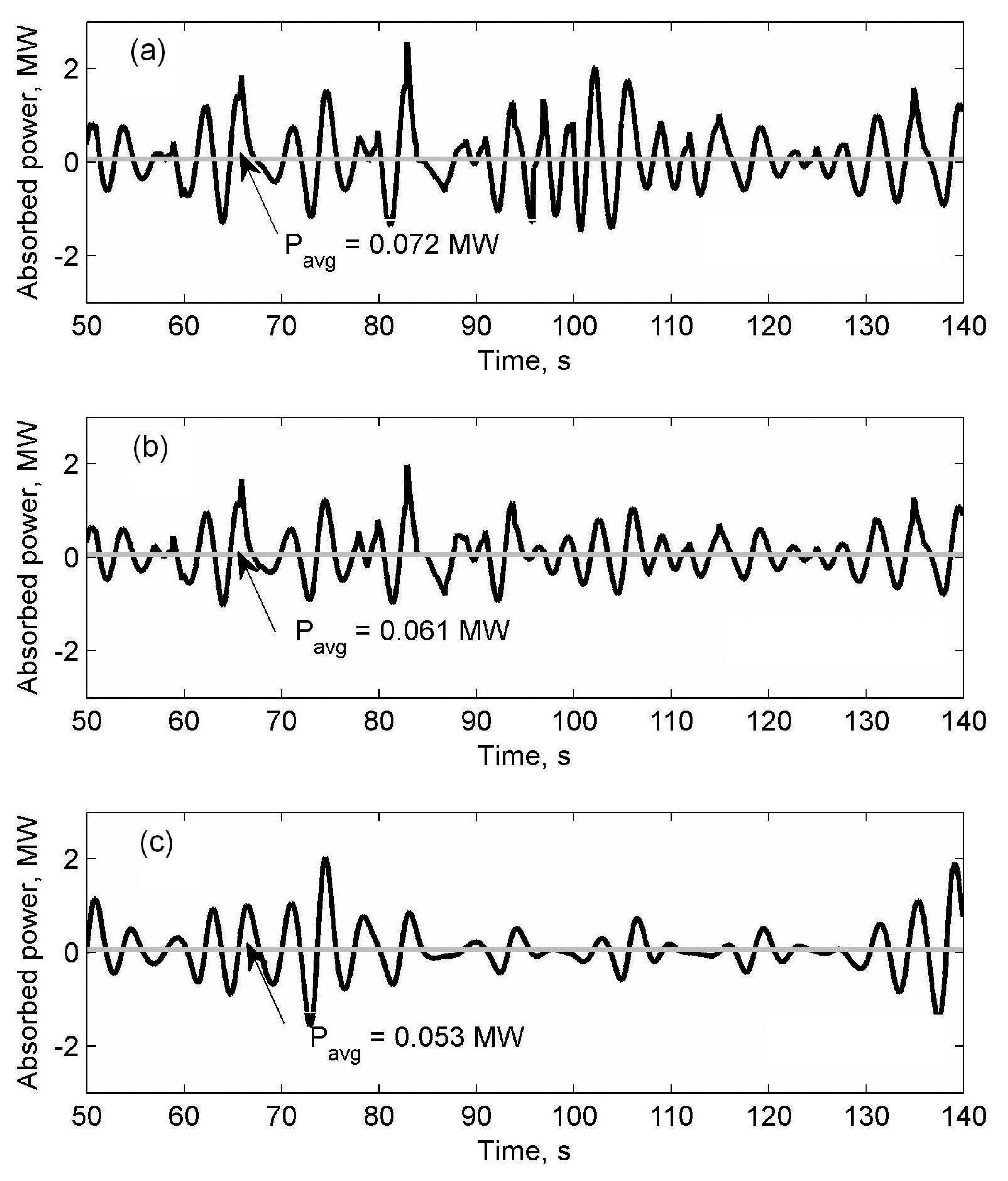
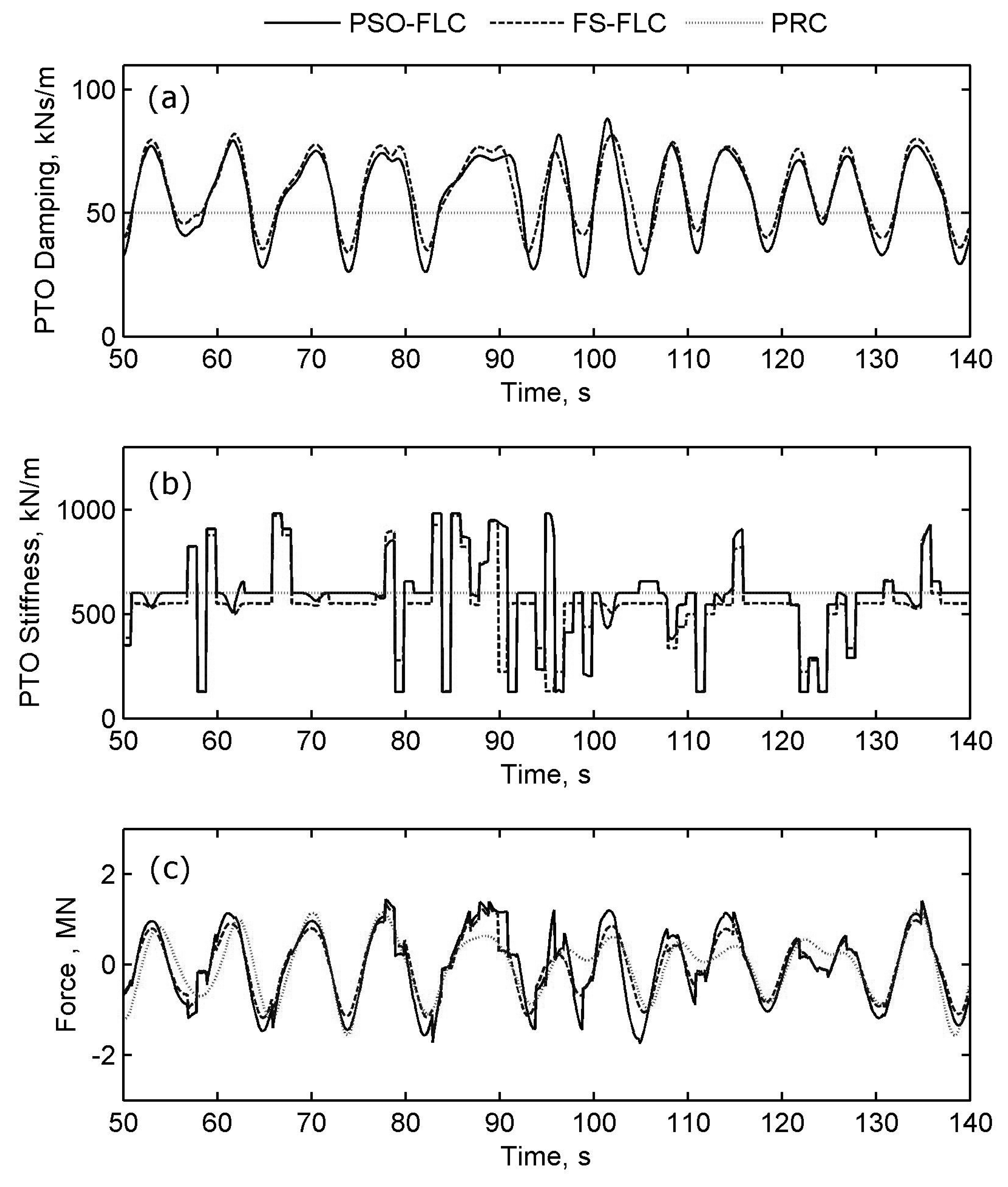
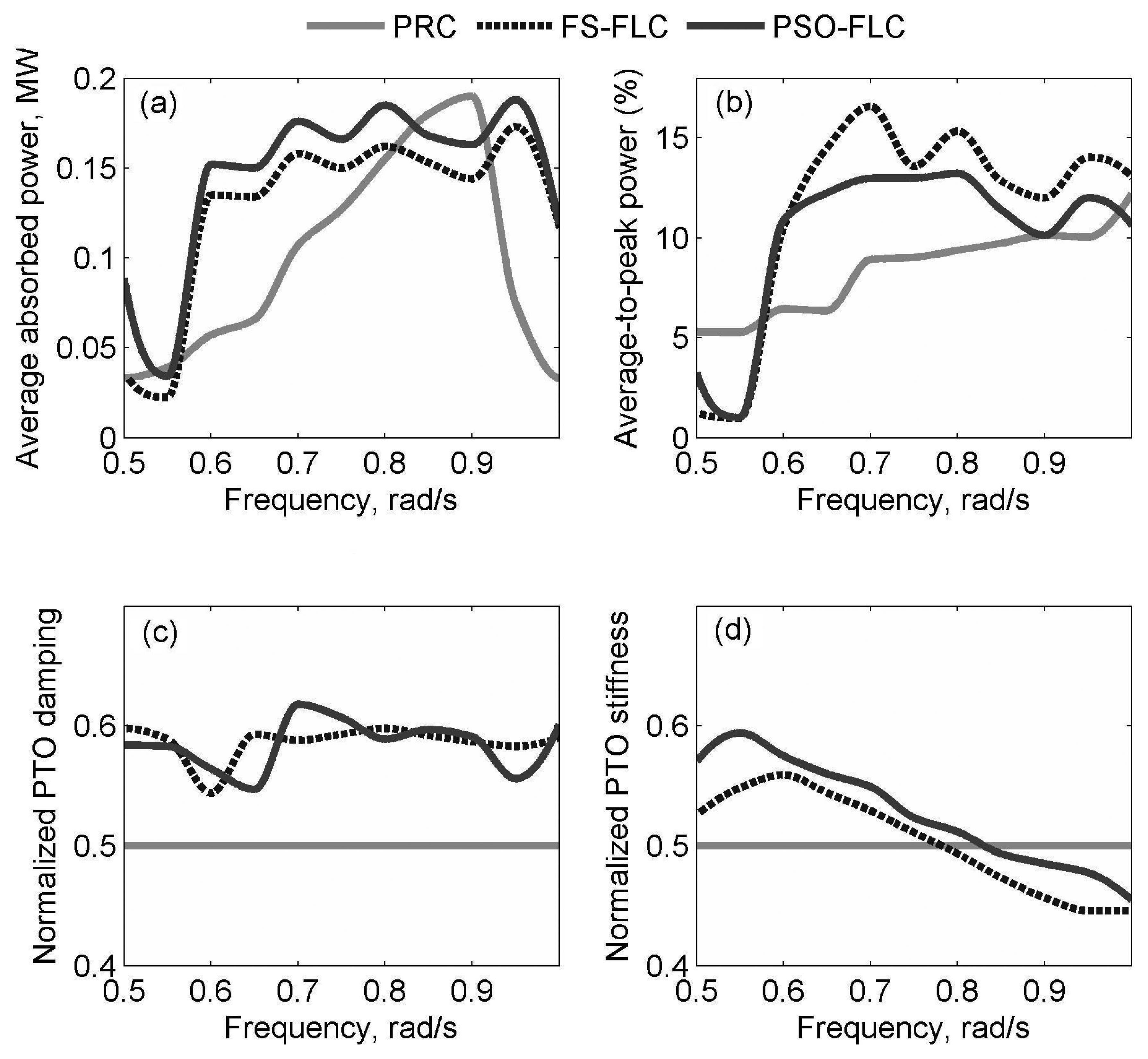
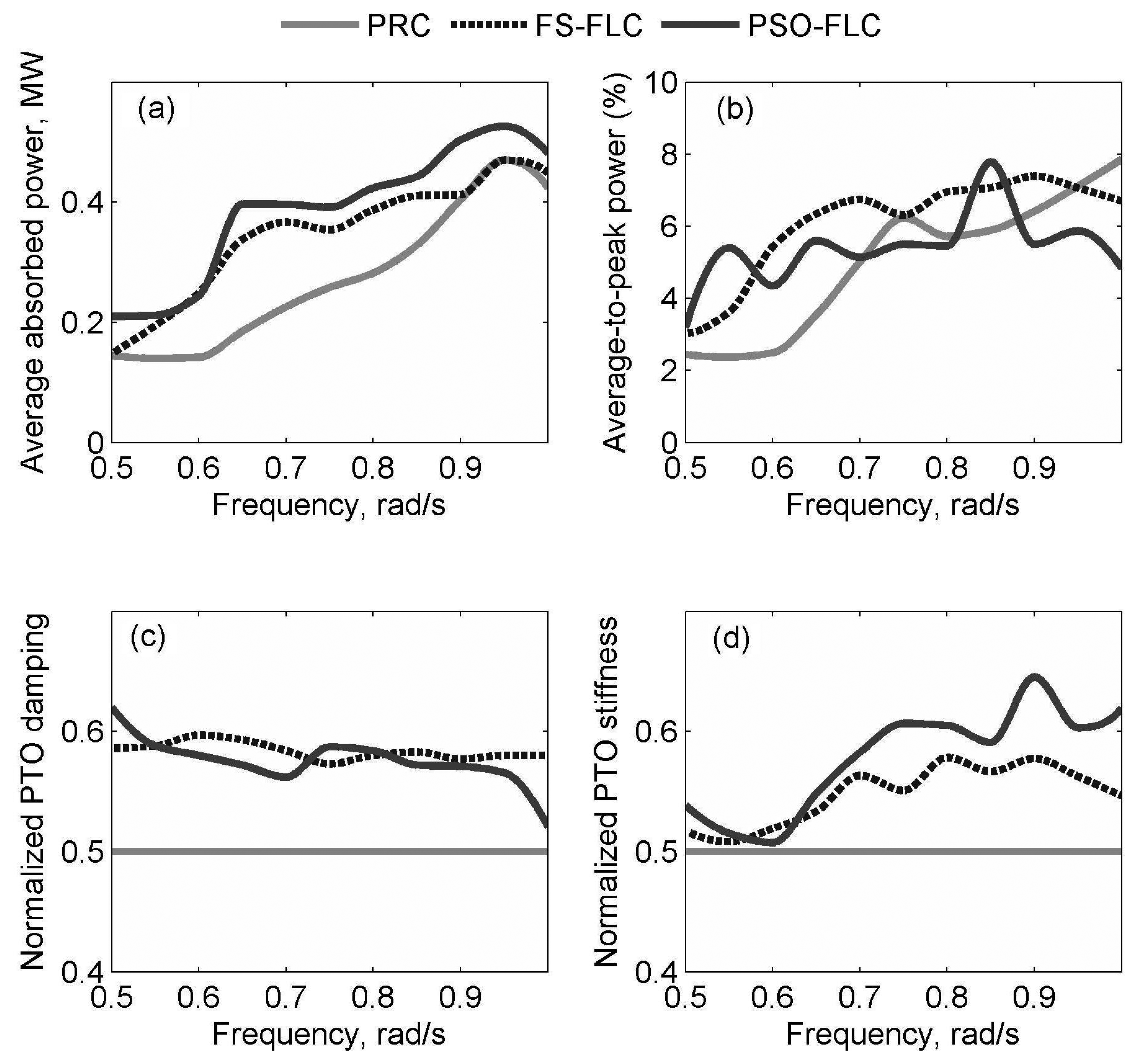
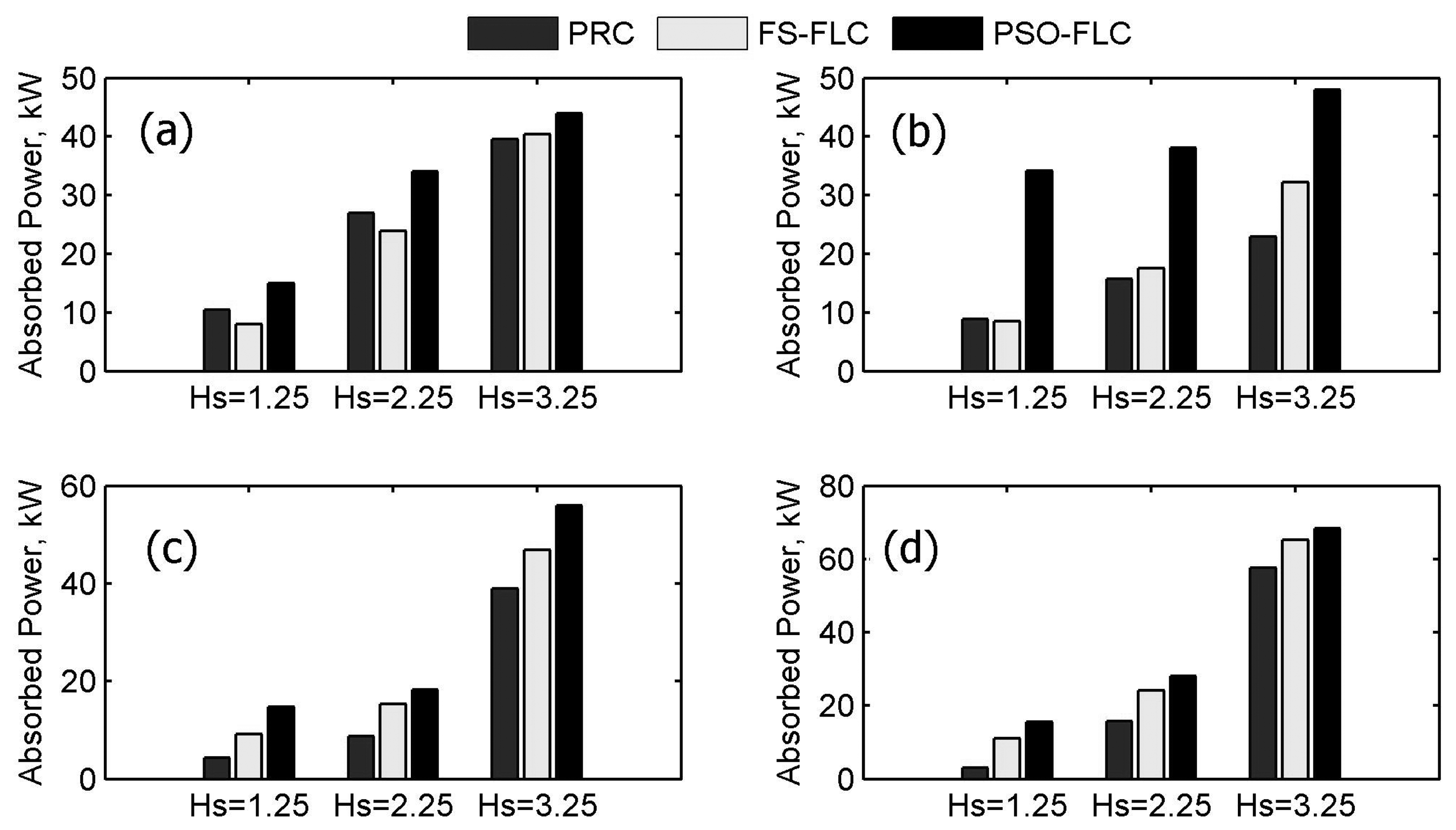
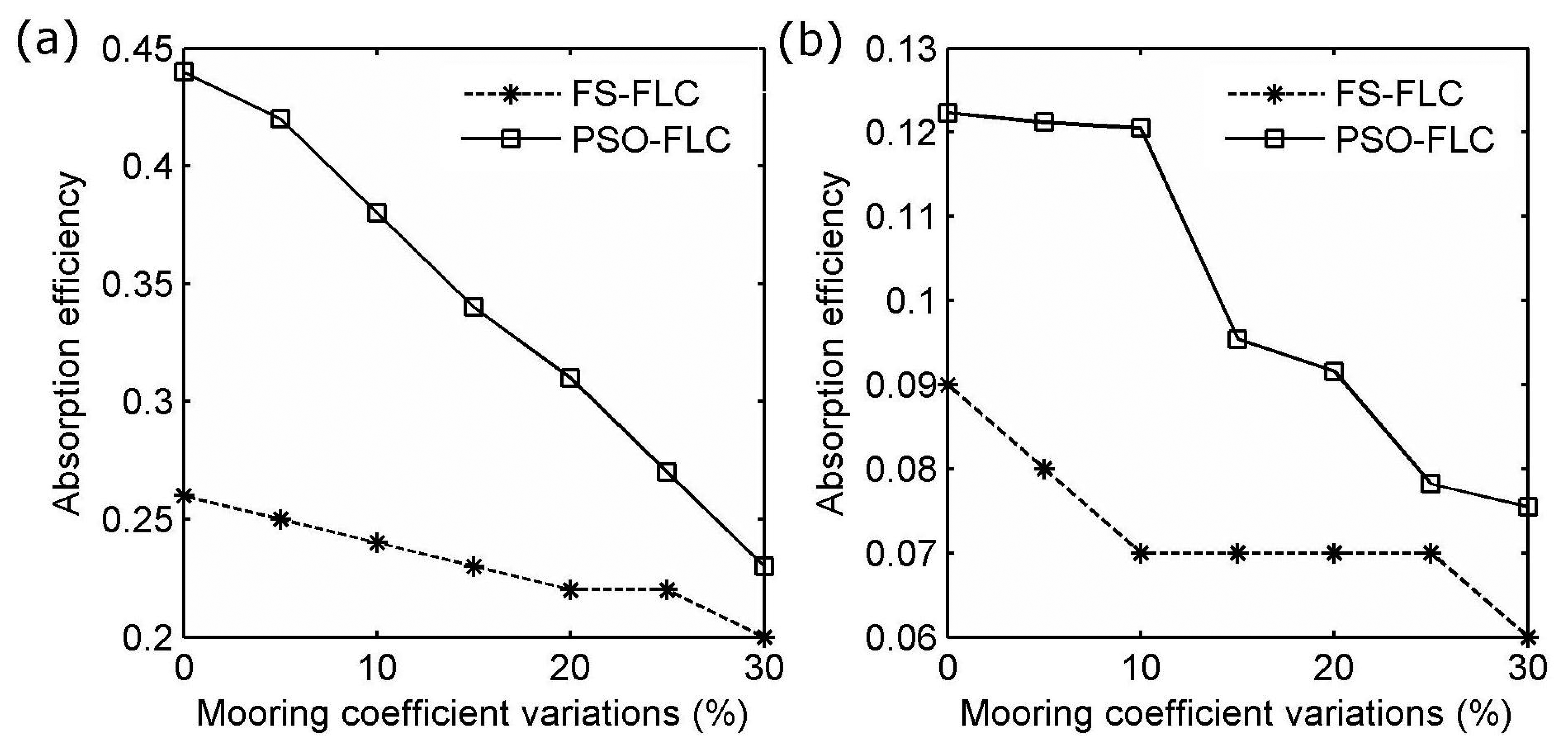
4.2. Simulation Results
5. Conclusions
Conflicts of Interest
References
- Valerio, D.; Beirao, P.; Mendes, M.J.G.; Sa da Costa, J. Comparison of control strategies performance for a wave energy converter. Proceedings of the 2008 16th Mediterranean Conference on Control and Automation, Ajaccio, France, 25–27 June 2008; pp. 773–778.
- Falcao, A.F.O. Wave energy utilization: A review of the technologies. J. Renew. Sustain. Energy Rev. 2010, 14, 899–918. [Google Scholar]
- Price, A. New Perspectives on Wave Energy Converter Control. Ph.D. Thesis, University of Edinburgh, Edinburgh, UK, 2009. [Google Scholar]
- Babarit, A.; Clement, A.H. Optimal latching control of a wave energy device in regular and irregular waves. Appl. Ocean Res. 2006, 28, 77–91. [Google Scholar]
- De La Villa JaÃl'n, A.; Andrade, D.E.M.; Santana, A.G. Increasing the efficiency of the passive loading strategy for wave energy conversion. J. Renew. Sustain. Energy 2013, 5. [Google Scholar] [CrossRef]
- Tedeschi, E.; Molinas, M. Tunable control strategy for wave energy converters with limited power takeoff rating. IEEE Trans. Ind. Electron. 2012, 59, 3838–3846. [Google Scholar]
- Slotine, J.; Li, W. Applied Nonlinear Control; Prentice Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
- Valerio, D.; Mendes, M.J.G.C.; Beirao, P.; da Costa, J.S. Identification and control of the AWS using neural network models. J. Appl. Ocean Res. 2008, 30, 178–188. [Google Scholar]
- Brekken, T. On model predictive control for a point absorber wave energy converter. Proceedings of the 2011 IEEE Trondheim PowerTech, Trondheim, Norway, 19–23 June 2011; pp. 1–8.
- Schoen, M.P.; Hals, J.; Moan, T. Wave prediction and robust control of heaving wave energy devices for irregular waves. IEEE Trans. Sustain. Energy 2011, 26, 627–638. [Google Scholar]
- Jama, M.; Wahyudie, A.; Noura, H.; Assi, A. Fuzzy logic based reactive controller for heaving wave energy converters. Proceedings of the 2012 International Conference on Renewable Energies for Developing Countries (REDEC), Beirut, Lebanon, 28–29 November 2012; pp. 1–5.
- Jama, M.; Wahyudie, A.; Noura, H.; Assi, A. Self-tunable fuzzy logic controller for the optimization of heaving wave energy converters. Proceedings of the 2012 International Conference on Renewable Energy Research and Applications (ICRERA), Nagasaki, Japan, 11–14 November 2012; pp. 1–6.
- Kukolja, D.; Kuzmanovica, B.; Levi, E. Design of a PID-like compound fuzzy logic controller. Eng. Appl. Artif. Intell. 2001, 14, 785–803. [Google Scholar]
- Stalberg, M.; Waters, R.; Danielsson, O.; Leijon, M. Influence of generator damping on peak power and variance of power for a direct drive wave energy converter. J. Offshore Mech. Arct. Eng. 2008, 130. [Google Scholar] [CrossRef]
- Falnes, J. Principles for capture of energy of ocean from ocean waves. Phase control and optimum oscillation. Norw. Mar. Res. 1976, 6, 1–8. [Google Scholar]
- Falnes, J. Ocean Waves and Oscillating Systems; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Markus, R.; Mario, E.; Oliver, S.; Brekken, T. Nonlinear model predictive control of a point absorber wave energy converter. IEEE Trans. Sustain. Energy 2013, 4, 118–126. [Google Scholar]
- Jordan, M.A.; Beltran-Aguedo, R. Optimal identification of potential radiation hydrodynamics for moored floating structures-A new general approach in state space. Ocean Eng. 2004, 31, 1859–1914. [Google Scholar]
- Cummins, W.E. The impulse response functions and ship motions. Schiffstechnik 1961, 9, 101–109. [Google Scholar]
- Ogilvie, T. Recent progress towards the understanding and prediction of ship motions. Proceedings of the 5th Symposium on Naval Hydrodynamics, Bergen, Norway, 10–12 September 1964; pp. 3–80.
- WAMIT User Manual. Available online: http://www.wamit.com/manual.htm (accessed on 12 March 2013).
- Taghipoura, R.; Pereza, T.; Moan, T. Hybrid frequency-time domain models for dynamic response analysis of marine structures. Ocean Eng. 2008, 35, 685–705. [Google Scholar]
- Backer, G.D. Hydrodynamic Design Optimization of Wave Energy Converters Consisting of Heaving Point Absorbers. Ph.D. Thesis, Ghent University, Zwijnaarde, Belgium, 2009. [Google Scholar]
- Azadegan, A.; Porobic, L.; Ghazinoory, S.; Samouei, P.; Kheirkhah, A.S. Fuzzy logic in manufacturing: A review of literature and a specialized application. Int. J. Prod. Econ. 2011, 132, 258–270. [Google Scholar]
- Coban, R.; Can, B. A trajectory tracking genetic fuzzy logic controller for nuclear research reactors. Energy Convers. Manag. 2010, 51, 587–593. [Google Scholar]
- Karuppanan, P.; Mahapatra, K.K. PI and fuzzy logic controllers for shunt active power filter-A report. ISA Trans. 2012, 51, 163–169. [Google Scholar]
- Emani, M.R.; Golenberg, A.A.; Turksen, I.B. Fuzzy logic control of dynamic systems: From modeling to design. Eng. Appl. Artif. Intell. 2000, 13, 47–69. [Google Scholar]
- Shayeghi, H.; Jalili, A.; Shayanfar, H.A. Multi-stage fuzzy load frequency control using PSO. Energy Convers. Manag. 2008, 49, 2570–2580. [Google Scholar]
- Chang, Y.; Wu, Y. The genetic algorithm based tuning method for symmetric membership functions of fuzzy logic control systems. Proceedings of the International IEEE/IAS Conference on Industrial Automation and Control: Emerging Technologies, 1995, Torino, Italy, 22–27 May 1995; pp. 421–428.
- Chiou, J.-S.; Tsai, S.-H.; Liu, M.-T. A PSO-based adaptive fuzzy PID-controllers. Simul. Model. Pract. Theory 2012, 26, 49–59. [Google Scholar]
- Rama Mohan Rao, A.; Sivasubramanian, K. Multi-objective design of fuzzy logic controller using a self-configurable swarm intelligence algorithm. Comput. Struct. 2008, 86, 2141–2154. [Google Scholar]
- Jamaludin, J.; Rahim, N.A.; Hew, W.P. Development of a self-tuning fuzzy logic controller for intelligent control of elevator systems. Eng. Appl. Artif. Intell. 2009, 22, 1167–1178. [Google Scholar]
- Yang, X.S. Engineering Optimization: An Introduction With Metaheuristic Applications; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Lee, K.Y.; El-Sharkawi, M.A. (Eds.) Modern Heuristic Optimization Techniques: Theory and Applications to Power Systems; Wiley-IEEE Press: Piscataway, NJ, USA, 2008.
- Kennedy, J.; Eberhart, R.C.; Shi, Y. Swarm Intelligence; Morgan Kaufman Publishers: Burlington, MA, USA, 2001. [Google Scholar]
- Ljung, L. System Identification, Theory for the User; Prentice Hall: Englewood Cliffs, NJ, USA, 1999. [Google Scholar]
- Kumar, V.; Kumar, K. Spectral characteristics of high shallow water waves. Ocean Eng. 2008, 35, 900–911. [Google Scholar]
| IF | ΔA is Z | THEN | Ru is Z |
| ΔA is PS | Ru is NS | ||
| ΔA is PM | Ru is NM | ||
| ΔA is PB | Ru is NB and Su is PB | ||
| ΔA is NS | Ru is PS | ||
| ΔA isNM | Ru is PM and Su is NM | ||
| ΔA is NB | Ru is PB and Su is NB | ||
| IF | Δθ is Z | THEN | Su is Z |
| Δθ is PS | Su is PS | ||
| Δθ is PM | Su is PM | ||
| Δθ is PB | Su is PB | ||
| Δθ is NS | Su is NS | ||
| Δθ is NM | Su is NM | ||
| Δθ is NB | Su is NB | ||
| Initialize the population position vector and velocity vector randomly at j = 1, N is the population size |
| while(iteration limit is reached) |
| j = j + 1 |
| for loop over all dth dimensional N particles |
| Update using Equation (12) |
| Update using Equation (13) |
| Adjust the controller FIS |
| Evaluate the objective function |
| (Equation (16)) for current |
| Determine the current best for each |
| particle |
| end for loop |
| Determine the current global best ĝd |
| end while |
| Output the final ĝd and |
| Parameter (Symbol) | Value | Unit |
|---|---|---|
| Buoy radius (r) | 5 | m |
| Buoy mass (mb) | 2.68 × 105 | kg |
| Water plane area (Aw) | 78.54 | m2 |
| Submerged volume (Vs) | 261.80 | m3 |
| Drag coefficient (CD) | 0.5 | - |
| Buoyancy stiffness coefficient (Sb) | 7.89 × 105 | N/m |
| Restoring stiffness coefficient (Srs) | 2 × 105 | N/m |
| Added infinite mass (m∞) | 1.34 × 105 | kg |
| Resonance angular frequency (ωo) | 1.56 | rad/s |
| Seabed depth (d) | 80 | m |
| Losses resistance (Rl) | 0.4 × 105 | N.s/m |
| Mooring stiffness coefficient (Sm) | 1.5 × 105 | N/m |
| Mooring cable length (Lm) | 4 | m |
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Jama, M.; Wahyudie, A.; Assi, A.; Noura, H. An Intelligent Fuzzy Logic Controller for Maximum Power Capture of Point Absorbers. Energies 2014, 7, 4033-4053. https://doi.org/10.3390/en7064033
Jama M, Wahyudie A, Assi A, Noura H. An Intelligent Fuzzy Logic Controller for Maximum Power Capture of Point Absorbers. Energies. 2014; 7(6):4033-4053. https://doi.org/10.3390/en7064033
Chicago/Turabian StyleJama, Mohammed, Addy Wahyudie, Ali Assi, and Hassan Noura. 2014. "An Intelligent Fuzzy Logic Controller for Maximum Power Capture of Point Absorbers" Energies 7, no. 6: 4033-4053. https://doi.org/10.3390/en7064033
APA StyleJama, M., Wahyudie, A., Assi, A., & Noura, H. (2014). An Intelligent Fuzzy Logic Controller for Maximum Power Capture of Point Absorbers. Energies, 7(6), 4033-4053. https://doi.org/10.3390/en7064033




