Hydrodynamic Effects on Spectroscopic Water Detection in Gasoline Pipe Flow
Abstract
:1. Introduction
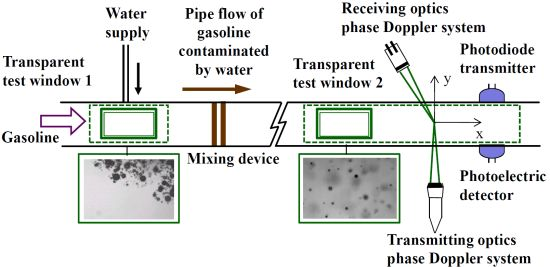
2. Experimental Setup and Procedures
2.1. Experimental Apparatus

2.2. Phase Doppler Particle Measurement System
| Optics | Specification | |
|---|---|---|
| Transmitting optics | Ar+ wavelength | 514.5 nm |
| Focal length | 250 mm | |
| Spot diameter | 233 μm | |
| Fringe spacing | 3.21 μm | |
| Fringe number | 72 | |
| Receiving optics | Focal length | 310 mm |
| Receiver aperture height | 2.0 mm | |
| Frequency shift | 40 MHz | |
| Scattering angle | 30 degree | |
| Phase to conversion factor | 0.955 μm/deg | |
2.3. Spectroscopic Water Detection
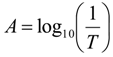

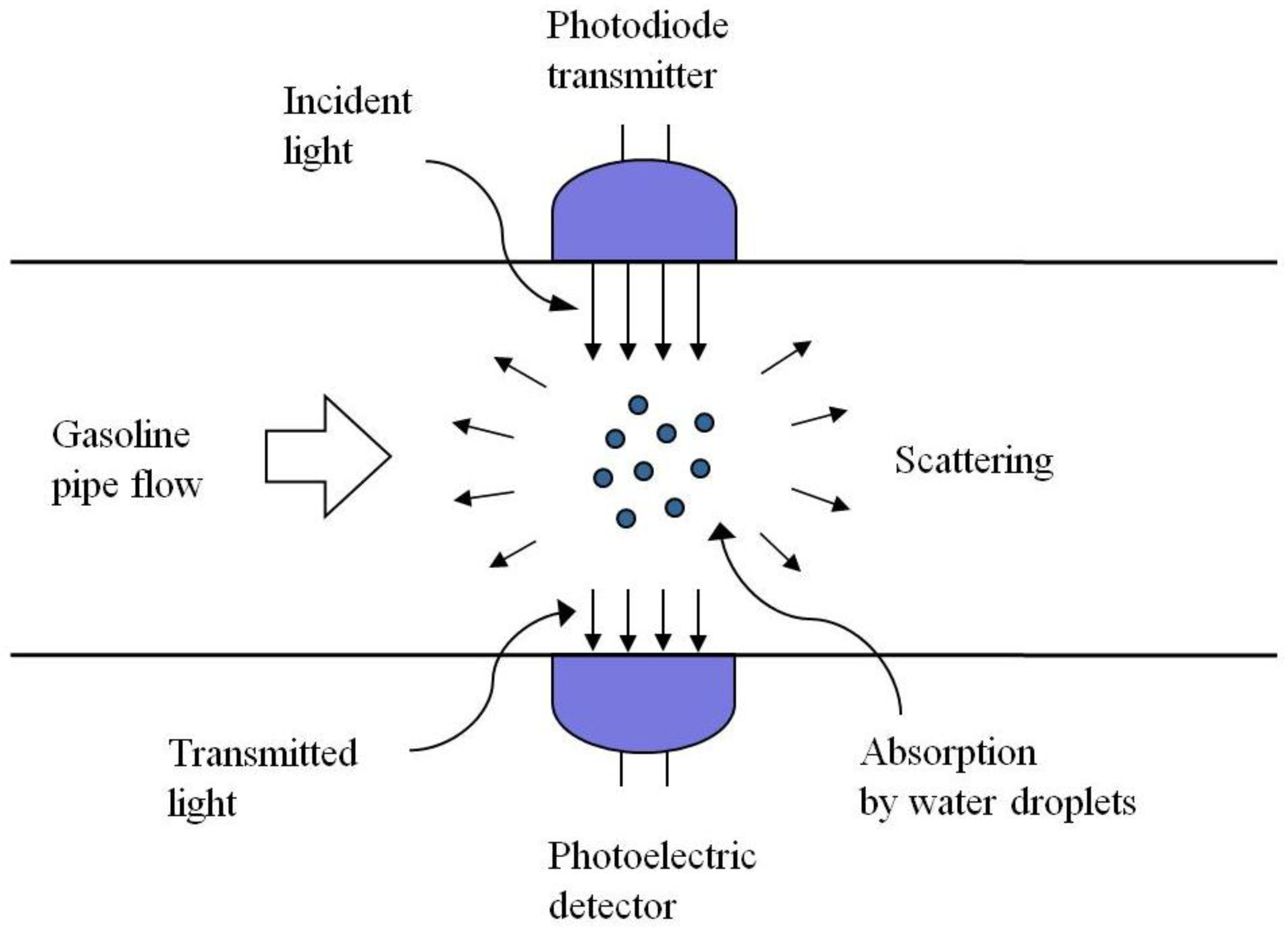
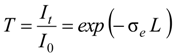
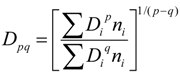
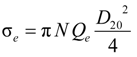
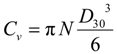
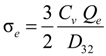
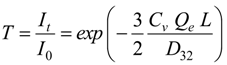
3. Results and Discussion
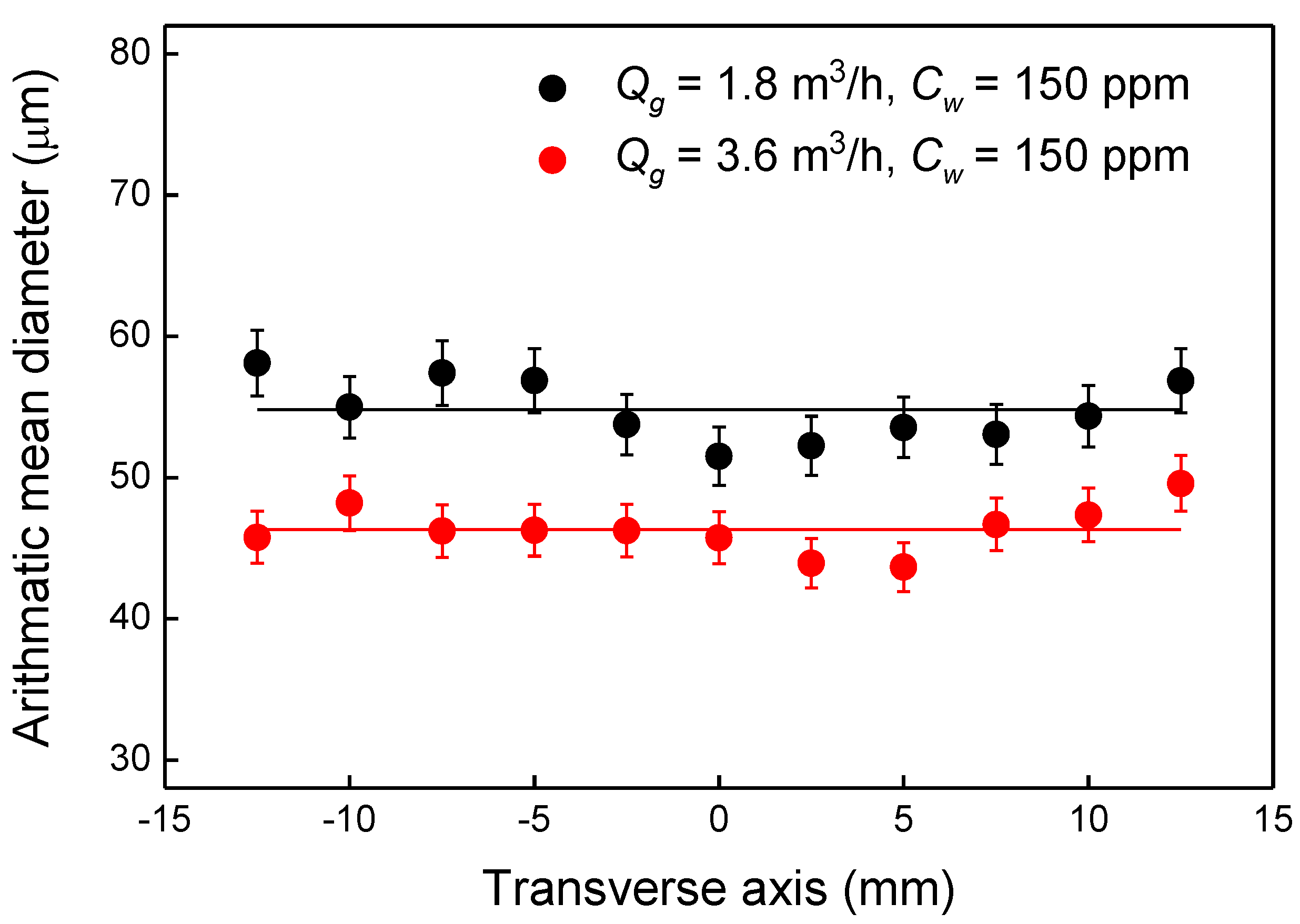
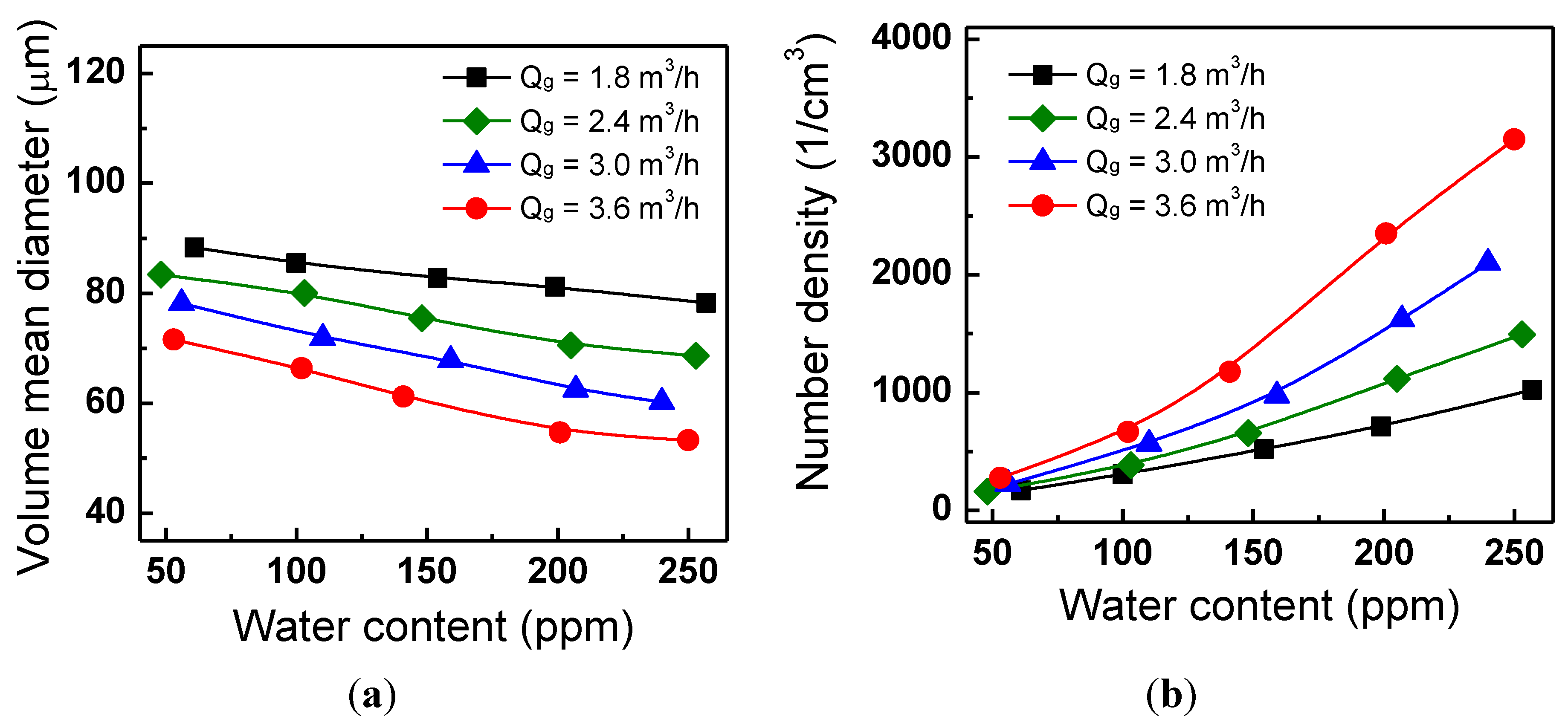
3.1. Water Droplet Characteristics

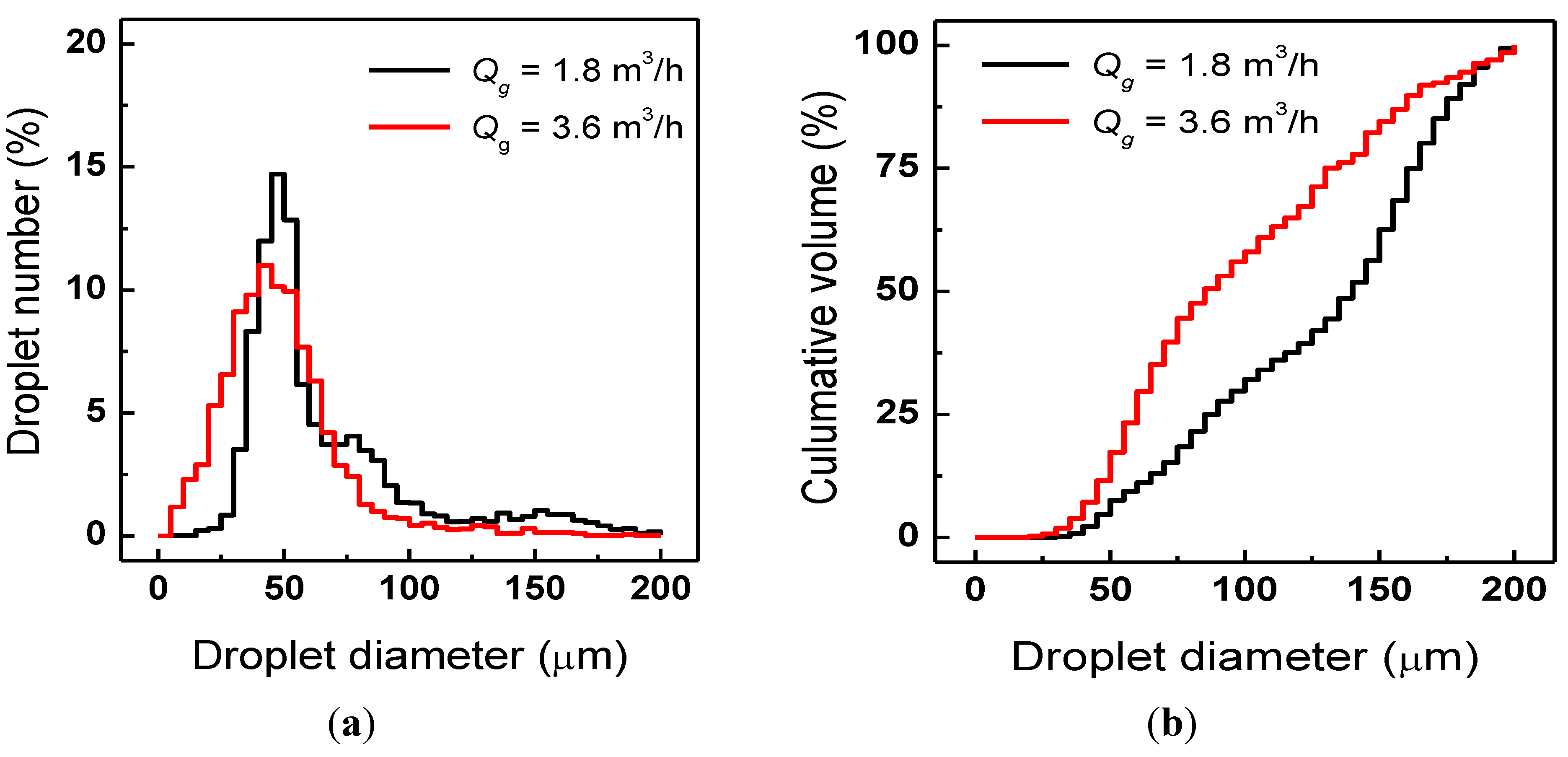
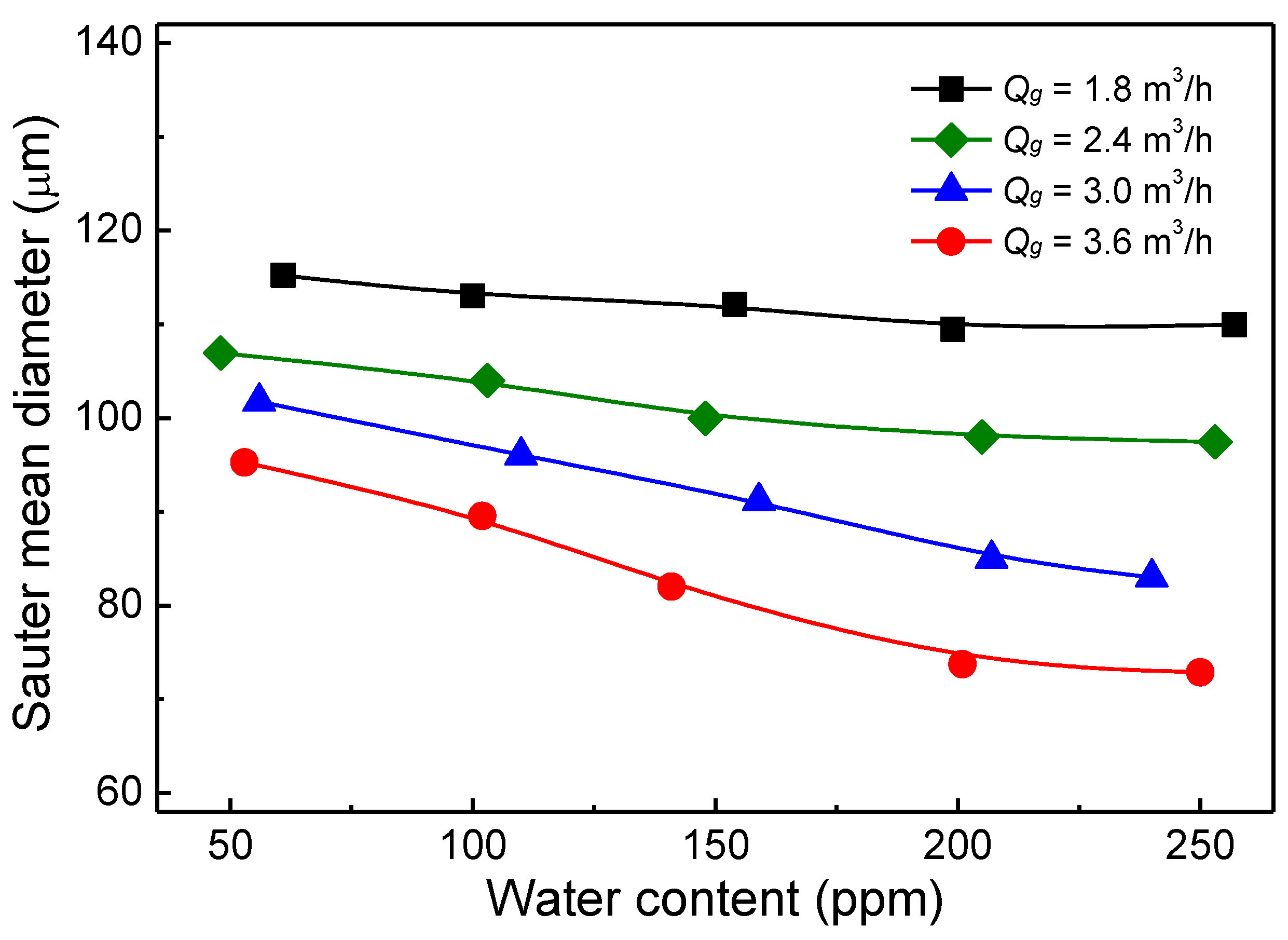
3.2. Spectroscopic Characteristics
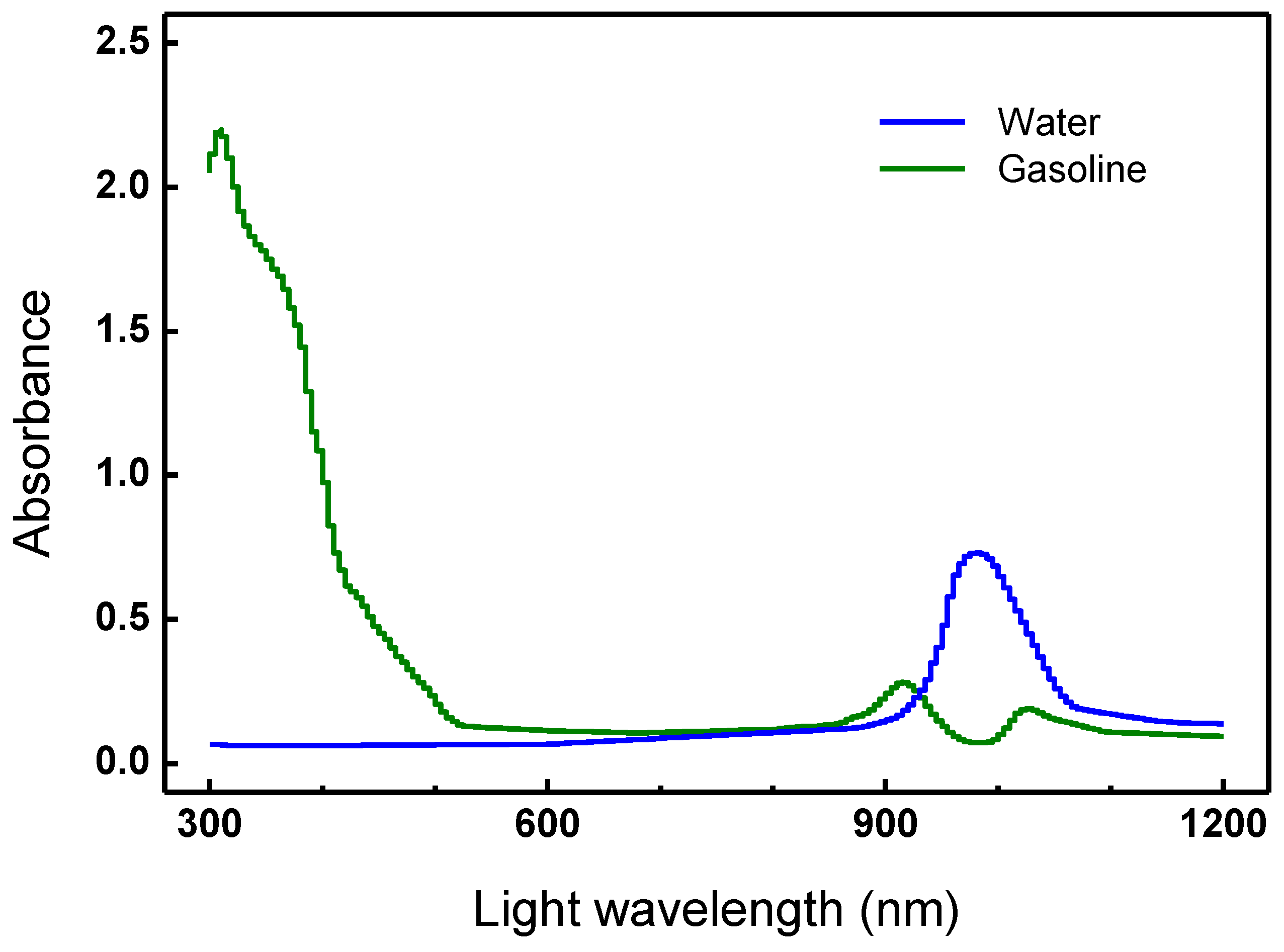


4. Conclusions
- In the gasoline pipe flow, the water from the nozzle disintegrated into small droplets by the hydrodynamic break-up mechanism through the mixing device, and the small spherical water droplets were sufficiently lean and dispersed almost homogeneously in the gasoline pipe flow. The water droplet size was significantly decreased with the increase of the flow rate of gasoline and water. When the water content varied from 50 to 250 ppm, the Sauter mean diameter decreased by about 5% at the gasoline flow rate of 1.8 m3/h, but decreased significantly by about 24% at the gasoline flow rate of 3.6 m3/h.
- The measurement results of spectral absorbance showed that gasoline was almost transparent at 980 nm wavelength of light while water showed peak absorption at this wavelength. Therefore, it was appropriate incident light for spectroscopic water detection.
- The light transmittance decreased linearly with increased water content, and the decreasing rate of the light transmittance with the water content was also gradually enlarged with decreased gasoline flow rate. When the water content increased from Cw = 50 to 250 ppm, the light transmittance was reduced by about 14% at a lower gasoline flow rate of Qg = 1.8 m3/h, but it was reduced largely by about 21% at a higher gasoline flow rate of Qg = 3.6 m3/h.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gong, J.-S.; Fu, W.-B. A Study on the effect of more volatile fuel on evaporation and ignitionfor emulsified oil. Fuel 2001, 80, 437–445. [Google Scholar] [CrossRef]
- Fu, W.-B.; Hou, L.-Y.; Wang, L.-P.; Ma, F.H.A. Study on ignition characteristics of emulsified oil containing flammable fuel. Fuel Process. Technol. 2003, 80, 9–21. [Google Scholar] [CrossRef]
- Alahmer, A. Influence of using emulsified diesel fuel on the performance and pollutants emitted from diesel engine. Energy Convers. Manag. 2013, 73, 361–369. [Google Scholar] [CrossRef]
- Attia, A.M.A.; Kulchitskiy, A.R. Influence of the structure of water-in-fuel emulsion on diesel engine performance. Fuel 2014, 116, 703–708. [Google Scholar] [CrossRef]
- Huo, M.; Lin, S.; Liu, H.; Lee, C.F. Study on the spray and combustion characteristics of water–emulsified diesel. Fuel 2014, 123, 218–229. [Google Scholar] [CrossRef]
- Chantrapornchai, W.; Clydesdale, F.; Julian, D.M. Influence of droplet characteristics on the optical properties of colored oil-in-water emulsions. Colloids Surf. A 1999, 155, 373–382. [Google Scholar] [CrossRef]
- Bae, C.; Kim, J.H.; Sheen, D.H. Optical Measurements of Water Droplet Characteristics in Turbulent Gasoline Pipe Flow; SAE Technical Paper 2001-01-1965; SAE International: Orlando, FL, USA, 2001. [Google Scholar]
- Bampi, M.; Scheer, A.P.; Castilhos, F. Application of near infrared spectroscopy to predict the average droplet size and water content in biodiesel emulsions. Fuel 2013, 113, 546–552. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: New York, NY, USA, 1999. [Google Scholar]
- Hinds, W.C. Aerosol Technology, 2nd ed; John Wiley & Sons: New York, NY, USA, 1999. [Google Scholar]
- Naqwi, A.A.; Durst, F. Light scattering applied to LDA and PDA measurements. Part. Part. Syst. Charact. 1991, 8, 245–258. [Google Scholar] [CrossRef]
- Kim, J.H.; Ikeda, Y.; Nakajima, T. Characteristic Measurements of Electrostatic Fuel Spray. In Proceedings of 9th International Symposium on Applications Laser Techniques to Fluid Mechanics, Lisbon, Portugal, 13–16 July 1998; pp. 21.5.1–21.5.6.
- Kim, J.H.; Nakajima, T. Aerodynamic influences on droplet atomization in an electrostatic spray. JSME Int. J. Ser. B 1999, 42, 224–229. [Google Scholar]
- Ingle, J.D.; Crouch, R. Spectrochemical Analysis; Prentice Hall: Englewood Cliffs, NJ, USA, 1988. [Google Scholar]
- Yin, J.; Pilon, L. Efficiency factors and radiation characteristics of spherical scatters in an absorbing medium. J. Opt. Soc. Am. A 2006, 23, 2784–2796. [Google Scholar] [CrossRef]
- Sudiarta, I.W.; Chylek, P. Mie scattering efficiency of a large spherical particle embedded in an absorbing medium. J. Quant. Spectrosc. Radiat. Transf. 2001, 79, 709–714. [Google Scholar] [CrossRef]
- Mugele, R.A.; Evans, H.D. Droplet size distribution on spray. Ind. Eng. Chem. 1951, 43, 1317–1324. [Google Scholar] [CrossRef]
- Lee, C.S.; Reitz, R.D. Effect of liquid properties on the breakup mechanism of high-speed liquid drops. At. Sprays 2001, 11, 1–19. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kim, J.H.; Lee, C.S. Hydrodynamic Effects on Spectroscopic Water Detection in Gasoline Pipe Flow. Energies 2014, 7, 3810-3822. https://doi.org/10.3390/en7063810
Kim JH, Lee CS. Hydrodynamic Effects on Spectroscopic Water Detection in Gasoline Pipe Flow. Energies. 2014; 7(6):3810-3822. https://doi.org/10.3390/en7063810
Chicago/Turabian StyleKim, Jeong Heon, and Chang Sik Lee. 2014. "Hydrodynamic Effects on Spectroscopic Water Detection in Gasoline Pipe Flow" Energies 7, no. 6: 3810-3822. https://doi.org/10.3390/en7063810