A Multi-Element Diffuser Augmented Wind Turbine
Abstract
: A new class of diffuser augmented wind turbines (DAWTs) is presented. The new diffuser concept exploits aero-dynamic principles for the creation of high-lift airfoil configurations known from the aircraft industry. Combining this with our objective of obtaining a compact power-efficient design has enabled creation of a family of DAWT designs with energy capture potentials which exceed the power efficiency based on the diffuser exit area by 50%. The paper presents the 1D momentum theory governing the DAWTs, and discusses upper limits for power extraction, similar to the Betz limit applicable for bare Horizontal-Axis Wind Turbines (HAWTs). Inviscid axisymmetric panel code calculations are then used to drive the diffuser design towards higher power coefficients. Axisymmetric actuator disk Navier-Stokes calculations reveal the types of stall that inhibit the functionality of the ideal inviscid optimum, leading the design towards the new class of DAWTs. DAWT performance has been differently measured over time, creating confusion. Proper comparison with performance of existing DAWT designs is therefore emphasized. This involves reference to established literature results, and recalculation of earlier DAWT designs in an attempt to project all results onto a common metric.1. Introduction
The quest for affordable cost-of-energy competitive renewable energy has driven the wind turbine industry to the mature stage of today. The past four decades have witnessed a tremendous up-scaling in terms of size and power. The concept winner judged from market penetration and achievable cost-of-energy is the bare 3-bladed front-runner modern HAWT also known as “the Danish concept”. The bulk of the market volume for modern HAWTs, including both onshore and offshore WTGs, lies in the MW-range roughly between 1 and 8 MW. In other words: large-scale wind power is comprised exclusively by modern HAWTs, and there is no indication of any changes in the foreseeable future. By contrast, small-scale wind power with WTGs up to 50 kW is undergoing a blooming of emerging designs and technologies. Household rural and urban applications are more influenced by other factors such as noise perception, visual disturbance, community regulations, etc., than large-scale wind power. Physically, small-scale wind is also different, due to higher turbulence levels and higher atmospheric shear levels, both caused by the decreased WTG hub height. This explains the persisting interest in alternative WTG designs for small-scale wind power applications. Ducted wind turbines have the virtue of full or partial visual shielding of the rotating parts, thereby reducing perceived visual disturbance. Although aero-acoustic noise is primarily dependent on the rotor blade tip-speed, the duct will shield the propagated noise emitted by the rotating blades. Additionally, ducted turbines are widely acclaimed for having a more compact energy capture. This is indeed the case when normalizing the generated power with the rotor area. Levels for the available power coefficient, Cp, in excess of the Betz limit of 16/27 (in the following referred to as Betz number) for bare propeller turbines are readily obtained. However, this is not the case when normalizing the generated power with the diffuser frontal area. This has fuelled many comments from DAWT sceptics as to why not just increase the rotor blade length to match the diffuser exit radius, which would be a more economical way for harvesting the same—or even a higher—level of energy. This paper will address the validity of that argument.
The DAWT exploits the Venturi effect, named after the Italian physicist Giovanni Venturi (1746–1822), which is the reduction of fluid pressure—and the associated increase of fluid velocity—that results when a fluid flows through a contraction. For a DAWT, the contraction is created by the diffuser in the throat of which is placed a rotor. The “throat” plane is the diffuser cross section perpendicular to the axisymmetric axis where the area inside the diffuser is smallest. Modern DAWT theoretical research can be traced back to the 1920s, where A. Betz studied the economic viability of DAWTs compared to bare HAWTs. During the 1950s English and Japanese groups conducted further research where the possibility for mass flow augmentation through the diffuser throat was confirmed and quantified, both theoretically [1,2] and experimentally [3]. The oil crisis in 1973 led to a renewed interest in diffuser augmented wind, and three independent groups started up experimental DAWT research led by Igra [4–8], Lewis [9], and Foreman at Grumman Aerospace [10,11], respectively. Engineering models and numerical tools at that time were not at a stage that allowed accurate prediction of performance and design optimization. Surface stall from the inner (suction) side of the diffuser was identified as a performance limiting factor, and especially the Grumman Aerospace group targeted their focus towards boundary layer separation control. This was achieved by the use of passive devises such as diffuser trailing edge flaps and boundary layer slots, which both inject higher-energy fluid into the adverse pressure boundary layer, with the purpose of stall suppression.
During the following decades up to the present time, the DAWT concept has attracted continuous interest as a niche concept overshadowed by the modern HAWT designs. Based on advances in analytical modelling and numerical simulation results, as well as lessons learned from failed commercial endeavors, e.g., Vortec Energy Limited, recognition has emerged that diffuser wind loads and structural cost increase prohibitively with size, so DAWTs cannot compete with modern HAWTs in large scale cost-of-energy. Focus has consequently shifted to the small scale.
At present, a handful of household wind turbine manufacturers have commercialized the DAWT. Most of these designs are single-ducted, some are double-ducted with a slot in-between to allow outside flow passing through to the inner-side duct to energize the boundary-layer in the adverse pressure gradient wake behind the rotor. Turbulent mixing between the rotor wake and the outside flow is exploited by a special class of DAWTs called Mixer-Ejector Wind Turbines (MEWTs), see [12,13]. The increase of energy capture potential by use of enhanced wake mixing is also investigated in [14]. A thorough review of the DAWT history and power performance can be found in [15].
This paper is organized as follows: in Section 2 the basic 1D momentum theory governing the DAWTs is presented. Section 3 quantifies the validity range of the momentum theory numerically, and investigates if it is possible within the assumptions of potential flow theory to exceed the Betz number when the entire DAWT frontal area is used as reference for the power efficiency. Stall-induced reduction in achievable DAWT power extraction is quantified and analyzed in Section 4 using Reynolds-Averaged Navier-Stokes Computational Fluid Dynamics (RANS CFD) with external forcing from an actuator disk. Diffuser designs that intend to circumvent the stall issue are suggested, leading to the new class of diffusers. Following a discussion about DAWT rotor efficiency in Section 5, Section 6 concludes this work and outlines perspectives for the new multi-element DAWT.
2. 1D Momentum Theory
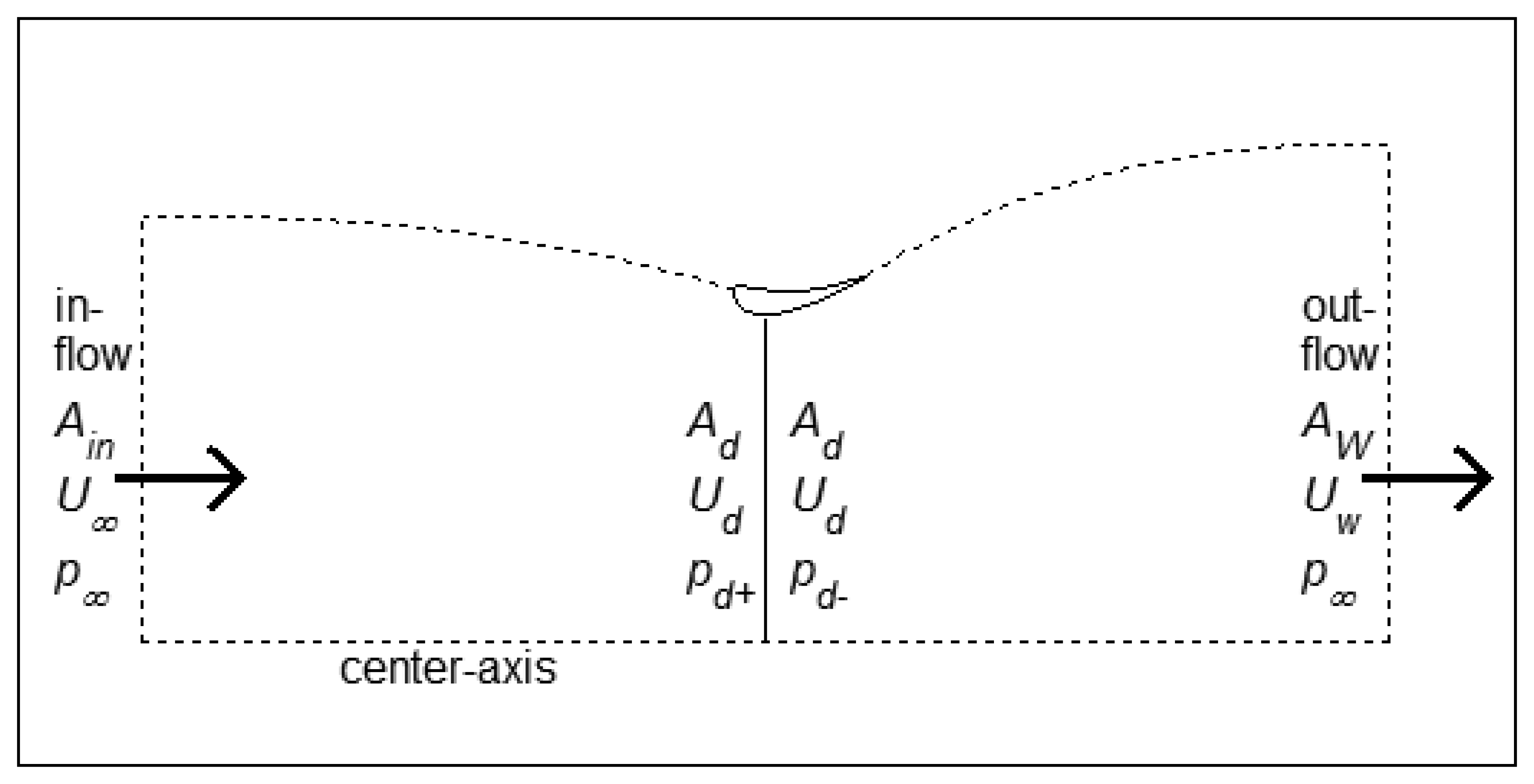
A control volume is defined by the center-axis, the dividing streamlines, the flow inlet, and the flow outlet, see Figure 1. The domain is axisymmetric in the direction perpendicular to the plane. The axisymmetric equivalent to a bladed rotor is the actuator disk, which is indexed “d” on the figure. Across the disk there is a pressure drop, pd+ − pd−. A small air gap between the diffuser airfoil surrounding the disk and the disk itself allows only a very small leakage, i.e., which is assumed negligible. This also means that the streamline bordering the wake flow and the surrounding flow emanates from the trailing edge (TE) of the ring-shaped diffuser airfoil.
2.1. Derivation
The axial momentum balance over the control volume is governed by the Navier-Stokes equations. Viscosity and compressibility effects are assumed negligible:
Force indices denote “disk” and “shroud” respectively. The axial flow velocity through the disk cannot be assumed constant, and will increase with increasing diffuser proximity. The flow tube through the disk is therefore divided into n annular elements as known from common BEM theory. Flow tube mass conservation upstream and downstream of the disk gives:
Note the implication in Equation (4) that the far wake velocity Uw is constant across all annular elements. The underlying assumption is that Fd per disk area is constant. This excludes uneven loading scenarios from the analysis. As will be argued and shown numerically, the optimal power take-out condition which is of primary interest is associated with even loading, for which this analysis is strictly valid. Eliminating Ain and Aw from Equations (1), (3), and (4):
The even loading constraint means that although pd+ and pd− will vary across the annular elements in accordance with the Ud(i) variation, the pressure drop, Δpd = pd+ − pd− will remain constant for all annular elements. The force exerted by the disk on the air can then be expressed as:
The axial force Fs exerted by the diffuser on the fluid is expressed using a Maclaurin series expansion (Taylor series centered around Δpd equal to zero) with the pressure drop Δpd across the disk as the free variable. Note that various choices as of how to express Fs exist. As will be shown in what follows, the chosen expression for Fs leads to a convenient definition of the involved diffuser constant Cs, when truncated to 1st order accuracy:
Inserting F from Equation (9) into the momentum balance Equation (5):
Applying the Bernouilli principle along a streamline upstream and downstream of the disk respectively:
Subtracting Equation (12) from Equation (11):
Elimination of Δpd through Equations (10) and (13) leads to:
The LHS of Equation (14) is the area-weighted average of the axial flow velocity through the disk, which will be named Ūd leading to:
Recall that Cs is the 1st order derivative term coefficient in a Maclaurin series expansion around Δpd = 0. At this operational point no power is taken out of the flow by the disk, so Uw will equal U∞:
The convenient definition of Cs is then expressed as the relative area-averaged speed-up of the flow through the disk at unloaded conditions minus one. Lower-case velocity quantities are non-dimensionalized by the free-stream velocity U∞:
2.2. Power-Optimal Operation
The power taken out of the flow by the actuator disk is the dot-product of exerted force times the passing fluid velocity integrated over all annuli. Bold types denote vector quantities. nd is the unit normal vector to the disk:
Substituting the RHS by using Equation (13), Equation (14) leads to:
Similarly, the thrust force on the actuator disk is expressed as:
The corresponding power- and thrust-coefficients become:
Now, setting dCP_disk/duw = 0 leads to the following results for power-optimal DAWT operation:
From Equations (23)–(27) we note that the DAWT power-optimal far wake velocity and disk thrust coefficients of 1/3 and 8/9 are independent of the diffuser and thus identical to the HAWT power optimum. Thus, for both the HAWT and the DAWT, optimal power take-out occurs when 8/9 of the fluid mechanical energy passing the disk is converted. For the optimal HAWT, 2/3 of the free-stream mass flow-rate through a disk-sized area will pass the actuator disk. Betz limit can be intuitively understood as the product of 8/9 and 2/3. Equation (24) tells us that for a DAWT, the optimal massflow-rate is a factor 1 + Cs higher than for a HAWT and since the same mechanical energy ratio of 8/9 of what passes through the disk is converted, the corresponding optimal power coefficient is the factor 1 + Cs higher for a DAWT, as stated by Equation (25).
These results coincide with references most notably van Bussel [16,17], Jamieson [18], and not least Werle and Presz [12,13] from whom the use of a shroud coefficient Cs as a convenient means of describing the diffuser impact was adapted. These references all disregard the non-uniformity of the axial flow velocity Ud over the disk, and do not properly explain the 1st order accuracy of the new variable(s) introduced in order to close the governing system of equations.
Bussel was the first to conclude that the obtainable power augmentation, based on the disk area, scales linearly with the velocity speed-up through the disk at unloaded conditions, as stated by Equation (25), that the power-optimal far wake velocity is 1/3 irrespective of the diffuser, as confirmed by Equation (23), and that the optimal disk thrust coefficient also is unchanged from the HAWT at a value of 8/9, Equation (26). In Bussel's momentum theory an additional station was defined at the diffuser exit. Instead of introducing a diffuser force coefficient, he defined a back pressure coefficient at the diffuser exit station, acknowledging that the pressure at the diffuser exit has still not recovered to ambient pressure, and that the wake will continue to expand downstream of the diffuser exit. Bussel made it very clear that high power efficiencies should be obtained through very low back pressures, such that further wake expansion downstream of the diffuser exit is maximized. In [17] Bussel's review also showed that no DAWT power performance has yet exceeded the Betz number—or conventional HAWT performance—when relating the converted power to the wind turbine frontally projected area, which for a DAWT means the diffuser exit area.
Jamieson's investigation [18] validated these findings. His derivation considered a system defined as the region in which axial induction is significantly influenced between the free stream and the far wake. The axial force interaction between the flow and the flow-augmentation device (i.e., the diffuser) is not included, so momentum balance over the entire control volume is absent. Instead, Jamieson argues that the far wake induction must equal a constant k times the change in disk induction from the unloaded state, expressed as aw = k(ad − ad0). In the absence of a control volume momentum balance, Jamieson closes the equations by using the inviscid theory result, that CT_disk = 0 for ad = 1. However, this corresponds to a non-physical condition where the far wake velocity aw is undefined. This is the case for the usual open-flow derivation. For a confined flow derivation, Werle [19] showed that the thrust singularity at CT_disk = 1 and can indeed be circumvented, and that CT_disk then will equal 1 (not zero) when approaching ad = 1 in the asymptotic limit where the flow confinement vanishes corresponding to open flow conditions. Nevertheless, Jamieson's results confirm Bussel's findings, and in a generic way that decouples from the flow-augmenting device and only uses the unloaded induction at the disk plane ad0 = 1 − ud0.
The approach devised by Werle and Presz [12,13], and from which the current momentum theory investigation departs, includes the flow-augmenting unit (i.e., the diffuser) in the momentum balance, and closes the equations by expressing the axial diffuser force as a linear function of the pressure drop across the disk, as in Equation (8). The optimum power extraction results are identical to Jamieson's, since Cs − ud0 − 1, thus connecting Jamieson unloaded disk induction parameter and Werle and Presz's shroud coefficient through the simple relation Cs = −ad0. Both Jamieson [18] and Werle and Presz [13] conclude that maximizing power goes through maximization of the flow augmentation capability of the diffuser at the unloaded condition. Jamieson further points out what was earlier stated by Hansen [20], that the diffuser flow augmentation capability should be optimized for the optimal power-takeout condition, and consequently not necessarily be optimal in the unloaded state.
Including the results presently obtained, there is good analytical evidence that CP_disk_opti can exceed the Betz number significantly. But really, the task of interest is to investigate whether CP_exit_opti based on the diffuser exit area instead of the disk area can also exceed the Betz number. Bussel concluded negatively based on his review of experimental and numerical results [17], but no theoretical limit has so far been identified.
3. Validation
The assumption of the optimality of a constant far wake velocity made in the derivation of the 1D momentum theory for diffusers exerting non-uniform flow augmentation will be validated numerically.
The validity of the 1st order approximation for the shroud force, i.e., the linear relation between Fs and Δpd in Equation (8) will also be quantified. To this end two computational codes will be used:
Panel code: A 2D axisymmetric potential flow panel code equipped with an actuator disk and a freely propagating wake. All bound and trailing vorticity is axisymmetrically formulated closely following the pioneering work of Lewis [21], which also includes source code. The expanding wake is computed iteratively by pseudo-time-stepping. The system of equations for the bound vorticity collocated on the panels of the diffuser is closed using the Kutta-condition. The merits of the panel code are execution speed and the ideal inviscid flow property, which precludes stall from occurring on the duct surface. This is practical from an investigative point of view, where surface stall initially can be regarded as an issue to be dealt with separately. The primary disadvantage of the panel code is the uniform collocation of circulation (vorticity) on the duct panels which serves to fulfil the Kutta-condition. The assumption of a uniform vorticity distribution over the panels is acceptable for some applications, but one must be aware that is represents a simplification of the real physics.
RANS CFD: A commercial Navier-Stokes solver by Comsol MultiPhysics® [22]. The system is again made 2-dimensional by use of the actuator disk approach. For details, see e.g., Mikkelsen [23] or Hansen [20]. The governing equations are the viscous, incompressible Reynolds-Averaged Navier-Stokes equations in axisymmetric coordinates. The applied turbulence model is the standard κ-ε formulation, where κ is the turbulent kinetic energy, and ε is the dissipation rate of turbulent energy. The advantage of RANS CFD is its physical correctness. The governing Navier-Stokes equations are an almost exact representation of the real physics. Still, notable model approximations are introduced through the use of a turbulence model (as opposed to resolving turbulence directly in time and space, which is computationally infeasible), the axisymmetric assumption, and discretization errors although small in 2D where mesh-independent results are easily obtainable. A discussion about the implication on modelling accuracy, power extraction, and possible pitfalls introduced by assuming non-swirl axisymmetry is given in a later chapter. The disadvantage of RANS CFD is the computational execution time. A converged solution for a 2D domain with 0.5 million mesh elements is obtained in approximately 1 hour on a high-end multi-core desktop pc.
Unless otherwise noted, the model dimensions, domain dimension, and discretization details will be as described below for all computations:
Panel code: The rotor disk is 1.0 m in radius, and placed at the “throat” location of the diffuser where the flow augmentation is maximized. The disk is one-dimensional due to the axisymmetric property, and aligned with the radial dimension. It is divided uniformly into 19 bound-vorticity line-segments. Trailing vorticity continues and propagates freely downstream from each end of each line-segment. Each of the trailing vorticity helices (which are tubes in 3D) are divided into 50 segments in the axial streamwise dimension. The streamwise discretization is non-uniform, with initial axial element length of 1.0 percent of the disk radius just behind the disk, and increasing gradually in length as the wake expansion settles further downstream. The last vorticity-tube continues infinitely downstream. The clearance distance between the disk tip at 1.0 m and the duct inner-most surface is 1.0 percent of the disk radius. 40 panels are used to represent the duct 2D geometry.
RANS CFD: Again, the rotor disk is 1.0 m in radius, and placed in the “throat” of the diffuser. Disk-duct clearance is 1.0 percent of the disk radius. From the disk and duct, the axisymmetric 2D domain extends 50 m axially upstream, downstream, and in the radial direction. The inlet boundary condition is of Dirichlet type, imposing constant velocity 10 m/s. Inlet turbulence intensity is 5% with a small length scale of 0.01 m. The radial and outlet boundary condition is of Neumann type, imposing a zero pressure gradient. Axial symmetry boundary condition is applied on the centreline, and a no-slip Dirichlet condition on all walls. The mesh is hybrid with unstructured isotropic triangular elements in open regions, and structured anisotropic quadrilateral elements adjacent to the duct walls. The complete mesh consists of 300,000–400,000 elements depending on the duct configuration, with a triangular element count of around 275,000. This is roughly 20–25 times more elements than the 16,640 elements employed by Hansen in [20] and quite sufficient to establish mesh independent results, even with the more complex diffuser geometries. The boundary element length is in the range 0.5–1.0 mm. The first boundary element height is 5–10 μm with a normal direction stretch factor of 1.1–1.2. The boundary layer mesh contains between 20 and 35 layers in the wall-normal direction. The disk in 2D is a rectangular sub-domain 1.0 m wide (the radius) and 2 mm thick, onto which volume forcing is applied, either constant-level or linearly increasing/decreasing from centreline to tip. For all RANS computations, the max-norm of the relative step-changes in field variables (u, v, p) converged from around unity to below 1.0 × 10−5. The turbulence variables (κ, ε) reached the same level of convergence, except for some simulations with disk loadings and/or diffuser geometries that caused massive wake separation, where convergence levelled off earlier at 1.0 × 10−3 or below.
The 1D HAWT/DAWT momentum theory, the panel code, and the RANS CFD are applied to a series of test cases. These test cases, and their relevance for the present investigation, are presented here:
Bare HAWT: The regular horizontal-axis wind turbine with no diffuser is well known in terms of performance, and therefore relevant as a validation test case. The bare HAWT is also very CP_exit efficient, not yet superseded by any DAWT, see [17], and will therefore be used as a baseline against which the other configurations (test cases) are benchmarked.
Hansen DAWT: This diffuser was analysed using 2D axisymmetric CFD [20], and serves a validation purpose. The validity of the assumption of power-optimality at constant disk loading used for the derivation of our 1D momentum theory is also quantified, as well as the valid range of the 1st order truncated expression for the duct loading, Fs, in Equation (8). Note that our Hansen DAWT computations are set up in accordance with [20]. Therefore, unit-length reference scale L is applied to the diffuser length instead of the disk radius. The disk radius is 0.4687 and the inlet flow velocity is determined such that the Reynolds number. Also note that Hansen used the κ-ω turbulence model, whereas we use the κ-ε model.
Circular cylinder (donut) DAWT: When applying circulation to a circular cylinder, a higher lift-coefficient can be obtained within potential flow theory than with any other geometry. 1D DAWT theory suggests that the obtainable power augmentation scales directly with the velocity augmentation at zero power take-out, which again scales with the inner surface suction created by the duct airfoil and hence its lift capacity. It is therefore interesting to see if the circular cylinder DAWT can exceed the bare HAWT Cp_exit performance. This test case offers insight of mostly theoretical nature, since stall issues are not dealt with.
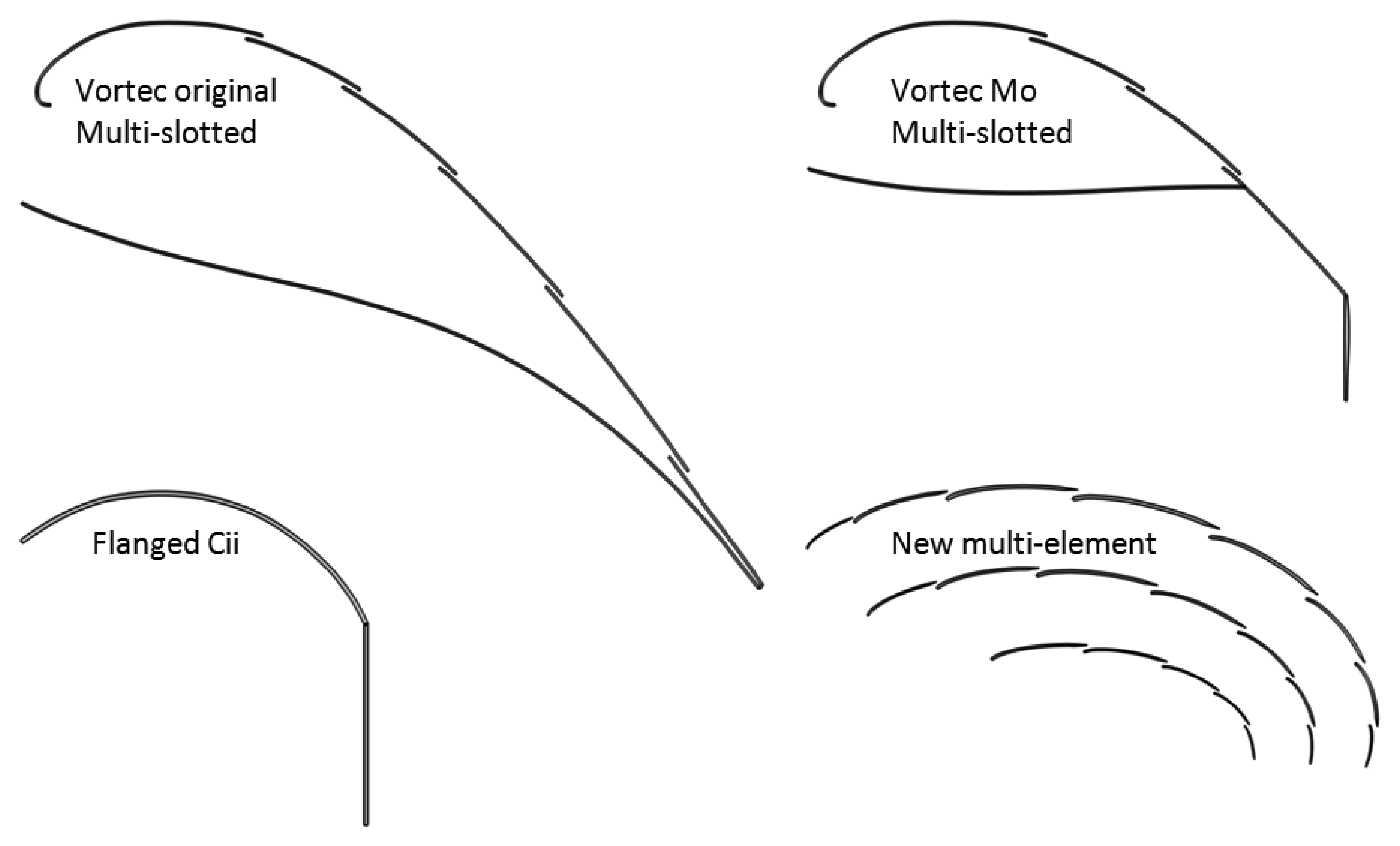
Vortec original multi-slotted DAWT: This is the 3rd generation DAWT from the Vortec project [15]. The Vortec research was initially based on the Grumman research [10,11] some decades earlier, and also reached the conclusion that high power-augmentation should be obtained through boundary-layer control of the flow over the duct suction side. The multi-slotted DAWT is state-of-the-art and therefore included in the series of test cases.
Vortec Mo multi-slotted DAWT: This is the 4th and final generation DAWT from the Vortec project. It combines the multi-slotted technology with a diffuser trailing-edge brim, quite similar to a Gurney flap known as a lift-enhancing device from regular airfoil sections.
Ohya Cii flanged DAWT: The flanged diffuser (a.k.a. brimmed diffuser) has been extensively and successfully tested by Ohya's research group [24]. Like the Vortec final designs, it represents state-of-the-art DAWT technology.
New multi-element DAWT: The new diffuser design of the present investigation.
The computation methods applied to each test case are listed in Table 1. Note that only RANS CFD is useful for the most complex cases, where complicated geometries and/or fluid stall mechanisms are present, which is beyond the applicability scope of the simpler methods.
3.1. Test Case: Regular HAWT
The left plot on Figure 2 shows the power efficiency CP_disk for a bare HAWT across the CT_disk loading range. The 1D momentum theory Betz point of CP_disk = 16/27 ≈ 0.593 at CT_disk = 8/9 is well confirmed by the panel code and RANS CFD. At lower disk loading the three methods match very well, and at disk loadings higher than the Betz point both simulation methods slightly over-predict compared to the analytical 1D momentum theory curve. At high disk loadings when the far wake velocity approaches zero and an unsteady turbulent wake is developed, turbulent mixing between the wake and the surrounding flow will increase. The mixing process will tend to energize the wake and slightly increase the potential for power take-out. The RANS CFD HAWT maximum CP_disk on Figure 2 is 0.604. If the κ-ε turbulence model is abandoned and no turbulence model applied, the simulation of the HAWT would yield a maximum CP_disk of 0.582. The reduction from 0.604 to 0.582 can be attributed to the lack of turbulent mixing.
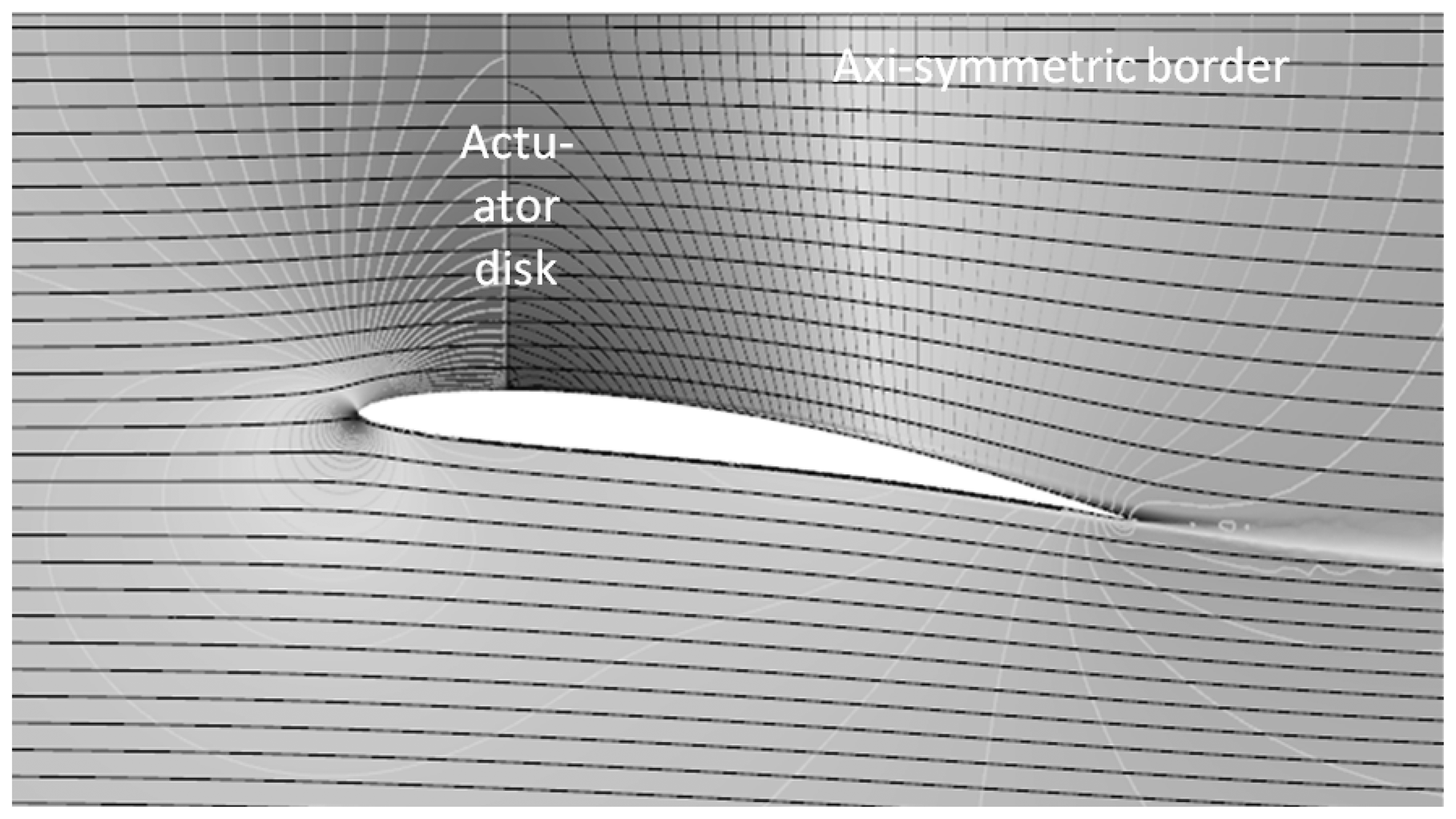
3.2. Test Case: Hansen DAWT
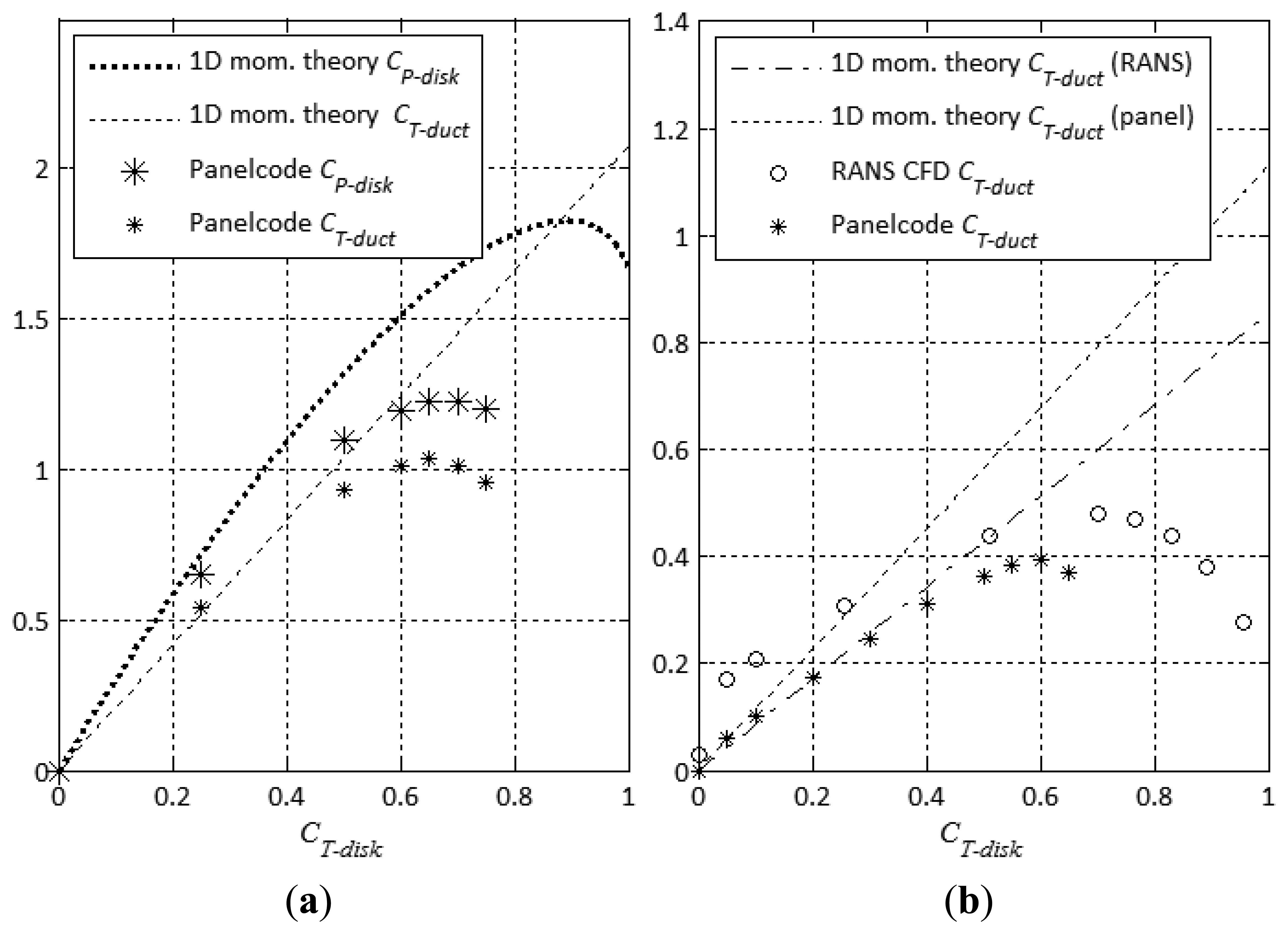
An axisymmetric cross section of the Hansen DAWT is depicted on Figure 3 with the streamlines propagating across and outside the rotor disk from left to right. The right plot on Figure 2 shows the power efficiency CP_disk for the Hansen DAWT across the CT_disk loading range computed by different methods. The dotted and dash-dot 1D momentum theory lines are calculated using the derived DAWT momentum theory. The unloaded average flow-augmentation factor used for calculating the dash-dot line is computed by the RANS CFD: ūd0 = 1.85, leading to a value for the shroud coefficient CS of 0.85 according to Equation (17). The similar unloaded average flow-augmentation factor computed by the panel code is 2.13, with a corresponding shroud coefficient CS of 1.13. This augmentation factor is then used to calculate the dotted line. The RANS CFD computed flow-augmentation agrees well with the value 1.83 reported by Hansen [20]. The duct suction-side flow is non-separated, but with a thick turbulent boundary-layer developing between 75% and 100% chord position, which is part of the explanation for the ūd0 discrepancy between the RANS CFD and the panel code. However, the main cause of the discrepancy is believed to be the constant circulation assumption used in panel methods in conjunction with the Kutta condition. It is known that the modeling precision of panel methods—despite their usefulness—is inferior to Navier-Stokes CFD even in the absence of viscous effects.
Still contemplating Figure 2 right plot, the RANS CFD results agree well with the Hansen reference. The increased discrepancy at high CT_disk values, where our maximum CP_disk is 0.91 compared to Hansen's 0.93, could be due to different turbulence models. The most striking result is the initial agreement between the analytically obtained momentum theory curves and the corresponding computational method at CT_disk values below 0.25, and the onset of apparent 2nd order effects (which were disregarded in the DAWT momentum theory due to the 1st order truncation of Equation (7b)). The lack of higher-order effects lead to a momentum theory over-prediction of CP_disk_opti by 21% and 43% respectively compared to the RANS CFD and the panel method. Furthermore the seemingly universal optimal thrust loading of 8/9 seems to be valid only within 1st order accuracy of Equation (7b), since both sets of RANS CFD results indicate a power-optimal thrust loading in the range of 0.75–0.80.
The right plot of Figure 4 shows CT_duct across the loading range for the Hansen DAWT. According to the 1D momentum theory for DAWTs, CT_disk and CT_duct are proportional by the factor CS, see Equations (20) and (21). Viscosity impacts from drag and slight stall obscures the RANS CFD comparison with the analytical curve below CT_disk values of 0.3. However for the panel code comparison with 1D momentum theory, higher-order effects kick in at CT_disk values even below 0.2, and both RANS CFD and the panel code indicate that the duct loading will actually decrease for disk loadings beyond the power-optimal level. These results further imply that 1D momentum theory for DAWTs is indeed quite approximate.
The rather narrow low-loading validity range of the 1st order approximation for the shroud force, i.e., the linear relation between FS and Δpd in Equation (8) is now quantified for the Hansen DAWT test case. It will be further quantified in the circular cylinder test case.
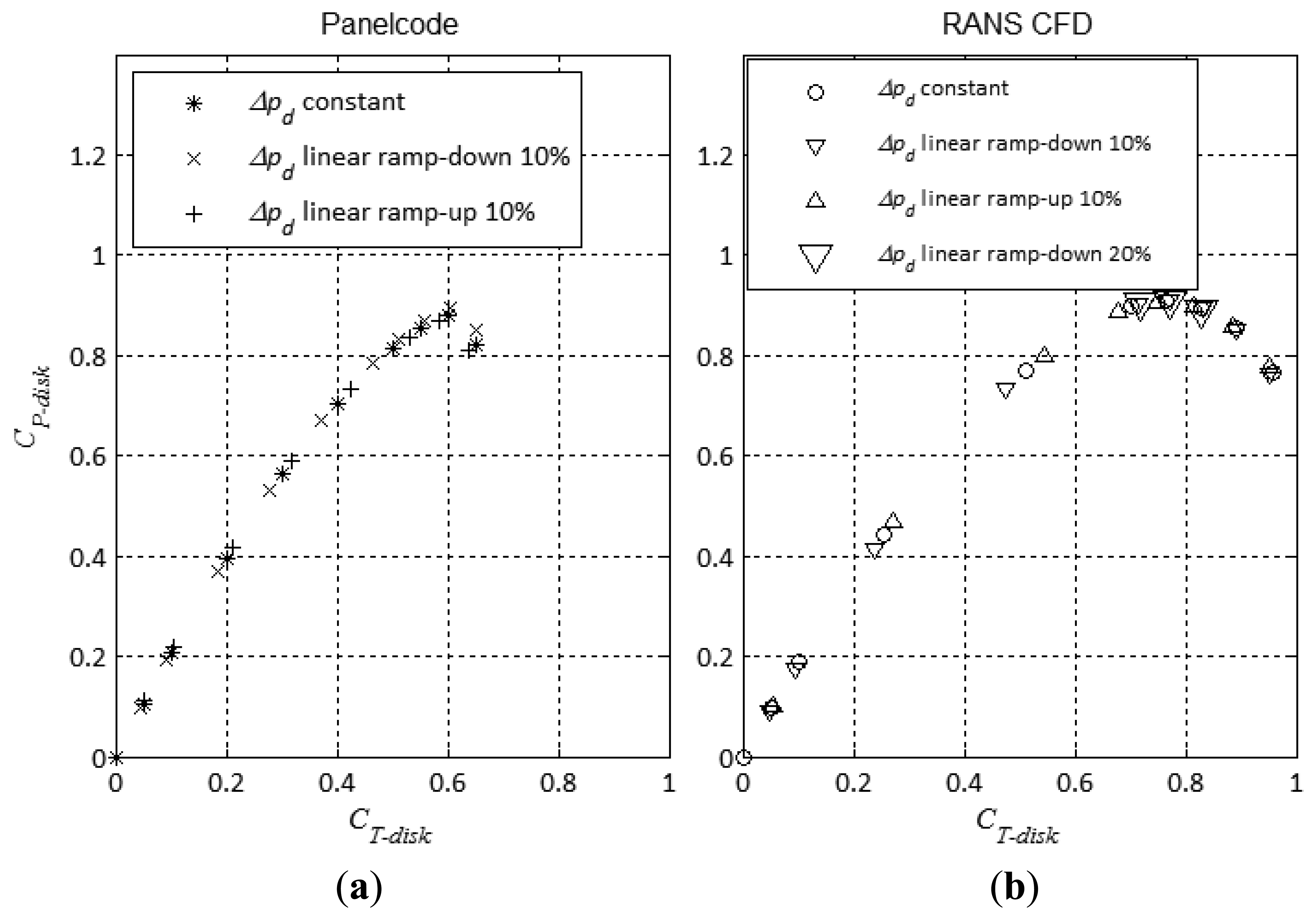
In Figure 5 we address the 2nd assumption made in the derivation of the DAWT momentum theory. We assumed that constant disk loading from the axisymmetric centerline to the disk tip was power-optimal. To this end we superimpose a linear load variation to the constant load. e.g., “Δpd ramp-up 10%” in the figure legend means that the pressure difference across the disk is 10% higher at the tip than at the root (centreline) and so forth. Different ramp-up and ramp-down combinations are made with each of the panel code and RANS CFD methods. Note that in the case of non-uniform disk loading, CT_disk is calculated as the area-weighted average over the disk. Observing the figure, the impact from non-uniform loading on CP_disk is seen to be negligible, although both methods show a small increase of CT_disk_opti when Δpd is ramped-down 10%. The increase is 1.4% and 0.1% respectively for the panel code and RANS CFD method. For the more accurate RANS CFD method it was found to be a local optimum, as 20% ramp-down lead to a slightly lower value of CP_disk_opti.
3.3. Test Case: Circular Cylinder (Donut) DAWT
The HAWT and Hansen DAWT test cases have validated the RANS CFD code, which gives results in close agreement with HAWT momentum theory and reference DAWT results [20]. The panel code also reproduces the HAWT momentum theory results, thereby validating the free-wake vortex-filament method. However, the colocation of constant bound vorticity over the duct panels in combination with the Kutta-condition as devised by Lewis [9] apparently leads to a slight under-estimation of CP_disk_opti compared to RANS CFD, and a not-so-slight under-estimation of the optimal thrust coefficient, CT_disk_opti. Still, the panel code is useful, especially when we deliberately want to exclude the detrimental impact from surface-stall from the investigation, at least temporarily.
As already noted, higher-order effects lead to an error in the prediction of CP_disk_opti using the 1st order accurate DAWT momentum theory of about 20% when using RANS CFD for the calculation of ūd0. Despite the error level, there is little doubt that the DAWT potential for power take-out scales predominantly linearly with the flow augmentation capability of the diffuser. In turn, the flow augmentation capability is proportional to the diffuser bound circulation, which scales with the duct airfoil lift capacity. Therefore, in the quest for a highly efficient DAWT, we should recognize that the duct airfoil—or airfoils—should represent a high-lift application.
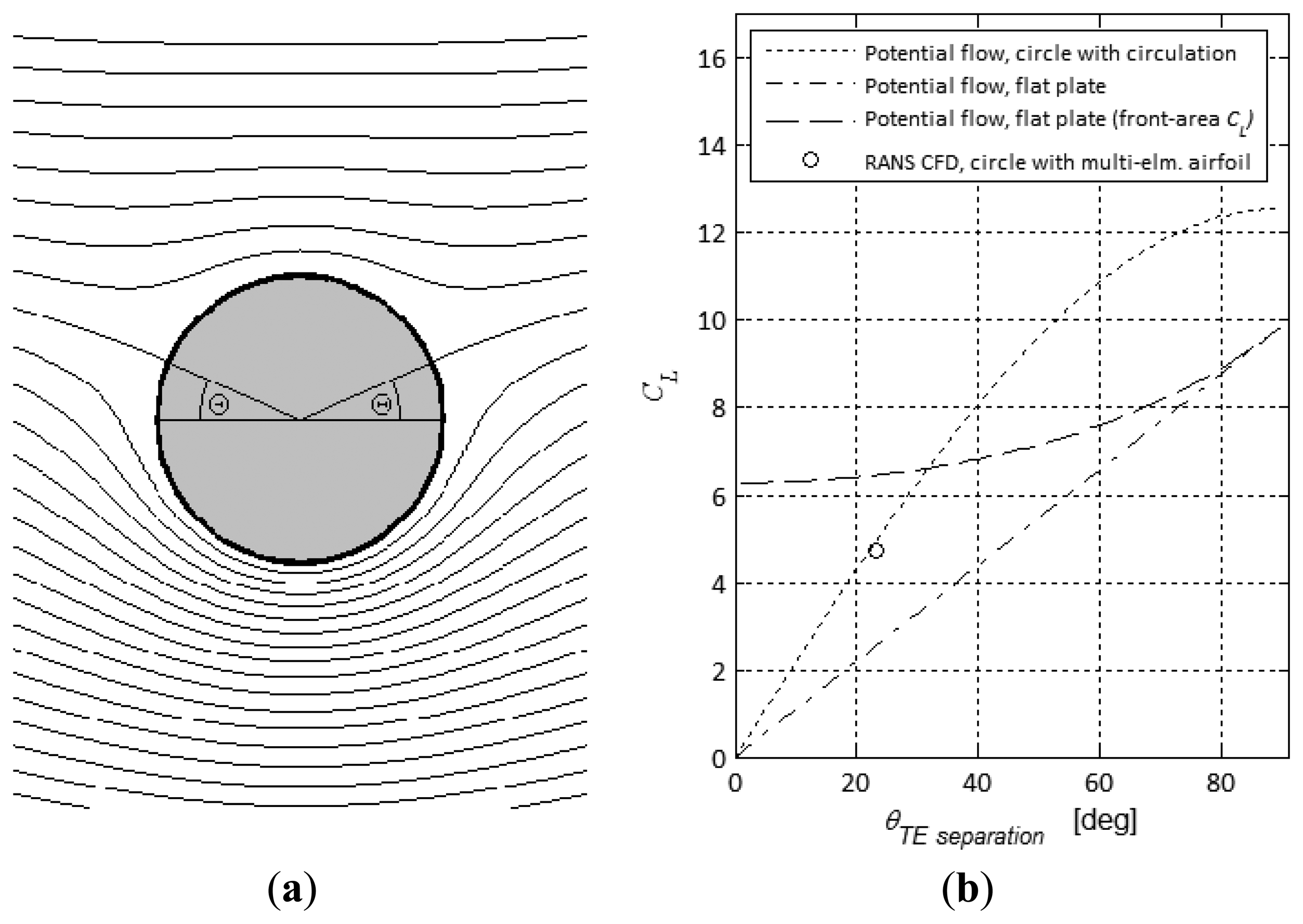
Turning our attention towards 2D airfoils, high-lift configurations are known e.g., from the aircraft industry, where airfoils are equipped with a leading edge slat and a series of trailing edge flaps that can be extracted during take-off and landing. The geometry of these high-lift multi-element configurations represents an engineering design compromise. In other words: Higher lift-coefficients may be possible, but probably not feasible for an airliner. Smith [25] identified the circular cylinder (with circulation) as the airfoil geometry with the highest possible lift coefficient, CL:
In the right plot of Figure 6 it is seen that the circle has higher maximum lift capacity than the flat plate, peaking at 4π and π2 respectively. Note that based on frontal area the plate offers higher CL values than the circle up to approximately 30 degrees. This means that the circle should be favoured over the flat airfoil only in cases where we believe that stall can be avoided up to very high angles.
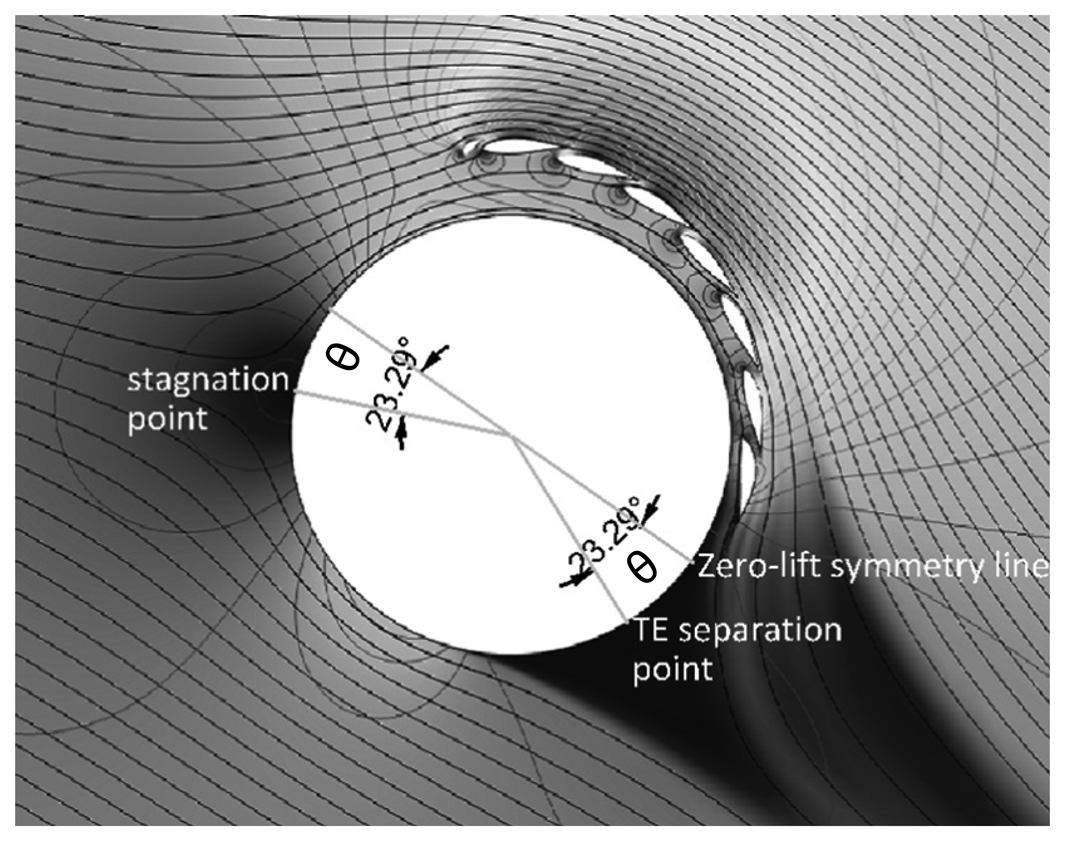
The circular marker at 23.3 degrees is a 2D viscous incompressible RANS CFD computation as visualized in Figure 7. The obtained CL is 4.73 based on the circle diameter and 4.02 based on the longest projected distance from leading slat to circle circumference on the opposite side. The multiple slats serve as guide vanes that prevent flow separation and stall on the suction side. Re number is 3.0 × 106 based on the circle diameter. Note the agreement with potential flow theory. Although the circular cylinder peak CL of 4π is unobtainable even with guide vanes, the result confirms the high-lift capacity of a circular cylinder. According to [25], the maximum lift coefficients passively obtained, based on the longest projected distance of the airfoil configuration, are roughly 3. Our value of 4.02 might be a record, although no vigorous attempt has been made by the authors to verify this claim. The CL/CD ratio is around 20, which is unacceptably low for any aerospace application, but for a wind turbine the viscous diffuser drag is dwarfed anyway by the thrust force created by the pressure drop across the rotor disk, and therefore not critical. Summarizing, we conclude that the circular cylinder is an interesting candidate as a high-lift airfoil suitable for a high-efficiency DAWT.
Consider again the circular cylinder but now as an axisymmetric (donut) DAWT instead of a 2D cylindrical section. θTE marks the position of the potential flow separation point on the circle's circumference measured from the horizontal line aligned with the free-stream as shown in Figure 6a. In the axisymmetric panel code, the location of θTE is easily controlled through the Kutta condition. Though guide vanes or similar are needed in a physical sense for obtaining the needed circulation and matching of the desired separation point, we simply impose θTE in the panel code. Let r be the radius of the circular donut DAWT cross-section and R be the radius of the actuator disk inside the donut diffuser. A 2-dimensional parameter-study is made, where r/R and ud0_max are varied systematically. ud0_max is the maximal local flow augmentation factor on the inner surface of the diffuser at the actuator disk location at zero power take-out, i.e., Ud0_max/U∞. For each value-combination of r/R and ud0_max four quantities are calculated and listed in Table 2:
ūd0: The disk-average flow augmentation factor at zero power take-out. Calculated by the panel code.
θTE: The angular position in degrees of the flow separation point on the diffuser circle's circumference, as sketched on Figure 6a. Calculated by the panel code.
CP_disk_opti: The optimal power efficiency, based on disk area, calculated by 1D DAWT momentum theory using Equations (17) and (25). ūd0 provided by the panel code.
CP_exit_opti: The optimal power efficiency, now based on diffuser frontal area (a.k.a. exit area). The clearance between disk and diffuser is 2.5% of the disk radius R.
In Table 2 focus is directed towards the CP_exit_opti results in the lower right section. Specifically, we observe that CP_exit_opti exceeds Betz number of 0.593 for many combinations of r/R and ud0_max. In line with intuition it is seen that higher flow augmentation at the diffuser throat location (i.e., higher ud0_max) leads to higher CP prediction according to the 1D DAWT momentum theory. In reality, when viscous effects and stall are included, an important limiting factor is the obtainable TE slip angle, θTE. For each value of ud0_max the most energy-efficient diffuser size r/R combination is greyed out in the lower right section in the cases where Betz number is exceeded. With increasing flow augmentation, CP_exit_opti increases from 0.63 to 1.06 and the corresponding slip angle θTE increases from 20.6° to 75.1°. This indicates, not surprisingly, that the challenge of overcoming the issue of flow separation and stall in real physics will increase with increasing flow augmentation. Note that non-physical combinations where the specified local flow augmentation ud0_max cannot be obtained are marked N.A. Concerning the relative diffuser size, a ratio r/R of around 0.10 seems optimal for obtaining a high CP_exit_opti. If focus is on maximizing CP_disk_opti higher values of r/R should be used.
The previous Hansen DAWT test case showed us that 1D DAWT momentum theory, being only 1st order accurate in the vicinity of the unloaded state, seems to over-predict the obtainable CP. The following circular cylinder (donut) DAWT configuration from Table 2 is therefore simulated under loaded conditions with the panel code:
r/R = 0.15
ud0_max = 6.0
The results are shown in Figure 4a. Again, higher-order effects not accounted for in the DAWT momentum theory leads to a lower CP_disk_opti value of 1.22 compared to 1.82 computed by 1D momentum theory, which is a 49% over-prediction. The tendencies observed in the analysis of the Hansen DAWT in the comparison of momentum theory and panel code results are largely repeated in the case of the circular cylinder (donut) DAWT. But the important result from Table 2 with these panel code simulations still remains: CP_exit_opti can obtain values exceeding the Betz number: The panel code CP_disk_opti of 1.22 from Figure 4 corresponds to a value for CP_exit_opti of 0.70. Be aware that the phrase “exceeding Betz” might be misleading, since Betz' limit cannot be exceeded by the class of turbines for which the Betz' limit applies, i.e., bare HAWTs. We simply investigate the findings by van Bussel [17] that no DAWT has yet outperformed the bare HAWT in terms of energy efficiency based on diffuser exit area (or frontal area in case of the donut DAWT, whichever is greater). The open question is, if DAWTs have not yet outperformed the bare HAWT because of a physical barrier, or if the DAWT designs simply have not yet reached their full potential for energy efficiency. Although inconclusive because of the potential flow simplification, the circular cylinder (donut) DAWT results seem to support the latter possibility.
4. DAWT Power Benchmarking
The next three test case diffusers serve the purpose of benchmarking against the bare HAWT as well as the new multi-element DAWT. In line with our conclusion from the previous test case, that flow augmentation should be maximized and that this will challenge the ability to maintain the flow attached on the diffuser suction side, some of these diffusers have boundary layer flow control. Others have high-lift devices such as the gurney flap (called “flange” in the diffuser case). Such a flange not only enhances lift, but will also create separation at the inner edge, thereby promoting turbulent mixing which to some extent will energize the low-energy wake behind the actuator disk. As to the authors' knowledge these three diffusers represent current DAWT state-of-the-art.
4.1. Test Case: Vortec Original Multi-Slotted DAWT
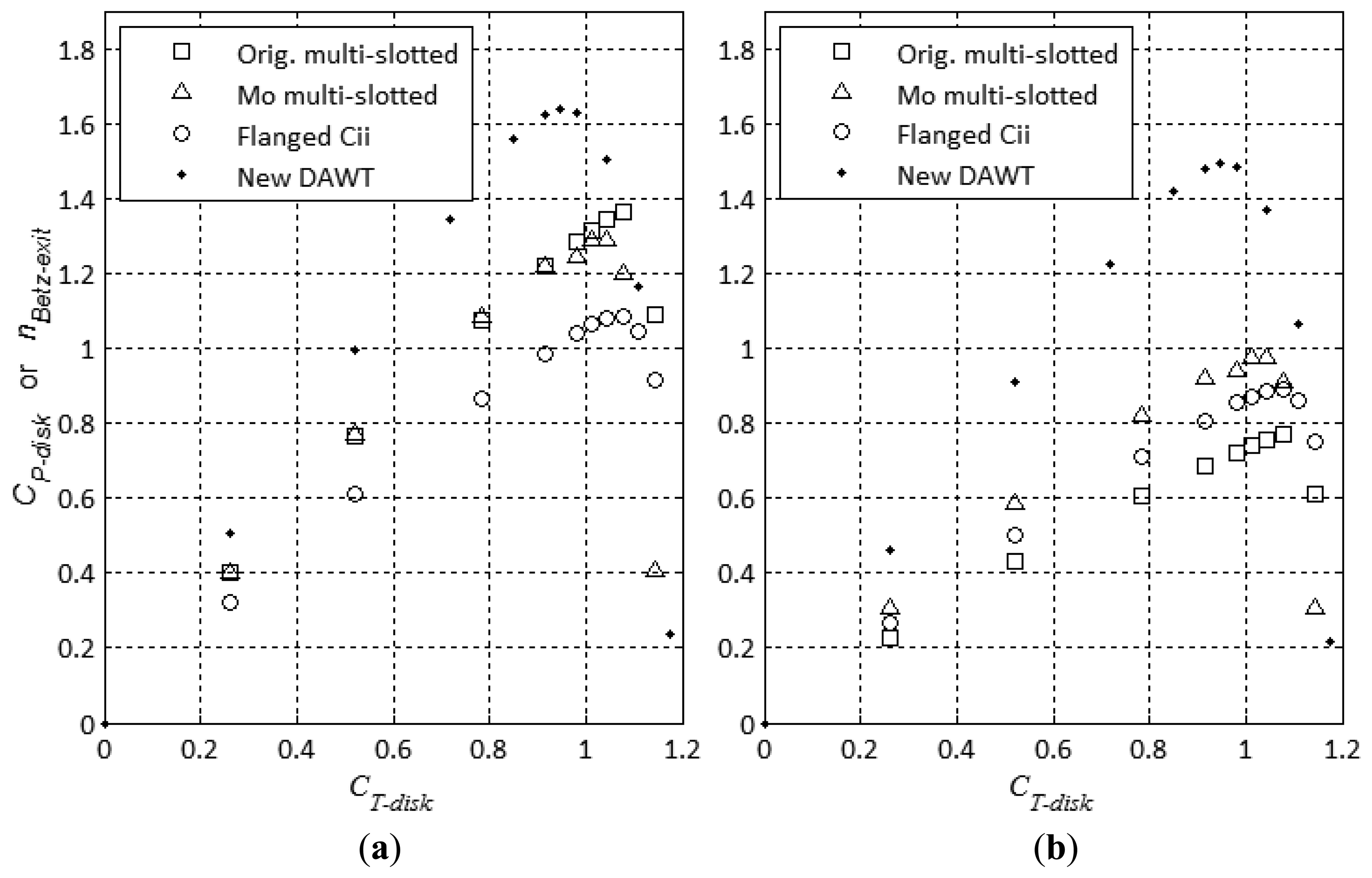
The plot on p.173 in [15] for available power augmentation based on disk area peaks at nBetz_disk = 2.40. The exit-to-disk area ratio is 3.0, thus yielding a reported value for nBetz_disk = 0.80. This agrees fairly well with our RANS CFD obtained value of 0.75, see right plot of Figure 10 and Table 3. The diffuser geometry is given on Figure 8, top-left. The flow solution at the power-optimal disk loading is shown on Figure 9 left. Despite the five passively powered boundary-layer flow-injection slots, the flow separates in close vicinity of the suction side diffuser wall causing a loss of lift. Relative to the exit-area this DAWT is less efficient than the much simpler Hansen DAWT.
4.2. Test Case: Vortec Mo Multi-Slotted DAWT
The plot on p. 255 in [15] only shows shaft power augmentation based on disk area. Contrary to Vortec's original multi-slotted DAWT available power augmentation is not reported. The plot shows a peak reduction in shaft power augmentation of 7% for the Vortec's Mo DAWT compared to their original DAWT. Assuming constant rotor efficiency for the two DAWTs, the assumed available power augmentation based on disk area becomes nBetz_disk = 2.23. The exit-to-disk area ratio for the Mo multi-slotted DAWT is 2.23, thus yielding a reported value for nBetz_disk = 1.00. This agrees very well with our RANS CFD obtained value of 0.98, see right plot of Figure 10 and Table 3. The diffuser geometry is given on Figure 8, top-right. The flow solution at the power-optimal disk loading is shown on Figure 9 right. Compared to the original multi-slotted DAWT the aft part of the diffuser has been truncated and a flange attached to the diffuser trailing edge. The result is a very similar turning of the flow, but with less structure and frontal area. Relative to exit area this is the most power-efficient DAWT yet analyzed, but still not better than the bare HAWT (Table 3).
4.3. Test Case: Ohya Cii Flanged DAWT
Peak shaft power coefficient based on exit area for the Cii type diffuser was measured experimentally to 0.54 in [24]. Assuming a rotor efficiency of 85% leads to an estimated available power coefficient based on exit area of nBetz_disk = 1.07. Our RANS CFD calculation of the same turbine predicts a somewhat lower value of 0.89. The diffuser geometry is given on Figure 8, bottom-left. The flow solution at the power-optimal disk loading is shown on Figure 11a. Compared to the Mo multi-slotted DAWT this flanged DAWT is similar but lacks the boundary-layer control provided by the suction slots. This should have a detrimental impact on area-specific power (as predicted by the RANS CFD), but since the flow behind the broad Cii-flange will cause large-scale turbulence, it is possible that large turbulent eddies will enhance mixing by causing wake-meandering which by nature cannot be captured by our 2D axisymmetric RANS CFD code.
4.4. Test Case: New Multi-Element DAWT
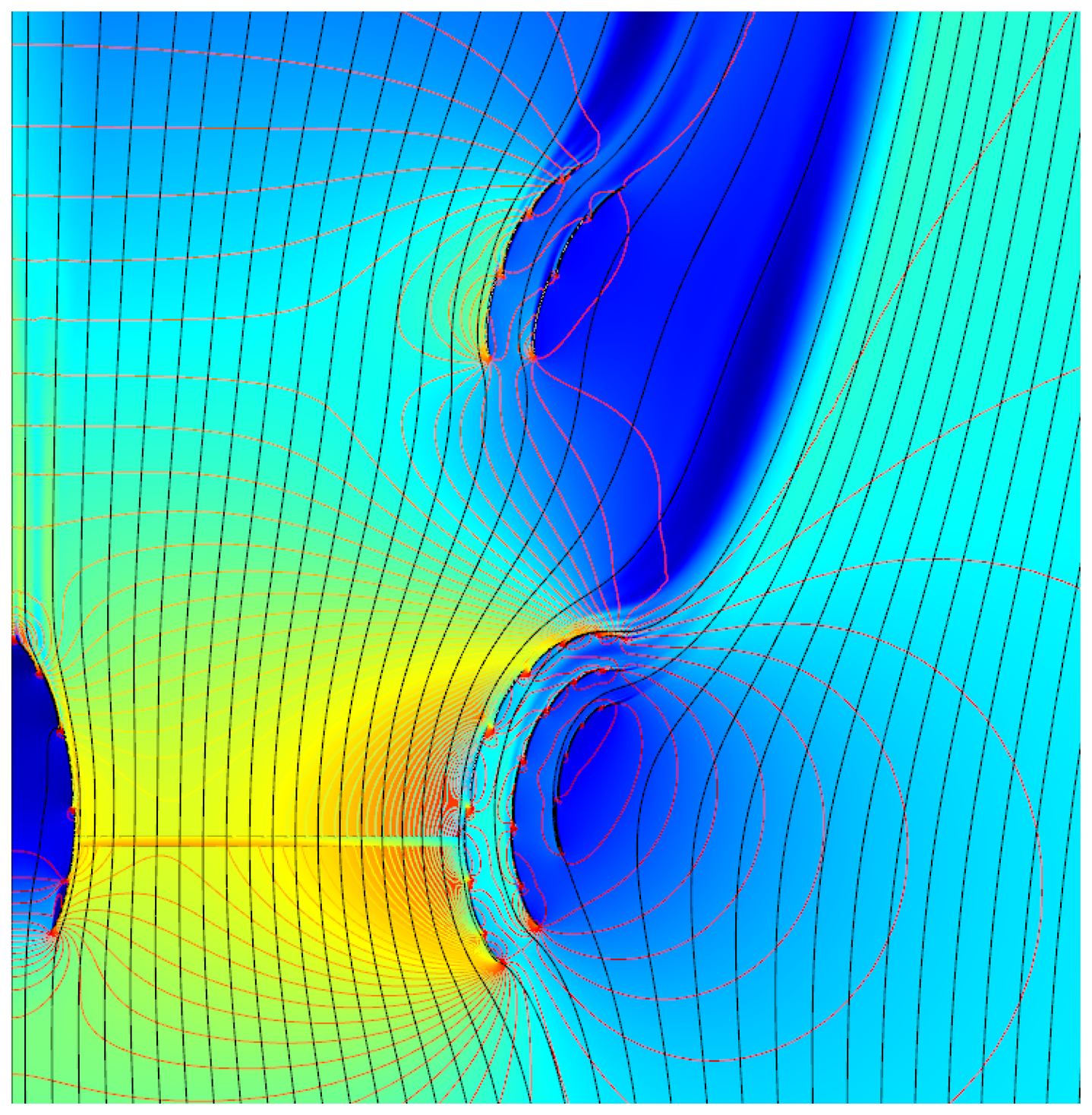
The last test case is our new multi-element DAWT. The RANS CFD calculation predicts a record exit-area-specific power-efficiency of nBetz_disk = 1.49. The diffuser geometry is given on Figure 8, bottom-right (patent pending, March 2014). The flow solution at the power-optimal disk loading is shown on Figure 11 right. The cross-section consists of three layers of multi-slotted guide vanes. Each guide vane is a variant of the Göttingen Goe417a airfoil, see e.g., [26], which was designed as a high-lift airfoil for low Re numbers of roughly 100,000 based on chord length. Furthermore it has the virtue of being one-sided which offers a structural advantage, at least when considering small diffuser structures. Similar designs with traditional airfoils for higher Re numbers, like the NACA-63618, were also made, and they would show better performance at higher Re numbers as expected. Initial cross-sectional designs were inspired by the Figure 7 configuration. In plain words, we know that lift is created as the flow turns, and scrutinizing the streamlines of Figure 7, it is seen that despite the high-lift capacity of that configuration, the flow on the pressure side actually turns “the wrong way”, thereby counter-acting optimal lift. Replacing the circle by auxiliary layers of multi-slotted vanes circumvented this deficiency, and boosted the power efficiency. If only the inner-most layer of vanes adjacent to the disk tip was kept, a slight power-drop was observed compared to the concept with one layer and a circle, e.g., as in Figure 7. During design iterations it became clear that multiple layers of vanes create a speedup amplification effect from the outermost layer to the next layer and so forth. The gradual increase in flow-velocity over the guide vane layers is seen on Figure 11 right, as well as the configuration's ability to turn the flow and maintain it attached.
None of the test cases include nacelle center-bodies. If the diffuser has high-lift capability, the center-body must have likewise; otherwise surface flow separation might occur. In the case of the new multi-element DAWT, a multi-slotted center-body is advised, see Figure 12.
The new multi-element DAWT flow showed in the left plot of Figure 11 also shows that suction surface stall has been effectively suppressed by the multi-slotting, and is therefore not a power-limiting factor. Instead, the boundary layers over the vanes propagate downstream of the trailing edges and form streaks of diffuser element wakes. If the wake velocity deficit and/or the pressure recovery in these wakes are sufficiently high, then wake flow reversal will occur during the wake expansion (i.e., the pressure recovery) and cause a different type of stall out of contact with any wall. Smith [25] described the phenomenon known from multi-element airfoil design for aircrafts, and named it “off-the-surface pressure recovery”. In Table 4 it is named “diffuser wake stall” as opposed to the normally occurring “diffuser surface stall”. Recognizing this stall mechanism for the new multi-element diffuser motivates us to categorize the lift-driven horizontal-axis turbines according to which types of stall impose an upper limit for energy extraction. The overview is presented in Table 4.
5. Discussion
It should be emphasized that the power taken out of the flow by the actuator disk for all three methods (1D momentum theory, panel code, and RANS CFD) is the so-called “available power”, which for the bare HAWT peaks at the Betz number of 16/27. Since power is converted through the operation of a spinning rotor with a discrete number of wind turbine blades, the available power represents an ideal optimum. Aerodynamic loss has the following sources: (1) Cross-sectional viscous and pressure drag along the span of the blade; (2) induced drag from the blade-tip trailing vorticity; (3) induced drag from the blade-root trailing vorticity; and (4) reduced power potential due to axial wake swirl created by the rotor. These losses typically reduce the available power by approximately 15%. The remaining mechanical power that enters the drivetrain is termed “shaft power”. It is relevant to contemplate whether the obtainable rotor efficiency, defined as the ratio between shaft and available power, is different between HAWTs and DAWTs.
Cross-sectional viscous and pressure drag along the span of the blade. The 2D lift and drag polar characteristics of the cross-sectional airfoils along the blade is unaffected by the presence of a diffuser.
Induced drag from the blade-tip trailing vorticity. The helical vortex emanating from the rotating blade tip is created by the downwash fluid motion from the pressure side to the suction side at the very tip. This downwash will in theory vanish when the tip is non-tapered such that the bound vorticity remains constant, and the tip is truncated arbitrarily close to the inside diffuser wall eliminating tip clearance and downwash. In reality, a certain tip clearance is necessary, but a certain reduction in induced drag should be anticipated, leading to reduced tip-loss for the DAWT compared to the HAWT.
Induced drag from the blade-root trailing vorticity. At least qualitatively, the flow augmentation created by the diffuser does not impact the shedding of helical root vortices. It is unclear if the pressure recovery of the vortex cores as they propagate downstream will accentuate the risk of inner wake recirculation, see next point. If so, the design of the blade root for DAWTs should aim at avoiding the operational shedding of concentrated root vortices.
Reduced power potential due to axial wake swirl created by the rotor. When the HAWT and the DAWT operate at comparable tip speed ratios, the wake losses that affect the inner part of the rotor where the swirl is highest should be quite similar. However, it is known from regular diffuser theory that axisymmetric expansion of an axial flow with swirl might be subject to inner core flow recirculation when propagating through the diffuser [27]. This rotor stall mechanism represents a possible pitfall in our analysis, since all methods employed in this work including the RANS CFD disregard swirl. Clausen established in [28] a semi-empirical rule for detecting inner core recirculation in regular diffusers based partly on experiments and partly on the theoretical results by Batchelor for steady axisymmetric flows with swirl in [27]. According to this rule, the square of the radial expansion ratio times the wake speed ratio must not exceed a value of 2. The wake speed ratio is the ratio between the diffuser throat flow tangential velocity at the containing wall radius and the axial velocity. Clausen's rule assumes constant cross sectional axial velocity and solid body type inlet flow rotation. None of these assumptions are fulfilled for a DAWT, so even though the criterion as such is easily fulfilled, this should be regarded as indicative only. To properly unveil the risk of swirl induced inner wake stall, full 3D actuator disk RANS CFD simulations with both axial and tangential forcing applied by the disk must be studied for a specific diffuser and rotor design. This is proposed as a further extending study to the present work.
6. Conclusions and Perspectives
The validity range of 1D momentum theory for DAWTs has been investigated, as well as the power performance limits, leading to a novel type of multi-element DAWT.
Conclusions
- -
1D momentum theory for DAWTs based on the unloaded flow augmentation ūd0 over-predicts CP_disk_opti by at least 20%. The duct loading agrees with the momentum theory predicted disk loading proportionality only up to disk loading coefficients, CT_disk, of around 0.25.
- -
Therefore, DAWT design efforts should focus on loaded performance optimization instead of unloaded flow augmentation optimization.
- -
Current DAWT designs have not yet reached their full potential for energy efficiency.
- -
CT_disk of the new multi-element DAWTs exceeds the Betz number by 50%, when employing a multi-layer duct-design with passive boundary-layer stall control. This is 50% higher than present state-of-the-art for any HAWT or DAWT.
The new multi-element DAWT might pave the road for improved future utilization of small-scale renewable energy.
Perspectives
- -
Financial value: The 50+ percent increased efficiency makes the DAWT technology become more Cost-of-Energy (CoE) attractive in two ways:
- ○
It increases the CoE competitiveness of DAWTs for small-scale wind.
- ○
The break-even size where HAWTs and DAWTs are equally competitive is pushed further up, possibly into the mid-scale wind utility range.
- -
Non-financial value: Besides energy augmentation, the diffuser helps shield the aero-acoustic noise propagation, and provides visual encapsulation of the rotating rotor. These are important considerations for small-scale wind in urban and sub-urban areas. Design of a low tip-speed-ratio rotor for the new multi-element DAWT will lead to a very silent application.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lilley, G.M.; Rainbird, W.J. A Preliminary Report on the Design and Performance of Ducted Windmills; Cranfield College of Aeronautics: Bedford, UK, 1956. [Google Scholar]
- Iwasaki, M. The Experimental and Theoretical Investigation of Windmills; Kyushu University, Research Institute for Applied Mechanics: Kyushu, Japan, 1953; Volume 2. [Google Scholar]
- Sanuki, M. Studies on biplane wind planes ventilation tubes and cup anemometers. Meteorol. Geophys. Jpn. 1950, 1, 279–290. [Google Scholar]
- Igra, O. Shrouds for aerogenerators. AIAA J. 1976, 14, 1481–1483. [Google Scholar]
- Igra, O. Design and performance of a turbine suitable for an aerogenerator. Energy Convert. 1976, 15, 143–151. [Google Scholar]
- Igra, O. Compact shrouds for wind turbines. Energy Convert. 1977, 16, 149–157. [Google Scholar]
- Igra, O. The shrouded aerogenerator. Energy 1977, 2, 429–439. [Google Scholar]
- Igra, O. Research and Development for Shrouded Wind Turbines. Proceedings of the European Wind Energy Conference, Hamburg, Germany, 22–26 October 1984.
- Lewis, R.I.; Williams, J.E.; Abdelghaffar, M.A. A theory and experimental investigation of ducted wind turbines. Wind Eng. 1977, 1, 104–125. [Google Scholar]
- Oman, R.A.; Foreman, K.M.; Gilbert, B.L. Investigation of Diffuser Augmented Wind Turbines, Parts I & II; Grumman Research Department Report RE-534, ERDA Report C00-2616-2; Grumman Aerospace: New York, NY, USA, 1977. [Google Scholar]
- Gilbert, B.L.; Oman, R.A.; Foreman, K.M. Fluid dynamics of diffuser-augmented wind turbines. J. Energy 1978, 2, 368–374. [Google Scholar]
- Werle, M.; Presz, W. Ducted wind/water turbines and propellers revisited. J. Propuls. Power 2008, 24, 1146–1150. [Google Scholar]
- Werle, M.; Presz, W. Shrouds and ejector augmentors for subsonic propulsion and power systems. J. Propuls. Power 2009, 25, 228–236. [Google Scholar]
- Ten Hoppen, P.D.C. An Experimental and Computational Investigation of a Diffuser Augmented Wind Turbine. M.Sc. Thesis, Delft University of Technology, Delft, The Netherlands, 2009. [Google Scholar]
- Phillips, D.G. An Investigation of Diffuser Augmented Wind Turbine Design. Ph.D. Thesis, University of Auckland, Auckland, New Zealand, 2003. [Google Scholar]
- Van Bussel, G.J.W. An Assessment of the Performance of Diffuser Augmented Wind Turbines. Proceedings of the 3rd ASME Joint Fluids Engineering Conference, San Francisco, CA, USA, 18–23 July 1999.
- Van Bussel, G.J.W. The science of making more torque from wind: Diffuser experiments and theory revisited. J. Phys. Conf. Ser. 2007, 75, 1–12. [Google Scholar]
- Jamieson, P. Generalized limits for energy extraction in a linear constant velocity flow field. J. Wind Energy 2007, 11, 445–457. [Google Scholar]
- Werle, M. Passing through the wind turbine thrust singularity. J. Propuls. Power 2011, 27, 908–912. [Google Scholar]
- Hansen, M.O.L. Effect of placing a diffuser around a wind turbine. J. Wind Energy 2000, 3, 207–213. [Google Scholar]
- Lewis, R.I. Vortex Element Methods for Fluid Dynamic Analysis of Engineering Systems; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- CFD Module User's Guide Version 4.4; Comsol Inc.: Burlington, MA, USA, 2013.
- Mikkelsen, R. Actuator Disc Methods Applied to Wind Turbines. Ph.D. Thesis, Technical University of Denmark, Kongens Lyngby, Denmark, 2004. [Google Scholar]
- Ohya, Y.; Karasudani, T. A shrouded wind turbine generating high output power with wind-lens technology. Energies 2010, 3, 634–649. [Google Scholar]
- Smith, A.M.O. High-lift aerodynamics. J. Aircr. 1975, 12, 501–530. [Google Scholar]
- Lyon, C.A.; Broeren, A.P.; Giguère, P.; Gopalarathnam, A.; Selig, M.S. Summary of Low-Speed Airfoil Data; SoarTech Publications, University of Illinois: Champaign, IL, USA, 1998; Volume 3. [Google Scholar]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 1967. [Google Scholar]
- Clausen, P.D.; Wood, D.H. A Possible Recirculation Limit for Expanding Swirling Flows. Proceedings of the 10th Australasian Fluid Mechanics Conference, Melbourne, Australia, 11–15 December 1989.



| Test Case | 1D mom. Theory | Panel Code | RANS CFD |
|---|---|---|---|
| Regular HAWT | X | X | X |
| Hansen DAWT | X | X | X |
| Circular cylinder (donut) DAWT | X | X | - |
| Vortec orig. multi-slotted DAWT | - | - | X |
| Vortec Mo multi-slotted DAWT | - | - | X |
| Ohya Cii flanged DAWT | - | - | X |
| New multi-element DAWT | - | - | X |
| ūd0 | r/R | ud0_max | θTE | r/R | ud0_max | ||||||||
| 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | ||||
| 0.025 | 1.04 | 1.22 | 1.39 | N.A. | N.A. | 0.025 | −0.7 | 24.3 | 52.3 | N.A. | N.A. | ||
| 0.05 | 1.08 | 1.35 | 1.61 | 1.88 | N.A. | 0.05 | −1.4 | 20.6 | 42.9 | 75.4 | N.A. | ||
| 0.10 | 1.15 | 1.54 | 1.92 | 2.31 | 2.69 | 0.10 | −2.5 | 16.0 | 32.9 | 50.5 | 75.1 | ||
| 0.15 | 1.21 | 1.68 | 2.14 | 2.61 | 3.07 | 0.15 | −3.5 | 12.9 | 27.0 | 40.4 | 54.4 | ||
| 0.2 | 1.26 | 1.78 | 2.31 | 2.84 | 3.36 | 0.2 | −4.5 | 10.4 | 22.7 | 33.9 | 44.9 | ||
| 0.3 | 1.34 | 1.95 | 2.56 | 3.17 | 3.77 | 0.3 | −6.3 | 6.5 | 16.7 | 25.6 | 33.6 | ||
| 0.4 | 1.41 | 2.07 | 2.74 | 3.41 | 4.07 | 0.4 | −7.8 | 3.5 | 12.4 | 20.0 | 26.7 | ||
| 0.5 | 1.47 | 2.17 | 2.88 | 3.58 | 4.29 | 0.5 | −9.2 | 1.1 | 9.1 | 15.8 | 21.7 | ||
| CP_disk_opti | r/R | ud0_max | CP_exit_opti | r/R | ud0_max | ||||||||
| 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | ||||
| 0.025 | 0.62 | 0.72 | 0.82 | N.A. | N.A. | 0.025 | 0.53 | 0.63 | 0.71 | N.A. | N.A. | ||
| 0.05 | 0.64 | 0.80 | 0.95 | 1.11 | N.A. | 0.05 | 0.51 | 0.63 | 0.75 | 1.01 | N.A. | ||
| 0.10 | 0.68 | 0.91 | 1.14 | 1.37 | 1.59 | 0.10 | 0.45 | 0.61 | 0.76 | 0.91 | 1.06 | ||
| 0.15 | 0.72 | 1.00 | 1.27 | 1.55 | 1.82 | 0.15 | 0.41 | 0.57 | 0.72 | 0.88 | 1.04 | ||
| 0.2 | 0.75 | 1.05 | 1.37 | 1.68 | 1.99 | 0.2 | 0.37 | 0.52 | 0.67 | 0.83 | 0.98 | ||
| 0.3 | 0.79 | 1.16 | 1.52 | 1.88 | 2.23 | 0.3 | 0.30 | 0.44 | 0.57 | 0.71 | 0.85 | ||
| 0.4 | 0.84 | 1.23 | 1.62 | 2.02 | 2.41 | 0.4 | 0.25 | 0.37 | 0.49 | 0.61 | 0.72 | ||
| 0.5 | 0.87 | 1.29 | 1.71 | 2.12 | 2.54 | 0.5 | 0.21 | 0.31 | 0.42 | 0.52 | 0.62 | ||
| Turbine | CT_disk | CT_duct | CP_disk | CP_exit | nBetz_exit | nBetz_exit (Refs.) |
|---|---|---|---|---|---|---|
| Regular HAWT | 0.89 | 0.00 | 0.60 | 0.60 | 1.02 | 1.00 |
| Hansen DAWT [20] | 0.77 | 0.47 | 0.91 | 0.49 | 0.83 | 0.86 [20] |
| Vortec orig. multi-slotted DAWT [15] | 1.04 | 2.03 | 1.34 | 0.45 | 0.75 | 0.80 [15] |
| Vortec Mo multi-slotted DAWT [15] | 1.04 | 1.57 | 1.29 | 0.58 | 0.98 | 1.00 [15] |
| Ohya Cii flanged DAWT [24] | 1.08 | 1.36 | 1.09 | 0.53 | 0.89 | 1.07 [24] |
| New multi-element DAWT | 0.95 | 1.85 | 1.64 | 0.88 | 1.49 | - |
| Turbine | Rotor surface stall | Rotor wake stall/blockage | Diffuser surface stall | Diffuser wake stall |
|---|---|---|---|---|
| HAWT | No | Yes (Betz) | - | - |
| Regular DAWT | No | Yes | Yes | No |
| New multi-element DAWT | No | Yes | No | Yes |
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Hjort, S.; Larsen, H. A Multi-Element Diffuser Augmented Wind Turbine. Energies 2014, 7, 3256-3281. https://doi.org/10.3390/en7053256
Hjort S, Larsen H. A Multi-Element Diffuser Augmented Wind Turbine. Energies. 2014; 7(5):3256-3281. https://doi.org/10.3390/en7053256
Chicago/Turabian StyleHjort, Søren, and Helgi Larsen. 2014. "A Multi-Element Diffuser Augmented Wind Turbine" Energies 7, no. 5: 3256-3281. https://doi.org/10.3390/en7053256





