Condition Parameter Modeling for Anomaly Detection in Wind Turbines
Abstract
: Data collected from the supervisory control and data acquisition (SCADA) system, used widely in wind farms to obtain operational and condition information about wind turbines (WTs), is of important significance for anomaly detection in wind turbines. The paper presents a novel model for wind turbine anomaly detection mainly based on SCADA data and a back-propagation neural network (BPNN) for automatic selection of the condition parameters. The SCADA data sets are determined through analysis of the cumulative probability distribution of wind speed and the relationship between output power and wind speed. The automatic BPNN-based parameter selection is for reduction of redundant parameters for anomaly detection in wind turbines. Through investigation of cases of WT faults, the validity of the automatic parameter selection-based model for WT anomaly detection is verified.1. Introduction
Supervisory control and data acquisition (SCADA) systems are used in almost all wind farms for monitoring the conditions of the wind turbines (WTs). Detection of WT faults with SCADA data is very helpful to improve the reliability of WTs and to reduce the operation and maintenance costs of wind farms. A SCADA system in a wind farm may contain massive amounts of data related to hundreds of parameters of the WTs and SCADA data has attracted great research interest in fault detection for WTs [1–5]. In [6] a normal behavior model for prediction of bearing faults by using SCADA data was presented. A generalized model, called virtual model, was presented in [7] for prediction of WT parameters based on SCADA data. Three WT condition parameters, including a main bearing temperature, a lubrication oil temperature of gearbox, and a winding temperature of the generator, were modeled through a BPNN for fault detection of WTs based on SCADA data [8]. BPNNs were also investigated in publications [9–12] for modeling WT parameters with SCADA data. A comparative analysis of two BPNN-based models and a regression-based model was presented in [12] for modeling parameters of gearbox bearing temperature and generator stator temperature.
Modeling parameters based on SCADA data is for the purpose of obtaining residual errors of the condition parameters used for fault detection of WTs. Given the hundreds of parameters of a SCADA system of wind farm, reducing the dimensionality of the data and establishing models with closely related parameters is a premise in simplifying models and ensuring prediction accuracy. In the above works, the condition parameters of WTs were determined empirically so as to obtain a small dataset for modeling parameters. The small dataset may not provide enough information about WT faults.
Moreover, parameter selection is an important step for anomaly detection of WTs [7] and its purpose is to determine target parameters with relevance to the initial condition parameters for modeling. However, few works have considered the correlation between the target parameters and the initial parameters of the SCADA systems of wind farms.
Considering the aforementioned problems, the authors propose a novel model for anomaly detection of WTs based on SCADA data. The model is a generalized model called automatic parameter selection (APS)-based model in this work, which involves automatic parameter selection using root-mean-square error (RMSE) of target parameters. Section 2 proposes the methodology of the APS-based model involving SCADA data collection, automatic parameter selection. Section 3 presents the selection of wind farm SCADA data and determination of initial WT condition parameters for modeling. Section 4 introduces the method for automatic parameter selection based on one BPNN for anomaly detection of WTs, and presents the other BPNN for prediction of RMSE of target parameters. Section 5 provides validation and analysis of the proposed method. The last section offers the conclusions of the work.
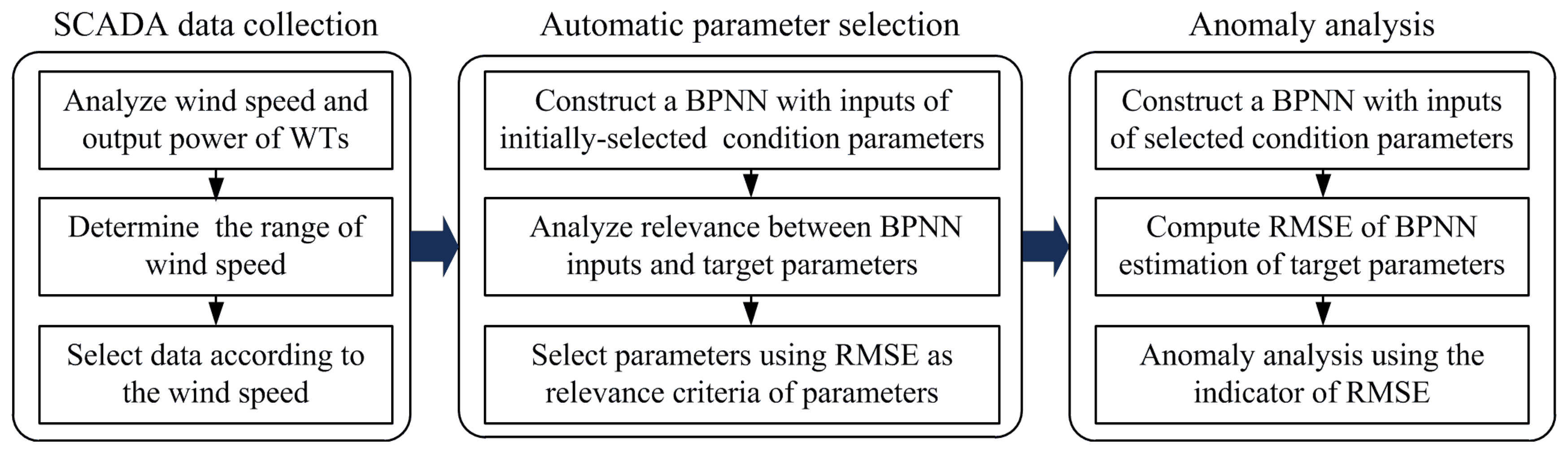
2. Methodology of the APS-based Model
Figure 1 presents the methodology of the APS-based model for anomaly detection of WT, which includes the following three parts:
- (1)
SCADA data collection includes data analysis and condition parameters for modeling. Data analysis is used to determine SCADA data for training and testing of the models in the work. Condition parameters from SCADA system of WT are described later.
- (2)
Automatic parameter selection is to select the appropriate input parameter of BPNN from condition parameters. Automatic parameter selection constructs a BPNN with input of initially-selected condition parameters and selects condition parameters using RMSE as criteria.
- (3)
Anomaly analysis is to build and use the model with selected condition parameters as input for anomaly detection. The RMSE of target parameter is computed in automatic parameter selection and anomaly analysis.
3. SCADA Data Collection
SCADA data were collected from a wind farm consisting of upwind and doubly-fed WTs with rated power of 1.5 MW, a cut-in wind speed of 3 m/s, a rated wind speed of 12 m/s, and a cut-out wind speed of 25 m/s. Each WT is equipped with a horizontal axis and an active yawing and pitch control system. Figure 2 presents an example of some WT condition parameters in the SCADA system of the wind farm. The SCADA data with a time interval of 10 min are used for the work. The descriptions of these WT condition parameters are concluded in Table 1. A total of 31 WTs of the same type are installed in the wind farm. The SCADA data of WTs 3, 10, 17, 23, and 31 are randomly selected for analysis of condition parameters.
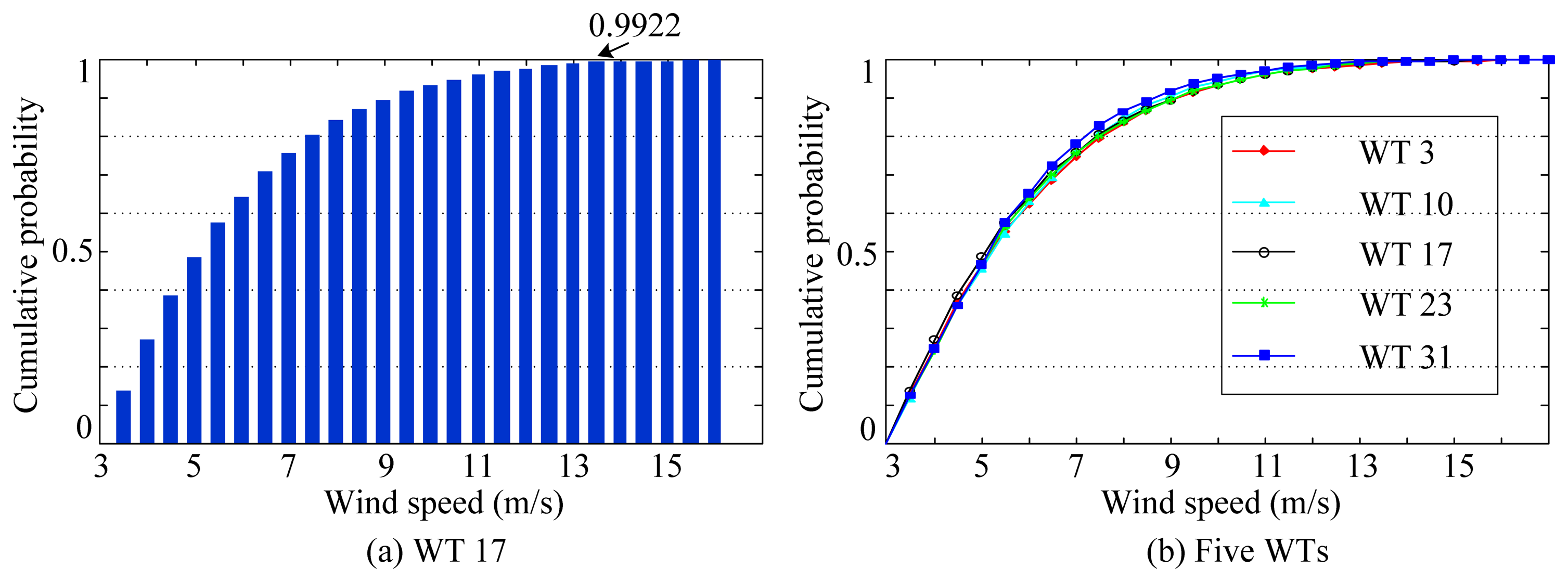
The SCADA data are selected with a criteria of wind speed. The Bin method [13] was used to analyze SCADA data. Figure 3 shows the wind speed probability distributions at five WTs in the wind farm. The cumulative probability of the wind speed of WT 17, as shown in Figure 3a, indicates 99.22% of wind speed values not exceeding 13.5 m/s. Figure 3b shows that the wind speed probability distributions of WTs 3, 10, 23, and 31 are identical with that of WT 17.
Figure 4 presents the distribution of the output power versus the wind speed of WT 17. The other four WTs have plots very similar to Figure 4. The wind speed range between 3 and 13.5 m/s is thus determined for SCADA data selection, where the wind speed of 3 m/s is the cut-in wind speed of the WTs. The blog in Figure 4 shows that the determined wind speed range covers most output power of each WT in the wind farm.
4. Automatic Parameter Selection
4.1. Construction of the BPNN
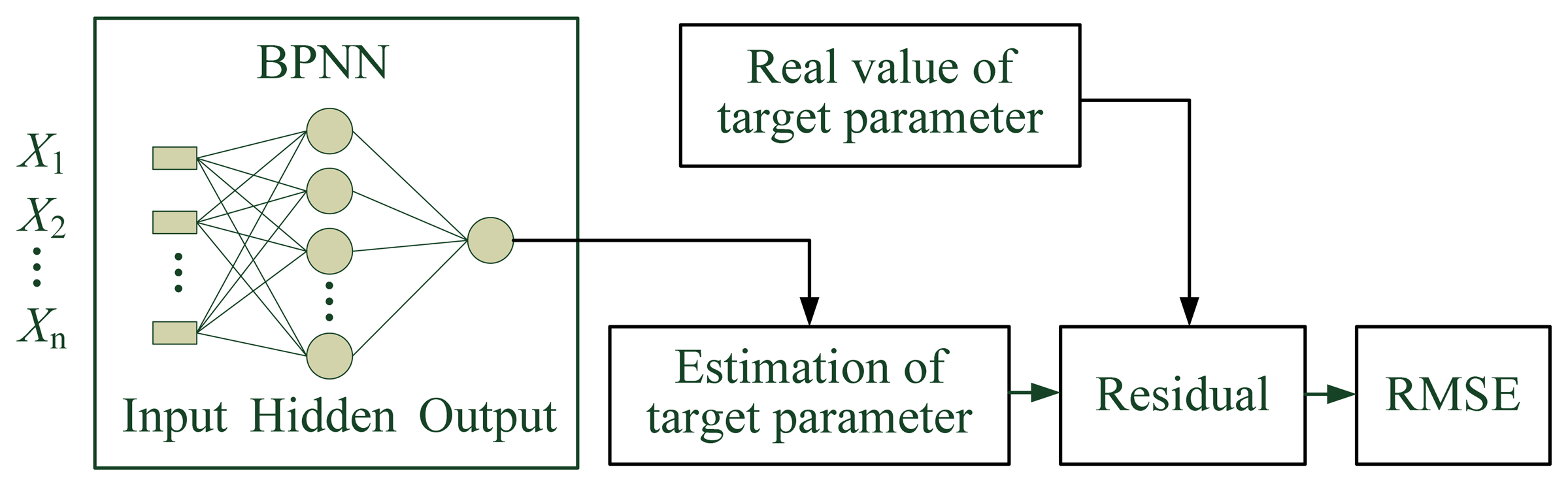
Figure 5 shows the modeling procedures based on a BPNN for estimating target parameters. Given one parameter in Table 1 as the target parameter of the BPNN, the other 19 parameters are considered as the inputs of the BPNN to be selected.
The BPNN is adopted for parameter selection. The BPNN is the most widely used neural network in many field [14]. Using neural networks to predict parameters has achieved good results [7]; thus, the BP neural network was used in the work to model the parameters in WTs. Given the time interval of 10 min, the models of the vibration parameters and some parameters with the fixed ranges are not established, including those of phase voltage and phase current. The 13 parameters are marked as “Yes”, as shown in the third column of Table 1. The BPNN for selection parameter has three layers with 19 nodes in the input layer and 1 node in the output layer. The 14 nodes in the hidden layer are determined by an empirical equation, i.e., Equation (1). And the hidden layer of all models in this paper has 14 nodes for comparative analysis:
A total of 30,000 data obtained under normal operating conditions are selected from the SCADA system of WT 17 for a year, including 27,000 training data and 3000 testing data. The optimal number of hidden nodes is dependent on the following condition: the number of nodes of input and output layer, the number of training data, network structure, activation function, training algorithm, etc. Now there is no ideal way to determine the number of hidden nodes of a neural network. Different hidden nodes are chosen according to empirical equations. However the optimal number of hidden nodes is not always obtained according to empirical equations sometimes. So the neural network is tested many times to determine the optimal number of hidden-layer nodes [15].
When the model is built, the number of nodes in the hidden layer is from 5 to 14. Through training the BP neural network, the model achieves better performance when the nodes of the hidden layer is 14. Figure 6 presents that the result for training the neural network by using the temperature of generator bearing B as an example. RMSEs of the temperature parameter of generator bearing B in Figure 6 change with the number of nodes in the hidden layer. So the hidden layer of all models in this paper has 14 nodes for comparative analysis.
4.2. Relevance Criteria for Condition Parameters Selection
Relevance between BPNN inputs and target parameters is analyzed using three steps as follows.
- (1)
The optimal model is obtained based on the training data described earlier. The model structure is 19:14:1.
- (2)
The model is tested with the test data, as shown in Equations (2) and (3). The average error is 0.0105 and the RMSE is 1.7656:
where ME is average error; RMSE is root-mean-square error; ri is raw data; r̂i is predicted value.- (3)
The inputs are successively increased and decreased by 5%. The model is tested. The average error and RMSE are recorded, and arranged in descending order of RMSEs, as shown in Table 2.
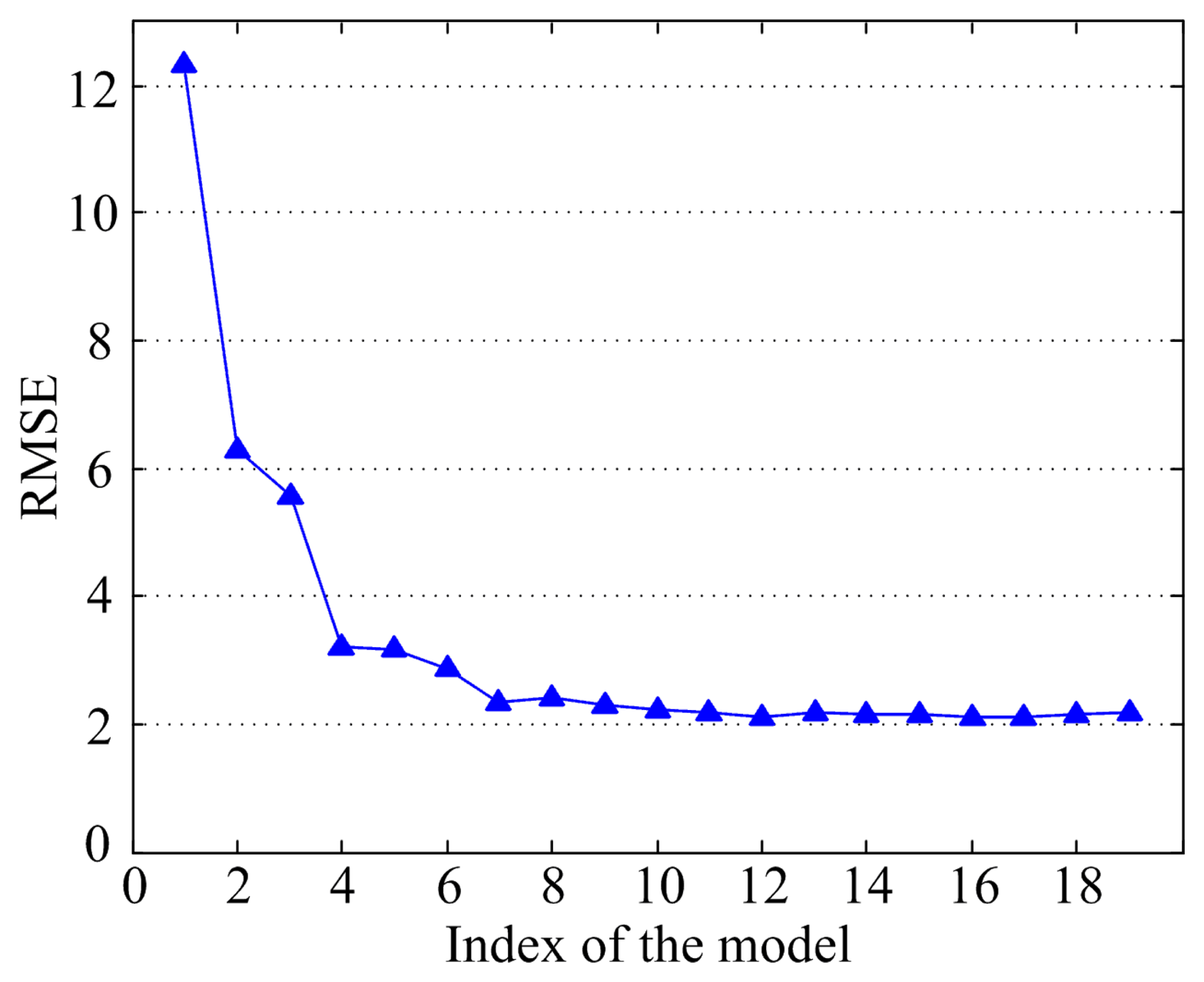
According to the order of the parameters shown in Table 2, the first 19 parameters are regarded as the input parameters of the model. The first model structure is 1:14:1, and the input parameter is the number 1 parameter. The second model structure is 2:14:1, and the input parameters are the first two parameters. By analogy, the nth model structure is n:14:1, and the input parameters are the first n parameters. Each model had 14 hidden nodes, and is trained 30 times with the same training data, and tested with the same test data. The average RMSE at 30 times is obtained, as shown in Figure 7.
As shown in Figure 7, the RMSEs drop sharply from the 1st to the 7th model, and the RMSE difference between the 7th and 19th models is smaller. The RMSE changes slightly after the 7th model and exhibited certain fluctuations, thus indicating that the subsequent parameter information is found in the first seven input parameters. According to the figure, the established model with the first seven input parameters exhibits good accuracy. Thus, the model built from input parameters that include phase voltage, as well as the temperatures of the output shaft, gearbox oil, generator bearing A, input shaft, top cabinet, and generator winding reflects the actual changing situation of the temperature in generator bearing B. It illustrates the validity of our model based on the parameter selection method according to the order listed in Table 2.
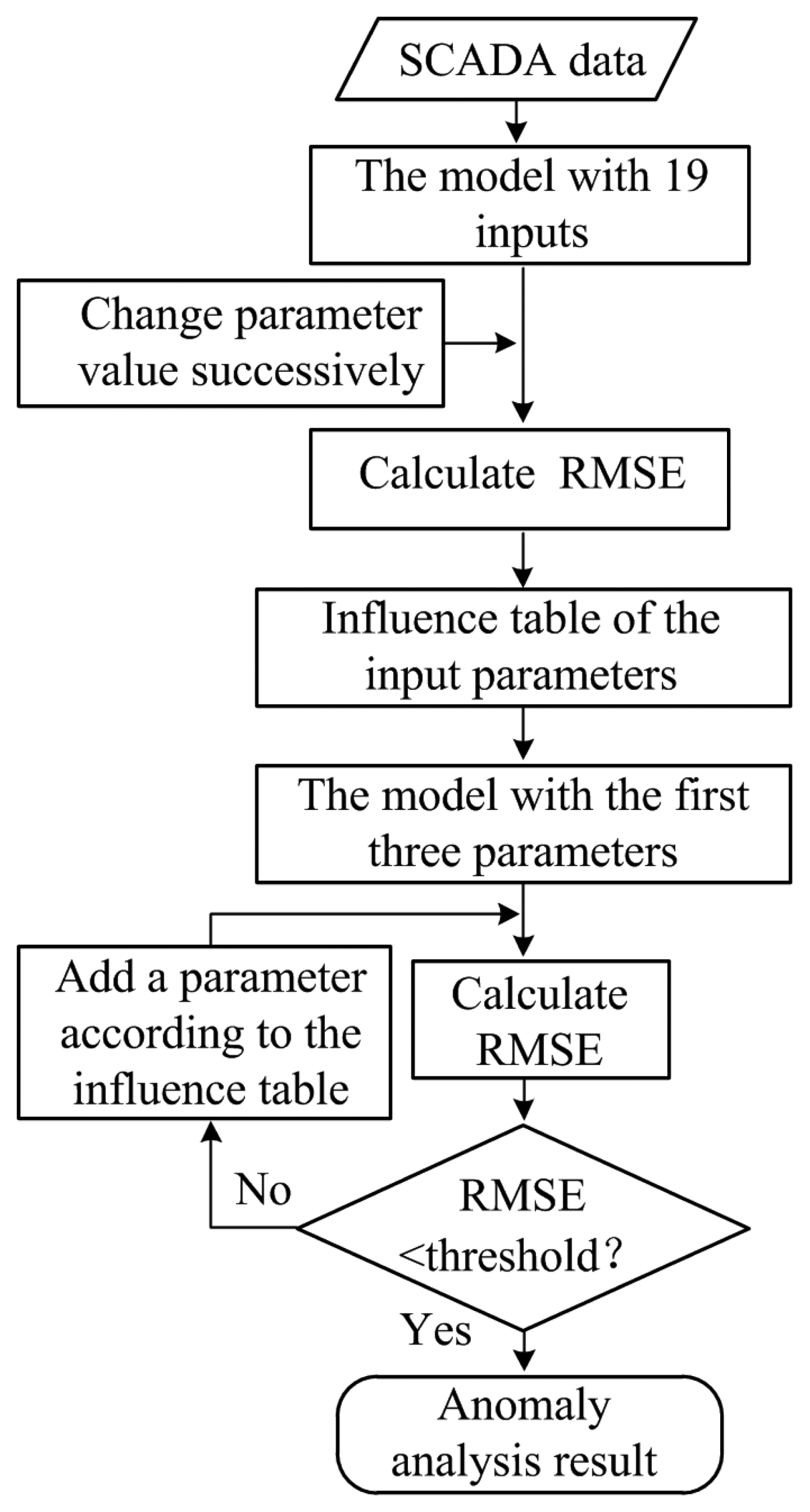
After the influence of various parameters on the target parameters are considered, the model for anomaly detection is established by the following steps (Figure 8):
- Step 1
The first three parameters with higher RMSEs are considered as the input parameters. The BPNN based model, with a model structure of 3:14:1, is built. The optimal model is established with the previous training data.
- Step 2
The newly built model is tested with the same test data. The RMSE is compared with that obtained from 19 initially built input parameters model.
- Step 3
When the difference of the two RMSEs is greater than the threshold, the parameter with the highest RMSE in the remaining parameters in Table 2 is added. The model is established by using the parameters as input parameters. Return to the step 2.
- Step 4
When the difference of the two RMSEs is smaller than the threshold, the model input parameters are finally determined.
When the input parameters of the model for different condition parameters of wind turbines are selected, the thresholds of the models for each parameter are different due to the different relationship between condition parameters of wind turbines. Two points are considered as follows: (1) the model must achieve a certain accuracy; (2) the accuracy of the model changes slightly. The threshold of the model of temperature of generator bearing B is 2.2 °C. And the thresholds chosen for the parameters are indicated in Table 3.
5. Anomaly Analysis
Anomaly detection research aims to identify data patterns that do not conform to the principle of expectation. Such patterns are called irregular or abnormal values [16]. Two cases are used for verifying automatic parameter selection based model for anomaly detection.
The model of the temperature of generator bearing B was analyzed with 3000 test data points obtained during normal operation. The residual of the model and its distribution are shown in Figure 9. As shown in Figure 9a, the errors were mostly found at approximately ±5 °C, and the RMSE was 2.6544. Through data processing, such as smooth filtering of data [12], errors can be effectively reduced. However, considering that a WT is a complex nonlinear system, a large residual does not signify an abnormal condition and data may contain useful information. Hence, research data were not processed in this study. According to Figure 9b, the residual distribution of the model agrees well with the Gaussian distribution. From a statistical perspective, the model accurately reflects actual changes in temperature of generator bearing B during normal operation.
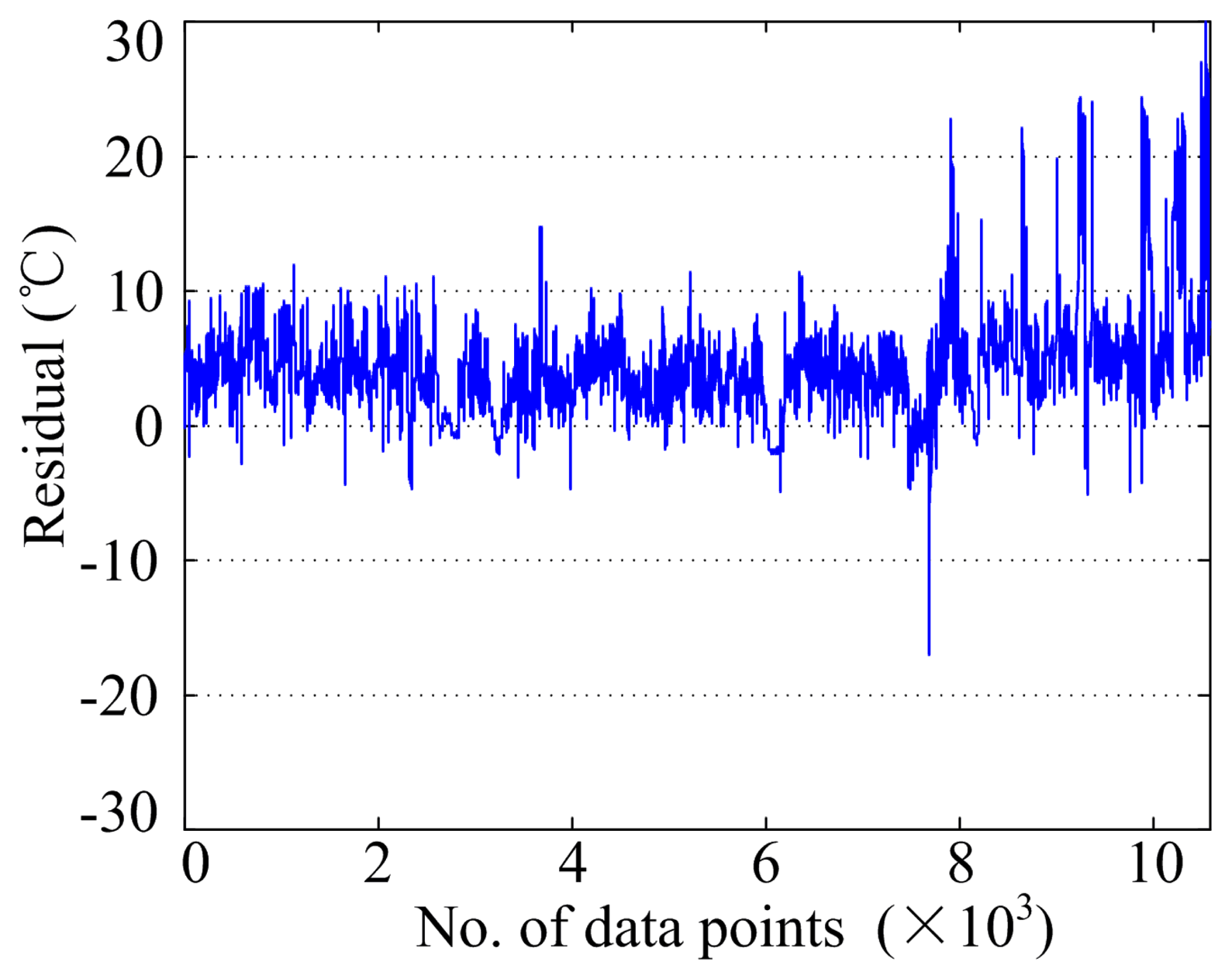
According to field records, the SCADA data of approximately 12,600 data points for three months before the failure of the generator bearing of WT 17 were selected. By building the model of the temperature of generator bearing B, the residual between the model result and the actual value was calculated by time sequence, as shown in Figure 10. From the beginning to around the 10,000th data point, residuals distributed approximately between −5 and 5 °C, and generator bearing B was in a normal condition. At about the 10,000th data point, the residual increased rapidly, up to 25 °C and decreased to −17 °C around the 10,810th data point. It became smaller during a short interval after the 10,810th data point, and turned into a great change of magnitude between −13 °C and 18 °C near the 12,000th data point.
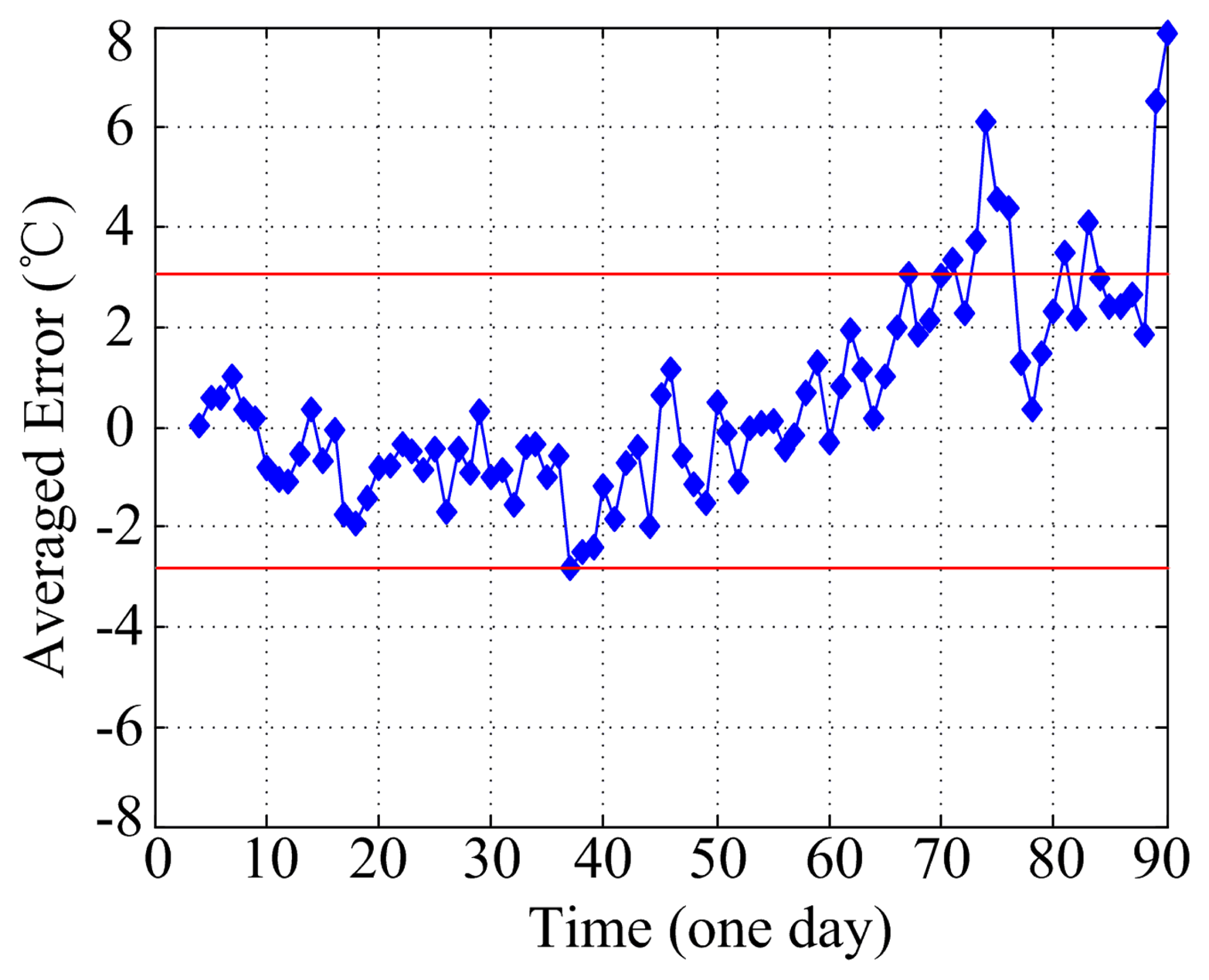
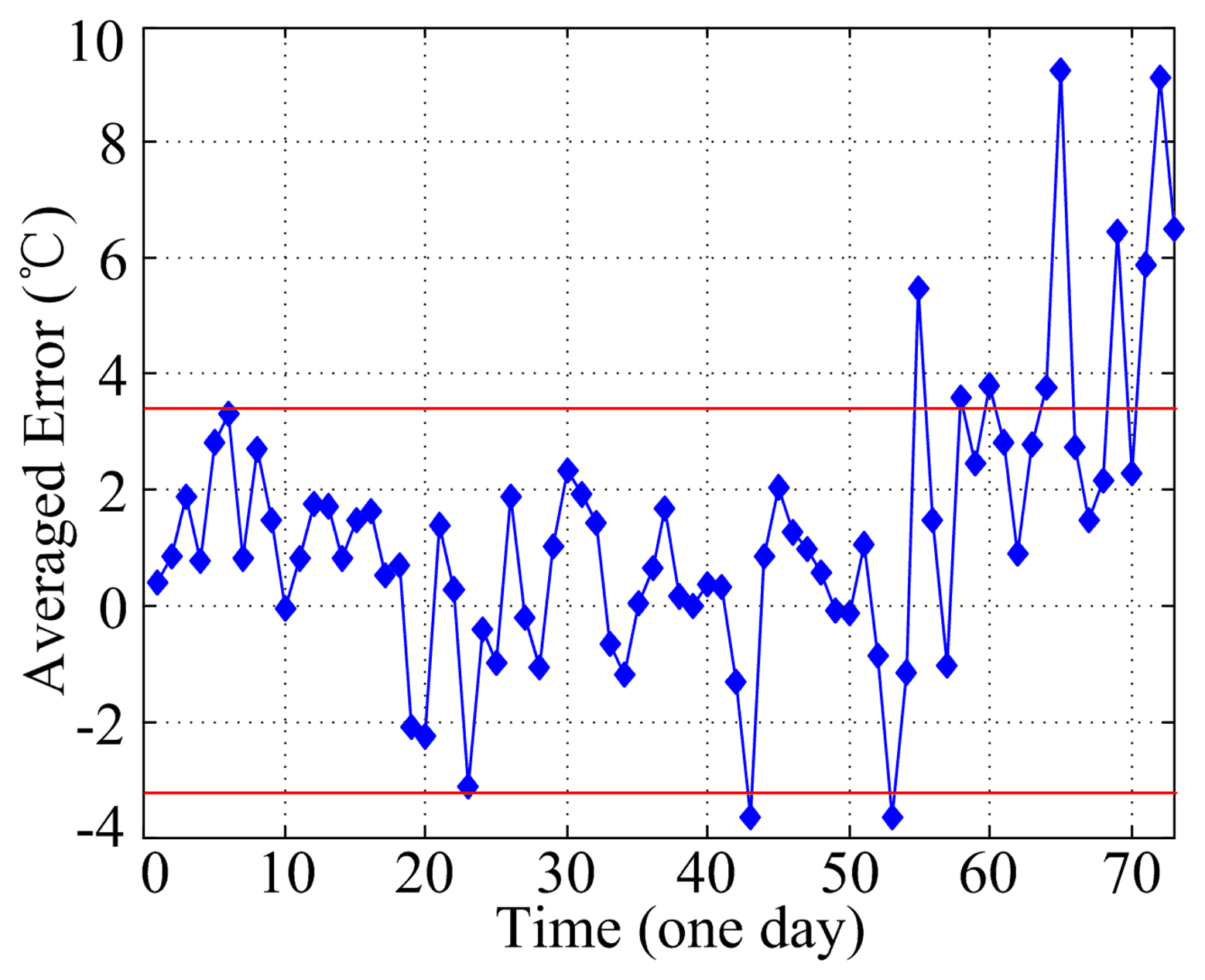
According to Figure 10, data points with the absolute value of the residual greater than 5 °C were less. In the normal condition, data points with the absolute value of the residual greater than 10 °C were observed; thus, identifying the outlier or the disturbance was difficult. Statistics on the average residual per day were recorded, as shown in Figure 11. From the beginning to the 70th day, the average residual error changed slightly, and was mainly distributed between −4 and 4 °C. On the 75th day, the average residual error reached 6 °C. This value became smaller later, until finally, it rapidly reached the maximum value before failure occurred. In Figure 11, during the normal condition of WTs, the average residual fluctuated up and down at 0 °C, with a smaller change in amplitude. Compared with Figure 10, the disturbance could be effectively eliminated by computing the daily average residual value. However, before the failure occurred, the average residual amplitude reached 6 °C and exhibited no significant difference with the average residual during the normal condition. Such result is not conducive to judging the abnormal condition.
Figure 12 shows the changing trend of the RMSE on a daily basis. From the 1st to the 70th day, the RMSE amplitude during normal operation was less than 4. It nearly reached 10 on the 75th day, then dropped to around 4, and increased rapidly one or two days before the fault occurred. As shown in Figure 12, the RMSE on the 75th day and before the fault occurred was significantly greater than that in the normal condition. Compared with the average residual, the RMSE better distinguished between the normal condition and the degradation condition of the temperature parameter of generator bearing B. It efficiently identified the initial stage of parameter degradation. Therefore, the RMSE can identify the abnormal condition of the temperature parameter of generator bearing B and is conducive to providing early warning for generator bearing B. Moreover, 15 days before the fault occurred (about the 75th day), the model exhibited a large RMSE amplitude, which provided a premise for determining the fault alarm time.
6. Case Study and Verification
6.1. Verification for Parameter Selection
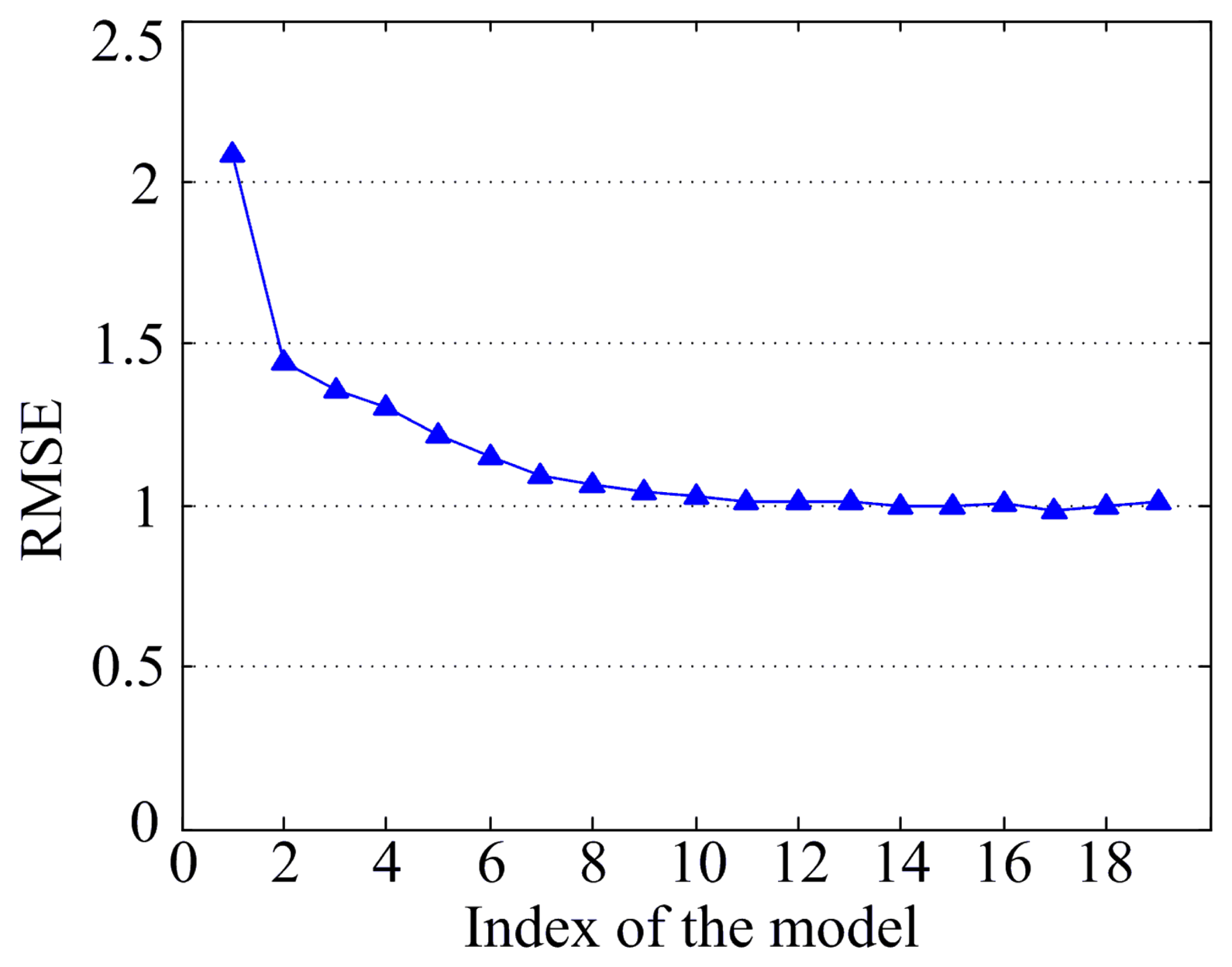
A total of 30,000 data points from the SCADA system mentioned previously are adopted. The model of the temperature of the output shaft of the gearbox is built by using the previously described methods to determine the influence of other parameters on the temperature of the output shaft, as shown in Table 4. Table 4 shows that the temperature parameters of the input shaft caused the RMSE of the model to change more dramatically than the other parameters. Therefore, the temperature of the input shaft will significantly influence the results of the model, i.e., the temperature of the input shaft is closely related to that of the output shaft, which is consistent with field experience.
Furthermore, based on Table 4 and the method of parameter selection discussed in the previous section, the RMSE of the model of the temperature of the output shaft that changes with the increase of the input parameters is obtained, as shown in Figure 13. According to the figure, a model can be obtained by using the first three parameters as inputs. The threshold is 1.3 °C. Based on field experience, the temperature of the input shaft of the gearbox, the oil temperature of the gearbox, and the inlet oil temperature of the gearbox are selected because they are closely related with the temperature of the output shaft, which verifies the effectiveness of the parameter selection method.
6.2. Verifying Anomaly Detection
Data from different WTs were used to verify the RMSE-based anomaly detection method. According to field records, WT 31 experienced an overheating fault in generator bearing B on 30 July, 2012. In this study, SCADA data from two months before the fault were analyzed, and a total of 10,500 data points were used, as shown in Figure 14. Though the bearing temperature showed higher fluctuations, it clearly did not exceed the limit. Before 30 July, the fault in generator bearing B is not judged from the temperature of the generator bearing B in Figure 14. The residuals of the model of the temperature of generator bearing B, the daily average residual, and the daily RMSE were obtained, as shown in Figures 15, 16 and 17.
The overall average residual and the RMSE of the model were observed to go upward over time, fluctuating up and down, possibly because of the following reasons: (1) the change of parameters caused by the volatility of wind speed and (2) the influence of the nonlinear control method of WTs on the condition parameters. Moreover, the upward trend in Figure 17 was more apparent than that in Figure 16; therefore, the average residual and the RMSE illustrated the validity of the method. Moreover, the RMSE-based detection method was effective in eliminating the disturbance and accurately judging condition degradation.
Residuals around the 8000th point in Figure 15, as well as average residual, and RMSE around the 56th day in Figures 16 and 17 exhibited greater difference compared with the previous results of the model. The condition of temperature parameter of generator bearing B can be judged approximately 16 days in advance, thus verifying the early warning time mentioned earlier.
From the model for the temperature parameter of the gearbox output shaft and the model for the temperature parameter of generator bearing B, the conclusion was drawn that the models of different parameters have different thresholds for judging the condition.
7. Conclusions
In this work, SCADA data from a wind farm are used to study the methods of condition parameters modeling and anomaly detection of WTs. The results and analysis can be summarized as follows:
- (1)
Appropriate parameters are determined for modeling. A reasonable wind speed range of monitoring data is obtained by analyzing the characteristics of the SCADA data from the wind farm.
- (2)
A neural network algorithm is adopted for automatic parameter selection, and the parameter selection method is proposed by using the temperature of generator bearing B as an example. The parameter selection method could effectively simplify the structure of the model.
- (3)
A comparative study of the anomaly detection method based on the average residual and the RMSE is made with the model, which illustrates that the RMSE-based anomaly detection method is more advantageous.
- (4)
The output of automatic parameter selection based model is consistent with the observed values. The results of the RMSE-based anomaly detection method could correctly reflect parameter anomalies.
The findings of this work can provide technical reference values for online monitoring, early warning, and condition-based maintenance of WTs.
Acknowledgments
The authors acknowledge the funding of the 973 Program (No. 2012CB215205). The work was supported in part by Specialized Research Fund for the Doctoral Program of Higher Education of China (SRFDP) (20110191130004) and the visiting scholar fund of State Key Lab of Power Transmission Equipment and System Security (SKLPES), Chongqing University, China. The National Natural Science Foundation of China (No. 51021005) and the 111 Project of the Ministry of Education, China (B08036) are also appreciated.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yang, W.X.; Court, R.; Jiang, J.S. Wind turbine condition monitoring by the approach of SCADA data analysis. Renew. Energy 2013, 53, 365–376. [Google Scholar]
- Charlotte, B.H.; Leif, R.; Alfredo, P.; Leo, E.J.; Pierre-Elouan, R. Wind Farm Wake: The Horns Rev Photo Case. Energies 2013, 6, 696–716. [Google Scholar]
- Kusiak, A.; Verma, A. A Data-Driven Approach for Monitoring Blade Pitch Faults in Wind Turbines. IEEE Trans. Sustain Energy 2011, 2, 87–96. [Google Scholar]
- Guo, P.; Infield, D. Wind Turbine Tower Vibration Modeling and Monitoring by the Nonlinear State Estimation Technique. Energies 2012, 5, 5279–5293. [Google Scholar]
- Li, H.; Hu, Y.G.; Chen, Z.; Ji, H.T.; Zhao, B. An improved fuzzy synthetic condition assessment of a wind turbine generator system. Int. J. Electr. Power Energy Syst. 2013, 45, 468–476. [Google Scholar]
- Kusiak, A.; Verma, A. Analyzing bearing faults in wind turbines: A data-mining approach. Renew. Energy 2012, 48, 110–116. [Google Scholar]
- Kusiak, A.; Li, W.Y. Virtual models for prediction of wind turbine parameters. IEEE Trans. Energy Convers. 2010, 25, 245–252. [Google Scholar]
- Zaher, A.; McArthur, S.D.J.; Infield, D.G.; Patel, Y. Online wind turbine fault detection through automated SCADA data analysis. Wind Energy 2009, 12, 574–593. [Google Scholar]
- Edzel, L.; Dustin, B.; Hossein, D.A.; David, S.; Jay, L. Wind turbine performance assessment using multi-regime modeling approach. Renew. Energy 2012, 45, 86–95. [Google Scholar]
- Mari, C.G.; Miguel, A.S.; Javier, P. SIMAP: Intelligent System for Predictive Maintenance: Application to the health condition monitoring of a wind turbine gearbox. Comput. Ind. 2006, 57, 552–568. [Google Scholar]
- Xiang, J.P.; Watson, S.; Liu, Y.Q. Smart monitoring of wind turbines using neural networks. Proceedings of the International Conference in Sustainability in Energy and Buildings, Brighton, UK, 29 April–1 May 2009.
- Schlechtingen, M.; Ferreira Santos, I. Comparative analysis of neural network and regression based condition monitoring approaches for wind turbine fault detection. Mech. Syst. Signal Process. 2011, 25, 1849–1875. [Google Scholar]
- IEC International Standard. IEC61400-12-1 Wind turbines–Part 12-1: Power Performance Measurements of Electricity Producing Wind Turbines; IEC: Geneva, Switzerland, 2005. [Google Scholar]
- Shi, Z.Z. Neural Networks; Higher Education Press: Beijing, China, 2009. [Google Scholar]
- Shi, Y.; Han, L.Q.; Lian, X.Q. Neural Nework Design Method and Case Study; Beuing University of Posts and Telecommunications Press: Beijing, China, 2009. [Google Scholar]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection: A survey. ACM Comput. Surv. 2009, 41, 15:1–15:58. [Google Scholar]
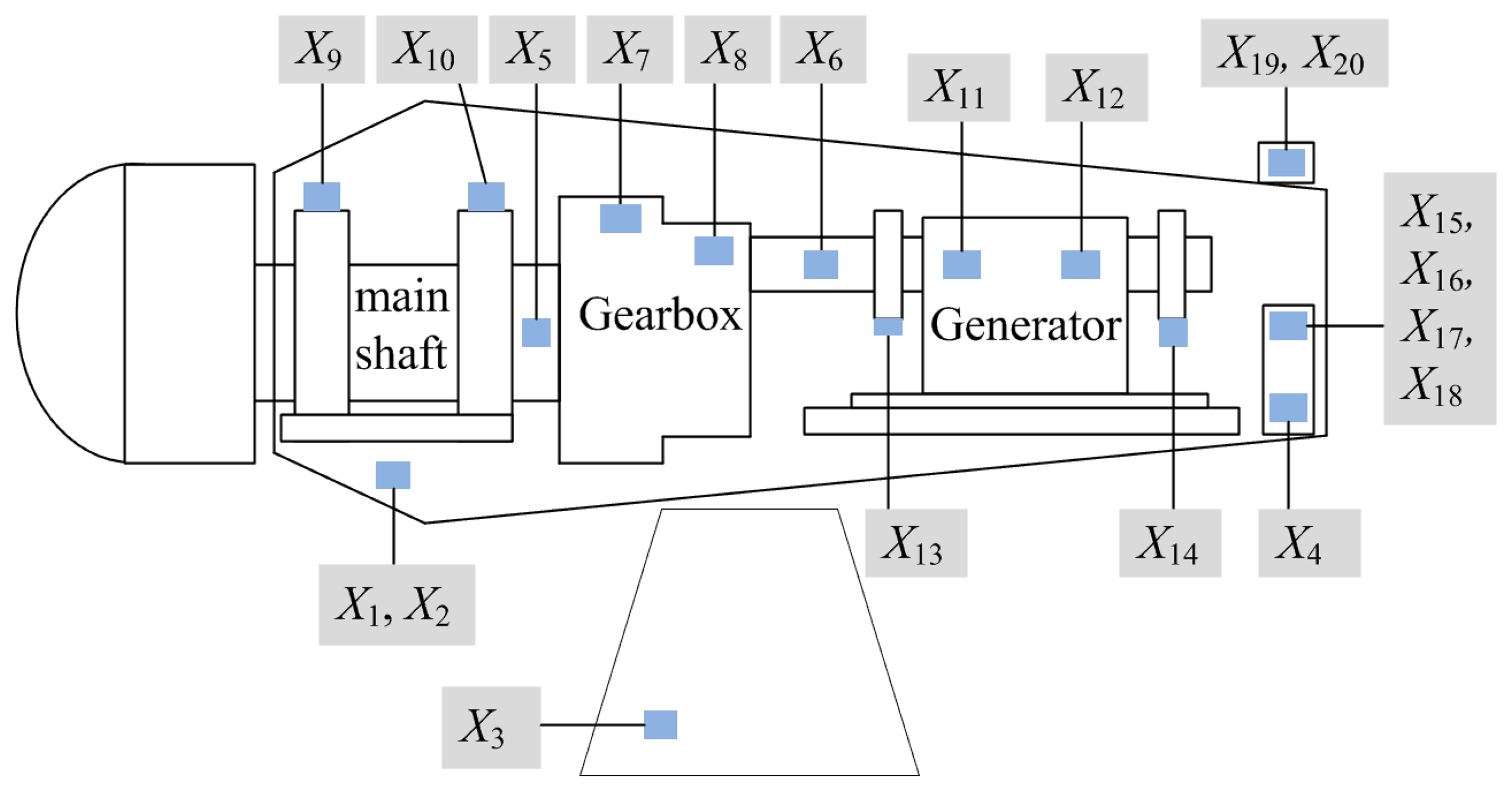







| Monitoring unit | Parameter | Description | Modeling or not |
|---|---|---|---|
| Nacelle | X1 | Nacelle vibration along X direction | No |
| X2 | Nacelle vibration along Y direction | No | |
| X3 | Temperature of base cabinet | Yes | |
| X4 | Temperature of top cabinet | Yes | |
| Gearbox | X5 | Temperature of input shaft | Yes |
| X6 | Temperature of output shaft | Yes | |
| X7 | Temperature of inlet oil | Yes | |
| X8 | Temperature of oil | Yes | |
| Bearing of main shaft | X9 | Temperature of rotor-side bearing | Yes |
| X10 | Temperature of gearbox-side bearing | Yes | |
| Generator | X11 | Temperature of winding | Yes |
| X12 | Temperature of cooling air | Yes | |
| X13 | Temperature of bearing A | Yes | |
| X14 | Temperature of bearing B | Yes | |
| Grid factors | X15 | Phase voltage | No |
| X16 | Phase current | No | |
| X17 | Active power | Yes | |
| X18 | Reactive power | No | |
| Environment factors | X19 | Wind speed | No |
| X20 | Temperature of ambient | No | |
| No. | Parameters | Average error | RMSE | |
|---|---|---|---|---|
| 1 | Phase voltage X15 | +5% | 0.0519 | 2.5363 |
| −5% | −0.3212 | 2.3748 | ||
| 2 | Temperature of output shaft X6 | +5% | −0.2040 | 2.2950 |
| −5% | 0.3330 | 2.5846 | ||
| 3 | Temperature of oil X8 | +5% | −0.3575 | 2.4915 |
| −5% | 0.2956 | 2.2599 | ||
| 4 | Temperature of bearing A X13 | +5% | −1.0219 | 2.2858 |
| −5% | 0.9809 | 2.2690 | ||
| 5 | Temperature of input shaft X5 | +5% | 0.0638 | 2.2428 |
| −5% | −0.0268 | 2.1590 | ||
| 6 | Temperature of top cabinet X4 | +5% | 0.7206 | 2.0841 |
| −5% | −0.8631 | 2.2222 | ||
| 7 | Temperature of winding X11 | +5% | −1.0278 | 2.1577 |
| −5% | 0.8946 | 2.1073 | ||
| 8 | Temperature of gearbox–side bearing X10 | +5% | −0.2745 | 2.1546 |
| −5% | 0.1743 | 2.0624 | ||
| 9 | Temperature of rotor–side bearing X9 | +5% | −0.2031 | 2.0581 |
| −5% | 0.0694 | 2.1309 | ||
| 10 | Temperature of cooling air X12 | +5% | 0.0690 | 1.9859 |
| −5% | −0.0850 | 1.9977 | ||
| 11 | Temperature of base cabinet X3 | +5% | −0.3296 | 1.9135 |
| −5% | 0.2301 | 1.8659 | ||
| 12 | Temperature of inlet oil X7 | +5% | 0.2204 | 1.8679 |
| −5% | −0.3223 | 1.9051 | ||
| 13 | Active power X17 | +5% | −0.0108 | 1.8538 |
| −5% | −0.0447 | 1.8698 | ||
| 14 | Temperature of ambient X20 | +5% | −0.0226 | 1.8416 |
| −5% | −0.0623 | 1.8607 | ||
| 15 | Phase current X16 | +5% | −0.0339 | 1.8572 |
| −5% | −0.0376 | 1.8403 | ||
| 16 | Wind speed X19 | +5% | −0.0148 | 1.8219 |
| −5% | −0.0459 | 1.8177 | ||
| 17 | Reactive power X18 | +5% | −0.0263 | 1.8193 |
| −5% | −0.0345 | 1.8190 | ||
| 18 | Nacelle vibration along X direction X1 | +5% | −0.0297 | 1.8192 |
| −5% | −0.0308 | 1.8190 | ||
| 19 | Nacelle vibration along Y direction X2 | +5% | −0.0311 | 1.8192 |
| −5% | −0.0294 | 1.8189 | ||
| Parameters | Threshold |
|---|---|
| Temperature of base cabinet X3 | 2.3 °C |
| Temperature of top cabinet X4 | 2.1 °C |
| Temperature of input shaft X5 | 1.5 °C |
| Temperature of output shaft X6 | 1.3 °C |
| Temperature of inlet oil X7 | 1.7 °C |
| Temperature of oil X8 | 2.0 °C |
| Temperature of rotor-side bearing X9 | 2.3 °C |
| Temperature of gearbox-side bearing X10 | 2.1 °C |
| Temperature of winding X11 | 1.2 °C |
| Temperature of cooling air X12 | 1.9 °C |
| Temperature of bearing A X13 | 1.8 °C |
| Temperature of bearing B X14 | 2.2 °C |
| Active power X17 | 60.02 kW |
| No. | Parameters | Average error | RMSE | |
|---|---|---|---|---|
| 1 | Temperature of input shaft X5 | +5% | −3.2198 | 3.5499 |
| −5% | 3.3400 | 3.7244 | ||
| 2 | Temperature of oil X8 | +5% | 0.4570 | 1.2283 |
| −5% | −0.4076 | 1.2070 | ||
| 3 | Temperature of inlet oil X7 | +5% | 0.1690 | 1.0884 |
| −5% | −0.1720 | 1.0308 | ||
| 4 | Phase voltage X15 | +5% | 0.0445 | 1.0122 |
| −5% | −0.0913 | 1.0131 | ||
| 5 | Temperature of gearbox–side bearing X10 | +5% | 0.2463 | 1.0065 |
| −5% | −0.0266 | 0.9626 | ||
| 6 | Temperature of rotor–side bearing X9 | +5% | 0.0784 | 0.9459 |
| −5% | 0.0739 | 0.9440 | ||
| 7 | Temperature of cooling air X12 | +5% | −0.0111 | 0.9161 |
| −5% | 0.0405 | 0.9156 | ||
| 8 | Temperature of bearing B X14 | +5% | −0.0170 | 0.9169 |
| −5% | 0.0407 | 0.9090 | ||
| 9 | Active power X17 | +5% | 0.0299 | 0.9177 |
| −5% | 0.0402 | 0.9043 | ||
| 10 | Temperature of top cabinet X4 | +5% | 0.0716 | 0.9148 |
| −5% | −0.0495 | 0.9061 | ||
| 11 | Phase current X16 | +5% | 0.0189 | 0.9033 |
| −5% | 0.0434 | 0.9128 | ||
| 12 | Temperature of winding X11 | +5% | 0.0438 | 0.9067 |
| −5% | −0.0043 | 0.9060 | ||
| 13 | Temperature of bearing A X13 | +5% | 0.0336 | 0.9041 |
| −5% | −0.0067 | 0.9081 | ||
| 14 | Temperature of ambient X20 | +5% | −0.0233 | 0.8976 |
| −5% | 0.0576 | 0.9077 | ||
| 15 | Temperature of base cabinet X3 | +5% | 0.0179 | 0.8986 |
| −5% | 0.0164 | 0.8978 | ||
| 16 | Wind speed X19 | +5% | 0.0177 | 0.8981 |
| −5% | 0.0169 | 0.8974 | ||
| 17 | Nacelle vibration along X direction X1 | +5% | 0.0165 | 0.8978 |
| −5% | 0.0178 | 0.8975 | ||
| 18 | Nacelle vibration along Y direction X2 | +5% | 0.0186 | 0.8981 |
| −5% | 0.0157 | 0.8972 | ||
| 19 | Reactive power X18 | +5% | 0.0215 | 0.8971 |
| −5% | 0.0122 | 0.8979 | ||
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Yan, Y.; Li, J.; Gao, D.W. Condition Parameter Modeling for Anomaly Detection in Wind Turbines. Energies 2014, 7, 3104-3120. https://doi.org/10.3390/en7053104
Yan Y, Li J, Gao DW. Condition Parameter Modeling for Anomaly Detection in Wind Turbines. Energies. 2014; 7(5):3104-3120. https://doi.org/10.3390/en7053104
Chicago/Turabian StyleYan, Yonglong, Jian Li, and David Wenzhong Gao. 2014. "Condition Parameter Modeling for Anomaly Detection in Wind Turbines" Energies 7, no. 5: 3104-3120. https://doi.org/10.3390/en7053104





