A Simulation Framework for Optimal Energy Storage Sizing
Abstract
: Despite the increasing interest in Energy Storage Systems (ESS), quantification of their technical and economical benefits remains a challenge. To assess the use of ESS, a simulation approach for ESS optimal sizing is presented. The algorithm is based on an adapted Unit Commitment, including ESS operational constraints, and the use of high performance computing (HPC). Multiple short-term simulations are carried out within a multiple year horizon. Evaluation is performed for Chile's Northern Interconnected Power System (SING). The authors show that a single year evaluation could lead to sub-optimal results when evaluating optimal ESS size. Hence, it is advisable to perform long-term evaluations of ESS. Additionally, the importance of detailed simulation for adequate assessment of ESS contributions and to fully capture storage value is also discussed. Furthermore, the robustness of the optimal sizing approach is evaluated by means of a sensitivity analyses. The results suggest that regulatory frameworks should recognize multiple value streams from storage in order to encourage greater ESS integration.1. Introduction
Energy targets and support policies have acted as a driving force in the increased adoption of renewable energy. Furthermore, it is expected that the share of electricity generation from variable renewables—such as wind, photovoltaic, tidal and wave power—will continue to increase rapidly [1]. It is foreseen that the increased integration of variable and partially dispatchable energy sources will call for greater flexibility in the operation and planning of power systems [2]. Options such as demand-side management, improved forecasting, cross-border interconnection and Energy Storage Systems (ESS) have been identified as a promising alternatives for addressing current and future challenges posed by large scale incorporation of variable renewables [3–6].
ESS are suitable for several applications to support integration of renewable energy. In [5,6] authors presented an extensive updated review of storage technologies, focusing on their appropriateness for different applications. Pump Hydro Storage (PHS), Compressed Air Energy Storage Systems (CAES), and Lithium-ion and Flow batteries appear to be the most suitable technologies for bulk applications, with longer-term storage capacities ranging from hours to days.
Despite increasing interest in ESS, quantification of the technical and economic benefits for each application remains a challenge and major barrier to their acceptance and development of ESS [4]. There is a broad consensus that ESS can enhance grid performance and security. However, there is uncertainty in the optimal sizing of the storage units from the standpoint of overall economic efficiency. Several approaches [7–17], detailed in Section 2, have been used to address this problem.
The particular challenge of assessing bulk ESS optimal size is to take into account for all the relevant factors. These can be divided into short and long-term effects. In the first cases, short-term, integration of ESS increases short-term system operation flexibility, permitting a greater participation of renewables, whilst also reducing impacts on conventional power plants. Economic assessments of such effects is carried out using realistic and detailed short-term simulations, characterizing the charging-discharging process and the impacts on the rest of the system. Technical operational constraints and intraday power variability modeling for renewable resources are necessary to accurately understand the benefits, which are included in the Unit Commitment (UC) formulation [16]. Additionally, because of load and the nature of renewable energy, it is essential to internalize yearly seasonal patterns, which may show large fluctuations throughout the year depending on the particular system under evaluation.
At the same time, the contributions of ESS to power systems may also vary from one year to another. The development of the electricity sector (electricity demand, generation mix according to renewable energy targets, and fuel costs) will play a key role in their future contribution. The benefits of storage—and consequently its optimal size—therefore depend on the specific year evaluated, making a long-term horizon necessary. To determine the optimal ESS sizing, the balance of investment costs and the resulting savings on the system's operating costs should be calculated over a long-term horizon, which could range from five to thirty years, depending on the technology's lifespan. The system future development could also involve other initiatives such as demand-side management, improved forecasting, cross-border interconnections or flexible generating technologies (hydro o natural gas units) that may impact its flexibility. Such initiatives would also affect the future contribution of ESS and a long-term evaluation, therefore, needs to be considered.
Moreover, since storage can simultaneously provide multiple services, different value streams must be taken into account in order to accurately estimate the potential benefits of ESS. In this case, the control strategies evaluated must reflect storage limitations to provide multiple services. The joint provision of different services (co-optimization) can be expected to yield a better return on investment than single-purpose use, thereby increasing the value of the ESS.
The contribution of the present work comprises a simulation approach to optimal ESS sizing, based on an adapted Unit Commitment formulation that includes ESS operational constraints [18] and the use of high performance computing (HPC) in order to perform detailed short-term system operation simulations over a multiple year horizon. The proposed methodology permits analysis of the key technical challenges and impacts of including ESS in short-term operation as well as its contribution in the long-term, striking a balance between detailed modeling and trackable solution times.
It demonstrates the importance of long-term evaluations rather than current state-of-the-art approaches, which consider a single year when determining optimal ESS sizing. A realistic test-bed is used to determine optimal storage size for the Chile's Northern Interconnected Power System (SING). Additionally, it is shown that optimal size depends on the services provided by the ESS, such as primary, and secondary reserves, and energy arbitrage. Recognition of multiple value streams for storage increases its economic value, and therefore, encourages greater integration of ESS into the grid.
The paper is organized as follows: Section 2 presents a review of existing approaches to optimal ESS sizing. The proposed evaluation framework is presented in Section 3, and the results of computational simulation are presented and discussed in Section 4. Finally, Section 5 sets out the conclusions of this work.
2. Approaches to Optimal ESS Sizing
Different approaches to assessing the value of ESS and determining optimal size—rated power and energy—in a given system can be found in the literature. Endogenous models that optimize ESS size are found in [7–10]. In [7], Brown et al. studied the sizing of a PHS for energy arbitrage in a small isolated system. This model takes daily and seasonal variability into account using hourly steps and a set of “typical days” or representative scenarios. Its results showed that the value of storage and, therefore, optimal size depend on the system's security criteria, indicating that inclusion of operational constraints would result in different ESS sizes. In [8], an Optimal Power Flow (OPF) framework is proposed in order to include locational aspects. Time slices are defined to reduce the size of the problem and simplifications of the units' constraints and flexibility are considered. This evaluation does not take into account load or future system expansion during the period. Carpinelli et al. [9] analyzed optimal ESS sizing in an industrial facility's electricity distribution system, applying decision theory (min-max regret, stability areas and expected cost minimization) to determine the best alternative. This approach assumes future electricity prices as an exogenous parameter, and simulations are carried out just for one day of operation. Investment in CAES along with the plan for expansion of the German system through 2020 is studied in [10] by using a linear electricity market model. The Effects of different penetration levels in the generation mix were shown.
On the other hand, simulation approaches to studying the value and the optimal sizing of storage can be found in [10–14]. In [12] the authors use a stochastic optimization approach to evaluate the convenience of energy storage as a means of reducing the final cost of energy and to define the corresponding optimal rating of the storage devices. The value of a PHS in the 2020 Irish system is studied in [10]. A chronological simulation of the system is performed using a stochastic rolling planning model. The study considers different storage capacities and different wind penetration levels, concluding that the value of storage strongly depends on these aspects. Similarly, the benefits of different storage technologies for the Dutch system are studied in [12]. In [14], Zhang et al. evaluate optimal PHS size for the Jiangsu power system, using a chronological approach to simulate system operation for a year with hourly resolution. Multiple PHS sizes are considered. By comparing the total cost for each case, the optimal PHS was selected. In [17] the authors present a stochastic framework for optimal sizing of storage capacity along with renewable resources for an isolated system, subject to pre-defined reliability levels. Sequential Monte Carlo simulations in conjunction with pattern search algorithms are used, which are suitable for short-term operation system operation representation A single year horizon is used and fixed values are assumed for investment costs. In this approach, there is no trade-off evaluation of load curtailment, as no economic value is assumed in the optimization, so results are conditioned to the reliability index selected. In other approaches [15], authors use the Fourier transformation to determine the maximum feasible storage size, but, since they do not use cost models, fail to determine the optimal ESS size.
In order to carry out a detailed assessment of the feasibility, reliability, and economics of including ESS in the power system operation, some authors have proposed a detailed chronological simulation approach on a daily basis (365 UCs) with a resolution of one hour [14]. As mentioned above, the development of the electricity sector over subsequent years plays a key role in the contribution of ESS to the grid. In order to include long-term effects described above, chronological simulation approaches require intensive computing effort when evaluating multiple years, ESS sizes and services. In order to have traceable solution times, previous authors have simplified the scheduling model by using linear constraints or/and making use of fewer time periods [8,10]. Similarly, others studies have shown the importance of short-term constraints in ESS value determination [7].
3. Evaluation Framework for Optimal ESS Sizing
3.1. General Description
The evaluation framework presented in this paper uses HPC capabilities to run several UC simulations for multiple ESS configurations. By comparing the total investment and savings in operational costs for several ESS configurations and services, the optimal ESS size is determined.
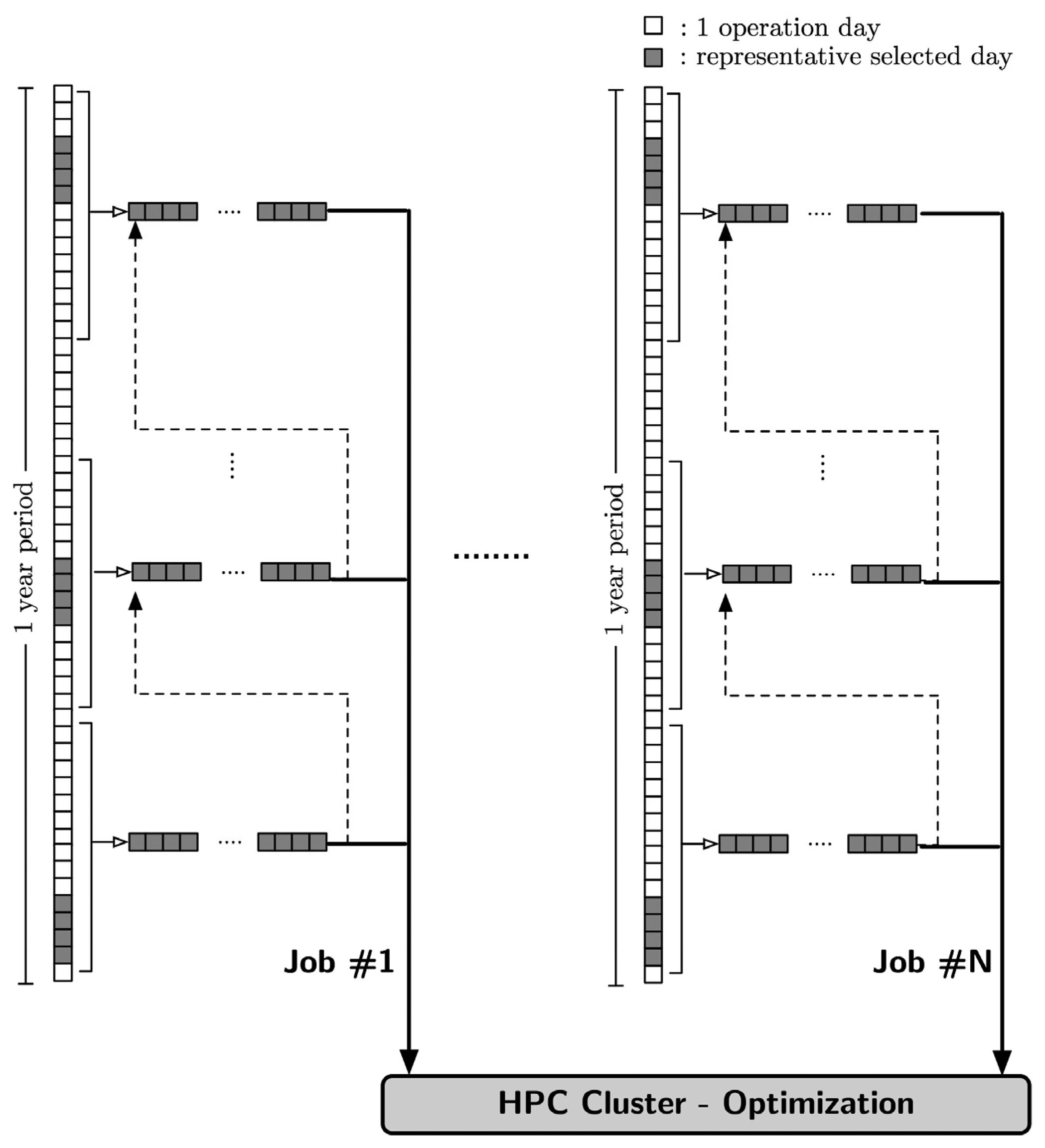
As shown above, none of the previous approaches has simultaneously addressed all the relevant aspects of evaluating optimal ESS size. In this paper, a simulation framework is presented in order to maintain detailed representation of short-term system operation over a long-term horizon whilst keeping solution times trackable. It considers UC simulations with an hourly resolution for selected representative days. Representative days are selected in such a way as to represent yearly operation, characterizing and summarizing the system's cycling pattern observed in demand and wind and solar radiation and to maintain representation of short-term operational characteristics. The aim is to achieve a trackable solution time whilst also extending the cases under analysis. The UC simulation includes inter-temporal units and technical constraints as well as system security constraints, permitting adequate representation of the ESS daily cycle as well as the seasonal and intra-day stochastic variability of renewable energy.
Similarly to [7], wind speed and solar radiation measurements, along with historic hourly system demand, are processed using hard-partitioning K-Medoids clustering analysis [19,20]. This results in a set of representative operating days, characterized by hourly system demand, wind and solar power plants' estimated hourly generation and generation units' maintenance schedule. The results obtained for selected representative days are weighted to characterize annual operating cost. This reduction seeks to approximate annual system operation, not by increasing the simulation time step—necessary to estimate the ESS daily cycle and represent hourly variability—but by reducing the number of daily UC simulations whilst reflecting short-term operational effects.
3.2. Mathematical Formulation of the Unit Commitment Model
The proposed UC model (1)–(23) minimizes the operation, start/stop, and unserved energy costs (1). The model is constrained to power supply balance (2), spinning and non-spinning reserves (3)–(9):
Subject to the following constraints:
Wind and solar spillage is considered explicitly in the model (3)–(4) and load shedding is allowed at a high Value of Lost Load (VOLL), in order to assure schedule feasibility. Demand side management has not been considered in the present formulation. Ramping constraints for thermal generators are included in (8) and (9). For the sake of simplicity, startup and shutdown flags are summarized in (10) and (11) respectively, along with other constraints such as minimum up and downtime constraints summarized in the subset Ω.
When incorporating ESS into the UC problem (14)–(25), it is necessary to incorporate power supply balance (2) charging (ct) and discharging (dt) process variables. Main technical constraints of storage are related to energy balance in the ESS (14), charging and discharging capacity limits (15)–(16), and also maximum and minimum levels of storage (17)–(18). The boundary condition is considered in (19):
In case that the ESS provides jointly energy arbitrage and spinning reserves, constraints (20)–(23) are needed:
The model assumes that the ESS is capable to change, in a short interval, between charge/discharge modes, so the ESS is able to participate in the provision of spinning reserves on a greater extent. Theoretically, the ESS may provide twice their power capacity for either up or down spinning reserve. Constraints (20) and (21) resume the ESS possibility to exploit this flexibility.
Since ESS has a limited energy capacity to provide these scheduled reserves if they are activated during real time operation, sufficient energy has to be stored to provide down reserves for over-frequency compensation. Likewise, during under-frequency events, a minimum energy level is required to provide up reserves. This is implemented by constraints (22) and (23) allowing ESS to cover worst-case foreseen deviations in every period.
The present model (1)–(23) guarantees that enough energy is available at the ESS in order to provide reserve services for a given charging/discharging pattern determined in the day-ahead market.
3.3. Long Term Evaluation and High Performance Computing
Due to computing capabilities, long-term system expansion planning has traditionally been carried out considering weekly or monthly intervals and load duration curve approximations, thereby losing the capability to model UC short-term operational constraints such as start-up costs, ramp rates and minimum up-and-down times [15,21–23]. ESS systems cannot be properly represented when the simulation time step is larger than ESS autonomy as well as the intra-day chronological operation in the case of using duration curves. For instance, in the case of short-term energy arbitrage, charge-discharge cycles occur within a day and cannot, therefore, be represented in weekly intervals. In a scenario of increasing variable generation, short-term constraints and the size of time steps are more significant. The system's flexibility—or lack of it—has to be taken into account in order to exploit the benefits of ESS under this new scenario.
Long-term system operation planning including short-term constraints and hourly resolution could result in prohibitive computing times. Therefore, it is a challenge to combine the necessary temporal granularity to accurately represent storage and short-term system operation—especially when evaluating short-term storage—and long-term expansion planning. These challenges for determining optimal storage size are addressed in the evaluation framework presented here by using representative days and HPC.
Figure 1 illustrates how UC simulations are carried out in the HPC infrastructure considering representative days as discussed above. The idea is to split a multiple-year horizon into single-year optimization. UC simulation for a given year is performed in a separated node of the HPC cluster, for each representative day consecutively. This permits solving short-term operation schedule for multiple years in parallel, whilst maintaining an acceptable solution time.
Using the proposed methodology it is possible to carry out the analysis of different scenarios in a reasonable period of time while considering: different ESS configurations (rated power, storage capacity, technologies and services) and performing several sensitivity analyses that include different renewable energy targets, future generation mix, and the long-term fuel price outlook.
3.4. Proposed Methodology
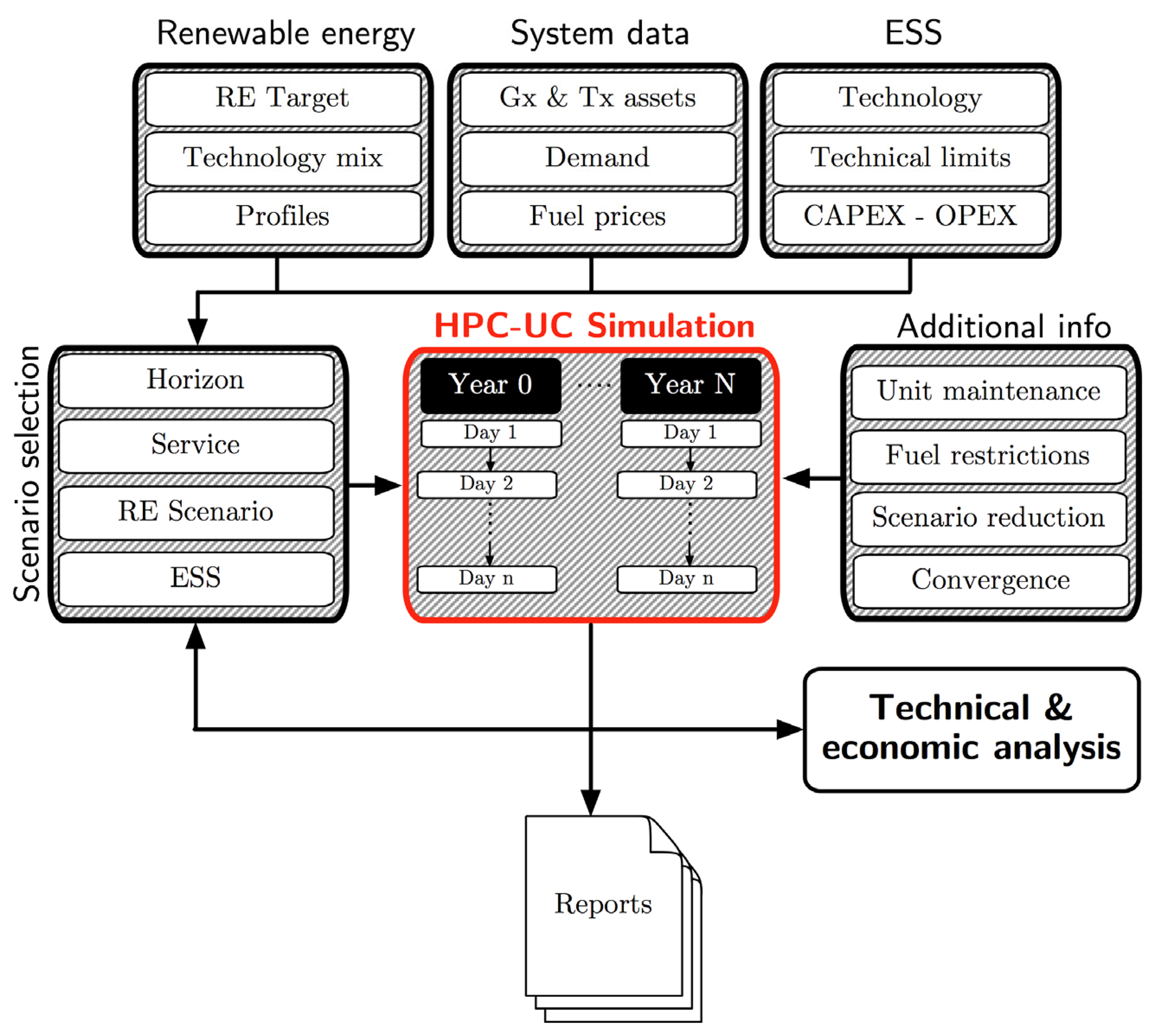
The evaluation framework used in this paper to determine optimal sizing of ESS in a particular power system is illustrated in Figure 2.
The proposed methodology can be summarized as follows:
- Step 1.
An expansion plan for the system is determined, including generation mix for each year, future fuel costs and system demand growth. Size—energy and power—and service provision for the ESS are evaluated.
- Step 2.
For each year, scenarios of hourly wind energy, solar energy, energy demand, and generation units maintenance programs are generated, based on historical data and clustering. This is carried out according to installed capacity depending on the generation mix for that year. The energy demand is scaled every according to expected annual energy growth.
UC simulations are performed for all the representative scenarios using HPC according to the methodology illustrated in Figure 1. Every operating year is optimized in a single computer node of the HPC infrastructure, solving UC for representative days on a rolling basis; the solution of a representative day i is used as the initial condition for the next consecutive representative day, i + 1.
- Step 3.
Steps 2 and 3 are repeated for each year of the evaluation horizon.
- Step 4.
Steps 1–4 are repeated for several ESS sizes and services (energy arbitrage, primary and secondary reserve). Different expansion plans and fuel costs can also be incorporated for particular sensitivities in order to explore the robustness of the decision.
- Step 5.
A summary of total ESS investment and system operating costs is drawn up for every ESS size and service under analysis.
This framework permits simultaneous analysis of different scenarios, depending on the available nodes of the HPC cluster, thereby facilitating determination of optimal ESS sizing. This approach can be used directly in thermal systems since operation in a given year does not impact operation in the following year. In the case of hydrothermal systems, where operation for several years is bundled, a considerable increase in computing time can be expected. However, an HPC approach is still suitable in this case, contributing to detailed analysis of ESS integration.
The benefits of including ESS in the power system operation are determined by means of a trade-off analysis. Investment costs are compared to a reduction in operational costs in the long-term (a 10 years evaluation period). The UC formulations (1)–(23) presented in Section 3.2 takes into account the main costs of real time operation, such as variable operation costs, start-up and shut-down costs, primary, secondary and tertiary requirement fulfillment, while considering technical constraints for generating units such as minimum up-time and minimum down-time for thermal units (Coal and CCGT units), among other considerations. Additional constraints are considered to include ESS into the UC problem while accounting for their technical constraints to jointly provide energy arbitrage and reserves. More details can be found in [18]. The number of cycles that an ESS can do before failing has not been considered in this work.
The proposed methodology can be improved through the usage of traditional derivate-based optimization, surface response approaches or by implementing other type of algorithms to avoid exploring the entire spectrum of energy/power configuration for ESS. Nevertheless, HPC infrastructure enabled the evaluation of a large range of configurations without compromising solution time. In any case, it is important to remark that global optimal solution cannot be guaranteed, only local optimal values where founded in all study cases.
As stated, the total investment costs and operational savings are crucial factors for optimal ESS sizing. In this way, ESS configuration is selected through maximization of social welfare understood as balance of investment cost and consequent savings in operational costs. In every case, annuity of investment cost and operational savings are included to determine the net present value of the cash flow considering a rate of discount of 10%.
3.5. The Levque Cluster
The HPC infrastructure used for this study is part of the Center for Mathematical Modeling (CMM) and comprises 66 nodes, each equipped with two quad-core Intel Xeon X5550 processors running at 2.67 GHz (each computer node has eight physical cores) and 24 GB RAM [24]. The UC model is based on mixed integer programming and was implemented using Java and solved using CPLEX 12.1 with a MIP gap of 0.1%.
4. Results
4.1. Realistic Case Study
Computational simulations were carried out for the SING which is a thermal isolated system and a centralized cost-based market. In 2012, the SING had a peak load of 2167 MW and energy generation was divided into coal (82%), natural gas (14%) and diesel (3%), with hydro and cogeneration accounting for the other 1%. Coal units exhibit large up/down time and a high minimum stable operating point, without cross-border interconnections. In the SING, there are also a larger number of diesel/fuel-oil units, incorporated in response to past uncertainty about fuel availability. Currently, the grid has two lithium-ion storage plants, totaling 32 MW, which were developed by A123 Systems. They are designed to maintain output for 15 minutes and provide primary reserve to support system frequency control [25].
Since mining companies account for 90% of electricity demand in the SING, its demand profile is unusually flat, with only small differences between peak and off-peak hours. Moreover, since no wind or solar power generation as yet exists, intra-day variability is low. In the following years, and mainly due to increasing number of mining processes in the area, the SING demand is expected to grow by 4% to 8% per year [26].
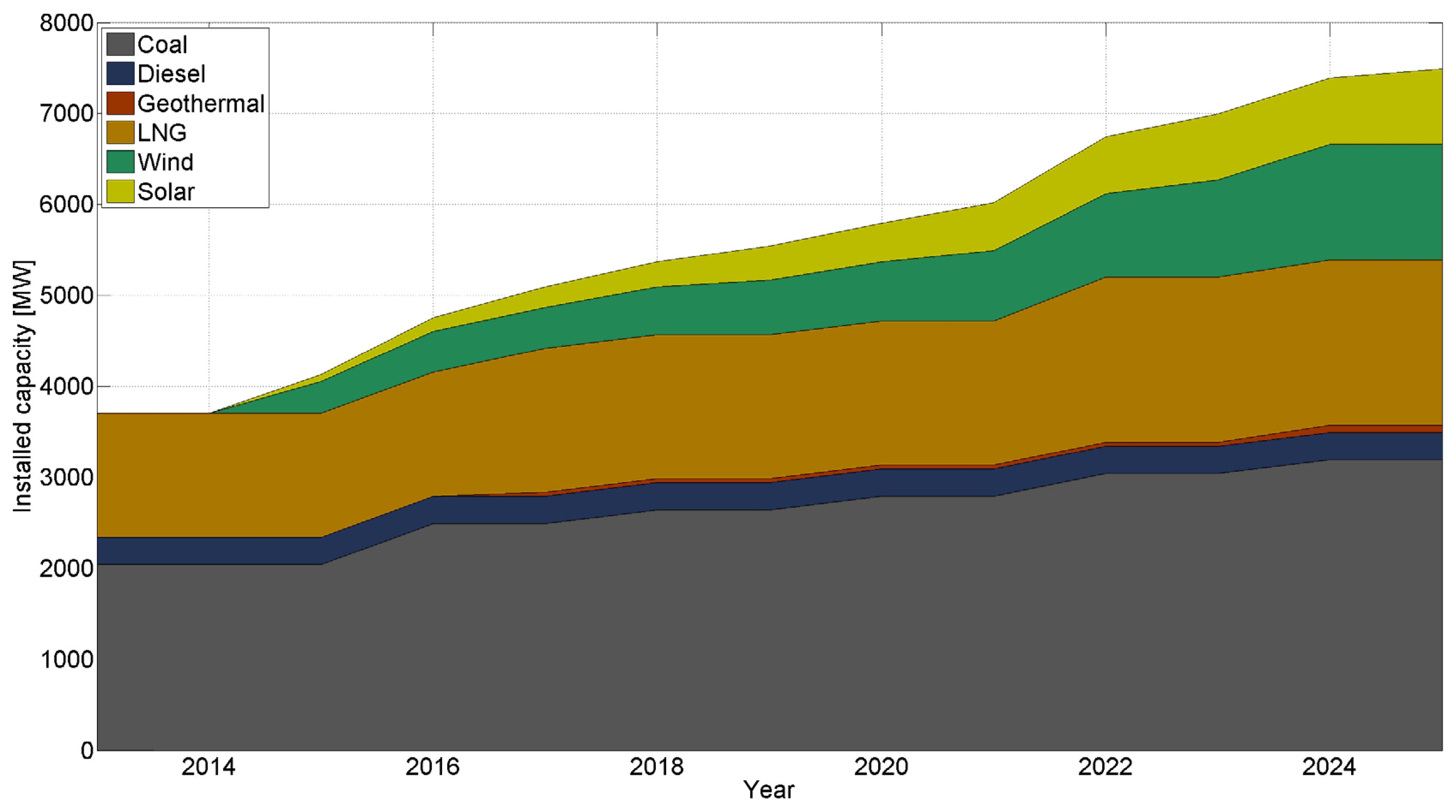
Chile is debating renewable targets in order to reduce carbon emissions, aiming for a renewable portfolio standard of 20% by 2024. The SING is, moreover, in a geographical area with exceptional solar radiation, windy areas and nearby geothermal reservoirs. Over the coming years, renewable energies are, therefore, expected to become an important part of its matrix, as illustrated in Figure 3. Following the increase in deployment of renewable energy, an unprecedented variability and uncertainty in real time operation is expected in the SING in the coming years. Such increase in the usage of renewable sources is justified due to the decrease in the investment cost and national support through renewable portfolio standard obligation [27].
Since the generation sector is considered as a competitive market in Chile, future generation mixes cannot be assured for the following years. From all the eligible technologies that can be incorporated into the SING, the generation companies will invest in those that result to be more competitive to supply demand. This work considered two feasible scenarios for the future generation mix: 10% of renewables by 2024 or 20% of renewables by 2024 [28]. The case study also considers unit maintenance, fuel constraint, fuel price projections and wind/solar patterns for incoming facilities, using public data from technical studies requested by the Ministry of Energy [29].
4.2. Performance Evaluation
For the particular case analyzed here, a total of 108 representative days were used to approximate 365 operating days. The clustering was performed following the presented methodology, considering 36 consecutive days. Each year was split into three seasons: summer, fall-winter and spring, permitting characterization of the seasonal behavior of wind speed and solar radiation in the region. The Atacama Desert has the planet's highest level of solar radiation, with very predictable resources, so solar power profiles are considered deterministic, seasonally variable and uniform throughout the region.
The period used to assess the benefits of incorporation of ESS in the SING is from 2020 (when ESS is assumed to be installed) through to 2030. ESS integration in short-term operation planning is analyzed for three kinds of services—primary and secondary reserve provision and energy arbitrage—which are integrated into the UC formulation following [18] implemented in AMEBA. To maximize the contribution of storage into the power system operation multiple value streams from ESS are included in the evaluation. Energy arbitrage and provision of secondary spinning reserve are then jointly evaluated for different configurations of rated power and storage capacity.
The results presented below summarize more than 260,000 optimizations carried out for different ESS configurations, services and renewable energy targets. The optimal ESS configuration is selected by maximizing social welfare defined as the balance of investment outlay and the resulting savings on operating costs. An evaluation of investment costs for each particular ESS configuration is discussed in order to make the methodology suitable for different ESS technologies.
4.3. Primary Reserve Evaluation
Spinning reserve provision by generating units entails its partial loading, in order to compensate for shortfalls/surpluses in generation/demand and maintain system frequency in a specified band. ESS reserve provision permits the shift of generators' unloaded spare capacity to energy production, increasing overall system efficiency. This is, in fact, the case of the two existing ESS systems in the SING, installed for the provision of primary reserve.
To study the benefits of ESS for this purpose, eight cases of power capacity—10, 20, 30, 40, 50, 60, 70 and 80 MW—are studied. According to current SING security standards, primary reserves must be deployed within ten seconds of a disturbance in frequency, and maintained for a maximum of twenty minutes. This determines the minimum MWh storage capacity needed in each case, depending on the rated power installed.
Figure 4 sets out the results obtained for reductions in annual operating costs for the case of primary reserve. As shown, cost reductions depend on the year under evaluation since development of the entire system changes from year to year. The results, therefore, support the hypothesis that multiple-year analysis is required in order to accurately determine the benefits of ESS integration into power systems. As illustrated, savings on operating costs tend to decline since additional capacity of conventional units (coal and gas fired, according to Figure 3) increases the availability of reserves for primary frequency control, reducing the value of storage for primary reserve provision.
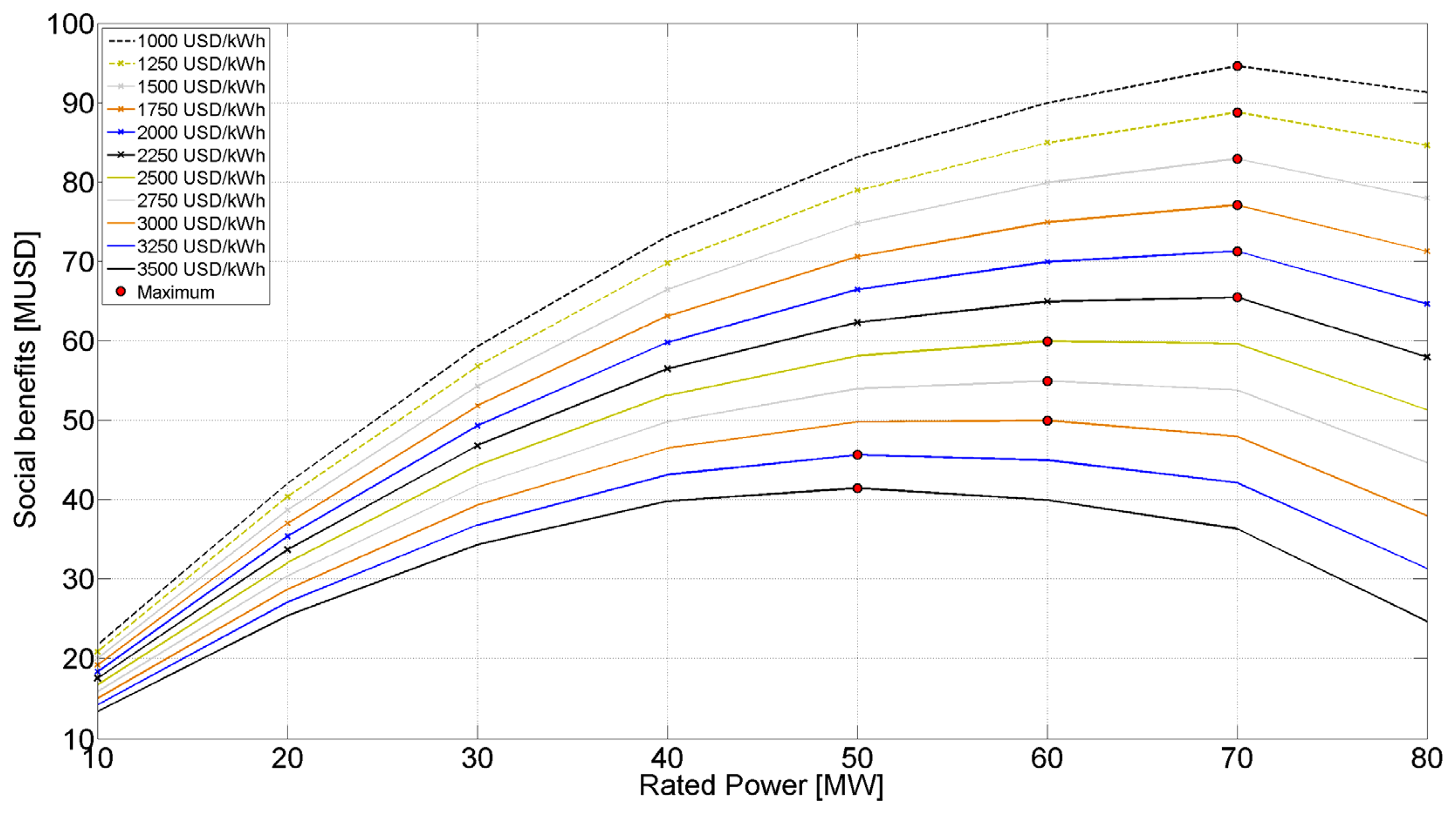
In order to evaluate the optimal ESS size for providing primary reserve, the net social benefit is calculated as cost savings minus investment outlay. A 10% discount rate and a life expectancy of ten years are assumed, the latter as an average value for technologies such as Li-ion or NaS [5,6] suitable for this purpose. Figure 5 shows the net benefit in millions of US dollars (MUSD) for different investment costs (USD/kWh).
For the sake of simplicity in presenting the results, the investment cost of power capacity is assumed fixed at 400 USD/kW, and no assumptions are made about the relationship in between power and energy capacities as expected in some chemical batteries. The cost of providing primary reserve and satisfying the technical requirements for deploying and maintaining the response in MW for 20 min is obtained as follows:
In Figure 5 it can be seen that for a given investment cost, there is an optimal size that maximizes the net benefit. For instance, the results indicate that for investment costs of up to 2250 USD/kWh, the optimal size is 70 MW. For higher costs, the optimal size for ESS to provide primary reserve is smaller—as expected—yet non-zero. Considering the current technologies costs [5,6] these results indicate, for ESS technologies to become an efficient and attractive alternative for providing primary reserves in the SING, the price threshold is high. This means that technologies such as Li-ion batteries are suitable in technical and economic terms for installation in the SING to provide primary reserve.
For a given ESS technology with a fixed power to energy relationship, it is still possible to evaluate their optimal size by obtaining the equivalent cost. For instance, for current primary reserve requirements of 20 min at rated power, a power-to-energy ratio of three is needed. If a given battery chemistry with a cost of 1500 USD/kWh has a ratio of six, this means that its rated power can only be maintained for ten minutes. Thus, the ESS should be dimensioned with twice the capacity, giving an equivalent cost of 3000 USD/kWh. With this correction, according to Figure 5, the optimal size would be 60 MW not 70 MW.
It is important to note that the range of benefits—0.2% to 1.4%—is greater than the solver tolerance used in this work for mixed integer optimizations (MIP gap). This is crucial in order to obtain a reliable estimate of such a small difference in operating costs. Using an optimization model that solves larger but simplified problems calls for the relaxation of the MIP gap in order to maintain practical execution times. In contrast, the use of a simulation approach based on HPC allows the use of greater modeling detail, as well as a smaller MIP gap solver tolerance. In any case, is important to maintain a MIP gap smaller than reductions in operating costs (in percentage terms) to preserve confidence in the results.
4.4. Energy Arbitrage and Secondary Reserve Evaluation
Joint provision of energy arbitrage and ancillary services is also studied. In this case, the evaluation considers six power capacities (50, 100, 150, 200, 250 and 300 MW) with storage capacity ranging from one hr to twelve hrs. Since evaluation focuses in grid scale sizes, PHS is considered as the target technology since it offers a number of advantages for provision of grid scale storage and maturity.
Costs for PHS are very site-specific, ranging from 450–2500 USD/kW and 5–60 USD/kWh [30], characterized on site geology, water availability, access to the grid and overall construction costs. A life expectancy of 40 years is used to evaluate the annuity of investment costs and obtain the present value of net annual benefits. In this case, the total investment costs of the ESS configuration is obtained as follows:
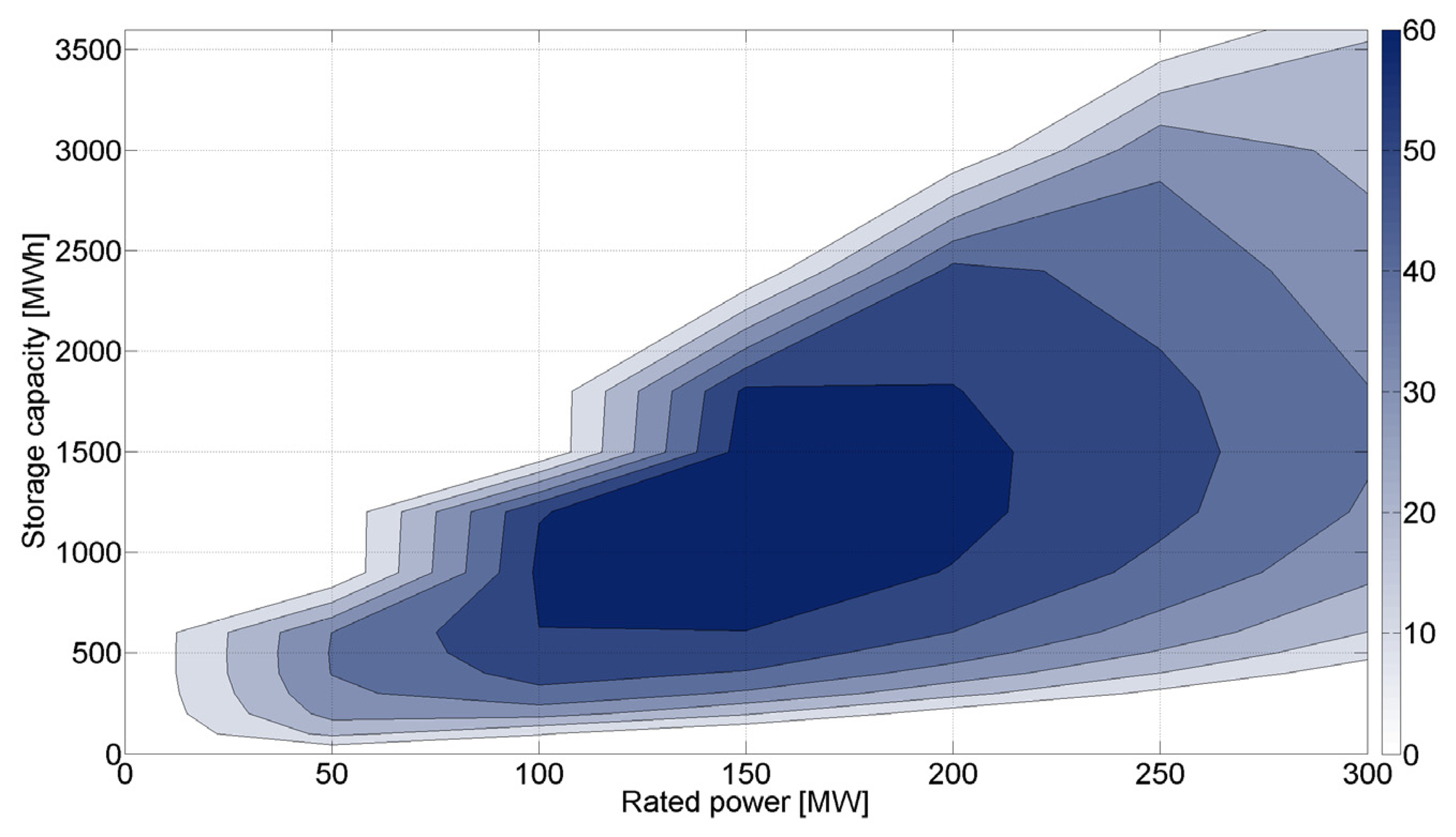
As expected, optimal ESS size for the provision of energy and secondary reserve depends on the capital costs of ESS. Figure 6 shows net social benefits (cost savings minus investment outlay) obtained when considering a capital cost of 500 USD/kW and 20 USD/kWh, for different ESS configurations (rated power and storage capacity). As shown, maximum net social benefits, i.e., optimal ESS size, are reached when installing approximately 150 MW and 1200 MWh and, in this case, reach around 60 MUSD.
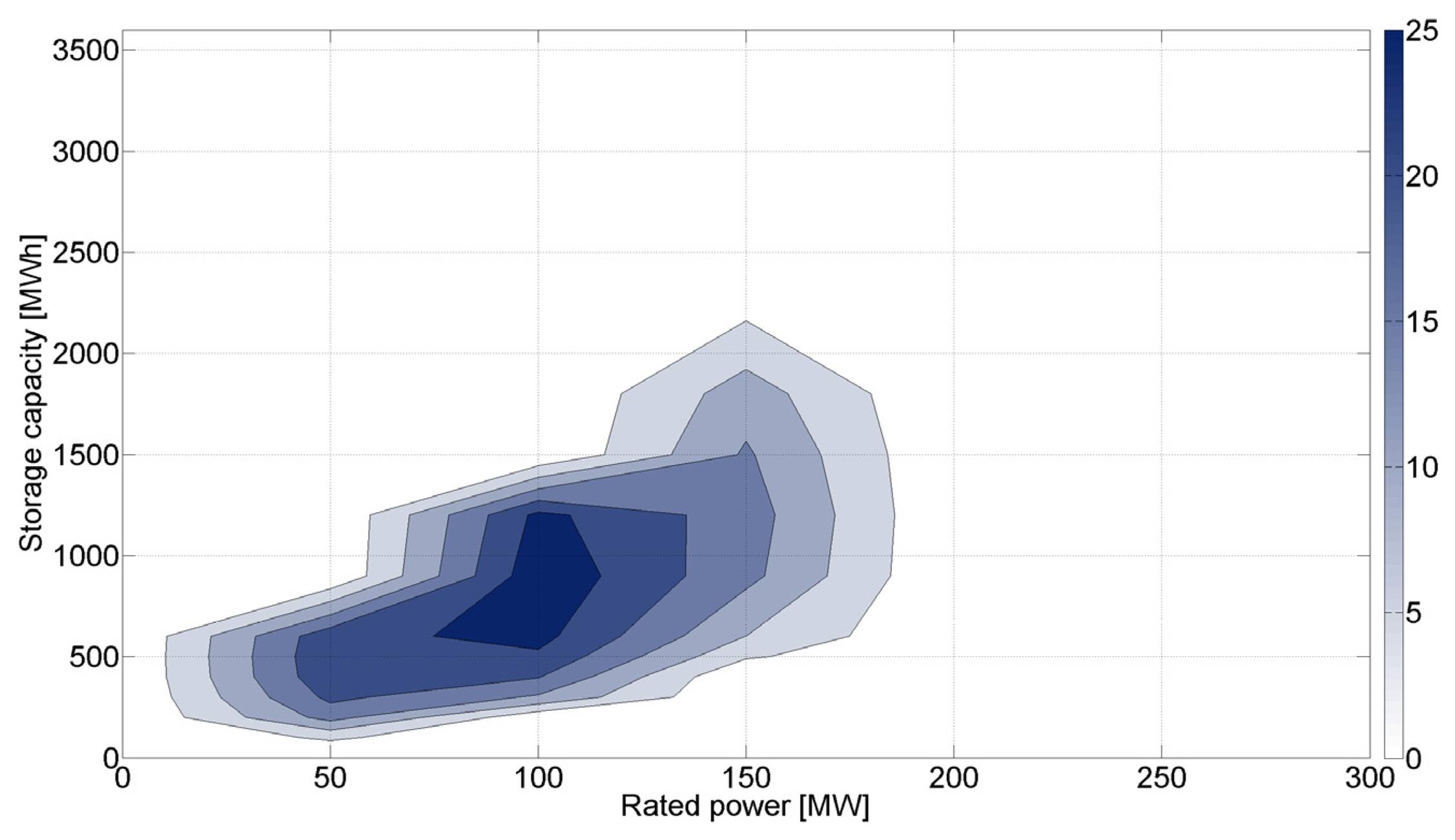
When considering a higher investment cost—for example, 1000 USD/kW—the optimal ESS size changes, as shown in Figure 7. In this case, the configuration of 100 MW and 900 MWh maximizes social benefits which reach a value of 25 MUSD. Figure 6 and Figure 7 show that ESS configurations which contribute to social welfare depend strongly on the investment cost as in the case of an ESS configuration of 200 MW and 2000 MWh. For an investment cost of 500 USD/kW, the social benefit reaches almost 40 MUSD, but no benefits are obtained if costs rise to 1000 USD/kW. In that case, it would not be advisable to use ESS of this capacity to provide energy arbitrage and secondary reserve.
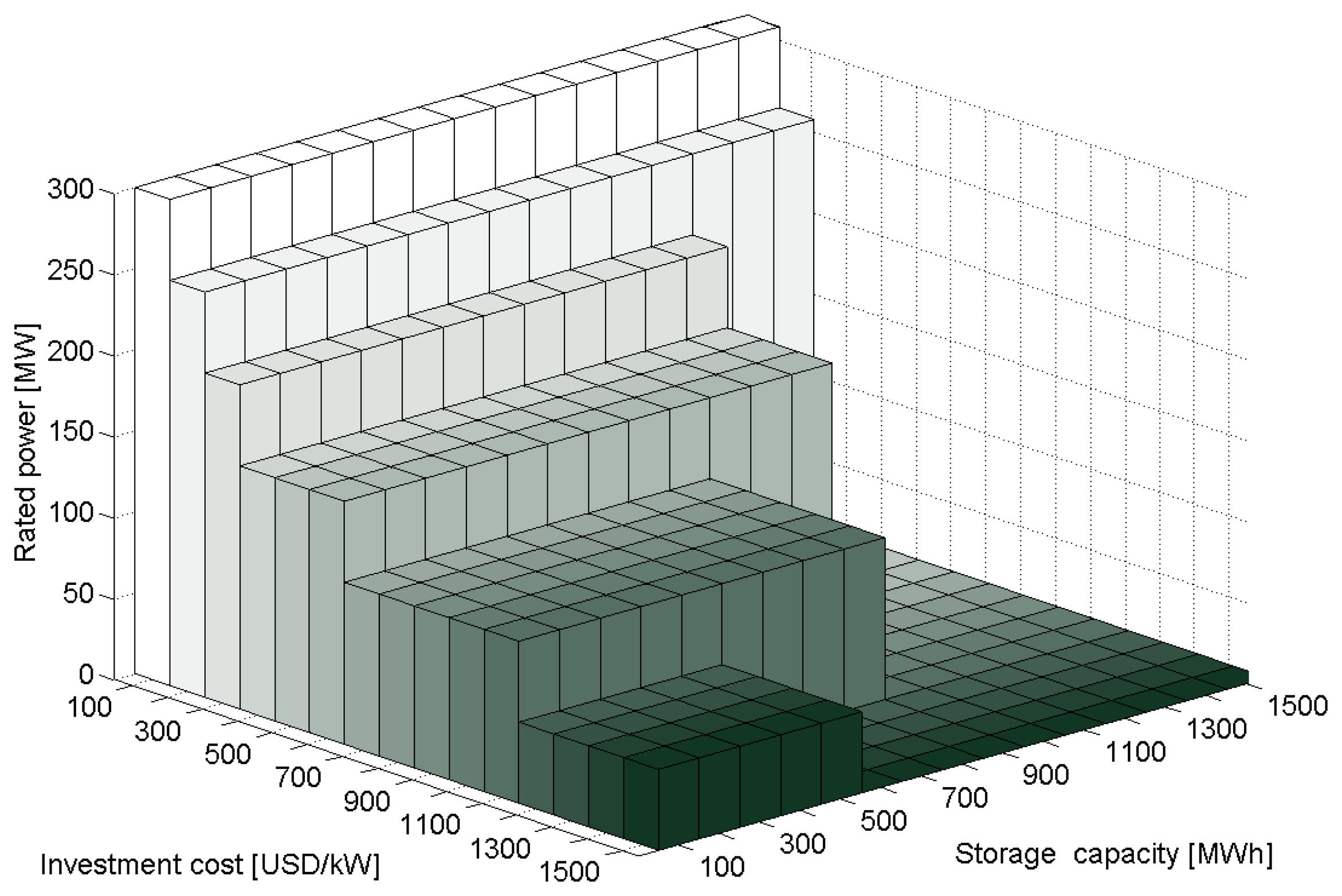
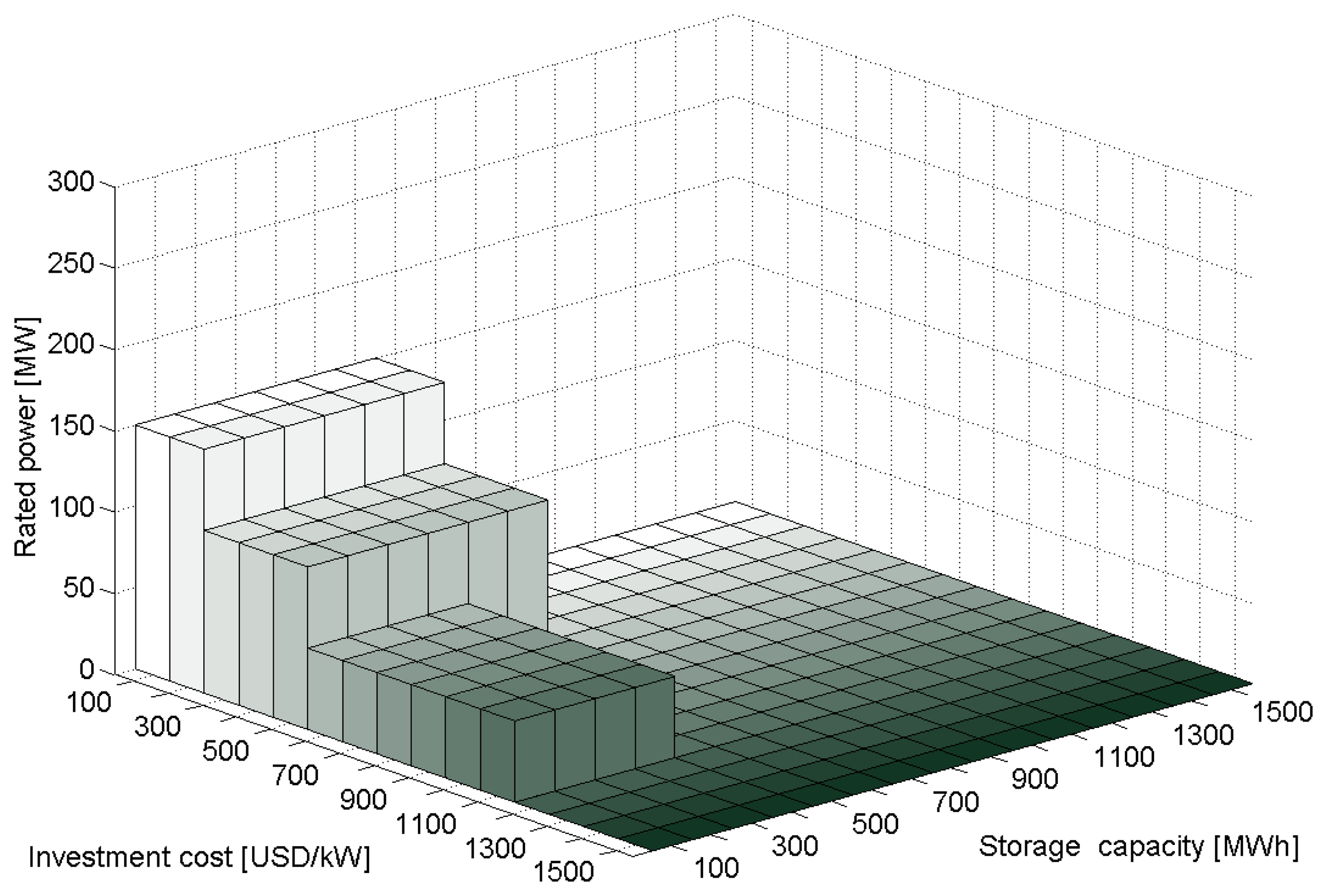
In order to explore how optimal ESS size changes, a sensitivity analysis for different investment costs is shown in Figure 8.
In this analysis, one of the costs of power/energy capacity is fixed to facilitate understanting and presentation of the results. Since the capital cost of power capacity is greater in PHS, the cost of energy capacity in this case is fixed at 20 USD/MWh. Thus, for a given investment cost of power capacity in USD/kW, an optimal ESS configuration—rated power and storage capacity—is determined.
It can be seen that optimal size increases—both in power and energy capacity—as investment costs drop. Figure 8 shows optimal size as stacked bars in order to illustrate how optimal size changes for different investment costs. It is important to remark that for a given investment cost, it has been found a single optimal size for an ESS and, therefore, Figure 8 should not be interpreted as multiple optimal values for a given cost in USD/kW. The optimal sizes for 500 and 1000 USD/kW discussed above are shown. The results underline the importance of precise determination of the ESS's investment cost, since under-estimation of the total cost could lead to an over-installation of storage capacity.
4.5. Energy Arbitrage Service Evaluation
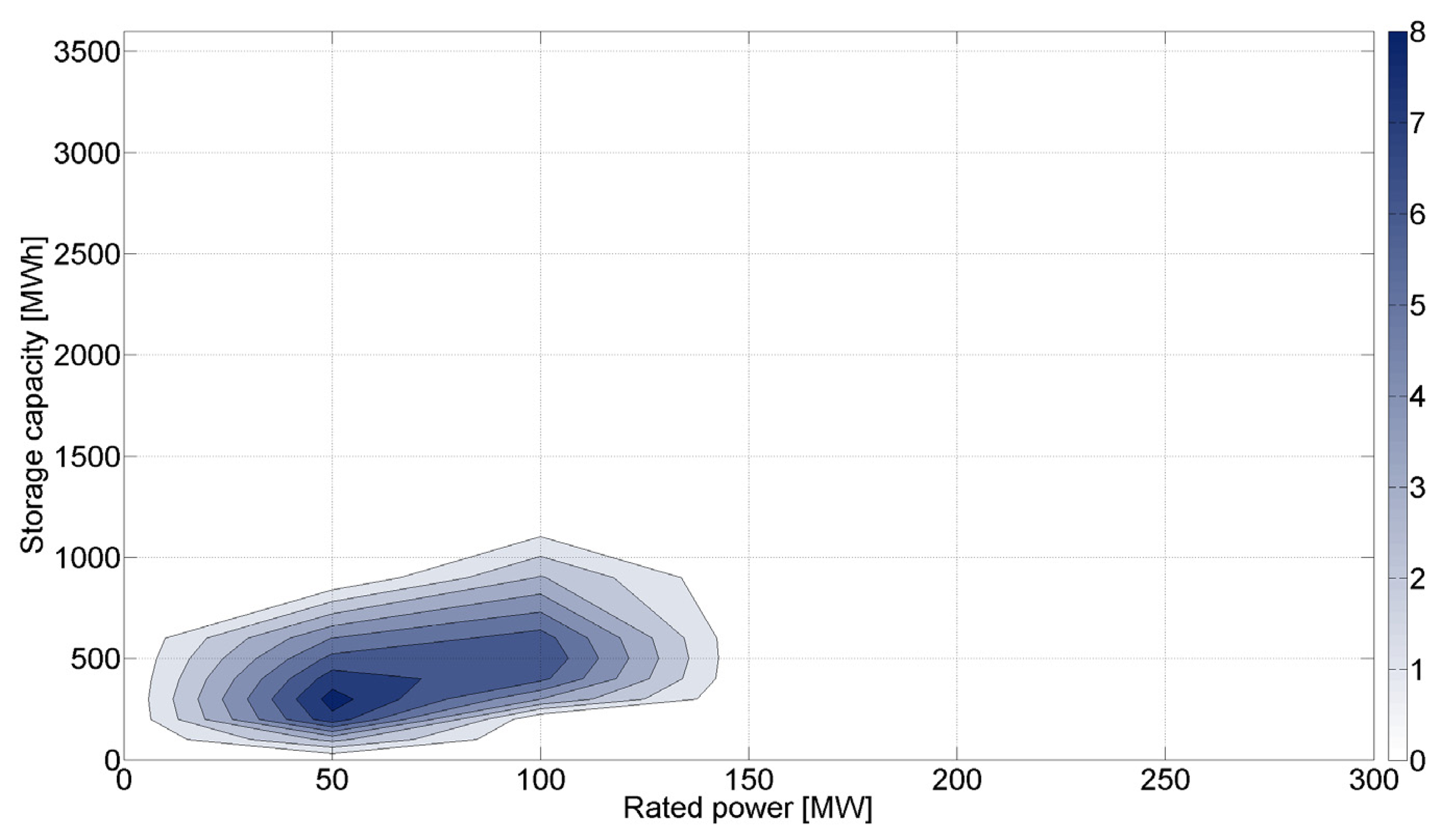
Use of ESS to provide multiple services increases their competitiveness. Simulations show that in the case of an ESS providing only energy arbitrage, social benefits tend to decrease dramatically. Figure 9 shows the results for investment costs of 500 USD/kW, where benefits drop significantly to 3.5 MUSD, with optimal ESS size of about 50 MW/250 MWh. This represents a reduction in social benefits of about 60 MUSD obtained in the case of joint provision of energy arbitrage and reserve previously shown in Figure 6.
Recognition of multiple value streams from ESS is relevant when evaluating the convenience of storage in a particular system. Although ESS can deploy technically different services, each power system's regulatory framework must recognize and foster these capabilities. This will yield greater benefits to the system, resulting in a more efficient incorporation of ESS into the grid.
In order to estimate monetary benefits, system operation modeling must internalize the capability to provide multiple services and also take into account the technical limitations of particular technologies. For instance, when providing operating reserves, it is crucial to determine availability of the energy stored so as to be sure that the ESS can provide the reserve in real time operation when this is required.
4.6. Renewable Energy Target
The energy sector's future development is currently being debated in the context of public policies to reduce carbon emissions. The case of a target of 10%, rather than 20%, for variable renewables—solar and wind—as a percentage of total electricity generation by 2024 is, therefore analyzed. The results for an ESS jointly providing energy and secondary reserve are shown in Figure 10. Compared to the case of 20% by 2024 (Figure 8), it can be seen that, for the entire range of costs, the optimal size of storage drops and it is not convenient to incorporate an ESS into the SING with an investment cost of more than 1200 USD/kW while, in the case of 500 USD/kW, the optimal storage size drops to 100 MW/600 MWh.
Hence, the future development of the energy matrix has a very important impact on the amount of storage needed. In this case, the incorporation of renewable energy, principally solar and wind technologies, in the SING will add variability to its operation. The incorporation of variable resources encourages the inclusion of storage technologies to manage variability and lack of predictability, thereby increasing the value of storage. As shown, this will depend on a number of variables that must be taken into account when evaluating the value of storage and determining optimal ESS incorporation. These variables include the future development of the energy matrix, cross-border interconnection, demand-side management and the evolution of fuel prices.
4.7. Evaluation Horizon
A multiple-year horizon is relevant in assessing optimal storage size since the energy matrix will see a shift to variable renewable energy over the coming decade. A detailed comparison of optimal ESS sizes obtained for different evaluation horizons is, therefore, presented. The multiple year evaluation—whose results were presented in Section 4.3–4.5—is compared with a single-year horizon (2020). The single-year evaluation considers only the cost savings of that year and the annuity of capital costs while the multiple-year evaluation uses present value with a 10% discount rate as discussed above.
In the case of primary reserve services, Table 1 summarizes the results of Figure 5 and shows the optimal size for the single-year evaluation. It can be seen that, for higher costs, the single year evaluation gives higher optimal ESS capacities. Table 2 presents the optimal sizing when considering different evaluation horizons for the joint provision of energy arbitrage and secondary reserve.
In this case, the results indicate that, for an investment cost of 1000 USD/kW, the optimal size obtained in a ten-year evaluation will increase by 50% (25 MUSD) as compared to the results obtained using a one-year evaluation period.
Analysis of the contribution of ESS in the long term is important since optimal sizing depends on this evaluation. A one-year approach could lead to a sub-optimal long-term planning decision. If results for a one-year simulation produce an over-estimation of the expected long-term benefits, this will lead to sub-optimal storage overcapacity.
4.8. Technical Effects
In addition to determining optimal ESS sizing, the methodology presented here permits analysis of different technical effects related to short-term operation and its expected evolution as the energy sector develops in the future
The incorporation of more renewables into the grid will affect the current operation of traditional generating units. In systems with a high participation of thermal units, flexibility is crucial in real-time operation.
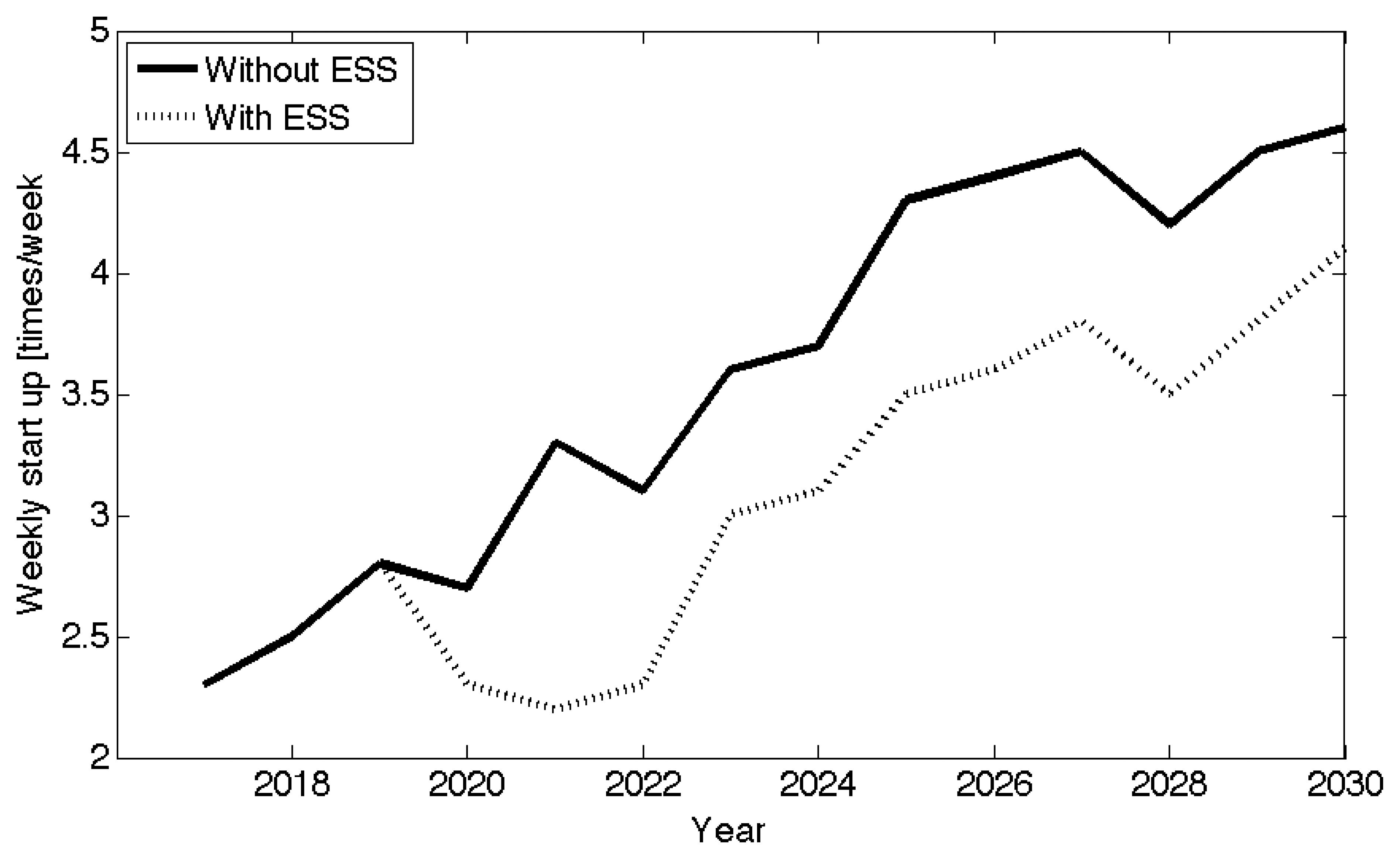
Figure 11 shows the average weekly start-up of combined cycle gas turbines (CCGTs) in the SING. The results indicate an increase in start-up both without ESS and when incorporating a 200 MW/600 MWh PHS in 2020. The start-up and shut-down schedule of CCGT units is affected by the introduction of ESS. Thus, an overall reduction in equivalent operating hours (EOH) is achieved as a result of lower variability in net demand. The introduction of ESS could lead to a decrease in EOH of approximately 14% for CCGT units. The quantitative impacts illustrated above may have an impact in reducing maintenance costs, improving power plant availability, maximizing periods of operation between inspections and overhauls and extending components' lifetime. The importance of performing detailed simulation in order to fully capture storage value is apparent.
5. Conclusions
This paper presents a simulation approach to the determination of optimal ESS sizing, based on UC simulations, suggested adaptations and the use of HPC. The ability to run UC simulations in parallel by using HPC infrastructure permits analysis of multiple years, using a detailed short-term system operation model. This, in turn, permits analysis of the inclusion of ESS in short-term operation and its contribution in the long term. Using the simulation framework presented, it is possible to determine the impacts of ESS and compare technologies for different applications.
Computational simulations were carried out for Chile's Northern Interconnected Power System (SING). The results show the importance of evaluating ESS in the long term. The particular evaluation of the SING indicates that optimal solutions for a given generation mix could lead to sub-optimal development of storage in other conditions. ESS configuration is, in other words, extremely dependent on the future incorporation of renewables in northern Chile. Similarly, multiple-year evaluation is found to be crucial for adequate assessment of ESS contributions. This paper presents valuable results, suggesting that the regulatory framework should recognize multiple value streams from storage in order to encourage greater integration of ESS into the grid. The authors show the importance of performing detailed simulation for several years, using the methodology presented, so as to fully capture storage value and of performing particular sensitivity analyses to explore the robustness of the decision.
Future work will focus on the impacts of operating policy in ESS lifetime expectancy for a more accurate assessment. Further analyses of the lifespan of ESS should be carried out depending on the storage technology considered. To clearly determine the value of storage, the impact of ESS on the future development of transmission and avoided generating facilities should be incorporated.
Acknowledgments
The authors want to thank the partial support of the Ministry of Energy, Government of Chile, under the project named “Sistemas de almacenamiento de energía para habilitar la integración de ERNC”, 2012, D.E.0593-2011 and the supercomputing infrastructure of the NLHPC (ECM-02). Likewise, R.P.B would like to thank the partial support of CONICYT/FONDAP/15110019 and FONDECYT Grant 1120317. C.S.M thanks the CIGRE National Working Group named “Energías Renovables No Convencionales. Incorporación de ERNC en los Sistemas Eléctricos Nacionales.”
Conflicts of Interest
The authors declare no conflict of interest.
References
- Renewables 2012 Global Status Report. 2013. REN21 Web site. Available online: http://www.ren21.net (accesed on 21 April 2014).
- Manz, D.; Piwko, R.; Miller, N. Look before you leap: The role of energy storage in the grid. IEEE Power Energy Mag. 2012, 10, 75–84. [Google Scholar]
- Denholm, P.; Ela, E.; Kirby, B.; Milligan, M. The Role of Energy Storage with Renewable Electricity Generation; NREL Report No. TP-6A2-47187. National Renewable Energy Laboratory: Golden, CO, USA, January 2010; pp. 1–61. Available online: http://digitalscholarship.unlv.edu/cgi/viewcontent.cgi?article=1005&context=renew_pubs (accessed on 21 April 2014).
- Eyer, J.; Corey, G. Energy Storage for the Electricity Grid: Benefits and Market Potential Assessment Guide; SAND2010-0815. Sandia National Laboratories: Albuquerque, NM and Livermore, CA, USA, February 2010. Available online: http://www.sandia.gov/ess/publications/pubslist_06.html (accessed on 21 April 2014).
- Beaudin, M.; Zareipour, H.; Schellenberglabe, A.; Rosehart, W. Energy storage for mitigating the variability of renewable electricity sources: An updated review. Energy Sustain Dev. 2010, 14, 302–314. [Google Scholar]
- Díaz-González, F.; Sumper, A.; Gomis-Bellmunt, O.; Villafáfila-Robles, R. A review of energy storage technologies for wind power applications. Renew Sustain. Energy Rev. 2012, 16, 2154–2171. [Google Scholar]
- Brown, P.D.; Peas Lopes, J.A.; Matos, M.A. Optimization of pumped storage capacity in an isolated power system with large renewable penetration. IEEE Trans. Power Syst. 2008, 23, 523–531. [Google Scholar]
- Oh, H.S. Optimal planning to include storage devices in power systems. IEEE Trans. Power Syst. 2011, 26, 1118–1128. [Google Scholar]
- Carpinelli, G.; di Fazio, A.R.; Khormali, S.; Mottola, F. Optimal sizing of battery storage systems for industrial applications when uncertainties exist. Energies 2014, 7, 130–149. [Google Scholar]
- Swider, D.J. Compressed air energy storage in an electricity system with significant wind power generation. IEEE Trans. Energy Convers. 2007, 22, 95–102. [Google Scholar]
- Tuohy, A.; O'Malley, M. Pumped storage in systems with very high wind penetration. Energy Policy 2011, 39, 1965–1974. [Google Scholar]
- Tedeschi, E.; Sjolte, J.; Molinas, M.; Santos, M. Stochastic rating of storage systems in isolated networks with increasing wave energy penetration. Energies 2013, 6, 2481–2500. [Google Scholar]
- Ummels, B.C.; Pelgrum, E.; Kling, W.L. Integration of large-scale wind power and use of energy storage in The Netherlands' electricity supply. IET Renew. Power Gener. 2008, 2, 34–46. [Google Scholar]
- Zhang, N.; Kang, C.; Kirschen, D.S.; Xia, Q.; Xi, W.; Huang, J.; Zhang, Q. Planning pumped storage capacity for wind power integration. IEEE Trans Sustain. Energy 2013, 4, 393–401. [Google Scholar]
- Makarov, Y.V.; Du, P.; Kintner-Meyer, M.C.W.; Jin, C.; Illian, H.F. Sizing energy storage to accommodate high penetration of variable energy resources. IEEE Trans. Sustain. Energy 2012, 3, 34–40. [Google Scholar]
- Daneshi, H.; Srivastava, A.K. Security-constrained unit commitment with wind generation and compressed air energy storage. Gener. Transm Distrib IET 2012, 6, 167–175. [Google Scholar]
- Arabali, A.; Ghofrani, M.; Etezadi-Amoli, M.; Fadali, M.S. Stochastic performance assessment and sizing for a hybrid power system of solar/wind/energy storage. IEEE Trans. Sustain. Energy 2014, 5, 363–371. [Google Scholar]
- Suazo-Martinez, C.; Pereira-Bonvallet, E.; Palma-Behnke, R.; Zhang, X.-P. Impacts of Energy Storage on Short Term Operation Planning Under Centralized Spot Markets. IEEE Trans. Smart Grid. 2014, 5, 1110–1118. [Google Scholar]
- Li, Q.; Huang, X. Research on Text Clustering Algorithms. Proceedings of the 2010 2nd International Workshop on Database Technology and Applications (DBTA), Wuhan, China, 27–28 November 2010; pp. 1–3.
- Abonyi, J.; Feil, B. Clustering Toolbox for MATLAB. Available online: http://www.fmt.vein.hu/softcomp/ (accessed on 21 April 2014).
- Palmintier, B.; Webster, M. Impact of Unit Commitment Constraints on Generation Expansion Planning with Renewable. Proceedings of the 2011 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 24–29 July 2011; pp. 1–7.
- Nweke, C.I.; Leanez, F.; Drayton, G.R.; Kolhe, M. Benefits of Chronological Optimization in Capacity Planning for Electricity Markets. Proceedings of the 2011 IEEE International Conference on Power System Technology (POWERCON), Auckland, New Zealand, 30 October–2 November 2012; pp. 1–6.
- Epperly, T.; Edmunds, T.; Lamont, A.; Meyers, C.; Smith, S.; Yao, Y.; Drayton, G. High-Performance Computing for Electric Grid Planning and Operations. Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–4.
- High Performance Computing Group@CMM of the Center for Mathematical Modeling (CMM) Homepage. Available online: http://hpclab.cmm.uchile.cl/ (accesed on 21 April 2014).
- A123 Energy Solutions Homepage. Available online: http://www.a123systems.com/smart-grid-storage.htm (accesed on 21 April 2014).
- Fijación de precio nudo octubre de 2013, Sistema Interconectado del Norte Grande (SING). Informe Técnico Definitivo, 2013. National Comission of Energy Website. (In Spanish). Available online: http://www.cne.cl (accesed on 21 April 2014).
- Propicia la ampliación de la matriz energética, mediante fuentes renovables no convencionales. Law in Spanish, October 2013. Available online: http://www.leychile.cl/Navegar?idNorma=1055402 (accessed on 21 April 2014).
- Sistemas de Almacenamiento de Energía para Habilitar Integración de Energías Renovables no Convencionales; Energy Centre, University of Chile: Santiago, Chile, 2012. In Spanish). Available online: http://www.minenergia.cl/documentos/estudios/2013.html (accesed on 21 April 2014).
- Expansión de Largo Plazo Para Distintos Escenarios de Desarrollo ERNC en el Sistema Interconectado del Norte Grande (SING); Energy Centre; University of Chile: Santiago, Chile, 2011. In Spanish). Available online: http://www.minenergia.cl/documentos/estudios/2013.html (accesed on 21 April 2014).
- Zach, K.; Auer, H.; Lettnet, G. D2.1 Report Summarizing the Current Status, Role, and Costs of Energy Storage Technologies; StoRE-Project Report for Facilitating Energy Storage to Allow High Penetration of Intermittent Renewable Energy; WIP Renewable Energies: Munich, Germany; March; 2012. [Google Scholar]
Nomenclature
| Pess | Power capacity of ESS in MW |
| Eess | Energy capacity of ESS in MWh |
| Ctotal | Total ESS investment cost |
| Cmw | Cost of power capacity in USD/MW |
| Cmwh | Cost of energy storage capacity in USD/MWh |
| tdept | Minimum deployment time for primary reserve in minutes |
| G | Set of all generation units, g ∈ G |
| GSL | Sub set of slow start units. GSL |
| GFS | Sub set of fast start units |
| E | Set of all ESS, e ∈ E |
Maximum capacity limit for generator g | |
Minimum capacity limit for generator g | |
| βg | Variable cost generator g |
Start-up cost generator g | |
Stop cost generator g | |
Up ramp limit generator g | |
Down ramp limit generator g | |
Available wind power, hour t | |
Available solar power, hour t | |
| lt | System load, hour t |
Maximum storage capacity, ESS e | |
Minimum required level stored energy, ESS e | |
Maximum discharge capacity, ESS e | |
Maximum charge capacity, ESS e | |
| ηd, e | Discharge efficiency, ESS e |
| ηc, e | Charge efficiency, ESS e |
| Pt, g | Power output, generator g, hour t |
Up spinning reserve, generator g, hour t | |
Down spinning reserve, generator g, hour t | |
Non-spinning reserve, generator g, hour t | |
| Wt | Wind power output, hour t |
| St | Solar power output, hour t |
| Wst | Wind power spillage, hour t |
| Sst | Solar power spillage, hour t |
| Ut | Unserved energy, hour t |
| Et, e | Energy stored, ESS e, hour t |
| ct, e | Charging level, ESS e, hour t |
| dt, e | Discharging level, ESS e, hour t |
Up spinning reserve, ESS e, hour t | |
Down spinning reserve, ESS e, hour t | |
| ut, g | Unit Commitment, generator g, hour t |
| vt, g | Start-up flag, generator g, hour t |
Turn-off flag, generator g, hour t | |
| Cop(pt, g) | Operation cost, generator g, hour t |
| Cstart(vt, g) | Start-up cost, generator g, hour t |
| Cstop(bt, g) | Shut-down cost, generator g, hour t |
| CENS(Ut) | Unserved energy cost, hour t |

| 10 years evaluation 2020–2029 | 1 year evaluation 2020 | 1 year evaluation 2025 | |
|---|---|---|---|
| Investment cost (USD/kWh) | Rated power (MW) | Rated power (MW) | Rated power (MW) |
| 1000 | 70 | 70 | 70 |
| 1500 | 70 | 70 | 70 |
| 2000 | 70 | 70 | 70 |
| 2500 | 60 | 70 | 70 |
| 3000 | 60 | 70 | 70 |
| 3500 | 50 | 60 | 60 |
| 10 years evaluation 2020–2029 | 1 year evaluation 2020 | 1 year evaluation 2025 | ||||
|---|---|---|---|---|---|---|
| Investment cost (USD/kW) | Power (MW) | Storage (MWh) | Power (MW) | Storage (MWh) | Power (MW) | Storage (MWh) |
| 200 | 250 | 1500 | 150 | 600 | 200 | 800 |
| 400 | 150 | 1200 | 100 | 600 | 150 | 600 |
| 600 | 150 | 1200 | 100 | 600 | 150 | 600 |
| 800 | 100 | 900 | 50 | 400 | 100 | 600 |
| 1000 | 100 | 900 | 50 | 400 | 50 | 400 |
| 1200 | 50 | 500 | 50 | 400 | 50 | 400 |
| 1400 | 50 | 500 | 50 | 400 | 50 | 400 |
| 1500 | 50 | 500 | 50 | 400 | 50 | 400 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland.. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Suazo-Martínez, C.; Pereira-Bonvallet, E.; Palma-Behnke, R. A Simulation Framework for Optimal Energy Storage Sizing. Energies 2014, 7, 3033-3055. https://doi.org/10.3390/en7053033
Suazo-Martínez C, Pereira-Bonvallet E, Palma-Behnke R. A Simulation Framework for Optimal Energy Storage Sizing. Energies. 2014; 7(5):3033-3055. https://doi.org/10.3390/en7053033
Chicago/Turabian StyleSuazo-Martínez, Carlos, Eduardo Pereira-Bonvallet, and Rodrigo Palma-Behnke. 2014. "A Simulation Framework for Optimal Energy Storage Sizing" Energies 7, no. 5: 3033-3055. https://doi.org/10.3390/en7053033




