Energy-Efficient Power Allocation Using Probabilistic Interference Model for OFDM-Based Green Cognitive Radio Networks
Abstract
: We study the energy-efficient power allocation techniques for OFDM-based cognitive radio (CR) networks, where a CR transmitter is communicating with CR receivers on a channel borrowed from licensed primary users (PUs). Due to non-orthogonality of the transmitted signals in the adjacent bands, both the PU and the cognitive secondary user (SU) cause mutual-interference. We assume that the statistical channel state information between the cognitive transmitter and the primary receiver is known. The secondary transmitter maintains a specified statistical mutual-interference limits for all the PUs communicating in the adjacent channels. Our goal is to allocate subcarrier power for the SU so that the energy efficiency metric is optimized as well as the mutual-interference on all the active PU bands are below specified bounds. We show that the green power loading problem is a fractional programming problem. We use Charnes-Cooper transformation technique to obtain an equivalent concave optimization problem for what the solution can be readily obtained. We also propose iterative Dinkelbach method using parametric objective function for the fractional program. Numerical results are given to show the effect of different interference parameters, rate and power thresholds, and number of PUs.1. Introduction
The demand for ubiquitous wireless broadband data access and multimedia services is constantly growing in the crowded consumer radio bands while wider spectral ranges of already licensed frequency bands are barely used. To cope with this unequal spectrum access and usage, spectrum pooling is identified as one of the potential techniques that enables public access to licensed frequency bands. The key idea of spectrum pooling is to merge spectral ranges from different spectrum owners into a common pool and the cognitive or secondary users may borrow/rent spectrum from the pool. The coexistence of both the licensed users and cognitive users are realized by filling the time-frequency gaps of the primary network when they are idle.
Orthogonal frequency division multiplexing (OFDM) has been identified as a feasible modulation technique due to its flexible spectral shape that can adaptively fill the idle gaps for such a co-existence scenario. However, due to the non-orthogonality of the transmit signals, both primary and secondary systems introduce mutual interference and it is crucial that the sum of the interference from all the subcarriers does not exceed acceptable limits. In this paper, our goal is to greenwise design a cognitive radio (CR) system that optimizes energy efficiency under probabilistic interference quality of service (QoS) constraints for primary users (PUs), and throughput and power QoS constraints for secondary users (SUs). We assume that each PU has its own statistical interference limits depending on its own QoS requirements. The SU sharing the spectrum has knowledge of all these individual statistical interference limit of the PUs. OFDM has already been deployed in different broadband broadcast wireless standards, such as, Digital Video Broadcasting (DVB), Digital Audio Broadcast (DAB), etc. because of its many desirable features, such as high spectral efficiency, multipath delay spread tolerance, immunity to the frequency selective fading channels and power efficiency. However, in a downlink broadcasting network most of the power is consumed in the transmitter. Therefore, it is very crucial to design an energy-efficient broadcasting transmission strategy. Below we discuss some works in broadcasting situations that deals with OFDM.
In [1], the authors presented an overview of peak-to-average power ratio (PAPR) reduction techniques for multiuser OFDM broadband communication systems. The mutual interference issues for OFDM-based spectrum pooling techniques between the primary and cognitive systems are studied in [2]. The authors in [3] studied an mutual interference minimization and subcarrier power allocation technique for OFDM-based CR. Different mutual interference suppression techniques are compared using laboratory test on real OFDM signals for spectrum pooling CR systems in [4]. In [5], the authors developed a dynamic subcarrier allocation algorithm for multi-user downlink communications using OFDM technique. Their algorithm attempts to allocate group of subcarriers to the user that have highest average channel gain. Conflict resolution technique is also studied to avoid the case when two or more users attempt to select the same channel partition. The authors also employed adaptive modulation techniques for each user on the allocated channel partitions.
While accessing PU's spectrum, it is crucial to limit interference so that PU's operation is not hampered. Different form of interference limit has been used in the literature, such as, instantaneous hard interference limit, average interference limit, PU outage limit, or soft statistical interference limit. The authors in [6] proposed a distributed power control framework that satisfy tight QoS constraints for SU and interference level threshold constraints for PUs. In [7], cross-layer tradeoff of power, sensing time and throughput is studied under a PU interference threshold constraint. Peak and average interference power constraints for protecting PUs in cognitive radio networks is studied in [8]. Using outage constraint for PU, a power allocation algorithm for OFDM-based cognitive radio is studied in [9]. In [10], optimal power allocation strategies for the secondary user is studied in order to maximize its capacity under transmit power constraint of the SU and outage constraint of the PU. Distributed subcarrier and power allocation technique for the maximization of throughput subject to constraints on the interference and power is studied in [11] for ad hoc cognitive radio networks. Using statistical constraint on interference, a joint admission control, and rate and power allocation for SUs in a CR network is developed in [12]. The authors studied outage probabilities for SUs and interference constraint violation probabilities for PUs for the dynamic fair spectrum sharing scenario. In [13], optimal and suboptimal power loading techniques are studied using statistical interference constraints for CR systems.
In [14], adaptive subcarrier allocation and power distribution technique for multi-antenna orthogonal frequency division multiple access (OFDMA) systems that provide multicast service is studied. The problem is formulated as maximizing sum capacity with constraints on the total power. The authors in [15] studied two-dimensional mapping of incoming requests for wireless OFDMA systems, where a base station (BS) is transmitting to a group of subscriber station (SS) using a broadcast channel in downlink. They presented run-time efficient heuristic solutions for the problem, where the objective function is the spatial efficiency. The performance of multimedia streaming over an IEEE802.11b wireless local area network using quality-oriented adaptive scheme is studied in [16]. The performance is assessed in terms of the average user quality of experience, number of concurrent streaming sessions, loss rate, delay, jitter and total throughput. In [17], the resource allocation problem of assigning a set of subcarriers and determining the number of bits to be transmitted for each carrier in OFDMA-based broadband wireless access systems is considered. The authors considered fairness and efficiency of the optimal and suboptimal algorithms.
In [18], an energy efficient structure for beacon signal transmission is proposed for the protection of PU, which is incumbent wireless microphone. The authors in [19] investigate energy-efficient design of CR in order to protect incumbent users, where power allocation and transmission duration are determined by exploiting multiple channels. In [20], the green network planning of single frequency networks based on OFDM schemes is investigated. A genetic algorithm optimization method is proposed to maximize energy-efficiency there. The problem of energy-efficient communication in the downlink OFDMA network is studied in [21]. For multi-cell OFDMA downlink networks with cooperative base stations, the energy-efficiency is discussed in [22]. In [23], a mathematical framework for energy-efficiency is presented.
Energy-efficient green communications techniques and network designs are of special importance for future generation communications in order to reduce carbon dioxide gas emission due to exponential increase on energy consumption in our daily lives [24]. To cope with the exponential increase of wireless data traffic in overly crowded consumer radio spectra, CR is identified as a very important technology for future wireless communication networks. CR communications technology will provide a way to opportunistically and efficiently utilize unused piece of spectrum that is currently statically assigned to other services (such as, TV band, amateur radio, etc.). Since the activity state of the incumbent PU is hidden from the SUs, the main research challenges in CR are to design efficient spectrum sensing, interference-management, and optimized accessing techniques.
While wireless handheld devices are playingan ever-increasing integral role in human daily activities, wireless systems as a whole invariably contribute to a significant global carbon footprint. A recent study shows that information and communication technology (ICT) is responsible for about 3%–5% of the worldwide total energy consumptions [25]. Data-hungry applications, such as wireless cloud computing and wireless machine-to-machine communications, are getting increasingly more attention in emerging wireless networks. The increase in telecommunications data volume is found to be approximately 10 times every 5 years, and the corresponding increase in energy consumption is 16%–20%. As a result, the research attention to energy-efficient environment-friendly wireless communications networks and architecture design are increasing worldwide among telecommunication researchers, operators and government bodies. While most of research in the last decades deals with throughput maximization, little attention is paid on energy-efficiency issues. Future generation wireless networks need to be optimized using energy-efficiency metric as an objective [26]. Energy-efficiency in its simplest form is defined as the effective throughput per unit transmitted power. Some other research works that deals with energy aware communications using green cost functions discussed above can be found in [27–34].
From the discussion above it can be seen that there are two streams of studies for cognitive radio networks in the literature: some authors studied the maximization of capacity with statistical interference constraint, and some authors addressed the maximization of EE without considering statistical interference model. In this paper, we address the deficiencies in both streams by combining them. We address a generalized formulation for green cognitive radio networks. Therefore, although downlink power allocation techniques for wireless broadcast channels exist in the literature, energy-efficient green power allocation technique with statistical interference constraint is not explored yet. Also, most of spectrum access techniques in cognitive radio networks deal with either throughput maximization or power minimization in interweave manner (cognitive user transmit when the primary user is off). In this paper, we addressed EE maximization problem considering three important constraints that are not addressed before together, but for cognitive radio scenario.
The main contributions of this paper are as follows:
We propose an energy-efficiency maximization framework in a cognitive radio scenario, where the transmitter judiciously allocates total power over multiple subcarriers. The transmitter maintains specified statistical interference limits for the individual PUs and minimum throughput for the SUs. We formulate the resulting problem as a fractional program;
Since the optimal solution of the formulated fractional program may be hard to obtain due to non-concavity of the objective function, we show using Charnes-Cooper Transformation (CCT) technique that the problem is equivalent to a concave optimization problem. Suitable concave optimization solution technique can be used to obtain optimal subcarrier powers for the equivalent concave optimization problem;
We discuss the special structure of the solution analytically and show that the power allocation follows a water-filling type distribution for the special case when the sum rate throughput is greater than the specified threshold;
We propose and study an iterative technique based on Dinkelbach method to obtain ε-optimal solution of the problem, where the objective function is transformed into a parametric form. A comparison of both techniques is also studied;
With numerical analysis, we show the performance of the green cognitive radio network with different operational parameters. We also compare the convergence of iterative method with equivalent CCT problem.
The rest of the paper is organized as follows. The system model and problem formulation are presented in Section 2. The transformation technique of the non-linear non-concave problem into a concave problem is discussed in Section 3 and iterative technique based on Dinkelbach method using parametric objective is given in Section 4. Simulation results are presented in Section 5 and conclusion is drawn in Section 6.
2. System Model
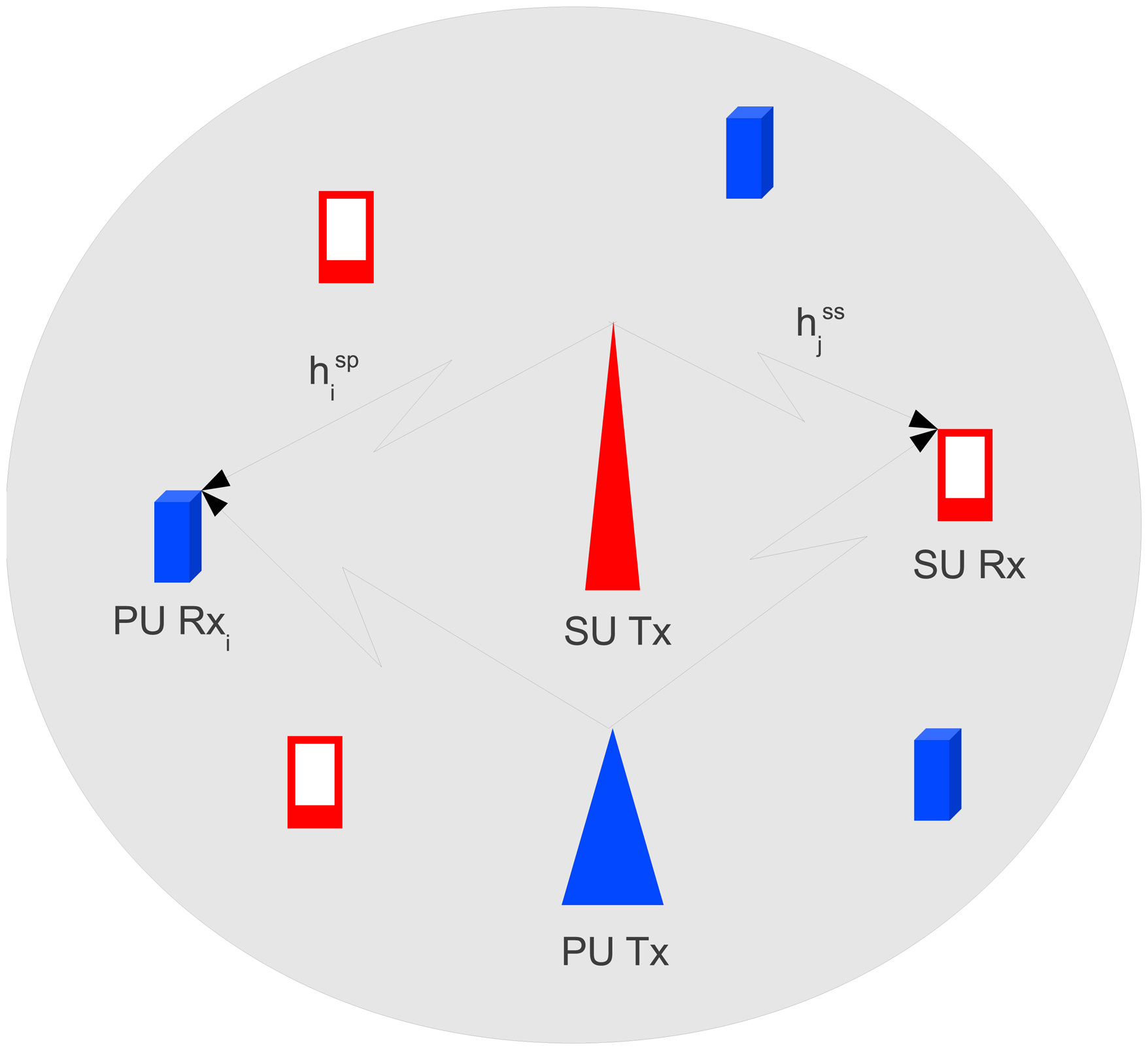
We consider a cognitive radio network as shown in a simplified Figure 1, where a cognitive transmitter (base station) is transmitting to its cognitive users in the downlink direction over pooled wireless spectrum from the primary users (who are also communicating in the adjacent spectrum at the same time). The primary users are the licensed owners of the spectrum and secondary users have the capability to use the unused spectrum opportunistically in time and/or frequency. When the SUs transmit on the adjacent pooled spectra, it inherently causes the mutual interference to the PUs. PUs cause mutual interference to the SUs as well. We assume that the interference due to PU's transmission can be estimated perfectly. Unless specified otherwise, we use A, a, and a to represent matrix, vector and an element of a vector respectively. When ai ≥ 0 for all components i of a vector a, we use a ≥ 0. The notations for most common variables are given at the end of this paper.
Let M denote the number of PUs that co-exist side-by-side with the CR user pair and Bi, ∀i ∈ denote the bandwidth of the frequency band of the ith PU pair, where = {1, 2, 3, …, M}. We assume that the SUs use orthogonal frequency division multiplexing (OFDM) technique for transmission of data. The SUs divide the acquired bandwidth into N subcarriers, where Δf is the bandwidth of each subcarrier. Let us denote the set of subcarriers by

The channel state between the CR transmitter and the CR receiver varies randomly in both time and frequency domain due to fading, and
denotes the channel fading gain of the associated SUs in the jth subcarrier. We assume that the channel state information (CSI) of all subcarriers are perfectly estimated at the receiver and are fed back to the transmitter for power loading on the subcarriers. Without losing generality, we assume that the set of achievable rate points for the broadcast channel can be computed using any methods, such as, frequency division, time-division, superposition coding (SPC), etc. [35]. For example, in SPC, the users are ordered based on their channel gains, from strong to weak and the first user is encoded last. For simplicity, we carry out our discussions using last user rate, which gives us the lower bound of the energy-efficiency that must be maintained across all the users for QoS guarantee. If pj, j = 1, 2, 3…, N, where pj ∈

2.1. Problem Formulation
The performance of the green radio systems are usually measured in terms of energy-efficiency metric, which is defined as the total achievable rate throughput per unit total transmitter power. Let Γ(p) denote the energy-efficiency in information bits per Joule as,
We assume that the fading channel between the SU transmitter and ith PU receiver can be described by Rayleigh distribution with fading gain denoted as . The probability density function (pdf) of the channel power gain is exponentially distributed and can be written as,
Note that the terms Kji, ∀j ∈

The detailed derivation of Equation (7) is given in Appendix A. Equation (7) means that the weighted sum of all the subcarrier powers is upper bounded by the channel between the secondary transmitter and the primary receiver, and PU's QoS requirement in terms of required interference thresholds.
The problem in Equation (3) is a non-linear and non-concave problem. Below, via suitable transformation, we transform it into a concave optimization problem that can be solved easily.
3. Transformation to Equivalent Concave Programming
The fractional programming problem in Equation (3) can be expressed in the following generalized form [36]:
Problem (8) is a concave fractional program (CFP) [36] since it satisfies the following properties: (i) the function f(p), g(p), and hi(p), ∀i ∈ are all real-valued functions that are defined on the set



A CFP with affine denominator can be transformed to an equivalent concave program with Charnes-Cooper Transformation (CCT) with the following transformations: y = tp and . With CCT, we can write equivalent concave program for Equation (3) as follows:
The concave program (9) can be solved using any standard optimization techniques and/or using mathematical programming software (e.g., MATLAB, CPLEX, MINOS, etc.). When the constraint C2 is a strictly inequality, we show that the power allocation in the subcarriers has water-filling type policy. We express this by the following theorem:
Theorem 1
The optimal power allocation rule that maximizes the total energy efficiency in Equation (9) is given by the following relation when the capacity is greater than the threshold in constraint C2:
Proof
The proof of Theorem 1 is given in Appendix B.
4. Iterative Algorithm using Parametric Optimization
Another mathematically less cumbersome technique that does not require the transformation is an iterative solution technique of the fractional programming problem based on the Dinkelbach method [39]. In this algorithm, the objective of the fractional programming problem is first transformed into a parametric optimization problem, then ε-optimal solutions are obtained iteratively, where ε is the tolerance of convergence. Let q ∈ ℝ denote a real-valued parameter such that F(p, q) = maxp∈S [f(p) − qg(p)]. Therefore, F(p, q) is continuous for q ∈ ℝ, strictly monotonic and concave over ℝ [39]. There is a one-to-one relationship between the solutions of the fractional programming formulation and iterative concave programming with parametric objective as stated by the following theorem:
Dinkelbach Theorem [39]
if and only if, maxp∈ S f(p) − q* g(p) = f(p*) − q* g(p*) = 0.
Therefore, the problem formulated in Equation (3) can be solved by replacing the fractional objective function with the parametric objective function F(p, q) using ε-optimal Dinkelbach algorithm as given in Algorithm 1.
| Algorithm 1 : Iterative algorithm based on the Dinkelbach method |
| Initialization: |
| Parameter q = 0, tolerance ε = 10−6, iteration i = 0, maximum iteration I = 100, |
| Convergence = false, |
| Define: |
| while (Convergence = false) and (i ≤ I) do |
| p ← argmaxp{F(p, q) ∣ C1 to C4 of Equation (3)} |
| if F(p, q) = 0 then |
| Optimal power, p* ← p |
| Convergence = true |
| else if F(p, q) ≤ ε then |
| ε-optimal power, pε ← p |
| Convergence = true |
| else |
| update, |
| update, i ← i + 1 |
| end if |
| end while |
5. Numerical Results
In this section, we present numerical simulation results for the channel access probability, average energy efficiency and average total transmitted power with different interference parameters, power and rate thresholds, and number of interfering primary users using both the CCT and Dinkelbach formulations. Both the CCT and Dinkelbach formulations give the same optimal values. We conduct Monte Carlo simulations by generating several set of channel samples for Rayleigh fading channel and average the optimal energy efficiency and the optimal total power over the number of set of samples. Unless specified otherwise, the values for different system parameters for the Monte Carlo simulations are as follows: the duration of OFDM symbol, Ts = 1 μs, static circuit power, pc = 10−6 mW, noise power variance, σ2 = 0.1 mW, the total transmitter power threshold, PT = 50 mW, number of subcarriers, N = 16, bandwidth of each subcarrier, Δf = 312.5 kHz, average channel power gain of the SU link, , average channel power gain between SU transmitter and PU receiver, , number of PU channels, M = 10, the rate threshold, Cth = 5 × 106 bits/sec, interference threshold, , interference probability threshold , bandwidth of each PU, B = 1 MHz, interference contribution of each PU is Rayleigh distributed with standard deviation 10−4.
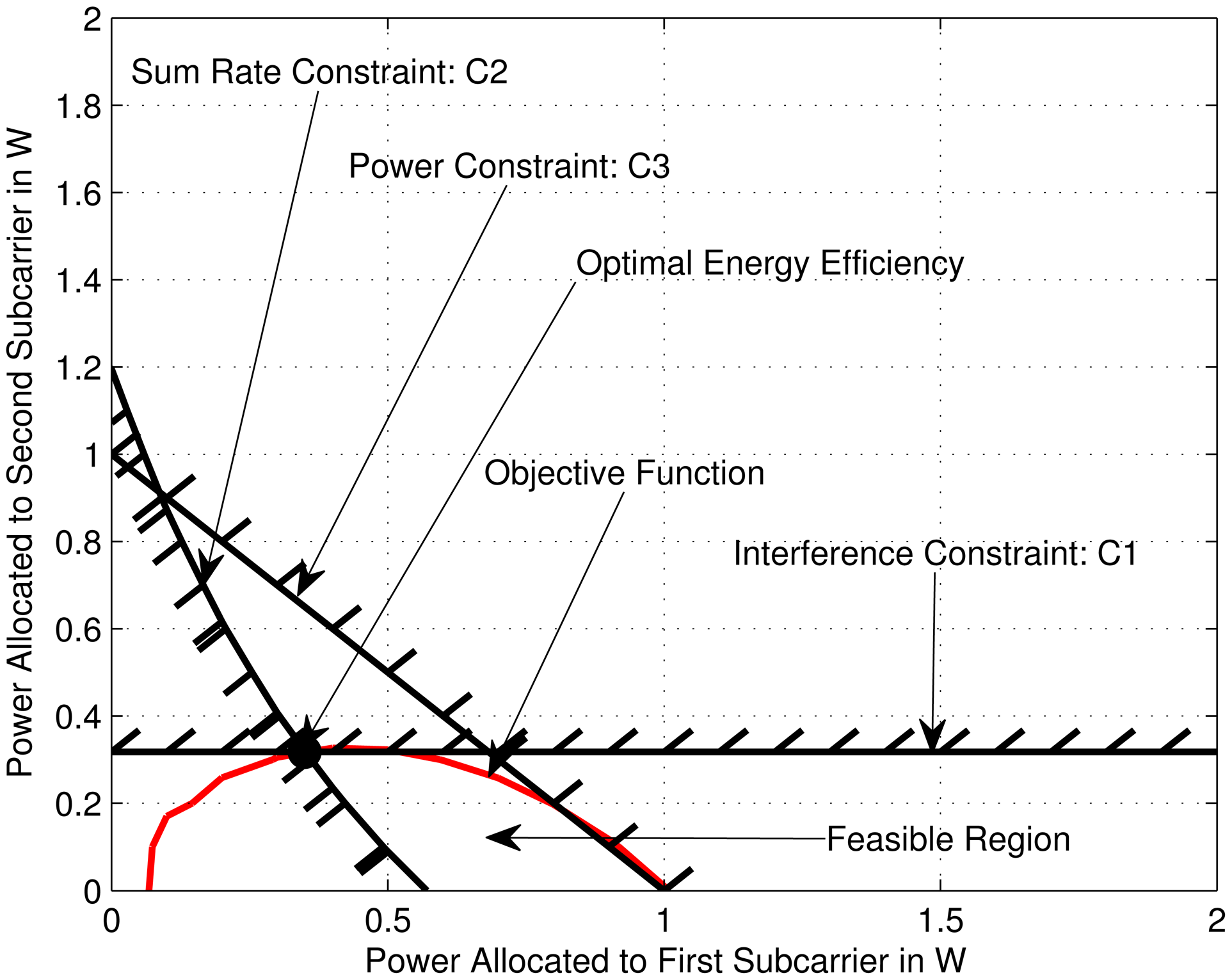
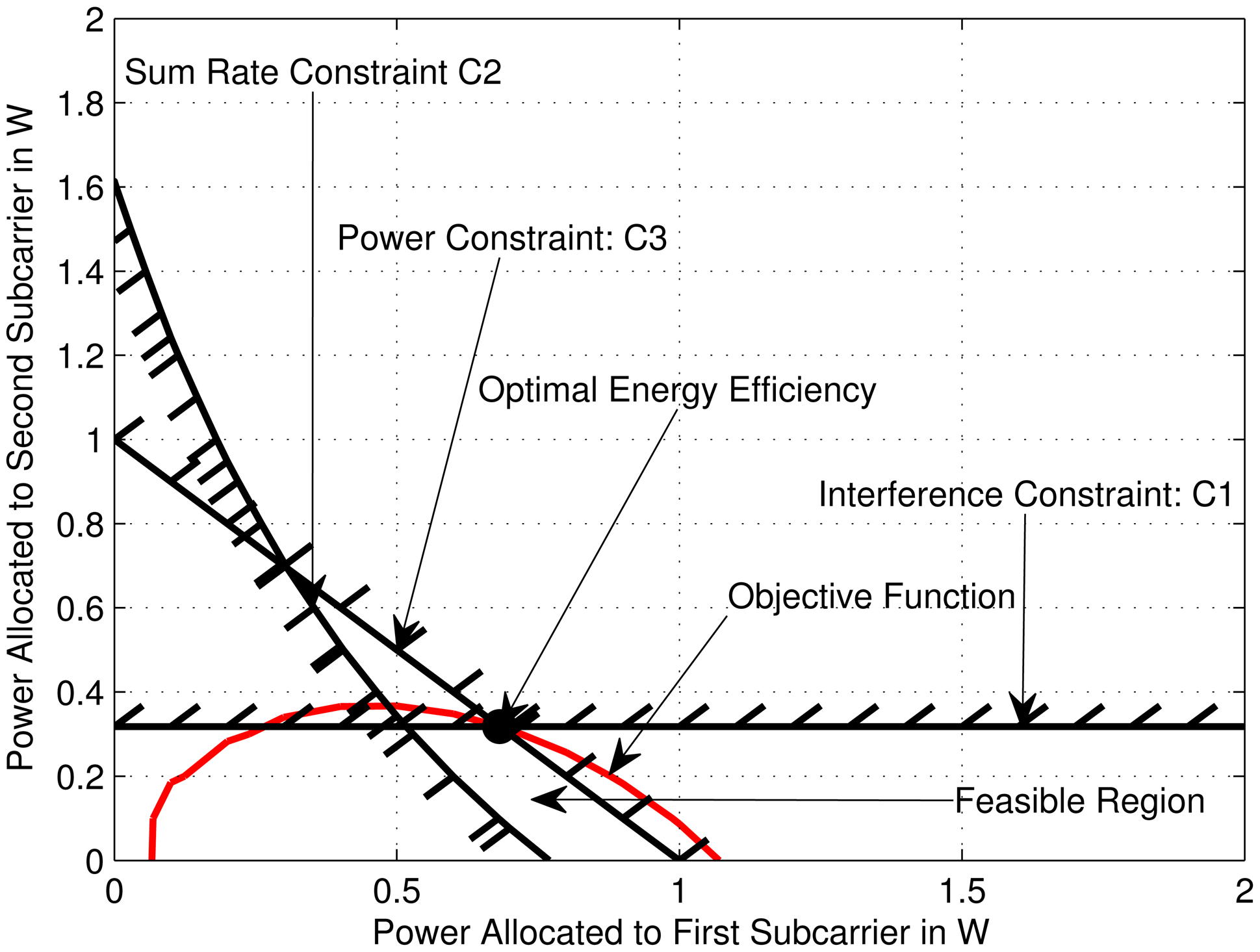
For a given set of data and channel realization, all the constraints must satisfy together and they form a region where all the possible solution points lie in. However, for a particular set of channel samples, there may not be any feasible region at all. Meaning, there is no solution point that can simultaneously satisfy all the constraints. For that channel scenario and constraint thresholds, the SU cannot access the channel. One or more thresholds must be relaxed in order to transmit for that channel conditions. The channel access probability is defined as the average number of samples for which a feasible region and hence an optimal solution exists for the problem. First let us see the how the three main constraints, i.e., the interference, rate and power affect the feasible region and consequently the optimal solution of the problem.
Figures 2 and 3 show two typical scenarios for two different rate thresholds respectively, where we show the feasible regions and optimal solution points. Note that as mentioned previously the feasible region is the set of solution points where all the constraints are simultaneously satisfied. However, one of the solution point in the feasible region will optimize the objective function and it is the optimal energy-efficiency In these figures, the common area inside hatched lines is the feasible region and the solid circular point is the optimal solution point (optimal energy efficiency point), where the value of energy efficiency is the maximum. These plots show how the rate threshold Cth affects the feasible region and the optimal energy-efficiency The values for different parameters for Figures 2 and 3 are as follows: number of subcarriers, N = 2, number of PU, M = 1, bandwidth of each subcarrier, Δf = 1 MHz, signal-to-noise and interference ratio (SINR) for subcarriers are 1.3 and 0.62. For Figure 2, the total transmitter power threshold, PT = 1 W and the rate threshold, Cth = 0.8 Mbits/sec. The optimal sum of subcarrier powers, the optimal rate and the optimal energy efficiency are found to be 0.6675 W, 0.8 Mbits/sec and 1.1985 Mb/Joule respectively by calculating the optimal point. Note that sum rate constraint is the active constraint (i.e., the optimal point lies on the sum rate constraint) here. In Figure 3, the rate threshold is increased to Cth = 1.0 Mbits/sec for the same power threshold. The resulting optimal sum of subcarrier powers, the optimal rate and the optimal energy efficiency are 1.0 W, 1.1754 Mbits/sec and 1.1754 Mb/Joule respectively. It can be seen that the power constraint is the active constraint here. Although the value of optimal rate is increased, the energy efficiency is decreased. Therefore, it is evident from the results that maximizing energy efficiency does not maximize the capacity. In fact, they may be sometimes conflicting goals in wireless networks, as was discussed in [26] also for general wireless network.
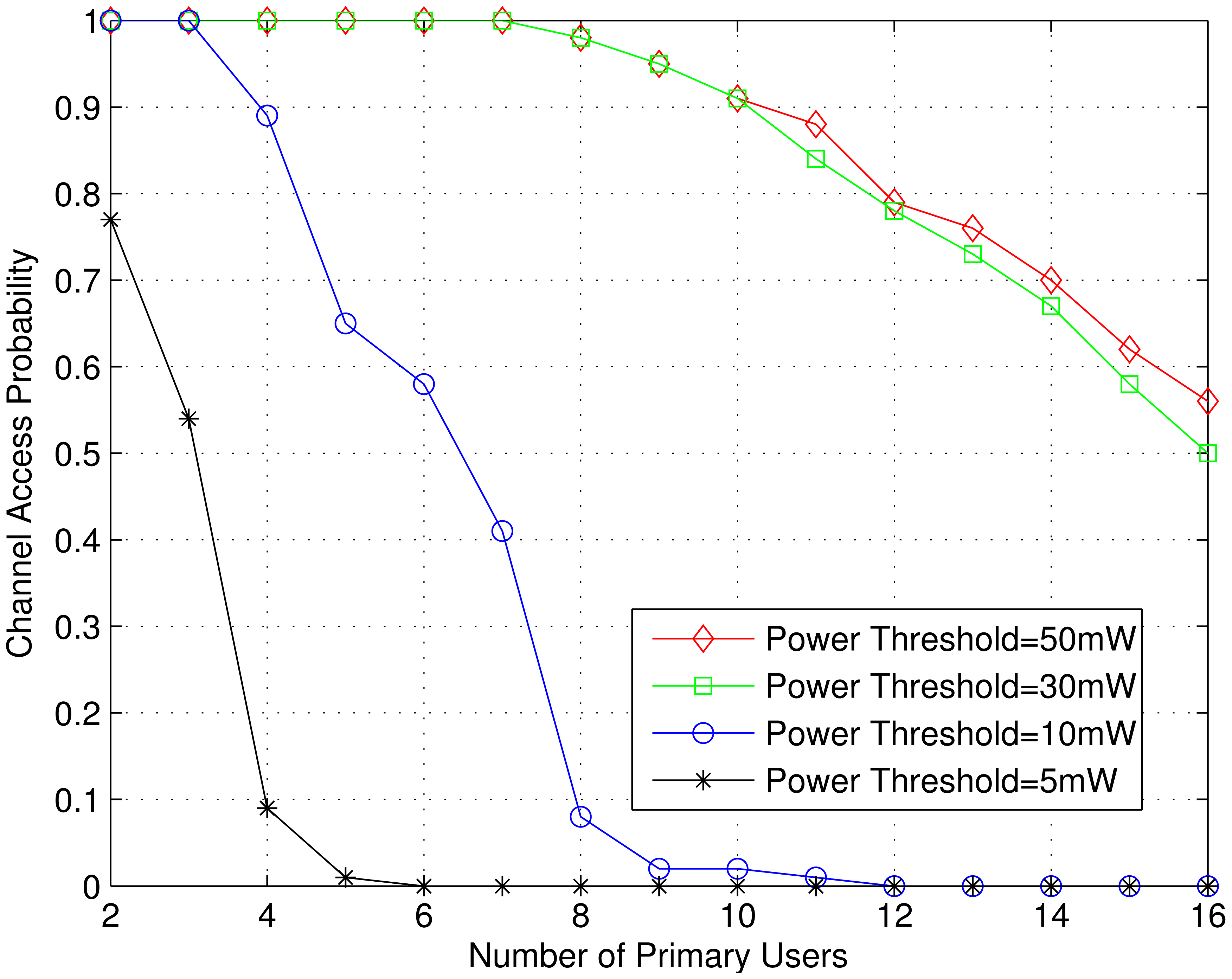
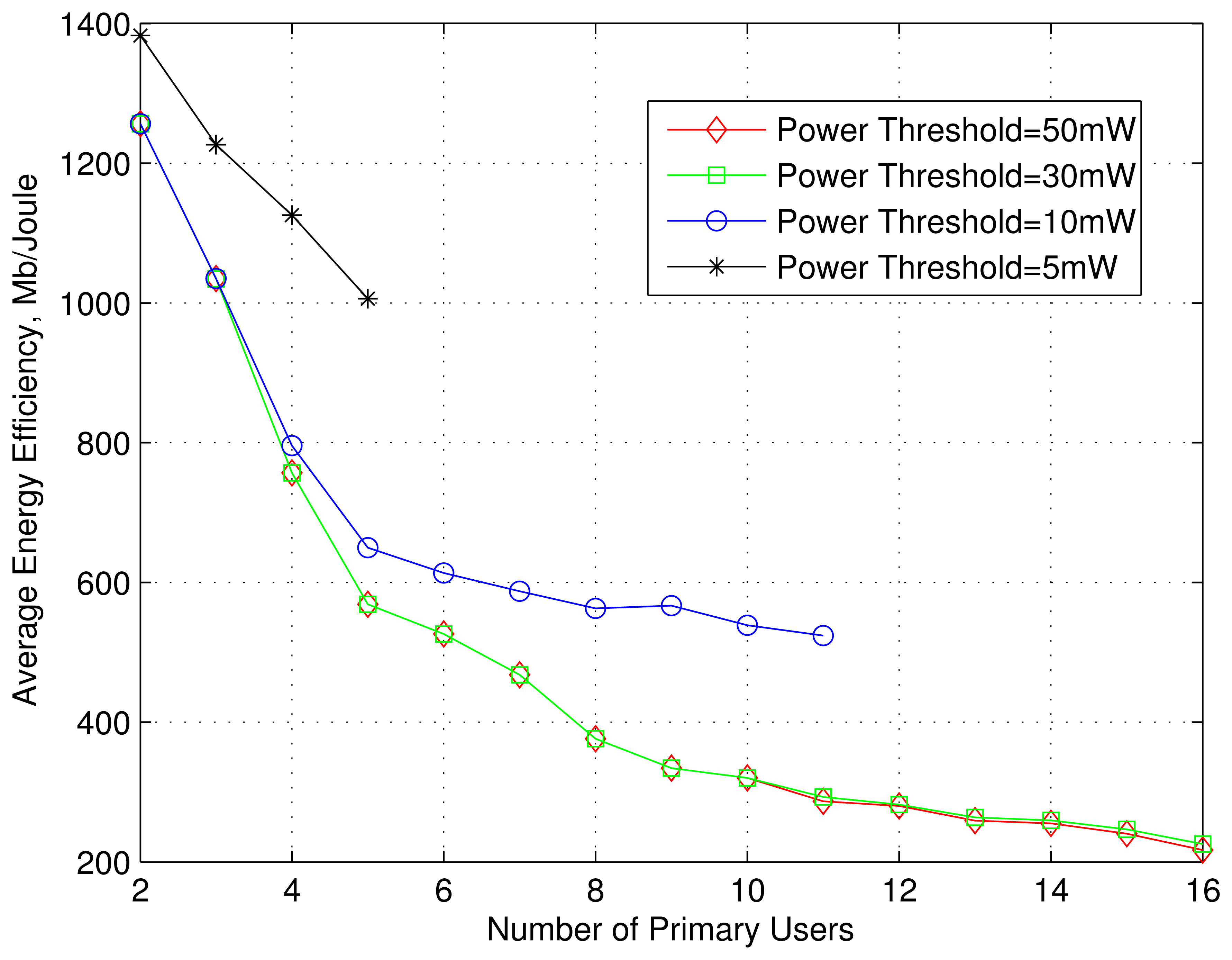
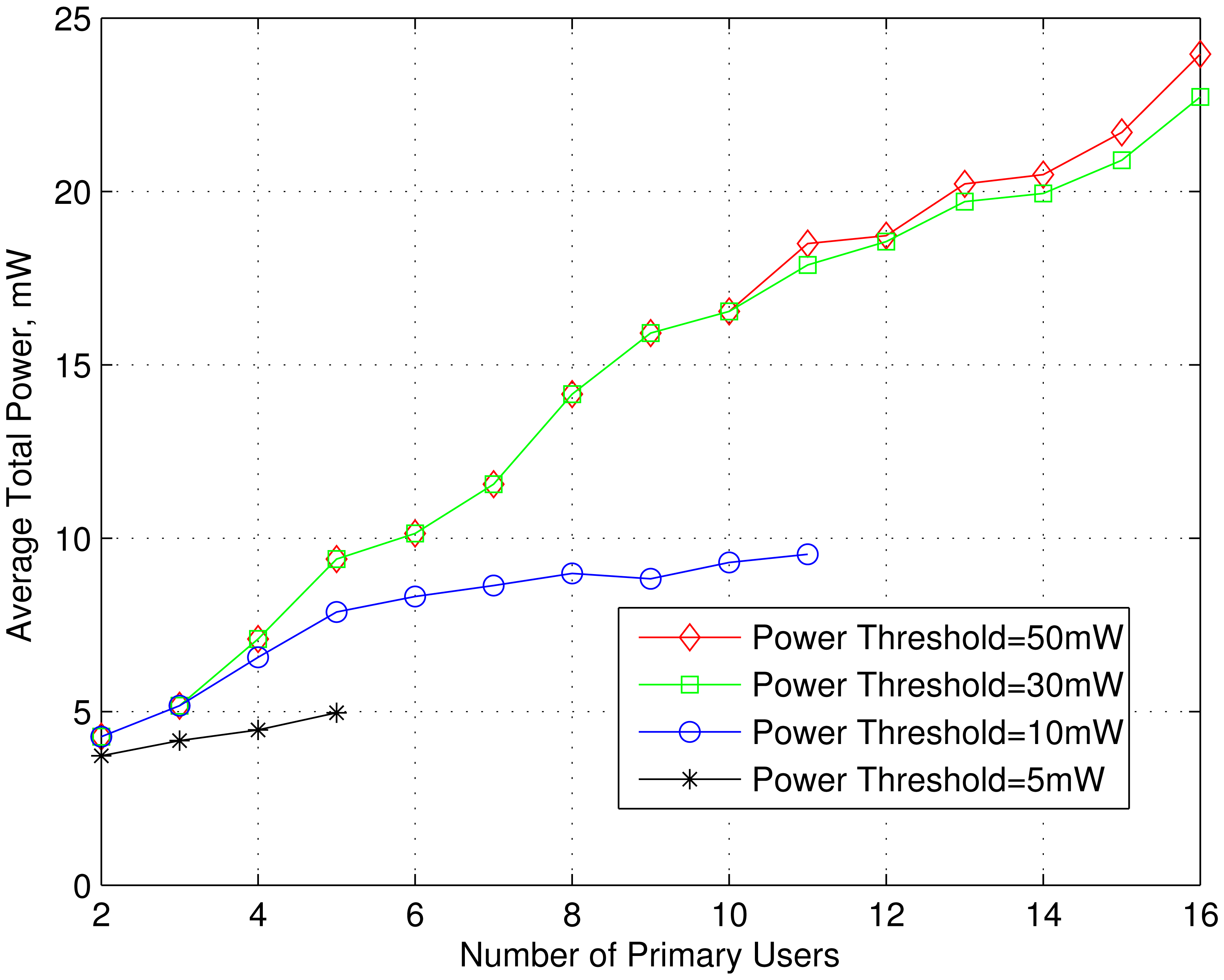
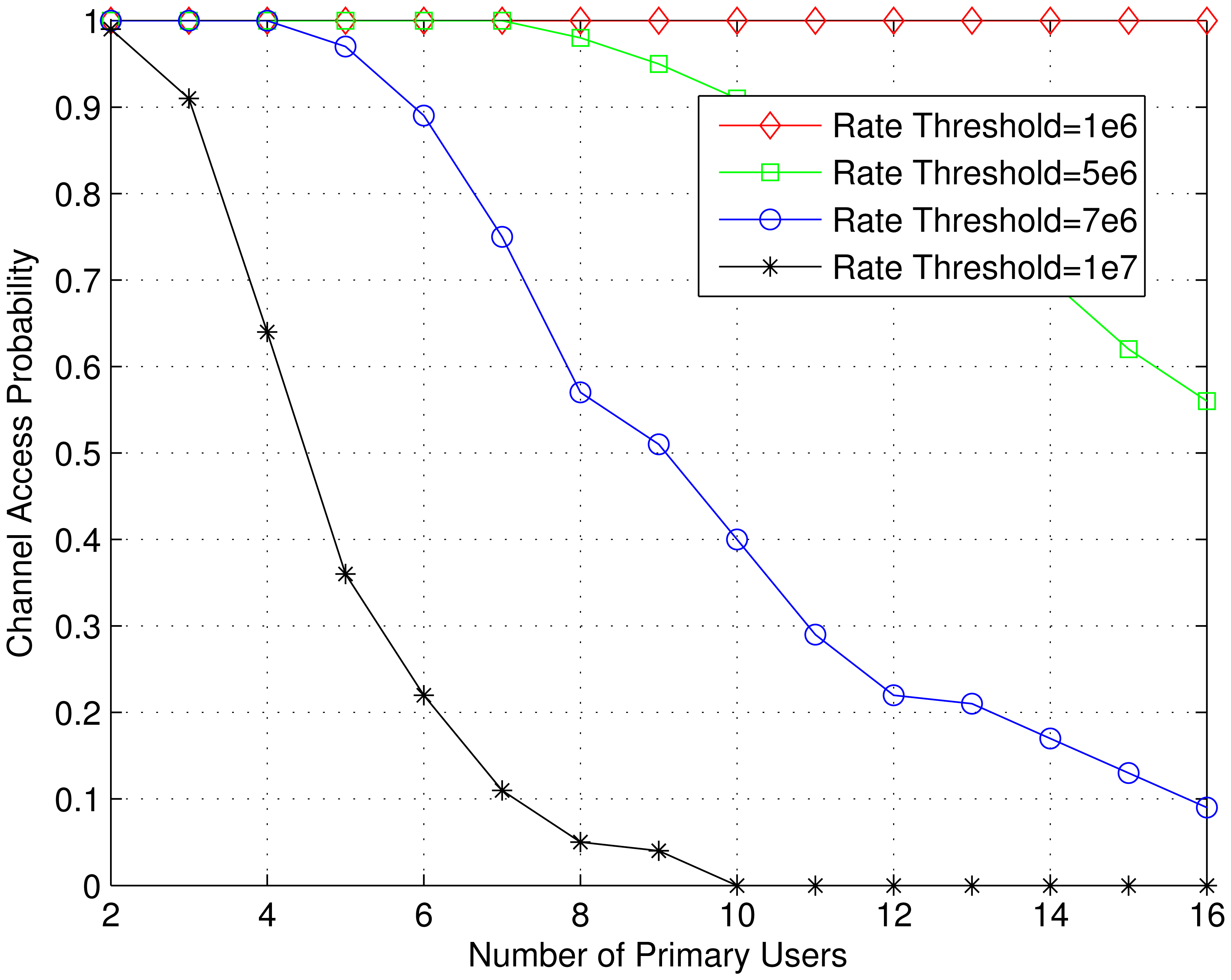
In Figures 4, 5 and 6, we have shown the effect of number of PUs on the channel access probability, average total subcarrier power and average energy efficiency for different power thresholds. For a particular value of power threshold, the channel access probability decreases with the increase of number of PUs. Because more PUs causes more interference to the SU's receiver. Also, the SU transmitter need to maintain interference constraints of additional PUs. As a results, the average numbers of channel realization for which all the constraints, given other bounds remain the same, need to satisfied decreases. Thus, the SU need to raise the power to counteract the increased number of PUs, as can be seen from Figure 6. Since for the same rate threshold the power increases, the energy efficiency decreases with the increase of number of PUs as in Figure 5. It is also seen that as the power threshold decreases, the channel access probability also decreases. For PT = 5 mW, the channel access probability is zero for M = 6 or more PUs. The effect of rate threshold on the channel access probability is shown in Figure 7. It is seen that for a particular number of PUs, the channel access probability decreases as the rate threshold increases. Because in order to achieve higher rate, the SU transmitter need to use higher transmitter power, which in turns disqualify many sets of channel samples for which there existed a feasible region before.
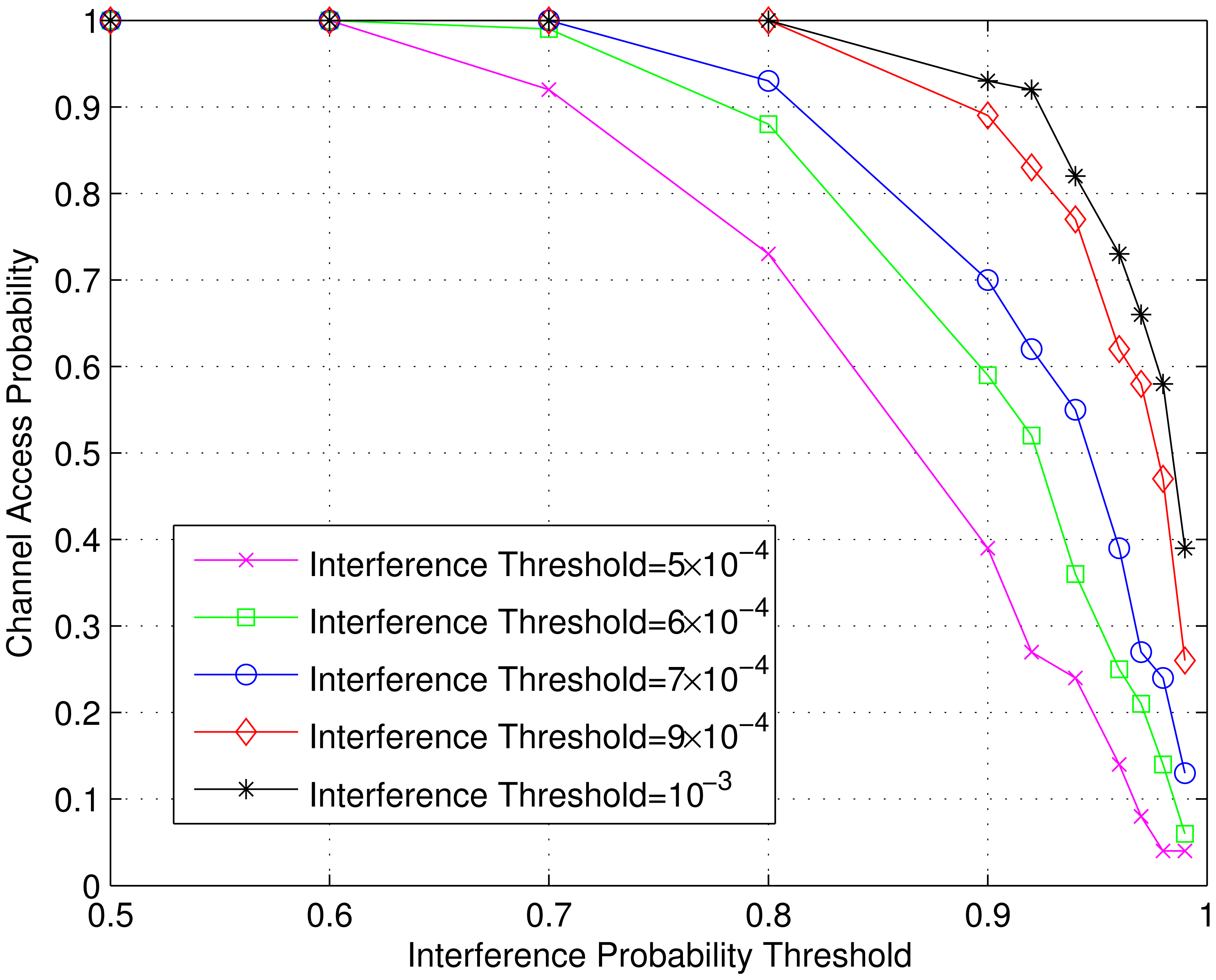
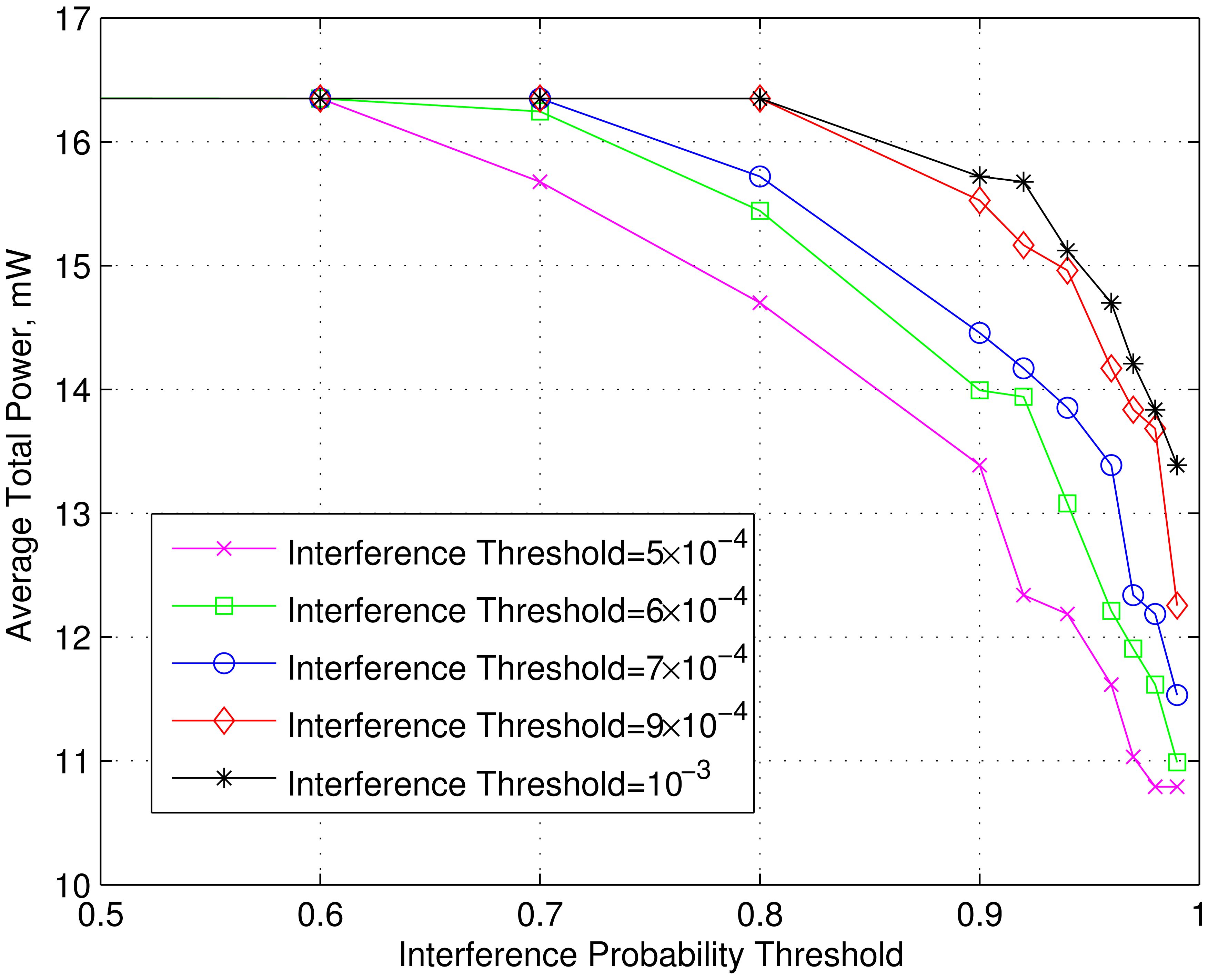
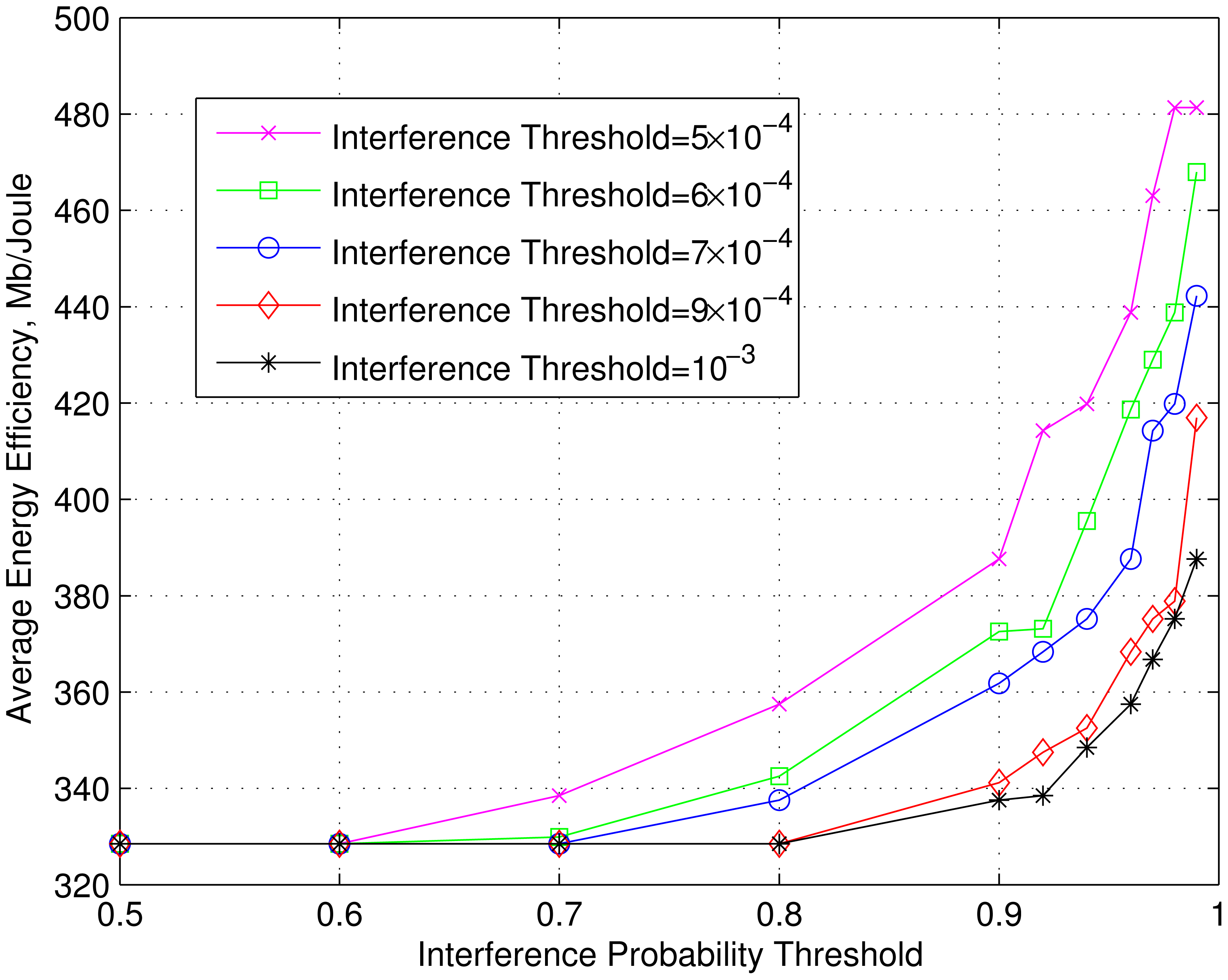
The effect of interference probability threshold on the channel access probability, total power and energy efficiency are shown in Figures 8, 9 and 10 respectively for different interference thresholds. Note that these two interference parameters, namely the interference threshold and interference probability threshold, are specified by the PU networks depending on its QoS requirements. These curves show the performance of SU for different pairs of these parameters. It can be seen from the Figure 8 that the channel access probability decreases with the interference threshold for a particular interference probability threshold. It makes sense because as the interference threshold gets tighter, less channel realization can give a feasible region and hence the channel access probability decreases. The SU transmitter need to use less power in order to meet the interference constraints (7) for the tighter interference threshold as can be seen in Figure 9. Since the total power decreases, the energy efficiency in Figure 10 increases. For a particular value of interference threshold, similar effect is seen for tighter interference probability threshold. It can be explained similarly using Equation (7) since tighter bound requires use of less power in order to satisfy interference constraint, which makes rate thresholds infeasible for greater number of sets of channel realizations.
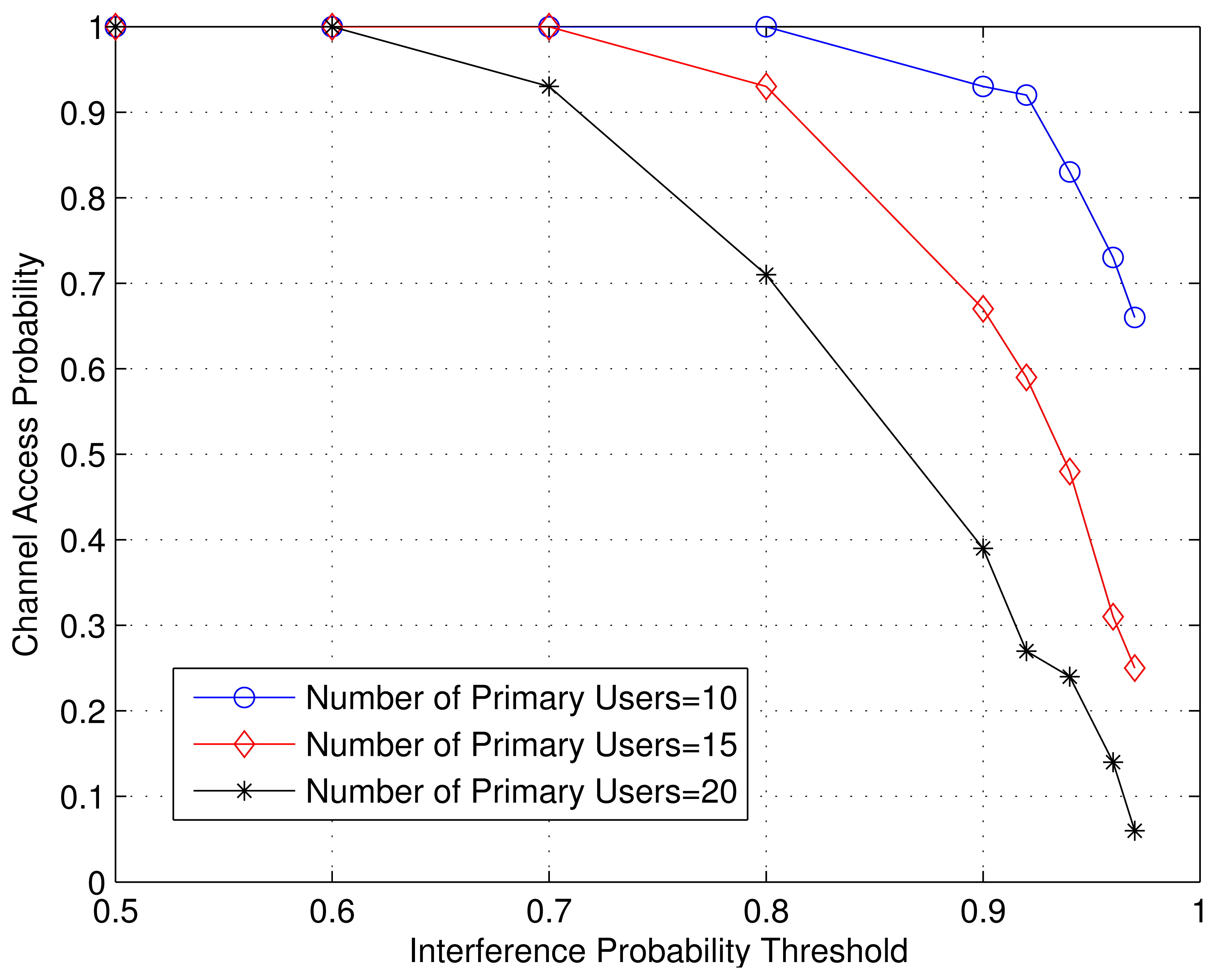
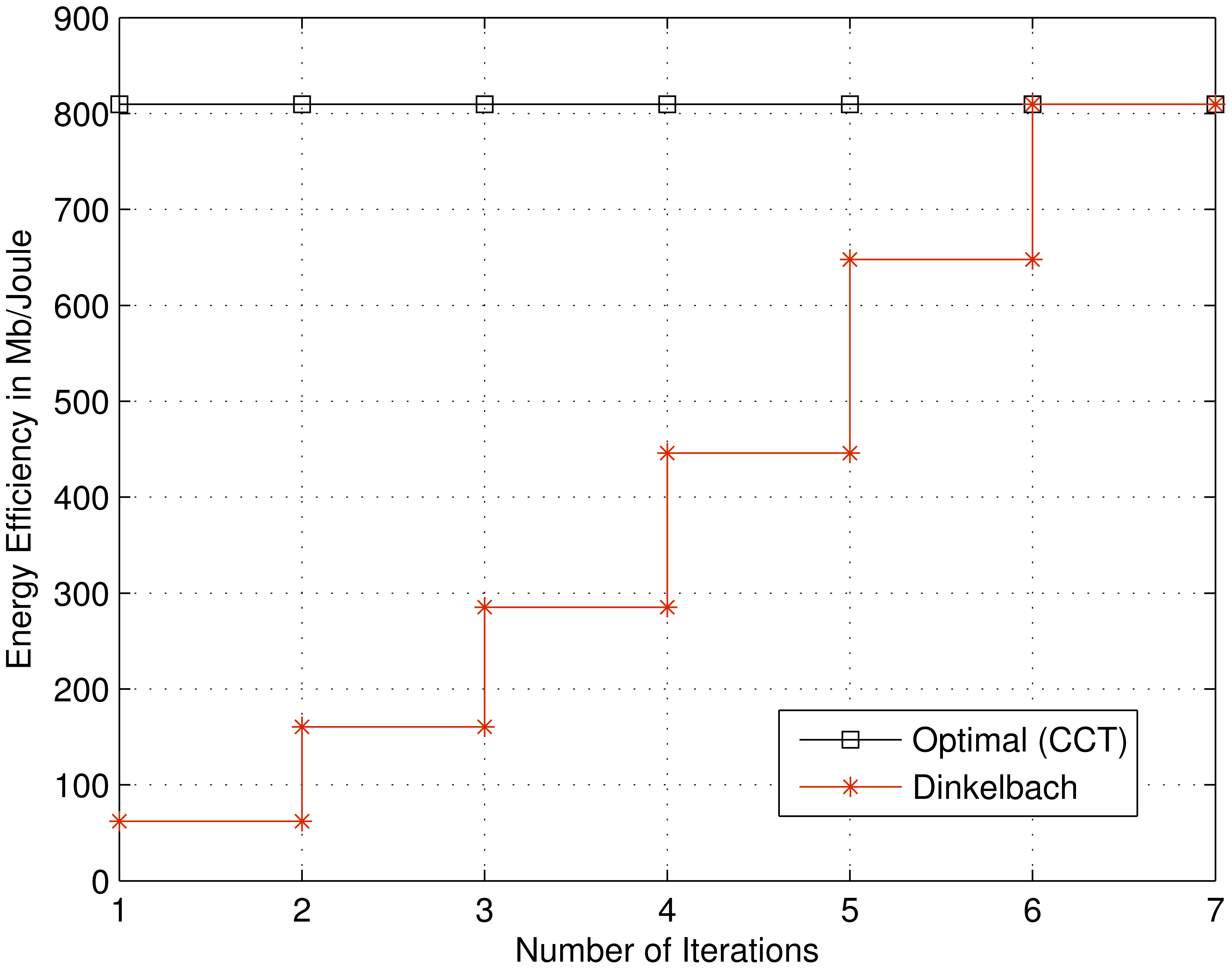
In Figure 11, the effect of interference probability threshold on the channel access probability is shown for different number of PUs. It is seen that the channel access probability decreases as the number of PUs increases. Since now more interference is coming from the increasing number of PUs, the SU transmitter must increase power to maintain the rate threshold, which on the other hand violates interference threshold for many channel situations. Therefore, number of channel condition realizations for which there existed a feasible region decreases. The convergence of Dinkelbach iterative algorithm is shown in Figure 12 and compared it with the CCT optimal solution point. It is found through a large number of simulation cases that the Dinkelbach algorithm converges to optimal solution in less than 8 iterations in most cases.
6. Conclusions
In this paper, we studied energy-efficient downlink power allocation techniques for OFDM-based green cognitive radio systems. We assumed that the primary and secondary users coexist in adjacent bands. In this scenario, the mutual interference is very important to control. We formulated the problem using a fraction programming technique, where the objective is to maximize the energy efficiency that is defined as the ratio of capacity and transmitted power. We first provided the optimal solution of the problem through Charne-Cooper transformation that gives us concave form of the problem from fractional form. Although the original fractional program is quasi-concave for which global optimal point is not guaranteed, the equivalent concave problem is easier to solve using standard optimization technique and also has only one global optimal point. Therefore, finding a local optimal point is enough. Then we investigated the Dinkelbach method, where the fractional objective function is converted into parametric objective function. We provided the proof of one-to-one relationship of the solution between the fractional programming method and the Dinkelbach method. The resulting parametric problem is solved using iterative techniques and ε-optimal solution is found. It is found that Dinkelbach method provides optimal solution very quickly, it converges mostly in 6–10 iterations. We also provided numerical simulation results to show the channel access probability, average total subcarrier power and average energy efficiency performance for different system parameters, such as, interference limits, number of primary users, rate and power thresholds.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix
A. Derivation of Constraint C1 in Equation (7)
Combining constraint C1 of Equations (3) and (6), we can write,
B. Proof of Theorem 1
Let us assume that and . Therefore, we can rewrite Equation (9) in the following standard form:
The Lagrangian function of Equation (A4) can be given by,
Suppose, and t* denote the optimal solution of the Lagrangian function (A5), then the Karush-Kuhn-Tucker (KKT) conditions can be written as follows:
Substituting L from Equation (A5) into Equation (A23) and after some manipulation, we can write following relation:
References
- Jiang, T.; Wu, T. An overview: Peak-to-average power ratio reduction techniques for OFDM signals. IEEE Trans. Broadcast. 2008, 54, 257–268. [Google Scholar]
- Weiss, T.; Hillenbrand, J.; Krohn, A.; Jondral, F. Mutual interference in OFDM-based spectrum pooling systems. Proceedings of the Vehicular Technology Conference (VTC'2004), Milan, Italy, 17–19 May 2004; Volume 4, pp. 1873–1877.
- Rahman, M.J.; Wang, X.; Primak, S.L. Efficient mutual interference minimization and power allocation for ofdm-based cognitive radio. Proceedings of the IEEE Global Communications Conference (GLOBECOM'09), Honolulu, HI, USA, 30 November–4 December 2009; pp. 1–6.
- Malon, K.; Lopatka, J. Efficient methods of interference suppression for spectrum pooling cognitive radios using OFDM signals. Proceedings of the Signal Processing and Communication Systems (ICSPCS'2011), Honolulu, HI, USA, 12–14 December 2011; pp. 1–6.
- Alen, T.C.H.; Madhukumar, A.S.; Chin, F. Capacity enhancement of a multi-user OFDM system using dynamic frequency allocation. IEEE Trans. Broadcast. 2003, 49, 344–353. [Google Scholar]
- Durowoju, O.; Arshad, K.; Moessner, K. Distributed power control for cognitive radios with primary protection via spectrum sensing. Proceedings of the IEEE Vehicular Technology Conference Fall (VTC'2010-Fall), Ottawa, ON, Canada, 6–9 September 2010; pp. 1–5.
- Hamdi, K.; Letaief, K.B. Power, sensing time, and throughput tradeoffs in cognitive radio systems: A cross-layer approach. Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC'2009), Budapest, Hungary, 5–8 April 2009; pp. 1–5.
- Zhang, R. On peak versus average interference power constraints for protecting primary users in cognitive radio networks. IEEE Trans. Wirel. Commun. 2009, 8, 2112–2120. [Google Scholar]
- Son, K.; Jung, B.C.; Chong, S.; Sung, D.K. Power allocation for ofdm-based cognitive radio systems under outage constraints. Proceedings of the IEEE International Conference on Communications (ICC'2010), Cape Town, South Africa, 23–27 May 2010; pp. 1–5.
- Kang, X.; Zhang, R.; Liang, Y.-C.; Garg, H. Optimal power allocation strategies for fading cognitive radio channels with primary user outage constraint. IEEE J. Sel. Areas Commun. 2011, 29, 374–383. [Google Scholar]
- Ngo, D.T.; Le-Ngoc, T. Distributed resource allocation for cognitive radio networks with spectrum-sharing constraints. IEEE Trans. Veh. Technol. 2011, 60, 3436–3449. [Google Scholar]
- Kim, D.I.; Le, L.B.; Hossain, E. Joint rate and power allocation for cognitive radios in dynamic spectrum access environment. IEEE Trans. Wireless Commun. 2008, 7, 5517–5527. [Google Scholar]
- Bansal, G.; Hossain, M.J.; Bhargava, V. Adaptive power loading for OFDM-based cognitive radio systems with statistical interference constraint. IEEE Trans. Wirel. Commun. 2011, 10, 2786–2791. [Google Scholar]
- Xu, J.; Lee, S.-J.; Kang, W.-S.; Seo, J.-S. Adaptive resource allocation for MIMO-OFDM based wireless multicast systems. IEEE Trans. Broadcast. 2010, 56, 98–102. [Google Scholar]
- Ben-Shimol, Y.; Kitroser, I.; Dinitz, Y. Two-dimensional mapping for wireless OFDMA systems. IEEE Trans. Broadcast. 2003, 52, 388–396. [Google Scholar]
- Muntean, G.-M.; Cranley, N. Resource efficient quality-oriented wireless broadcasting of adaptive multimedia content. IEEE Trans. Broadcast. 2007, 53, 362–368. [Google Scholar]
- Ergen, M.; Coleri, S.; Varaiya, P. QoS aware adaptive resource allocation techniques for fair scheduling in OFDMA based broadband wireless access systems. IEEE Trans. Broadcast. 2003, 49, 362–370. [Google Scholar]
- Lei, Z.; Chin, F. A reliable and power efficient beacon structure for cognitive radio systems. IEEE Trans. Broadcast. 2008, 54, 182–187. [Google Scholar]
- Li, L.; Zhou, X.; Xu, H.; Li, G.Y.; Wang, D.; Soong, A.C.K. Energy-efficient transmission for protection of incumbent users. IEEE Trans. Broadcast. 2011, 57, 718–720. [Google Scholar]
- Koutitas, G. Green network planning of single frequency networks. IEEE Trans. Broadcast. 2010, 56, 541–550. [Google Scholar]
- Venturino, L.; Risi, C.; Buzzi, S.; Zappone, A. Energy-efficient coordinated user scheduling and power control in downlink multi-cell OFDMA networks. Proceedings of the IEEE Personal Indoor and Mobile Radio Communications (PIMRC'2013), London, UK, 8–11 September 2013; pp. 1655–1659.
- Kang, X.; Zhang, R.; Liang, Y.-C.; Garg, H.K. Energy-efficient resource allocation in multi-cell OFDMA systems with limited backhaul capacity. IEEE Trans. Wirel. Commun. 2012, 11, 3618–3631. [Google Scholar]
- Isheden, C.; Chong, Z.; Jorswieck, E.; Fettweis, G. Framework for link-level energy efficiency optimization with informed transmitter. IEEE Trans. Wirel. Commun. 2012, 11, 2946–2957. [Google Scholar]
- Fehske, A.; Fettweis, G.; Malmodin, J.; Biczook, G. The global footprint of mobile communications: The ecological and economic perspective. IEEE Commun. Mag. 2011, 49, 55–62. [Google Scholar]
- Han, C.; Harrold, T.; Armour, S.; Krikidis, I.; Videv, S.; Grant, P.; Haas, H.; Thompson, J.; Ku, I.; Wang, C.-X.; et al. Green radio: Radio techniques to enable energy-efficient wireless networks. IEEE Commun. Mag. 2011, 49, 46–54. [Google Scholar]
- Li, G.; Xu, Z.; Xiong, C.; Yang, C.; Zhang, S.; Chen, Y.; Xu, S. Energy-efficient wireless communications: Tutorial, survey, and open issues. IEEE Wirel. Commun. Mag. 2011, 18, 28–35. [Google Scholar]
- Gelenbe, E.; Gunduz, D. Optimum power level for communications with interference. Proceedings of 24th Tyrrhenian International Workshop on Digital Communications—Green ICT (TIWDC), Genoa, Italy, 23–25 September 2013; pp. 1–6. [CrossRef]
- Gelenbe, E.; Oklander, B. Cognitive users with useful vacations. Proceedings of the International Conference on Communications (ICC'2013) Workshops, Budapest, Hungary, 9–13 June 2013; pp. 370–374.
- Oklander, B.; Gelenbe, E. Optimal Behaviour of Smart Wireless Users. In Information Sciences and Systems; Gelenbe, E., Lent, R., Eds.; Springer International Publishing: New York, NY, USA, 2013; pp. 87–95. [Google Scholar]
- Gelenbe, E.; Lent, R. Information Sciences and Systems 2013. Proceedings of the 28th International Symposium on Computer and Information Sciences (ISCIS) 2013, Paris, France, 28–29 October 2013; Gelenbe, E., Lent, R., Eds.; Springer Lecture Notes in Electrical Engineering: New York, NY, USA, 2013; Volume 264, pp. 87–95. [Google Scholar]
- Gelenbe, E.; Morfopoulou, C. A framework for energy-aware routing in packet networks. Comput. J. 2011, 54, 850–859. [Google Scholar]
- Sakellari, G.; Morfopoulou, C.; Gelenbe, E. Investigating the tradeoffs between power consumption and quality of service in a backbone network. Futur. Internet. 2013, 5, 268–281. [Google Scholar]
- Gelenbe, E. Energy Packet Networks: ICT Based Energy Allocation and Storage. In Green Communications and Networking 2012; Springer Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering: Heidelberg, Germany; Volume 51, pp. 186–195.
- Rodrigues, J.; Zhou, L.; Chen, M.; Kailas, A. Green Communications and Networking. Proceedings of the 1st International Conference, GreeNets 2011, Colmar, France, 5–7 October 2011; Springer: Berlin/Heidelberg, Germany, 2012; Volume 51. [Google Scholar]
- Goldsmith, A.J. Wireless Communications; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Schaible, S.; Ibaraki, T. Fractional programming. Eur. J. Oper. Res. 1983, 12, 325–338. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Charnes, A.; Cooper, W.W. Programming with linear fractional functionals. Naval Res. Logist. Q. 1962, 9, 181–186. [Google Scholar]
- Dinkelbach, W. On nonlinear fractional programming. Manag. Sci. 1967, 13, 492–498. [Google Scholar]
Notations
| M | Number of primary users (PUs) |
| Bi | Bandwidth of ith PU |
| N | Number of subcarriers of the secondary user's (SU's) transmitter |
| Δf | Bandwidth of a subcarrier |
Channel fading gain of jth subcarrier | |
Channel power gain of jth subcarrier | |
Channel fading gain between SU transmitter and ith PU | |
Channel power gain between SU transmitter and ith PU | |
| pj | Power allocated to jth subcarrier |
| Iji | Interference by jth subcarrier to ith PU |
Interference threshold | |
Interference probability threshold | |
| Cj | Capacity/Rate of jth subcarrier in bits/sec |
| Cth | Capacity/Rate threshold |
| PT | Maximum transmitted power over all subcarriers |
| Jij | Interference by ith PU to jth subcarrier |
| Ts | OFDM symbol duration |
| dji | Spectral distance between jth subcarrier and ith PU |
| f(p) | Numerator of fractional program |
| g(p) | Denominator of fractional program |
| y | = tp, Charnes-Cooper transformation variable |
| t | = g(p)−1, Charnes-Cooper transformation variable |
| ε | Convergence tolerance parameter in Dinkelbach method |
| q | Real-valued parameter so that F(q) = maxp[f(p) − qg(p)] |
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Karmokar, A.; Naeem, M.; Anpalagan, A.; Jaseemuddin, M. Energy-Efficient Power Allocation Using Probabilistic Interference Model for OFDM-Based Green Cognitive Radio Networks. Energies 2014, 7, 2535-2557. https://doi.org/10.3390/en7042535
Karmokar A, Naeem M, Anpalagan A, Jaseemuddin M. Energy-Efficient Power Allocation Using Probabilistic Interference Model for OFDM-Based Green Cognitive Radio Networks. Energies. 2014; 7(4):2535-2557. https://doi.org/10.3390/en7042535
Chicago/Turabian StyleKarmokar, Ashok, Muhammad Naeem, Alagan Anpalagan, and Muhammad Jaseemuddin. 2014. "Energy-Efficient Power Allocation Using Probabilistic Interference Model for OFDM-Based Green Cognitive Radio Networks" Energies 7, no. 4: 2535-2557. https://doi.org/10.3390/en7042535
APA StyleKarmokar, A., Naeem, M., Anpalagan, A., & Jaseemuddin, M. (2014). Energy-Efficient Power Allocation Using Probabilistic Interference Model for OFDM-Based Green Cognitive Radio Networks. Energies, 7(4), 2535-2557. https://doi.org/10.3390/en7042535



