An Asymmetrical Fuzzy-Logic-Control-Based MPPT Algorithm for Photovoltaic Systems
Abstract
: In this paper, a fuzzy-logic-control (FLC) based maximum power point tracking (MPPT) algorithm for photovoltaic (PV) systems is proposed. The power variation and output voltage variation are chosen as inputs of the proposed FLC, which simplifies the calculation. Compared with the conventional perturb and observe (P&O) method, the proposed FLC-based MPPT can simultaneously improve the dynamic and steady state performance of the PV system. To further improve the performance of the proposed method, an asymmetrical membership function (MF) concept is also proposed. Two design procedures are proposed to determine the universe of discourse (UOD) of the input MF. Comparing with the proposed symmetrical FLC-based MPPT method, the transient time and the MPPT tracking accuracy are further improved by 42.8% and 0.06%, respectively.1. Introduction
In recent years, the concerns over greenhouse gas emission and the ever rising fuel prices have stimulated urgent demands for alternative energy. Government incentives and the soaring cost of fossil fuels have significantly promoted the development of renewable energies. Among them, solar energy is one of the most important green energy resources due to its environmental sustainability and inexhaustibility [1–3]. Since the I–V characteristic curve of photovoltaic (PV) cells varies nonlinearly with the insolation and temperature, it is crucial to operate PV system to a specific point to extract maximum solar energy. This technology is normally named as maximum power point tracking (MPPT). Many MPPT methods have been developed and implemented in previous studies, including perturb and observe (P&O), incremental conductance (IncCon), fractional open-circuit voltage, fractional short-circuit current, line approximation, ripple correlation control (RCC) and fuzzy logic control (FLC) approaches. These techniques have high tracking accuracy under steady weather conditions, but still exhibit some trade-offs between tracking speed and tracking accuracy when insolation changes [4,5]. Taking the P&O method for instance, it determines the perturbation directions of the control value (i.e., PV voltage, PV current or duty cycle) of the system according to the measured power in prior state and current state. With larger perturbation steps, it will take less time for the PV system to track the maximum power point (MPP) from one steady state to another. However, the power loss caused by perturbation in the steady state will also increase. On the other hand, a smaller perturbation step can improve the power loss caused by perturbation in the steady state but will slow down the tracking speed. Therefore, how to determine the perturbation step becomes an important issue [6]. To deal with this problem, variable-step size MPPT methods are proposed in many literatures [7–13]. The basic operating principle of these kinds of methods is that when operating point is far from the MPP, larger perturbation step will be used to improve tracking speed. On the other hand, when operating point is close to the MPP, smaller perturbation step will be used to improve steady-state efficiency. However, since PV system is a nonlinear system, how to determine the scaling factor of the perturbation step becomes significant when realizing these variable-step size MPPT algorithms. On the other hand, FLC has advantages that its parameters can be determined without precise and complicate mathematical model and it is capable of operating under highly nonlinear system. As a result, the FLC-based MPPT algorithm attracts many research interests. Recently, numerous MPPT techniques based on FLC have been proposed in the literatures [14–34]. In comparison with conventional P&O algorithm, FLC-based MPPT provides superior tracking performance. However, the design consideration and realization complexity for different kinds of FLC-based MPPT techniques vary greatly.
In terms of the input variable selection, most FLC-based MPPT techniques take the error [e(t), usually defined as dPPV/dVPV or dPPV/dIPV] and the error variation [Δe(t)] as inputs [14–19]. For these methods, divisions is required therefore increases the computation complexity. Moreover, derivative operation may induce large amounts of errors from merely small amounts of measurement noise. Therefore, additional considerations are required during implementation. In contrast, [20–24] take power variation (ΔPpv) and voltage or current variation (ΔVpv or ΔIpv) as inputs, which avoids the precision loss and overflow problem when dealing with fixed-point division, thus simplifies the calculation. The inputs in [25] are dPPV/dIPV and e(t) (defined as PMPP − PPV), while the inputs in [26] are error [e(t)] (defined as PMPP − PPV) and error variation [Δe(t)]. Since the information of MPP should be acquired in prior, these methods are not suitable for practical realization. In [27–34], solar irradiation and cell temperature are used as FLC inputs. However, most of the small PV systems do not equip irradiation and temperature sensors; hence these methods are not suitable for cost-sensitive systems.
Regarding the design of input/output membership functions (MFs), it is known that the input/output MFs design has a great impact on FLCs' performance. In order to deal with this issue, genetic algorithm (GA), particle swarm optimization (PSO) and Hopfield artificial neural network (ANN) are proposed in the literatures to optimize the FLC MFs [15–17,24]. As for control schemes, typical dual-input fuzzy logic controller is adopted by [14–26]. These controllers employ nine to 49 rules in the rule table, depending on the numbers of linguistic variables in input MFs. However, these methods share similar implementation complexity. Ref. [27–31] uses ANN to assist FLC. ANN technique needs a great amount of training data to acquire reasonable result, thus the solar irradiance and cell temperature are often taken as input variables in such methods, this could limit its application. In order to enhance the FLC efficiency, fuzzy cognitive networks [18,32] and Takagi-Sugeno (T-S) fuzzy technique [33,34] are employed to improve the tracking speed. Comparing with conventional FLC, these methods are difficult to be realized using low-cost microcontrollers due to their complicated computation. Moreover, FLC can be used to adaptively tune the gains of the PID controller utilized in the MPPT controller [35].
The aim of this paper is to design a low cost, high efficiency MPPT algorithm. In this paper, power variation (ΔPpv) and output voltage variation (ΔVpv) are chosen as the inputs of the proposed FLC. The design of the FLC scheme and rule table will be introduced in detail first. To further improve the performance of the proposed MPPT method, an asymmetrical MF concept is proposed. A systematic design procedure verified by grid-search method will be proposed to determine the universe of discourse (UOD) of the input MF. Finally, a low cost digital signal controller (DSC) will be used to realize the proposed method. Experiments are then conducted to validate the correctness and effectiveness of the proposed system. According to the experimental results, the proposed asymmetrical FLC-based MPPT method can simultaneously shorten the tracking time and increase the tracking accuracy comparing with the traditional P&O and symmetrical FLC-based MPPT algorithm.
2. System Configuration
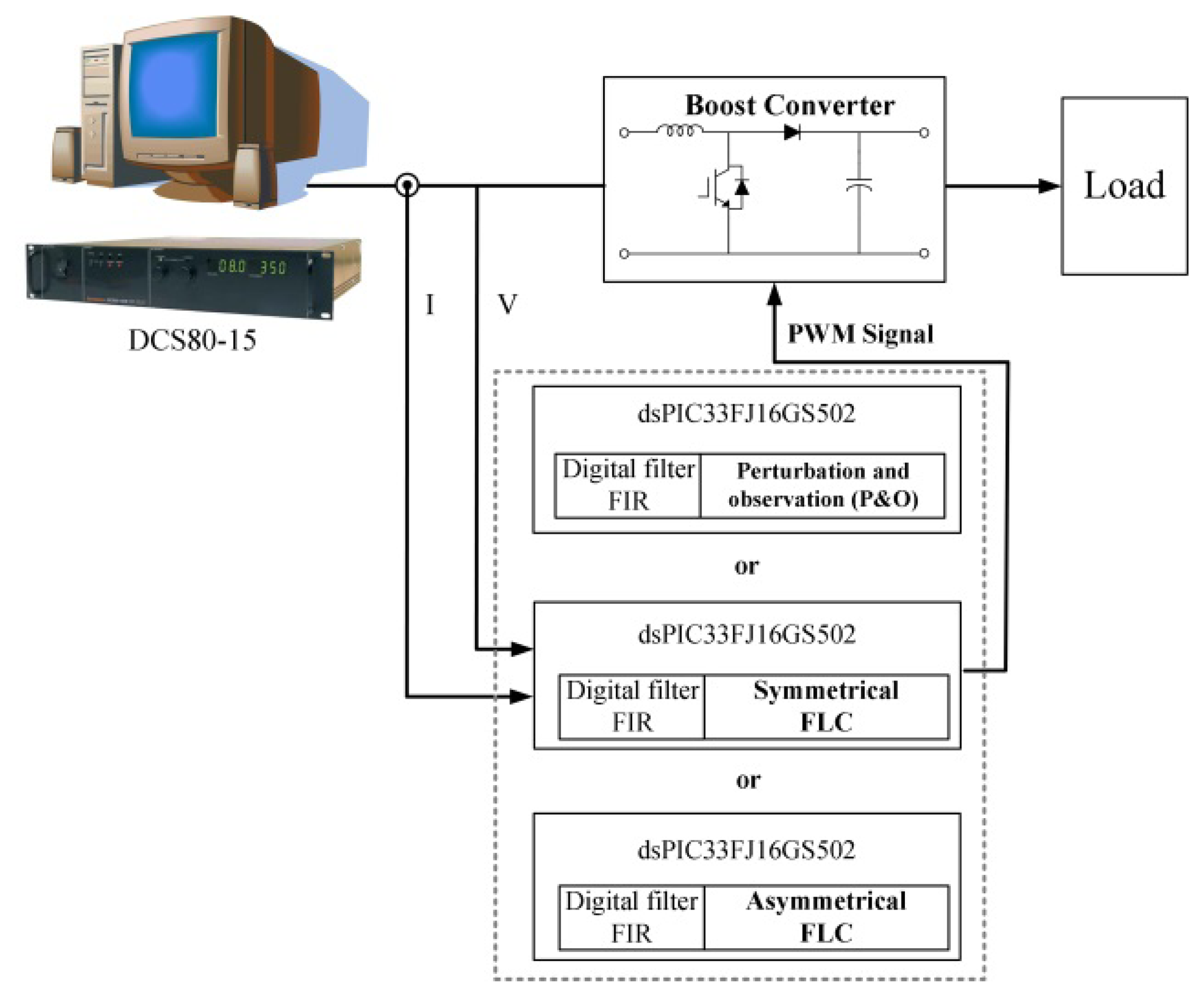
The block diagram of the proposed system is shown in Figure 1. In this study, a low cost DSC dsPIC33FJ16GS502 from Microchip Corp. (Chandler, AZ, USA) is used to implement the developed MPPT algorithm. The utilized DSC provides the required gating signal for the power switch in the power converter and gathers data from the signal conditioning circuits. From Figure 1, the whole system can be divided into three major parts: energy conversion unit, main control unit and data logging system. Detailed descriptions about each unit will be given in the following subsections:
- (a)
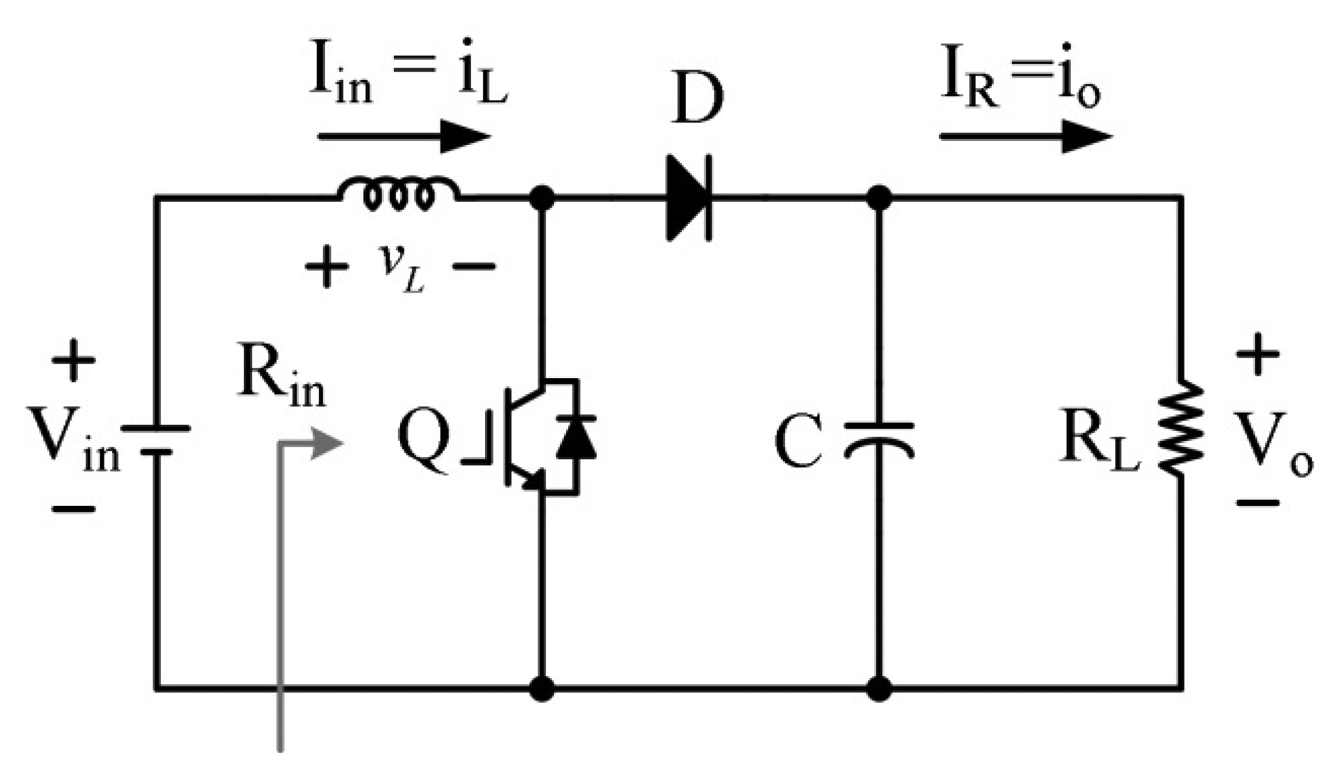
Energy conversion unit: the energy conversion unit is used to supply the power to the load. The topology of the energy conversion unit is illustrated in Figure 2. A simple boost type DC-DC converter is utilized in this paper. By adequately controlling the PWM gating signal, the energy conversion unit can transfer the maximum available PV energy to the load. The design and implementation of this part of circuit is conventional; therefore will not be discussed further here.
The relationship between output voltage and input voltage in boost converter can be expressed as:
where δ represents the duty cycle. Assuming the conversion efficiency of the boost converter is 100%, relationship between the output current and the input current can be written as:From Equations (1) and (2), when duty cycle varies, relationship between the input impedance and the output load of the boost converter can be described using Equation (3):
- (b)
Main control unit: As shown in Figure 1, the main control unit provides the PWM signal for the boost converter to track the peak power available from PV panel. The utilized DSC gathers and analyzes PV panel data (voltage and current) from the A/D module. After obtaining the required PV panel data, a digital filter is employed to smooth out the acquired signals. The digital filter used in the proposed system is a 24-order finite impulse response (FIR) filter. The equation describing a FIR filter can be expressed as in Equation (4):
where X is the filter input; Y is the filter output and ai is the corresponding coefficient of the designed FIR filter.After the filtered PV voltage and current are obtained, needed gating signals are then determined using the developed MPPT controller. In this paper, three different MPPT schemes will be implemented for performance comparison, detailed description of these MPPT methods will be provided in Section 3.
- (c)
Data logging system: In order to validate the effectiveness of the proposed method, long term recording of the operating condition is required. Solar array simulator (SAS) TerraSAS DCS80-15 from AMETEK Corp. (Berwyn, PA, USA) is adopted as the input power source in this paper. This simulator features long-term recording function with the recording time interval as short as 0.05s. The recorded data will be stored to a spreadsheet file for further analysis.
3. Derivation of the Proposed FLC-Based MPPT Controller
3.1. Derivation of the FLC-Based MPPT Controller
Figure 3 shows the equivalent circuit of the PV cell, the I-V characteristic of the PV cell can be mathematically described by Equation (5):
Figure 4a shows the I-V curves of the utilized Sanyo VBHN220AA01 solar panel under different irradiation levels, these curves are obtained using MATLAB simulation. The circular markers in the graph represent the calculated maximum power points. The corresponding P-V curve for 1000 W/m2 irradiation level is given in Figure 4b. Observing Figure 4b, the absolute value of dP/dV of a PV panel varies smoothly and is recommended in [10] as a suitable parameter for determining the step size of the IncCon algorithm. Thus, power variation (ΔPpv) and voltage variation (ΔVpv) from solar cell are also used as the inputs of the proposed FLC-based MPPT controller.
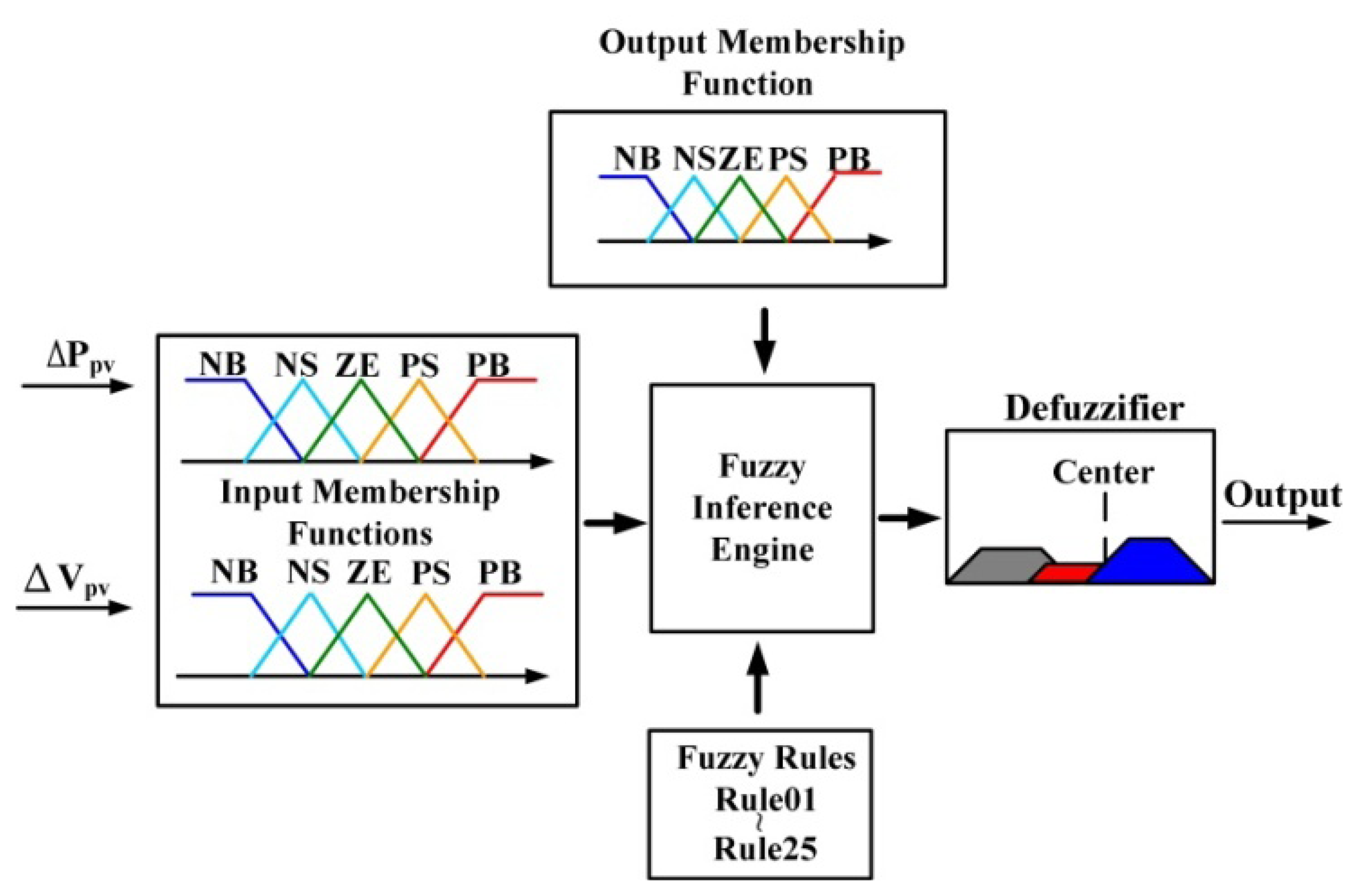
To achieve MPPT, a fuzzy controller is used to determine the required perturbation step size. The proposed fuzzy controller is carried out every 20 ms. The block diagram of the implemented FLC-based MPPT controller is shown in Figure 5.
In this paper, the inputs of the proposed MPPT controller are the power variation (ΔPpv) and the voltage variation (ΔVpv). The MFs of the utilized input and output variables for the proposed controller are illustrated in Figure 6. Figure 6a shows the MFs of the input variables; both ΔPpv and ΔVpv MFs are in triangular form. Figure 6b is the MF of the output (duty cycle step size ΔD), which is also in triangular form. In Figure 6, dP stands for power variation, dV represents voltage variation and dD denotes duty cycle variation. For linguistic variables, P represents positive, N represents negative, B, S, and ZE are defined as big, small and zero, respectively. From Figure 6, each of the input variables ΔPpv and ΔVpv is mapped into five different linguistic values. Therefore, the proposed FLC will contain 25 different rules. The complete set of the fuzzy control rules for the proposed system will be explained in Section 3b. The defuzzification method used in this paper is the commonly used center of gravity method as shown in Equation (6):
3.2. Parameters Design of FLC-Based MPPT Controller
It is known that the FLC performance will be affected by the design of MFs. Generally, the shape of MFs in FLC can be in triangular, trapezoidal, symmetric Gaussian function, generalized Bell curve and sigmoidal function forms. Since a low cost DSC will be used in this paper to realize the proposed FLC-based MPPT controller, triangular MF is adopted to reduce the computation complexity. Next, the UOD of the MFs will be determined by the following procedures:
- (1)
Designing the UOD of the output MF: In this paper, duty cycle variation is chosen to be the output variable. The advantage of using duty cycle as the control variable is its simplicity. For direct duty control, no close-loop control is needed to achieve voltage control for MPPT realization [10]. FLC-based MPPT algorithm can be regarded as an adaptive P&O method with its perturbation step automatically adjusted by FLC. For P&O method, a larger step can achieve better tracking dynamic but will increase fluctuation on steady state, and vice versa. Therefore, the maximum value of the perturbation step has to be determined first. In the paper, the maximum perturbation step in MPPT, dDmax, is set as 5%;
- (2)
Designing the UOD of input MFs: In this context, voltage variation ΔVpv and power variation ΔPpv are chosen to be input variables. The UOD of ΔVpv and ΔPpv can be determined by the following procedures:
With a 1% step size, a profile can be plotted by increasing duty cycle from 0% to 100% with x-axis represents duty cycle and y-axis represents voltage variation or power variation, as shown in Figure 7. In Figure 7, the simulation is conducted under the standard test condition (1000 W/m2, 25 °C). From Figure 7a, the maximum value of ΔV/ΔD will be utilized to determine the UOD of ΔVpv (denoted as dVmax). Likewise, the UOD of ΔPpv (denoted as dPmax) can be determined in similar ways. In this paper, dVmax is 1.5 V and dPmax is 8.2 W.
For control rule design, since ΔVpv and ΔPpv are taken as the inputs and ΔD is chosen as the output in this paper; therefore, the control rule should be determined according to the relationships between these variables. From Figure 6, each of the input variables ΔVpv and ΔPpv is mapped into five different linguistic values. Therefore, the rule base of the proposed FLC will contain 25 different rules. The basic principle of designing the rules is explained as follows:
As mentioned in Section 2, boost converter is utilized in the paper. As shown in Equation (3), the operating point will move from right to left along the P-V curve when duty cycle increases and vice versa. For the proposed system, a positive ΔP/ΔV value indicates that the operating point lies on the left-hand side of MPP. In this case, a negative value of ΔD is needed to make the operating point moving toward right to reach MPP. On the other hand, a negative ΔP/ΔV value represents that the operating point locates on the right-hand side of MPP. Therefore, a positive value of ΔD is needed. Consequently, the sign of the ΔP/ΔV can be used to determine the sign of the output variable ΔD. Next, the magnitude of the output variable ΔD can be determined using the following design principles. Figure 8 shows a typical P-V curve of a PV panel. Observing Figure 8, when the operating point is far from the MPP (like point A or B in Figure 8), a larger ΔD is required to rapidly reach the MPP. On the contrary, when the operating point is close to the MPP (like point C or D in Figure 8), a smaller ΔD can be used to reduce the fluctuation on steady state. Therefore, the value of |ΔP/ΔV| can be utilized to determine the magnitude of the output. Based on this concept, a complete set of fuzzy rules for the proposed FLC are summarized in Table 1. In Table 1, darker color represents larger number while lighter color indicates smaller number. Red represents positive value, green represents negative value and white represents zero.
4. Derivation of the Proposed Asymmetrical FLC-Based MPPT Controller
4.1. Grid Search Method to Determine the UOD of ΔPpv
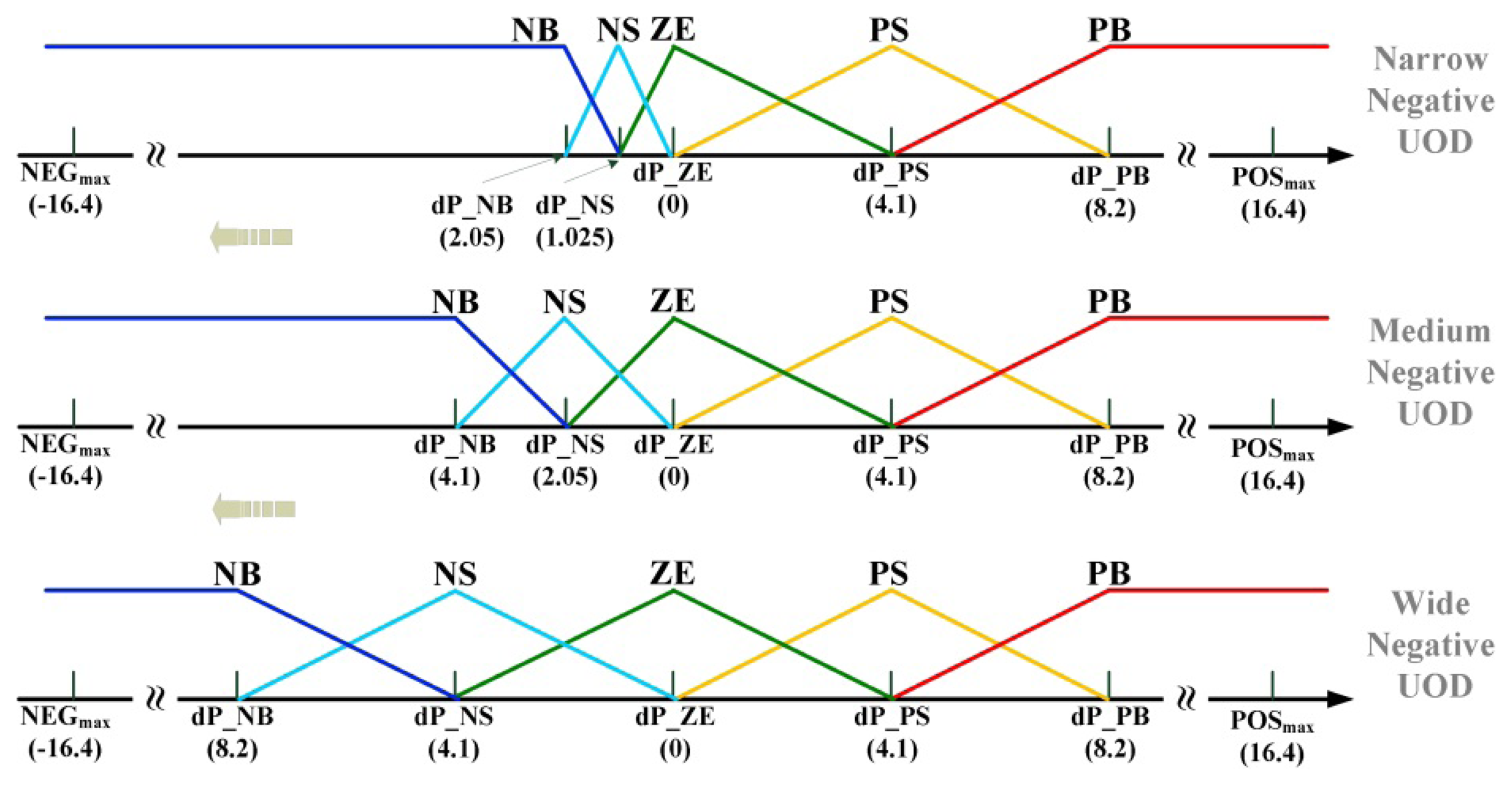
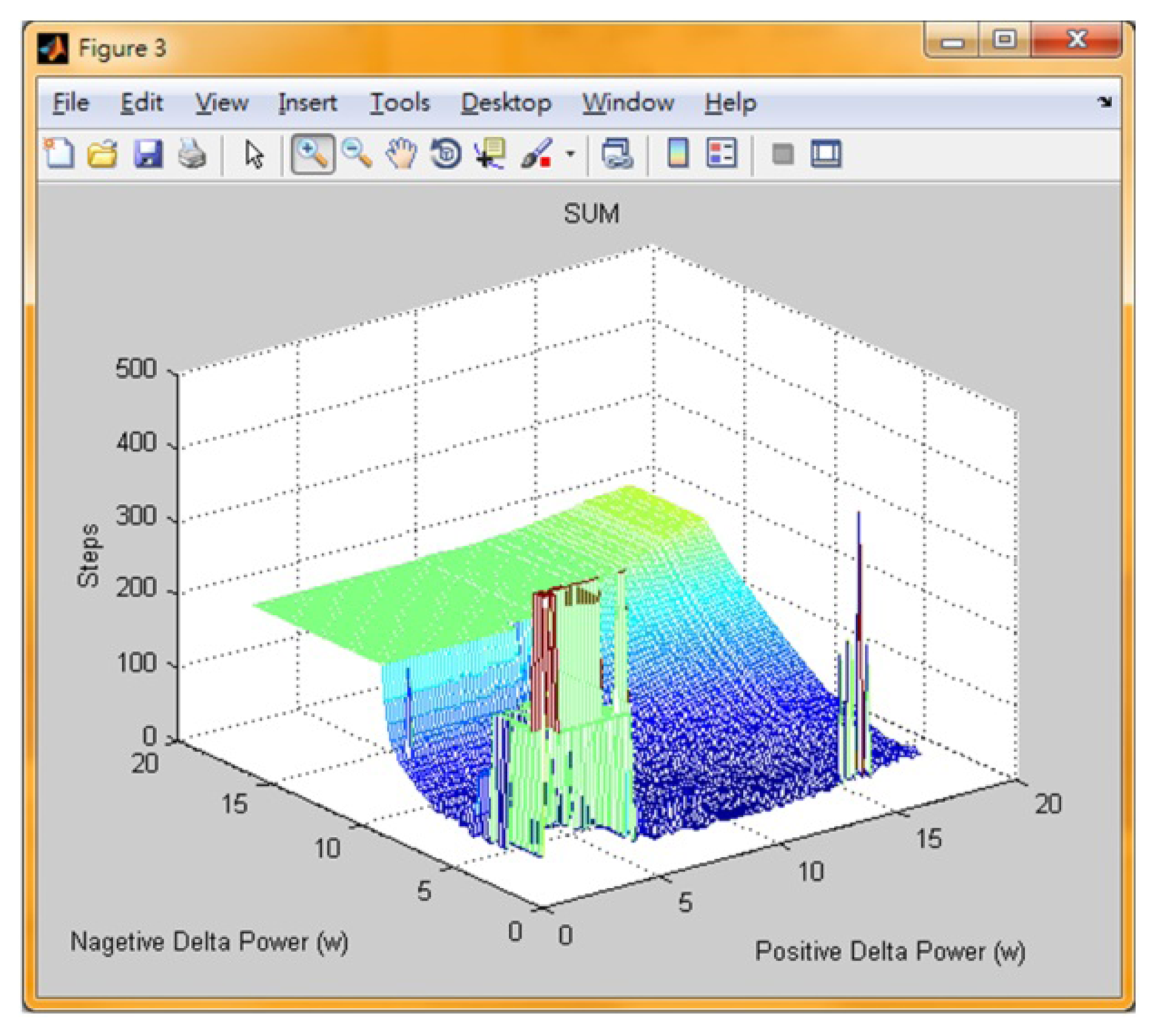
In Section 3, the design procedures of the proposed symmetrical FLC have been explained. To further improve the performance of the proposed FLC, the derivation of asymmetrical input MF technique will be explained. Figure 9 shows the dP/dV vs. duty cycle curve, which can be obtained by dividing Figure 7b with Figure 7a. Observing Figure 9, the dP/dV curve of a solar cell has different slopes on two sides. That is, when operating point locates at the left-hand/right-hand side of the MPP, the generated power variation will be larger/smaller under a fixed duty cycle variation. Thus, when designing the UOD of input variable ΔPpv, it is essential to take this phenomenon into consideration. To deal with this issue, a variety of artificial intelligent (AI) methods have been proposed in the literatures to obtain the optimal configuration of the MFs. These AI methods include GA, PSO and Hopfield ANN [15–17,24]. According to the experimental results, these AI approaches can acquire the optimal configuration in most cases. However, the problem of using AI techniques is that the parameters of these algorithms (for example, the population size, rate of crossover and rate of mutation in GA or the inertia factor, social rate and cognitive rate in PSO) are hard to determine. On the other hand, it can be observed that the UOD of ΔPpv has relatively larger impact on the proposed FLC-based MPPT controller, which implies that the problem complexity can be reduced if only the ΔPpv optimization is taken into account. Therefore, grid search technique is employed in this paper to obtain the optimal design of the UOD of ΔPpv Figure 10 shows the implementation concept of the grid search method used in this paper. First, this study fixed the dP_PB value at POSmax/100 W (referring to Figure 10, POSmax = 2 × dPmax in this paper), and the dP_NB value was gradually reduced from NEGmax/100 W to NEGmax W (NEGmax = −1 × POSmax) through a fixed increment of NEGmax/100, yielding a total of 100 points. Subsequently, the dP_PB value was increased to 2 × POSmax/100 W through a fixed increment of POSmax/100; with this new value, the previous procedure, in which the dP_NB value experienced a 100 point decrease, was repeated. This process was repeated until the dP_PB value is equal to POSmax W. This test method produced 10,000 (100 × 100) combinations of simulation test points. Then, according to these possible UOD combinations, simulation is conducted under a step change in solar irradiation from 0 to 1000 W/m2 for the proposed system. The steady-state tracking time can then be observed in a 3D plot in which the z-axis represents the numbers of tracking steps. Consequently, it can be concluded that the point with the lowest z-axis value indicates the optimal UOD combination. To reduce the complexity for optimization, the shape of the ΔPpv MF remains as triangle shape and the ratio of large value to small value remains as 2 to 1 (that is, dP_NS = (dP_NB/2); dP_PS = (dP_PB/2)). Additionally, to take every tracking situation into account, the simulation is carried out using two initial conditions—initial duty cycle value equals to 10% (representing the tracking from right to left along the P-V curve) and 90% (representing the tracking from left to right along the P-V curve). Then, the tracking time required for both cases is summed up as the total tracking time. Figure 11 shows the obtained 3D simulation result under different UOD configurations. The obtained optimal results are dP_PB = 7 W and dP_NB = −2.5 W.
4.2. Systematic Approach to Determine the UOD of ΔPpv
Because grid search method is capable of searching every possible region and its generated 3D surface is a smooth surface; therefore, the proposed grid search method can yield optimal results. However, grid search method requires large amount of simulations (20,000 simulations in this case), thus increases the complexity of design. Consequently, a simple design method which can be used to determine the UOD of the MF of ΔPpv is also proposed in this paper. It can also be observed from Figure 9 that the dP/dV values of fixed duty cycle variation on two sides of the MPP are not identical. After conducting integration for the dP/dV curves on both sides of MPP, the area under the curve on the left (area B) was 2093, the area under the curve on the right (area A) was 278, and the ratio of area B to area A was 7.53. Therefore, if the MF of ΔVpv remains unchanged, the asymmetrical UOD problem can be adequately addressed by setting the ratio dP_PB and dP_NB as 7.53 (i.e., dP_PB = 8.2 and dP_NB = −1.1). Although this method cannot guarantee to obtain the optimal solution, it can efficiently determine the configuration of the UOD of ΔPpv with quite satisfactory performance. Experimental results for these two methods will be provided in Section 5 for comparison.
5. Experimental Results
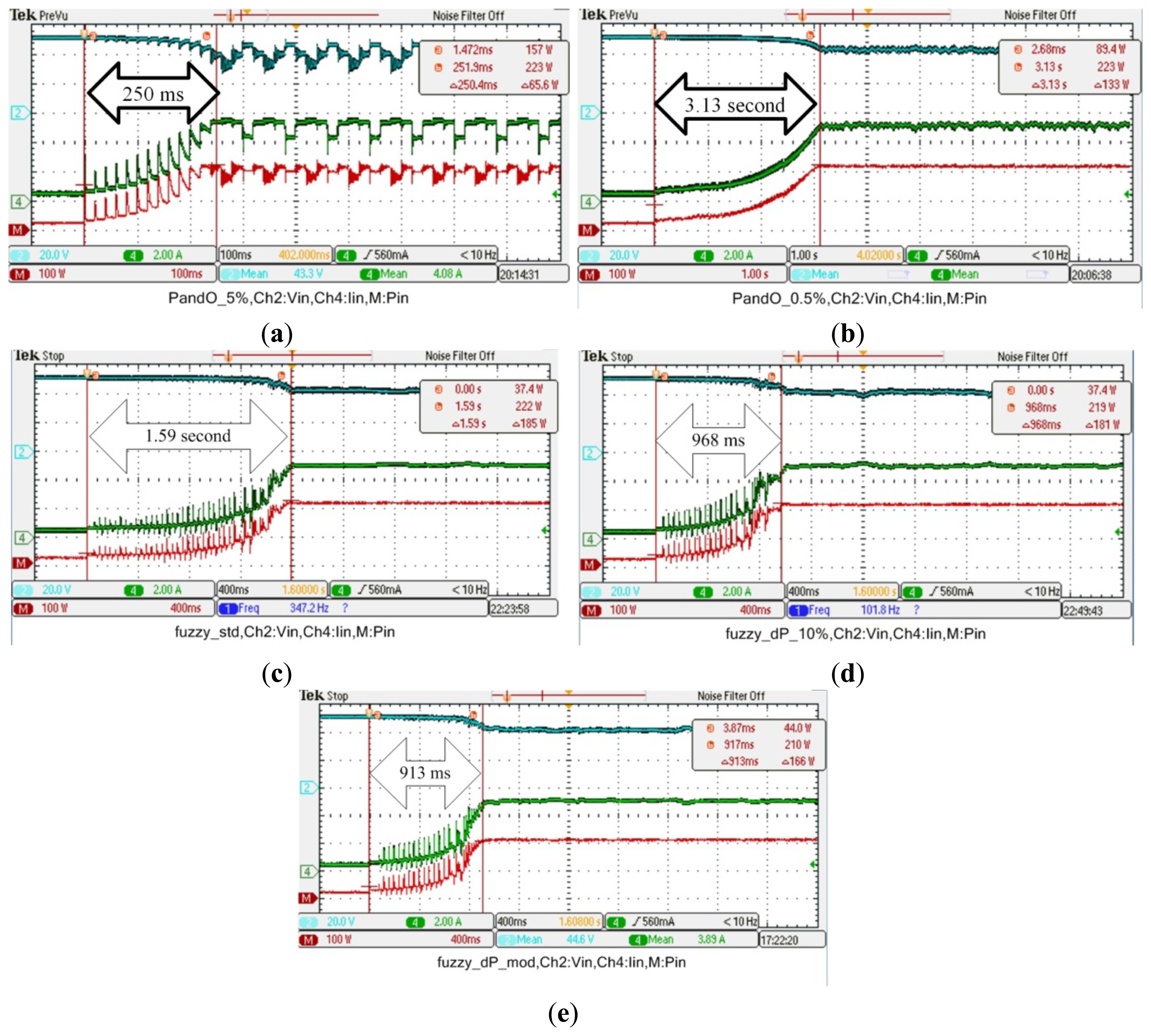
To verify the correctness of the proposed FLC-based MPPT controller, a 300 W prototyping circuit is implemented from which experiments are carried out accordingly. The proposed algorithm is validated using an AMETEK Solar Array Simulator TerraSAS DCS80-15 in SAS mode. The parameters of the utilized PV panel are listed in Table 2 and the specification of the utilized power converter is listed in Table 3. As shown in Figure 1, in order to validate the effectiveness of the proposed MPPT controller, experiments will be carried out on the following systems: Two P&O MPPT methods with different perturbation step settings, one proposed symmetrical FLC-based MPPT method and two proposed asymmetrical FLC-based MPPT methods with different settings. All experiments are conducted using the same power circuit to ensure the fairness. Table 4 shows the parameters used in each MPPT algorithm. In this paper, low cost DSC dsPIC33FJ16GS502 from Microchip Corp. is used to realize the aforementioned five kinds of algorithms. Using a 40 MHz oscillator, the required execution times of the P&O MPPT, the symmetrical FLC-based MPPT and the asymmetrical FLC-based MPPT are 1.5 μs, 120 μs and 120 μs, respectively. Figure 12 shows the starting waveform of these five methods for 1000 W/m2 solar irradiance and 25 °C PV panel temperature. From Figure 12, the transient times for the fixed step P&O method are 250 ms (for 5% fixed step) and 3.13 s (for 0.5% fixed step), respectively. Additionally, the transient time for the proposed symmetrical FLC-based MPPT controller, the proposed asymmetrical FLC-based MPPT controller (UOD obtained in Section 4.2) and the proposed asymmetrical FLC-based MPPT controller (UOD obtained in Section 4.1) are 1.59 s, 968 ms and 913 ms, respectively. Observing Figure 12, the P&O method with large step exhibits good dynamic performance but larger steady state oscillations; therefore, the MPPT accuracy is rather low. On the other hand, using a small step size can improve the tracking accuracy at the cost of slower dynamic performance. The proposed FLC-based MPPT methods solves this dilemma as evident from Figure 12. It can be seen from Figure 12 that although the transient time of the proposed method is slightly higher than the P&O method using large step size, the oscillation around the MPP for the proposed method is much smaller than that obtained from the P&O method using large step size.
The performances of the tested methods are summarized in Table 5. In Table 5, the tracking accuracy values are obtained using the built-in data logging function of the solar array simulator. The system begins to record the accuracy data when system reaches steady state and the total recorded data contains 125 points (recoding time is 6.25 s with sampling time equals 0.05 s). From Table 5, the tracking accuracies of the proposed methods are better than both of the P&O method. It can be seen that the proposed FLC-based MPPT controller can improve the dynamic and steady state performance of the PV system simultaneously. Moreover, it can also be learned from Table 5 that asymmetrical FLC-based MPPT methods can improve tracking speed over symmetrical FLC-based MPPT method. Although the asymmetrical FLC-based MPPT method obtained in Section 4b does not have optimal tracking speed and accuracy, the design procedure is simple and its performance is still better than that of the symmetrical FLC-based MPPT method. It is worth mentioning that the only difference between asymmetrical FLC-based MPPT method and symmetrical FLC-based MPPT method is the design of the UOD of ΔPpv MF; therefore, the implementation complexity of these two methods is the same. That is, asymmetrical FLC-based MPPT method can enhance the tracking speed and tracking accuracy over symmetrical FLC-based MPPT without increasing the calculation burden. To further validate the performance improvement of the proposed methods, simulations on the full day energy production are also provided. The obtained data is also provided in Table 5. In these simulations, the irradiance profile used is a built-in “standard sunny day” profile of the utilized solar array simulator (data obtained from the Sandia National Labs, Alameda, CA, USA). From Table 5, asymmetrical FLC-based MPPT methods also have the best full day energy yield.
6. Conclusions
In this paper, a FLC-based MPPT method is proposed for the first time. The design and implementation of the proposed method is discussed in detail in this paper. By using the power variation and voltage variation as the inputs, the calculation is simplified. Comparing with the conventional P&O method, the proposed MPPT method can satisfactorily address the tradeoff between the tracking speed and steady state oscillations. To further improve the performance of the proposed MPPT method, an asymmetrical membership function concept is proposed. Two design procedures are presented and experiments are carried out to validate the effectiveness of the proposed method. Comparing with the symmetrical FLC-based MPPT method, the transient time and the MPPT tracking accuracy are further improved by about 42.8% and 0.06%, respectively.
Acknowledgments
The authors are indebted to utility-scaled energy storage system and interconnection technology development project from the Bureau of Energy, Ministry of Economic Affairs for supporting this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lee, J.S.; Lee, K.B. Variable dc-link voltage algorithm with a wide range of maximum power point tracking for a two-string PV system. Energies 2013, 6, 58–78. [Google Scholar]
- Shen, C.L.; Tsai, C.T. Double-linear approximation algorithm to achieve maximum-power-point tracking for photovoltaic arrays. Energies 2012, 5, 1982–1997. [Google Scholar]
- Yau, H.T.; Wu, C.H. Comparison of extremum-seeking control techniques for maximum power point tracking in photovoltaic systems. Energies 2011, 4, 2180–2195. [Google Scholar]
- Reisi, A.R.; Moradi, M.H.; Jamasb, S. Classification and comparison of maximum power point tracking techniques for photovoltaic system: A review. Renew. Sustain. Energy Rev. 2013, 19, 433–443. [Google Scholar]
- Ishaque, K.; Salam, Z. A review of maximum power point tracking techniques of PV system for uniform insolation and partial shading condition. Renew. Sustain. Energy Rev. 2013, 19, 475–488. [Google Scholar]
- Femia, N.; Petrone, G.; Spagnuolo, G.; Vitelli, M. Optimization of perturb and observe maximum power point tracking method. IEEE Trans. Power Electron. 2005, 20, 963–973. [Google Scholar]
- Pandey, A.; Dasgupta, N.; Mukerjee, A.K. High-performance algorithms for drift avoidance and fast tracking in solar mppt system. IEEE Trans. Energy Convers. 2008, 23, 681–689. [Google Scholar]
- D'Souza, N.S.; Lopes, L.A.C.; Liu, X. Comparative study of variable size perturbation and observation maximum power point trackers for PV systems. Electr. Power Syst. Res. 2010, 80, 296–305. [Google Scholar]
- Abdelsalam, A.K.; Massoud, A.M.; Ahmed, S.; Enjeti, P.N. High-performance adaptive perturb and observe MPPT technique for photovoltaic-based microgrids. IEEE Trans. Power Electron. 2011, 26, 1010–1021. [Google Scholar]
- Liu, F.; Duan, S.; Liu, F.; Liu, B.; Kang, Y. A variable step size INC MPPT method for PV systems. IEEE Trans. Ind. Electron. 2008, 55, 2622–2628. [Google Scholar]
- Lalili, D.; Mellit, A.; Lourci, N.; Medjahed, B.; Berkouk, E.M. Input output feedback linearization control and variable step size MPPT algorithm of a grid-connected photovoltaic inverter. Renew. Energy 2011, 36, 3282–3291. [Google Scholar]
- Mei, Q.; Shan, M.; Liu, L.; Guerrero, J.M. A nove improved variable step-size incremental-resistance MPPT method for PV systems. IEEE Trans. Ind. Electron. 2011, 58, 2427–2434. [Google Scholar]
- Jiang, Y.; Qahouq, J.A.A.; Haskew, T.A. Adaptive step size with adaptive-perturbation-frequency digital MPPT controller for a single-sensor photovoltaic solar system. IEEE Trans. Power Electron. 2013, 28, 3195–3205. [Google Scholar]
- Messai, A.; Mellit, A.; Massi Pavan, A.; Guessoum, A.; Mekki, H. FPGA-based implementation of a fuzzy controller (MPPT) for photovoltaic module. Energy Convers. Manag. 2011, 52, 2695–2704. [Google Scholar]
- Larbes, C.; Ait Cheikh, S.M.; Obeidi, T.; Zerguerras, A. Genetic algorithms optimized fuzzy logic control for the maximum power point tracking in photovoltaic system. Renew. Energy 2009, 34, 2093–2100. [Google Scholar]
- Messai, A.; Mellit, A.; Guessoum, A.; Kalogirou, S.A. Maximum power point tracking using a GA optimized fuzzy logic controller and its FPGA implementation. Sol. Energy 2011, 85, 265–277. [Google Scholar]
- Letting, L.K.; Munda, J.L.; Hamama, Y. Optimization of a fuzzy logic controller for PV grid inverter control using S-function based PSO. Sol. Energy 2012, 86, 1689–1700. [Google Scholar]
- Kottas, T.L.; Boutalis, Y.S.; Karlis, A.D. New maximum power point tracker for PV arrays using fuzzy controller in close cooperation with fuzzy cognitive networks. IEEE Trans. Energy Convers. 2006, 21, 793–803. [Google Scholar]
- Algazar, M.M.; AL-monier, H.; EL-halim, H.A.; Salem, M.E.E.K. Maximum power point tracking using fuzzy logic control. Int. J. Electr. Power Energy Syst. 2012, 39, 21–28. [Google Scholar]
- Lalouni, S.; Rekioua, D.; Rekioua, T.; Matagne, E. Fuzzy logic control of stand-alone photovoltaic system with battery storage. J. Power Sources 2009, 193, 899–907. [Google Scholar]
- Alajmi, B.N.; Ahmed, K.H.; Finney, S.J.; Williams, B.W. Fuzzy-logic-control approach of a modified hill-climbing method for maximum power point in microgrid standalone photovoltaic system. IEEE Trans. Power Electron. 2011, 26, 1022–1030. [Google Scholar]
- Alajmi, B.N.; Ahmed, K.H.; Finney, S.J.; Williams, B.W. A maximum power point tracking technique for partially shaded photovoltaic systems in microgrids. IEEE Trans. Ind. Electron. 2013, 60, 573–584. [Google Scholar]
- Alajmi, B.N.; Ahmed, K.H.; Adam, G.P.; Williams, B.W. Single-phase single-stage transformer less grid-connected PV system. IEEE Trans. Power Electron. 2013, 28, 2664–2676. [Google Scholar]
- Subiyanto, S.; Mohamed, A.; Hannan, M.A. Intelligent maximum power point tracking for PV system using Hopfield neural network optimized fuzzy logic controller. Energy Build. 2012, 51, 29–38. [Google Scholar]
- Altas, I.H.; Sharaf, A.M. A novel maximum power fuzzy logic controller for photovoltaic solar energy systems. Renew. Energy 2008, 33, 388–399. [Google Scholar]
- Gounden, N.A.; Peter, S.A.; Nallandula, H.; Krithiga, S. Fuzzy logic controller with MPPT using line-commutated inverter for three-phase grid-connected photovoltaic systems. Renew. Energy 2009, 34, 909–915. [Google Scholar]
- Syafaruddin; Karatepe, E.; Hiyama, T. Artificial neural network-polar coordinated fuzzy controller based maximum power point tracking control under partially shaded conditions. IET Renew. Power Gener. 2009, 3, 239–253. [Google Scholar]
- Syafaruddin; Karatepe, E.; Hiyama, T. Polar coordinated fuzzy controller based real-time maximum-power point control of photovoltaic system. Renew. Energy 2009, 34, 2597–2606. [Google Scholar]
- Chaouachi, A.; Kamel, R.M.; Nagasaka, K. A novel multi-model neuro-fuzzy-based MPPT for three-phase grid-connected photovoltaic system. Sol. Energy 2010, 84, 2219–2229. [Google Scholar]
- Salah, C.B.; Ouali, M. Comparison of fuzzy logic and neural network in maximum power point tracker for PV systems. Electr. Power Syst. Res. 2011, 81, 43–50. [Google Scholar]
- Abu-Rub, H.; Iqbal, A.; Ahmed, S.M.; Peng, F.Z.; Li, Y.; Baoming, G. Quasi-Z-source inverter-based photovoltaic generation system with maximum power tracking control using ANFIS. IEEE Trans. Sustain. Energy 2013, 4, 11–20. [Google Scholar]
- Karlis, A.D.; Kottas, T.L.; Boutalis, Y.S. A novel maximum power point tracking method for PV systems using fuzzy cognitive networks (FCN). Electr. Power Syst. Res. 2007, 77, 315–327. [Google Scholar]
- Chiu, C.S. T-S fuzzy maximum power point tracking control of solar power generation systems. IEEE Trans. Energy Convers. 2010, 25, 1123–1132. [Google Scholar]
- Chiu, C.S.; Ouyang, Y.L. Robust maximum power tracking control of uncertain photovoltaic systems: A unified T-S fuzzy model-based approach. IEEE Trans. Control Syst. Technol. 2011, 19, 1516–1526. [Google Scholar]
- Dounis, A.I.; Kofinas, P.; Alafodimos, C.; Tseles, D. Adaptive fuzzy gain scheduling pid controller for maximum power point tracking of photovoltaic system. Renew. Energy 2013, 60, 202–214. [Google Scholar]






| ΔPpv | ΔVpv | ||||
|---|---|---|---|---|---|
| NB | NS | ZE | PS | PB | |
| NB | NS Rule1 | NB Rule6 | PB Rule11 | PB Rule16 | PS Rule21 |
| NS | ZE Rule2 | NS Rule7 | PS Rule12 | PS Rule17 | ZE Rule22 |
| ZE | ZE Rule3 | ZE Rule8 | ZE Rule13 | ZE Rule18 | ZE Rule23 |
| PS | ZE Rule4 | PS Rule9 | NS Rule14 | NS Rule19 | ZE Rule24 |
| PB | PS Rule5 | PB Rule10 | NB Rule15 | NB Rule20 | NS Rule25 |
| Parameters | Specification | Parameters | Specification |
|---|---|---|---|
| Maximum Power (Pmax) | 220 W | Short Circuit Current (Isc) | 5.65 A |
| Open Circuit Voltage (Voc) | 52.3 V | Maximum Power Current (Imp) | 5.17 A |
| Maximum Power Voltage (Vpm) | 42.7 V | Temperature Coefficient (αv) | −0.336%/°C |
| Parameters | Specification |
|---|---|
| Input Voltage (Vin) | 40–70 V |
| Rated Output Voltage (Vo) | 160 V |
| Rated Ouput Current (Io) | 2.5 A |
| Rated Output Power (Po) | 400 W |
| Switching Frequency (fs) | 50 kHz |
| Output Voltage Ripple (ΔVo/Vo) | <1% |
| No. | Description | Parameters | Note |
|---|---|---|---|
| 1 | P&O (0.5%) | Fixed Duty Cycle 0.5% | denoted as method 1 |
| 2 | P&O (5%) | Fixed Duty Cycle 5% | denoted as method 2 |
| 3 | Symmetrical FLC | dP_PB = 8.2W dP_NB = −8.2 W | denoted as method 3 |
| dV_PB = 1.5V dV_NB = −1.5 V | |||
| 4 | Asymmetrical FLC #1 | dP_PB = 8.2W dP_NB = −1.1 W | denoted as method 4 Parameters from Section 4b |
| dV_PB = 1.5V dV_NB = −1.5 V | |||
| 5 | Asymmetrical FLC #2 | dP_PB = 7.0W dP_NB = −2.5 W | denoted as method 5 Parameters from Section 4a |
| dV_PB = 1.5V dV_NB = −1.5 V |
| Methods | Average steady state output power | MPPT tracking accuracy | Transient time | Full day energy yield 1 |
|---|---|---|---|---|
| P&O (0.5%) | 206.89 W | 92.84% | 0.25 s | 1466.07 Wh |
| P&O (5%) | 222.45 W | 99.82% | 3.13 s | 1561.15 Wh |
| Symmetrical FLC | 222.58 W | 99.87% | 1.28 s | 1571.66 Wh |
| Asymmetrical FLC #1 | 222.65 W | 99.91% | 0.97 s | 1573.92 Wh |
| Asymmetrical FLC #2 | 222.69 W | 99.93% | 0.91 s | 1574.56 Wh |
1The full day energy production is 1580.45 Wh for ideal condition.
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Liu, C.-L.; Chen, J.-H.; Liu, Y.-H.; Yang, Z.-Z. An Asymmetrical Fuzzy-Logic-Control-Based MPPT Algorithm for Photovoltaic Systems. Energies 2014, 7, 2177-2193. https://doi.org/10.3390/en7042177
Liu C-L, Chen J-H, Liu Y-H, Yang Z-Z. An Asymmetrical Fuzzy-Logic-Control-Based MPPT Algorithm for Photovoltaic Systems. Energies. 2014; 7(4):2177-2193. https://doi.org/10.3390/en7042177
Chicago/Turabian StyleLiu, Chun-Liang, Jing-Hsiao Chen, Yi-Hua Liu, and Zong-Zhen Yang. 2014. "An Asymmetrical Fuzzy-Logic-Control-Based MPPT Algorithm for Photovoltaic Systems" Energies 7, no. 4: 2177-2193. https://doi.org/10.3390/en7042177
APA StyleLiu, C.-L., Chen, J.-H., Liu, Y.-H., & Yang, Z.-Z. (2014). An Asymmetrical Fuzzy-Logic-Control-Based MPPT Algorithm for Photovoltaic Systems. Energies, 7(4), 2177-2193. https://doi.org/10.3390/en7042177





