Sensitivity Analysis of Parameters Governing the Recovery of Methane from Natural Gas Hydrate Reservoirs
Abstract
: Naturally occurring gas hydrates are regarded as an important future source of energy and considerable efforts are currently being invested to develop methods for an economically viable recovery of this resource. The recovery of natural gas from gas hydrate deposits has been studied by a number of researchers. Depressurization of the reservoir is seen as a favorable method because of its relatively low energy requirements. While lowering the pressure in the production well seems to be a straight forward approach to destabilize methane hydrates, the intrinsic kinetics of CH4-hydrate decomposition and fluid flow lead to complex processes of mass and heat transfer within the deposit. In order to develop a better understanding of the processes and conditions governing the production of methane from methane hydrates it is necessary to study the sensitivity of gas production to the effects of factors such as pressure, temperature, thermal conductivity, permeability, porosity on methane recovery from naturally occurring gas hydrates. A simplified model is the base for an ensemble of reservoir simulations to study which parameters govern productivity and how these factors might interact.1. Introduction
Naturally occurring gas hydrates are regarded as an important future source of energy and considerable efforts are currently being invested to develop methods for an economically viable recovery of this resource. The recovery of natural gas from gas hydrate deposits has been studied by a number of researchers [1–6]. Depressurization is seen as a favourable method because of its lower energy requirements [7]. While lowering the pressure in the production well seems to be a straight forward approach to destabilize methane hydrates, the intrinsic kinetics of CH4-hydrate decomposition and fluid flow lead to complex processes of mass and heat transfer within the deposit. In order to develop a better understanding of the processes and conditions governing the production of methane from methane hydrates it is necessary to study the sensitivity of gas production to the effects of factors such as pressure, temperature, thermal conductivity, permeability, porosity on gas production. The main purpose of this paper is therefore to carry out a sensitivity study on methane recovery from naturally occurring gas hydrates using a reservoir simulation in order to determine which parameters govern productivity and how these factors might interact. In this model, the three primary mechanisms involved in the gas hydrate decomposition are considered to be: (1) heat transfer; (2) gas-water fluid flow; and (3) kinetics of hydrate decomposition.
1.1. Sensitivity Analysis-Theoretical Background
With the development of new computational techniques and robust numerical calculations in the last decades, reservoir simulation has evolved into a cost-effective tool for industries, not only for testing new production designs but also for maximizing the production by optimizing the process variables. It is in this context that sensitivity analysis can contribute to phenomenological understanding, key factor determination, and assessing interactions between factors, process optimization and production forecasting [8]. Sensitivity analysis is a technique for systematically changing factors in a model to determine the effect of such changes in either one or several response variables [9] and has been used in several numerical reservoir studies [8,10,11]. Two approaches were selected to carry out the sensitivity analysis: (1) one factor at a time (OFAT); and (2) factorial design. In this paper, the purpose of the sensitivity analysis will be the determination of the relative importance of selected process variables and physical properties on the cumulative gas produced from a hypothetical gas hydrate deposit.
1.2. OFAT
OFAT his is one of the most common methods to carry out sensitivity analysis by selecting a baseline for each factor and then sequentially varying each factor over its range with the other factors fixed at the initial (baseline) level [12]. Based on this approach any change observed in the output will unambiguously be due to the single factor changed. This increases the comparability of the results and minimizes the risk of a numerical model not converging, which is more likely to happen when several input factors are changed simultaneously [9]. The major disadvantage of this strategy is that it does not consider any interaction between the factors. An interaction, in this case, is characterized by the failure of one factor to produce the same effect on the response variable when another factor is also changed [12].
1.3. Factorial Design
In factorial design, all factors are varied together taking all possible combinations in the different levels of each factor. The analysis of the results is usually carried out using analysis of variance (ANOVA); which is a collection of statistical models in which the observed variance in a particular variable is partitioned into components attributable to different sources of variation [12]. The main advantage of this approach, when compared to OFAT, is that interaction effects between variables are considered. It allows the effect of a factor to be estimated at several levels of other factors and is thus more powerful than OFAT. The purpose of ANOVA is to test differences in means (for variables or groups) for statistical significance. This is achieved by partitioning the total variance in a measured outcome into its sources: The components that are due to differences between means (SS Effects); which means variance that can be explained, such as by a regression model or an experimental treatment assignment and a component that is due to true random error (SS Error), which means a variance that cannot be explained. These latter variance components are then tested for statistical significance using the F-test or the p-value [12]. In this paper, all the outcomes come from a simulation, thus, no true random error exists which causes ANOVA analysis to fail. In order to overcome this problem, it is assumed that high order interactions are negligible and combine their mean squares to estimate the error. This approach is based on the “sparsity of the effects principle” [12] which states that most systems are dominated by some of the main effects and lower interactions and higher order interactions are negligible. The calculation procedure will be presented in the subsequent sections.
2. Modeling CH4 Recovery from CH4-Hydrate Reservoirs
To study the characteristics of CH4-hydrate decomposition in porous media we developed a model based on the following considerations:
Reservoir is an unsteady-state open system;
Phases involved are: gas, aqueous, hydrate;
Components: CH4, H2O, CH4-hydrate;
Darcy's law will be used to describe the fluid flow in porous media;
Reservoir is a homogeneous and isotropic medium;
Gas hydrate molecule is assumed to be CH4•5.75H2O.
Gas hydrate decomposition can be represented by the following kinetic reaction:
CMG STARS™ [13] (Computer Modelling Group-Advanced Processes & Thermal Reservoir Simulator, Calgary, AB, Canada) was chosen as the tool to solve the mass and energy balances. Its suitability to represent methane production from gas hydrates in porous media and has been examined by other authors who validated it against other comparable software [14–17].
2.1. Reservoir Parameters and Component Properties
In the simulation of gas hydrate several parameters are considered as being important for the production of methane from CH4-hydrate deposits. The most important are: geometry of the reservoir (dimensions and shape), reservoir properties (porosity, permeability, etc.), initial conditions (temperature, pressure, gas/water saturation, and hydrate saturation), operational conditions (bottom hole pressure (BHP) and well radius). Table 1 summarizes the available data for methane production from gas hydrate reservoirs. Values from the literature were selected to create a base case and subsequently use value limits to verify their impact on methane recovery using a sensitivity analysis. The data selected for the base case and their variations will be presented in the subsequent sections.
As in the case for reservoir properties, a literature review was conducted for gas hydrate physical properties and it is summarized in Table 2 [1,5,16,18–20]. From those values, we selected representative data to be used in the base case.
Table 3 presents the values selected for our study [1,16,18].
2.2. Governing Equations and Model Design
The model was designed as a radially symmetrical model of a gas hydrate deposit. It includes all three rate-controlling mechanisms (multiphase fluid flow in porous media, kinetics of decomposition and heat transfer) that govern CH4 production from naturally occurring gas hydrates [16]:
Mass balance for CH4:
Fluid flow velocities are described by the following equations:
The velocity of gas along r-direction:
The velocity of gas along z-direction:
The velocity of water along r-direction:
The velocity of water along z-direction:
The rates of gas and water production and the rate of hydrate decomposition are represented by ġg, ġg and ġH, and are calculated using the Kim-Bishnoi model [25]:
The energy balance is described by the following equations:
2.3. Gas Hydrate Decomposition in STARS™
As mentioned before, the kinetics of methane hydrate decomposition follows the Kim-Bishnoi model [25]. The value for the heat of decomposition is taken from Liu et al. [1]:
Kinetic parameters ( E) were determined experimentally by Clarke and Bishnoi [26]. For pure components the fugacity of methane can be calculated as: fCH4 = φP; fe = φPe. Since STARS™ does not allow fugacity calculation the system is assumed to behave as an ideal gas, and we thus assigned the value φ = 1:
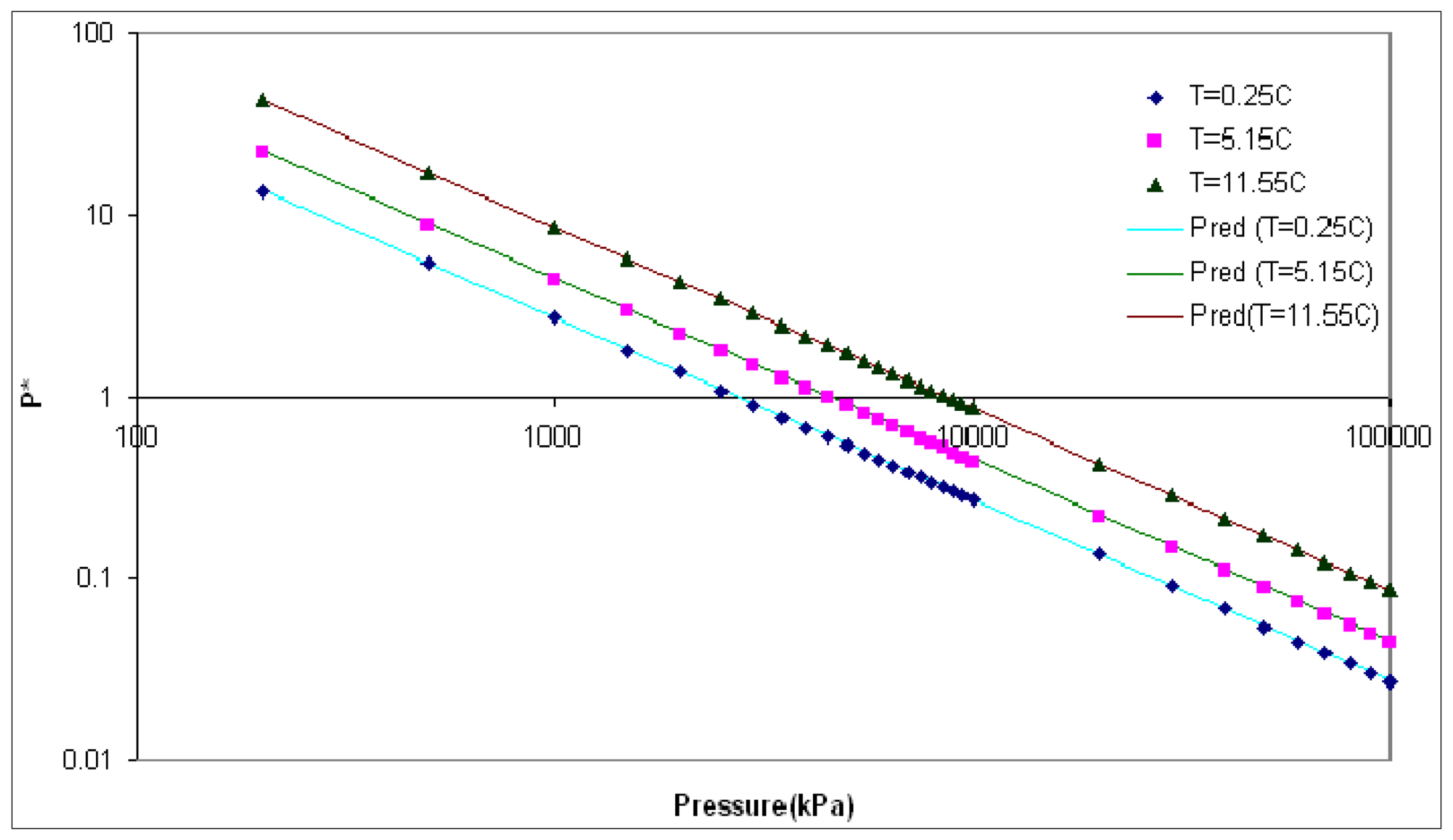
The equilibrium pressure equation is determined by regression from experimental data compiled by Sloan and Koh [27] (see Figure 1):
Gas hydrate decomposition affects reservoir properties such as permeability and porosity since solid gas hydrate partially blocks the reservoir pore space, thus decreasing its permeability. During the decomposition process the pore space is freed from solid gas hydrate, thus increasing its permeability, which favors fluid transport though the reservoir. To take into account the effect of hydrate saturation in the pore space, STARS™ offers the option to determine the reservoir absolute permeability, k0, with each time step using a Carmen-Kozeny type formula:
Gas and aqueous relative permeability are thus described by the following equations:
Capillary pressure between gaseous and aqueous phases is expressed as:
2.4. Geometrical Reservoir Characteristics and Exploitation Period
Following the simulation carried out by Hong [17], the chosen case study was a reservoir of cylindrical shape with a single production well located at the center. The pore space is occupied by mobile phase (gas and water) and immobile phase (methane hydrate). The reservoir formation is considered to be a homogeneous and isotropic medium. In the numerical simulation the system is allowed to lose or gain heat from the surroundings in order to make the model realistic. A schematic representation of the system is presented in Figure 2.
A trial and error method was used to determine the time of the simulation in order to ensure the development of the decomposition profile that makes best use of the available hydrates. Three periods of time were evaluated: 8, 12 and 20 years. The results of these simulations are shown in Figures 3, 4 and 5.
3. Results and Discussion
Before starting analyzing the different results, it is important to highlight that the purpose of this paper is to carry out a systematic sensitivity analysis of variables, thus, the selection of parameter's values is not done based on a single type of formation encountered on Earth, but rather, a collection of multiple combinations that although might create “non-possible” hydrate reservoirs will also contain all the hydrate reservoirs found in the different regions, allowing the authors to unveil the what the most important variables are and its different interactions among each other.
3.1. Base Case
The literature review presented in previous sections provided the parameter values that were selected to create the base case for a sensitivity study to investigate the influence of the chosen parameters on gas recovery from methane hydrates (Table 4).
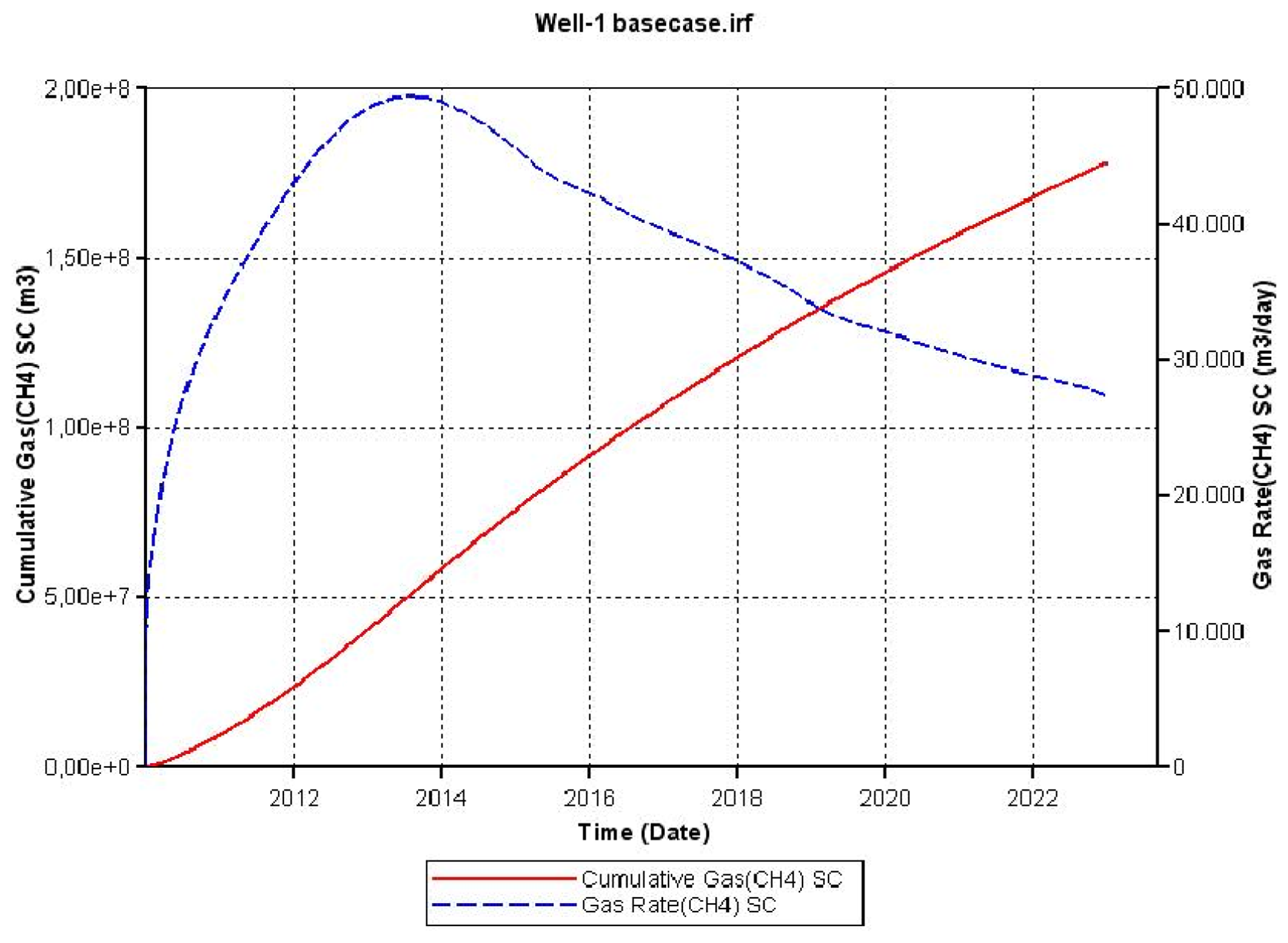
Figure 6 presents the cumulative amount of recovered methane and the rate of gas production obtained from the simulation of the base case. In this scenario, the cumulative amount of gas recovered from the reservoir increases almost constantly during the 12 years of operation. However, the rate of gas production reaches its peak in the first years of operation and subsequently declines.
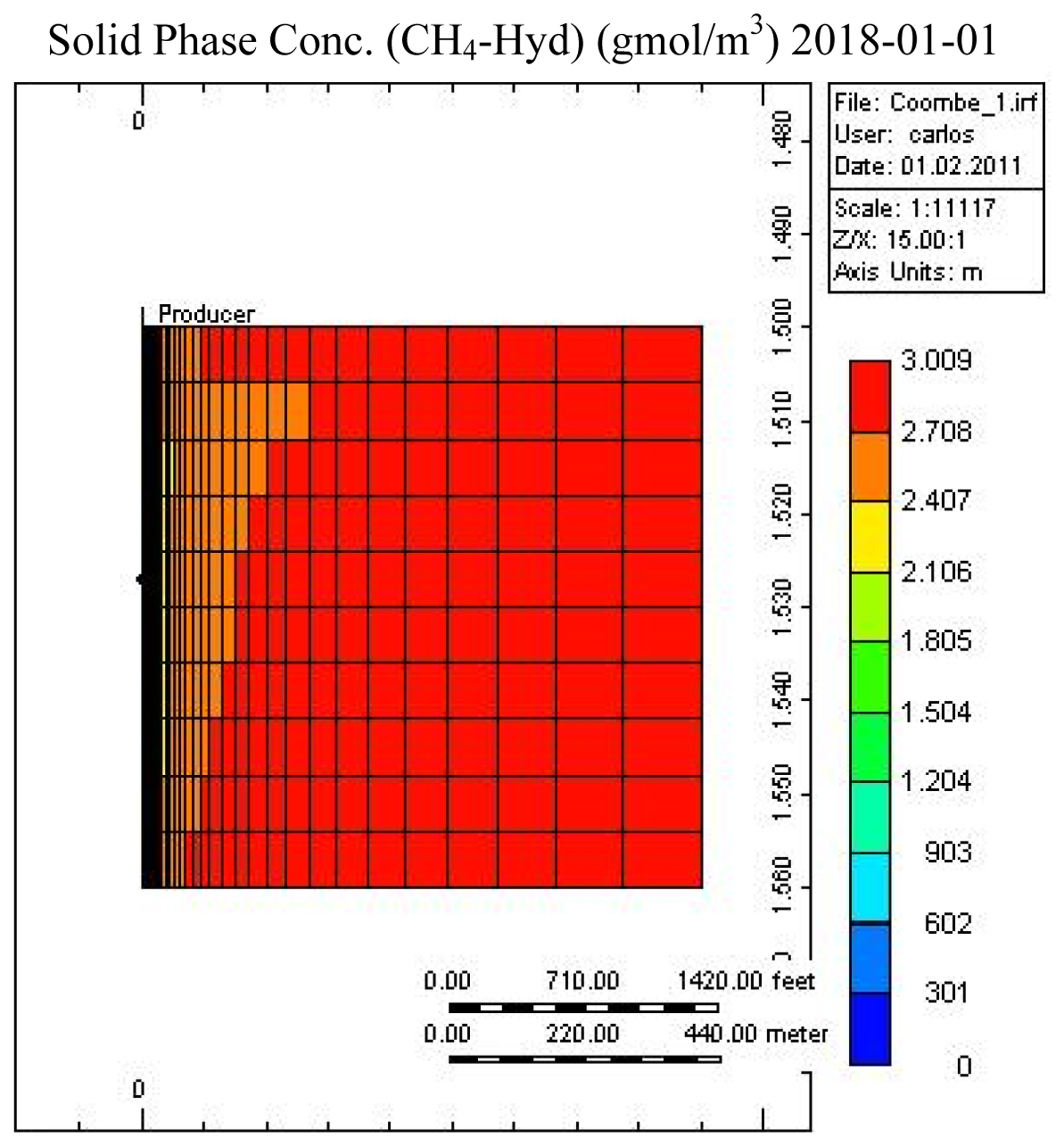
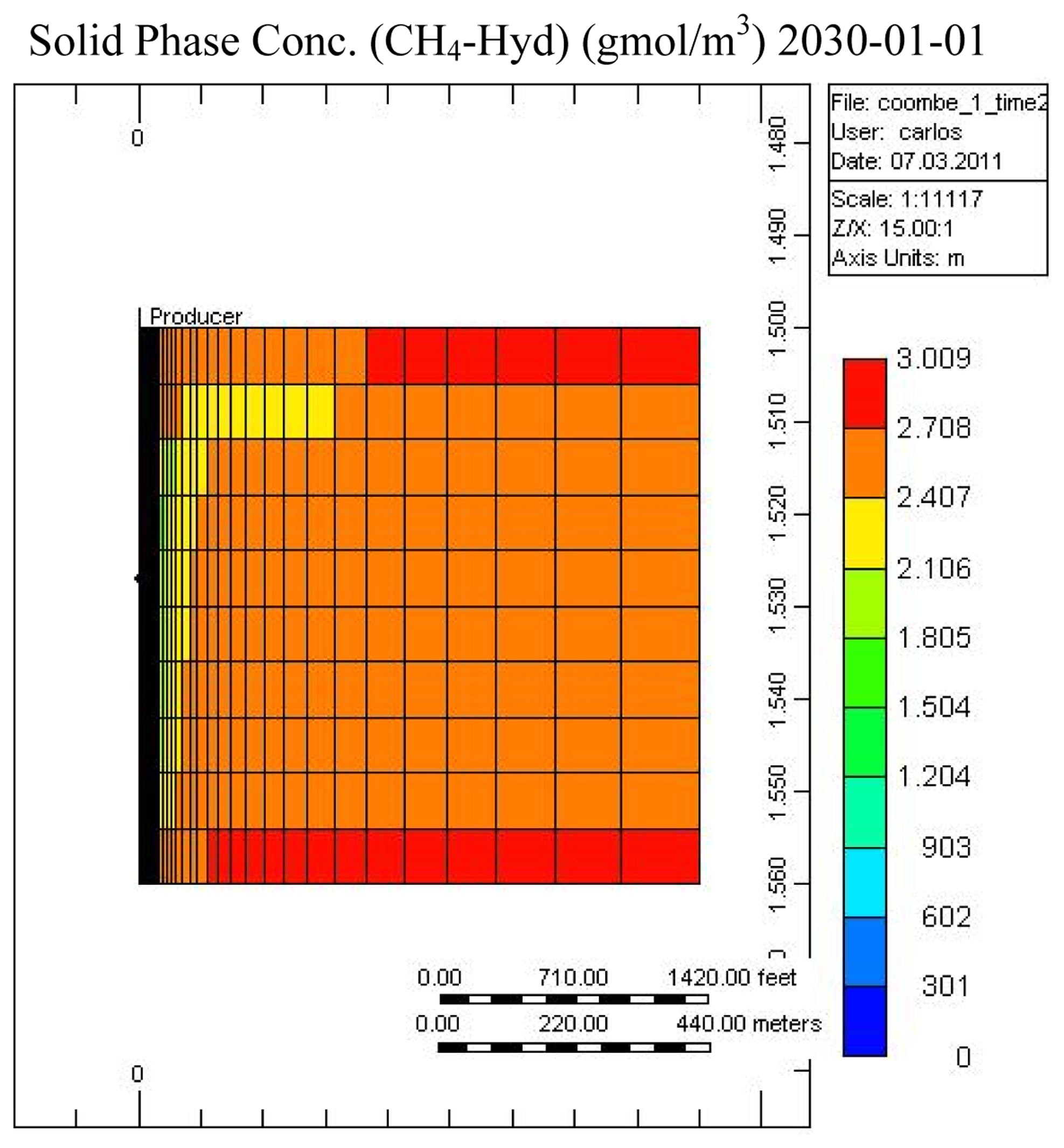
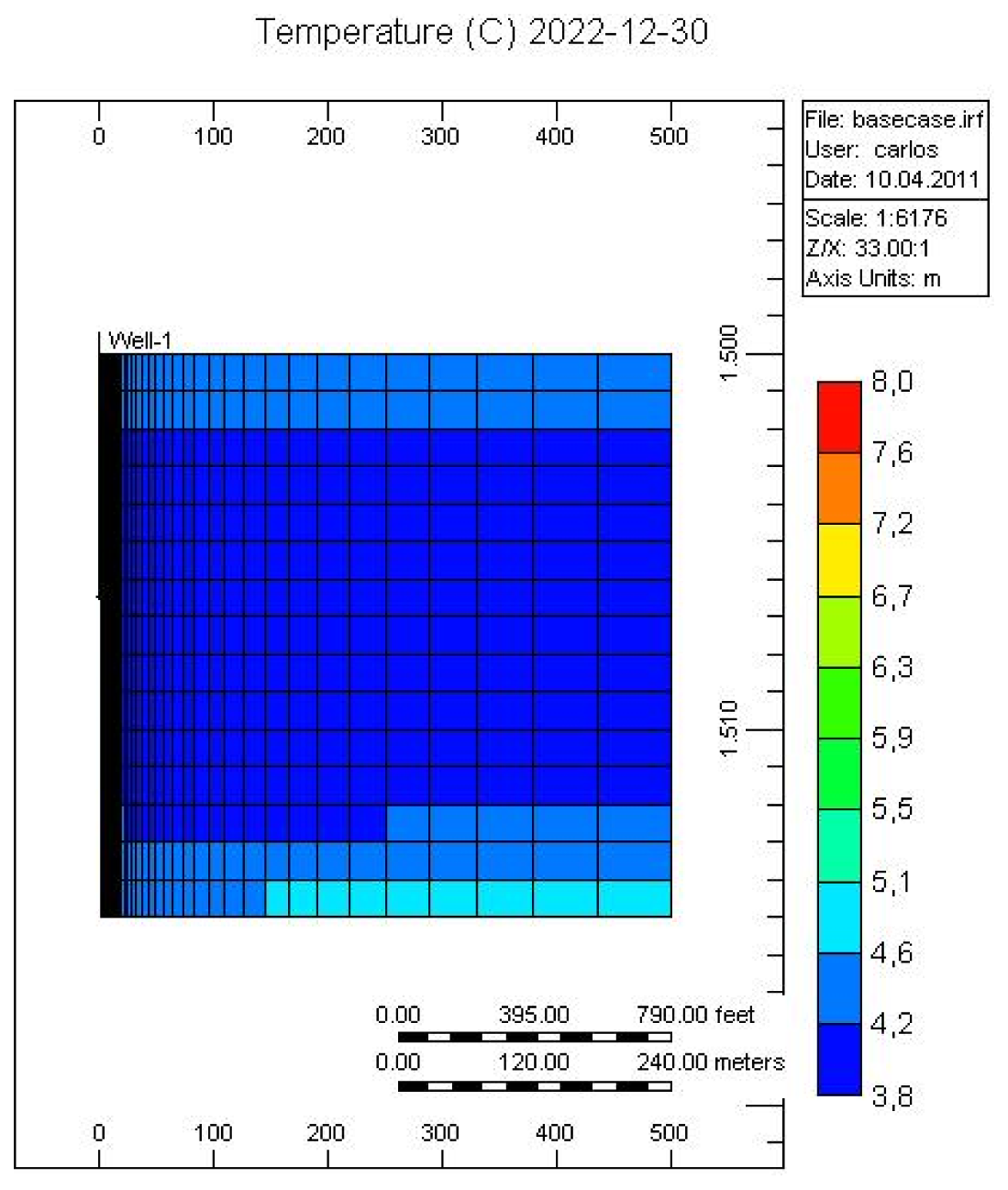
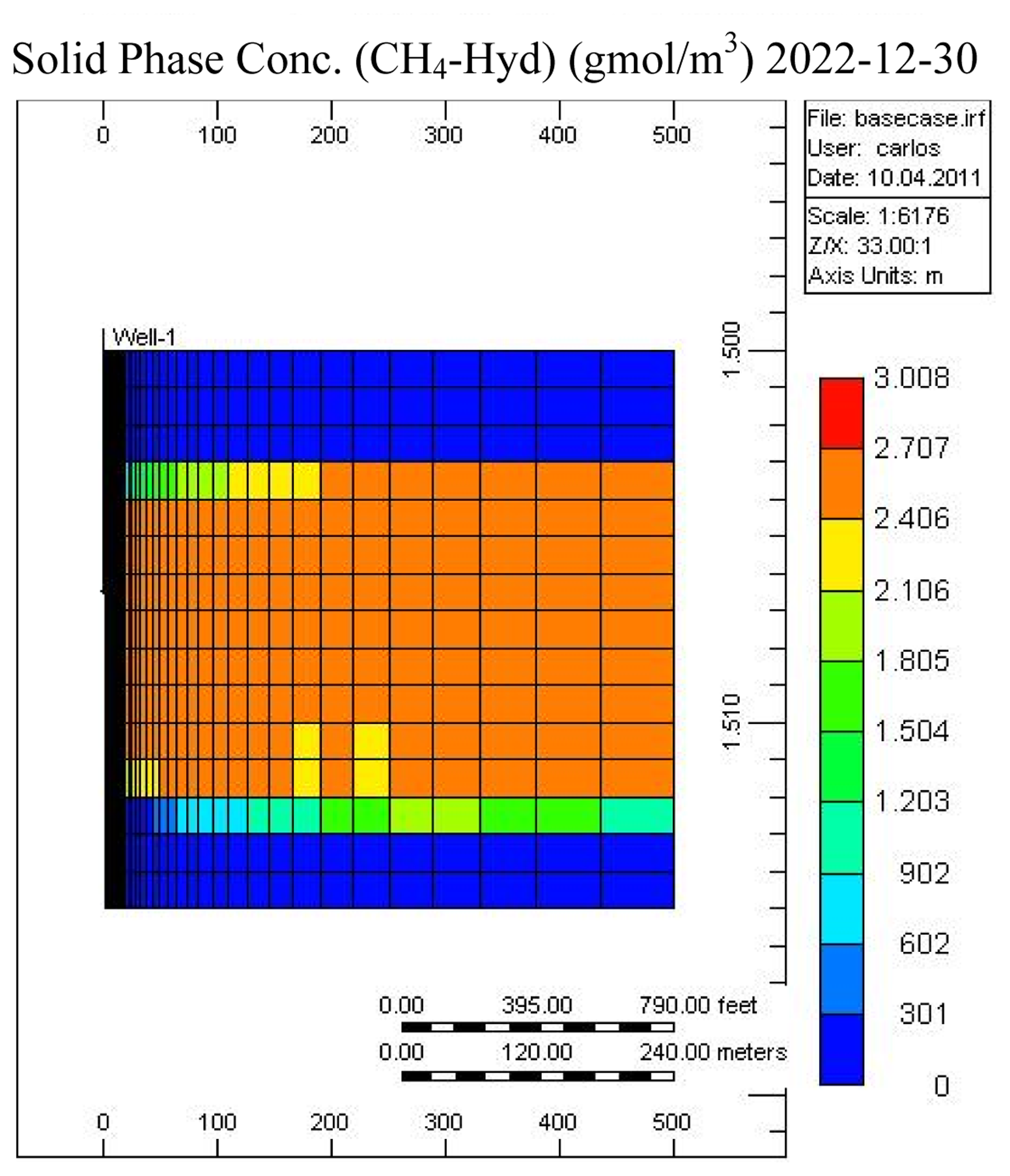
Figures 7 and 8 show the temperature and CH4-hydrate concentration distribution in the reservoir base case at the end of the operation. As noted, gas hydrates have decomposed in the area close to the over- and under-burden. Due to the endothermic nature of the hydrate decomposition process the temperatures in the reservoir decrease, slowing the decomposition process, while at the same time heat is provided from the surrounding over- and under-burden, which in turn accelerates the decomposition process.
To ensure that the results of the models are comparable through all modifications of the reservoir parameters we kept the total molar amount of gas hydrate in the reservoir constant. Two parameters-porosity and thickness of the hydrate layer-deserve special attention since any modification in these values causes a change in the formation pore volume and volume of the reservoir. In these two cases, it was necessary to modify the geometry of the system to keep the total volume of the reservoir constant.
3.2. OFAT
Table 5 summarizes the results of the OFAT. The parameters chosen for this sensitivity study were systematically changed to extreme values and the results compared with the base case.
Figures 9, 10, 11, 12, 13, 14 and 15 present the cumulative recovered methane and gas rate production obtained from the simulations of the variables when changed one at a time. As can be noted from these results, the main variables that produce significant changes in the total volume of gas that can be produced in a 12-year production period are absolute permeability (κ) and BHP.
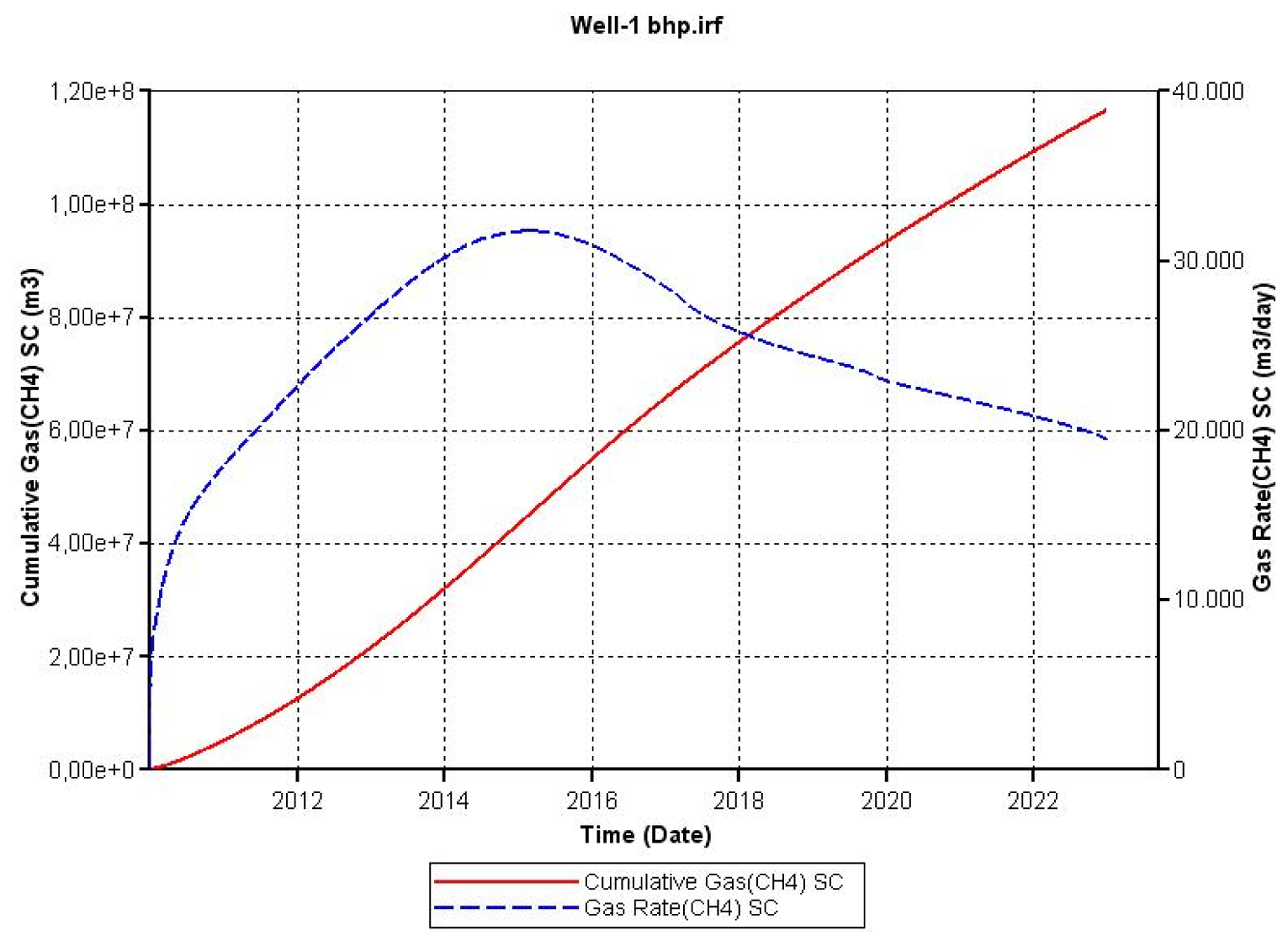
Figures 10 and 12 show how changes in these parameters result in distinctive changes in gas rate production. In the case of the absolute permeability, the gas rate production curve increases very sharply in the first year reaching a maximum and subsequently a quick drop in the gas rate; then during the following years, the gas rate seems to reach a plateau. BHP had a negative effect on the cumulative gas production of methane, since there is less driving force to produce gas. The gas rate production is delayed, producing a maximum peak at approximately five years to the subsequently decrease.
Variables such as thermal conductivity of the rock, initial pressure and well radius had a smaller effect on the response variable (cumulative gas production) indicating that their significances are low in comparison to absolute permeability and BHP. Gas rate production curves (Figures 9, 11 and 15) showed similar trends to the ones presented by the base case.
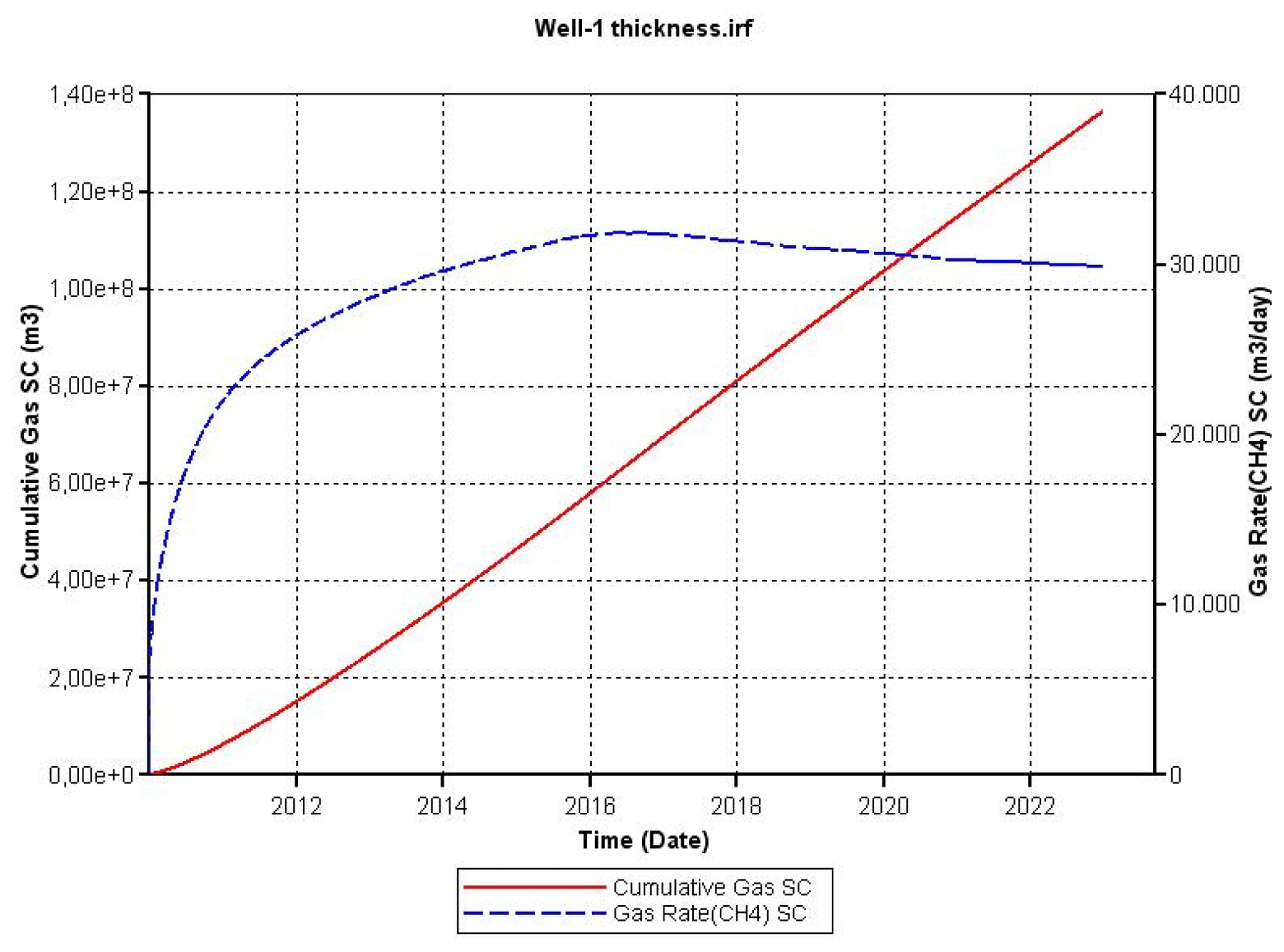
As noted above, changes in porosity and thickness of the hydrate layer affect the formation pore volume and the volume of the reservoir, respectively. In the case of a decreased porosity it was necessary to increase the thickness of the hydrate layer by a factor of 2.5 to compensate the change in porosity from 0.5 to 0.2. In the case of a reduced thickness of the gas hydrate it was necessary to increase the radius of the reservoir by a factor of 2.5 to compensate the change in thickness from 14 m to 7 m.
Figure 13 shows that in the case of porosity the cumulative recovered methane is higher than in the base case. Although, common sense would suggest that low porosity will produce less gas, the results show that in this case the cumulative production is higher. This case shows an increased ratio of formation rock against hydrates that results in a higher heat retention of the formation rock that subsequently result in a higher temperature in the host formation and subsequently temperatures remain higher due to the heat capacity of the rock, which in turn stimulates even more hydrate dissociation.
In the case of reducing the thickness of the hydrate layer, the radius of the reservoir was increased in order to keep the same initial volume. The result of this change was less cumulative methane production and is shown in Figure 14. In this case gas from hydrate decomposition had to travel a longer distance through the host rock and an increased time was needed for the pressure change to propagate through the formation.
3.3. Full Factorial Design
For our full factorial design we chose six parameters: BHP, initial pressure, thermal conductivity of the rock, absolute permeability, irreducible water saturation and well radius. The effects of each factor with respect to the response variable were studied in an ANOVA. The design bases for this analysis are:
Six factors and two levels; this design constitutes a total of 64 simulations (26);
Response variable: cumulative production of CH4;
Level of significance (α): 0.05;
Replicates: one (number of results per run).
Table 6 summarizes the factors and levels that are used in this analysis.
Table 7 summarizes the results of the 64 simulations required to study this system. A value of −1 represents a low level of the factor whereas a value of +1 represents a high level.
For instance, for Runs #9, 20 and 37; it is established that shown in Table 8.
The chosen parameter values were BHP = 4000 kPa; initial pressure = 6000 kPa; thermal conductivity = 0.5 W/(m·K); absolute permeability = 300 mD; irreducible water saturation = 0.2; well radius = 0.086 m. This run is labeled “ad” because the factors a (BHP) and d (absolute permeability) are at the high level. A similar structure is followed by Runs 20 and 37; where the highest levels are respectively: absolute permeability and well radius; thermal conductivity, absolute permeability and irreducible water saturation.
As mentioned before, this system is an unreplicated 26 factorial design. With only one replicate there is no internal estimate of error, which causes ANOVA analysis to fail. To overcome this problem, it is assumed that high order interactions are negligible (sparsity of effects principle) and combine their mean squares to estimate the error [12].
To carry out this type of ANOVA it is necessary to calculate its main components: Sum of squares (Sum Sq.) due to each source represent the difference between the various levels of each source and the grand mean; degrees of freedom (d.f.) represents the degree of freedom associated to the sum of squares; mean squares (Mean Sq.) of each source represent the variance of each source and is obtained by dividing the sum of squares by the associated d.f. F-test is obtained from the ratio between variance of the source and the variance of the error. P-value is the statistical test to determine if a factor is statistically important, in this case, P-value is less than the level of significance (α). Table 9 presents the results obtained from the ANOVA analysis.
From Table 9, using the 0.05 level of significance, it is possible to deduce that the factors BHP, K (thermal conductivity of the rock) and κ (absolute permeability), and the interactions BHP-K (BHP-thermal conductivity), BHP-κ (BHP-absolute permeability) and K-κ (thermal conductivity-absolute permeability), all have a value of p < 0.05 and thus make statistically important contributions to the response variable.
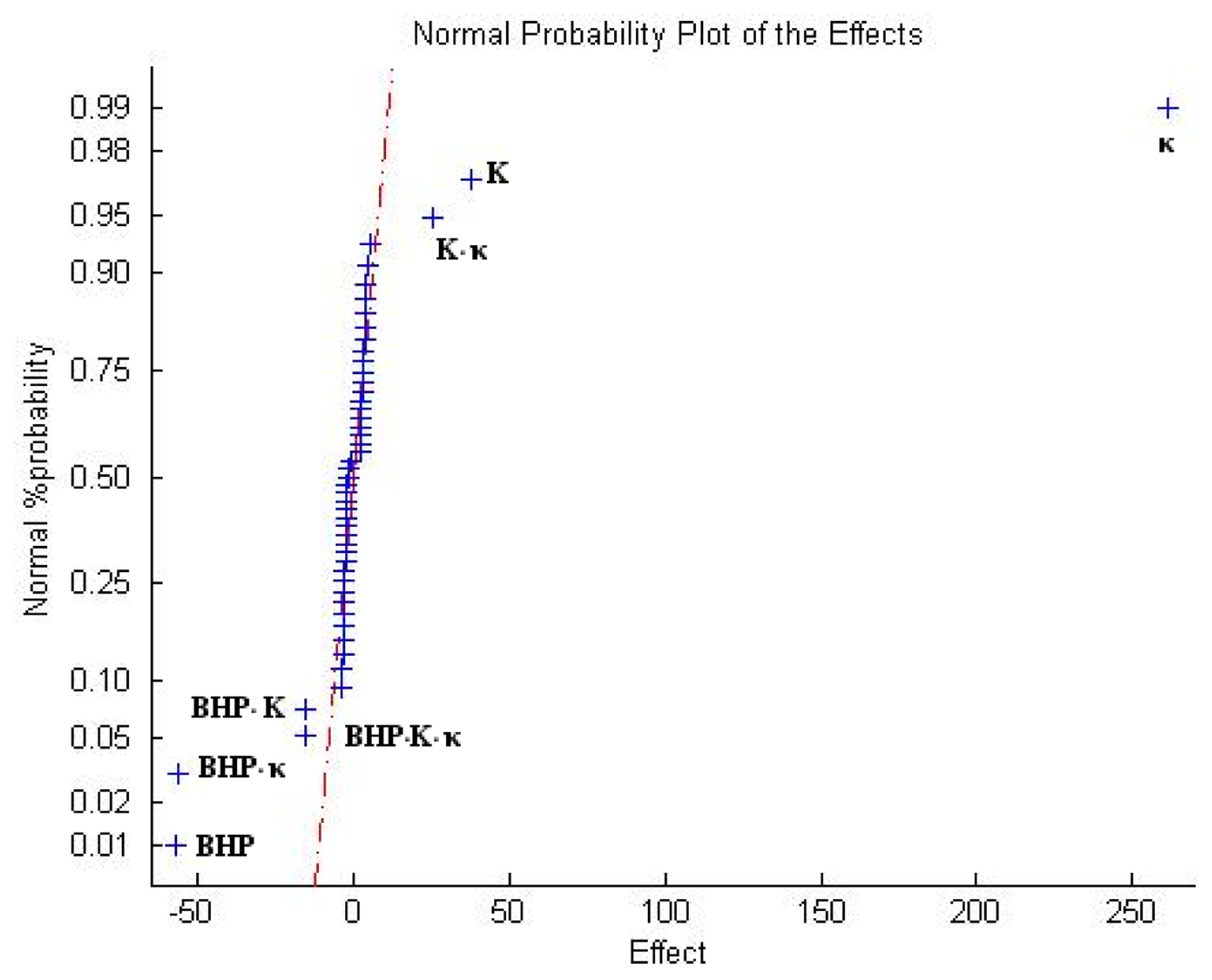
It is important now to rule out higher order interactions. Montgomery [12] proposes a method of analysis which is based on the normal probability plot of the estimates of the effects. In this method, the effects that are negligible are normally distributed, with mean zero and will tend to fall along a straight line on this plot, whereas significant effects will have non-zero means and will not lie along the straight line. In order to calculate the effects it is necessary to determine the contrasts for each effect. The general method is as follows
In general to estimate the contrast for effect the AB…K, expand the right hand side of the following equation:
Considering this, Figure 16 presents the normal probability plot of the effects. Figure 16 supports the conclusions obtained from the ANOVA analysis. It also shows that third order interactions are relatively important (BHP-thermal conductivity-absolute permeability).
In addition, Figure 17 presents the graphs of the main effects of the factors on the cumulative gas production; as noticed the absolute permeability and BHP are the most important variables since their graphs' slopes are the highest indicating that any change in their level greatly affect the response variable.
Figure 18 presents the graphs of the interaction effects on the cumulative gas production and confirms that the most important interactions are: BHP-K (BHP-thermal conductivity), BHP-κ (BHP-absolute permeability) and K-κ (thermal conductivity-absolute permeability) which can be determined from how parallel the lines are. For instance, the interaction BHP-rw is not statistically important (parallel lines) since the differences between the well radii are consistent for each value of BHP; however, the interaction BHP-κ is statistically important (non-parallel lines) since at 0.1 mD the average cumulative gas produced is almost the same at the two BHP levels, but at 300 mD there is a large difference.
An additional interpretation of the effects is possible; since the effects of initial pressure, irreducible water saturation and well radius and all their interactions are negligible it is possible to discard these variables so that the design becomes 23 with 8 replicates, this method is known in the literature as hidden replication. The ANOVA using this simplification is presented in Table 10. The results of this analysis confirm the conclusions obtained above.
4. Conclusions
The OFAT sensitivity study and the full factorial design analyzed using ANOVA showed that reservoir absolute permeability (κ), BHP and the thermal conductivity of the rock (K) had the most significant effects on the recovery of methane from gas hydrates. In addition, the full factorial design allowed to established important interactions such as BHP-K, κ-K, BHP-κ and κ-K-BHP that contribute to the response variable which cannot be concluded from the OFTA.
Considering the levels, by which these factors contribute to productivity, the most significant factors, by far, are those controlling the transport of gas to the well (κ and BHP). In comparison to factors governing the rate of transport, factors governing the rate of hydrate decomposition are of less importance, except for heat transfer (K) from the country rock to the hydrate deposit.
The design of this study will help to estimate the upper limits of productivity in natural gas hydrate deposits. In the field, further limitations will apply, such as trapped gas bubbles, inhomogeneous hydrate distribution or anisotropic permeability.
Acknowledgments
This research was funded by the German Federal Ministry of Economics and Technology as part of the project “Submarine Gas Hydrates” (SUGAR).
The authors would like to thank the reviewers for their helpful comments. The German Federal Ministry for Economic Affairs and Energy (BMWi) provided funding for this work through Research Grant 03SX250E.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, Y.; Strumendo, M.; Arastoopour, H. Simulation of methane production from hydrates by depressurization and thermal stimulation. Ind. Eng. Chem. Res. 2009, 48, 2451–2464. [Google Scholar]
- Selim, M.S.; Sloan, E.D. Modeling of the Dissociation of an In-Situ Hydrate. Proceedings of the Society of Petroleum Engineers (SPE) California Regional Meeting, Bakersfield, CA, USA, 27–29 March 1985.
- Sung, W.; Lee, H.; Lee, C. Numerical study for production performances of a methane hydrate reservoir stimulated by inhibitor injection. Energy Sources 2002, 24, 499–512. [Google Scholar]
- Yousif, M.H.; Abass, H.H.; Selim, M.S.; Sloan, E.D. Experimental and theoretical investigation of methane-gas-hydrate dissociation in porous media. SPE Reserv. Eng. 1991, 6, 69–76. [Google Scholar]
- Shahbazi, A.; Pooladi-Darvish, M.; Hassanzadeh, H. Coarse Grid Numerical Simulation of Reaction Kinetics Model in the Gas Hydrate Reservoirs. Proceedings of the 6th International Conference on Gas Hydrates (ICGH), Vancouver, BC, Canada, 6–10 July 2008.
- Schicks, J.; Spangenberg, E.; Giese, R.; Steinhauer, B.; Klump, J.; Luzi, M. New approaches for the production of hydrocarbons from hydrate bearing sediments. Energies 2011, 4, 151–172. [Google Scholar]
- Konno, Y.; Masuda, Y.; Hariguchi, Y.; Kurihara, M.; Ouchi, H. Key factors for depressurization-induced gas production from oceanic methane hydrates. Energy Fuels 2010, 24, 1736–1744. [Google Scholar]
- Myshakin, E.; Gamwo, I.; Warzinski, R. Experimental Design Applied to Simulation of Gas Productivity Performance at Reservoir and Laboratory Scales Utilizing Factorial ANOVA Methodology. Proceedings of the TOUGH Symposium, Berkeley, CA, USA, 14–16 September 2009.
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley & Sons: Chichester, UK, 2008. [Google Scholar]
- Friedmann, F.; Chawathe, A.; Larue, D.K. Assessing Uncertainty in Channelized Reservoirs Using Experimental Designs. Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 30 September–3 October 2001.
- White, C.; Royer, S. Experimental Design as a Framework for Reservoir Studies. Proceedings of the SPE Reservoir Simulation Symposium, Houston, TX, USA, 3–5 February 2003.
- Montgomery, D.C. Design and Analysis of Experiments, 7th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Advanced Process and Thermal Reservoir Simulator; CMG STARS, Version 2009; Computer Modelling Group Ltd.: Calgary, AB, Canada, 2009.
- Wilder, J.W.; Moridis, G.J.; Wilson, S.J.; Kurihara, M.; White, M.D.; Masuda, Y.; Anderson, B.J.; Collett, T.S.; Hunter, R.B.; Narita, H.; et al. An International Effort to Compare Gas Hydrate Reservoir Simulators. Proceedings of the 6th International Conference on Gas Hydrates (ICGH), Vancouver, BC, Canada, 6–10 July 2008.
- Uddin, M.; Wright, F.; Coombe, D. Numerical study of gas evolution and transport behaviours in natural gas-hydrate reservoirs. J. Can. Petrol. Tech. 2011, 50, 70–89. [Google Scholar]
- Uddin, M.; Coombe, D.; Wright, F. Modeling of CO2-hydrate formation in geological reservoirs by injection of CO2gas. J. Energy Resour. Technol. 2008, 130. [Google Scholar] [CrossRef]
- Hong, H.; Pooladi-Darvish, M.; Bishnoi, P.R. Analytical modelling of gas production from hydrates in porous media. J. Can. Pet. Technol. 2002, 42, 45–56. [Google Scholar]
- Gabitto, J.F.; Tsouris, C. Physical properties of gas hydrates: A review. J. Thermodyn. 2010, 2010. [Google Scholar] [CrossRef]
- Chen, Z.; Bai, W.; Xu, W.; Jin, Z. An analysis on stability and deposition zones of natural gas hydrate in Dongsha Region, North of South China Sea. J. Thermodyn. 2010, 2010. [Google Scholar] [CrossRef]
- Waite, W.F.; Santamarina, J.C.; Cortes, D.D.; Dugan, B.; Espinoza, D.N.; Germaine, J.; Jang, J.; Jung, J.W.; Kneafsey, T.J.; Shin, H.; et al. Physical properties of hydrate-bearing sediments. Rev. Geophys. 2009, 47. [Google Scholar] [CrossRef]
- Selim, M.S.; Sloan, E.D. Heat and mass transfer during the dissociation of hydrates in porous media. AIChE J. 1989, 35, 1049–1052. [Google Scholar]
- Kurihara, M.; Narita, H.; Masuda, Y. Gas Production from Methane Hydrate Reservoirs. Proceedings of the 7th International Conference on Gas Hydrates (ICGH), Edinburgh, UK, 17–21 July 2011.
- Tabatabaie, S.H.; Pooladi-Darvish, M. Analytical Solution for Gas Production from Tilted Gas Hydrate Reservoir. Proceedings of the Canadian Unconventional Resources and International Petroleum Conference, Calgary, AB, Canada, 19–21 October 2010.
- Howe, S.; Patil, S.; Dandekar, A.; Nanchary, N.; Ogbe, D.; Hunter, R.; Chukwu, G.; Reynolds, D. Production modeling of a potential methane hydrate accumulation on the north slope of Alaska. Petrol. Sci. Technol. 2009, 27, 923–932. [Google Scholar]
- Kim, H.C.; Bishnoi, P.R.; Heidemann, R.A.; Rizvi, S.S.H. Kinetics of methane hydrate decomposition. Chem. Eng. Sci. 1987, 42, 1645–1653. [Google Scholar]
- Clarke, M.A.; Bishnoi, P.R. Determination of the intrinsic rate constant and activation energy of CO2 gas hydrate decomposition using in-situ particle size analysis. Chem. Eng. Sci. 2004, 59, 2983–2993. [Google Scholar]
- Sloan, E.D.; Koh, C.A. Clathrate Hydrates of Natural Gases, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar]
- Parker, J.C.; Lenhard, R.J.; Kuppusamy, T. A parametric model for constitutive properties governing multiphase flow in porous media. Water Resour. Res. 1987, 23, 618–624. [Google Scholar]
Nomenclature
Symbol
| a | Constant in the phase equilibrium equation |
| Adec | Hydrate surface area per unit volume (m2m3) |
| ASH | Specific area of hydrate particles (m2m3) |
| b | Constant in the phase equilibrium equation (K) |
| BHP | Bottom hole pressure (kPa) |
| Cpg | Gas heat capacity (J/(gmol·K)) |
| d.f. | Degrees of freedom |
| E | Activation energy (J/mol) |
| feq | Equilibrium fugacity (kPa) |
| fg | Fugacity of the hydrate former in the vapor phase (kPa) |
| f | Fugacity (kPa) |
| g | Mass generation rate (kg/m3·s) |
| h | Specific enthalpy (J/kg) |
| iSw | Irreducible water saturation |
| k | Thermal conductivity (W(m2·s)) |
| kd | Decomposition rate constant (mol/(m2·Pa·s)) |
| k0d | Intrinsic decomposition rate constant (mol/(m2·Pa·s)) |
| M | Molecular mass (kg/mol) |
| ni | Number of moles of component i |
| pc | Capillary pressure (kPa) |
| P | Pressure (kPa) |
| Pe | Aspect ratio |
| QH | Heat of hydrate decomposition unit bulk volume (J/m3·s) |
| Qin | Direct heat input bulk volume (J/m3·s) |
| r | Radius (m) |
| rw | Well radius (m) |
| R | Universal gas constant, 8.314 J/(mol·s) |
| Si | Saturation of phase i |
| Swr | Irreducible water saturation |
| Sgr | Residual gas saturation |
| T | Temperature (K) |
| t | Time (s) |
| u | Specific internal energy (J/kg) |
| V | Volume (m3) |
| z | Axial axis in the reservoir (m) |
| Greek Letters |
|---|







| Parameter | Chen et al. [19] | Myshakin et al. [8] | Liu et al. [1] | Shahbasi et al. [5] | Uddin et al. [16] | Selim et al. [21] | Kurihara et al. [22] | White et al. [11] | Tabataibe et al. [23] | Howe et al. [24] | Sung et al. [3] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Porosity | 0.5 | 0.35 | 0.2 | 0.2 | 0.28 | 0.3 | 0.35 | 0.3 | 0.3 | 0.36 | 0.2 |
| Permeability (mD) | 0.1 | 1,000 | 4.2 | 1 | 20 | 140 | 1,000 | 1,000 | - | 300 | 10–100 |
| Thermal conductivity of the rock (W/m·K) | 1 | 0.5 | 2.73–5.57 | 1.5 | 1.5–8 | 2.7 | 2 | 0.5 | 1.5 | 1.7 | - |
| Thickness (m) | - | 60 | - | - | 10 | semiinfinite | 12.5 | 30 | 16 | 15 | 15 |
| Volumetric heat capacity (J/m3·K) | - | - | 1.76 × 106 | 2.12 × 106 | 2.12 × 106 | - | 2.60 × 106 | - | 2.12 × 106 | 2.35 × 106 | - |
| Radius (m) | - | 900 | 100 | - | 200 | - | 450 | 567 | 100 | - | - |
| Initial pressure (kPa) | 20,370 | 10,900 | - | 11,510 | 6,913 | - | 6800 | 10,670 | 8,540 | - | 5,514 |
| Initial temperature (°C) | 3.1 | 12.45 | 12–16 | 15 | 10 | - | 2.8 | 13.5 | 12 | 11 | 4.75 |
| BHP (kPa) | - | - | 3,000–4,000 | 2,000 | 4,300 | (2) | - | 4,000 | - | 2,068 | 3,446 |
| Gas saturation | - | - | - | - | 0.1 | - | 0 | - | 0 | 0.1 | 0.4 |
| Water saturation | - | - | - | - | 0.3 | - | 0.35 | - | 0.25 | 0.2 | 0.3 |
| Hydrate saturation | - | 0.4 | 0.19 | 0.4 | 0.6 | - | 0.65 | - | 0.75 | 0.7 | - |
(1) To improve readability, the explanation of the symbols used in the formulae has been moved to an appendix at the end of this article; and (2) Thermal stimulation method.
| Parameter | Gabitto et al. [18] | Chen et al. [19] | Lui et al. [1] | Waite et al. [20] | Shahbasi et al. [5] | Uddin et al. [16] |
|---|---|---|---|---|---|---|
| Heat capacity (J/kg·K) | 3,300 | - | 2,200 | 2,031 | 1,600 | 1,600.5 |
| Thermal conductivity (W/m·K) | 0.5 | - | 0.49 | 0.57 | 0.4 | 0.4 |
| Density (kg/m3) | 912 | 920 | 910 | 929 | 919.7 | 919.7 |
| Heat of reaction (kJ/mol) | - | - | 54.7 | - | 57 | 51.9 |
| Molecular weight (kg/kmol) | - | - | - | - | 119.5 | 119.5 |
| Basic parameter | CH4 hydrate | H2O | CH4 | Reference |
|---|---|---|---|---|
| Thermal conductivity (W/m·K) | 0.5 | 0.6 | 0.04 | Gabitto et al. [18] |
| Molecular weight (g/mol) | 119.5 | 18 | 16 | Uddin et al. [16] |
| Density (kg/m3) | 912 | 1,000 | (1) | Gabitto et al. [18] |
| Heat capacity (J/kg·K) | 2,200 | (2) | (3) | Liu et al. [1] |
(1) Calculated by Advanced Processes & Thermal Reservoir Simulator (STARS) using an equation of state;(2) From STARS database; and (3) Cpg(J/(mol·K)) = 19.251 + 5.213 × 10−2 × T + 1.197·× 10−5 × T2 − 1.132·× 10−8 × T3.
| Name | Value | Reference |
|---|---|---|
| System | Non-adiabatic | More realistic than adiabatic case |
| Hydrate layer radius (m) | 500 | [11,22] |
| Well radius (m) | 0.086 | Default value from STARS™ |
| Hydrate layer thickness (m) | 14 | [23,24] |
| Porosity | 0.5 | [19] |
| Absolute permeability (mD) | 10 | [3,16] |
| Thermal conductivity of rock (W/(m·K)) | 3 | [21] |
| Temperature (°C) | 8 | [16] |
| BHP (kPa) | 3,000 | [1] |
| Pressure (kPa) | 6,000 | [16,22] |
| Rock heat capacity (J/(m3·K)) | 2.6 × 106 | [22] |
| Initial gas saturation | 0.08 | [16] |
| Initial hydrate saturation | 0.4 | [8] |
| Initial water saturation | 0.62 | Determined by difference |
| Case | Cumulative production (m3 @Standard T&P) × 108 |
|---|---|
| Base case | 1.78 |
| Thermal conductivity of rock (8 W/(m·K)) | 1.88 |
| Absolute permeability (100 mD) | 3.12 |
| Initial pressure (7,000 kPa) | 1.78 |
| BHP (4,000 kPa) | 1.16 |
| Porosity (0.2). Thickness is increased 2.5 times. | 2.54 |
| Thickness of the hydrate layer (7 m). Radius is increased by a factor of 21/2. | 1.38 |
| Well radius (0.3 m) | 2.2 |
| Factors | Labels | Levels |
|---|---|---|
| BHP (kPa) | a | 3,000–4,000 |
| Initial pressure-P (kPa) | b | 6,000–6,500 |
| Thermal conductivity of rock-K (W/(m·K)) | c | 0.5–8 |
| Absolute permeability-κ (mD) | d | 0.1–300 |
| Irreducible water saturation-iSw | e | 0.2–0.35 |
| Well radius-rw (m) | f | 0.086–0.3 |
| Run number | Factors | Run label | Response variable | |||||
|---|---|---|---|---|---|---|---|---|
| BHP | Initial pressure | Thermal conductivity | Absolute permeability | Irreducible water saturation | Well radius | QCH4 (Sm3) × 106-total | ||
| 1 | 1 | 1 | −1 | −1 | −1 | −1 | a | 8.43 × 10−1 |
| 2 | −1 | −1 | −1 | −1 | −1 | −1 | b | 1.66 |
| 3 | −1 | −1 | 1 | −1 | −1 | −1 | c | 1.98 |
| 4 | −1 | −1 | −1 | 1 | −1 | −1 | d | 2.75 × 102 |
| 5 | −1 | 1 | −1 | −1 | 1 | −1 | e | 2.04 |
| 6 | −1 | −1 | −1 | −1 | −1 | 1 | f | 2.41 |
| 7 | 1 | −1 | −1 | −1 | −1 | −1 | ab | 8.83 × 10−1 |
| 8 | 1 | 1 | 1 | −1 | −1 | −1 | ac | 1.15 |
| 9 | 1 | −1 | −1 | 1 | −1 | −1 | ad | 1.82 × 102 |
| 10 | −1 | 1 | 1 | −1 | −1 | −1 | bc | 2.04 |
| 11 | 1 | −1 | −1 | −1 | 1 | −1 | ae | 1.07 |
| 12 | −1 | 1 | −1 | −1 | −1 | −1 | bd | 2.76 × 102 |
| 13 | 1 | −1 | 1 | −1 | −1 | 1 | af | 1.19 |
| 14 | −1 | 1 | −1 | −1 | 1 | −1 | be | 2.09 |
| 15 | −1 | −1 | −1 | 1 | −1 | −1 | cd | 3.56 × 102 |
| 16 | −1 | −1 | −1 | −1 | −1 | 1 | bf | 2.52 |
| 17 | −1 | −1 | 1 | −1 | 1 | −1 | ce | 2.47 |
| 18 | −1 | −1 | 1 | −1 | −1 | 1 | cf | 2.88 |
| 19 | −1 | −1 | −1 | 1 | 1 | −1 | de | 2.80 × 102 |
| 20 | −1 | 1 | −1 | 1 | −1 | 1 | df | 2.77 × 102 |
| 21 | −1 | 1 | −1 | −1 | 1 | 1 | ef | 3.01 |
| 22 | 1 | 1 | 1 | −1 | −1 | −1 | abc | 9.14 × 10−1 |
| 23 | 1 | −1 | −1 | 1 | −1 | −1 | abd | 1.83 × 102 |
| 24 | 1 | 1 | −1 | −1 | 1 | −1 | abe | 1.11 |
| 25 | 1 | −1 | 1 | 1 | −1 | −1 | acd | 2.15 × 102 |
| 26 | 1 | 1 | −1 | −1 | −1 | 1 | abf | 1.27 |
| 27 | 1 | −1 | 1 | −1 | 1 | −1 | ace | 1.16 |
| 28 | −1 | −1 | 1 | 1 | −1 | −1 | bcd | 3.57 × 102 |
| 29 | 1 | 1 | 1 | −1 | −1 | 1 | acf | 1.64 |
| 30 | 1 | −1 | −1 | 1 | 1 | −1 | ade | 1.86 × 102 |
| 31 | −1 | 1 | 1 | −1 | 1 | −1 | bce | 2.52 |
| 32 | 1 | 1 | −1 | 1 | −1 | 1 | adf | 1.84 × 102 |
| 33 | −1 | −1 | 1 | −1 | −1 | 1 | bcf | 3.03 |
| 34 | −1 | 1 | −1 | 1 | 1 | −1 | bde | 2.81 × 102 |
| 35 | 1 | −1 | −1 | −1 | 1 | 1 | aef | 1.51 |
| 36 | −1 | 1 | −1 | 1 | −1 | 1 | bdf | 2.79 × 102 |
| 37 | −1 | −1 | 1 | 1 | 1 | −1 | cde | 3.61 × 102 |
| 38 | −1 | −1 | −1 | −1 | 1 | 1 | bef | 3.13 |
| 39 | −1 | −1 | 1 | 1 | −1 | 1 | cdf | 3.60 × 102 |
| 40 | −1 | 1 | 1 | −1 | 1 | 1 | cef | 3.56 |
| 41 | −1 | 1 | −1 | 1 | 1 | 1 | def | 2.82 × 102 |
| 42 | 1 | 1 | 1 | 1 | −1 | −1 | abcd | 2.16 × 102 |
| 43 | 1 | 1 | 1 | −1 | 1 | −1 | abce | 1.34 |
| 44 | 1 | 1 | 1 | −1 | −1 | 1 | abcf | 1.68 |
| 45 | 1 | −1 | −1 | 1 | 1 | −1 | abde | 1.87 × 102 |
| 46 | 1 | 1 | −1 | 1 | −1 | 1 | abdf | 2.79 × 102 |
| 47 | 1 | −1 | 1 | 1 | 1 | −1 | acde | 2.19 × 102 |
| 48 | 1 | 1 | −1 | −1 | 1 | 1 | abef | 1.59 |
| 49 | 1 | −1 | 1 | 1 | −1 | 1 | acdf | 2.17 × 102 |
| 50 | −1 | 1 | 1 | 1 | 1 | −1 | bcde | 3.63 × 102 |
| 51 | 1 | −1 | 1 | −1 | 1 | 1 | acef | 2.04 |
| 52 | −1 | 1 | 1 | 1 | −1 | 1 | bcdf | 3.61 × 102 |
| 53 | 1 | 1 | −1 | 1 | 1 | 1 | adef | 1.87 × 102 |
| 54 | −1 | −1 | 1 | −1 | 1 | 1 | bcef | 3.78 |
| 55 | −1 | 1 | −1 | 1 | 1 | 1 | bdef | 2.83 × 102 |
| 56 | −1 | 1 | 1 | 1 | 1 | 1 | cdef | 3.65 × 102 |
| 57 | 1 | 1 | 1 | 1 | 1 | −1 | abcde | 2.05 × 102 |
| 58 | 1 | 1 | 1 | 1 | −1 | 1 | abcdf | 2.18 × 102 |
| 59 | 1 | −1 | 1 | −1 | 1 | 1 | abcef | 2.10 |
| 60 | 1 | 1 | −1 | 1 | 1 | 1 | abdef | 1.87 × 102 |
| 61 | 1 | −1 | 1 | 1 | 1 | 1 | acdef | 2.21 × 102 |
| 62 | −1 | 1 | 1 | 1 | 1 | 1 | bcdef | 3.67 × 102 |
| 63 | 1 | 1 | 1 | 1 | 1 | 1 | abcdef | 2.22 × 102 |
| 64 | −1 | −1 | −1 | −1 | −1 | −1 | (1) | 1.60 |
(1) All factors are at low level.
| BHP | Initial pressure | Thermal conductivity | Absolute permeability | Irreducible water saturation | Well radius | Run label |
|---|---|---|---|---|---|---|
| 1 | −1 | −1 | 1 | −1 | −1 | ad |
| −1 | −1 | −1 | 1 | −1 | 1 | df |
| −1 | −1 | 1 | 1 | 1 | −1 | cde |
| Source | Sum Sq. | d.f. | Mean Sq. | F-test | P-value |
|---|---|---|---|---|---|
| BHP | 52,574 | 1 | 52,574 | 230.26 | 0.00 |
| P | 149 | 1 | 149 | 0.65 | 0.42 |
| K | 10,590 | 1 | 10,590 | 46.38 | 0.00 |
| κ | 1,094,245 | 1 | 1,094,245 | 4,792.61 | 0.00 |
| iSw | 16 | 1 | 16 | 0.07 | 0.79 |
| rw | 390 | 1 | 390 | 1.71 | 0.20 |
| BHP-P | 89 | 1 | 89 | 0.39 | 0.54 |
| BHP-K | 3,896 | 1 | 3,896 | 17.06 | 0.00 |
| BHP-κ | 50,394 | 1 | 50,394 | 220.72 | 0.00 |
| BHP-iSw | 236 | 1 | 236 | 1.03 | 0.32 |
| BHP-rw | 134 | 1 | 134 | 0.59 | 0.45 |
| P-K | 183 | 1 | 183 | 0.80 | 0.38 |
| P-κ | 142 | 1 | 142 | 0.62 | 0.43 |
| P-iSw | 180 | 1 | 180 | 0.79 | 0.38 |
| P-rw | 187 | 1 | 187 | 0.82 | 0.37 |
| K-κ | 10,265 | 1 | 10,265 | 44.96 | 0.00 |
| K-iSw | 109 | 1 | 109 | 0.48 | 0.49 |
| K-rw | 64 | 1 | 64 | 0.28 | 0.60 |
| κ-iSw | 32 | 1 | 32 | 0.14 | 0.71 |
| κ-rw | 276 | 1 | 276 | 1.21 | 0.28 |
| iSw-rw | 106 | 1 | 106 | 0.46 | 0.50 |
| Error | 9,589 | 42 | 228 | - | - |
| Total | 1,233,846 | 63 | - | - | - |
| Source | Sum Sq. | d.f. | Mean Sq. | F | P-value |
|---|---|---|---|---|---|
| BHP | 52,574 | 1 | 52,574 | 366.86 | 0.00 |
| K | 10,590 | 1 | 10,590 | 73.90 | 0.00 |
| κ | 1,094,245 | 1 | 1,094,245 | 7,635.68 | 0.00 |
| BHP-K | 3,896 | 1 | 3896 | 27.19 | 0.00 |
| BHP-κ | 50,394 | 1 | 50,394 | 351.65 | 0.00 |
| K-κ | 10,265 | 1 | 10,265 | 71.63 | 0.00 |
| BHP-K-κ | 3,857 | 1 | 3,857 | 26.92 | 0.00 |
| Error | 8,025 | 56 | 143 | - | - |
| Total | 1,233,846 | 63 | - | - | - |
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Giraldo, C.; Klump, J.; Clarke, M.; Schicks, J.M. Sensitivity Analysis of Parameters Governing the Recovery of Methane from Natural Gas Hydrate Reservoirs. Energies 2014, 7, 2148-2176. https://doi.org/10.3390/en7042148
Giraldo C, Klump J, Clarke M, Schicks JM. Sensitivity Analysis of Parameters Governing the Recovery of Methane from Natural Gas Hydrate Reservoirs. Energies. 2014; 7(4):2148-2176. https://doi.org/10.3390/en7042148
Chicago/Turabian StyleGiraldo, Carlos, Jens Klump, Matthew Clarke, and Judith M. Schicks. 2014. "Sensitivity Analysis of Parameters Governing the Recovery of Methane from Natural Gas Hydrate Reservoirs" Energies 7, no. 4: 2148-2176. https://doi.org/10.3390/en7042148





