Large Eddy Simulation of Vertical Axis Wind Turbine Wakes
Abstract
: In this study, large eddy simulation (LES) is combined with a turbine model to investigate the wake behind a vertical-axis wind turbine (VAWT) in a three-dimensional turbulent flow. Two methods are used to model the subgrid-scale (SGS) stresses: (a) the Smagorinsky model; and (b) the modulated gradient model. To parameterize the effects of the VAWT on the flow, two VAWT models are developed: (a) the actuator swept-surface model (ASSM), in which the time-averaged turbine-induced forces are distributed on a surface swept by the turbine blades, i.e., the actuator swept surface; and (b) the actuator line model (ALM), in which the instantaneous blade forces are only spatially distributed on lines representing the blades, i.e., the actuator lines. This is the first time that LES has been applied and validated for the simulation of VAWT wakes by using either the ASSM or the ALM techniques. In both models, blade-element theory is used to calculate the lift and drag forces on the blades. The results are compared with flow measurements in the wake of a model straight-bladed VAWT, carried out in the Institute de Méchanique et Statistique de la Turbulence (IMST) water channel. Different combinations of SGS models with VAWT models are studied, and a fairly good overall agreement between simulation results and measurement data is observed. In general, the ALM is found to better capture the unsteady-periodic nature of the wake and shows a better agreement with the experimental data compared with the ASSM. The modulated gradient model is also found to be a more reliable SGS stress modeling technique, compared with the Smagorinsky model, and it yields reasonable predictions of the mean flow and turbulence characteristics of a VAWT wake using its theoretically-determined model coefficient.1. Introduction
Revived attention towards vertical axis wind turbines (VAWTs) has been observed in recent years. VAWTs are claimed to have several advantages over the conventional horizontal axis wind turbines (HAWTs), such as: insensitivity to the wind direction and, consequently, the absence of any yaw equipment; lower noise, due to the lower tip-speed of the blades; and placement of the drive train system on the ground [1]. Recently, Dabiri [2] has claimed that the power density of wind farms consisting of counter-rotating VAWTs can be potentially greater than HAWT wind farms by an order of magnitude. To understand the performance of VAWTs better, detailed knowledge of the flow through them and the wakes behind them is necessary. Furthermore, to optimize the efficiency of a single VAWT or an array of VAWTs in a wind farm, an accurate and reliable prediction of the flow field behind the turbines is essential. For this purpose, numerical simulations can provide valuable quantitative understanding of VAWT wakes in a relatively fast and cheap way.
Almost 40 years after Darrieus’ patent was registered (in 1931), researchers, mainly from some North American institutes (such as the National Research Council of Canada, NASA Langley Research Center and the Sandia National Laboratories), started to study VAWTs extensively. Rigorous and exhaustive experimental data from both wind tunnel and field measurements for different sizes of VAWTs were collected by these institutes in the 1970s and 1980s [3–8]. These experiments and other wind tunnel and field measurements, which were done during those years [9–14], mainly focused on overall rotor performance (e.g., power and torque) and loading on the blades. The first attempts to experimentally study the wake behind a VAWT date back to the late 1970s, when Muraca and Guillotte [15] performed velocity measurements in the near wake of a VAWT in a wind tunnel, and Vermeulen et al. [16] carried out flow measurements in the wake of a full-scale VAWT in the natural wind environment. None of them reported wake turbulence data. Later, in the 1980s, Strickland et al. [17] and Brochier et al. [18] carried out water channel experiments to quantify the flow field downstream of a model straight-bladed VAWT. Bergeles et al. [19] performed hot-wire measurements in the near wake of a Troposkein-shaped VAWT in a wind tunnel and reported the profiles of mean velocity and turbulence intensity for different tip-speed ratios and two downstream positions. More recently, Battisti et al. [20] carried out wind tunnel measurements on the wake of a VAWT and provided data on time-averaged and phase-resolved velocity and turbulence intensity in a vertical plane located 1.5 rotor diameters downstream of the turbine axis. They showed that large-scale aerodynamic unsteadiness is greater in the tip region than in the central region. With the emergence of particle image velocimetry (PIV) techniques, some flow visualizations and measurements have been done to study the dynamic stall phenomenon and vortex evolution inside and behind a VAWT [21–24]. Tescione et al. [24] has reported contours of average velocity and vorticity up to about 1.5 rotor diameters downstream of the turbine in a wind tunnel.
Besides experimental investigations, analytical and numerical studies have also been employed with the aim of VAWT performance prediction. The aerodynamic models that have been proposed for VAWTs can be classified in two main groups: streamtube models [1] (e.g., single streamtube model, multiple streamtube model, double multiple streamtube model) and vortex models (e.g., fixed-wake vortex model [25] and free-wake vortex model [17]). In streamtube models, the time-averaged forces on the blades are equated to the change in the streamwise momentum of the wind. Although, in principle, with vortex models, one can obtain the flow field downstream of a VAWT, the main focus of both models has been on the prediction of forces on the blades and overall rotor performance.
Simulation of VAWTs by solving the Navier–Stokes equations with numerical techniques was pioneered by Rajagopalan and Fanucci [26], who introduced the actuator swept-surface method in a two-dimensional space as a cylindrical porous shell on which the time-averaged blade forces continuously act on the fluid. This method was extended to a three-dimensional actuator swept-surface model for a curved-bladed VAWT in Rajagopalan et al. [27]. In both studies, the flow was considered laminar. Fortunato et al. [28] applied the same turbine modeling and solved the 2D compressible laminar Euler equation with a finite difference method. Shen et al. [29] used a 2D Navier–Stokes solver, using the k − ω shear stress transport turbulence model, to obtain the flow field past a VAWT. They modeled the turbine blades as two rotating actuator surfaces, on which the body forces are distributed. In the above works, mainly power coefficients and forces acting on the blades are quantitatively compared with experimental data, while the wake flow field is only demonstrated qualitatively. Moreover, considering the highly turbulent wake of a VAWT, the application of a numerical turbulence-resolving technique can potentially improve the quality of the wake prediction.
The present work aims at simulating the turbulent wake of a VAWT in a large eddy simulation (LES) framework by solving the full filtered Navier–Stokes equations in three dimensions, using an actuator swept-surface and an actuator line method to model the turbine effects on the flow and two turbulence modeling techniques to parameterize the subgrid-scale (SGS) stresses. It is worth mentioning that it is the first time that LES has been applied and validated for the simulation of VAWT wakes by using either the actuator swept-surface model (ASSM) or the actuator line model (ALM) techniques. The LES framework and model formulations are presented in Section 2. Next, we simulate the wake behind a straight-bladed VAWT for one special case and compare the results with corresponding experimental data. The numerical and experimental setups are described in Section 3, and the results are presented in Section 4. A summary of the study is given in Section 5.
2. Large Eddy Simulation Framework
LES solves the filtered incompressible Navier–Stokes equations, which can be written in rotational form as:
2.1. Turbulence Closure Models
Two closure models for parameterizing the SGS stresses are considered: the traditional Smagorinsky model and the modulated gradient model.
2.1.1. The Smagorinsky Model
The traditional Smagorinsky model [33] for the deviatoric part of the SGS stress is:
2.1.2. The Modulated Gradient Model
The modulated gradient model (MGM), which was proposed by Lu and Porté-Agel [37], is an alternative to standard eddy-viscosity closure models. In the MGM, the SGS stress tensor is modeled as:
If Δ̃x, Δ̃y and Δ̃z are taken to be filter sizes in the x-, y- and z-directions, then G̃ij is defined as:
To evaluate the SGS kinetic energy, ksgs, the local equilibrium hypothesis is used, which assumes there is a local balance between SGS energy production, P, and dissipation, ε. These two terms are calculated as:
Replacing the above expression for ksgs in Equation (7) gives the following equation for the SGS dissipation, ε:
To ensure numerical stability and that energy does not transfer locally from unresolved to resolved scales, we use the following clipping procedure:
With Equation (10), the set of equations for the MGM model is closed, and τij is fully expressed in terms of resolved variables. The model has been successfully validated in the simulation of a neutral atmospheric boundary layer [37,40,41] and a boundary layer over a 2D block using the immersed boundary method [42].
2.2. Parameterization of VAWT-Induced Forces
In this study, two methods are used to model the turbine-induced forces: (a) the actuator swept-surface model (ASSM); and (b) the actuator line model (ALM). Both models are based on blade-element theory, and therefore, they do not require resolving the boundary-layer flow around the turbine blade surfaces, which greatly reduces the computational cost requirements. In the blade-element theory, the turbine blades are divided into N blade elements that are assumed to behave aerodynamically as two-dimensional airfoils. The aerodynamic forces are determined using the lift and drag characteristics of the airfoil type, as well as the local flow conditions.
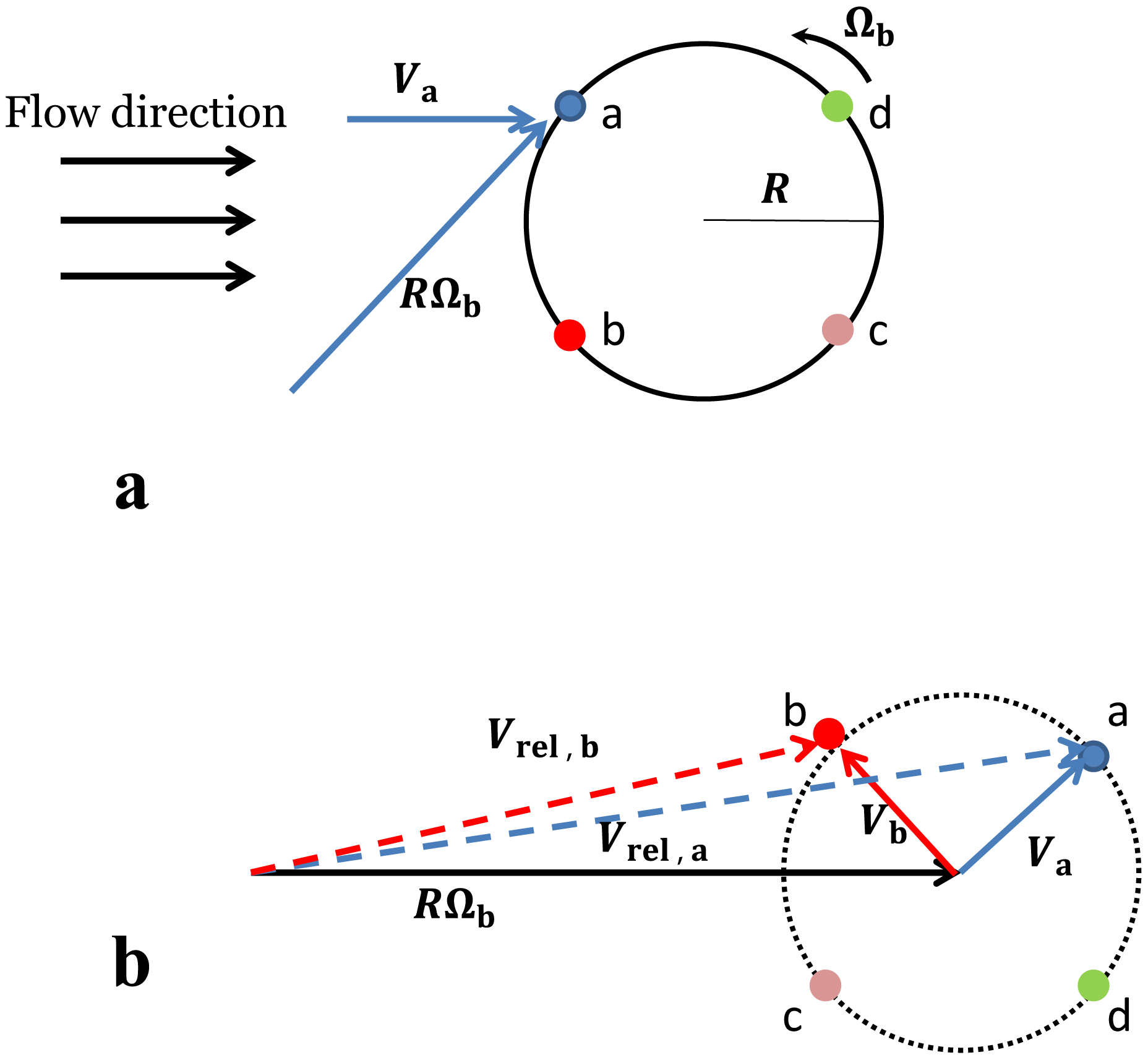
Figure 1 shows a horizontal cross-section of a blade in Darrieus motion in an arbitrary angular position, θ. In this figure, Ωb is the rotor angular velocity, R is the radius of the rotor, u∞ is the unperturbed wind velocity magnitude and Vlocal is the local wind velocity vector at the position of the blade. Denoting the radial and tangential components of the local wind velocity in the inertial frame of reference as Vlocal,n and Vlocal,s, respectively, the local relative wind velocity vector with respect to the rotating blade can be written as Vrel = Vlocal,nen + (Vlocal,s − ΩbR)es, where en and es are unit vectors in the radial and tangential directions, respectively. As is common for VAWTs, the airfoil is considered to be symmetrical, and the chord-line is assumed to be normal to the rotor radius; thus the angle of attack can be written as:
The lift and drag forces (see Figure 2) are calculated as:
2.2.1. Actuator Swept-Surface Model
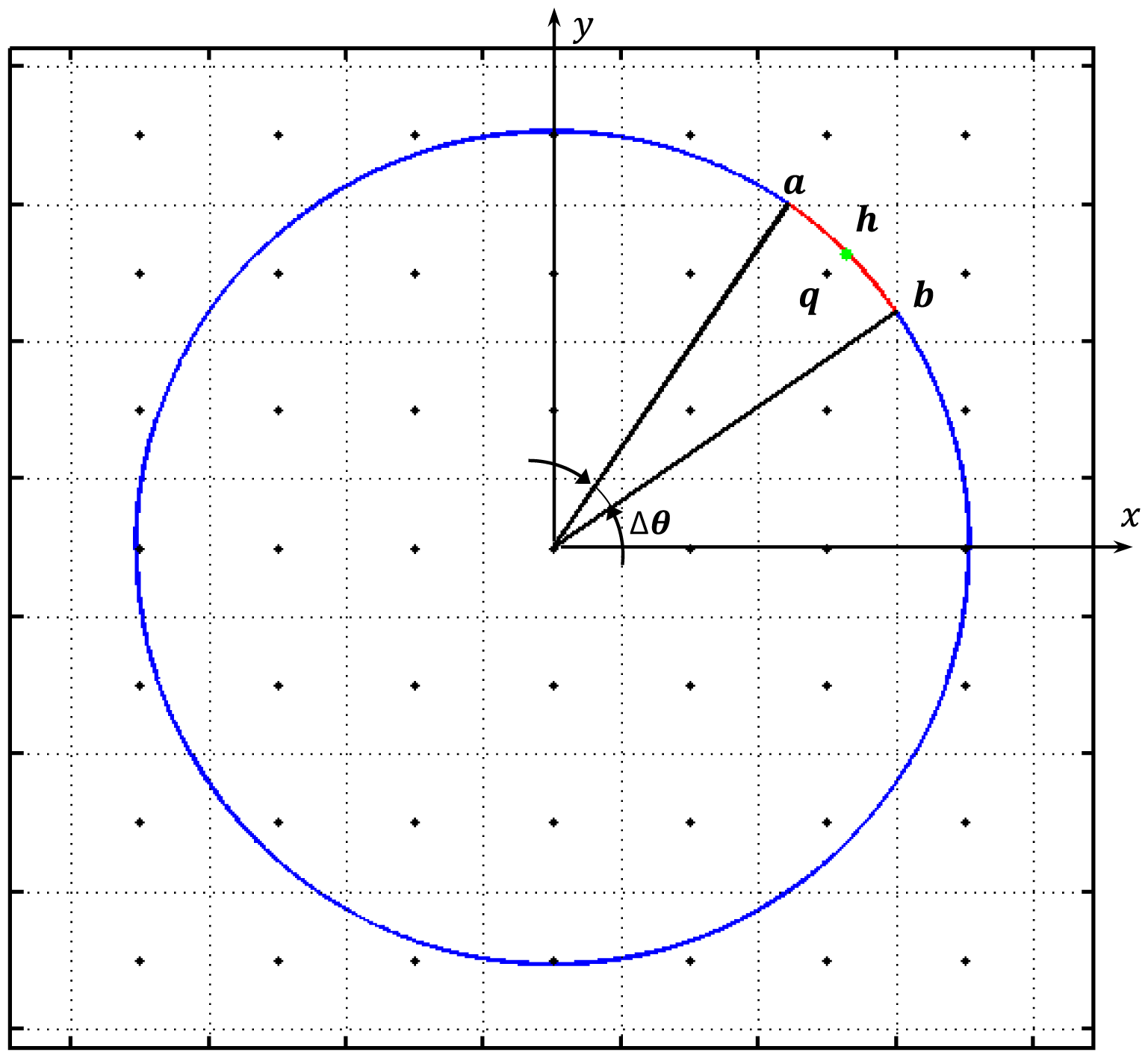
In the ASSM approach, the actuator swept surface is defined as the surface swept by the blades. For example, in the case of a straight-bladed VAWT, this actuator swept surface is an actuator cylinder. We distribute the time-averaged turbine-induced forces on this surface and integrate them over time and space. Figure 3 shows a horizontal cross-section of the actuator swept surface in the computational mesh, where the black points are grid points and the dashed lines show the control volumes surrounding them.
For illustration reasons and for the sake of clarity, the size of the grid cells with respect to the diameter of the rotor is shown as being much bigger than in the simulations. The turbine forces are distributed among grid points, whose corresponding control volumes intersect the actuator swept surface. For instance, arc with an angle of Δθ is located inside the control volume of grid point q in Figure 3. We take the midpoint, h, as a representative point of this arc and calculate Vrel, CL and CD on this point. The time fraction that each blade spends in arc is (Δθ/Ωb) × (Ωb/2π), and considering the number of blades, B, the time-averaging weight for the calculated force on this point is BΔθ/2π. Finally, the term, fi/ρ, in the Navier–Stokes equations [Equation (2)] for a given grid point, q, is calculated as:
2.2.2. Actuator Line Model
In the ALM, the turbine forces are distributed vertically along lines that represent the blades of the wind turbine. In this model, which was introduced by Shen and Sørensen [43] and has already been implemented for horizontal-axis wind turbines [43–47], there is no need to time-average the forces, because the blades are tracked in each time-step, and the forces are applied only at the physical position of the blades.
First, each grid point whose corresponding control volume encompasses the blade line is identified, and then, the airfoil data and subsequent loading are determined by computing local angles of attack from the movement of the blades and the local flow field. For instance, in Figure 4, it can be seen that the blade is located at point h, which is within the control volume of grid point q; hence, theoretically, the term, fi/ρ, in the Navier–Stokes equations [Equation (2)] should only be assigned to this grid point with the following formula:
By explicitly representing the individual blade motions, the ALM enables us to capture in more detail the complex and unsteady vortical structure of the near-wake flow. Consequently, it is likely to improve the near-wake predictions with respect to the ASSM. The application of the ALM seems particularly crucial for VAWTs, since, in contrast to HAWTs, a blade of a VAWT passes through the wakes generated by other blades, as well as its own wake; this fact makes the ALM approach attractive, because it allows us to study the blade-wake interaction phenomenon more realistically.
3. Numerical and Experimental Setups
In this section, the details of the numerical simulations, as well as the experimental setup, with which our results are compared, are presented. We have chosen the experimental study by Brochier et al. [18] to compare our simulation results with, because it contains data on mean velocity and turbulence intensity at several downstream positions in the wake of a model VAWT, even though it was conducted under uniform flow conditions. In fact, in previous VAWT wind tunnel experiments, the turbine has never been placed in a turbulent boundary layer flow, which is the regular flow regime, where full-scale turbines are located. It should be mentioned that more systematic and rigorous experimental studies on VAWT wakes, especially in a turbulent boundary layer flow, are still needed to deepen our understanding of the flow structure and behavior.
3.1. Experimental Setup
In 1986, Brochier et al. [18] conducted a water channel experiment with a straight-bladed Darrieus wind turbine under controlled-rotation conditions in the Institute de Méchanique et Statistique de la Turbulence (IMST) water channel. Velocity measurements were made using a laser-Doppler velocimeter (LDV), and quantitative profiles of mean velocity and turbulence intensity were provided.
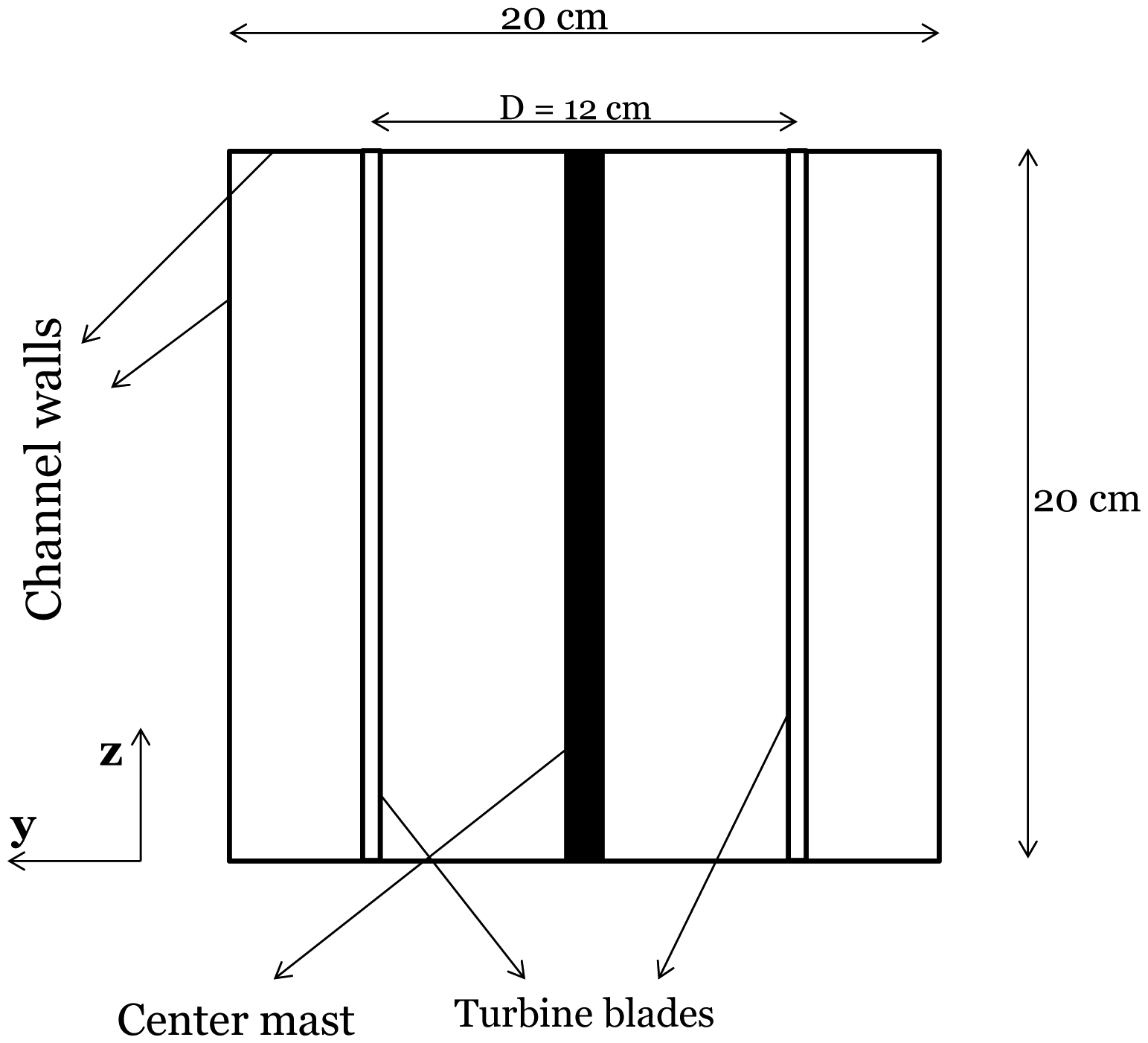
The water channel was vertical, and the driving force of the flow was gravity. The length of the channel in the streamwise direction (vertical direction in the experiment) was 1.5 m, and the cross-section of the channel (normal to the streamwise direction) was a square of a side length of 20 cm (see Figures 5 and 6). The walls of the channel were transparent (made of plexiglass) to allow for LDV measurements and flow visualization. The model rotor was made up of two straight blades with a chord length of 2 cm. The blades are composed of a NACA 0018 airfoil. The length of the blades was 20 cm, and the diameter of the rotor was 12 cm. The center column of the turbine had a diameter of 1 cm. The measurements were obtained for two tip speed ratios of 2.14 and 3.85. The flow speed in the water channel was 15 cm/s, and the center of the turbine was located 13 chord lengths downstream of the nozzle plane through which the inflow enters the test section.
3.2. Numerical Setup
The LES code is a modified version of the code described by Albertson and Parlange [32], Porté-Agel et al. [35] and Porté-Agel et al. [47]. A 3D structured mesh is employed, which has Nx and Ny nodes in the x- and y-directions, respectively, and Nz nodes in the z-direction. The mesh is staggered in the z-direction; this means the layers in which the vertical component of velocity (w) is stored are located halfway between the layers in which all the other main flow variables (u, υ, p) are stored. The first w—nodes are located on the z = 0 plane, while the first uυp—nodes are located on the plane.
To compute the spatial derivatives, a Fourier-based pseudospectral scheme is used in the horizontal directions, and a second-order finite difference method is used in the vertical direction. The governing equations for conservation of momentum are integrated in time with the second-order Adams–Bashforth scheme.
The boundary conditions in the horizontal directions are mathematically periodic. For the bottom and top boundary conditions, the instantaneous surface shear stress is calculated using the Monin–Obukhov similarity theory [48] as a function of the local horizontal velocities at the nearest (to the wall) vertical grid points ( for the bottom wall and for the top wall) (see, for instance, [49–51]).
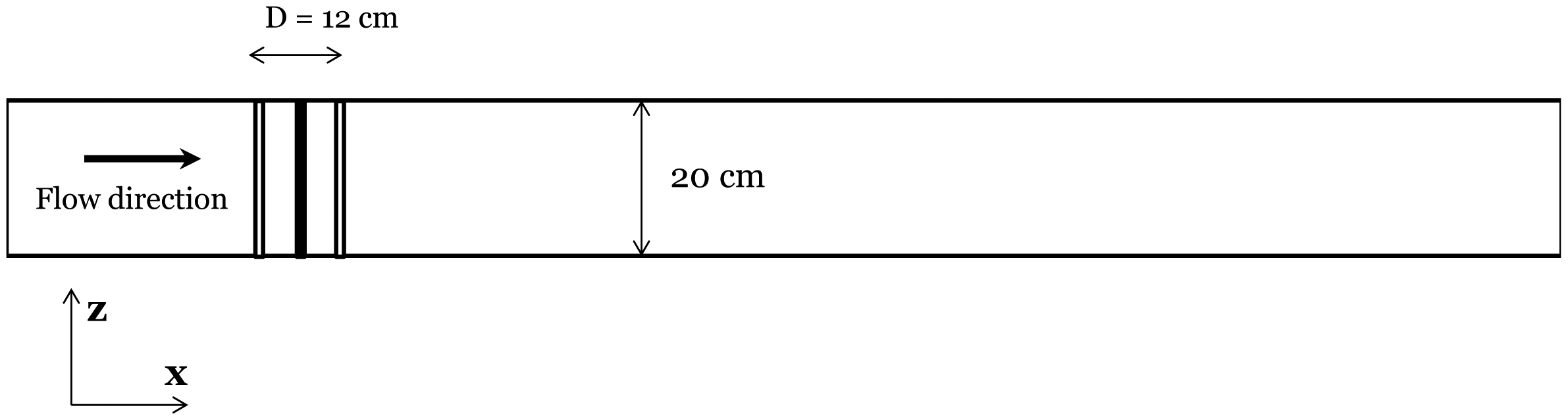
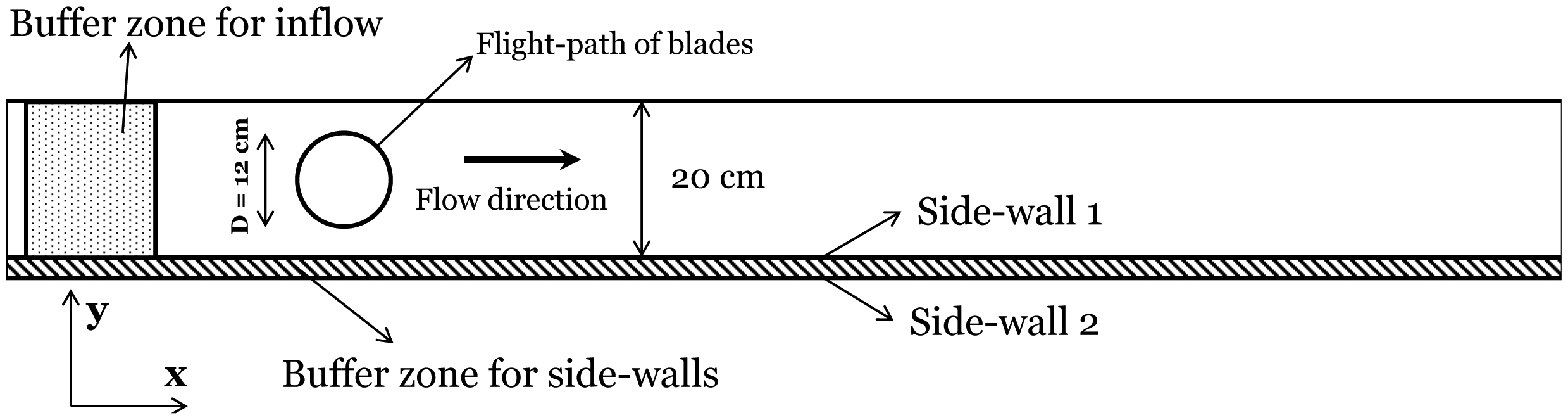
In the simulations for this case, the same dimensions as in the experiment are used in the y- and z-directions, while in the streamwise direction, the domain is taken longer than the channel length, because of the presence of a buffer zone (which will be described later). Thus, the domain dimensions are Lx = 200 cm, Ly = 20 cm (not including the width of the buffer zone for side-walls) and Lz = 20 cm in the streamwise, spanwise and vertical directions, respectively. Regarding the computational mesh, the number of grid points in each of the three directions is Nx = 240, Ny = 30 (not including the 4 auxiliary grid points within the buffer zone for side-walls), and Nz = 80.
Because of the periodic boundary conditions in the x- and y-directions, it is implicitly assumed that there are similar turbines upstream, downstream and on both sides of the VAWT under consideration. To eliminate the effects of the upstream turbine wake on the flow and to ensure that we have a uniform inflow (as in the experiment), a buffer zone upstream of the turbine is employed to adjust the flow to an undisturbed uniform inflow condition. The use of this technique, i.e., using an inflow boundary condition in a direction in which the flow variables are discretized using Fourier series, has been shown to be successful in the works of Tseng et al. [52], Wan and Porté-Agel [53] and Wu and Porté-Agel [54].
In the y-direction, to account for the effect of the side walls, an immersed boundary technique is used. We have set the wall-normal velocity component (υ) to zero at the location of the walls and have also modified the τxy component of the stress tensor for the grid points, which are located on the side walls, to a value obtained from assuming a logarithmic velocity profile near the side walls. The computational domain is shown in Figure 7. In this figure, the location of Side-wall 2 can be assumed to be at the other end of the y-direction axis (because of the periodic boundary condition in y-direction), so that Side-wall 1 and Side-wall 2 represent the two side walls of the experiment, which are 20 cm apart.
As discussed in Subsection 2.2, for both VAWT models (ASSM and ALM), we need tabulated data for lift and drag coefficients. The conventional source for aerodynamic characteristics of symmetrical airfoils, used in VAWTs, is the tabulated data of Sheldahl and Klimas [55]; however, for low Reynolds numbers (which is the case for this experiment), these data show some anomalies for low angles of attack (i.e., the lift coefficient tends to be negative). This data anomaly has been reported by Shen et al. [29], Kumar et al. [56] and Hara et al. [57]. As a solution, for low angles of attack, the data of Kumar et al. [56] is used, and for high angles of attack, the data of Sheldahl and Klimas [55] is used (for NACA 0018 airfoil). This approach to obtain the lift and drag coefficients has been employed by Hara et al. [57], as well. To account for the dynamic stall phenomenon and to consider its effect on CL and CD curves, the modified MIT dynamic stall model is employed [58]. It is worth mentioning that the the dynamic stall phenomenon has a significant effect on the values of the airfoil lift and drag coefficients and, hence, on the turbine performance [1,29,59].
The turbine center mast is also modeled as a cylindrical body, which applies a drag force on the fluid. The drag coefficient for the mast is considered to be equal to 1.0. In our simulations, the tip speed ratio (defined as the ratio between the velocity of the blades and the incoming flow velocity) of the turbine is taken to be 3.85 to match that of the experiment. The inflow of the simulation is a uniform flow with a velocity of 15 cm/s and a turbulent intensity of 2.5%, as in the experiment.
4. Results and Discussion
In this section, the results of our simulations for the above-described case are presented for five different combinations of the turbine and SGS models. Three simulations are performed for the ALM (with the MGM and the traditional Smagorinsky model with CS = 0.1 and 0.2), and two are done for the ASSM (with the MGM and the traditional Smagorinsky model with CS = 0.1).
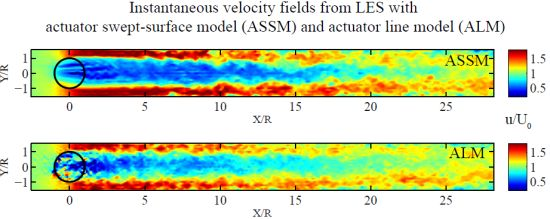
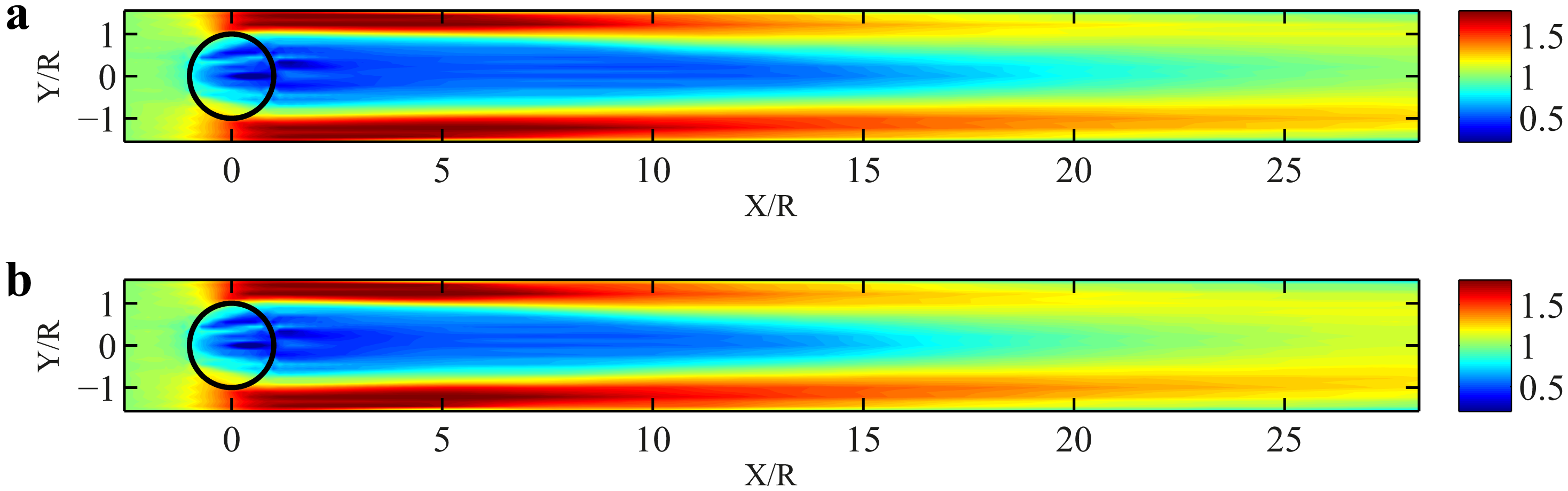
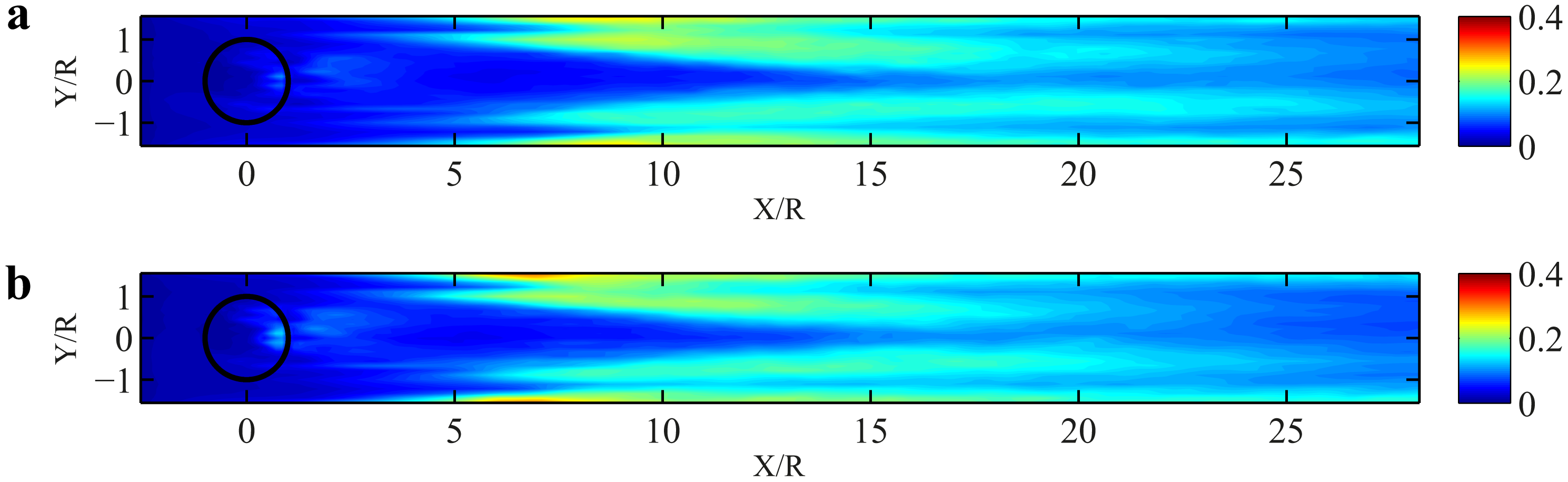
Figures 8 and 9 show time-averaged streamwise velocity contours on a horizontal plane (top view) at the equator height of the turbine for the actuator swept-surface and actuator line models, respectively. The black circle in each figure represents the flight path of the turbine blades, which rotate in the counter clockwise direction. It is obvious from the figures that the turbine extracts momentum from the flow, resulting in a low velocity region in its wake. As can be seen in the contours, when we go further downstream of the turbine, the wake recovers by entraining the neighboring high velocity fluid. In these figures, the blockage effect is evident near the channel side-walls (two ends of the y-axis), where the streamwise velocity magnitude is substantially larger than the incoming flow velocity. This is due to the narrow channel in which the experiment was performed. It should be noted that the presence of the blockage effect affects the recovery rate of the wake, due to the higher velocity gradients at the edge of the wake with respect to unconfined VAWTs. In these velocity maps, the effect of the turbine wake can be seen at downstream distances as large as 20 rotor radii. In all the following figures the streamwise (X) and spanwise (Y) distances are non-dimensionalized by the rotor radius, R, and the velocities are normalized by the incoming uniform flow velocity, U0.
As can be observed in the figures, the wake of a VAWT is not symmetric in the spanwise direction (y-direction). This lack of symmetry, which is a typical behavior of VAWT wakes, was also reported by Battisti et al. [20], Simao Ferreira et al. [60] and Brochier et al. [18]. We can see that in the region where the streamwise component of the blade velocity is in the opposite direction of the inflow velocity, i.e., upcoming blade region, (positive y in the figure), the wake is stronger than in the region where these two velocities are in the same direction, i.e., retreating blade region, (negative y in the figure). The primary reason behind this observation can be found by inspecting the velocity triangles at two typical blade positions in these two regions, as shown in Figure 10. In Figure 10a, the black circle is the flight path of the blades, on which four typical blade positions are highlighted. From the point of view of an observer who sits on the blades, the blade velocity is a constant vector (with a magnitude of RΩb) and the induced flow velocity at the point of the blade is a vector that rotates with the same average frequency as Ωb. The dotted circle in Figure 10b is the locus of the endpoint of the induced velocity vector, and the four points that correspond to the highlighted blade positions in Figure 10a are illustrated on this circle, as well. It is clear from the velocity triangles of points a and b that the relative velocity at point a is larger than the one at point b. As the blade forces are proportional to the square of the relative velocity at the blades, this explains why the velocity deficit is stronger at points a and d as compared to points b and c. It is noteworthy that in this analysis, for the sake of simplicity, the induced velocities at all blade positions are considered to be the same; however, it is evident that the induced velocities at points d and c are smaller than the ones at points a and b. This is because the downwind half of the rotor is located in the wake of the upwind half.
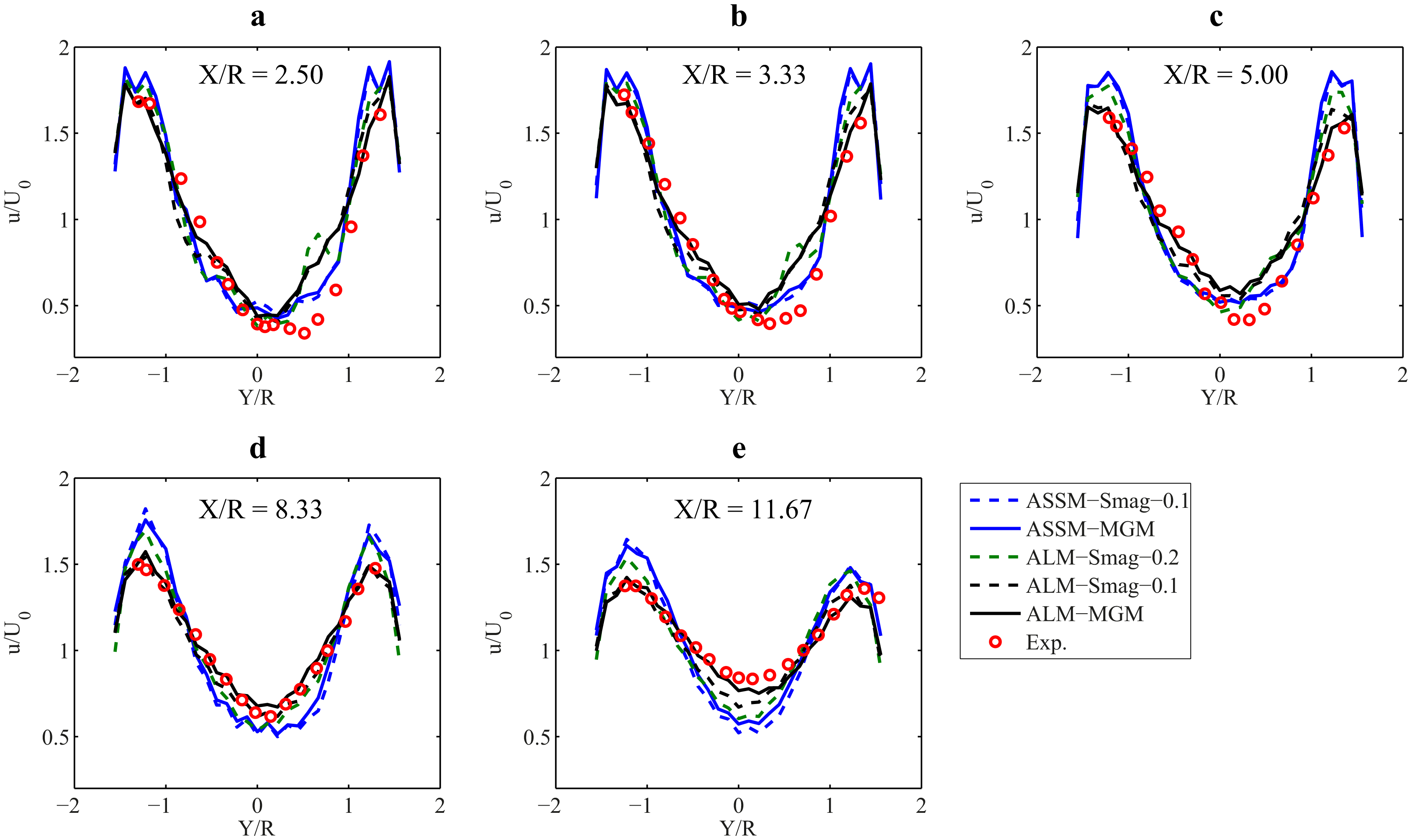
To obtain a more quantitative understanding of the turbine wake, mean velocity profiles in the spanwise direction and at the equator height of the rotor are plotted in Figure 11 for five downstream locations: x/R = 2.50, 3.33, 5.0, 8.33, 11.67. In these plots, the five combinations of SGS and VAWT models are compared together and also with experimental data. As can be seen in the figure, although both turbine models are able to predict the evolution of the wake in a fairly acceptable manner, the agreement between the ALM results and the experimental data is slightly superior to that of the ASSM results. One important feature that can be observed in this figure (and also in Figures 8 and 9) is the different ability of each model in predicting the wake recovery rate. Clearly, the wake recovers more slowly in the simulations run with the ASSM than in the ones with the ALM. This relatively slow wake recovery is also observed for the Smagorinsky model with Cs = 0.2. Since the wake recovery rate is closely correlated to the turbulence intensity level in the flow (e.g., Wu and Porté-Agel [61] for horizontal-axis wind turbines), it would be insightful to look at how the VAWT generates turbulence in the flow.
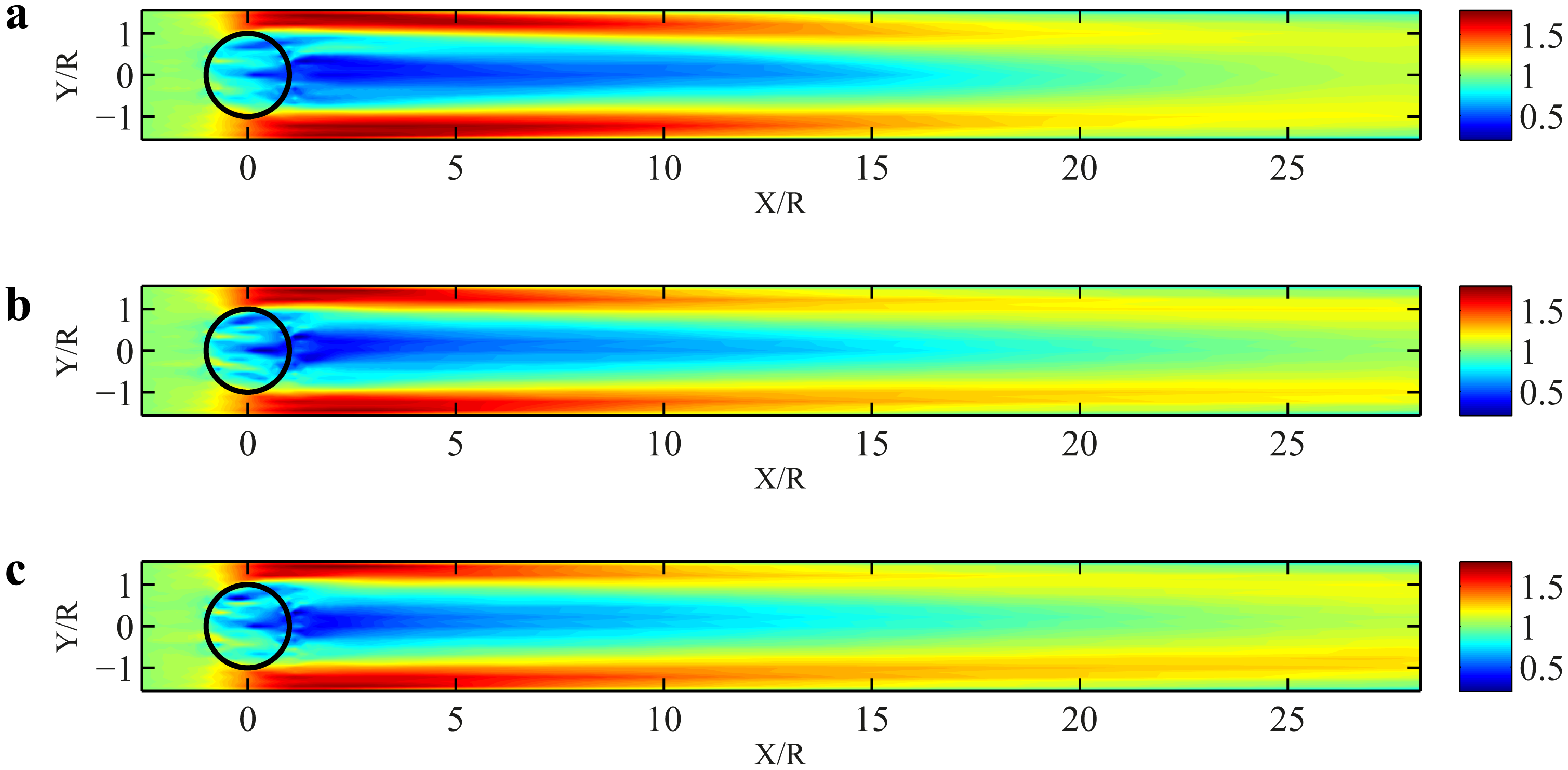
Figures 12 and 13 show contours of the mean streamwise turbulence intensity (TI) in a horizontal plane at the equator height of the rotor for the ASSM and the ALM, respectively. As can be understood readily from these contours, the difference between the ASSM and the ALM is even more pronounced considering the distribution of turbulence intensity. In these figures, one should pay attention to the trends in turbulence intensity distribution in the spanwise and streamwise directions. In the spanwise direction, all of the models qualitatively predict two regions of relatively high turbulence intensity in the vicinity of the wake edges. More details on the spanwise variation of TI will be discussed later. While in the spanwise direction, the same trends exist, in the streamwise direction, the differences between different models are more obvious. As can be seen in the contours, for the ASSM model, we have very low levels of TI in the turbine region and also in the near wake; then, TI gradually increases, until a point where it reaches a maximum (x/R around 10), and then, it starts to decrease. However, for the ALM, we observe a very high TI in the turbine region and in the near wake, and it decreases as we go downstream. Of these two trends, the one obtained by the ALM is qualitatively in better agreement with the experiments of Brochier et al. [18]. Looking at instantaneous velocity fields (Figure 14) can shed more light on the dissimilar effects of the two turbine models on the near wake flow. In Figure 14b (the ALM simulation), the wavy and wiggling edges of the wake near the turbine are clearly distinguishable from the rather straight and smooth wake edges in the same region in the ASSM simulation (Figure 14a). One can attribute this difference to the fact that the ALM can better capture the vorticity shed from the blades in the near wake by resolving the motion of individual blades. Another interesting observation that can be made in Figure 13 is the existence of four locations on the flight path of the blades around which the TI is maximum. This is likely due to the fact that, in those locations, the magnitude of the forces induced by the flow on the blades is locally maximum.
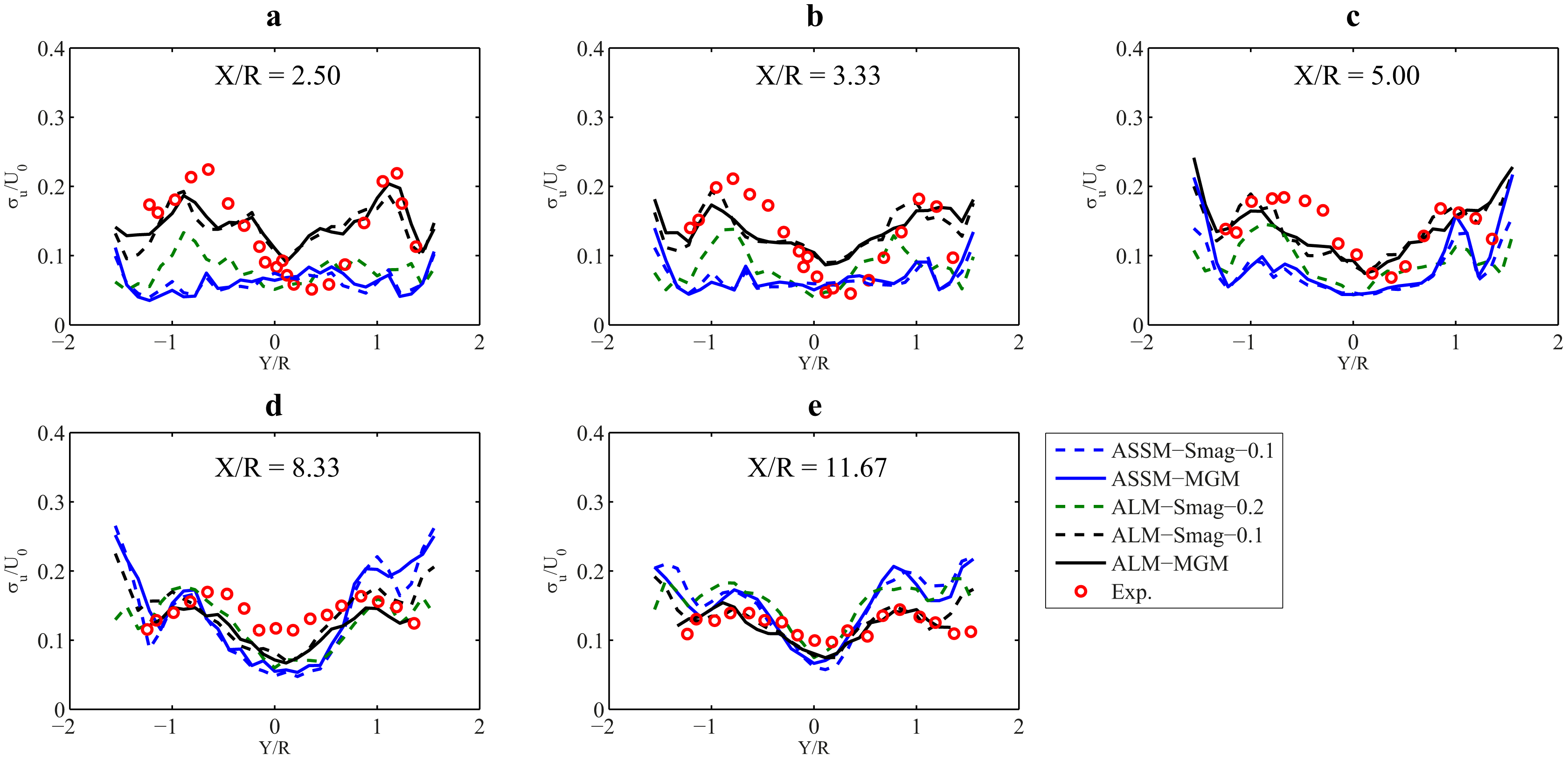
In Figure 15, where the spanwise variation of TI is shown for five downstream locations (x/R = 2.50, 3.33, 5.0, 8.33, 11.67), the above-discussed streamwise trends can be seen more clearly for the ASSM (blue lines) and the ALM (black lines). Also seen in this figure is the fact that in the spanwise direction the TI profile has two maxima, which are located on the edges of the wake. This is due to the unsteady shed vorticity from the blades and is reported in the works of Fujisawa and Shibuya [21], Battisti et al. [20] and Brochier et al. [18]. Moreover, we see different behavior of the flow turbulence in the spanwise direction for different turbine models. The ASSM overestimates the difference of TI between the retreating-blade half of the domain (negative y) and the upcoming-blade half of the domain (positive y); in contrast, the TI profiles obtained from the ALM show a better agreement with the measurements. This can be attributed in part to the inability of the ASSM to capture the unsteady-periodic nature of the flow, especially in the near wake region. This is, in contrast to the ALM, that, by resolving the unsteadiness of the blade forces, which improves the prediction of the turbulent behavior of the flow, particularly in the retreating-blade half of the domain.
At this point, we are able to draw conclusions regarding the links between the mean velocity field and the turbulence predictions of different models. First of all, as discussed earlier, the fact that the ASSM predicts lower levels of TI in the near wake leads to slower wake recovery. This can be seen clearly in Figure 11e, where the ASSM simulations (blue lines) overestimate the velocity deficit at x/R = 11.67 with respect to the ALM simulations (black lines) and also the measurements. Regarding the SGS models, we can see that, as expected, the high SGS dissipation rate forced by the Smagorinsky model with CS = 0.2 leads to lower resolved turbulence intensity predictions (Figure 15, green line) and, consequently, to a slower wake recovery (Figure 11e, green line).
By observing the presented results, one can conclude that the ALM, coupled with the MGM or the Smagorinsky model with CS = 0.1, gives the best agreement with the measurements. However, it should be noted that the MGM has a clear advantage over the Smagorinsky model in that it does not need tuning for its model coefficient [41]. In contrast, even though the value of CS = 0.1 gives the best agreement of the Smagorinsky model results with experimental data for this specific problem, the optimum value could be different for other experimental or field conditions. Specifically, this advantage of the MGM is expected to be even more decisive in the case of VAWTs placed in turbulent boundary layer flows, for which the MGM has been shown to provide better predictions (without turbines) than the standard Smagorinsky model [37,40,41]. Another advantage of the MGM over the Smagorinsky model (in fact, all Smagorinsky-based models) is the ability of the MGM to calculate the unresolved part of the TI in addition to its resolved part. This is due to the fact that in the MGM, the complete SGS stress tensor is modeled, which is in contrast to Smagorinsky-based models for which only the deviatoric part of the SGS stress tensor is parameterized. In our case, the unresolved part of the TI was about 5% of the total TI throughout the domain.
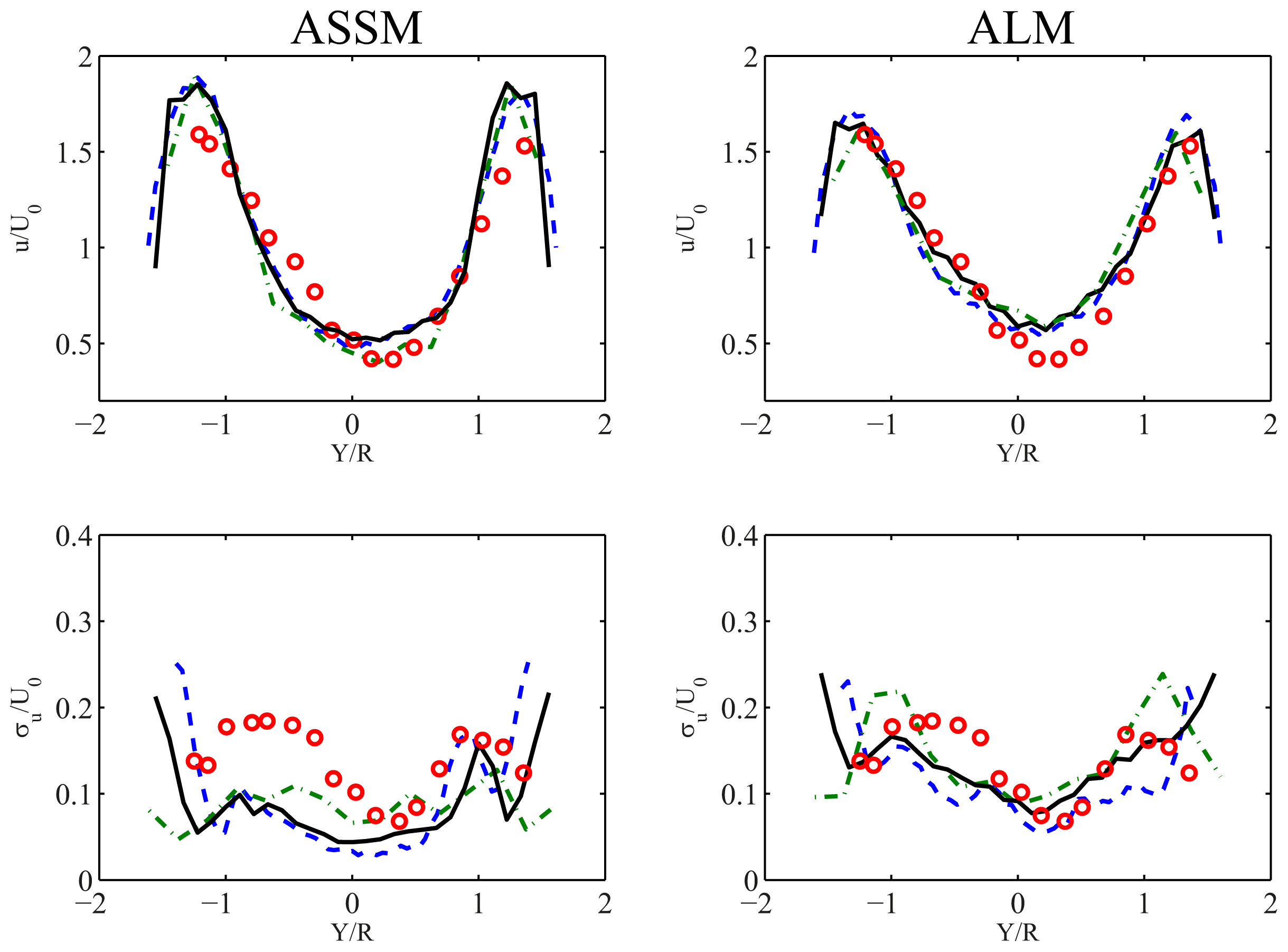
To show the grid resolution sensitivity of the computational results, we performed simulations for the ALM-MGM and ASSM-MGM model combinations with three different grid resolutions (the resolution is varied in the horizontal directions, which is critical in capturing the blade motions). It was observed that, for the range of resolutions considered here, resolution had only a small effect on the results. Figure 16 shows spanwise plots of mean streamwise velocity and turbulence intensity in the middle downstream position (x/R = 5.0) for the three grid resolutions.
5. Summary
In this study, large eddy simulation (LES), coupled with a turbine model, is used to investigate the 3D unsteady turbulent wake flow behind a vertical-axis wind turbine (VAWT). To model the SGS momentum fluxes, two SGS models are used, namely, the traditional Smagorinsky model and the modulated gradient model (MGM) [37]. To parameterize the effects of a VAWT on the flow, two VAWT models are developed: (a) the actuator swept-surface model (ASSM), in which the time-averaged turbine-induced forces are distributed on a surface swept by the turbine blades, i.e., the actuator swept-surface; and (b) the actuator line model (ALM), in which the instantaneous blade forces are only spatially distributed on lines representing the blades, i.e., the actuator lines. In both models, blade-element theory is used to calculate the lift and drag forces acting on the blades. This is the first time that LES has been applied and validated for the simulation of VAWT wakes by using either the ASSM or the ALM technique. The results are compared with flow field measurements in the wake of a model straight-bladed VAWT, carried out in the Institute de Méchanique et Statistique de la Turbulence (IMST) water channel.
Different combinations of VAWT and SGS models are tested and compared against each other, and a fairly good agreement with the experimental data is observed. It is found out that, in general, the results obtained with the ALM agree better with the measurements and also with the physics of the flow than the ones from the ASSM. The inherent advantage of the ALM in resolving the periodic location of the blade forces allows one to capture the unsteady-periodic nature of the wake and, thus, the blade-wake interaction, which is a characteristic of the aerodynamics of a VAWT rotor. The slight superiority of the ALM over the ASSM was shown quantitatively in the better prediction of the turbulence intensity and, consequently, of the wake recovery, which is very important in designing and optimizing potential VAWT arrays. However, it is worth bearing in mind that the ASSM could potentially be the preferable turbine model in simulations of VAWT wind farms, due to its lower grid resolution requirement. Regarding the SGS models, although both tested models showed reasonable turbulence modeling capabilities, it should be noted that the traditional Smagorinsky model needs its model coefficient to be optimized, depending on the local flow characteristics, while the MGM proved that it can, with its theoretically-determined model coefficient, capture the mean flow and turbulent characteristics of a VAWT wake. This advantage of the MGM is expected to be even more decisive in the case of VAWTs placed in turbulent boundary layer flows, where the MGM has previously been shown to have a superior prediction ability (without turbines) compared with the standard Smagorinsky model [37,40,41].
Potential sources of the observed discrepancies between simulation results and measurement data can be summarized as: (a) inherent limitations of the proposed numerical model; (b) inherent measurement errors in the experiment; and (c) inaccuracies in the tabulated airfoil data. It is worth noting that, in effect, the final results are considerably dependent on the lift and drag coefficient curves as a function of the angle of attack.
As mentioned by Paraschivoiu [1], the most important shortcoming that VAWTs are suffering from, at present, is that they have not benefited from research and development as much as HAWTs. Therefore, more rigorous and systematic studies on different technical aspects of VAWTs are still needed. For the aerodynamic aspect, high-resolution wind tunnel measurements of the flow field in the wake of VAWTs placed in a boundary layer flow would be highly valuable. Furthermore, for the numerical simulation of the wake, the authors believe that, if one lesson has to be learned from the development of HAWTs, it is that the most feasible and practical way of taking into account the effects of the turbine on the flow is through using immersed-body-force approaches, such as an actuator swept surface, actuator line or rotating actuator surface. With these techniques, the simulation, optimization and design of VAWT wind farms will be an attainable and realizable objective in the near future.
Acknowledgments
This research was supported by EOS (Energie Ouest Suisse) Holding, the Swiss National Science Foundation (grant 200021-132122 and grant IZERZ0-142236) and the Swiss Innovation and Technology Committee (CTI) within the context of the Swiss Competence Center for Energy Research “FURIES: Future Swiss Electrical Infrastructure”. Computing resources were provided by the Swiss National Supercomputing Centre (CSCS) under project ID s306. Special thanks go to Charles Meneveau for his sage and insightful suggestions. We thank the two anonymous reviewers whose constructive comments helped improve this work. We also thank Jacques Boppe and Fabien Mandrillon from Bogga Ltd. (Lausanne, Switzerland) for the useful discussions during the early stages of this project.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Paraschivoiu, I. Wind Turbine Design—With Emphasis on Darrieus Concept; Polytechnic International Press: Montreal, QC, Canada, 2002. [Google Scholar]
- Dabiri, J.O. Potential order-of-magnitude enhancement of wind farm power density via counter-rotating vertical-axis wind turbine arrays. J. Renew. Sustain. Energy 2011, 3, 043104. [Google Scholar] [CrossRef]
- Blackwell, B.F.; Sheldahl, R.E.; Feltz, L.V. Wind Tunnel Performance Data for the Darrieus Wind Turbine with NACA 0012 Blades; Technical Report; Sandia National Laboratories: Albuquerque, NM, USA, 1976. [Google Scholar]
- Sheldahl, R.E.; Blackwell, B.F. Free-Air Performance Tests of a 5 Meter Diameter Darrieus Turbine; Technical Report SAND77-1063; Sandia National Laboratories: Albuquerque, NM, USA, 1977. [Google Scholar]
- Sheldahl, R.E.; Klimas, P.C.; Feltz, L.V. Aerodynamic performance of a 5-meter-diameter Darrieus turbine. AIAA J. Energy 1980, 4, 227–232. [Google Scholar]
- Proceedings of the Vertical-Axis Wind Turbine (VAWT) Design Technology Seminar for Industry, Albuquerque, NM, USA, 1–3 April 1980; Technical Report SAND80-0984; Johnston, S.J., Jr., Ed.; Sandia National Laboratories: Albuquerque, NM, USA, 1980.
- Worstell, M.H. Aerodynamic performance of the DOE/Sandia 17-m-diameter vertical-axis wind turbine. AIAA J. Energy 1981, 5, 39–42. [Google Scholar]
- McNerney, G.M. Accelerometer Measurements of Aerodynamic Torque on DOE/Sandia 17-m Vertical-Axis Wind Turbine; Technical Report; Sandia National Laboratories: Albuquerque, NM, USA, 1981. [Google Scholar]
- South, P.; Rangi, R.S. An Experimental Investigation of a 12 Ft. Diameter High Speed Vertical-Axis Wind Turbine; Technical Report TR-LA-166; National Research Council of Canada: Ottawa, ON, Canada, 1975. [Google Scholar]
- Nguyen, V.D.; Vittecoq, P.; Bourassa, P.; Mercadier, Y. Étude en Souflerie d'un Rotor de Type Darrieus; Technical Report MEC-81-2; Mechanical Engineering Department, University of Sherbrooke: Sherbrooke, QC, Canada, 1981; in French. [Google Scholar]
- Vittecoq, P.; Laneville, A. Étude en Souflerie d'un Rotor de Type Darrieus; Technical Report MEC-82-2; Mechanical Engineering Department, University of Sherbrooke: Sherbrooke, QC, Canada, 1982; in French. [Google Scholar]
- Penna, P.J.; Kuzina, J.C. Magdalen Islands VAWT Summary and Index of Experimental Data, 1980–1982; Technical Report; National Research Council of Canada: Ottawa, ON, Canada, 1984. [Google Scholar]
- Schienbein, L.A. Development, Installation and Testing of a Wind Turbine Diesel Hybrid—Final Report; DAF Indal Ltd.: Mississauga, ON, Canada, 1979. [Google Scholar]
- Richards, B. Initial Operation of Project Eole 4MW Vertical-Axis Wind Turbine Generator. Proceedings of the Windpower’87, Annual Conference of American Wind Energy Association, San Francisco, CA, USA, 5–8 October 1987.
- Muraca, R.J.; Guillotte, R.J. Wind Tunnel Investigation of a 14 ft Vertical-Axis Windmill; Technical Report NASA TMX-72663; National Aeronautics and Space Administration, Langley: Hampton, VA, USA, 1976. [Google Scholar]
- Vermeulen, P.; Builtjes, P.; Dekker, J.; Bueren, G. An Experimental Study of the Wake Behind a Full-Scale Vertical-Axis Wind Turbine; Technical Report 79-06118; TNO: Delft, The Netherlands, 1979. [Google Scholar]
- Strickland, J.H.; Webster, B.T.; Nguyen, T. A Vortex Model of the Darrieus Turbine: An Analytical and Experimental Study; Technical Report SAND-81-7017; Sandia National Laboratories: Albuquerque, NM, USA, 1981. [Google Scholar]
- Brochier, G.; Fraunie, P.; Beguier, C.; Paraschivoiu, I. Water Channel Experiments of Dynamic stall on Darrieus wind turbine blades. AIAA J. Propuls. Power 1986, 2, 445–49. [Google Scholar]
- Bergeles, G.; Michos, A.; Athanassiadis, N. Velocity vector and turbulence in the symmetry plane of a Darrieus wind generator. J. Wind Eng. Ind. Aerodyn. 1991, 37, 87–101. [Google Scholar]
- Battisti, L.; Zanne, L.; Dell’Anna, S.; Dossena, V.; Persico, G.; Paradiso, B. Aerodynamic measurements on a vertical axis wind turbine in a large scale wind tunnel. J. Energy Resour. Technol. 2011, 133, 031201:1–031201:9. [Google Scholar]
- Fujisawa, N.; Shibuya, S. Observations of dynamic stall on darrieus wind turbine blades. J. Wind Eng. Ind. Aerodyn. 2001, 89, 201–214. [Google Scholar]
- Simao Ferreira, C.J.; van Bussel, G.J.W.; Scarano, F.; van Kuik, G. 2D PIV Visualization of Dynamic Stall on a Vertical Axis Wind Turbine. Proceedings of the AIAA/ASME Wind Energy Symposium, Reno, NV, USA, 8–11 January 2007.
- Hofemann, C.; Simao Ferreira, C.J.; van Bussel, G.J.W.; Van Kuik, G.A.M.; Scarano, F.; Dixon, K.R. 3D Stereo PIV Study of Tip Vortex Evolution on a VAWT. Proceedings of the EWEC, Brussels, Belgium, 31 March–3 April 2008.
- Tescione, G.; Ragni, D.; He, C.; Simao Ferreira, C.J.; van Bussel, G.J. Experimental and Numerical Aerodynamic Analysis of Vertical Axis Wind Turbine Wake. Proceedings of the International Conference on Aerodynamics of Offshore Wind Energy Systems and Wakes, Lyngby, Denmark, 17–19 June 2013.
- Wilson, R.E.; Walker, S.N. Fixed-Wake Analysis of the Darrieus Rotor; Technical Report SAND81-7026; Sandia National Laboratories: Albuquerque, NM, USA, 1981. [Google Scholar]
- Rajagopalan, R.G.; Fanucci, J.B. Finite difference model for vertical-axis wind turbines. AIAA J. Propuls. Power 1985, 1, 432–436. [Google Scholar]
- Rajagopalan, R.G.; Berg, D.E.; Klimas, P.C. Development of a three-dimensional model for the Darrieus rotor and its wake. AIAA J. Propuls. Power 1995, 11, 185–195. [Google Scholar]
- Fortunato, B.; Dadone, A.; Trifoni, V. A two-dimensional methodology to predict vertical axis wind turbine performance. J. Sol. Energy Eng. 1995, 117, 187–193. [Google Scholar]
- Shen, W.; Zhang, J.; Sørensen, J. The actuator surface model: A new Navier–Stokes based model for rotor computations. J. Sol. Energy Eng. 2009, 131, 011002:1–011002:9. [Google Scholar]
- Orszag, S.; Pao, Y.H. Numerical computation of turbulent shear flows. Adv. Geophys. 1975, 18A, 225–236. [Google Scholar]
- Ferzinger, J.H.; Perć, M. Computational Methods for Fluid Dynamics; Springer-Verlag: New York, NY, USA, 1996. [Google Scholar]
- Albertson, J.D.; Parlange, M.B. Surfaces length scales and shear stress: Implications for land-atmosphere interactions over complex terrain. Water Resour. Res. 1999, 35, 2121–2132. [Google Scholar]
- Smagorinsky, J. General circulation experiments with the primitive equations. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar]
- Mason, P.J.; Thomson, D.J. Stochastic backscatter in large-eddy simulations of boundary layers. J. Fluid Mech. 1992, 242, 51–78. [Google Scholar]
- Porté-Agel, F.; Meneveau, C.; Parlange, M.B. A scale-dependent dynamic model for large-eddy simulation: Application to a neutral atmospheric boundary layer. J. Fluid Mech. 2000, 415, 261–284. [Google Scholar]
- Wan, F.; Porté-Agel, F.; Stoll, R. Evaluation of dynamic subgrid-scale models in large-eddy simulations of neutral turbulent flow over a two-dimensional sinusoidal hill. Atmos. Environ. 2007, 41, 2719–2728. [Google Scholar]
- Lu, H.; Porté-Agel, F. A modulated gradient model for large-eddy simulation: Application to a neutral atmospheric boundary layer. Phys. Fluids 2010, 22, 015109. [Google Scholar] [CrossRef]
- Yoshizawa, A.; Horiuti, K. A statistically-derived subgrid-scale kinetic energy model for the large-eddy simulation of turbulent flows. J. Phys. Soc. Jpn. 1985, 54, 2834–2839. [Google Scholar]
- Kim, W.-W.; Menon, S. A New Dynamic One-Equation Subgrid-Scale Model for Large Eddy Simulations. Proceedings of the 33rd Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9℃12 January 1995.
- Lu, H.; Porté-Agel, F. A modulated gradient model for scalar transport in large-eddy simulation of the atmospheric boundary layer. Phys. Fluids 2013, 25, 015110:1–015110:17. [Google Scholar]
- Lu, H.; Porté-Agel, F. On the development of a dynamic nonlinear closure for large-eddy simulation of the atmospheric boundary layer. Bound.-Layer Meteorol. 2014. in press. [Google Scholar]
- Cheng, W.C.; Porté-Agel, F. Evaluation of subgrid-scale models in large-eddy simulation of flow past a two-dimensional block. Int. J. Heat Fluid Flow 2013, 44, 301–311. [Google Scholar]
- Shen, W.; Sørensen, J. Numerical modeling of wind turbine wakes. J. Fluids Eng. 2002, 124, 393–399. [Google Scholar]
- Troldborg, N.; Sørensen, J.; Mikkelsen, R. Actuator line simulation of wake of wind turbine operating in turbulent inflow. J. Phys. Conf. Ser. 2007, 75. [Google Scholar] [CrossRef]
- Ivanell, S.; Sørensen, J.; Mikkelsen, R.; Henningson, D. Analysis of numerically generated wake structures. Wind Energy 2009, 12, 63–80. [Google Scholar]
- Lu, H.; Porté-Agel, F. Large-eddy simulation of a very large wind farm in a stable atmospheric boundary layer. Phys. Fluids 2011, 23, 065101. [Google Scholar]
- Porté-Agel, F.; Wu, Y.T.; Lu, H.; Conzemius, R.J. Large-eddy simulation of atmospheric boundary layer flow through wind turbines and wind farms. J. Wind Eng. Ind. Aerodyn. 2011, 99, 154–168. [Google Scholar]
- Monin, A.; Obukhov, M. Basic laws of turbulent mixing in the ground layer of the atmosphere. Tr. Akad. Nauk SSSR Geophiz. Inst. 1954, 24, 163–187. [Google Scholar]
- Moeng, C. A large-eddy simulation model for the study of planetary boundary-layer turbulence. J. Atmos. Sci. 1984, 46, 2311–2330. [Google Scholar]
- Stoll, R.; Porté-Agel, F. Effect of roughness on surface boundary conditions for large-eddy simulation. Bound. Layer Meteorol. 2006, 118, 169–187. [Google Scholar]
- Abkar, M.; Porté-Agel, F. A new boundary condition for large-eddy simulation of boundary-layer flow over surface roughness transitions. J. Turbul. 2012, 13, 1–18. [Google Scholar]
- Tseng, Y.H.; Meneveau, C.; Parlange, M.B. Modeling flow around bluff bodies and predicting urban dispersion using large eddy simulation. Environ. Sci. Technol. 2006, 40, 2653–2662. [Google Scholar]
- Wan, F.; Porté-Agel, F. Large-eddy simulation of stably-stratified flow over a steep hill. Bound.-Layer Meteorol. 2011, 138, 367–384. [Google Scholar]
- Wu, Y.T.; Porté-Agel, F. Large-Eddy simulation of wind-turbine wakes: Evaluation of turbine parametrisations. Bound. Layer Meteorol. 2011, 138, 345–366. [Google Scholar]
- Sheldahl, R.E.; Klimas, P.C. Aerodynamic Characteristics of Seven Airfoil Sections through 180 Degrees Angle of Attack for Use in Aerodynamic Analysis of Vertical Axis Wind Turbines; Technical Report SAND80-2114; Sandia National Laboratories: Albuquerque, NM, USA, 1981. [Google Scholar]
- Kumar, V.; Paraschivoiu, M.; Paraschivoiu, I. Low reynolds number vertical axis wind turbine for Mars. Wind Eng. 2010, 34, 461–476. [Google Scholar]
- Hara, Y.; Suzuki, T.; Ochiai, Y.; Hayashi, T. Velocity Field Measurements in Wake of a Straight-Bladed Vertical Axis Wind Turbine. Proceedings of the ASME-JSME-KSME 2011 Joint Fluids Engineering Conference, Hamamatsu, Japan, 24–29 July 2011; Volume 1, pp. 1839–1849.
- Noll, R.B.; Ham, N.D. Dynamic Stall of Small Wind Systems; Aerospace Systems Inc.: Burlington, MA, USA, 1983. [Google Scholar]
- Scheurich, F.; Brown, R. Effect of dynamic stall on the aerodynamics of vertical-axis wind turbines. AIAA J. 2011, 49, 2511–2521. [Google Scholar]
- Simao Ferreira, C.J.; van Kuik, G.; van Bussel, G.J. Wind Tunnel Hotwire Measurements, Flow Visualization and Thrust Measurement of a VAWT in Skew. Proceedings of the AIAA/ASME Wind Energy Symposium, Reno, NV, USA, 9℃12 Januray 2006.
- Wu, Y.T.; Porté-Agel, F. Atmospheric turbulence effects on wind-turbine wakes: An LES study. In Energies; 2012; Volume 5, pp. 5340–5362. [Google Scholar]





© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Shamsoddin, S.; Porté-Agel, F. Large Eddy Simulation of Vertical Axis Wind Turbine Wakes. Energies 2014, 7, 890-912. https://doi.org/10.3390/en7020890
Shamsoddin S, Porté-Agel F. Large Eddy Simulation of Vertical Axis Wind Turbine Wakes. Energies. 2014; 7(2):890-912. https://doi.org/10.3390/en7020890
Chicago/Turabian StyleShamsoddin, Sina, and Fernando Porté-Agel. 2014. "Large Eddy Simulation of Vertical Axis Wind Turbine Wakes" Energies 7, no. 2: 890-912. https://doi.org/10.3390/en7020890