Remaining Useful Life Prediction of Lithium-Ion Batteries Based on the Wiener Process with Measurement Error
Abstract
: Remaining useful life (RUL) prediction is central to the prognostics and health management (PHM) of lithium-ion batteries. This paper proposes a novel RUL prediction method for lithium-ion batteries based on the Wiener process with measurement error (WPME). First, we use the truncated normal distribution (TND) based modeling approach for the estimated degradation state and obtain an exact and closed-form RUL distribution by simultaneously considering the measurement uncertainty and the distribution of the estimated drift parameter. Then, the traditional maximum likelihood estimation (MLE) method for population based parameters estimation is remedied to improve the estimation efficiency. Additionally, we analyze the relationship between the classic MLE method and the combination of the Bayesian updating algorithm and the expectation maximization algorithm for the real time RUL prediction. Interestingly, it is found that the result of the combination algorithm is equal to the classic MLE method. Inspired by this observation, a heuristic algorithm for the real time parameters updating is presented. Finally, numerical examples and a case study of lithium-ion batteries are provided to substantiate the superiority of the proposed RUL prediction method.1. Introduction
Lithium-ion batteries have been widely used in many fields, e.g., consumer electronics, electric vehicles, marine systems, aircrafts, satellites, etc., due to their high power density, low weight, long lifetime, low self-discharge rate, no memory effect and other advantages [1,2]. The demand for lithium-ion batteries demonstrates the necessity to evaluate their reliability. Failure of lithium-ion batteries could lead to performance degradation, operational impairment, and even catastrophic failure [3–5]. For example, in 2006, the National Aeronautics and Space Administration's Mars Global Surveyor stopped working due to the failure of batteries [6]. In 2013, all Boeing 787 Dreamliners were indefinitely grounded due to battery failures that occurred on two planes [7]. Therefore, monitoring the degradation process, evaluating the state of health and predicting the remaining useful life (RUL) have become increasingly important for lithium-ion batteries.
Prognostics and health management (PHM) has emerged as one of the key enablers to improve system safety, increase system operations reliability and mission availability, decrease unnecessary maintenance actions, and reduce system life-cycle costs [8,9]. As a very important step of PHM, the RUL prediction based on the condition monitoring (CM) information plays an important role in maintenance strategy selection, inspection optimization, and spare parts provision [9,10]. The RUL of lithium-ion batteries is defined as the length of time from present time to the end of useful life. Since the failure data is scarce in reality, the degradation information is often chosen to describe the health status through a degradation model [11]. For the lithium-ion batteries, the capacity induced by the charge-discharge operational cycle is a suitable feature to characterize the long-term degradation process [12,13]. Then, the issue of estimating the battery's RUL could be transformed to predict the time when its capacity crosses a predefined failure threshold.
There are two main approaches for prognostics in PHM, i.e., physics-of-failure (PoF) and data-driven. As the PoF based prognostic methods depend on the knowledge of a battery's life cycle loading condition, material properties, failure mechanisms, etc., it is difficult to apply for complicated systems with unclear physical failure mechanism. However, this is most frequently encountered in practice. In contrast, data-driven techniques extract features from performance data such as current, voltage, capacity and impedance, and thus they are less complex than the PoF-based approaches. The current research about the RUL prediction of lithium-ion batteries focuses mainly on data-driven approaches. Saha et al. [14] presented an empirical model to describe battery behavior and predicted the RUL by the particle filter (PF) algorithm. Dalal et al. [15] provided details on how the PF algorithm could be used for prognostics. To improve the accuracy of the PF algorithm, Rao-Blackwellized PF and unscented PF algorithm are used [16,17]. To fully utilize the degradation data of congeneric batteries, He et al. [18] applied the Dempster-Shafer theory to evaluate the initial model parameters. Other new prognostics-related methods and models, e.g., autoregressive model, Verhulst model, fusion prognostic algorithm, adaptive bathtub-shaped function, relevance vectors, etc., can be found in [19–25].
In the above works, the probability distribution function (PDF) of the RUL is approximated by the Monte Carlo method, which is time-consuming. To solve this problem, the Wiener process has been reported to predict the RUL of batteries [12,13]. The Wiener process can provide a good description of system's dynamic characteristic due to its non-monotonic property, infinite divisibility property and physical interpretations. As such, it has been widely used to model degradation process, such as bridge beams [26], milling machines [27], light-emitting diodes (LEDs) [28,29], micro electro mechanical systems (MEMS) [30], laser generators [31], continuous stirred tank reactors [32], and gyros [33–35]. The RUL prediction based on the Wiener process, which is a type of statistics-based data driven methods, has gained much attention in recent years [36]. In this paper, we address the issue of applying the Wiener process to predict the RUL of batteries, with an emphasis on the effect of measurement error (ME) in the measured data [12,13].
In the literature, the current research about the Wiener process with ME (WPME) focuses on the following three aspects. The first aspect is studying the influence of the ME to the RUL prediction and finding the PDF of the RUL or the lifetime. Si et al. [37] presented the analytical form of the RUL distribution for the linear WPME by considering the uncertain of the ME. Feng et al. [13] presented an analytical form of the RUL distribution for the nonlinear case. Wang et al. [38] and Tang et al. [39] proposed the RUL distributions for the WPME by incorporating the uncertainties of the ME and the degradation trend simultaneously. However, when the ME is involved, the degradation state must be estimated from the measurements with ME. Suppose that the failure threshold is w and the actual CM data at the current time is xk which is a random value, it should be satisfied that w > xk if the item is not failed at the current time. Thus, w − xk has a nonzero probability to be negative. Particularly, when the degradation state approaches the failure threshold, this nonzero probability will increase and cannot be ignored. Otherwise, if we use the traditional normal distribution to model w − xk, an underestimated probability density function of the estimated RUL will be generated and thus lead to unsuccessful prognostics. Therefore, the task of this paper is to ensure the condition that w > xk is satisfied by introducing a truncated normal distribution (TND) based modeling approach.
The second aspect is the offline parameters estimation. The maximum likelihood estimation (MLE) method is most commonly used to estimate the fixed model parameters of the WPME. Whitmore [40] did a pioneering work for the modeling and parameters estimation of the WPME for a single item. Peng and Tseng [31] incorporated the random effects into the modeling of the WPME and presented a MLE method for a type of items. Then, this method has been applied to the nonlinear Wiener process [33] and the WPME when using first differences of the observations [12,39,41,42]. However, the drift parameter is assumed to be random for a specific item, which is not consistent with the modeling assumptions, as detailed in Section 3.
The last aspect is updating the random parameters of the WPME. The updating algorithm of the WPME is developed from the updating algorithm for the basic linear Wiener process. In this paper, we review the updating algorithm for the basic linear Wiener process and WPME together. A classic work about the updating of the random parameters is proposed by Gebraeel et al. [43], whose model established a linkage between the past and current degradation data of the congeneric items by a Bayesian mechanism. Following Gebraeel et al. [43], some related issues and many variants and applications have been studied and reported [39,44–46]. The work about this Bayesian updating mechanism for the WPME is also been studied in [41]. Another updating algorithm is combining the Bayesian updating and expectation maximization (EM) algorithm, where the Bayesian updating includes the basic Bayesian algorithm, Kalman filtering, strong tracking filter, extended Kalman filter, etc., [13,32,34,35,47]. In this combination algorithm, the Bayesian updating is used to update the random parameters of the model and the EM algorithm is used to estimate the fixed parameters. However, the relationship between the Bayesian method and the combination algorithm is still unclear.
To address the above issues, we firstly use the TND to model w − xk and in this case an exact and analytical RUL distribution is obtained. This leads to the first contribution of the paper. Secondly, we present a two-step MLE method to estimate the parameters for satisfying the assumption that the random drift parameter is fixed for a specific item. This is another contribution of the paper since this two-step method makes the estimated variance of the drift parameter positive. Then, we find an interesting result about the relationship between the Bayesian method and the combination algorithm, and based on this result we present a heuristic algorithm for the parameters updating. This is the third contribution of this paper, which is not fully explored before. Finally, some numerical examples and a case study regarding the lithium-ion batteries are presented to verify the results derived in this paper and to illustrate the application and superiority of the proposed method.
The remainder of this paper is organized as follows: Section 2 develops the ME model and derives the RUL distribution; in Section 3, we present a two-step MLE method to estimate the fixed parameters; in Section 4, we discuss the parameters updating for the WPME and propose a heuristic algorithm; numerical examples and a case study are provided in Section 5; and Section 6 draws the main conclusions.
2. Degradation Modeling and RUL Prediction
2.1. Degradation Model
The Wiener process with a linear drift is typically used for modeling the degradation process. Let X (t) denote the degradation value at time t; the degradation process can be represented as follows:
Generally speaking, the degradation data obtained from routine CM are inevitably contaminated by the uncertainty during the measurement process [48,49]. If the measurement process of X(t) contains ME, only the variable with ME can be observed, which is represented as follows [40]:
Generally, the lifetime of the system is defined by the concept of the first hitting time (FHT) of the degradation process as:
In the sense of the FHT, it is well-known that the Wiener process crossing a constant threshold w obeys an inverse Gaussian distribution [50]. Accordingly, the PDF, mean and variance of the lifetime can be obtained as follows:
2.2. Modelling the ME
For the degradation process with ME, the lifetime Te can be defined as:
Therefore, the lifetime Te can be calculated by the time of {Y(t), t ≥ 0} hitting the threshold wε = w + ε. Given the probability distribution of the ME, such as normal distribution, the PDF of the RUL can be derived by the law of total probability [31,40]. However, the restriction that w − xk > 0 is not satisfied in References [31,40]. As mentioned above, we use the TND to solve this problem. If Z ∼ N(μ, σ2) and Z is truncated by Z > 0, then this type of TND can be written as Z ∼ TN(μ, σ2). Suppose that Z ∼ TN(μ, σ2), the PDF and mean of Z can be written as [51]:
If μ ≫ σ, then we have Φ(μ/σ) ≈ 1 and exp(−μ2/σ2) ≈ 0. Thus, the TND approximately turns into the traditional normal distribution. The key issue of the RUL prediction with ME is to derive the PDF of the RUL, which is addressed in the following subsection.
2.3. Real Time RUL Prediction with ME
In this subsection, the RUL prediction method at a particular point of time tk is proposed. Define Y0:k = {y0,y1,y2,…,yk} as the observed degradation and X0:k = {x0,x1,x2,…,xk} as the actual degradation at CM times t0, t1, t2,…,tk, which could be irregularly spaced. Once the actual degradation process X0:k is available at tk, the process {X(t),t ≥ tk} can be transformed into [34,35]:
Therefore, the RUL at time tk is equal to the FHT of the process {φ(lk), lk ≥ 0} crossing the threshold wk = w − xk. Accordingly, the RUL can be defined as:
As a result, once X0:k is available at tk, the PDF of the RUL with considering the uncertainty of λ in the sense of FHT can be written as [34,35]:
However, for the degradation process with ME, X0:k is unobserved. Only the degradation process with ME, i.e., Y0:k, can be directly measured. Thus, the true value of xk is a random value with uncertainty. To derive the PDF of the RUL with ME, the following lemma is given first:
Lemma 1 If Z ∼ TN(μ,σ2), and B ∈ R, C ∈ R+, then:
The proof is given in the Appendix.
As the ME , it follows that . On condition that w − xk > 0, we have . Then, based on Lemma 1 and Equation (11), the PDF and mean of the RUL based on the updated λ can be obtained by the law of total probability, which is summarized in following theorem:
Theorem 1 Once Y0:k is available at tk the PDF and mean of the RUL with considering the uncertainty the estimated λ and ME can be written as:
The proof is given in the Appendix.
Similarly, if the is set to be zero, the result of Theorem 1 reduces to the result of Equation (11). This indicates that the result of Theorem 1 is a generalization of Equation (11). If μw,k ≫ σε, we obtain that and Λ(z) = 1/2z based on the approximation property of the Dawson integral function. Hence, we have E(Lk|Y0:k) ≈ w,k/ μλ,k. This result is desired since the expectation of the RUL is required in some maintenance strategies [45,46]. In the following, we develop a parameters estimation algorithm to estimate and update the parameters in Equations (13) and (14).
3. Offline Parameters Estimation Method
An offline parameters estimation method is needed to estimate the fixed parameters of the WPME, which represents population-based degradation character. The results of this estimation could provide the prior information for updating the online parameters. To represent the heterogeneity among different items, the drift parameter of the Wiener process is usually assumed as a random parameter with mean μ0 and variance [12,31]. Strictly speaking, the drift parameter is assumed to be random for the population but fixed for a specific item. Peng and Tseng [31] presented a MLE method to estimate the unknown parameters of the WPME. This method has been further applied for the cases of nonlinear Wiener process [33], and the WPME when using the first differences of observations to develop the sample likelihood function (SLF) [12,39,41]. For more details of this MLE method, refer to Reference [31]. However, if the drift parameter λ is assumed to be random for a specific item, the estimated variance of the drift parameter may be evaluated to be negative by the MLE method presented in Reference [31]. This phenomenon is not consistent with the modeling assumptions and the actual conditions. To solve this problem, we develop a two-step MLE method. The first step is estimating the parameters , where λn denotes the mean degradation rate for a specific item. The second is estimating the randomness of λ, i.e., . In the following, we present the two-step MLE method in detail.
We use the first differences of the observations to develop the SLF, similarly to References [12,41]. It is assumed that there are N tested items, and the degradation of the nth item is measured at times t1,n, t2,n,…, tmn,n, where mn denotes the available number of degradation measurements of the n-th item, and n = 1,2,…N. Let Yn = {ΔY(t1,n),ΔY(t2,n),…,ΔY(tm,n)}′ , where ΔY(ti,n) = Y(ti,n) − Y(ti−1,n). In addition, define Tn = {ΔT1,n, ΔT2,n,,…, ΔTmn,n}′ with ΔTi,n = ti,n − ti−1,n. Then, according to the properties of the Wiener process, Yn follows a multivariate normal distribution with mean and covariance given by:
Note that the value in the first row and the first column of Pn, i.e., Pn(1,1), is equal to one, which is different from the result in Reference [40]. The reason is that Reference [40] ignored the observation at the first time. Recently, Ye et al. [41,42] corrected this mistake and set Pn(1,1) as 1.
To facilitate the inference, we re-parameterize the parameters by and . Then, the log-likelihood function of can be written as:
Taking the first partial derivatives of ln L(Θ|Y) with respect to yields:
Then, by setting these derivatives with respect to to zeros, the results of the MLE for λ1,λ2,…,λN and can be written as:
Substituting Equations (19) and (20) into Equation (16), we obtain the profile likelihood function for σ͂2 in terms of the estimated as follows:
The MLE for can be obtained by maximizing the profile log-likelihood function in Equation (21) through a one-dimensional search. In this paper, we use the MATLAB function “FMINSEARCH” to find the estimates of σ͂2. Then, the estimates of can be obtained by substituting the estimates of into Equations (19) and (20). Finally, the estimate of can be calculated as follows:
Remark 1. In the MLE method presented by Peng and Tseng [31], Yn follows a multivariate normal distribution with the mean μ0ΔYn and covariance . It can be observed that the main diagonal of Σn is always positive, i.e., , or . However, at the maximizing process of the lnL(Θ|Y), it cannot be ensured that on condition that is the sum of , and . If is not restricted that , it could be negative when searching the best Θ to maximize ln L(Θ|Y) by the MLE method presented in Reference [31].
Remark 2 Whitmore [40] presented two ways to develop the SLF of the WPME for a single item, i.e., the observations at each point (referred to as SLF1) and the first differences of the observations (referred to as SLF2). SLF1 has been used in References [31,33], and SLF2 in References [12,39,41]. However, to our knowledge, the issue that which one should be selected for the MLE method has not been studied before. Here, we give a simple numerical example to illustrate this issue. For a single item, let (0, 0.9, 1.6, 4.7, 4.3, 5.6, 5.4) be the observed data at time (0, 0.8, 2, 4.2, 5, 7.5, 8.9); then the estimated log-likelihood function (log-LF), λ, , and based on SLF1 are 7.5002, 0.63424, 0.32989, and 0.16090, respectively. Interestingly, the estimated results based on SLF2 equals to those based on SLF1. This indicates that the SLFs developed by these two ways could derive the same results. This phenomenon also occurs for the nonlinear Wiener process and the Wiener process with random effects. Note that Pn(1,1) is equal to 1 in the numerical example, it verifies the remedy of the variance matrix by Ye et al. [41] to some extent. Additionally, since the covariance matrix in the SLF2 is the symmetric tridiagonal matrix, it is easy to calculate its inverse [52,53]. Thus, the SLF2, i.e., by the first differences of the observations, is suggested.
4. Online Parameter Updating
Online parameter updating is used to make the estimation adapt to the item's individual characteristic and reduce the uncertainty of the estimation. As mentioned above, there are two commonly used updating methods, i.e., the Bayesian method and the combination algorithm. From a comparative perspective, the advantage of Bayesian method is that the prior information and the in situ degradation data could be reasonably incorporated. However, it is sensitive to the prior information [34]. In contrast, the merit of the combination algorithm is its robustness over the selection of these prior parameters. Essentially, the estimation by the Bayesian method could partially reflect the population information, while the combination algorithm is more adaptable to the individual information of a specific item. In this section, we attempt to find the relationship between the Bayesian method and the combination algorithm, and then present a heuristic parameters updating algorithm. We first present the combination algorithm for the WPME.
4.1. The Combination Algorithm for Parameters Updating
Parameters updating via newly observed CM data is an important part for the real time RUL prediction. To estimate the PDF of the RUL based on the in situ CM data Y0:k, Si et al. [34] proposed a general process for the estimation of the unknown parameters through the combination of Bayesian updating and EM algorithm. Inspired by this algorithm, we use both Bayesian updating and EM algorithm to estimate the unknown parameters for the linear WPME. However, the result of the EM algorithm can be directly derived and an interesting result is obtained.
For the combination algorithm, the estimate of the unknown parameters includes the following steps:
- Step 1
Determine the prior information for the unknown parameters.
First, to update the PDF of the RUL, the unknown parameters need to be estimated by the history degradation data, lifetime data or accelerated degradation data. The initial parameters are estimated by the MLE method presented in the above section. Additionally, in order to simplify the updating process, it is assumed that the prior distribution of λ0 follows . Consequently, such prior distribution falls into the conjugate family of sampling distribution p(Y0:k|λ), and the posterior estimate of λ conditional on Y0:k is still normal, that is, .
- Step 2
Update the posterior distribution of the random parameter.
Given that , based on the Bayesian theorem, the posterior distribution of λ can be obtained as follows:
where Δyk = {y1−y0,y2−y1,…,yk−yk−1}, and Δtk = {t1−t0,t2−t1,…,tk−tk−1}. Due to the property of the normal distribution of λ | Y0:k, we have:with:- Step 3
Estimate the unknown parameters via the EM algorithm.
For simplicity, the linear WPME is referred to as Model 0, and the basic linear Wiener process as Model 1. The unknown parameters of Model 0 are , , and the parameters μ0 and in prior distribution p(λ), denoted by . Accordingly, Model 1 includes three unknown parameters, i.e., . For the real time RUL prediction, once new observation yk is available, the unknown parameters can be calculated by the MLE method as follows:
where p(Y0:k|Φ) is the joint PDF of the observed degradation data Y0:k.
However, it is difficult to maximize the log-likelihood function due to the random effect and unobservability of λ. Generally, the EM algorithm provides a possible way to solve this problem [54]. The fundamental principle of the EM algorithm is to manipulate the relationship between p(Y0:k|Φ) and p(Y0:k,λ|Φ) via the Bayesian theorem so that the estimating of Φ can be achieved by two steps:E-step and M-step:
E-step:
where denotes the estimated parameters in the i-th step of the EM algorithm conditional on Y0:k.M-step:
Then, the E-step and M-step are iterated multiple times until a criterion of convergence is satisfied. The commonly used criterion of convergence is that the difference between and falls below a pre-defined threshold. For more details of the convergence properties of the EM algorithm, see [54].
For Model 0, we first evaluate the complete log-likelihood function as follows:
Given as the estimate in the i-th step based on Y0:k. The expectation of ln p(Y0:k,λ|Φ) can be calculated as follows:
After deriving , the results of the estimated parameters in the (i + 1)-th step can be summarized in the following theorems:
Theorem 2.
- (1)
, by maximizing , is given by:
where:and C denotes a generic constant that may change from line to line throughout the paper.- (2)
is uniquely determined and located at the maximum.
The proof is given in Appendix. From Theorem 2, it can be observed that the M-step can be solved analytically and each iteration of the EM algorithm can be performed with only a single computation. To further simplify the computation, we propose the following Theorem.
Theorem 3.
- (1)
The iteration result of the combination algorithm is:
where:- (2)
The result of the EM algorithm is equal to the estimate via the MLE method by assuming a fixed λ.
The proof is given in Appendix.
Based on Theorem 3, we can obtain similar results for Model 1 as follows:
Corollary 1
- (1)
The result of the combination algorithm for Model 1 is:
- (2)
It is equal to the estimate via the MLE method by assuming a fixed λ.
The proof of Corollary 1 can be easily obtained by setting in the proof of Theorem 3.
The reason why the EM algorithm obtains the same results with the MLE method can be explained as follows. The EM algorithm is used to find the maximum likelihood estimate of , where μ0 and are the mean and variance of λ represent the heterogeneity among different items. However, λ is a fixed value for a specific item, therefore, the maximum likelihood estimate of by the EM algorithm should be zero. And thus the EM algorithm turns into the traditional MLE method.
The second result of Theorem 3 indicates that the EM algorithm can overcome the impact of improper prior information on the RUL prediction. However, it completely gets rid of the impact of prior information and only depends on the in situ observed data. Therefore, how to reasonably integrate the prior information and in situ information is an important issue in the real time RUL prediction. The following subsection attempts to address this issue.
4.2. A Heuristic Parameter Updating Method
Note that the convergent result of the combination algorithm equals to maximum likelihood estimate. Consequently, if no iteration is performed, it is the traditional Bayesian updating method. As the number of iterations increases, the estimation depends more on the in situ information, i.e., the individual characteristic. To integrate the prior information and in situ information, the following two basic guidelines should be followed. The first is that the less confident on the prior information, the more iterations. The second is that the more in situ degradation data are observed, the more iteration times are performed.
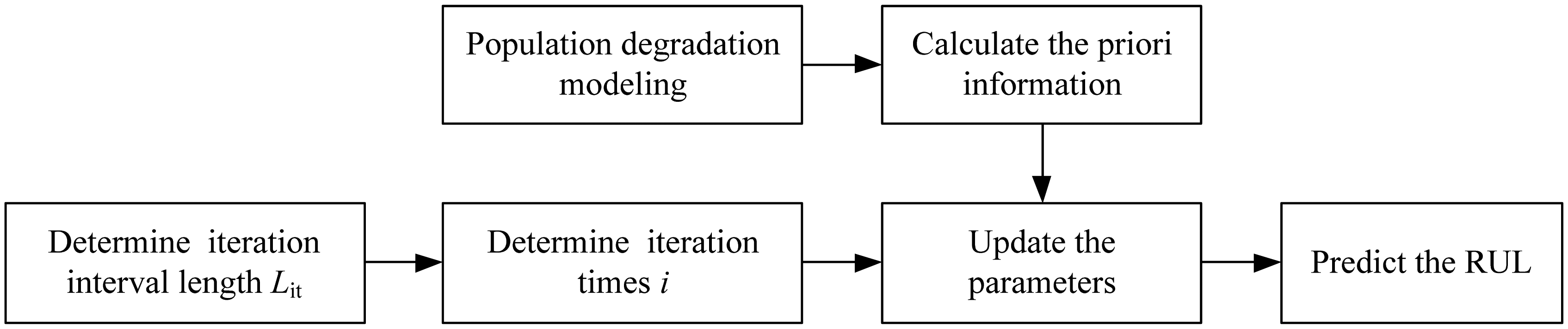
Based on the above two guidelines, we present a heuristic parameter updating algorithm as shown in Figure 1.
The heuristic algorithm includes three main steps as follows:
- Step 1
Calculate the priori information by the estimation method presented in Section 3, i.e., ;
- Step 2
According to the confidence of the priori information, determine the length of iteration interval;
- Step 3
Suppose that there are k degradation data observed. If (k −1)/Lit ≤ i < k/Lit, the EM algorithm presented in Section 4.1 is performed i times of the iteration, where Lit is the iteration interval length determined in Step 2. Then, the RUL is predicted based on the updated parameters.
As the drift parameter λ is assumed as a random parameter to represent the heterogeneity among different items, and are assumed to be fixed which are common to all items, we only update the drift parameter by the heuristic algorithm in this paper. As more degradation data are observed, the iteration times of the EM algorithm increase and thus the estimation depends more on the in situ information. This is consistent with the second basic guideline presented above. Additionally, it can be observed that the key issue of the heuristic method is to determine the iteration interval length via the prior information. In this paper, the iteration interval length is determined by the historical experience or expert's information. The selection of Lit should base on the following principle. The more confidence there is on the prior information, the smaller Lit is.
5. Experimental Studies
In this section, we provide several numerical examples to analyse the effect without considering the restriction that w − xk > 0, to compare the performance of the fixed MLE method with the existing method in the literature, and to verify the interesting consequence derived in this paper. Then, a practical case study of the lithium-ion batteries is illustrated to demonstrate the application of the developed method for the real time RUL prediction.
5.1. Numerical Examples
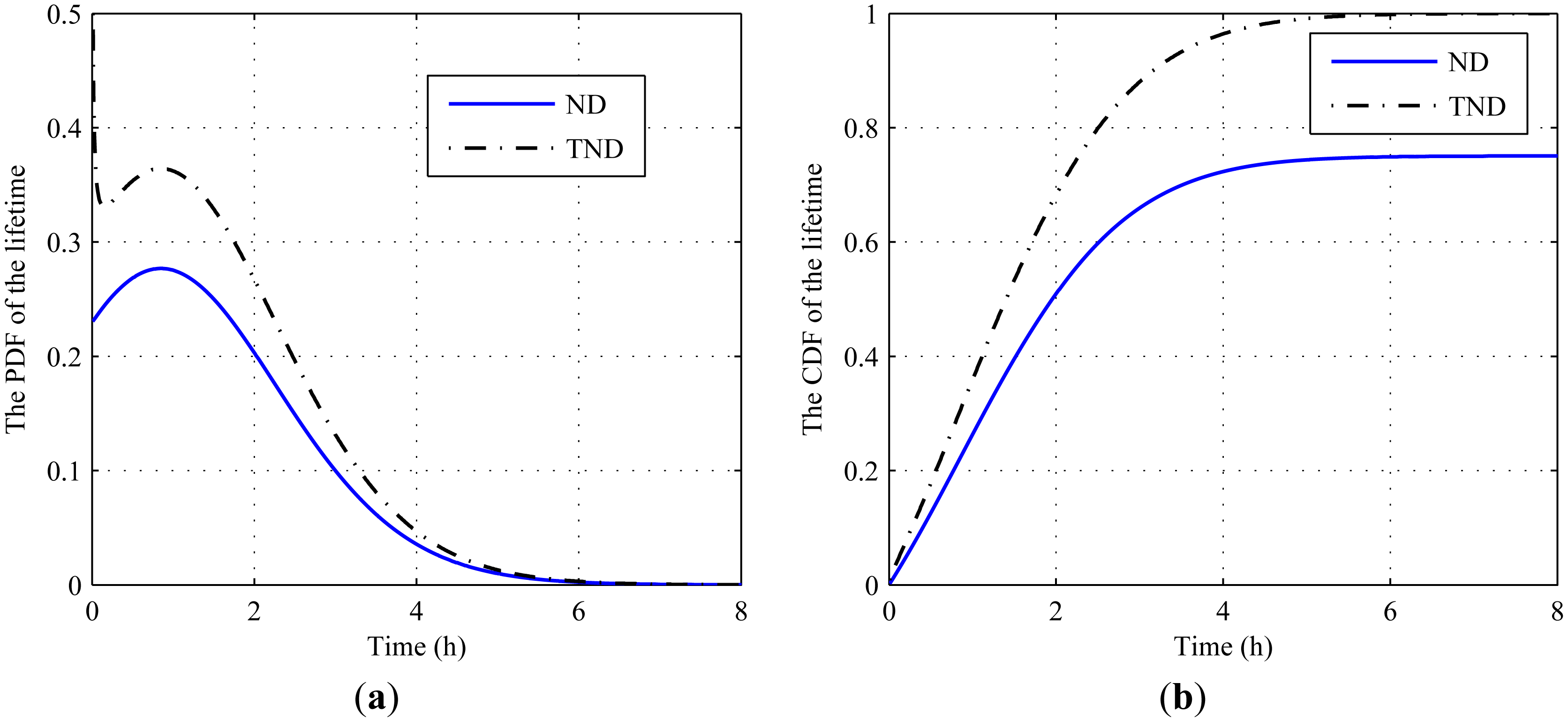
First, we provide a numerical example to show the effect without considering the restriction that w − xk > 0. For illustrative purposes, the parameters in the degradation process are assumed as w = 10, yk = 9 and Φ = {1,0.01,0.09,2} . Then, the corresponding PDF and CDF of the lifetime are illustrated in Figure 2, where ND represents the traditional normal distribution. Obviously, the PDF and CDF by the traditional normal distribution are smaller than those by the TND.
The reason why the traditional normal distribution obtains smaller PDF and CDF can be explained as follows. When the traditional normal distribution is used, the PDF and CDF of the RUL can be calculated by the law of total probability as follows:
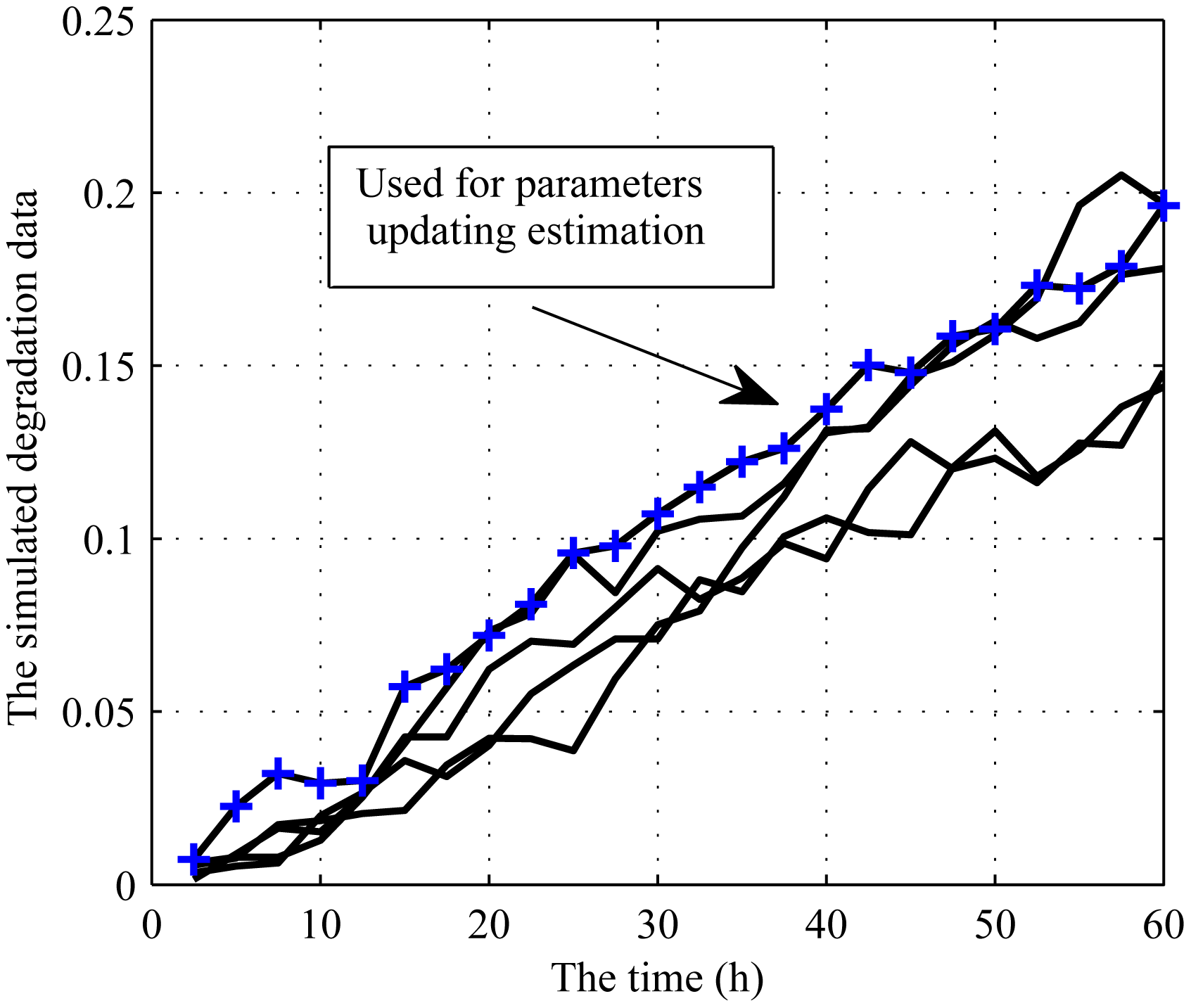
Then, five degradation paths are generated to demonstrate the validity of the proposed offline MLE method. For illustrative purposes, the parameters for the degradation process are assumed as Φ = {3×10−3,4×10−8, 1×10−5,2×10−5} . The degradation paths are simulated by the Euler approximation method with measurement frequency of 2.5 h, as shown in Figure 3.
For simplicity, the MLE method proposed in this paper is referred to as MA, the method presented by Reference [31] as MB. Then, the estimation results of the parameters and the log-likelihood function value are shown in Table 1 for comparison. From Table 1, it can be observed that the estimate of by MB is negative. This demonstrates the better performance of the presented model. If the is restricted as in the process of maximizing the log-likelihood function, the estimation results are given in the last line of Table 1. Compared with MB, our method produces closer estimations of the unknown parameters to the real results and has better fit in terms of the log-LF.
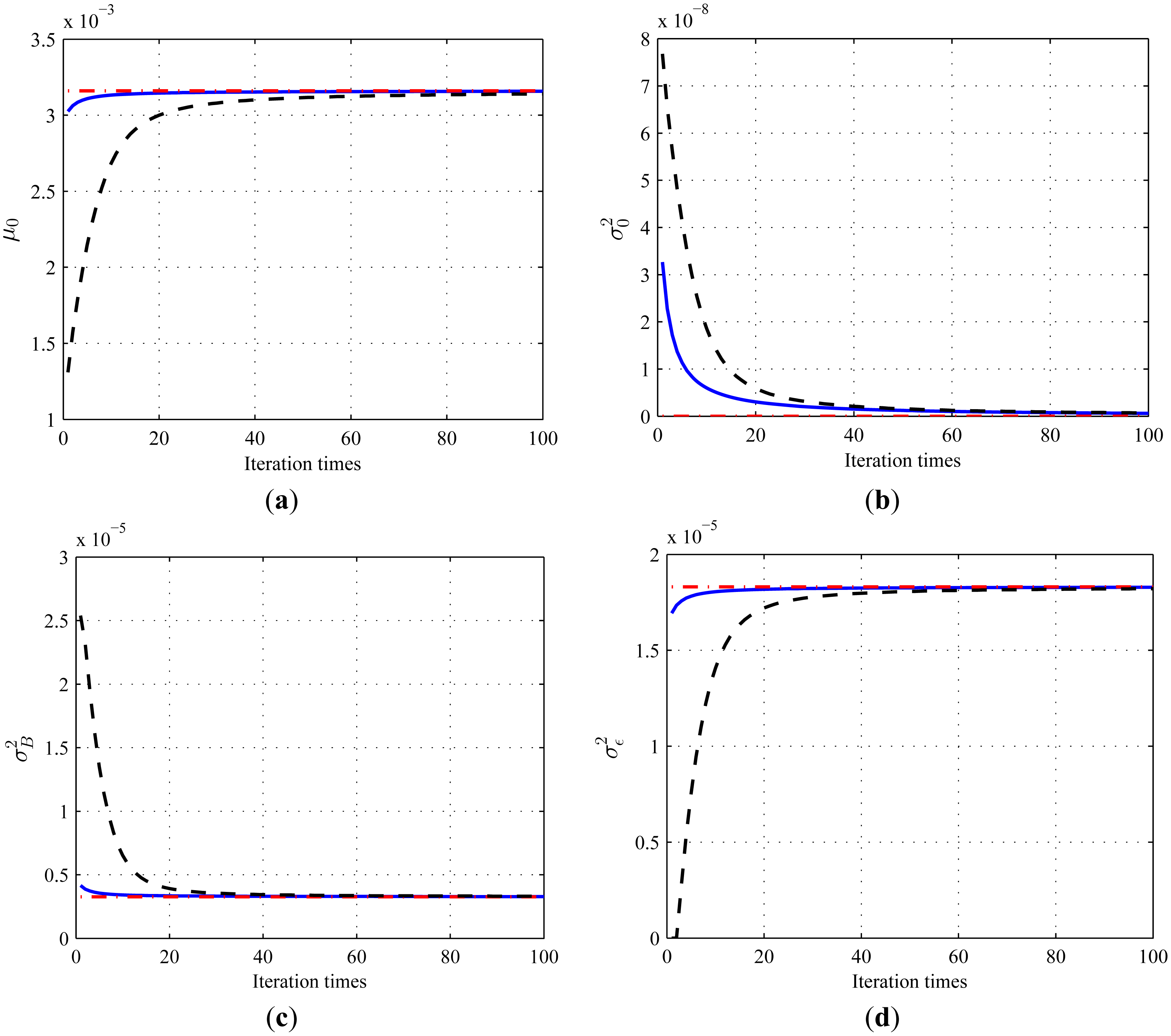
To demonstrate the interesting consequence derived in this paper, we use the third simulated degradation paths to illustrate the iteration process of the combination algorithm of the Bayesian updating and EM algorithm through estimating the unknown parameters of a specific item. Using the MLE method in Reference [40], the estimated results are Φ̂ |MLE = {3.3279×10−3,0,1.3245×10−6,2.3885×10−5} . The real and random prior parameters are respectively used for the parameters updating, where the random prior parameters are chosen as Φ = {1×10−3,9×10−8,3×10−5,1×10−5}. The iterative process of 100 times is illustrated in Figure 4. It is shown that the iteration based on the right prior parameters converges faster than that under the random prior parameters. However, they all converge to the results by using the MLE directly.
5.2. A Practical Case Study
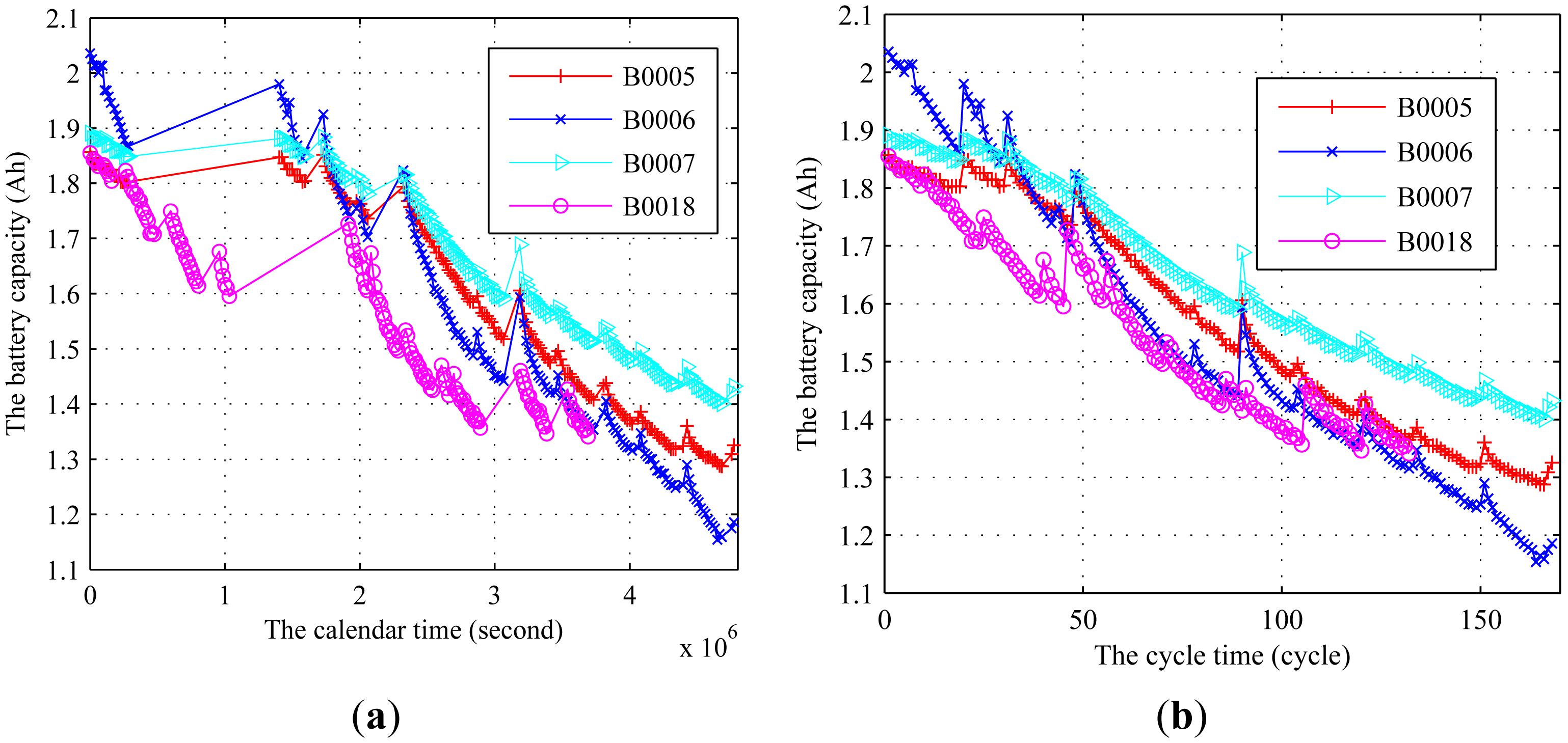
In this experiment, we use the data collected from the National Aeronautics and Space Administration (NASA) Ames Prognostics Center of Excellence to demonstrate the effectiveness of our algorithm [55]. The degradation data includes four Li-ion batteries run through three different operational profiles (charge, discharge and impedance) at room temperature. The use of the lithium-ion battery is a process of repeatedly charging and discharging. Based on the analysis of the available performance measures of the lithium-ion batteries presented by Jin et al. [12], the capacity can be used to characterize the long-term degradation process induced by the charge-discharge operational cycle. The cycle life of the battery is defined as the number of times a battery can be recharged before its capacity has faded beyond acceptable limits (20%∼30% of the rated capacity). The degradation data from NASA included two time scales, i.e., calendar time and cycle time [12]. The degradation data based on the two time scales are shown in Figure 5.
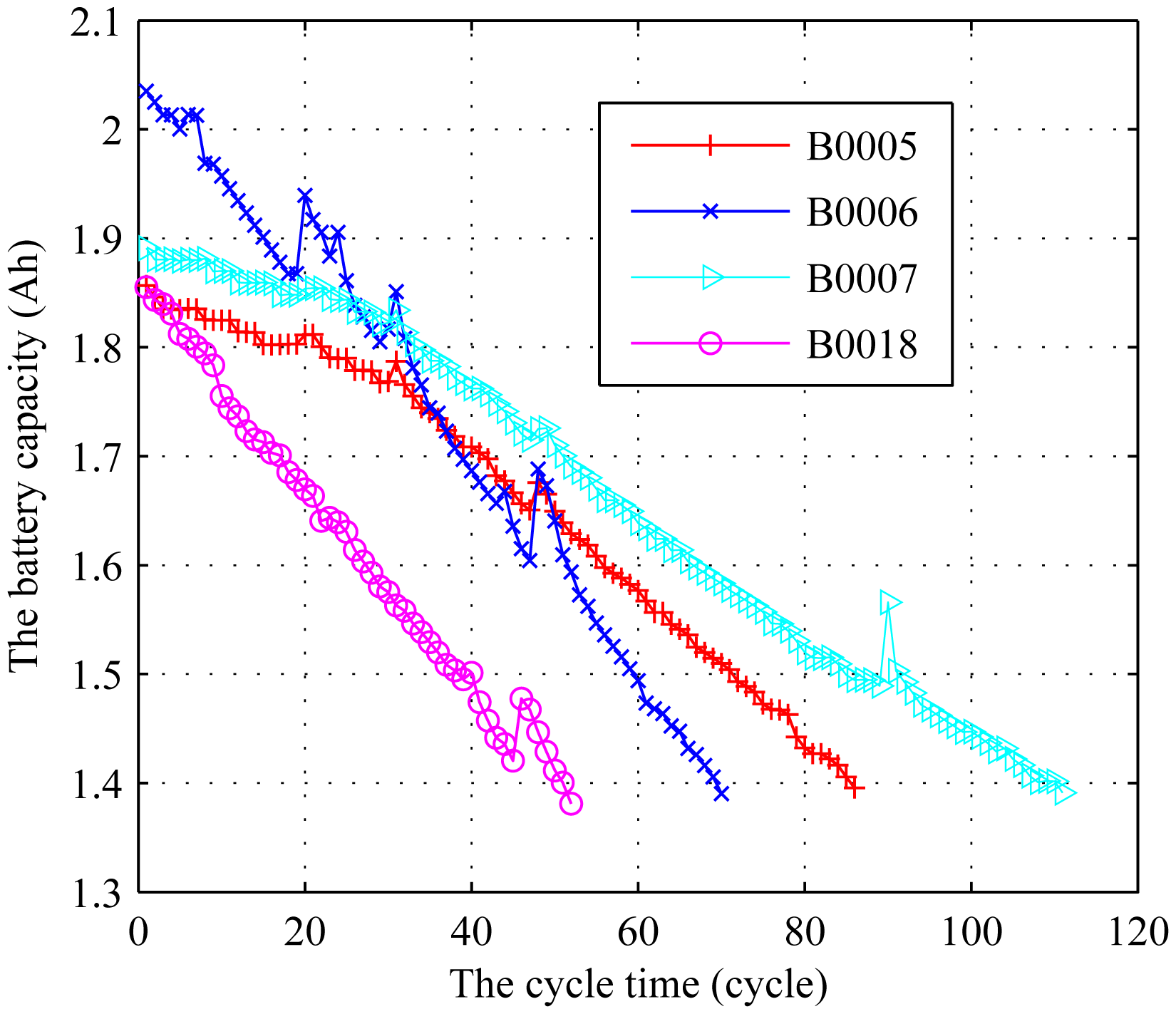
It can be observed that some rest time exists in the experiment, which leads to the recovery of the battery. This phenomenon, called relaxation effect, increases the available capacity for the next cycle [12]. Due to the uncertainty of the rest time, the RUL could not be accurately predicted. Therefore, the relaxation effect should be extracted to study the RUL prediction of the cycle time. Jin et al. [12] used an exponential function of the calendar time presented in Reference [14] to extract the relaxation effect. For more details about how to extract the relaxation effect, see Reference [14]. In this paper, we also extract the relaxation effect by the method presented in Reference [14]. The transformed data by extracting the relaxation effect is illustrated in Figure 6, where the data is collected until failure. When the full charge capacity is reduced to below 70% of its rated value (1.4 A h), it is considered as the end of life and the battery needs to be replaced.
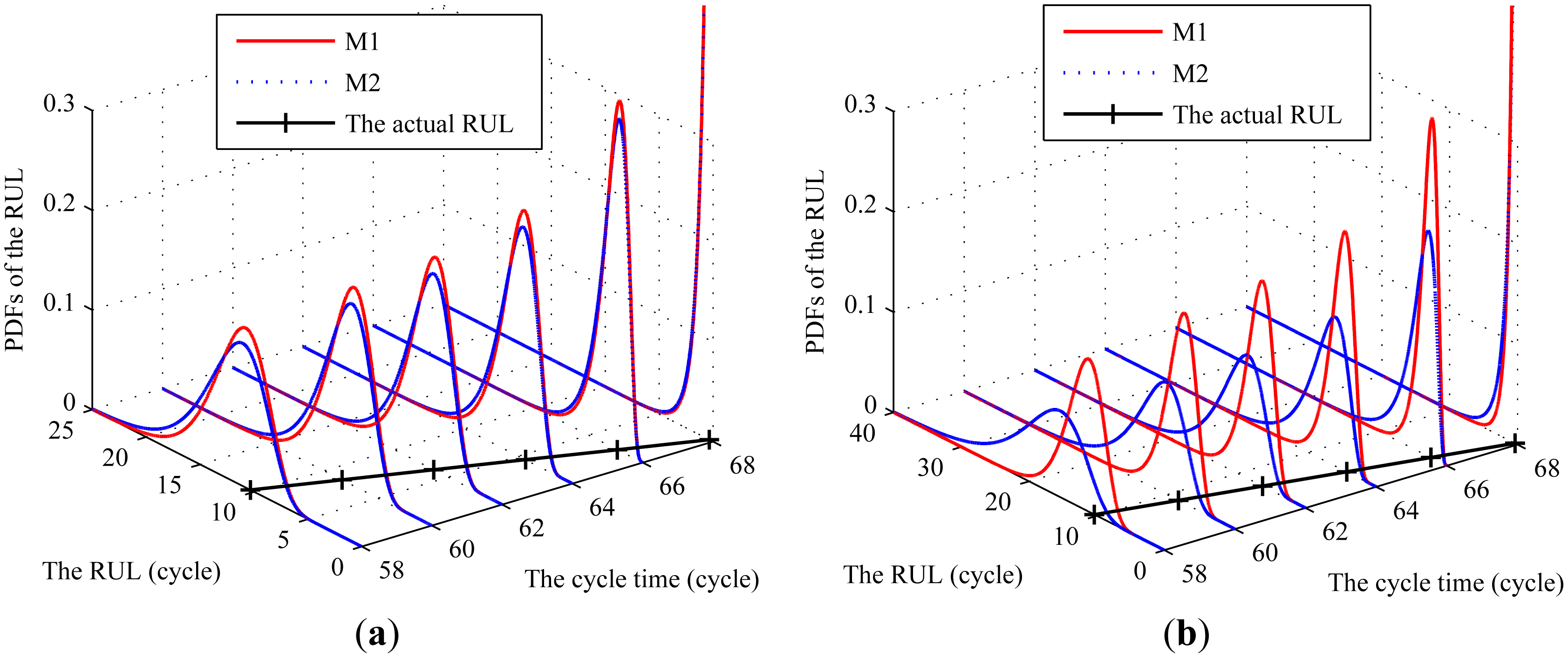
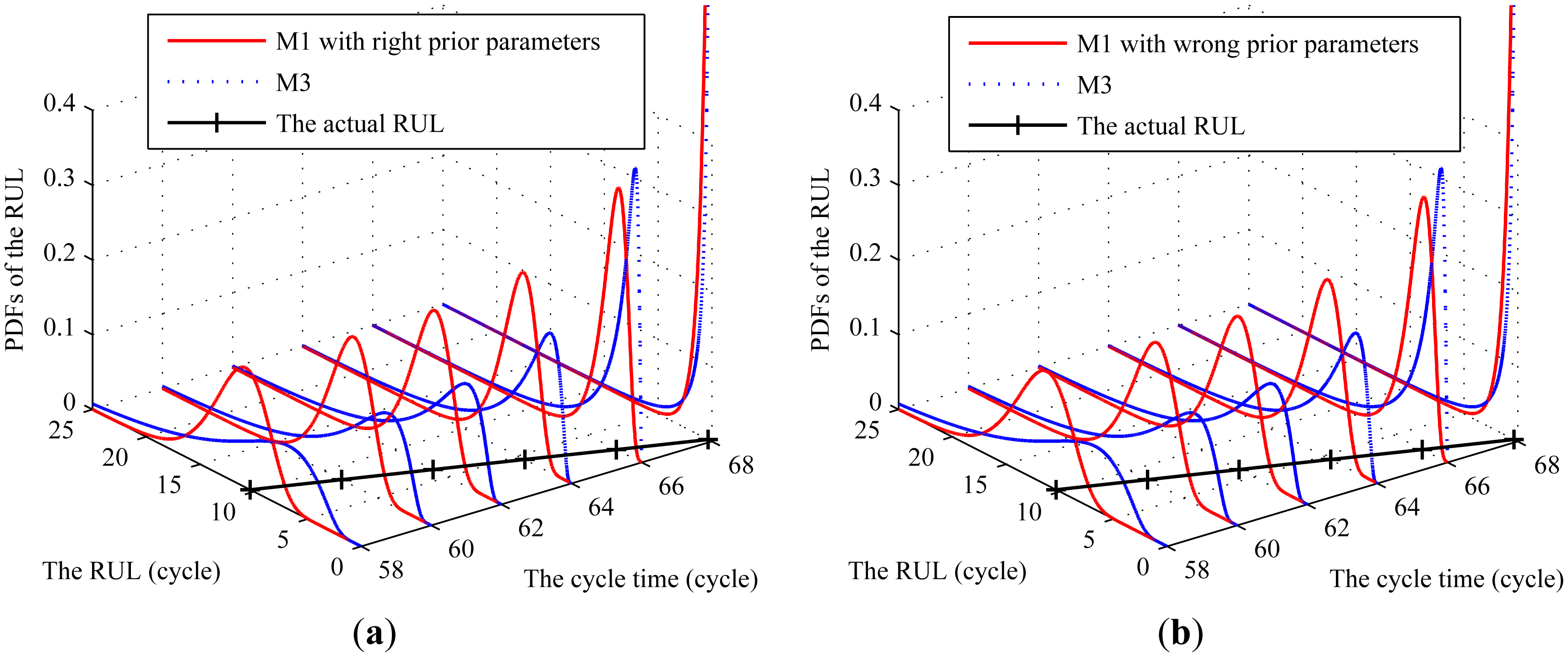
In the following, we compare our method with Bayesian algorithm [43]. For simplicity, the method proposed in this paper is referred to as M1, the method based on the Bayesian updating algorithm as M2, and the method based on the MLE method as M3. To evaluate the proposed method, B0006 is chosen to compare these methods at different CM times and the data of other items are used to evaluate the prior parameters, the results of which are Φ = {−6.30×10−3,3.92×10−6,4.51×10−5,2.55×10−5} . For comparison, the inappropriate prior parameters are chosen as μ0 = −2.10 × 10−3 and .
We set iteration interval length Lit = 10 for the RUL prediction with right prior information and Lit = 5 for that with inappropriate prior information. The corresponding PDFs of RULs under M1 and M2, and the actual RULs at some different CM points are shown in Figure 7. From Figure 7, it can be observed that, for the case with the right prior information, the range of the PDFs of the RULs based on both methods could cover the actual RUL. However, the uncertainty in the estimated RULs of M1 is less than that by M2. For the case with inappropriate prior information, the PDFs based on M1 could cover the actual RULs. However, the PDFs based on M2 could not cover the actual RULs and thus the maintenance is delayed if such predictive result is applied in maintenance schedule. This indicates that the proposed method could obtain desirable results regardless of the quality of the prior information.
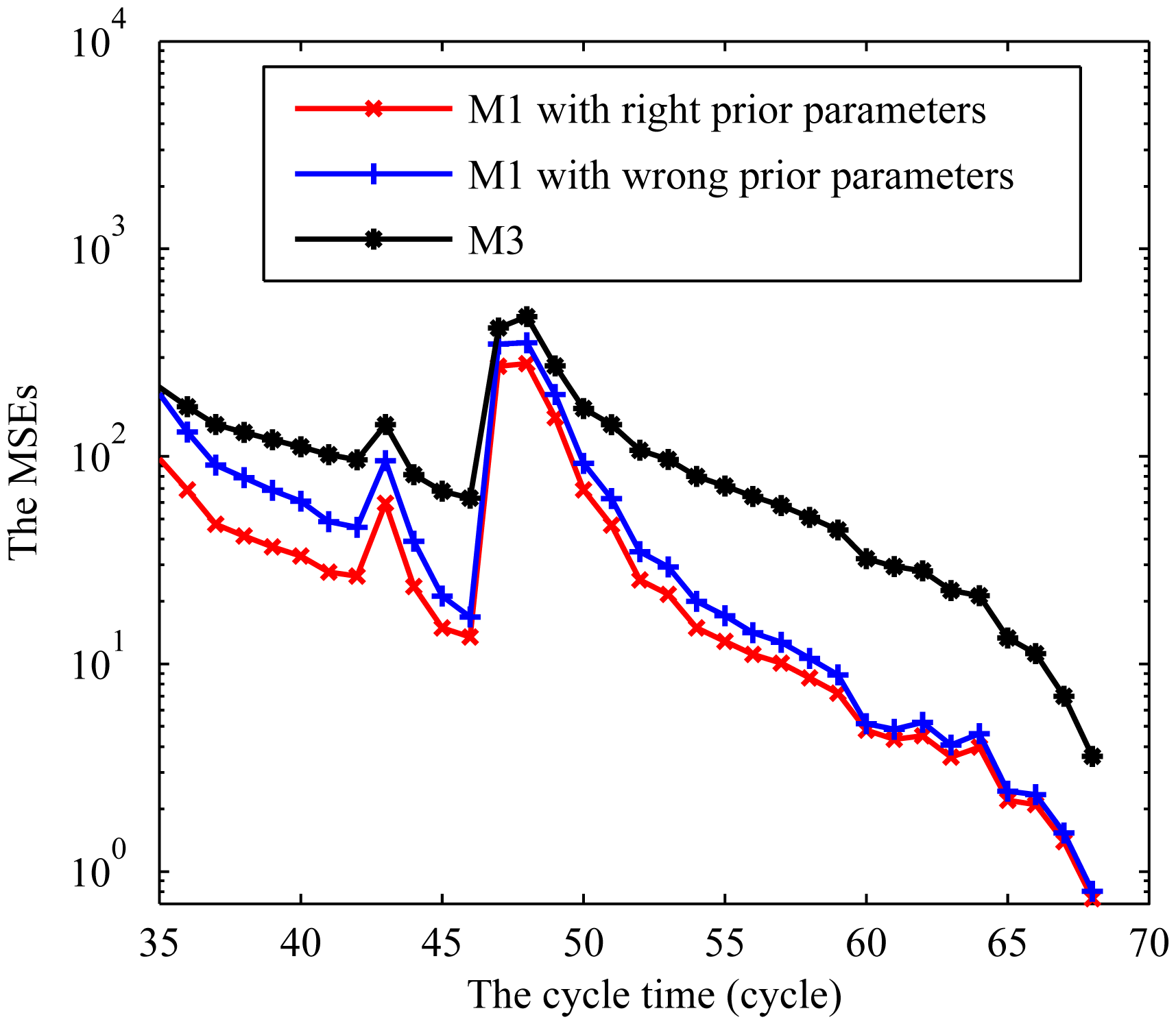
To further test the goodness of fit, we use the mean square error (MSE) to compare the methods in terms of the total prediction error of the RUL. The MSE at each observation point is calculated as follows:
Since the combination of the Bayesian method and the EM algorithm is actually the MLE method for a fixed degradation rate [40], we further compare our method with the MLE method. The corresponding PDFs of RULs and the actual RULs at some different CM points are shown in Figure 9. From Figure 9, we observe that all the PDFs could cover the actual RUL. However, the MLE method has a wider distribution, and has low probability for the time close to the actual RUL values.
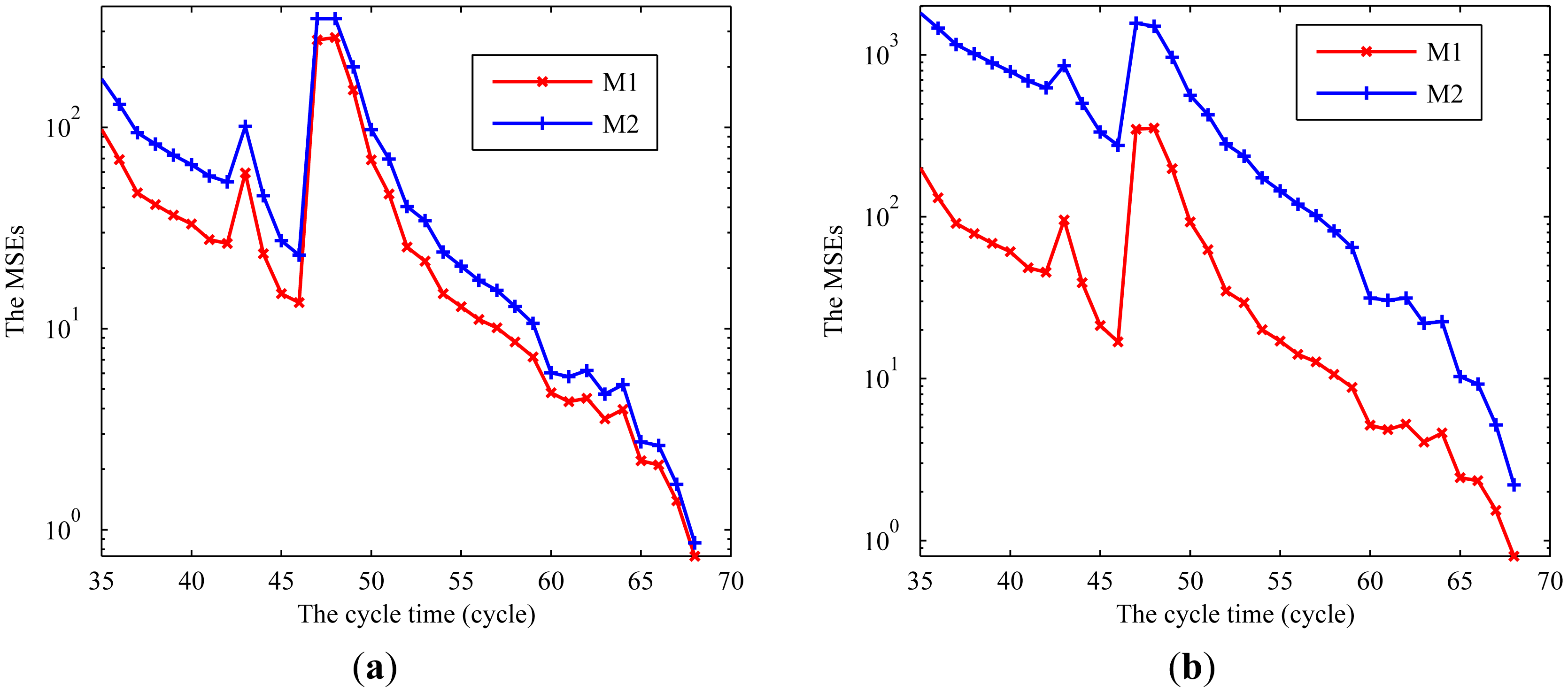
Additionally, we give the results of the MSEs at some CM points as shown in Figure 10. It can be observed that the proposed method obtains better accuracy than the MLE method and has certain robustness over the selection of the prior information. Moreover, the MLE method cannot apply the prior information for the RUL prediction. This further demonstrates the superiority of the proposed method.
Overall, the numerical examples and the practical study demonstrate that our developed method can work well and efficiently. Moreover, we verify that reasonably integrating the prior information and in situ information into degradation modeling can improve the accuracy of the RUL prediction.
6. Conclusions
This paper proposes a novel RUL prediction algorithm for lithium-ion batteries based on the WPME. First, some issues regarding the RUL prediction for the WPME have been studied. In order to ensure that w − xk > 0, we use the TND to model the estimated state w − xk and obtain an exact and closed-form RUL distribution by considering the ME and the distribution of the estimated drift parameter simultaneously. A new likelihood function is established for the offline parameters estimation, and thus the requirement of a fixed drift parameter for a specific item is satisfied. For the online parameter updating, we infer that the combination of the Bayesian updating algorithm and the EM algorithm derives the same results with that by the MLE method with a fixed drift parameter, and verify the interesting consequence through numerical examples. Based on this interesting result, we propose a heuristic parameter updating algorithm. Finally, the usefulness of the proposed method is demonstrated by a real-world degradation data of lithium-ion batteries from NASA. Compared with the existing approach, the proposed method can generate better results in predicting the RUL and has application potential.
We primarily discuss the issues associated with estimating the RUL for the batteries with linear degradation characteristic. However, in many cases, lithium-ion batteries exhibit nonlinear degradation trend, especially when they approach the end of life. Therefore, using Wiener process for the RUL estimation of lithium-ion batteries with nonlinear degradation trend is necessary in future research. Additionally, the relaxation effect could lead to the recovery of the battery, i.e., increases the available capacity for the next cycle. This phenomenon gives rise to a new studying issue that how to set the rest time for increasing the utilization of the batteries. Moreover, the heuristic parameter updating algorithm proposed in this paper is still preliminary, the issue regarding how to reasonably incorporate the prior information and in situ information together should be further exploited.
Acknowledgments
The authors thank the editor and four anonymous reviewers for their valuable and constructive suggestions that led to considerable improvements of this paper. This work was supported by the Nature Science Foundation of China (NSFC) Grant #61272428, #41174162, #61174030, #61104223, and #61374126, and the Ph.D. Programs Foundation of Ministry of Education of China for funding the Project of #20120002110067.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix
A. The Proof of Lemma 1
Duo to the limited space, it is only summarized the main results below:
By substituting Equations (A2) and (A3) into Equation (A1), the final result of Theorem 2 can be obtained after some manipulations. This completes the proof.
B. The Proof of Theorem 1
As , from Equation (11) and using the law of total probability, it can be obtained that:
Let B = μλ,klk and , the PDF of RUL can be obtained straightforwardly using Theorem 1.
Let Λ() be the Dawson function, from Theorem 2, the mean of RUL can be formulated as [31]:
C. The Proof of Theorem 2
- (1)
By taking the first partial derivatives of the expectation of the complete log-likelihood function in Equation (30) with respect to , and , and setting the three derivatives to zero, we obtain restricted estimate of , and . Substituting the restricted estimate into Equation (30) and simplifying, gives the profile log-likelihood function only regarding to ϕ as . By maximizing the profile log-likelihood function, we get Then, substitute into the restricted estimate, we obtain the estimate for , and , as shown in Equation (31).
- (2)
Let , we have:
where:
Set and calculate the order principal minor determinant, then we have:
This proves that the matrix in Equation (C1) is negative definite at . It indicates that given , is the only solution satisfying . Moreover, as is the only solution of the profile log-likelihood function, is uniquely determined and located at the maximum. This completes the proof.
D. The Proof of Theorem 3
- (1)
Substituting Equations (25) and (31) and setting , we have:
Consequently, the result of the EM algorithm is the solution of the above equations. By solving the above equations, we can obtain the result of the EM algorithm.
- (2)
Set , then from Equation (15) we have:
By maximizing the above equation, we can derive the result of the estimation by the MLE method, which is the same as the result of the EM algorithm. This completes the proof.
References
- He, Z.; Gao, M.; Wang, C.; Wang, L.; Liu, Y. Adaptive state of charge estimation for Li-ion batteries based on an unscented kalman filter with an enhanced battery model. Energies 2013, 6, 4134–4151. [Google Scholar]
- Williard, N.; He, W.; Osterman, M.; Pecht, M. Comparative analysis of features for determining state of health in lithium-ion batteries. Int. J. Progn. Health Manag. 2013, 1, 1–7. [Google Scholar]
- Zhang, J.; Lee, J. A review on prognostics and health monitoring of Li-ion battery. J. Power Sources 2011, 196, 6007–6014. [Google Scholar]
- Liu, D.; Wang, H.; Peng, Y.; Xie, W.; Liao, H. Satellite lithium-ion battery remaining cycle life prediction with novel indirect health indicator extraction. Energies 2013, 6, 3654–3668. [Google Scholar]
- Xing, Y.; Ma, E.W.M.; Tsui, K.L.; Pecht, M. Battery management systems in electric and hybrid vehicles. Energies 2011, 4, 1840–1857. [Google Scholar]
- Goebel, K.; Saha, B.; Saxena, A.; Celaya, J.R.; Christophersen, J.P. Prognostics in battery health management. IEEE Instrum. Meas. Mag. 2008, 11, 33–40. [Google Scholar]
- Williard, N.; He, W.; Hendricks, C.; Pecht, M. Lessons learned from the 787 Dreamliner issue on lithium-ion battery reliability. Energies 2013, 6, 4682–4695. [Google Scholar]
- Pecht, M.G. Prognostics and Health Management of Electronics; John Wiley & Sons, Ltd.: New York, NY, USA, 2008. [Google Scholar]
- Bo, S.; Shengkui, Z.; Rui, K.; Pecht, M.G. Benefits and challenges of system prognostics. IEEE Trans. Reliab. 2012, 61, 323–335. [Google Scholar]
- Camci, F.; Chinnam, R.B. Health-state estimation and prognostics in machining processes. IEEE Trans. Autom. Sci. Eng. 2010, 7, 581–597. [Google Scholar]
- Carr, M.J.; Wang, W. An approximate algorithm for prognostic modelling using condition monitoring information. Eur. J. Oper. Res. 2011, 211, 90–96. [Google Scholar]
- Jin, G.; Matthews, D.E.; Zhou, Z. A Bayesian framework for on-line degradation assessment and residual life prediction of secondary batteries inspacecraft. Reliab. Eng. Syst. Saf. 2013, 113, 7–20. [Google Scholar]
- Feng, L.; Wang, H.; Si, X.; Zou, H. A state-space-based prognostic model for hidden and age-dependent nonlinear degradation process. IEEE Trans. Autom. Sci. Eng. 2013, 10, 1072–1086. [Google Scholar]
- Saha, B.; Goebel, K. Modeling Li-Ion Battery Capacity Depletion in a Particle Filtering Framework. Proceedings of the Annual Conference of the Prognostics and Health Management Society, San Diego, CA, USA, 27 September–1 October 2009; pp. 1–10.
- Dalal, M.; Ma, J.; He, D. Lithium-ion battery life prognostic health management system using particle filtering framework. J. Risk Reliab. 2011, 225, 81–90. [Google Scholar]
- Saha, B.; Goebel, K.; Poll, S.; Christophersen, J. Prognostics methods for battery health monitoring using a Bayesian framework. IEEE Trans. Instrum. Meas. 2009, 58, 291–296. [Google Scholar]
- Miao, Q.; Xie, L.; Cui, H.; Liang, W.; Pecht, M. Remaining useful life prediction of lithium-ion battery with unscented particle filter technique. Microelectron. Reliab. 2013, 53, 805–810. [Google Scholar]
- He, W.; Williard, N.; Osterman, M.; Pecht, M. Prognostics of lithium-ion batteries based on Dempster-Shafer theory and the Bayesian Monte Carlo method. J. Power Sources 2011, 196, 10314–10321. [Google Scholar]
- Long, B.; Xian, W.; Jiang, L.; Liu, Z. An improved autoregressive model by particle swarm optimization for prognostics of lithium-ion batteries. Microelectron. Reliab. 2013, 53, 821–831. [Google Scholar]
- Xian, W.; Long, B.; Li, M.; Wang, H. Prognostics of lithium-ion batteries based on the Verhulst model, particle swarm optimization and particle filter. IEEE Trans. Instrum. Meas. 2013, 63, 2–17. [Google Scholar]
- Liu, J.; Wang, W.; Ma, F.; Yang, Y.B.; Yang, C.S. A data-model-fusion prognostic framework for dynamic system state forecasting. Eng. Appl. Artif. Intell. 2012, 25, 814–823. [Google Scholar]
- Xing, Y.; Ma, E.W.M.; Tsui, K.-L.; Pecht, M. An ensemble model for predicting the remaining useful performance of lithium-ion batteries. Microelectron. Reliab. 2013, 53, 811–820. [Google Scholar]
- Omar, N.; Monem, M.A.; Firouz, Y.; Salminen, J.; Smekens, J.; Hegazy, O.; Gaulous, H.; Mulder, G.; van den Bossche, P.; Coosemans, T.; et al. Lithium iron phosphate based battery—Assessment of the aging parameters and development of cycle life model. Appl. Energy 2014, 113, 1575–1585. [Google Scholar]
- Chen, Y.; Miao, Q.; Zheng, B.; Wu, S.; Pecht, M. Quantitative analysis of lithium-ion battery capacity prediction via adaptive bathtub-shaped function. Energies 2013, 6, 3082–3096. [Google Scholar]
- Wang, D.; Miao, Q.; Pecht, M. Prognostics of lithium-ion batteries based on relevance vectors and a conditional three-parameter capacity degradation model. J. Power Sources 2013, 239, 253–264. [Google Scholar]
- Wang, X. Wiener processes with random effects for degradation data. J. Multivar. Anal. 2010, 101, 340–351. [Google Scholar]
- Wei, M.; Chen, M.; Zhou, D. Multi-sensor information based remaining useful life prediction with anticipated performance. IEEE Trans. Reliab. 2013, 62, 183–198. [Google Scholar]
- Tseng, S.-T.; Tang, J.; Ku, I.-H. Determination of burn-in parameters and residual life for highly reliable products. Nav. Res. Logist. 2003, 50, 1–14. [Google Scholar]
- Liao, C.; Tseng, S. Optimal design for step-stress accelerated degradation tests. IEEE Trans. Reliab. 2006, 55, 59–66. [Google Scholar]
- Ye, Z.; Shen, Y.; Xie, M. Degradation-based burn-in with preventive maintenance. Eur. J. Oper. Res. 2012, 221, 360–367. [Google Scholar]
- Peng, C.; Tseng, S. Mis-specification analysis of linear degradation models. IEEE Trans. Reliab. 2009, 58, 444–455. [Google Scholar]
- Wang, W.; Carr, M.; Xu, W.; Kobbacy, K. A model for residual life prediction based on Brownian motion with an adaptive drift. Microelectron. Reliab. 2011, 51, 285–293. [Google Scholar]
- Si, X.; Wang, W.; Hu, C.-H.; Zhou, D.-H.; Pecht, M.G. Remaining useful life estimation based on a nonlinear diffusion degradation process. IEEE Trans. Reliab. 2012, 61, 50–67. [Google Scholar]
- Si, X.; Wang, W.; Chen, M.; Hu, C.; Zhou, D. A degradation path-dependent approach for remaining useful life estimation with an exact and closed-form solution. Eur. J. Oper. Res. 2013, 226, 53–66. [Google Scholar]
- Si, X.S.; Wang, W.; Hu, C.H.; Chen, M.Y.; Zhou, D.H. A Wiener-process-based degradation model with a recursive filter algorithm for remaining useful life estimation. Mech. Syst. Signal Process 2013, 35, 219–237. [Google Scholar]
- Si, X.; Wang, W.; Hu, C.; Zhou, D. Remaining useful life estimation—A review on the statistical data driven approaches. Eur. J. Oper. Res. 2011, 213, 1–14. [Google Scholar]
- Si, X.; Chen, M.; Wang, W.; Hu, C.; Zhou, D. Specifying measurement errors for required lifetime estimation performance. Eur. J. Oper. Res. 2013, 231, 631–644. [Google Scholar]
- Wang, X.; Guo, B.; Cheng, Z.; Jiang, P. Residual life estimation based on bivariate Wiener degradation process with measurement errors. J. Cent. South Univ. 2013, 20, 1844–1851. [Google Scholar]
- Tang, S.; Guo, X.; Zhou, Z.; Zhou, Z.; Zhang, B. Real time remaining useful life prediction based on nonlinear Wiener based degradation processes with measurement errors. J. Cent. South Univ. 2014. in press.. [Google Scholar]
- Whitmore, G.A. Estimating degradation by a wiener diffusion process subject to measurement error. Lifetime Data Anal 1995, 1, 307–319. [Google Scholar]
- Ye, Z.-S.; Wang, Y.; Tsui, K.-L.; Pecht, M. Degradation data analysis using wiener processes with measurement errors. IEEE Trans. Reliab. 2013, 62, 772–780. [Google Scholar]
- Ye, Z.; Chen, N.; Tsui, K.-L. A Bayesian approach to condition monitoring with imperfect inspections. Qual. Reliab. Eng. Int. 2013. [Google Scholar] [CrossRef]
- Gebraeel, N.Z.; Lawley, M.A.; Li, R.; Ryan, J.K. Residual-life distributions from component degradation signals: A Bayesian approach. IIE Trans. 2005, 37, 543–557. [Google Scholar]
- Gebraeel, N. Sensory-updated residual life distributions for components with exponential degradation patterns. IEEE Trans. Autom. Sci. Eng. 2006, 3, 382–393. [Google Scholar]
- Kaiser, K.A.; Gebraeel, N.Z. Predictive maintenance management using sensor-based degradation models. IEEE Trans. Syst. Man Cybern. A Syst. Hum. 2009, 39, 840–849. [Google Scholar]
- You, M.; Liu, F.; Wang, W.; Meng, G. Statistically planned and individually improved predictive maintenance management for continuously monitored degrading systems. IEEE Trans. Reliab. 2010, 59, 744–753. [Google Scholar]
- Wang, X.; Guo, B.; Cheng, Z. Residual life estimation based on bivariate Wiener degradation process with time-scale transformations. J. Stat. Comput. Simul. 2012, 84, 545–563. [Google Scholar]
- Curcurù, G.; Galante, G.; Lombardo, A. A predictive maintenance policy with imperfect monitoring. Reliab. Eng. Syst. Saf. 2010, 95, 989–997. [Google Scholar]
- Xu, Z.; Ji, Y.; Zhou, D. Real-time reliability prediction for a dynamic system based on the hidden degradation process identification. IEEE Trans. Reliab. 2008, 57, 230–242. [Google Scholar]
- Folks, J.L.; Chhikara, R.S. The inverse Gaussian distribution and its statistical application—A review. J. R. Stat. Soc. Ser. B Methodol. 1978, 40, 263–289. [Google Scholar]
- Greene, W.H. Econometric Analysis, 5/e; Pearson Education India: Delhi, India, 2003. [Google Scholar]
- Meurant, G. A review on the inverse of symmetric tridiagonal and block tridiagonal matrices. SIAM J. Matrix Anal. Appl. 1992, 13, 707–728. [Google Scholar]
- Peng, C.-Y.; Hsu, S.-C. A note on a Wiener process with measurement error. Appl. Math. Lett. 2012, 25, 729–732. [Google Scholar]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B Methodol. 1977, 39, 1–38. [Google Scholar]
- Saha, B.; Goebel, K. Battery Data Set. In NASA Ames Prognostics Data Repository; National Aeronautics and Space Administration (NASA)'s Ames Research Center: Moffett Field, CA, USA, 2007. Available online: http://ti.arc.nasa.gov/tech/dash/pcoe/prognostic-data-repository/ (accessed on 22 January 2014). [Google Scholar]
| Methods | μλ | Log-LF | |||
|---|---|---|---|---|---|
| Real value | 3 × 10−3 | 4 × 10−8 | 1 × 10−5 | 2 × 10−5 | - |
| MA | 2.8735 × 10−3 | 1.6847 × 10−7 | 1.0467 × 10−5 | 1.8566 × 10−5 | 416.48 |
| MB | 2.8750 × 10−3 | −6.9337 × 10−8 | 1.3679 × 10−5 | 1.4693 × 10−5 | 414.50 |
| MB (with restriction) | 2.8747 × 10−3 | 0 | 1.2749 × 10−5 | 1.5704 × 10−5 | 414.39 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Tang, S.; Yu, C.; Wang, X.; Guo, X.; Si, X. Remaining Useful Life Prediction of Lithium-Ion Batteries Based on the Wiener Process with Measurement Error. Energies 2014, 7, 520-547. https://doi.org/10.3390/en7020520
Tang S, Yu C, Wang X, Guo X, Si X. Remaining Useful Life Prediction of Lithium-Ion Batteries Based on the Wiener Process with Measurement Error. Energies. 2014; 7(2):520-547. https://doi.org/10.3390/en7020520
Chicago/Turabian StyleTang, Shengjin, Chuanqiang Yu, Xue Wang, Xiaosong Guo, and Xiaosheng Si. 2014. "Remaining Useful Life Prediction of Lithium-Ion Batteries Based on the Wiener Process with Measurement Error" Energies 7, no. 2: 520-547. https://doi.org/10.3390/en7020520




