Analysis of the Dynamic Performance of Self-Excited Induction Generators Employed in Renewable Energy Generation
Abstract
: Incentives, such as the Feed-in-tariff are expected to lead to continuous increase in the deployment of Small Scale Embedded Generation (SSEG) in the distribution network. Self-Excited Induction Generators (SEIG) represent a significant segment of potential SSEG. The quality of SEIG output voltage magnitude and frequency is investigated in this paper to support the SEIG operation for different network operating conditions. The dynamic behaviour of the SEIG resulting from disconnection, reconnection from/to the grid and potential operation in islanding mode is studied in detail. The local load and reactive power supply are the key factors that determine the SEIG performance, as they have significant influence on the voltage and frequency change after disconnection from the grid. Hence, the aim of this work is to idengify the optimum combination of the reactive power supply (essential for self excitation of the SEIG) and the active load (essential for balancing power generation and demand). This is required in order to support the SEIG operation after disconnection from the grid, during islanding and reconnection to the grid. The results show that the generator voltage and speed (frequency) can be controlled and maintained within the statuary limits. This will enable safe disconnection and reconnection of the SEIG from/to the grid and makes it easier to operate in islanding mode.1. Introduction
World energy use increased more than tenfold over the 20th century, predominately from fossil fuels and this is estimated to increase by 60% by 2030 [1]. Increased price of energy resources and concerns regarding climate change and the need to limit greenhouse gas emissions are driving energy policy makers towards improved energy efficiency and renewable energy sources. The integration of renewable energy sources into the grid brings with it technical, economical and social barriers to be bridged [2]. The Self-Excited Induction Generations (SEIG) represents a significant segment of the potential Small Scale Embedded Generation (SSEG). It is the most cost effective machine for applications in the Medium Voltage (MV) and Low Voltage (LV) Distribution Network (DN). This is due to its merits such as low cost, simple construction, low maintenance requirements and inherent overload capability. As the induction generator does not have a separate field winding, a capacitor bank (connected in parallel with the generator) is needed to build up the terminal voltage. Under present UK distribution network code, the EG would shut down by either the “G59/1” [3] protection located on the SSEG interface protection [4], or by an inter-tripping signal originating at the circuit breaker tripping on fault. The G59/1 protection to prevent islanding typically includes under/over voltage, under/over frequency and loss of mains. The key issues behind preventing islanding in the distribution network are: the island may not be able to maintain the frequency and voltage within the statutory limits; possibilities of an unearthed neutral in the islanded network and absence of synchronising equipment. The main difficulty of SEIG is the lack of ability to control the machine terminal voltage and frequency under un-predicted load and speed conditions, such as disconnection/reconnection to the grid or when it operates in an islanding mode.
The literature available in the area of SEIG is focused on three main areas. The first is the characteristics of the isolated self-excited operation of the induction generators [5–7]. The second area is the selection of the capacitance required for self-excitation and build up of the machine terminal voltage. This has been addressed for two different topologies; a fixed capacitor connected in shunt or in series with the machine stator winding [8–10] or a reactive power compensator connected across the machine terminals [11,12]. The reactive power is controlled to support the machine terminal voltage against load variations. The third area studied is the control of ballast load connected to the IG busbar in order to compensate the variations of the main customer loads [13–15]. In this case, the required reactive power is obtained by connecting fixed capacitors across the SEIG stator terminals.
The aforementioned research is focused on the SEIG operation in standalone mode with respect to load variation. The work presented in [16,17] discusses the SEIG islanding operation under random settings of the local active and reactive load. There has been some interesting research published recently concerning the impacts of wind generation on the power grid and its stability [18–20]. However, there is no research published on the dynamic performance and the exact contribution of the active and reactive load to both voltage and frequency variations during disconnection/reconnection events and islanding of the SEIG. The focus of this paper is to analyse the effect of local active and reactive power control on the SEIG during disconnection/reconnection and islanding operation in order to define the optimum conditions for the SEIG. The optimum setting eliminates the risks of violating the frequency and voltage limits that are usually associated with islanding and disconnection/reconnection of the SEIG in power networks.
The analysis presented in this paper attempts to define the available operating regions, boundaries and limits for the induction generator and potential schemes to support the generator stable operation, such as demand side management. This analysis should help designers of wind energy conversion systems, whether using conventional or new power electronic converters based technologies to exploit the full possible stable operating range of the system.
The methodology implemented in this research is to use the steady-state analysis of the SEIG to idengify various parameters affecting its performance under different operating conditions. These parameters are then used to analyse the SEIG “dynamic” operation during the transition from one steady-state to another; e.g., from grid connection (where the balance of active and reactive power is supported by the grid) to another state where the SEIG and its local demand and resources have to be self-sufficient.
2. Induction Generator System Analysis
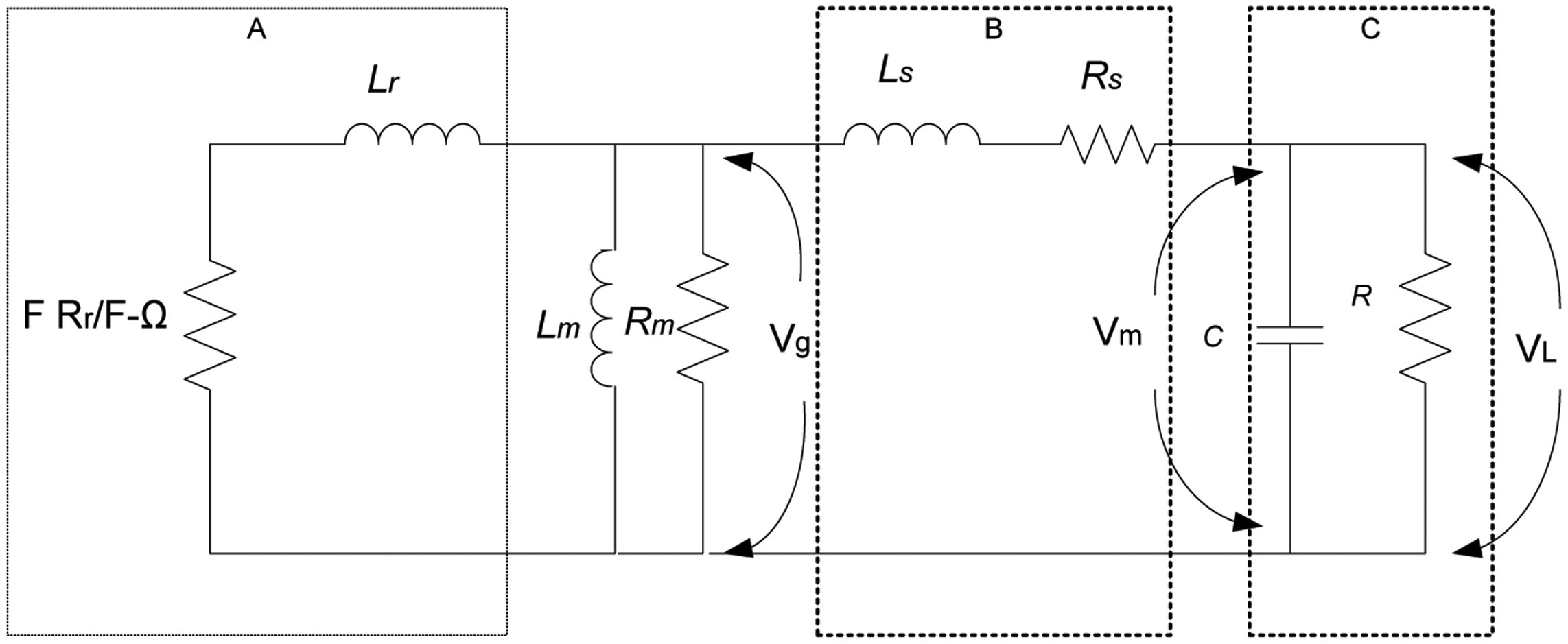
The single-phase equivalent circuit of a 2-pole induction generator is shown in Figure 1:
where:
| Rr,Lr | Rotor resistance and leakage inductance |
| Lm | Magnetizing inductance |
| Rm | Core loss Resistance |
| Rs,Ls | Stator resistance and leakage inductance |
| C | Excitation capacitance |
| R | Load resistance |
| Ω,F | Speed and Frequency in radian per second |
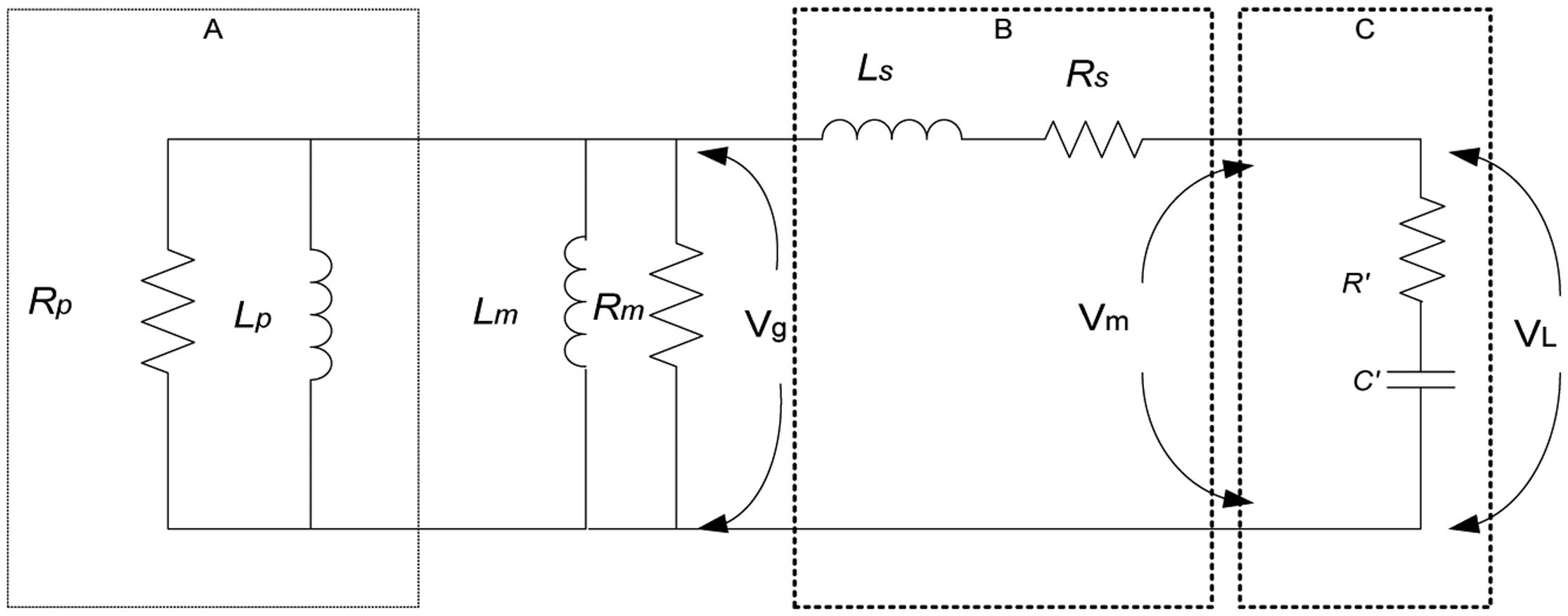
In order to simplify the analysis, the series/parallel impedances of the IG model and load circuit shown in Figure 1 (boxes A and C, respectively) are converted to their parallel/series equivalent impedances. This results in the simplified circuit shown in Figure 2. The rotor parallel circuit parameters of the IG marked in box A are given as [5]:
And the load series circuit parameters (resistance and excitation capacitance, marked in box C) are given as [5]:
Hence, the machine equivalent circuit is given as:
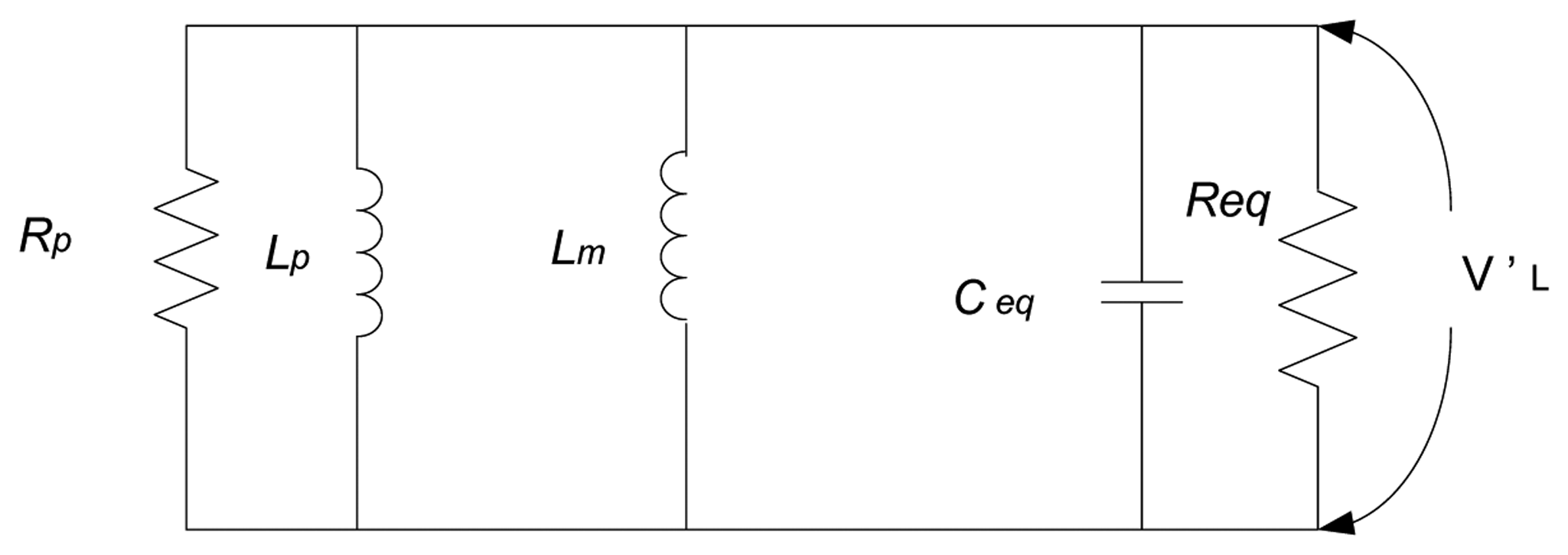
The parallel equivalent impedance for the circuit is shown in Figure 3 and is described as follows:
In order to provide excitation current, Equation (7) must be capacitive reactance. The equivalent of the machine terminal resistance defined in Equation (6) and the core losses can be modelled by Req as shown in Figure 4.
Under steady-state operation of the IG, the stator current cannot be zero. With reference to Figure 4, the following two Equations are valid:
Substituting from Equation (1) into Equation (9) yields:
Hence:
Re-arranging Equation (10) yields:
The magnetizing characteristic of the induction machine can be approximated in the area of saturation as follows [14]:
where, b and k are constants:
Substituting for Lp, Ceq, Lm and im from Equations (2), (7), (13) and (14) respectively into Equation (15) yields:
From Equations (12) and (16), it is clear that both the SEIG frequency and voltage depend on three elements which are speed, excitation capacitance and the load impedance. The induction generator is widely used in wind energy conversion systems, where the rotational speed is variable and dependent on the wind speed. Consequently, the wind speed is assumed to be an independent uncontrollable variable. Thus, both excitation capacitance and load impedance may be used to regulate the IG voltage and frequency in particular during islanding or the transient period during disconnection/reconnection of the SEIG from/to the grid.
3. Selection of Optimum Operation of the IG
From the analysis described in Section 2, Equations (12) and (16) can be solved numerically at the steady state operating points of load impedance and speed to compute the magnetizing inductance and the machine terminal voltage and frequency. Once the load is changed, the machine voltage magnitude and frequency (speed) will vary accordingly. Also, when the IG is connected/disconnected to/from the grid, it experiences a significant variation in terminal voltage magnitude and frequency if it does not have the right combination of self excited capacitance and local load. In this section, the optimum match between the excitation capacitance and local load will be idengified in order to minimize the change in voltage and frequency in order to ensure the smooth operation of the IG during reconnection to the grid or when operating in isolation from the grid.
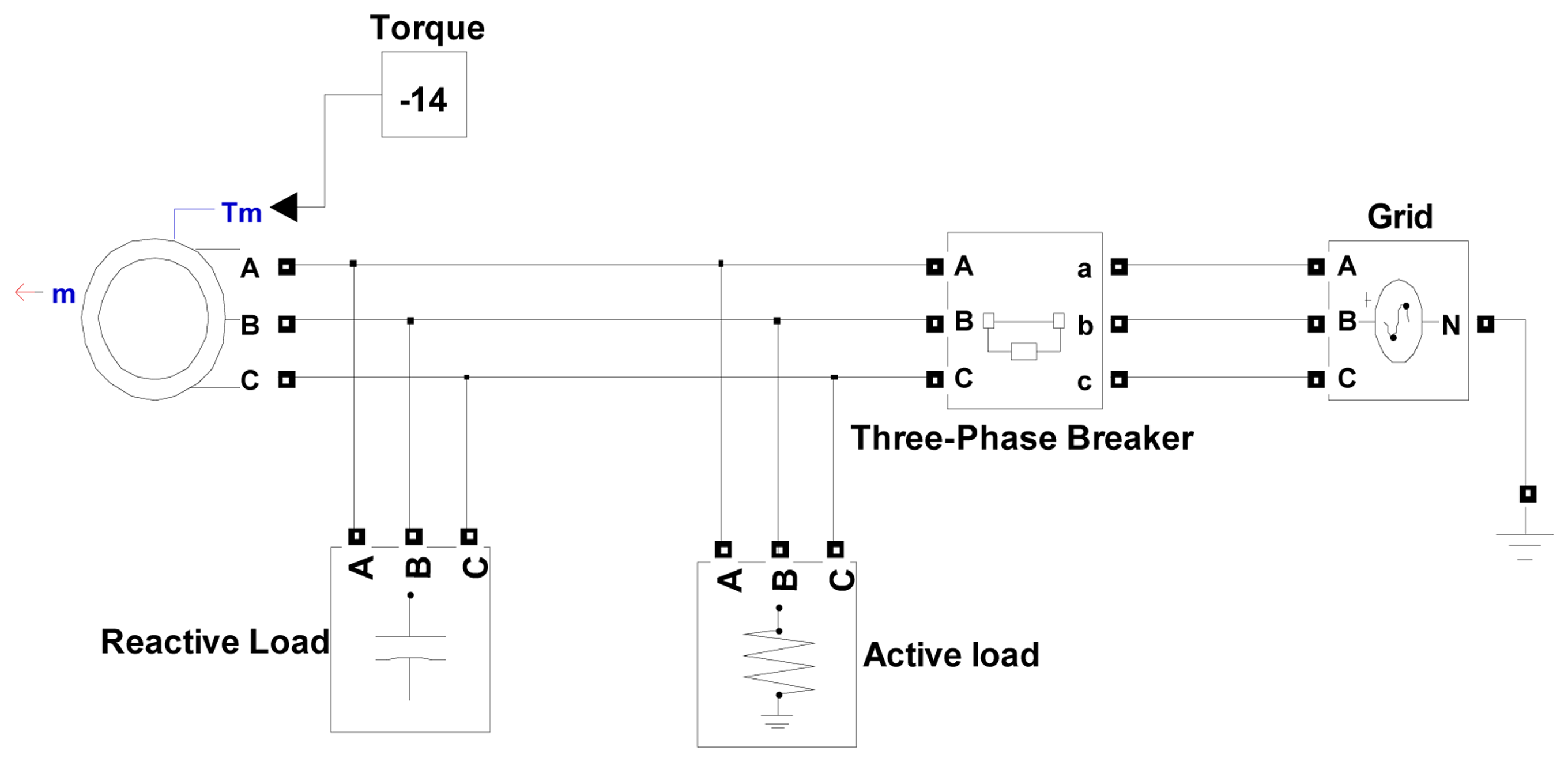
A three-phase IG (specification: 2.3 kVA, 230 V, 50 Hz, Rs = 1.115 Ω, Ls = 0.005974 H, Rr = 1.083 Ω, Lr = 0.005974 H, Lm = 0.2037 H, Inertia = 2 × 10−4) was considered to investigate the dynamic performance of the IG and determine the optimum values for local load and excitation capacitance. A MATLAB/SimPowerSystem model was used to analyse the IG performance as shown in Figure 5.
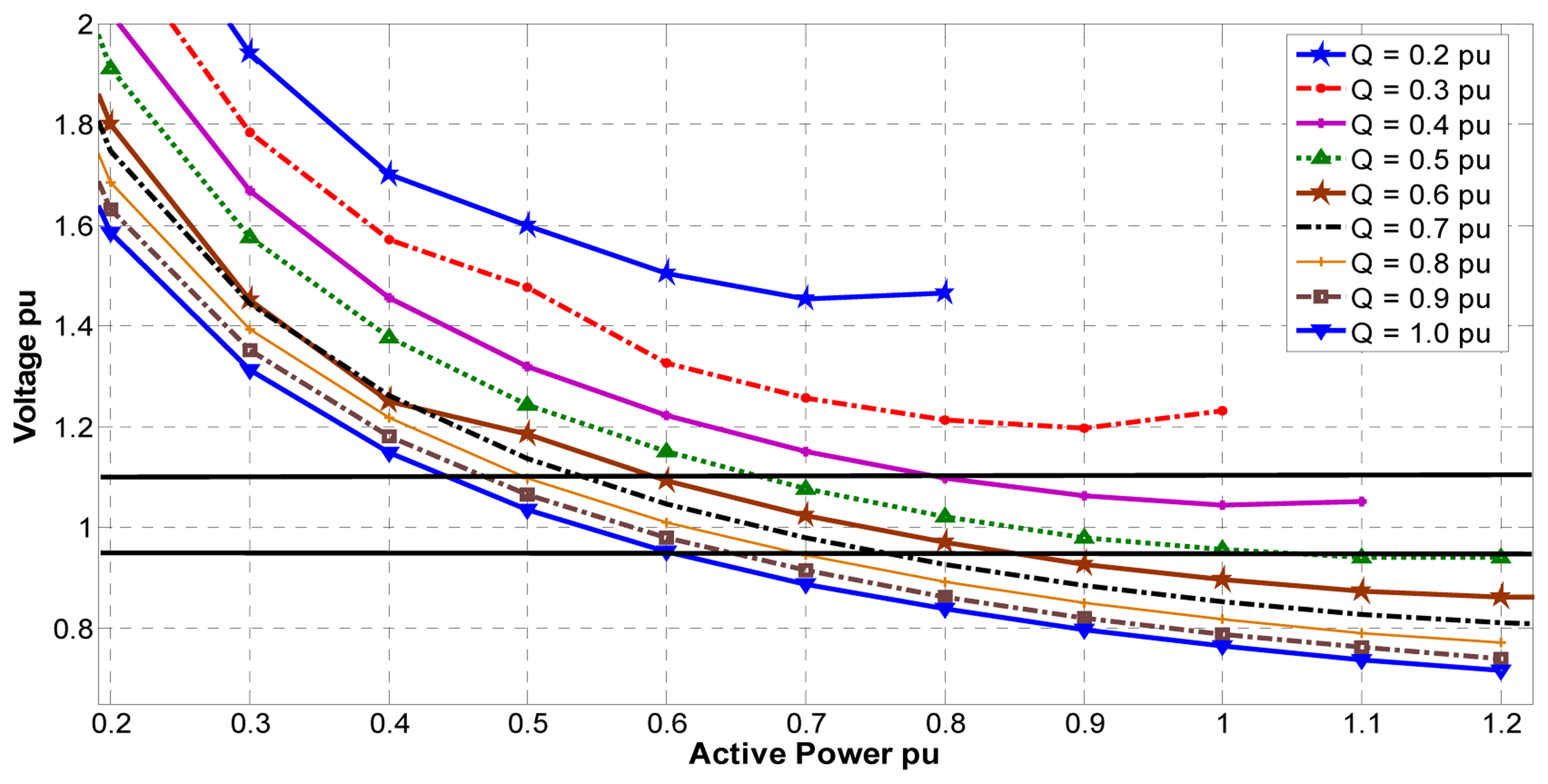
Variation of the IG terminal voltage for different local loads at different ratings of the shunt excitation capacitance (represented as a percentage of the machine rating) is shown in Figure 6. It is seen that for fixed excitation capacitance the terminal voltage decreased with the increase of the local load active power. If the machine is under-loaded to a small fraction of its rating, the terminal voltage will be very large. This would normally trigger the over-voltage protection scheme to switch the machine off. Also, it is worth noting that with excitation capacitance less than approximately 30% of the machine rating, the terminal voltage will never reach its rated value (1.0 pu) irrespective of the value of the active load. If the machine is disconnected from the grid while overloaded, the terminal voltage may drop to a value that would trigger the under-voltage protection (depending on the excitation level). Figure 6 shows that it is possible to keep the terminal voltage within the standard limits (+10%, −6% for the low-voltage distribution system), for a wide range of IG loading if the excitation is appropriately controlled between 0.4 pu and 0.6 pu
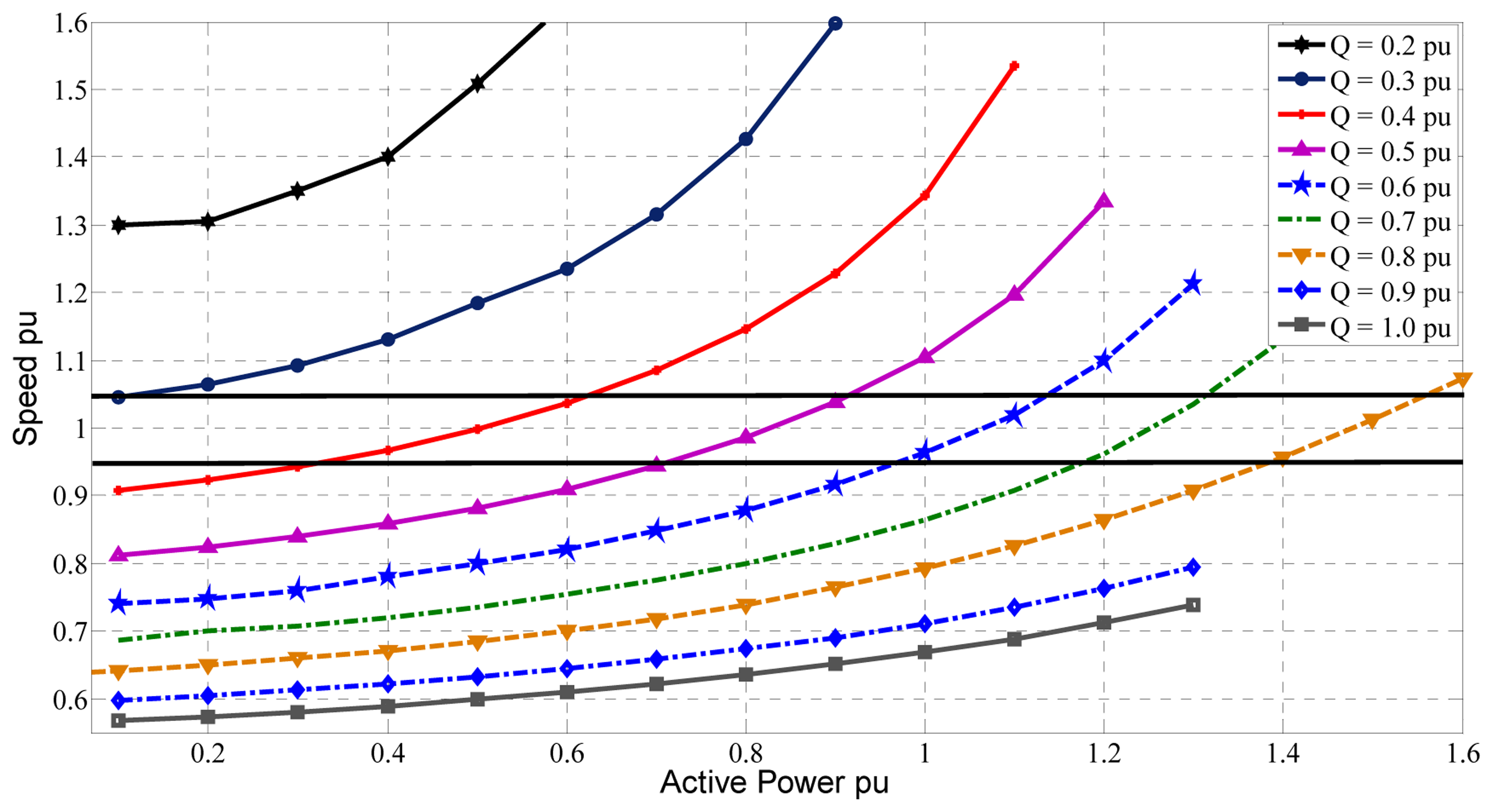
Similarly, variation of the machine speed (frequency of the generated voltage) with the local load power at different excitation capacitance is shown in Figure 7. It is clear that for a fixed excitation capacitance, the machine speed (frequency) increases with the increase of local load power. If the machine is lightly loaded and the excitation capacitance is too high, its speed drops and the machine may stall. This would trigger the under-speed protection. As noticed in Figure 7, when the excitation capacitance is low (less than approximately 30% of the machine rating), the machine speed will always be above the rated value (1 pu) irrespective of the value of the active load. If the machine is islanded while overloaded, the machine speed will abruptly increases and may trigger the over-speed protection. Also, examining the curves shown in Figure 7 (of local load power for various excitation capacitance within the standard speed limits), show that it is possible to keep the speed (and hence the frequency of generated voltage) within acceptable limits for a wide range of load variations if the excitation is controlled in the range 0.3–0.6 pu
Optimum Operating Point
The operating point of the IG when it is connected to the grid is not affected by the local load and the excitation capacitance. Any difference in the active or reactive power between local generation and demand will be balanced by the grid. However, when the IG is islanded or disconnected/reconnected from/to the grid, the machine performance is largely determined by the local active/reactive load. Based on the above analysis, the following section attempts to define the optimum matching of active/reactive load for the IG to enable a stable operation.
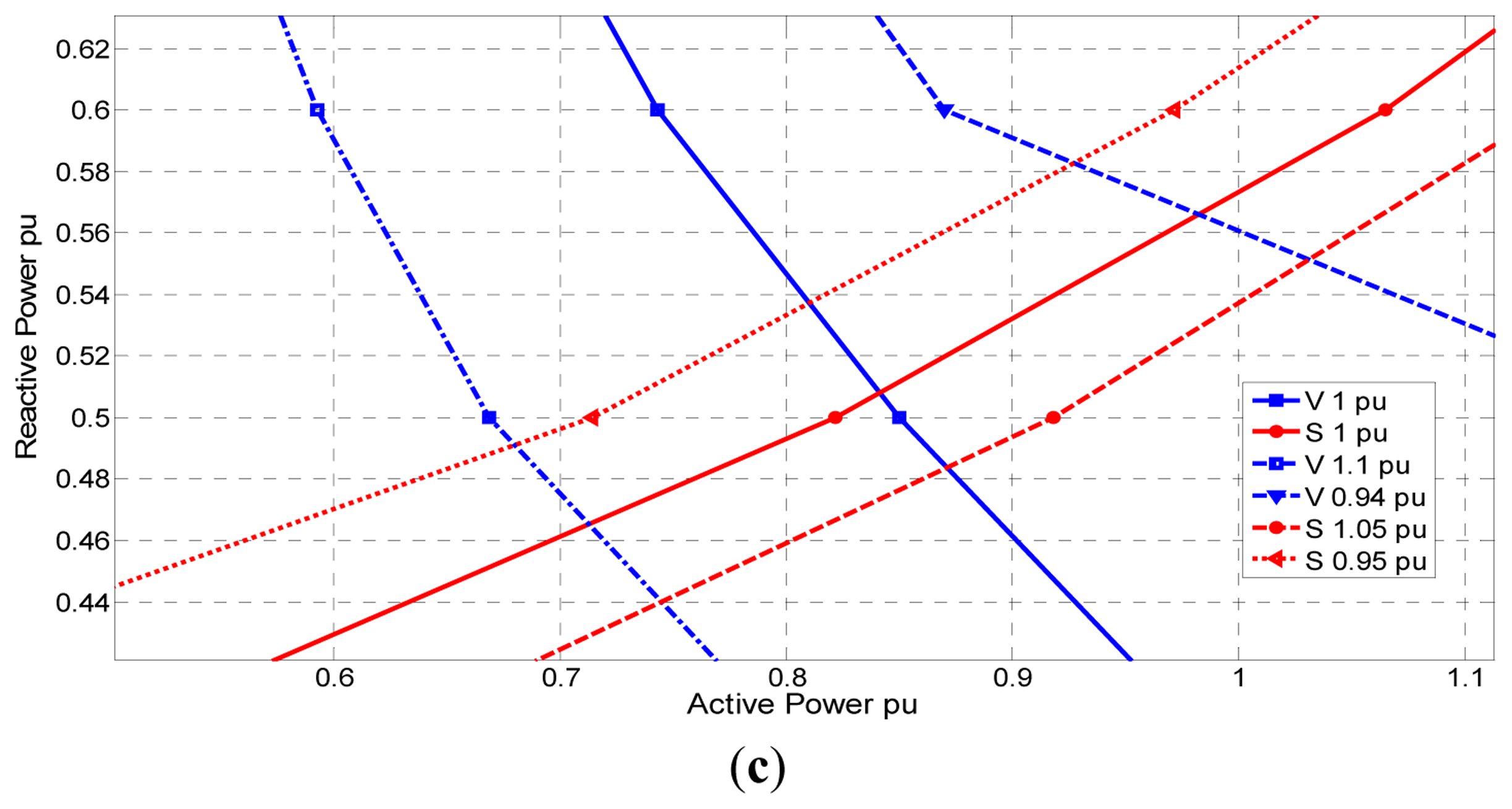
The operating points of the IG to produce terminal voltage magnitude and frequency (as defined in Figures 6 and 7, respectively) within the acceptable standard, are redrawn in Figure 8a. It is clear from this figure that there is only one operating point at which the IG will run at optimal values for both voltage and speed (frequency). This point is the intersection between the two curves defined as 1 pu voltage and 1 pu speed. The operating point represented by 0.8473 pu for local load active power and 0.5081 pu for local load reactive power (excitation capacitance) is the optimum active/reactive load for the induction generator to operate at. Figure 8b shows the feasible operating area for the IG machine when the terminal voltage is limited within the boundary of the standards (+10%, −6%) and the machine speed is limited to ±1%. It is clear that the IG machine can operate satisfactorily if the local active load is controlled between 0.71 pu and 0.99 pu and the reactive power excitation is regulated between 0.46 pu and 0.57 pu If the speed limit is relaxed to ±5% (for example, in case of a grid fault or emergency), the feasible operating area increases significantly, as shown in Figure 8c.
4. System Simulation
The purpose of the simulation conducted in this section is to verify the proposed concept of the optimum local active/reactive power control of the IG. This is to enhance the dynamic operation of the IG during disconnection/reconnection from/to the grid as well as during operation in islanding mode. The system shown in Figure 5 was used in the simulation. The impacts of different load combinations on the optimum operating point during islanding and reconnecting the IG to the grid are considered. To simplify the analysis presented in the following sections, the wind speed is assumed to be constant. However, as the controller can be designed to have a fast time response (faster than the wind speed variation), it will respond equally well for variable wind speed, as shown below.
4.1. Islanding of IG from the Grid
4.1.1. Open Loop Investigation
Scenario 1: The IG is disconnected without local active/reactive load. In this case the machine would not be able to continue its operation in this islanding mode; once it loses its local active and reactive loads and the support from the grid, the protection scheme is triggered to switch it off.
Scenario 2: As shown in Section 3, the IG needs capacitive support of at least one third of its rating to build up the nominal terminal voltage. Therefore, in this scenario, the IG is disconnected from the grid with a terminal capacitor equal to 40% of the machine rating. The presence of the reactive source causes self-excitation and consequently the generator terminal voltage builds up to a very high level (with the absence of appropriate local active load) which may trigger the protection circuit to switch the machine off.
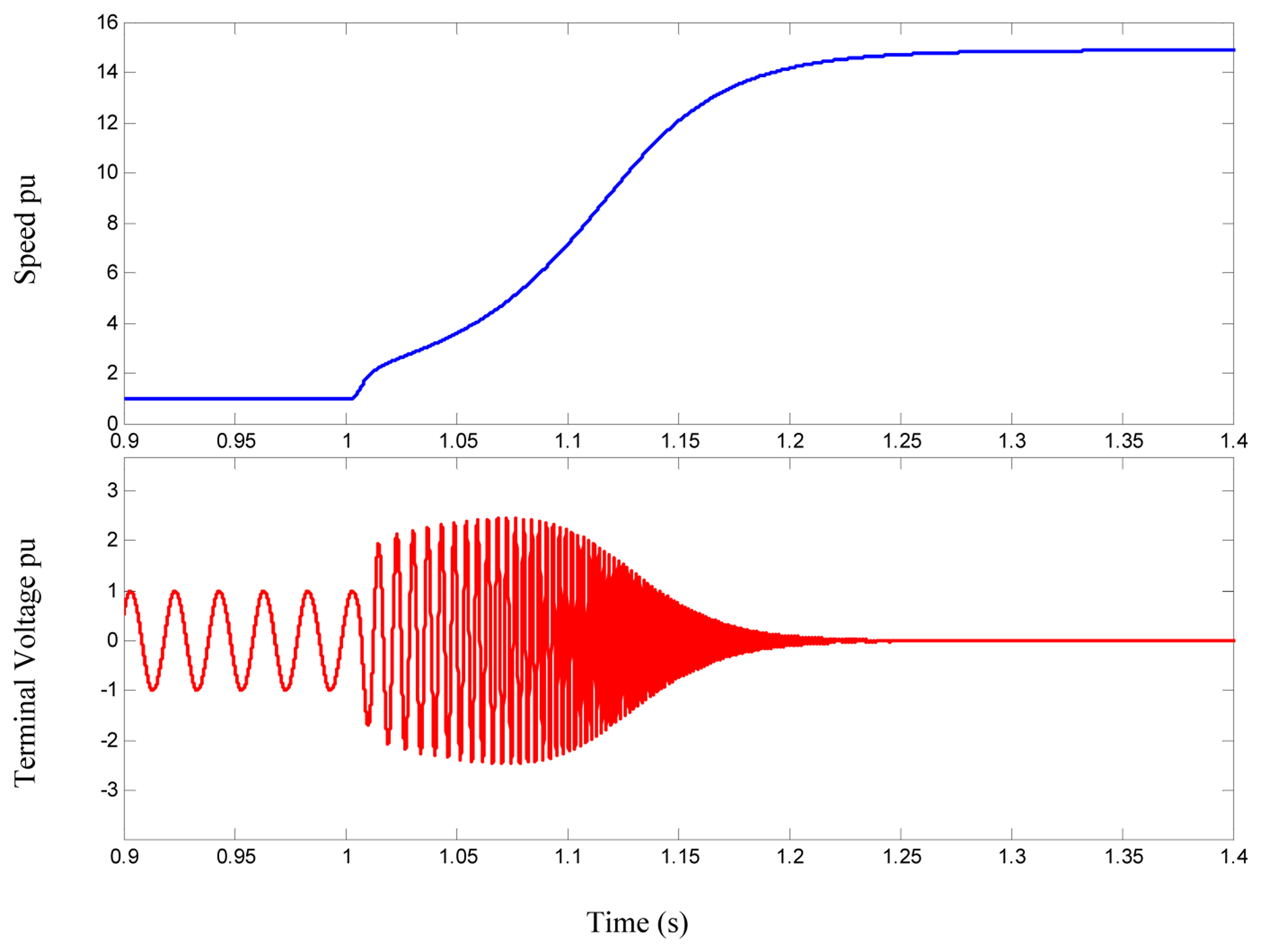
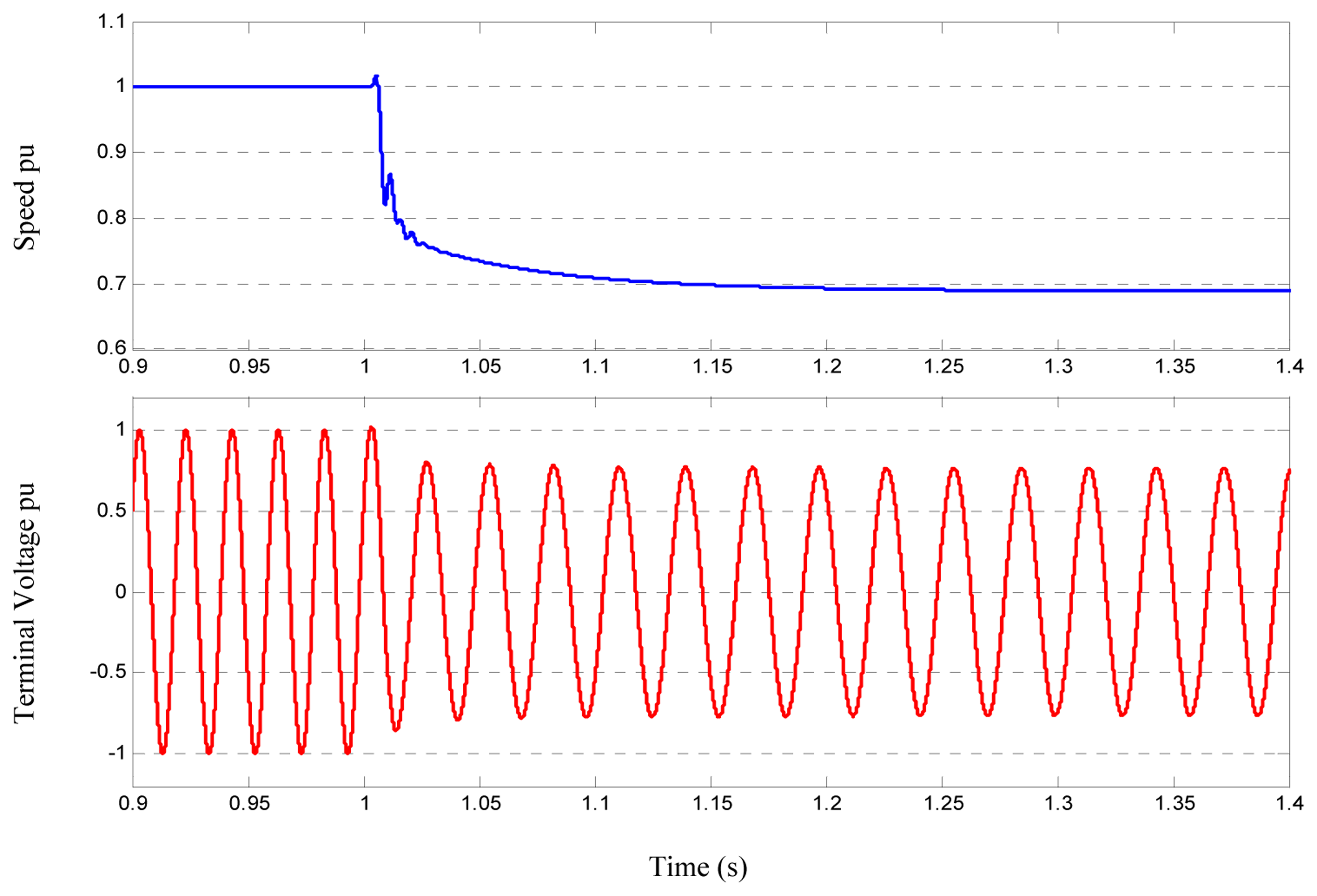
Scenario 3: In this case, the IG is disconnected from the grid with a local active load equal to 40% of the machine rating and no local excitation (capacitor). The absence of the excitation reactive power causes the machine terminal voltage to collapse. As shown in Figure 9, the machine voltage initially increases, but due to lack of local excitation, it is unable to maintain the terminal voltage. Also, the speed increases dangerously high.
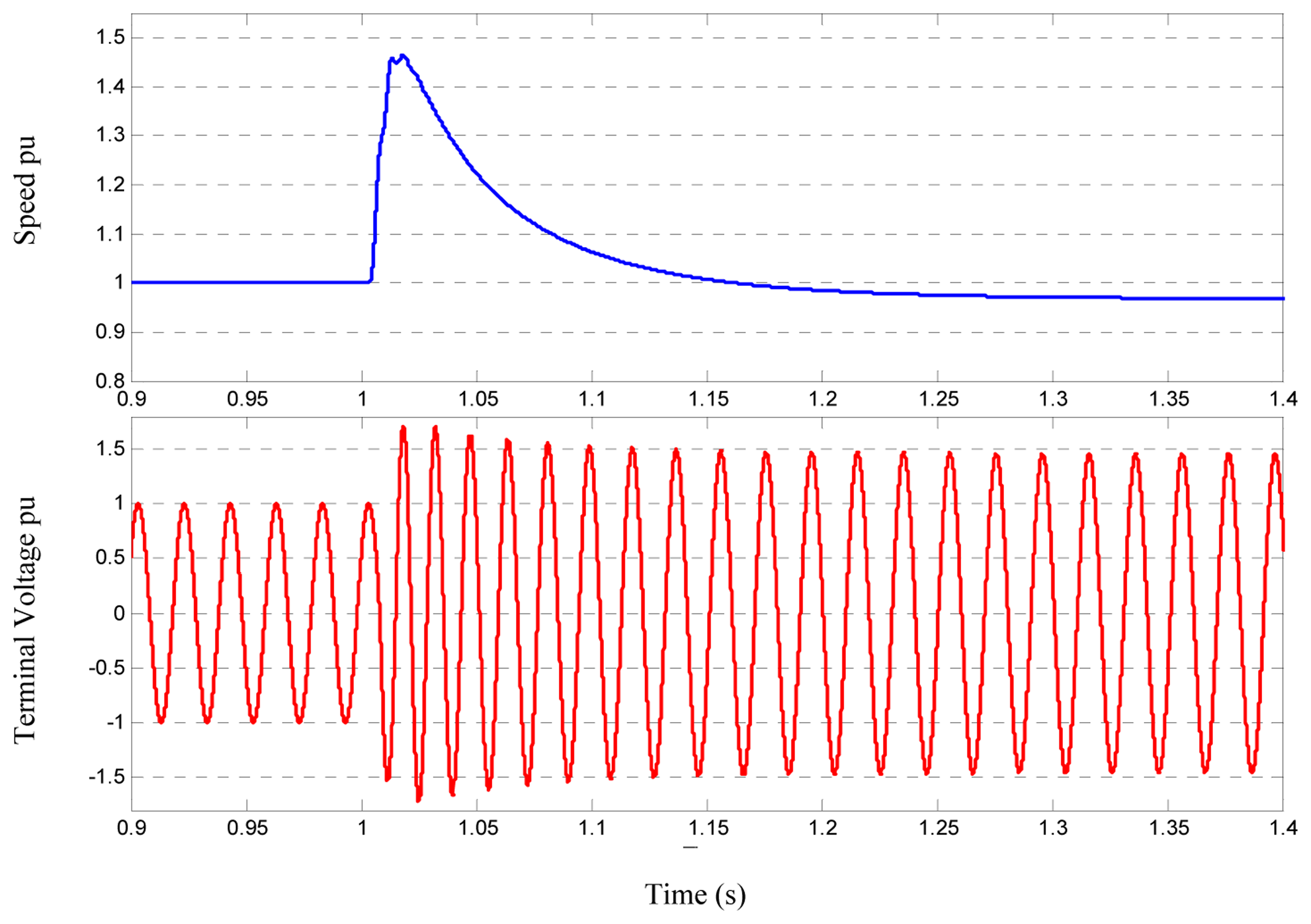
Scenario 4: In this case, the machine is disconnected from the grid with active load equal to 40% and capacitive excitation of 40% of the machine rating. As shown in Figure 10, the machine's terminal voltage rises to a level higher than the nominal grid voltage and the speed (and frequency) decreases.
Scenario 5: in this case, the IG is disconnected from the grid with active load and reactive load each equals to the machine rating. As the total load exceeds the machine rating, the terminal voltage and the machine speed decrease, as shown in Figure 11.
Scenario 6: The IG local load is set to the optimum active and reactive values defined in Section 3: 0.8473 pu active load and 0.5081 pu reactive load. The machine is disconnected from the grid at 1 sc. and continues to run and supply its local load. As shown in Figure 12, the terminal voltage and the machine speed are constant with an error of only 0.02% following to the islanding event. Therefore, islanding the IG will be safe only if the local load is kept constant within the optimum range.
4.1.2. Closed Loop Investigation
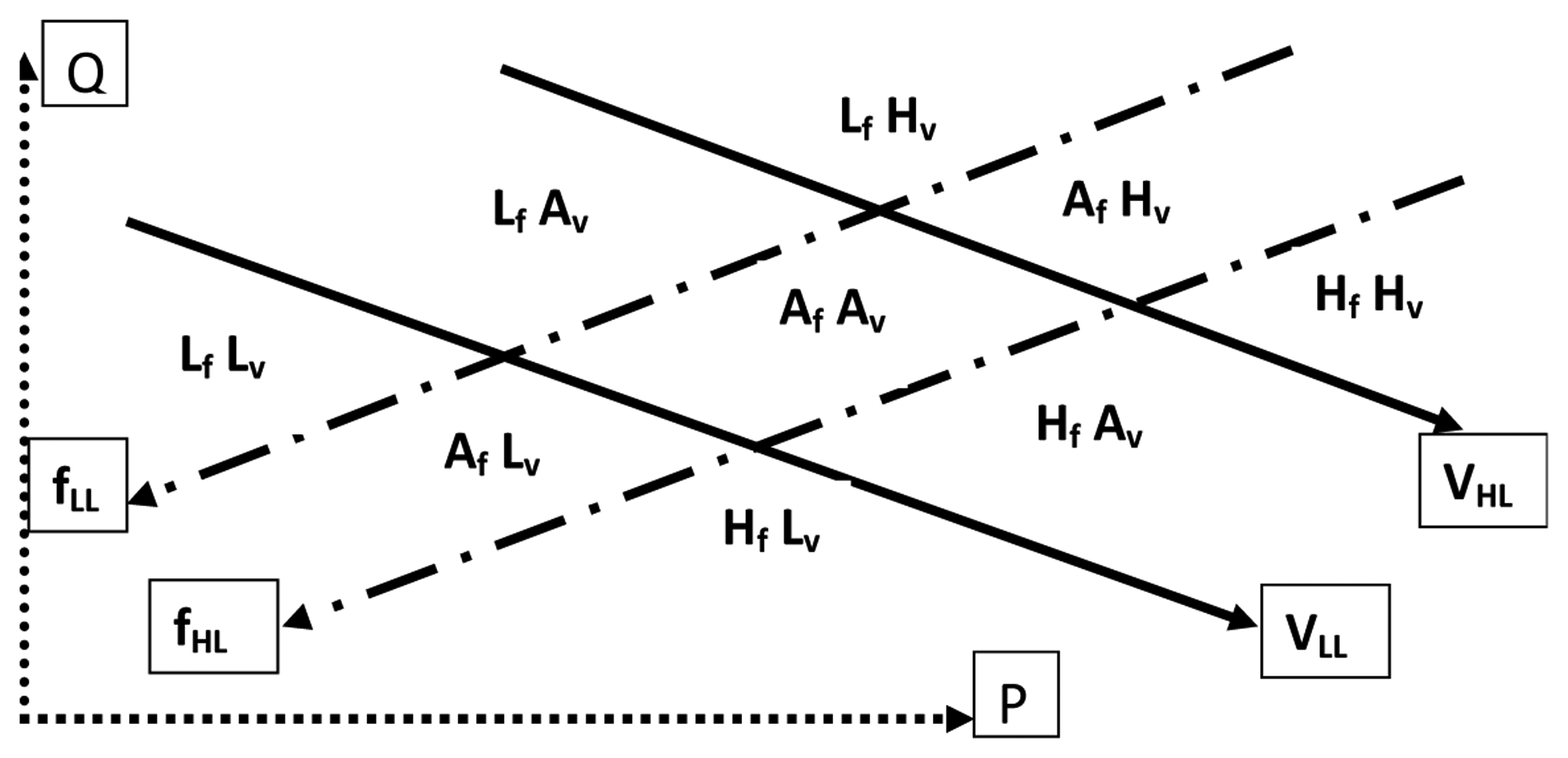
Based on the feasible operating area shown in Figure 8, a closed loop controller was developed in order to regulate the operation of the IG at different operating conditions. First, the operating points outside the accepted operating area and the corresponding control action are defined. As shown in Figure 13, eight regions surrounding the feasible (desirable) operating area are defined and clearly marked according to the corresponding voltage magnitude and machine speed (frequency), this defined by the low voltage and frequency limits VLL and fLL and the corresponding high limits VHL and fHL. The control action to be taken in each sub-region is defined in Table 1. For instance, in the sub-region defined by high voltage and high frequency (Hf and Hv), the local active power load need to be reduced and the excitation reactive power should be increased.
For the purpose of illustration, a conventional PI controller has been used, as shown in Figure 14, to control the local active load connected to the IG when it is islanded under different loading conditions. The controller is designed to monitor the machine's terminal voltage and frequency and control these by using a PWM control of a dummy local load. In a real system, local domestic loads (including Electric Vehicles chargers) may be controlled through demand side management. Reactive power control would be an added resource and this is achieved via thyristor-switched-capacitors as shown in Figure 14.
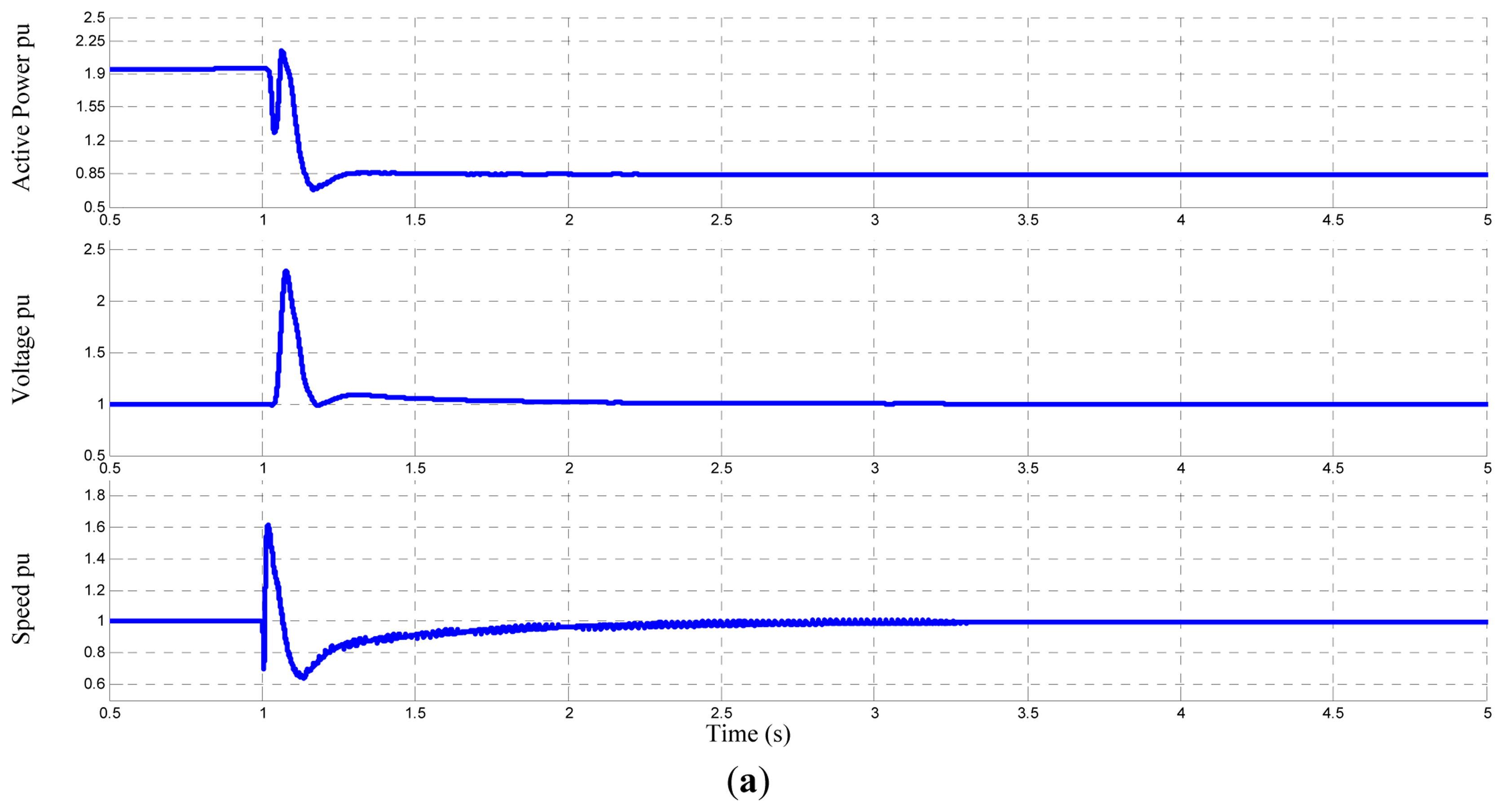
Research published recently describes the use of domestic loads to provide primary frequency response to the UK grid [21], where about 45% of the domestic loads can be locally controlled without disturbing the household life style. Similarly, these loads may be used to control the operation of the IG when operating in islanded mode. As shown in Figure 15a, the IG is islanded while the local active load is about double the machine rating, the controller managed to change the local load in order to maintain the voltage and speed at the predetermined values. Figure 15b, shows the controller performance when the machine local load was initially less than the IG rating, it is very clear that a dummy load needs to be available and controlled in order to maintain the voltage and speed (frequency) at the desired values.
With wider use of SEIG in small and medium wind generation, it is important to investigate the impacts of wind fluctuation on the controller performance and this is presented in Figure 15c, where the IG is islanded from the grid at time 3 s, then the wind speed is changed at slow rate of 2 m/s at time 5 s from 8 m/s to 11 m/s. It is clear from the system response that the algorithm is robust enough to keep the local active power and terminal voltage within the operating region.
4.2. Reconnection of IG to the Grid
Here two cases are studied to evaluate the impact of reconnecting the IG to the grid on machine behaviour.
Scenario 1: In this case, the IG was running in isolation from the grid with 0.5 pu local active load and 0.5 pu reactive excitation capacitance.
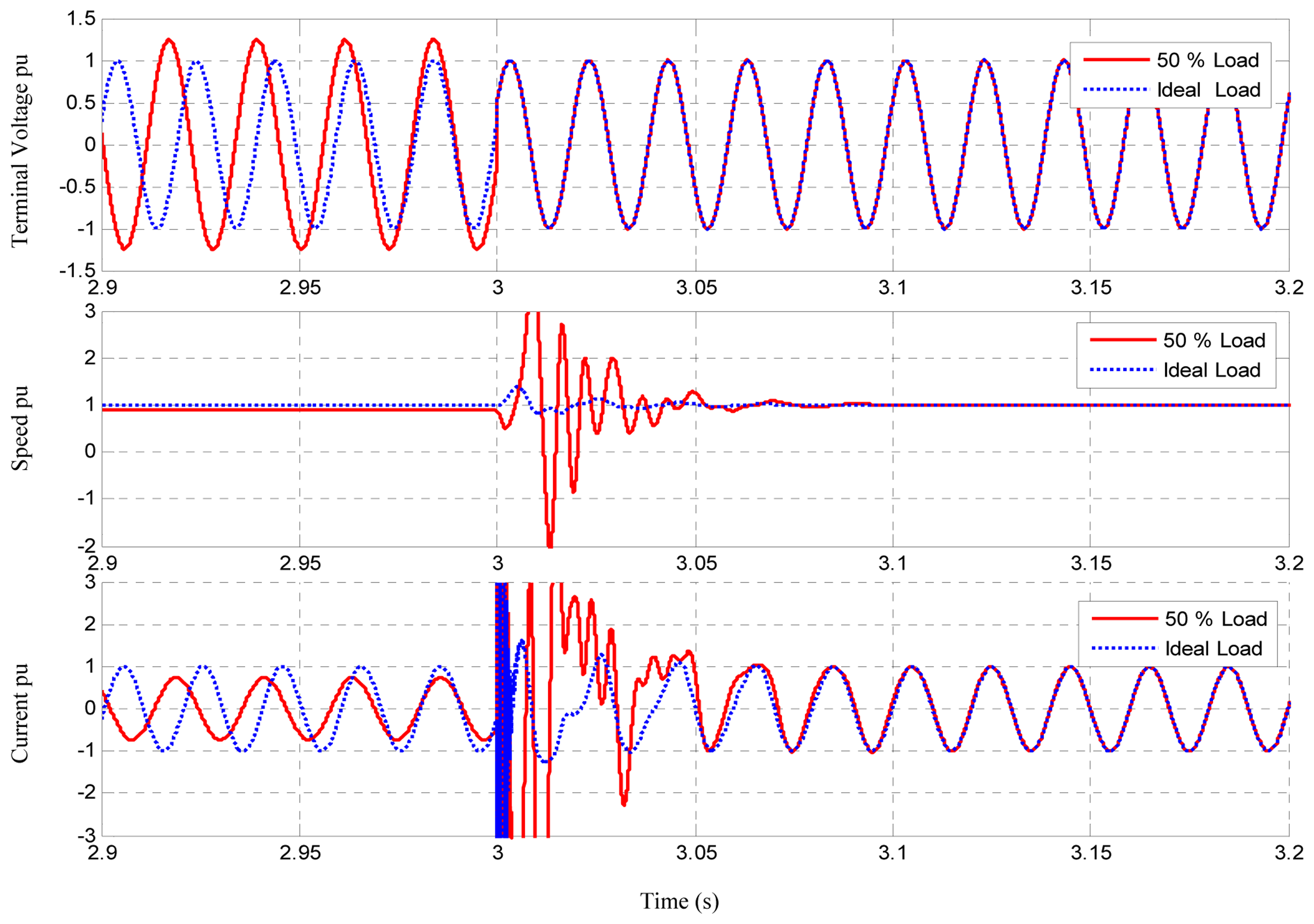
Scenario 2: In this case, the IG was running according to the optimal combination of active and reactive load as described in Section 3. The results of these two cases are shown in Figure 16. The top part of the figure shows the machine terminal voltage for both cases before and after reconnection to the grid. It is obvious that there is no risk of over-voltage during both scenarios.
The middle part of the figure shows the machine speed for both cases before and after the reconnection. It is clear that the response following the reconnection is better for the case with optimum loading and excitation. The results also show that it is better if the machine is reconnected to the grid at the appropriate point on the voltage waveform.
The bottom part of the figure shows the machine current in both cases. It is clear that although the machine working better under optimum load, there is an inrush current in both cases which can be cleared using a soft starter [17]. Inrush current problem and mitigation are well covered in the literature and therefore are not considered in this paper.
5. Conclusions
This paper presents an analysis of the dynamic performance of self excited induction generators during disconnection and reconnection to the grid as well as when operating in stand-alone mode (islanding operation). The paper also presents the effects of active and reactive local demand on the voltage magnitude and frequency of a self-excited induction generator, when it is islanded and reconnected to the grid. The optimum setting of both reactive and active loading is determined, implemented and verified. It is shown that the SEIG can work safely according to the distribution network engineering recommendations if the local active (required for load balancing) and reactive load (required for self excitation of the generator) are set to the optimum values.
Conflicts of Interest
The authors declare no conflict of interest.
References
- International Energy Agency. Available online: http://www.iea.org (accessed on 12 June 2012).
- Starbac, G.; Jenkins, N.; Hird, M.; Djapic, P.; Nicholson, G. Integration of Operation of Embedded Generation and Distribution Networks; Technical Report; Project URN 02/1145; Department of Trade and Industry: London, UK, 2002. [Google Scholar]
- Electricity Network Association. ENA Engineering Recommendations; G59/1; Electricity Network Association: London, UK, 1991. [Google Scholar]
- Econnect Ltd. Assessment of Islanded Operation of Distribution Networks and Measures for Protection; ETSU Project URN 01/1119; Department of Trade and Industry: London, UK, 2001. [Google Scholar]
- Murthy, S.S.; Malik, O.P.; Tandon, A.K. Analysis of self-excited induction generators. IEE Proc. C Gener. Transm. Distrib. 1982, 129, 260–265. [Google Scholar]
- Grantham, C.; Sutanto, D.; Mismail, B. Steady state and transient analysis of self-excited induction generators. IEE Proc. B Electr. Power Appl. 1989, 136, 61–68. [Google Scholar]
- Arrillaga, J.; Watson, D.B. Static power conversion from self-excited induction generators. Proc. Inst. Electr. Eng. 1978, 125, 743–746. [Google Scholar]
- Bim, E.; Szajner, J.; Burian, Y. Voltage compensation of an induction generator with long-shunt connection. IEEE Trans. Energy Convers. 1989, 4, 526–530. [Google Scholar]
- Shrindhar, L.; Singh, B.; Jha, C.S.; Singh, B.; Murthy, S.S. Selection of capacitors for the self regulated short shunt self-excited induction generator. IEEE Trans. Energy Convers. 1995, 10, 10–17. [Google Scholar]
- Tiwari, A.K.; Murthy, S.S.; Singh, B.P.; Shrindhar, L. Design based performance evaluation of two-winding capacitor self-excited single-phase induction generator. Electr. Power Syst. Res. 2003, 10, 89–97. [Google Scholar]
- Al-saffar, M.A.; Nho, E.C.; Lipo, T.A. Controlled Shunt Capacitors Self-Excited Induction Generator. Proceedings of the IEEE Industry Applications Conference, St. Louis, MO, USA, 12–15 October 1998; Volume 2, pp. 1486–1490.
- Wekhande, S.; Agarwal, V. A new variable speed constant voltage controller for self-excited induction generator. Electr. Power Syst. Res. 2001, 59, 157–164. [Google Scholar]
- Ekanayake, J.B. Induction generators for small hydro schemes. Power Eng. J. 2002, 16, 61–67. [Google Scholar]
- Bonert, R.; Rajakaruna, S. Self-excited induction generator with excellent voltage and frequency control. IEE Proc. Gen. Trans. Dist. 1998, 145, 33–39. [Google Scholar]
- Stein, W.M.; Manwell, J.F.; McGowan, J.G. A power electronics based power shedding control for wind diesel systems. Int. J. Ambient Energy 1992, 13, 65–73. [Google Scholar]
- Tamura, J.; Nakamichi, R.; Nakazawa, C.; Chihara, I. Analysis of an Isolated Self-Excited Induction Generator. Proceedings of the International Conference on Electrical Machines, (ICEM), Espoo, Finland, 28–30 August 2000; pp. 519–522.
- Ramachandran, J.; Putrus, G.A. Dynamic Behaviour of Single-Phase Induction Generator during Disconnection and Reconnection to the Grid. Proceedings of the Power Systems Computation Conference (PSCC), Glasgow, UK, 14–18 July 2008.
- Dahraie, M.V.; Najafi, H.R.; Ebadian, M. Analytical investigation of the effect of wind farm equipped with SCIG on voltage stability. Proceedings of the 2012 Second Iranian Conference on Renewable Energy and Distributed Generation, Tehran, Iran, 6–8 March 2012; pp. 121–126.
- Srivastava, A.K.; Kumar, A.A.; Schulz, N.N. Impact of distributed generations with energy storage devices on the electric grid. IEEE Syst. J. 2010, 6, 110–117. [Google Scholar]
- Abdelkader, S. Voltage Stability Assessment for Systems with Large Wind Power Generation. Proceedings of the 44th International Universities Power Engineering Conference (UPEC), Glasgow, UK, 1–4 September 2009; pp. 1–5.
- Samarakoon, K.; Ekanayake, J.; Jenkins, N. Investigation of domestic load control to provide primary frequency response using smart meters. IEEE Trans. Smart Grid 2012, 3, 282–292. [Google Scholar]





| Frequency (f) | Voltage (V) | Reactive power (Q) | Active power (P) |
|---|---|---|---|
| L | L | DEC | INC |
| L | A | DEC | NA |
| L | H | DEC | DEC |
| A | L | NA | INC |
| A | A | NA | NA |
| A | H | NA | DEC |
| H | L | INC | INC |
| H | A | INC | NA |
| H | H | INC | DEC |
L: low, H: high, A: accepted, INC: increase, DEC: decrease, NA: no action.
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Farrag, M.E.A.; Putrus, G.A. Analysis of the Dynamic Performance of Self-Excited Induction Generators Employed in Renewable Energy Generation. Energies 2014, 7, 278-294. https://doi.org/10.3390/en7010278
Farrag MEA, Putrus GA. Analysis of the Dynamic Performance of Self-Excited Induction Generators Employed in Renewable Energy Generation. Energies. 2014; 7(1):278-294. https://doi.org/10.3390/en7010278
Chicago/Turabian StyleFarrag, Mohamed E. A., and Ghanim A. Putrus. 2014. "Analysis of the Dynamic Performance of Self-Excited Induction Generators Employed in Renewable Energy Generation" Energies 7, no. 1: 278-294. https://doi.org/10.3390/en7010278





