1. Introduction
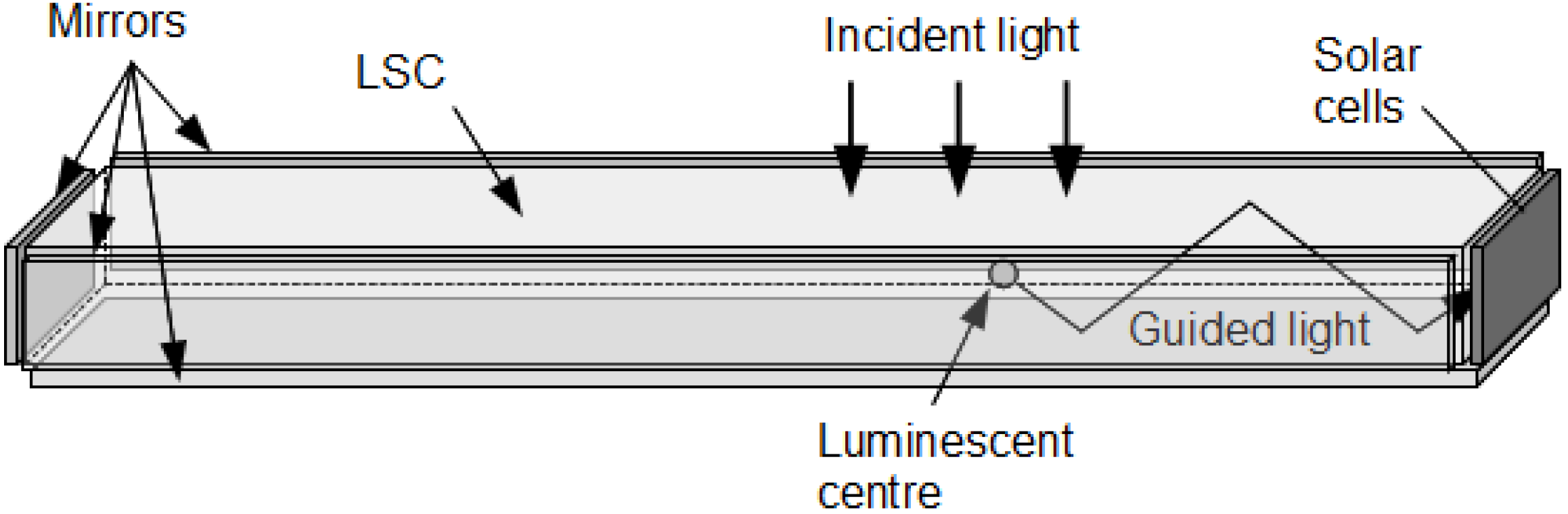
The luminescent solar concentrator (LSC) is a non-imaging optical device that can concentrate sunlight onto a small area of solar cells to generate electricity. In this way, a large area of solar cells required in a standard flat-plate PV panel can be replaced by an inexpensive concentrator, hence reducing the cost of the module and thus the cost per unit electricity generated [
1].
The LSC typically consists of a polymer plate doped with a luminescent material, with solar cells attached to the plate edges.
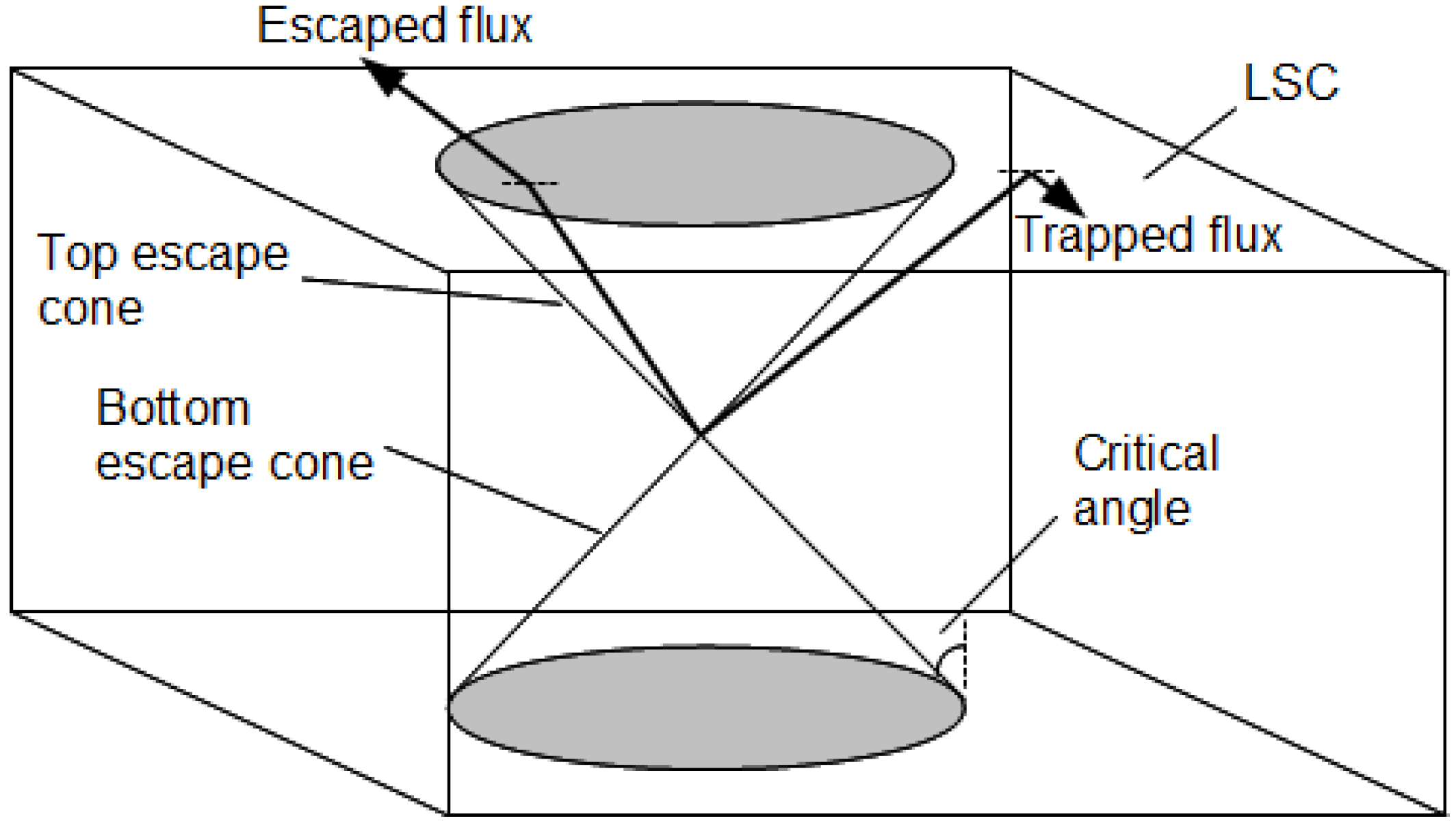
Figure 1 shows a diagram of the simplest type of luminescent solar concentrator. Higher efficiency can be achieved by matching the peak quantum efficiency of the solar cells to the peak emission of the concentrator. Several types of luminescent materials can be used in LSCs, such as laser dyes or organic dyes, semiconductor quantum dots [
2], rare earth materials [
3], and semiconducting polymers [
4]. To further improve the efficiency of LSCs, materials such as photonic layers [
5] and liquid crystals [
6] have also been used to reduce the losses.
Figure 1.
Luminescent solar concentrator.
Figure 1.
Luminescent solar concentrator.
LSCs have several advantages over conventional geometric solar concentrators. LSCs can accept both direct and diffuse sunlight and indeed it is believed that LSCs can perform better under diffuse light than under direct light, so a sunlight tracking system is not necessary. The extended surface area of LSCs enables effective heat dissipation, hence avoiding the need for any cooling systems and allowing solar cells coupled at the edges to operate at the optimum temperature. In addition, LSCs can be used as building facades such as roofs, windows, walls or pavements. The electricity generated by LSC systems is consumed directly by electricity customers. Transmission of the solar electricity across electrical distribution systems can be avoided. As a result, power transmission losses can be reduced and technical issues caused by the integration of renewable energy sources with the distribution networks can be avoided [
7,
8,
9].
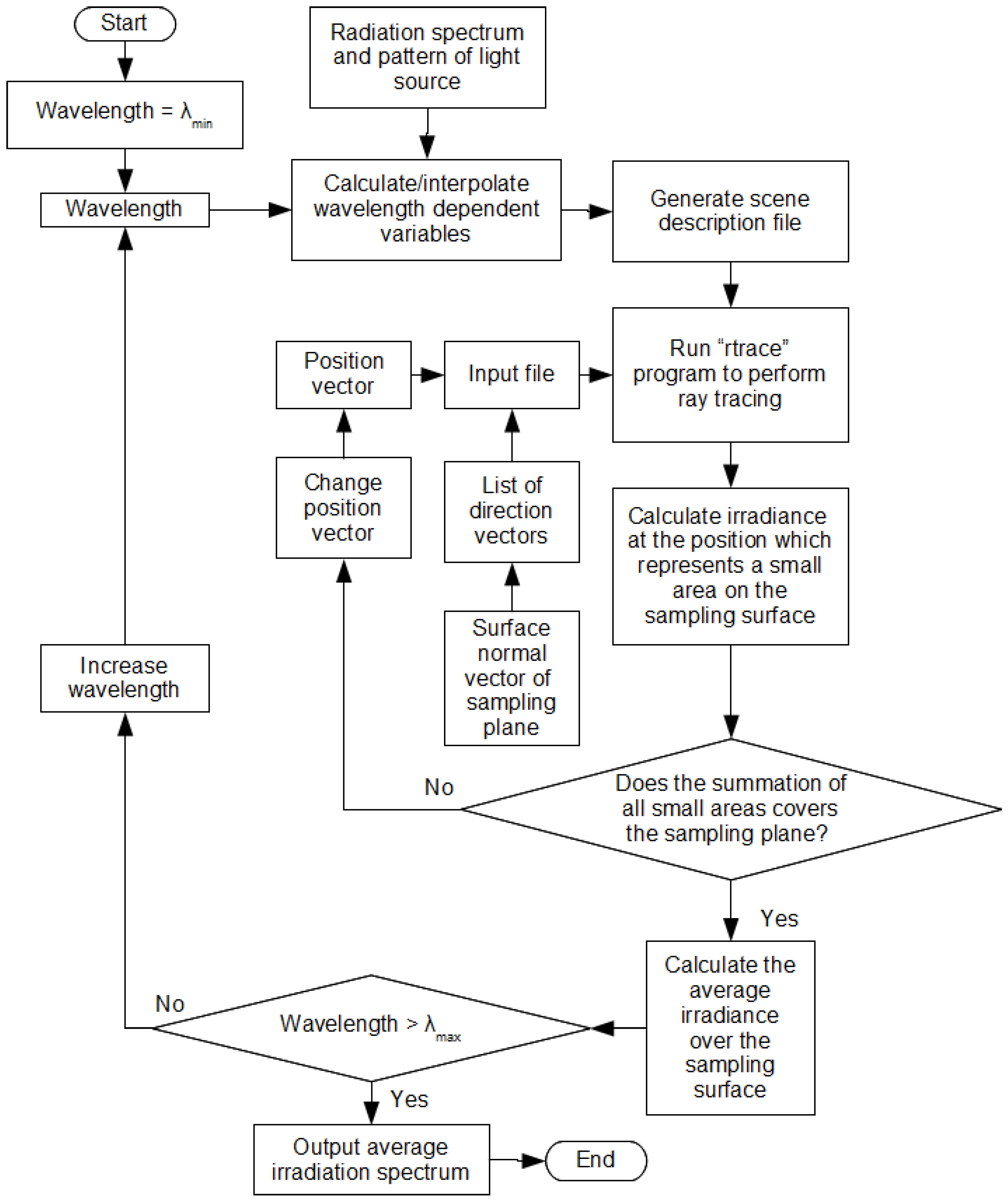
To improve the radiation transfer of LSCs, computer modeling of LSCs becomes very essential as it can be used to determine the optimum design parameters of LSCs. Those parameters are the quantum efficiency of luminescent materials, concentration of luminescent materials, refractive index of the host, red-shift of the luminescent materials, thickness of LSCs, geometries of LSCs, diffuse or direct sunlight and surface contour of LSCs. Computer simulation of LSCs is required to fine-tune each of the parameters in order to achieve the maximum emission at the edge of LSCs.
Currently, there are two approaches of modeling LSCs, namely thermodynamic modeling [
10] and ray-tracing modeling [
11]. Thermodynamic modeling is a detailed balance model which is based on the radiative energy transfer between mesh points in the concentrator, whereas ray-tracing modeling is used to track every incoming photon and determine its fate [
12]. Thermodynamic and tray-tracing models have been used to simulate the performance of LSCs under direct sunlight conditions in order to optimize the performance of LSC with respect to the size of luminescent quantum dots, inclusion of mirrors and multi-layers of the LSC [
10,
11,
12,
13,
14]. The accuracies of thermodynamic and ray-tracing models are about 4% and 11%, respectively.
Both thermodynamic and ray-trace modeling provide useful tools for optimizing the performance of a LSC and predicting the electrical output. Thermodynamic modeling can be easily used to simulate a simple rectangular LSC shape under direct sunlight. However, it is not flexible enough to model various geometries and the surface contours of LSCs under diffuse sunlight. Ray-tracing modeling is able to model various surface geometries of LSCs under direct and diffuse sunlight. However, this modeling requires a substantial amount of input measurement data from a case study. As described in [
13,
14], the ray-tracing modeling requires a collection of emission spectra from a luminescent material at various different excitation wavelengths in addition to the dimension, refractive index and extinction coefficient of LSC, quantum yield of dye, light source spectra and light intensity distribution. Also, the simulation time required by the ray-tracing method is enormous because forward ray-tracing is used to trace a large amount of photons from the source to their final destinations.
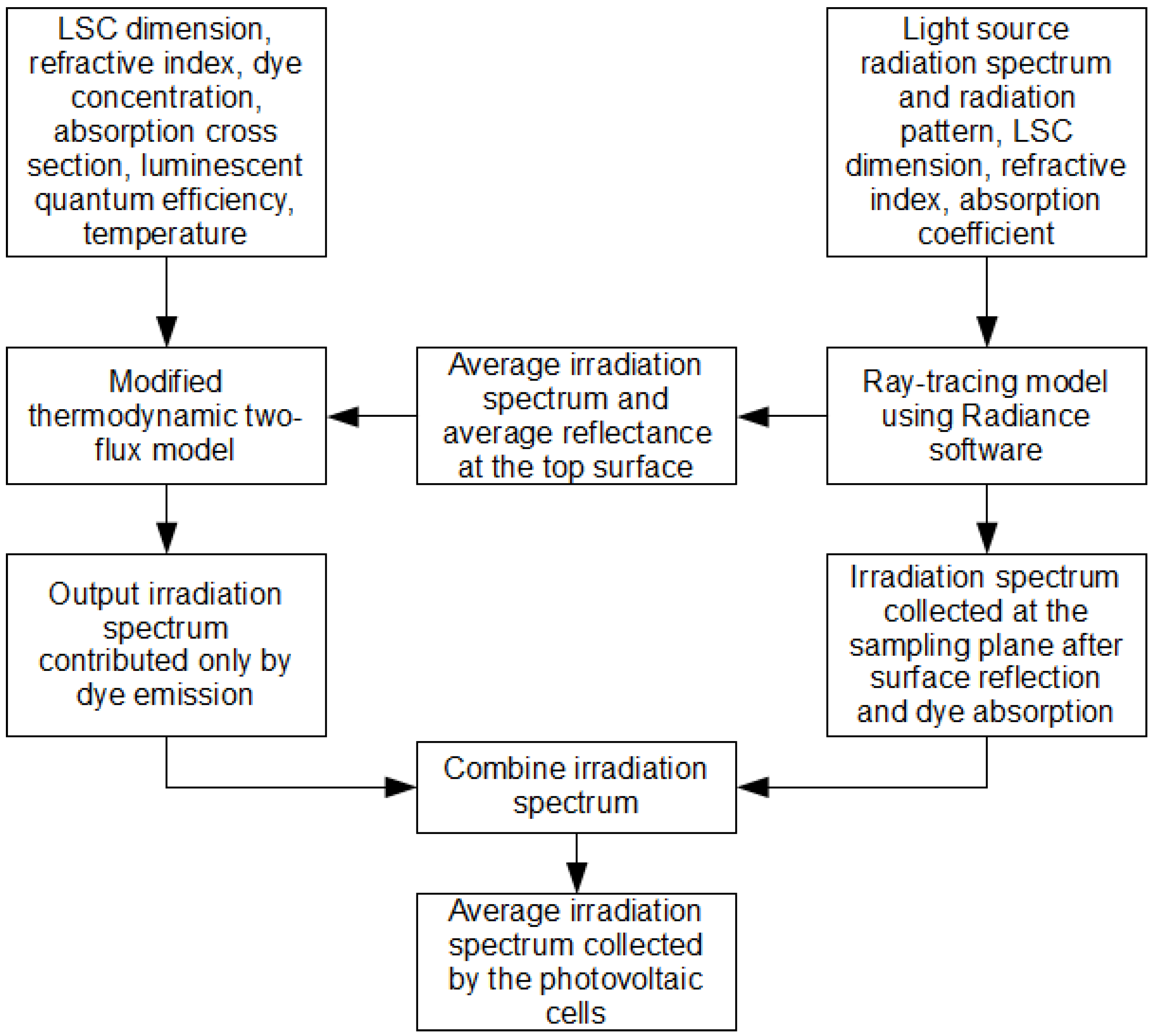
The objective of this research work was to study the performance of a LSC with various orientations under direct and diffuse sunlight conditions. The novelty of this hybrid model is the idea of integrating the thermodynamic model with the backward ray-tracing model. This model is a compromise tool that can off-set the weaknesses of the individual models. Therefore, it could be a fast, effective and powerful tool to simulate the performance of LSCs with various orientations under diffuse and direct sunlight. As a result, the technical and economical viability of using LSCs as building facades can be established.
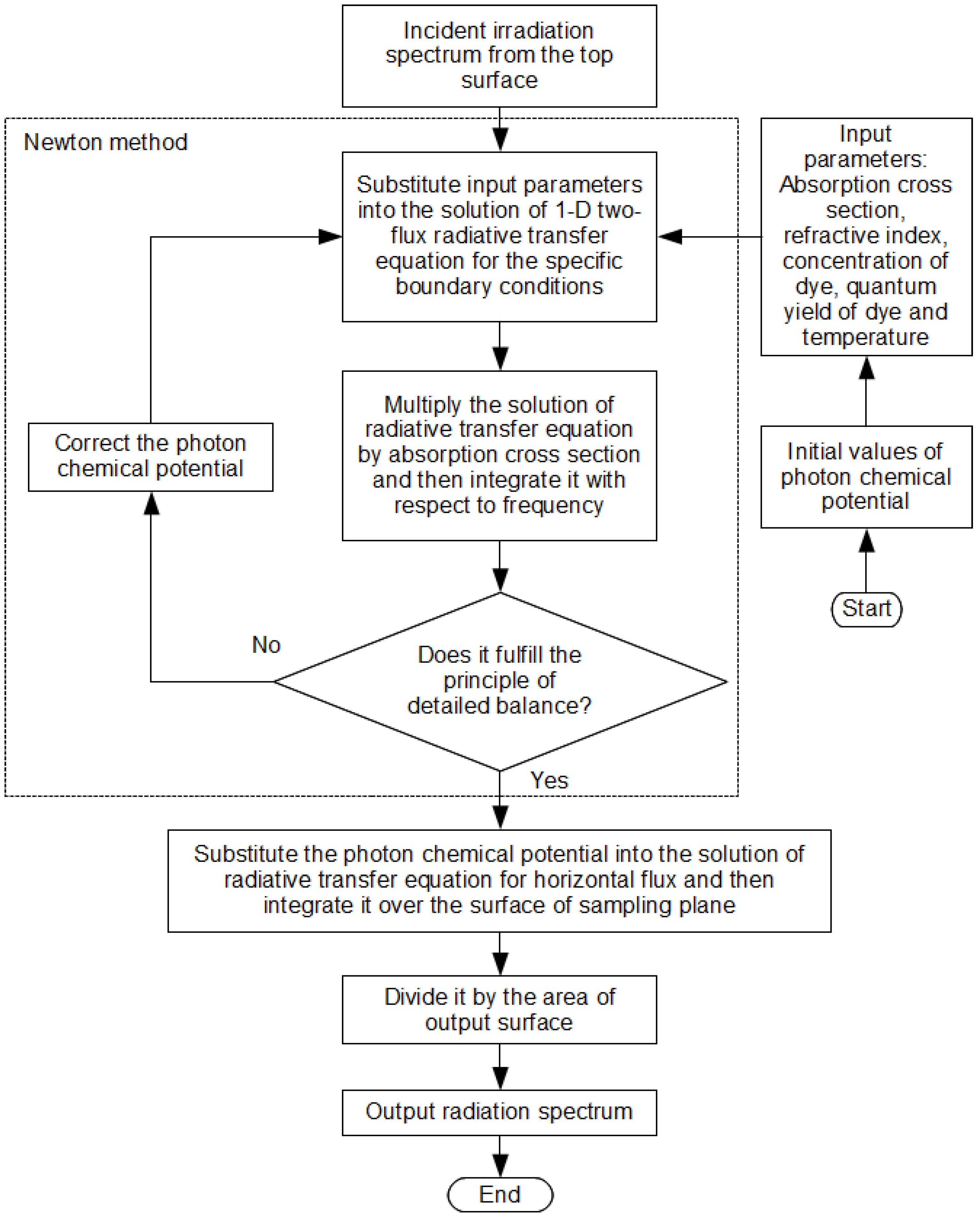
In this hybrid algorithm, thermodynamic modeling is to calculate the luminescence at the edge of LSC due to the embedded luminescent materials. Then ray-tracing modeling is to determine the light intensity collected at the edge of LSC as a result of the unabsorbed portion of the incoming light. This ray-tracing modeling does not consider the emission of the luminescent materials in LSC. Therefore, the input data of the emission spectra at various different excitation wavelengths are not required in this hybrid algorithm. Furthermore, the simulation time required by the ray-tracing modeling is reduced substantially because this hybrid algorithm uses backward ray-tracing that only traces photons arriving at the target. As a result, this hybrid approach has the advantages of simplicity derived from the thermodynamic modeling which requires a minimum data input, and flexibility from the ray-tracing approach where different LSC surface geometries under direct and diffuse sunlight can be studied with reduced simulation effort.
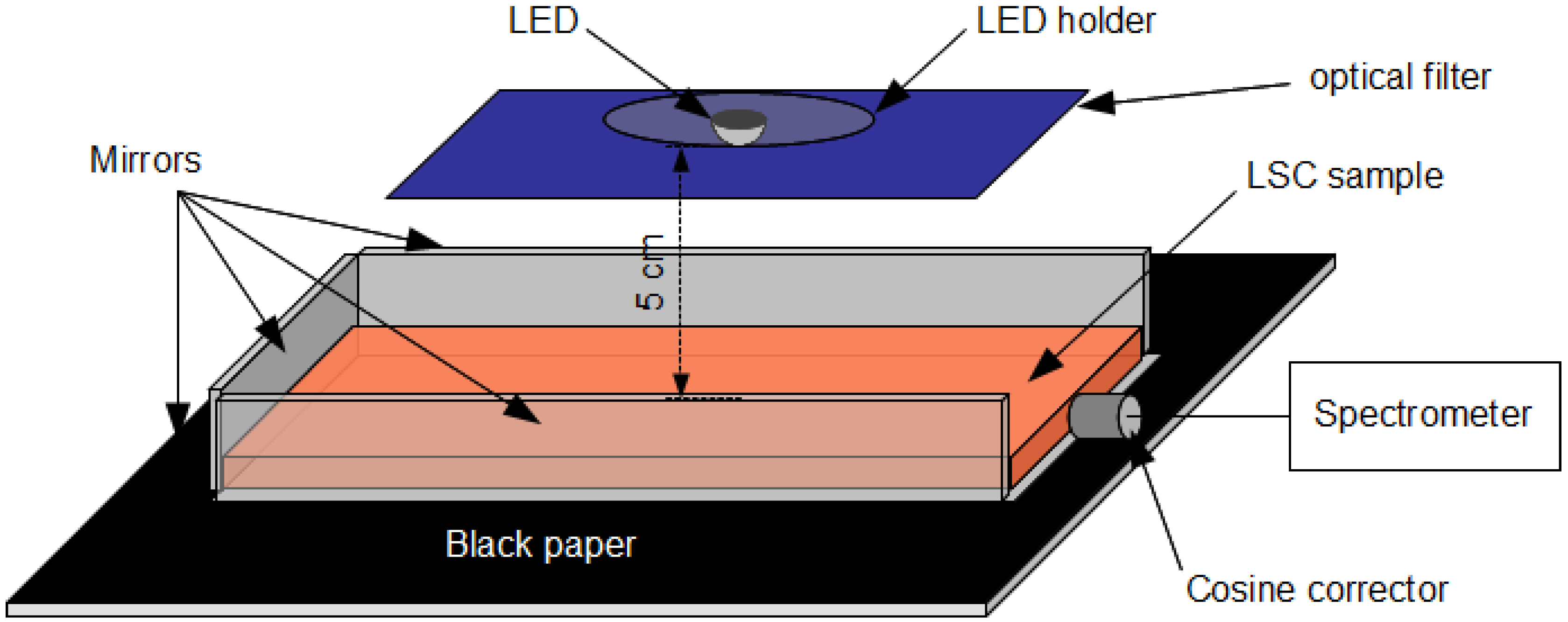
In this article, the details of the hybrid simulation approach are presented. To verify the simulation approach, a LSC with the dimension of 10 cm (length) × 5 cm (width) × 0.5 cm (thick) was constructed using unsaturated polyester as the host matrix and Rhodamine 6G as the organic dye. This LSC was placed under a filtered LED light source. The absorption spectrum of the LSC was measured by a calibrated USB4000 spectrometer. The emission spectra were measured at the edge of the LSC. The simulation model of the LSC was developed using the hybrid algorithm. The simulated emission spectra were then generated and compared with the experimental spectra. The simulated results were in a good agreement with the experimental ones.
4. Simulation of the Experimental Setup
The purpose of the experiment is to verify the solution obtained from the proposed simulation approach. Therefore the program was modified to introduce the effect of cosine corrector and the small air gap between the LSC edge surface and the cosine corrector diffuser surface. The cosine corrector was modeled as a perfect diffuser collecting light from a 180 degree field of view. The simulation input parameters are listed in
Table 1, together with the corresponding measured values.
Table 1.
Simulation input parameters versus the actual measured values.
Table 1.
Simulation input parameters versus the actual measured values.
| Property | Simulation Input Parameter | Measured Value/Spectrum |
|---|
| Dimension | 10 cm × 5 cm × 0.5 cm | 9.8 cm × 4.9 cm × 0.5 cm |
| Refractive index | 1.58 | 1.57 |
| Luminescent quantum efficiency | 0.95 1 | Not measured. |
| Concentration | 3.75 × 10−5 mol/dm3 | 3.75 × 10−5 mol/dm3 |
| Temperature | 25 °C | Not measured |
| Absorption cross section (dye) | Refer to Figure 9 | Refer to Figure 9 |
| Absorption cross section (sample) | Refer to Figure 10 | Refer to Figure 10 |
| Incident light | Refer to Figure 13 | Refer to Figure 13 |
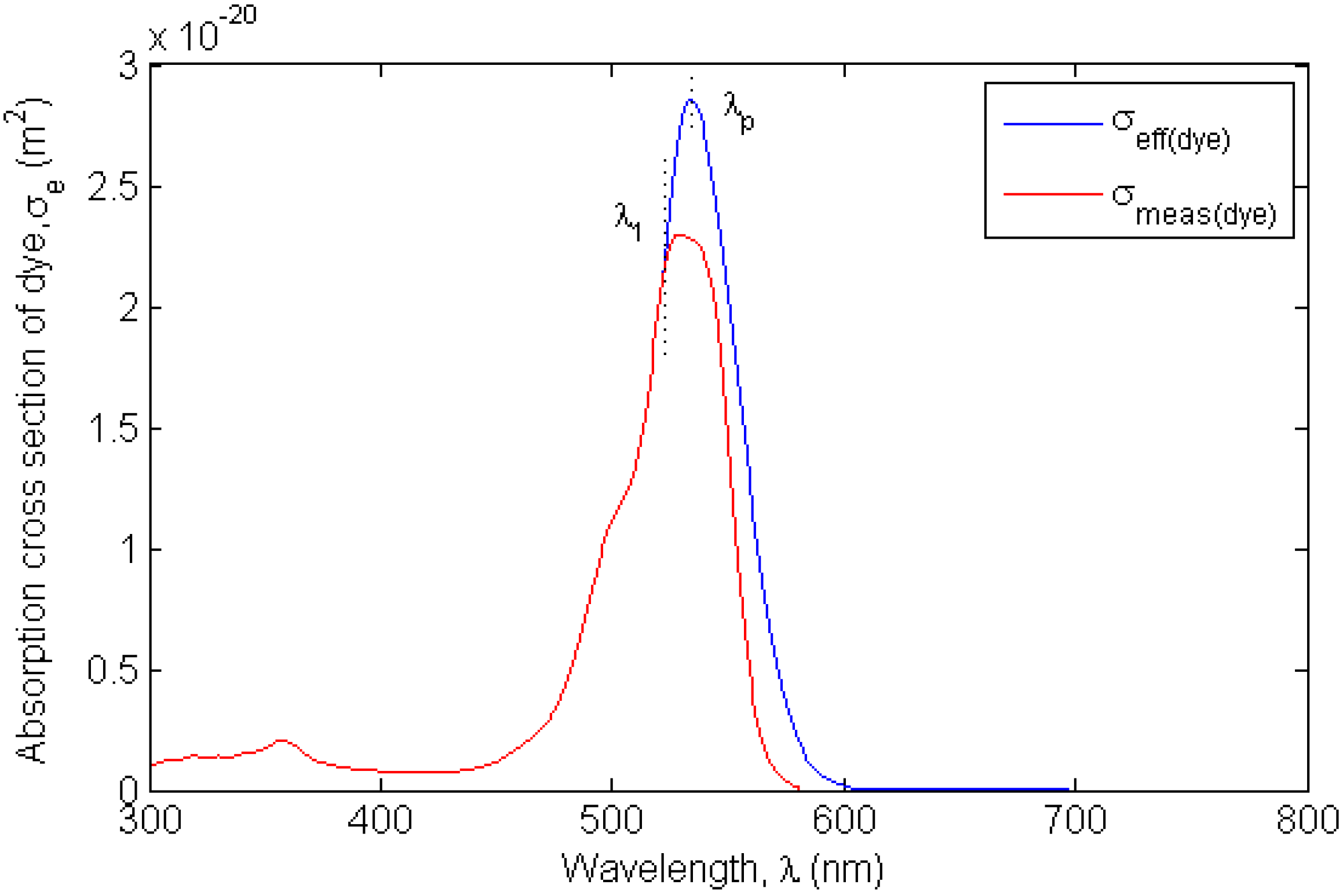
The absorption cross-section of the dye (Rhodamine 6G) was measured from a mixture of UP resin, Rhodamine 6G and MMA in the same proportion as in the hardened LSC sample. The mixture was put inside a 1 cm cuvette, with the mixture of UP resin and MMA as the reference solution. The absorbance was measured using a wavelength-calibrated Ocean Optics USB4000 spectrometer connected to the Ocean Optics CUV-ALL-UV cuvette holder, with the Mikropack HL-2000-HP-FHSA halogen light source connected to the cuvette holder at the opposite direction. The absorbance spectrum was then converted to absorption cross section spectrum, as shown in
Figure 9.
Figure 9.
Dye absorption cross section.
Figure 9.
Dye absorption cross section.
The absorbance of the sample was measured by fixing the solid LSC sample vertically in between two Ocean-Optics-84-UV-25 collimating lens mounted on an optical table. The Mikropack HL-2000-HP-FHSA halogen light source was connected to one of the collimating lens, while another lens was connected to the Ocean Optics USB4000 spectrometer. No reference sample was prepared in this case since there was some difficulty in preparing an ideal well-polished flat plate sample of 5 mm thickness for spectroscopic measurement. Therefore the reflection at the air-to-LSC boundary was ignored in the measurement. The absorbance spectrum was then converted to absorption cross section spectrum, as shown in
Figure 10.
Figure 10.
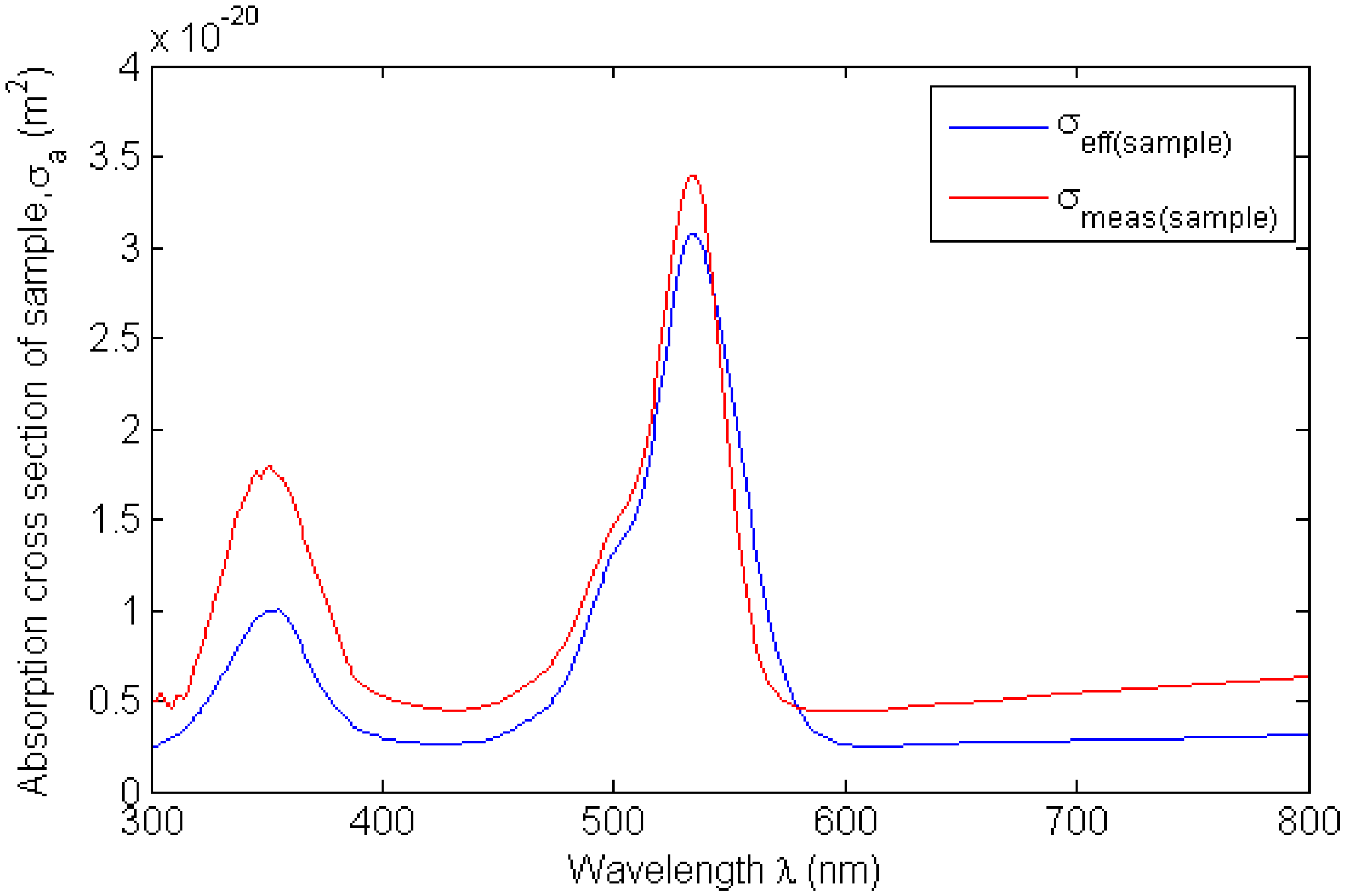
Sample absorption cross section.
Figure 10.
Sample absorption cross section.
The red lines in
Figure 9 and
Figure 10 represent the experimental data, which is not the pure absorption cross sections of the dye and LSC plate because the data contains some unwanted effects such as the reflectance and absorption of the cuvette, reflectance of the LSC surfaces and emission of the dye. As a result, the experimental data could not be used directly as the input data to the simulation model. Attempts were carried out to remove all the distortions from the measurement data by using analytical approach. In these attempts, all the distortions were measured and fed into the analytical equations in the hope that the effective absorption cross sections of the dyes and LSC plate could be determined. However, it was found that none of the analytical equations took into account all the unwanted effects correctly. In fact, the analytical equations became relatively complicated in the situation where the top and bottom surfaces of LSC were not perfectly uniform and flat. Therefore, it was decided to use empirical approach to determine the effective absorption cross sections of the dye and LSC plate.
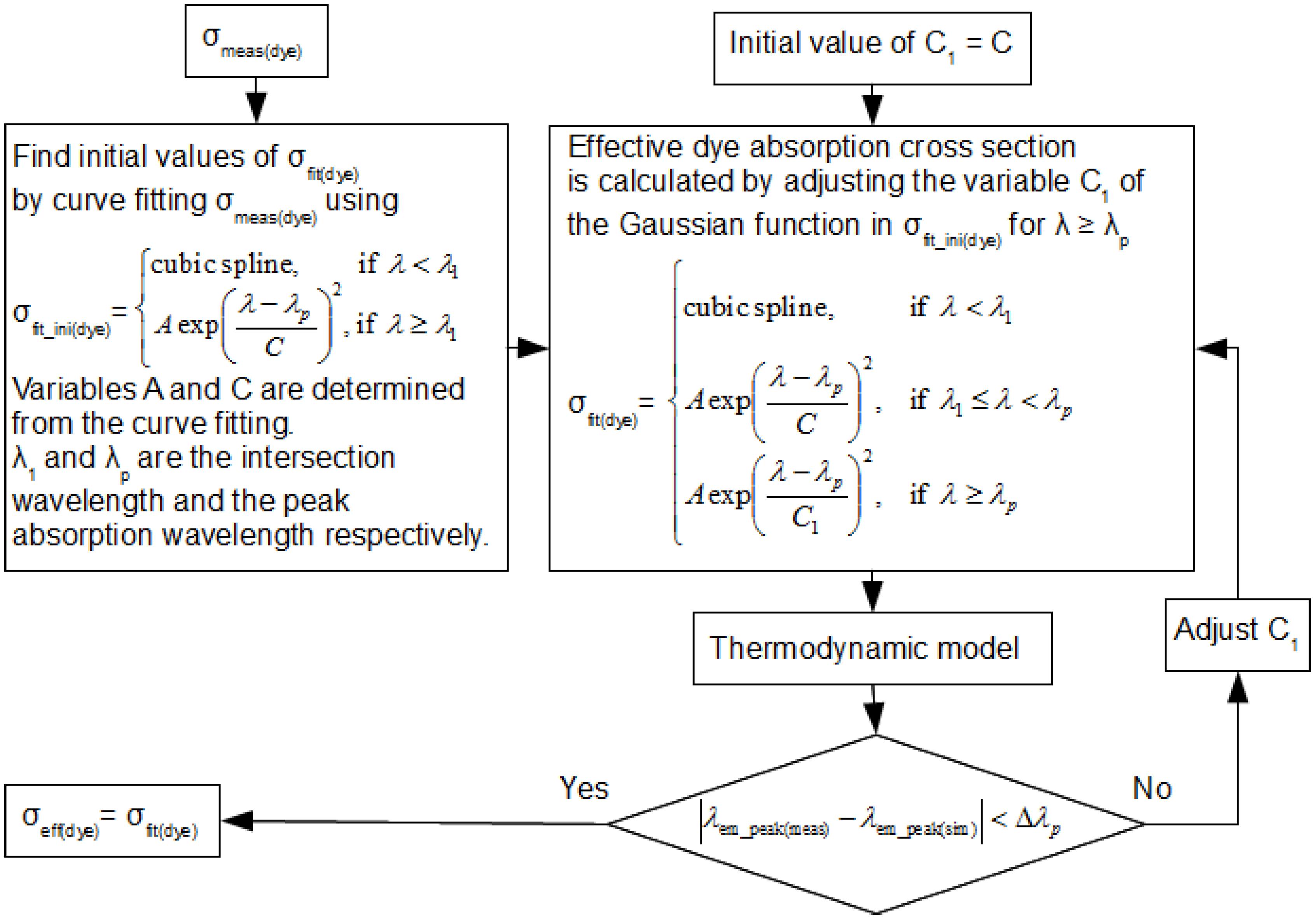
Figure 11 describes the empirical approach used to find the effective absorption cross section of the dye. This absorption cross section spectrum,
σmeas(dye), is used as the initial spectrum to be curve fitted. A Gaussian function and a cubic spline function are used to curve fit
σmeas(dye). The result of the curve fitting
σfit_ini(dye) is fed into the thermodynamic model to generate an emission spectrum with a peak wavelength of
λem_peak(sim). It is noticed that the absorption cross section spectrum of the dye affects predominantly the wavelength of the peak. Therefore,
λem_peak(sim) is used to compare with peak wavelength in measured emission spectrum
λem_peak(meas). The difference between the two is used to adjust a constant, C
1. This new constant value is used in the Gaussian function in
σfit(dye) to produce a new absorption cross section spectrum which in turn is fed into the thermodynamic model. This adjustment process is repeated until the difference between
λem_peak(meas) and
λem_peak(sim) is less than a specified tolerance. The effective absorption cross section of the dye,
σeff(dye), is then determined.
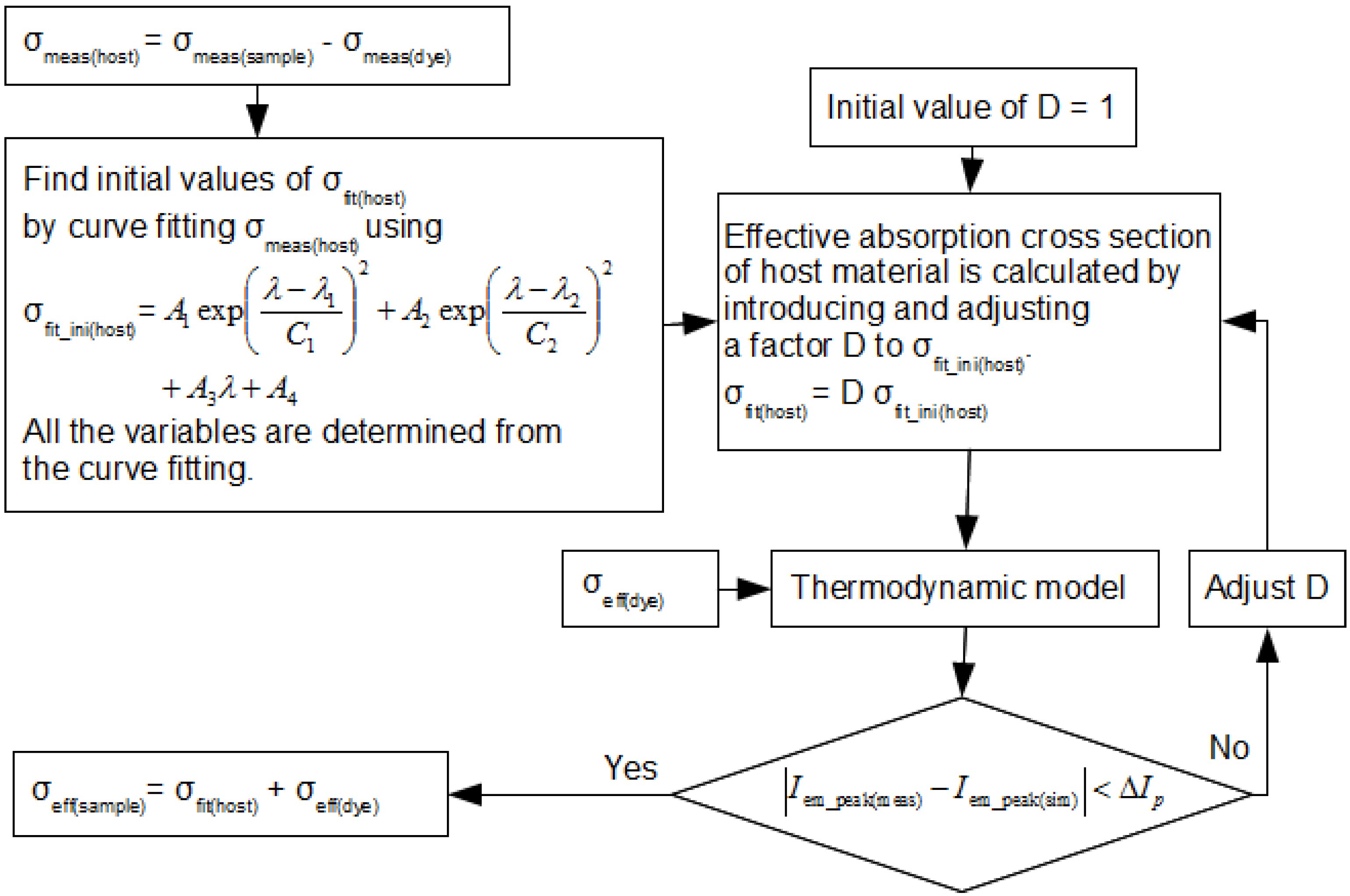
Figure 12 describes the empirical approach used to find the effective absorption cross section of the LSC sample,
σeff(sample). LSC sample means the host material with the dye. Firstly, the absorption cross section of the host material without the dye,
σmeas(host), is determined by subtracting the measured absorption cross section of the LSC sample,
σmeas(sample), from that of the dye,
σmeas(dye).
Figure 11.
Flow chart for calculating the effective absorption cross section of the dye.
Figure 11.
Flow chart for calculating the effective absorption cross section of the dye.
Figure 12.
Flow chart for calculating the effective absorption cross section of the sample.
Figure 12.
Flow chart for calculating the effective absorption cross section of the sample.
A combination of linear and Gaussian functions was used to curve fit σmeas(host) in order to generate a function, σfit_ini(host). The magnitude of the function, σfit_ini(host), is then multiplied by a factor D, in order to correct the effect of the imperfection on the surface of the solid LSC sample. The factor D is always less than one. Then the corrected function, σfit(host), and the effective absorption cross section of the dye, σeff(dye), are fed into thermodynamic model to generate the emission spectrum. It is noticed that the absorption cross section spectrum of the host material mainly affects the magnitude of the peak. Therefore, the magnitude of the peak in the emission spectrum, Iem_peak(sim), is used to compare with the measured peak magnitude, Iem_peak(meas). The difference between the two is used to adjust the factor D, which in turn is used in Gaussian functions to generate a new function. The adjustment process is repeated until the difference (Iem_peak(meas) − Iem_peak(sim)) is less than a specified tolerance. The effective absorption cross section of LSC sample, σeff(sample), is then determined.
The effective absorption cross sections of the dye and the sample are represented by the blue lines in
Figure 9 and
Figure 10. These effective absorption cross sections of the dye and the sample were used in various case studies with different LSC settings. The simulation results generated from one setting were found to match well with the experimental results from the same setting. This is how the effective absorption cross section of the dye and the sample were verified.
There are two peaks in
Figure 10. The peak at the wavelength of 350 nm is the absorption cross section of the host material or unsaturated polyester without considering the dye. The peak at wavelength of 530 nm is the absorption cross section of the dye. It can be noticed that the peak at wavelength of 530 nm is the same as that in
Figure 9. The peak at 530 nm is higher than that at 350 nm because the host material itself is more transparent than the dye.
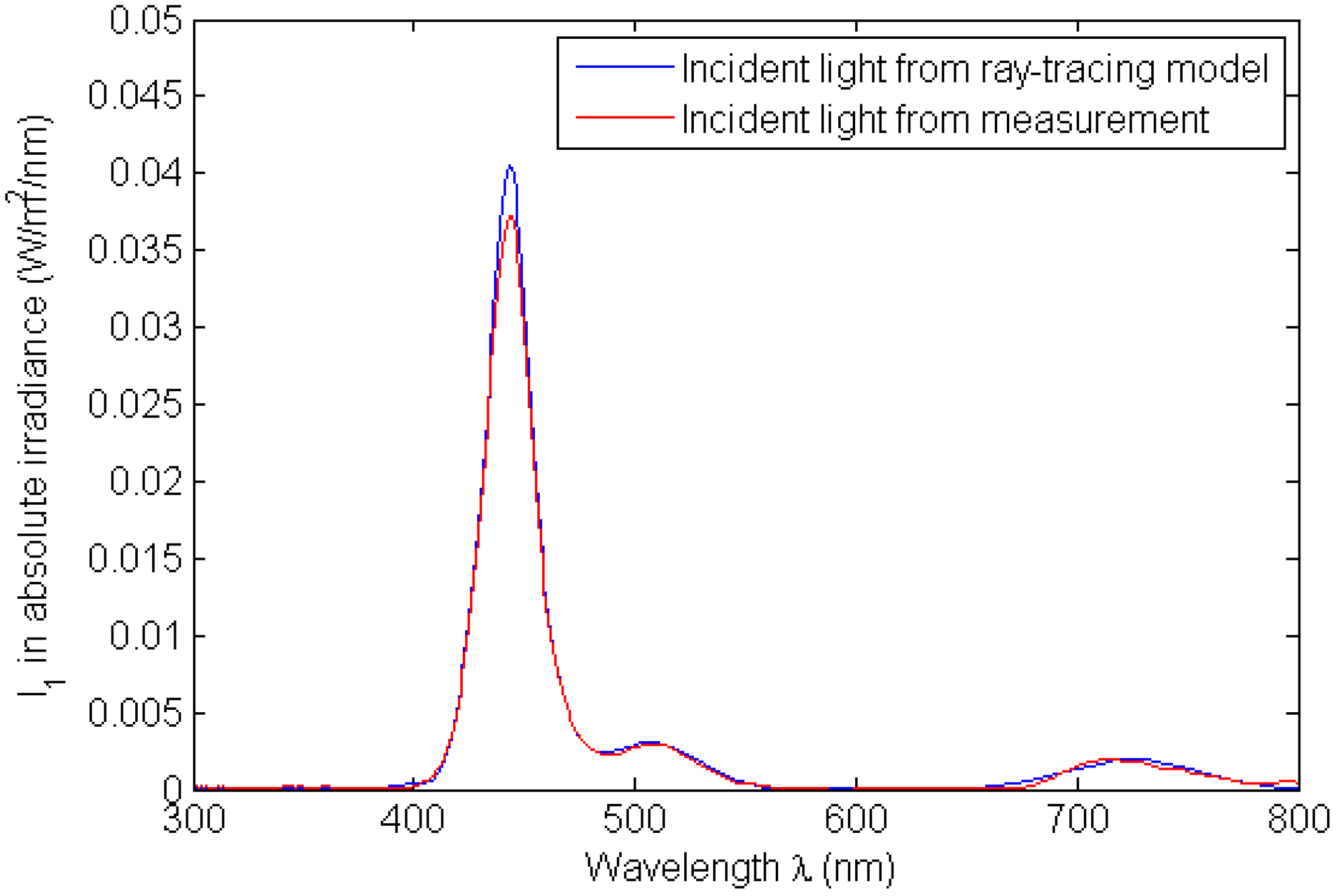
The incident light source irradiance spectrum as shown in
Figure 13 was measured using the Avantes spectrometer connected to a cosine corrector via an optical fiber, by pointing the cosine corrector upward to the center of the LED after the optical filter, at a distance of 5 cm from the LED. The LED and the optical filter was lumped together and modeled as a round shape isotropic area source having a diameter of 3 mm and radiance value of
LFilteredLED calculated using Equation (5) in the Radiance scene description:
where:
Emeasured = Measured incident light spectrum;
d = Diameter of the LED (0.3 cm);
D = Distance between the sample and the light source (5 cm).
The incident light spectrum was sampled in Radiance by generating a scene that consists of the light source only, representing the experiment setup which measures the incident light irradiance spectrum. The irradiance collected by the vertically upward sampling plane over a hemisphere at a point 5 cm below the light source is obtained using the calculation in
Appendix A. The minimum values of
Mθ and
Mφ were determined by increasing their values gradually until the sampled spectrum matches the measured incident irradiance spectrum reasonably well. The sampled spectrum as shown in
Figure 13 is used as the input parameter in the thermodynamic model. For this experiment, the average reflectance at the top surface of LSC was calculated using Equation (B.12) from
Appendix B, since it was assumed that the top surface of the LSC sample in the experiment is a perfectly flat surface where the average reflectance can be easily calculated.
Figure 13.
Incident light spectrum.
Figure 13.
Incident light spectrum.
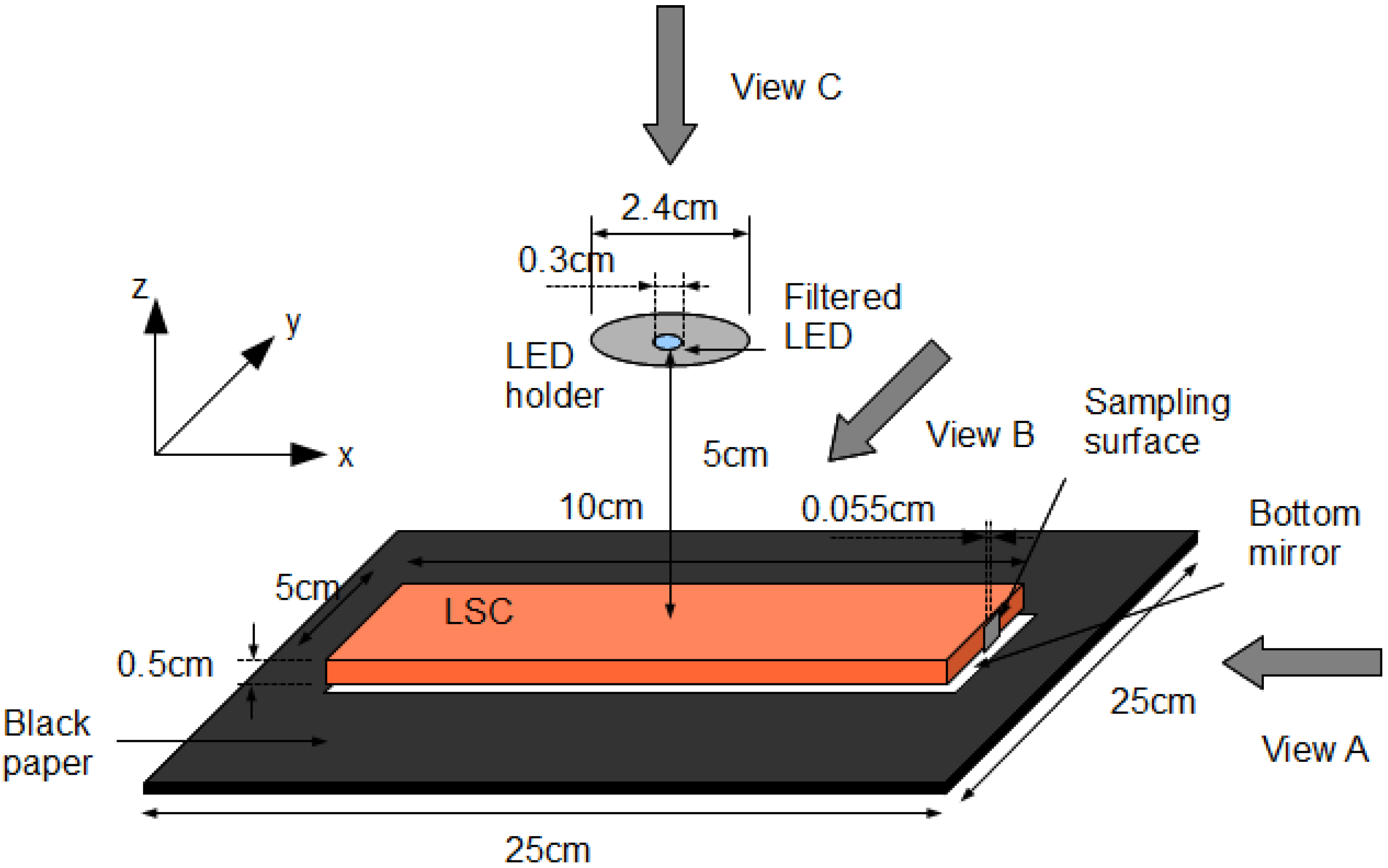
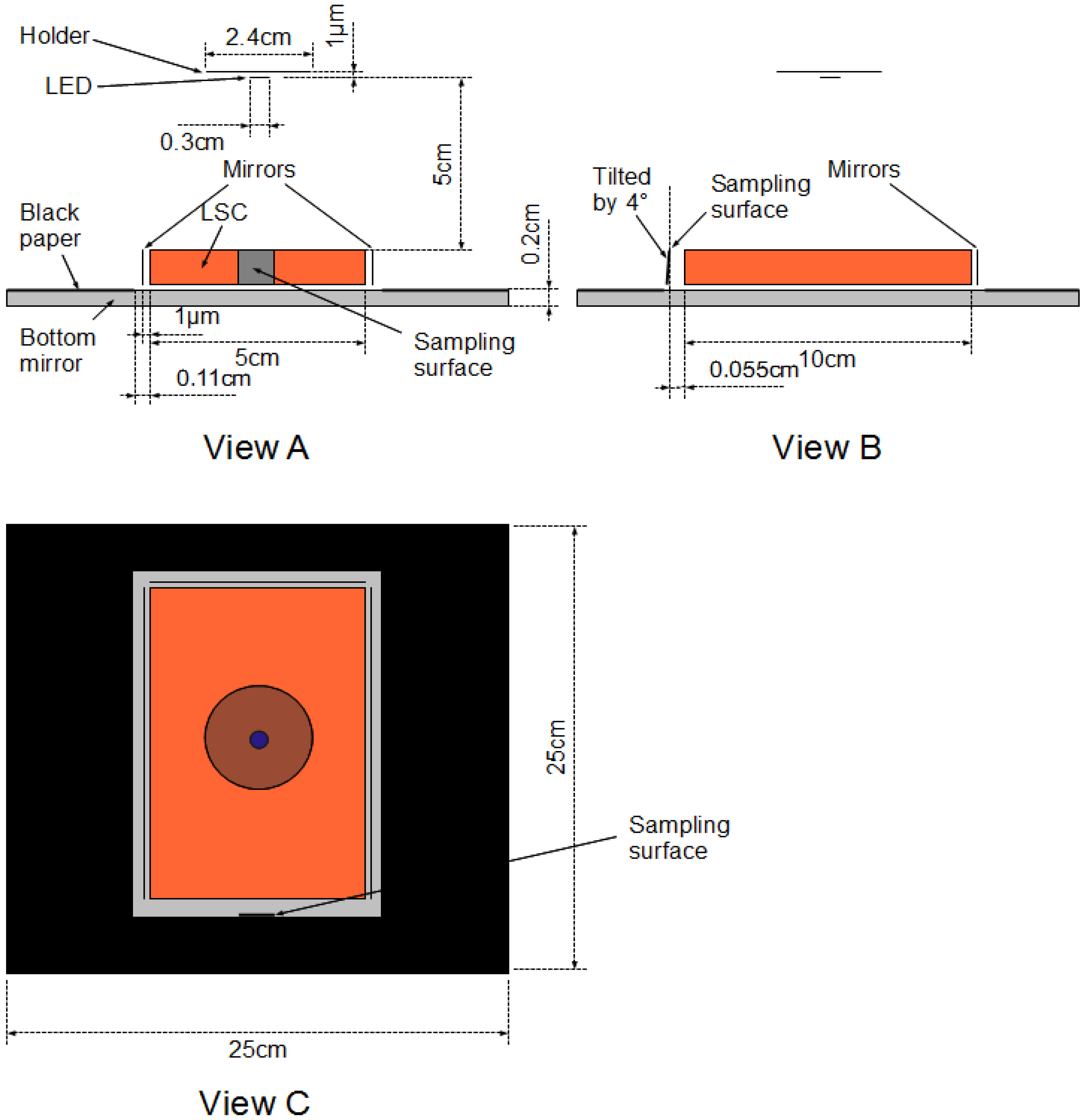
The scene description file used by the ray-tracing model created by the Shell script model the scene set up which is shown in
Figure 14 and
Figure 15. The dimension in the scene was determined from the actual experiment setup. The tilt angle of the sampling plane was due to the structure of the connector connecting the optical fiber and the cosine corrector, which has a diameter slightly larger than the diameter of the cosine corrector, and causes a small tilt when the cosine corrector was put on the flat surface.
Figure 14.
Ray-tracing simulation model.
Figure 14.
Ray-tracing simulation model.
The filter holder surface was included to account for the small reflection from that surface, which was collected by the cosine corrector directly. The black paper was modeled as a plastic type surface having reflectance of 0.05, specularity fraction of 0.1 and roughness of 0.15. The LSC was modeled by a combination of dielectric surfaces with the specified refractive index and the mist type material to account for the absorption. A 2 mm dielectric with refractive index of 1.52 was included for the bottom mirror to model the thin layer of glass on the mirror used in the experiment. The mirrors at the 3 edges were modeled by metal type surface with reflectance of 1, specularity of 1 and zero roughness.
Figure 15.
Two-dimensional view of the ray-tracing simulation model.
Figure 15.
Two-dimensional view of the ray-tracing simulation model.
5. Results and Discussion
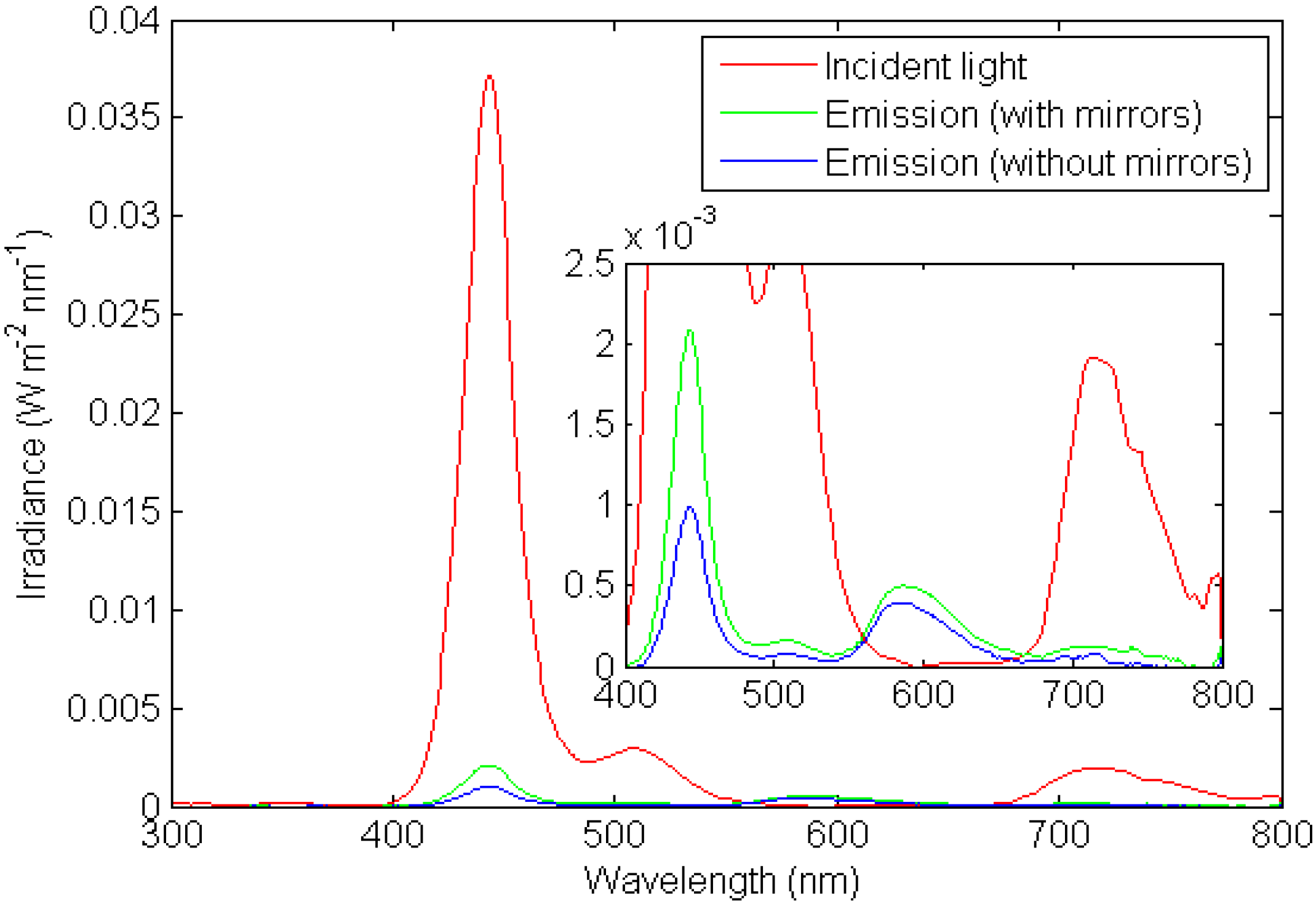
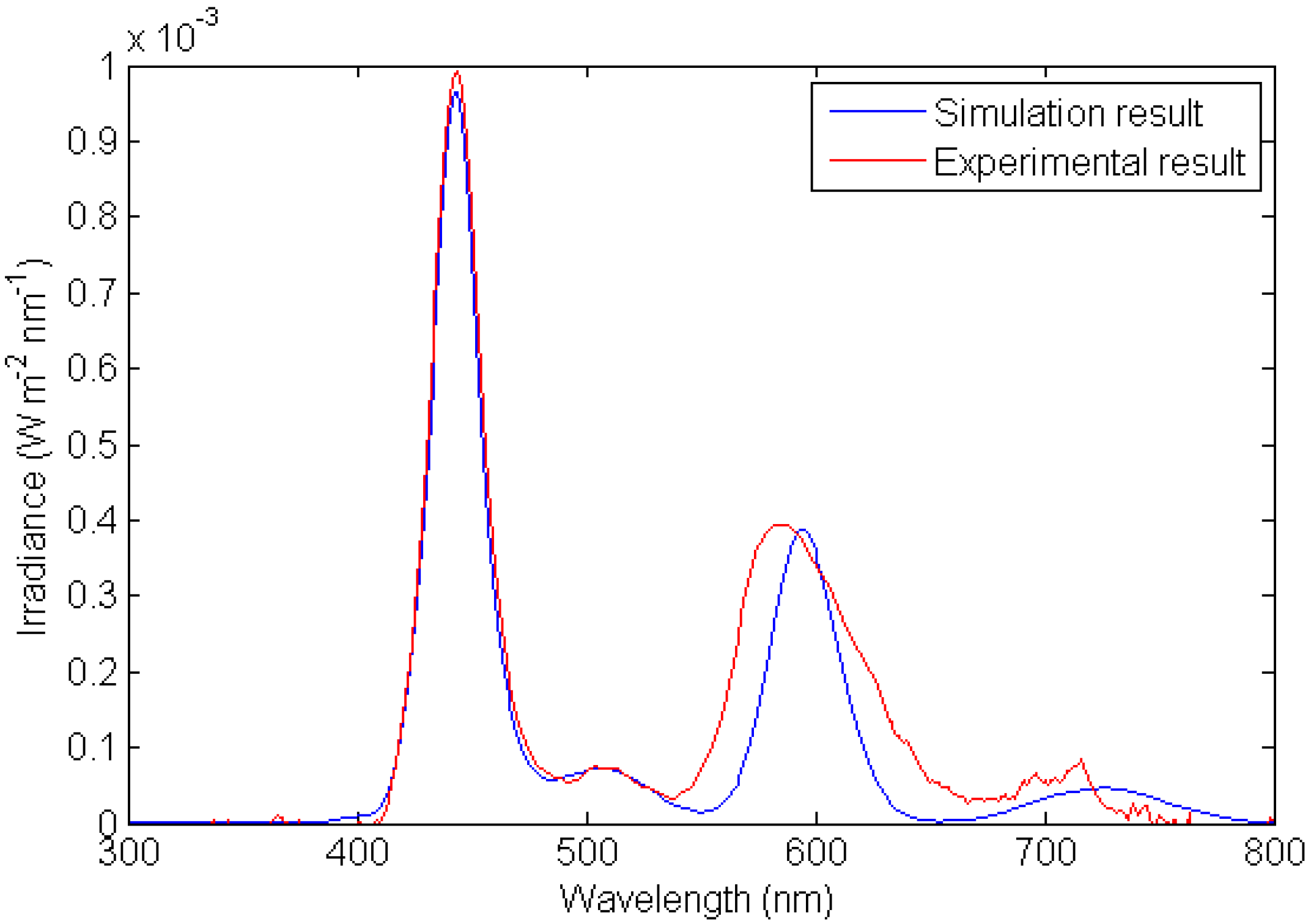
The measurement result is shown in
Figure 16, together with its magnified graph in the middle. Incident light was attenuated by the optical filter in the region of wavelength between 550 nm to 650 nm so that the dye emission can be clearly observed in the measured emission spectrum from the edge.
The emission spectrum in
Figure 16 represents both luminescent emission plus light confinement. Since theoretically the separate components come from splitting the solution of radiative transfer equation into two parts where one part is affected by the incident light only, and another part affected by the dye emission. Therefore, it is not possible to separate them in real measurement and verify each contribution separately.
Figure 16.
Experimental measurement result.
Figure 16.
Experimental measurement result.
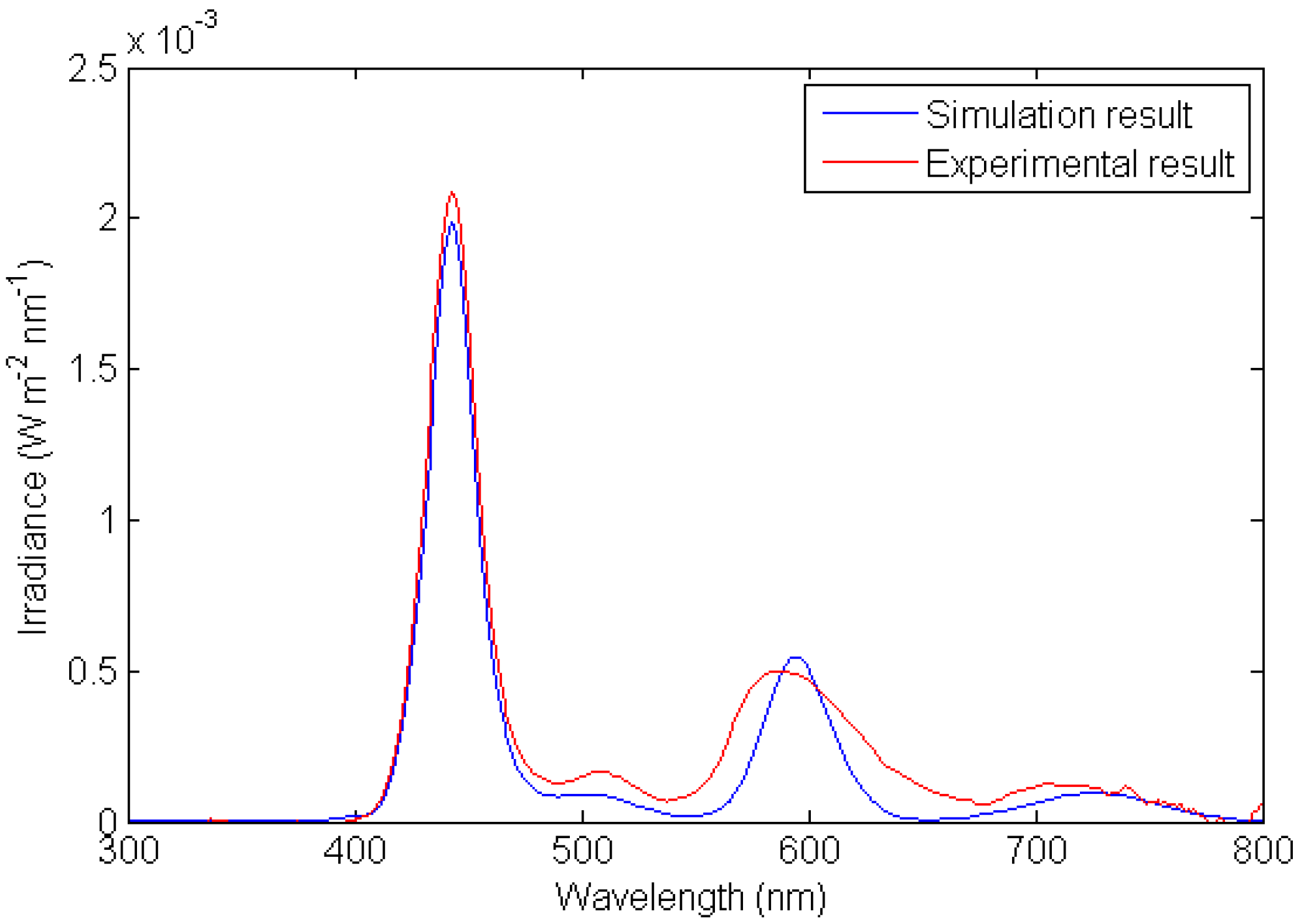
The simulation results for the cases of LSC with mirrors and without any mirror are shown in
Figures 17 and
Figure 18 respectively, together with the experimental result for comparison. Two peaks were observed in the experimental result.
Figure 17.
Simulation result versus experimental result for the case with mirrors.
Figure 17.
Simulation result versus experimental result for the case with mirrors.
Figure 18.
Simulation result versus experimental result for the case without any mirror.
Figure 18.
Simulation result versus experimental result for the case without any mirror.
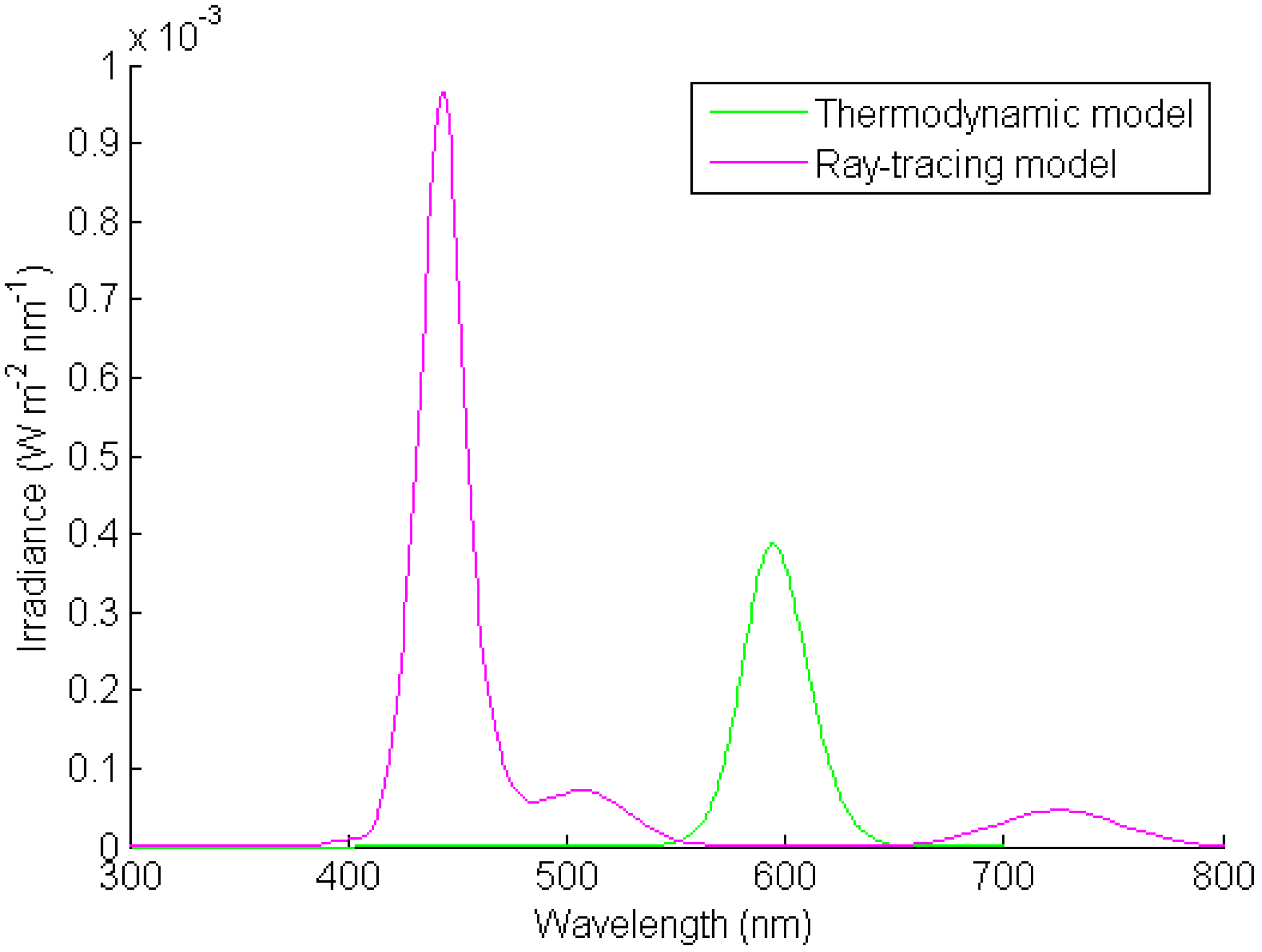
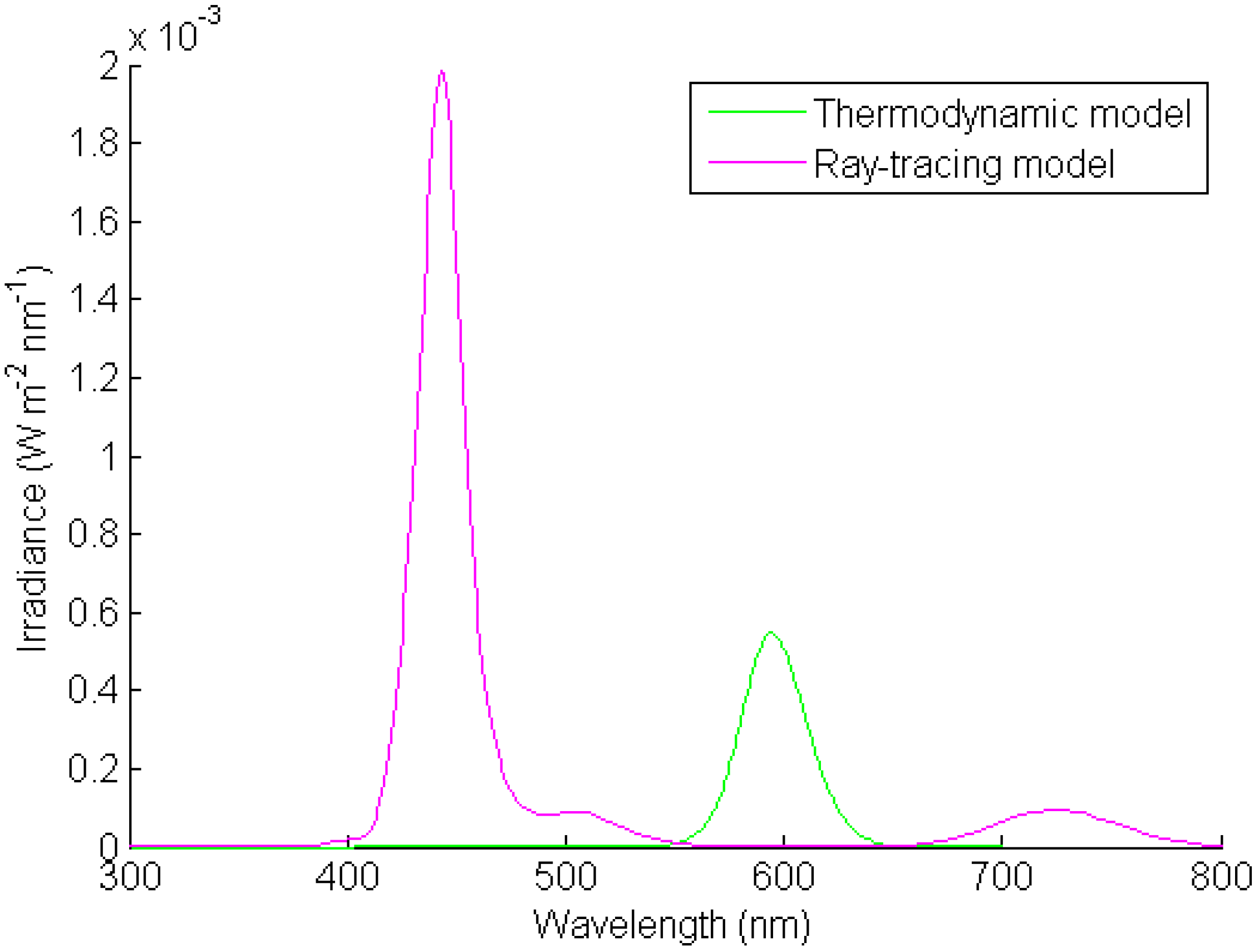
The separate contributions from each model are shown in
Figures 19 and
Figure 20. The irradiance values of the peaks and the corresponding wavelengths are listed in
Table 2, together with the calculated values from simulation result. The simulation output can predict the peak irradiance and wavelength in the measurement result for the case without any mirror accurately using the same set of parameters adjusted to match the measurement result for the case with mirrors. Therefore it validates the adjustment of parameters described in
Section 4.
Two peaks are observed from the output irradiance spectral of LSC. The first peak at 443 nm is contributed by the trapped light. The second peak at 594 nm is from the luminescence of the dye. The first peak is much higher than the second peak. The surface of LSC is able to capture the incident light and guide the light to the edge. The contribution of the trapped light to the output irradiance of LSC is significant. Therefore, it is important to consider the contribution of the trapped light into the design of LSC.
Figure 19.
Separate contribution from the two models for no-mirror case.
Figure 19.
Separate contribution from the two models for no-mirror case.
Figure 20.
Separate contribution from the two models for with-mirror case.
Figure 20.
Separate contribution from the two models for with-mirror case.
Table 2.
Peak irradiance and wavelength in irradiance spectrum.
Table 2.
Peak irradiance and wavelength in irradiance spectrum.
| Peak in Irradiance Spectrum | Simulation | Experiment |
|---|
| Irradiance (W/m2/nm) | Wavelength (nm) | Irradiance (W/m2/nm) | Wavelength (nm) |
|---|
| 1st peak, with mirrors | 1.99 × 10−3 | 443 | 2.09 × 10−3 | 443 |
| 1st peak, without mirrors | 9.66 × 10−3 | 443 | 9.92 × 10−3 | 444 |
| 2nd peak, with mirror | 5.48 × 10−4 | 594 | 5.02 × 10−4 | 586 |
| 2nd peak, without mirror | 3.89 × 10−4 | 594 | 3.89 × 10−4 | 588 |
Total irradiance in
Table 3 is calculated by integrating the irradiance spectrum with respect to the wavelength. The differences between the predicted total irradiance values from simulation and the measured values are 22% for the case with mirrors, and 16% for the case without any mirror.
Table 3.
Comparison of total irradiance from simulation result and experimental result.
Table 3.
Comparison of total irradiance from simulation result and experimental result.
| Total Irradiance | Simulation (W/m2) | Experiment (W/m2) | % Difference |
|---|
| With mirrors | 0.0872 | 0.1125 | 22% |
| Without mirrors | 0.0489 | 0.0579 | 16% |
The reasons of the mismatch between the simulation output and the experimental measurement include the scattering effect which occurs in the transparent host material and the difficulties to model the non-perfectly-flat LSC surfaces correctly.
In the simulation cases studies, the reflectors at the bottom and edges of LSC are specular reflector, however the hybrid model can also be used for diffuse reflectors as long as the effective reflectance of the diffuse reflectors is first modeled using ray-tracing. The thermodynamic and ray-tracing models can handle various values of effective reflectance of the diffuse reflectors. This study on this effect can contribute to a second publication.
6. Conclusions
A new hybrid simulation approach is developed based on a combination of thermodynamic and ray-tracing modeling. This hybrid approach has the ability to study the transfer of energy across a LSC with different surface geometries under direct and diffuse sunlight with minimum data input and reduced simulation efforts. To verify the simulation approach, unsaturated polyester and Rhodamine 6G were used to construct a LSC with dimensions of 10 cm (length) × 5 cm (width) × 0.5 cm (thick). This LSC was placed under a solar simulator. Several input parameters such as absorption cross section of the dye, absorption cross section of the host material and incident light were measured and fed into the simulation program.
The irradiance spectrum produced by the hybrid simulation approach is able to accurately predict the peak irradiance and the corresponding wavelength to be received at the edge of LSC. The spectrum output from the simulation can be used as the input parameter for photovoltaic cell simulation model for a more accurate analysis on the performance of the photovoltaic cells attached to LSC. Therefore this hybrid simulation approach is suitable to study the performance of photovoltaic cells attached to LSCs with different surface geometries under various sunlight conditions.
A hybrid LSC simulation model was developed using the idea of combining the thermodynamic and Radiance ray-tracing simulation models. The thermodynamic model has been well-developed. The ray-tracing simulation model is well-established free software. It can simulate various scenarios accurately, taking into account the effect such as the diffuse inter-reflection between building walls and physically based reflection model. Therefore, the development of the hybrid simulation model did not require any extensive modification and improvement on the programming code of the ray-tracing and thermodynamic models. This hybrid model can be a fast, powerful and cost-effective tool for the design of LSCs for building facades.
The hybrid model was used to carry out two case studies. The first case study was to determine the output irradiance of LSC with mirrors attached to the edges and bottom of LSC. The second case study was the one without mirrors. The output irradiance of LSC with mirrors was about 2 times higher than that without mirrors. The simulation results showed that the trapped light contributed significantly to the output of LSC. The accuracy of the hybrid model is about 18% as compared to the measurements. The possible reasons for the mismatch between the simulation output and the experimental measurement are the ray scattering effect which occurs in the transparent host material and the non-perfectly-flat surfaces of LSC.
The immediate tasks to be carried out will be to incorporate the ray scattering effect into the hybrid simulation model, to study the electrical performance of solar cells attached to the LSC and finally to investigate the effect of replacing the specular reflector at the LSC bottom by diffuse and Lambertian reflector.